Macroscale variation in resting-state neuronal activity and connectivity assessed by simultaneous calcium imaging, hemodynamic imaging and electrophysiology

Abstract

Functional imaging of spontaneous activity continues to play an important role in the field of connectomics. The most common imaging signal used for these experiments is the blood-oxygen-level-dependent (BOLD) functional MRI (fMRI) signal, but how this signal relates to spontaneous neuronal activity remains incompletely understood. Genetically encoded calcium indicators represent a promising tool to study this problem, as they can provide brain-wide measurements of neuronal activity compared to point measurements afforded by electrophysiological recordings. However, the relationship between the calcium signal and neurophysiological parameters at the mesoscopic scale requires further systematic characterization. Therefore, we collected simultaneous resting-state measurements of electrophysiology, along with calcium and hemodynamic imaging, in lightly anesthetized mice to investigate two aims. First, we examined the relationship between each imaging signal and the simultaneously recorded electrophysiological signal in a single brain region, finding that both signals are better correlated with multi-unit activity compared to local field potentials, with the calcium signal possessing greater signal-to-noise ratio and regional specificity. Second, we used the resting-state imaging data to model the relationship between the calcium and hemodynamic signals across the brain. We found that this relationship varied across brain regions in a way that is consistent across animals, with delays increasing by 0.6 sec towards posterior cortical regions. Furthermore, while overall functional connectivity (FC) measured by the hemodynamic signal is significantly correlated with FC measured by calcium, the two estimates were found to be significantly different. We hypothesize that these differences arise at least in part from the observed regional variation in the hemodynamic response. In total, this work highlights some of the caveats needed in interpreting hemodynamic-based measurements of FC, as well as the need for improved modeling methods to reduce this potential source of bias.

Introduction

Measurements of spontaneous brain activity by blood-oxygen-level-dependent (BOLD) functional MRI (fMRI) have already proven to be a valuable tool in the field of connectomics (Biswal et al., 2010), and more recently have played a critical role in defining the most detailed atlas of the human brain to date (Glasser et al., 2016). In performing functional connectivity MRI (fcMRI) experiments, the goal is to make inferences about neuronal connectivity or sometimes disease-driven changes in neuronal connectivity. BOLD fMRI is valuable to this end because this signal is coupled to neuronal activity and can be measured noninvasively. However, the BOLD signal is an indirect measure of the underlying neuronal activity, which effectively blurs the activity in both time and space.

This relationship between neuronal activity and the BOLD signal has long been a topic of research because of its obvious importance for understanding and interpreting fMRI data (Duong et al., 2001; Goense and Logothetis, 2008; Kim et al., 2000; Logothetis et al., 2001; Mukamel et al., 2005; Niessing et al., 2005; Shmuel and Leopold, 2008). However, most of these studies aim to understand how a stimulus-induced change in neuronal activity evokes a change in the BOLD signal, while much less is known about neurovascular coupling during spontaneous activity, commonly referred to resting-state activity. In human studies, functional connectivity measurements taken by electrocorticography or magnetoencephalography detect networks similar to those measured by BOLD fMRI (Brookes et al., 2011; de Pasquale et al., 2010; Mantini et al., 2007), providing support to a neuronal basis for connectivity measured by fMRI. Recent animal work has also demonstrated a significant relationship between neuronal activity (measured by electrophysiology) and simultaneously acquired hemodynamic signals. These studies typically report that local field potentials (LFPs) are the best neuronal correlate of the BOLD signal, but whether that is the LFP in the higher gamma band (>25 Hz) (Hermes et al., 2012; Niessing et al., 2005; Shmuel and Leopold, 2008), or in the ultra-slow band (<0.5 Hz) (He et al., 2008; Pan et al., 2013) remains a topic of debate.

Calcium imaging is emerging as a valuable tool to investigate neurovascular coupling not only at discrete points (i.e., at the site of an electrode), but across large areas of the brain. Du et al. used an injectable calcium indicator in the rat somatosensory cortex to show that low-frequency spontaneous calcium fluctuations are both present and correlated with simultaneously measured hemodynamic signals (Du et al., 2014). Our group (Vazquez et al., 2014) as well as Matsui et al. (Matsui et al., 2016) have leveraged transgenic mouse models expressing calcium indicators in excitatory neurons throughout the cortex to study the relationship between connectivity measured by calcium and hemodynamic signals. These studies agree that maps of functional connectivity measured by calcium are significantly correlated with maps measured by the hemodynamic signal. More recently, Ma et al. also used simultaneous calcium and hemodynamic measurements to investigate the relationship between the two signals on a pixel-by- pixel basis, demonstrating the neuronal basis for the spontaneous hemodynamic signal and how it is modulated by urethane anesthesia (Ma et al., 2016).

Nonetheless, gaps in knowledge remain that are addressable in a similar mouse model. First, what is the relationship (both in time and space) between both imaging signals and spontaneous neuronal activity? Even while the calcium signal is being used as a gold standard for neuronal activity in these studies, its relationship to electrophysiology has not been systematically investigated in a widefield imaging setup. Second, does this relationship between the calcium and hemodynamic signals vary across the brain in a way that is systematic across animals? Several studies have investigated variability in the hemodynamic response function (HRF) in humans and the impact of this variability on fMRI processing (Aguirre et al., 1998; Handwerker et al., 2012; Handwerker et al., 2004; Heinzel et al., 2013). However, these studies often do not consider how variability in the HRF may vary across regions in a way that is systematic across subjects. This type of systematic variation could not simply increase variance but produce bias in the functional connectivity estimates.

Therefore, in this work we utilize the Thy1-GCaMP3 mouse model (Chen et al., 2012) to make measurements of electrophysiology, along with simultaneous mesoscopic or macroscale imaging of the calcium and hemodynamic signals. With these simultaneous measurements, we can assess the relationship between the imaging signals and spontaneous neuronal activity both across time and space, and as a function of electrophysiological frequency. Furthermore, we test the hypothesis that the relationship between the calcium and hemodynamic signals varies systematically across the brain, and then evaluate how estimates of functional connectivity measured by the hemodynamic signal are related to estimates made by the calcium signal.

Methods

Animal preparation

All procedures performed were approved by the University of Pittsburgh Institutional Animal Care and Use Committee and in accordance with standards for humane animal care and use as set by the Animal Welfare Act and the National Institutes of Health Guide for the Care and Use of Laboratory Animals. We imaged 6 transgenic mice expressing GCaMP3 in excitatory neurons throughout the nervous system (strain B6.CBA(Thy1-GCaMP3)8Gfng, 28–36 g, 2.5–3.5 months old) obtained from Jackson Laboratory (Bar Harbor, ME). The mice were initially anaesthetized with an intra-peritoneal (IP) injection of a ketamine (75 mg/kg) and xylazine (10 mg/kg) cocktail. We also placed an IP line for the administration of fluids (5% dextrose in saline). The animals were placed in a stereotaxic frame (Narishige, Tokyo, Japan) and provided blow-by oxygen at a rate of 500 ml/min. Electrocardiogram leads were placed subcutaneously in the abdomen, and heart rate was used to assess physiological condition and anesthesia depth. Body temperature was maintained at 38 °C using a heating pad controlled by feedback from a thermal probe placed under the animals’ abdomen (40-90-8C, FHC, Inc., Bowdoinham, ME, USA). Heart rate and body temperature were recorded throughout each experiment using Acknowledge polygraph data acquisition software (Biopac Systems, Inc., Goleta, CA, USA). To prepare the animals for imaging, the superior surface of the skull was first exposed over both hemispheres and an acrylic cement well was made of approximately 9x7 mm² centered approximately 1 mm posterior to Bregma. We then used a dental drill to remove the skull over each hemisphere and filled the well with 1% agarose gel at body temperature. Finally, we waited at least 15 minutes before beginning data collection, which was performed under 0.5% isoflurane.

Data acquisition

For each animal, two 5-minute runs of spontaneous activity were acquired including simultaneous measurements of electrophysiology, calcium-sensitive images, and optical intrinsic signal images. Electrophysiology was recorded using a glass-insulated carbon fiber microelectrode (1Mohm Carbostar-1, Kation Scientific, Minneapolis, MN) and a Plexon MAP system (Plexon Inc., Dallas TX) at a sampling frequency of 20 kHz. Local field potentials (LFPs) and multi-unit activity (MUA) were filtered between 1–150Hz and 300–9000Hz, respectively, for further analysis. The electrode was placed in the forelimb area of somatosensory cortex using a micro-manipulator (Narishige Inc., Tokyo, Japan) to record activity from the center of a distinct region. Electrophysiology was recorded at a depth of 300 μm. The forelimb area was determined by a short imaging experiment where mild electrical pulses were delivered subcutaneously to the forelimb pad (1.0mA, 0.5ms at a frequency of 5Hz for 2 sec repeated 10 times every 16 sec). Although the goal of this study is to examine neuronal and hemodynamic signals during spontaneous activity, to verify the presence of calcium and hemodynamic responses evoked by sensory stimulation, forelimb stimulation experiments were also acquired where the stimulus period lasted 4 seconds, repeated every 60 seconds (5 trials recorded from each animal).

Calcium-sensitive images were collected over an 11.9 × 8.9 mm² field of view using an Olympus MVX-10 epi-fluorescence microscope (Tokyo, Japan). GCaMP was excited using a mercury lamp light source coupled to a low-noise power supply (Opti Quip, Highland Mills, NY) with an appropriate excitation filter (470 ± 20 nm). The fluorescence emission, filtered at 525 ± 25 nm, was imaged with a digital cooled-CCD camera (CoolSnap HQ2, Photometrics, Princeton, NJ). The exposure of each image was 100 ms for a 10 Hz frame rate. The spatial bin factor was set to 3 to increase signal-to-noise ratio (SNR) and maintain the desired temporal resolution, for an effective pixel size of 26 μm.

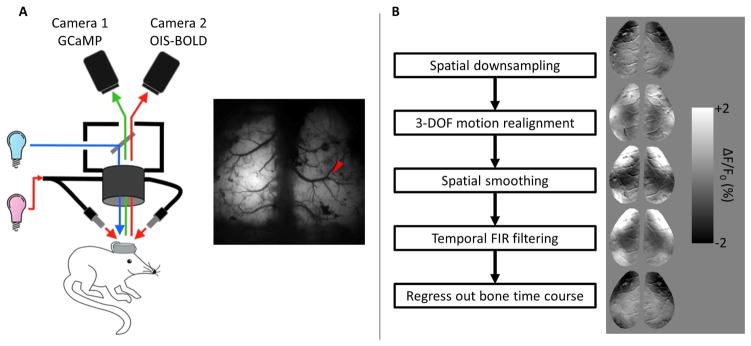
Optical intrinsic signal images sensitive to blood oxygenation (OIS-BOLD) were acquired simultaneously with an analog CCD camera (Sony XT-75, Tokyo, Japan) over the same field of view. A halogen light source (Thermo-Oriel, Stratford, CT) provided light via oblique light guides. A barrier filter was placed before the camera (620 ± 7 nm) corresponding to a region in the hemoglobin absorption spectrum that is dominated by deoxyhemoglobin. OISBOLD data were acquired at 30 Hz with a pixel size of 14 μm. This optical setup is summarized in Figure 1a.

Figure 1.

A. Summary of optical setup. GCaMP3 was excited by blue light and following light-splitting was filtered into the green emission (525 nm) band just prior to Camera 1. Intrinsic signal was acquired with red light to provide sensitivity to blood oxygenation. Reflected light was filtered into the desired band (620 ± 7 nm) with a filter just prior to Camera 2 following light-splitting. Red arrow shows the insertion location of the electrode for electrophysiological recording. B. Summary of the image preprocessing pipeline (left) and example GCaMP difference images after each step (right).

Data analysis

Image preprocessing

The image processing pipeline is summarized in Figure 1b, including example preprocessed GCaMP images in the right panel. Additional single-frame GCaMP images are shown in Supplementary Figure 1, as well as the simultaneously acquired OIS-BOLD images. To further increase SNR, GCaMP images were spatially binned by a factor of 2 (final pixel size of 52 μm) and OIS-BOLD images were binned by a factor of 3 (final pixel size of 42 μm). OISBOLD images were also temporally binned by a factor of 3 to match the temporal resolution of the GCaMP images. Images were then realigned to correct for small brain motion by co-registering each image in the time series to the first using a 3 degree of freedom, rigid body transformation. The images were then spatially smoothed by Gaussian kernel with a standard deviation of 1 pixel (i.e., 52 μm for GCaMP images, 42 μm for OIS-BOLD images). Next, the data were temporally filtered using a finite impulse response filter with a Hamming window of length n=1001. For characterizing temporal properties of the data, images were high-pass filtered with a cutoff frequency of 0.01 Hz. When characterizing spatial properties of the data, band-pass filtered data were also evaluated with cutoff frequencies of 0.01 and 0.1 Hz. Filtering was performed in the forward and backward directions to leave the phase of the signal unchanged. Finally, we regressed out the average time course extracted from the skull just posterior to lambda (to account for unwanted fluctuations in the light source). Each time course was then normalized by adding back and dividing by its mean and subtracting 1.

Correlation between electrophysiology and imaging signals

For comparison with imaging signals, electrophysiological data were summarized in sliding 1 s windows centered on each image. Local field potentials were summarized in 5 frequency bands by computing the power spectrum in each window and then calculating the mean power in the entire signal as well as the following bands: Delta (1–3 Hz), Theta (4–7 Hz), Alpha (8–12 Hz), Beta (13–25 Hz), and Gamma (25–90 Hz). This window length was chosen to provide 1 Hz resolution in the power spectrum and allow for separation of the specified frequency bands. Spikes were counted in the same 1 s windows for consistency by thresholding the filtered electrophysiological recording (high-pass filtered with 1 kHz cutoff) at the mean minus 4 standard deviations. An example MUA recording with the detected spikes is shown in Supplementary Figure 2. Imaging signals were summarized by computing the mean signal within 100 μm of the electrode while excluding visible surface vessels.

The relationship between the electrophysiology and the imaging signals was then modeled in two levels. First, we computed the cross-correlation function for each run of the data by holding the electrophysiological time course constant and sliding the imaging time course in a window of −10 to +10 seconds. Second, the mean correlation coefficient at each time lag was computed with a mixed effects model with only a constant fixed-effect term and random intercepts to account for multiple measurements from each animal. Three consecutive p values less than 0.05 were considered significant (based on simulation to control family-wise type I error at 0.05 for 201 samples).

Impulse response function estimation for predicting imaging signal from multi-unit activity

We opted to use spiking activity to predict the imaging signals in the proceeding sections of this work because the imaging signals are most correlated with spiking activity and can be computed without smoothing. To predict the imaging signal, we used matrix deconvolution to estimate the impulse response function (IRF). In this fashion, the predicted signal is obtained by the convolution of the spike rate with the estimated IRF. This calculation was first performed separately for each run in the data set where the signal stemmed from the 100-μm circular ROI centered on the insertion location of the electrode (excluding surface vasculature). Next, we counted the number of spikes during each imaging period, mua(t), over each 100 ms imaging window. The following linear model was used to fit the data and obtain the estimated IRF (b’s) for each run:

$$\mathrm{s}(\mathrm{t})=\mathrm{a}+{\sum }_{\mathrm{i}=-10\mathrm{s}}^{+10\mathrm{s}}{\mathrm{b}}_{\mathrm{i}}\ast \mathit{mua}(\mathrm{t}+\mathrm{i})+\epsilon$$

Before summarizing these IRFs across all animals, the baseline was set to 0 by subtracting the mean of the parameters in the window of 10 to 5 seconds prior to the spike, and then parameters were normalized by dividing by the maximum absolute value. Next, the mean IRF at each time point was estimated using a mixed effects model with only a fixed intercept and random intercepts for each animal. Three consecutive p values less than 0.05 were considered significant.

Temporal relationship between imaging signals and spiking activity

For each run, we computed the predicted imaging signal by convolving the spike count with the previously estimated IRF, and then computed its correlation coefficient with the time course measured near the electrode. The mean correlation coefficient was then calculated for each modality, and differences between the GCaMP and OIS-BOLD signals were tested using a mixed effects model with random intercepts for each animal.

Spatial relationship between imaging signals and multi-unit activity

To characterize the spatial relationship between spiking activity and the images, we first computed correlation maps in two ways for each run in the data set. To investigate the relationship between multi-unit activity and the image signals, we first calculated the predicted signal (spike rate convolved with the mean IRF) and correlated it with the time course of every pixel in the image. This map compares the spiking activity-estimated imaging signals in the reference region (S1) to those across the brain. To investigate spatial autocorrelation in the imaging data, we computed the mean time course within 100 μm of the electrode and correlated it with every pixel in the image. This allowed us to consider sources of variation not captured by the IRF model. To make the correlation coefficients normally distributed for statistical modeling, we applied the Fisher r-to-z transform to each correlation map. Then, the relationship between correlation and distance from the electrode was modeled with a mixed effects model with random slopes and intercepts by concatenating the measurements from each run for pixels that are within 2 mm of the electrode. A natural spline basis was used to allow the model to fit an arbitrary functional form, with knots placed every 250 μm starting at 250 μm from the electrode and ending at 1750 μm. To test for significant differences in this relationship between the GCaMP and OIS-BOLD signals, two models were compared using a likelihood ratio test. The first model had predictors that included distance from the electrode, a categorical variable for signal type, and the interaction between distance and signal type. The restricted model used only distance from the electrode as the predictor. A p value of less than 0.05 was considered significant. This analysis was performed for both high-pass and band-pass filtered data, with analogous filtering performed both on the time course of interest and the imaging data.

Relationship between GCaMP and OIS-BOLD signal across the brain

To establish regions of interest (ROIs) for this analysis, a functional group atlas was constructed using the resting-state GCaMP data. The GCaMP data was chosen because of its sensitivity to neuronal activity. The images from all animals were co-registered to the first animal using a 5 degree of freedom affine registration with a normalized correlation coefficient cost function. The images were spatially binned by a factor of 2 and temporally binned by a factor of 5 to reduce dimensionality. Then the time courses from each pixel were concatenated across all runs. Noise was reduced using principal component analysis to keep 90% of the variance both for each run (48.9 components kept on average) and then again for the fully concatenated data (44 components kept). Finally, ROIs were estimated using k-means clustering with 8 clusters and a correlation distance metric. To improve reproducibility of the cluster assignments, the algorithm was run 25 times selecting the run that minimized total distance from the cluster centroids. The number of clusters was determined empirically under the assumption that the regions should be bilaterally symmetric. Therefore, we increased the number of clusters until symmetry was no longer observed. The resulting atlas had 7 roughly symmetric ROIs in each hemisphere (6 clusters were bilateral with 2 clusters contained in one hemisphere), and is shown in Supplementary Figure 3 along with an analogous atlas constructed using OIS-BOLD data.

With these ROIs, the relationship between the GCaMP and OIS-BOLD signal across the brain was modeled in two levels. First, we extracted the mean time course from each ROI excluding vessels for each animal and imaging modality and then computed the cross-correlation function between the GCaMP (held stationary) and OIS-BOLD signal in the window of −10 to +10 s. Second, these cross-correlation functions were modeled at each time lag in three ways using a mixed effects model (listed in order of increasing complexity):

1. The simplest model included only a fixed-effect constant term and random intercepts for each animal, r_ij(t) = b₀(t) + u_j(t) + ε_ij(t), where r_ij(t) is the correlation in region i (a single global region in this model) and animal j at time t, b₀ is a fixed-effect constant term (i.e., the mean correlation coefficient across animals and regions), u_j are random intercepts for each animal, and ε_ij are the residuals.

2. Model 1 plus additional categorical fixed effects for brain region where regions were defined as 7 bilateral, symmetric regions, r_ij(t) = b_i(t) + u_j(t) + ε_ij(t), where r_ij(t) is the correlation in region i and animal j at time t, b_i are fixed-effects equal 1 if pixel is in region i and 0 otherwise for 1 ≤ i ≤ 7 (i.e., mean correlation in each region), u_j are random intercepts for each animal, and ε_ij are the residuals.

3. Model 1 plus additional categorical fixed effects for brain region where left and right regions each treated as 14 individual unilateral regions, r_ij(t) = b_i(t) + u_j(t) + ε_ij(t), where r_ij(t) is the correlation in region i and animal j at time t, b_i are fixed-effects equal 1 if pixel is in region i and 0 otherwise for 1 ≤ i ≤ 14 (i.e., mean correlation in each region), u_j are random intercepts for each animal, and ε_ij are the residuals.

Differences between models were tested at each time point using a likelihood ratio test at each time point with three consecutive p values less than 0.05 were considered significant. The best-fitting model was then defined as the simplest model that explained significantly more variance than other candidate models. More specifically, model 2 was compared to model 1 across all time points, and considered a better model if any significant improvement in model fit was detected according to the above test. Model 3 was then compared to model 2 in a similar fashion. From the best-fitting model, we then constructed maps of the maximum correlation coefficient between the imaging signals, as well as the time lag at which that maximum occurs.

Relationship between functional connectivity measured by GCaMP and OIS-BOLD

Using the group atlas, graphs of functional connectivity (FC) were computed for each run by extracting the mean time course from each ROI, computing all possible pair-wise correlation coefficients, and performing a Fisher r-to-z transformation. The relationship between FC measured by each modality was tested with a mixed-effects model in which FC measured by OIS-BOLD (FC_OIS-BOLD) was predicted by both fixed- and random-effects of FC measured by GCaMP (FC_GCaMP) and a constant. The difference between the two measurements was tested for each edge in the graph using a mixed-effects model with a fixed intercept and a random intercept for each animal. P values for the intercept of less than 0.05 were considered significant. P values uncorrected for multiple comparisons were used because this threshold was more conservative than applying false discovery rate correction.

Results

Imaging signals increasingly correlated with electrophysiology with increasing frequency

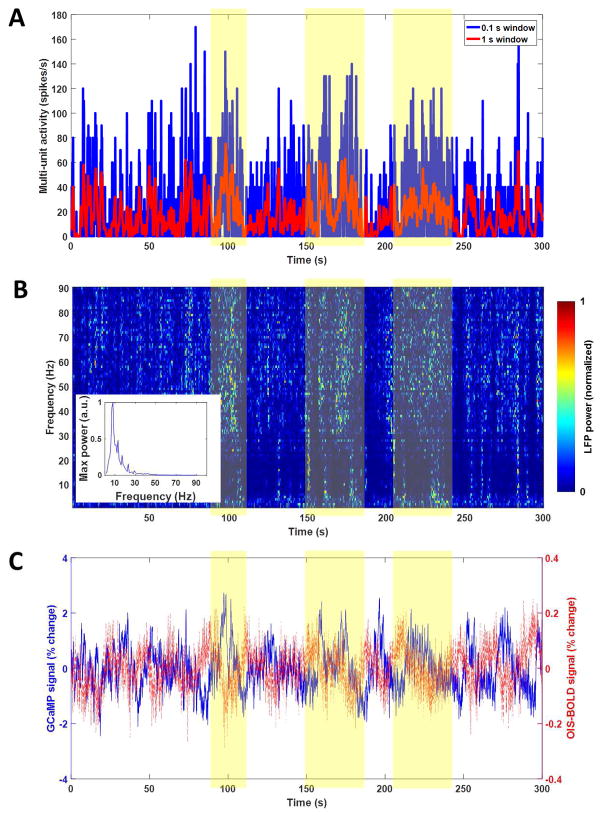
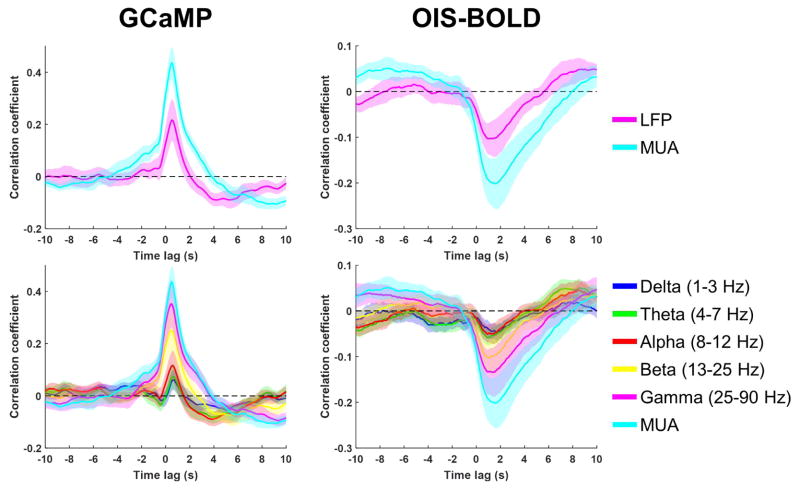
Example time courses from a single run of data collected during spontaneous activity are shown in Figure 2, including simultaneous measurements of spiking activity (Fig. 2A), local field potentials (Fig. 2B), and calcium and hemodynamic imaging signals (Fig. 2C, blue and red lines, respectively). Time courses from the first 30 seconds are shown in Supplementary Figure 4 for more detail. These data show robust and continuous activity throughout the data acquisition period that generally corresponds with changes in calcium signal. Neuronal-activity evoked increases in GCaMP signal were confirmed by forelimb stimulation experiments, as expected (Supplementary Fig. 5). The spontaneous activity electrophysiological and imaging data were then used to compute the mean cross-correlation functions between each imaging signal and the electrophysiological data in various frequency bands, which are summarized across all animals and runs in Figure 3. For both GCaMP and OIS-BOLD, multi-unit activity (MUA) was a better predictor of the imaging signal compared to both total LFP power (top row) and LFP power in any given band (bottom row). The maximum absolute value of correlation increases with higher frequency bands, with the correlation generally increasing as the LFP frequency band increased and maximized by the use of multi-unit activity (MUA) as the measure of electrophysiology. This correlation is 0.44 for GCaMP with a time lag of 0.5 s, and −0.20 for OIS-BOLD with a time lag of 1.6 s. Note that the lags are systematically longer due to the lower temporal resolution data used for this calculation. The apparent relationship between the imaging data and LFP activity over the same frequency bands is altered when the LFP power in each window is normalized by the total power in that window (Supplementary Fig. 6). For both imaging modalities, we observe diminished correlation in the high frequency bands, and a reversal of the sign of correlation in low frequency bands, similar to previously reported correlations that implemented this normalization (Niessing et al., 2005).

Figure 2.

Example time course data from one experimental run acquired during spontaneous activity. Panel A shows the multi-unit activity measured in spikes per second in either 0.1 s windows (blue) or 1 s windows (red). Panel B shows the LFP spectrogram that is normalized by dividing the time course of each frequency by its own maximum value. The maximum value for each frequency is also shown in an inset plot indicating the expected 1/f distribution.. Panel C shows the imaging signals extracted from a region within 100 μm of the electrode. Shaded region denotes areas where high periods of activity are present and similar responses to GCaMP and OIS-BOLD (negative) were generally observed.

Figure 3.

Summary of correlation between spontaneous electrophysiology and imaging signals as a function of frequency band. Each panel shows the cross-correlation function computed by holding the electrophysiological signal stationary and shifting the imaging signal in a window of −10 to +10 s. The line and shaded regions represent the mean and standard error, respectively, across 6 animals (2 runs each) estimated by a linear mixed-effects model.

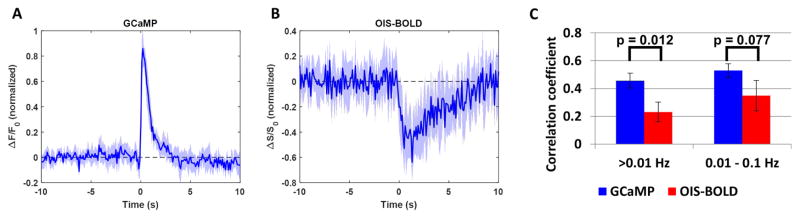
GCaMP impulse response function has larger magnitude and faster return to baseline compared to OIS-BOLD

Since multi-unit activity was the best correlate of the imaging signals and since spike rate can be computed without smoothing, we used this measure to predict the imaging signals in the proceeding portion of this work. We performed deconvolution of the imaging signals with the spike rate using linear modeling in order to estimate the impulse response function (IRF). This IRF for each modality is summarized in Figure 4. In Figure 4A, the mean GCaMP IRF becomes significantly different from zero at time equal to 0 peaking at 200 ms and then remains significantly greater than zero until 1.8 seconds after the spike, with the mean IRF crossing back over 0 at 3.2 s. These temporal changes are in agreement with those previously reported for this mouse model (Chen, 2012). In Figure 4B, the mean OIS-BOLD IRF becomes significantly different from zero at 200 ms post-spike peaking at 1.3 s, remains significantly lower than zero until 2.6 s post-spike, with the mean IRF crossing 0 once more at 6.3 s. The larger magnitude of the GCaMP IRF compared to the OIS-BOLD IRF is evidence of superior signal-to-noise ratio for the GCaMP signal.

Figure 4.

Summary of temporal correlation between multi-unit activity and imaging signals. The estimated impulse response function (IRF) for the resting-state GCaMP data is shown in panel A (mean ± 95% confidence interval, n = 6 × 2 runs, likelihood ratio test on intercept term of a linear mixed-effects model at each time point). The estimated resting-state OIS-BOLD IRF is shown in panel B. Panel C displays a comparison of temporal correlation between the imaging signal and the MUA-predicted signal (bar graph shows mean ± standard error, n=6 × 2 runs, F-test on fixed-effect for difference between GCaMP and OIS-BOLD).

GCaMP signal tends to provide better temporal correlation with multi-unit activity compared to OIS-BOLD

To estimate the temporal relationship between the spontaneous MUA and the imaging signals, we computed the predicted imaging signals by convolving the spikes counts with each IRF and then tested for correlation with the measured imaging signals. These correlation coefficients are summarized in Figure 4C. Using high-pass filtering, the mean correlation was significantly larger (p=0.012) using the GCaMP signal (0.46 ± 0.057, mean ± standard error, 2 runs from 6 animals estimated by a mixed model) compared to the OIS-BOLD signal (0.23 ± 0.071). Using band-pass filtering, the mean correlation was 0.53 ± 0.058 using the GCaMP signal and 0.36 ± 0.10 using the OIS-BOLD signal. This difference did not meet the level of statistical significance (p=0.077). Examples of the predicted and measured time courses using band-pass filtered data are shown in Supplementary Figure 7.

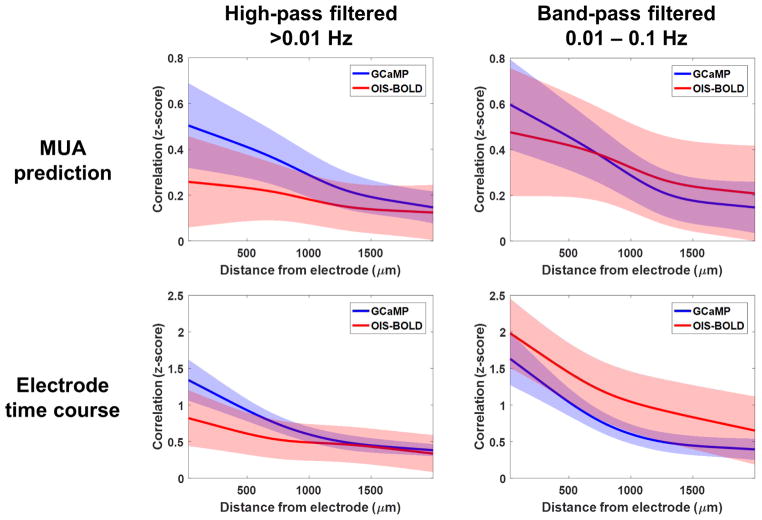
Spatial correlation between GCaMP and multi-unit activity is larger and more regionally specific than OIS-BOLD

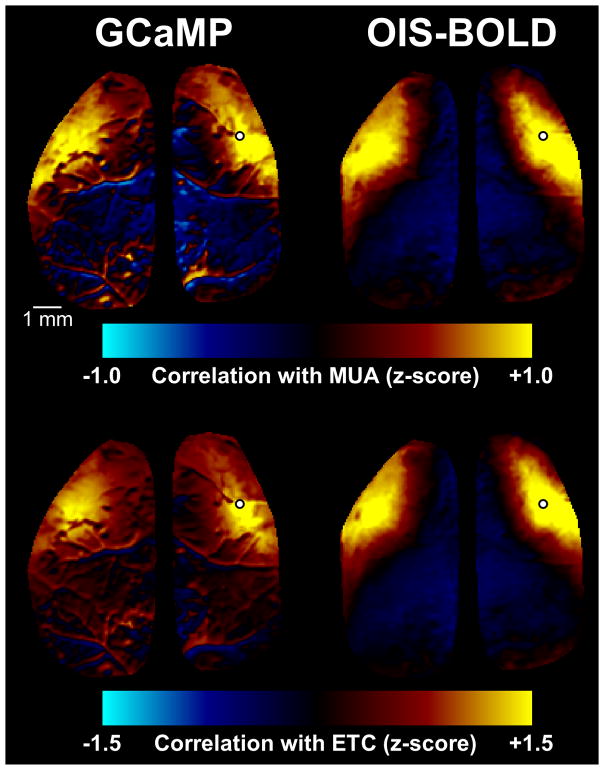
To estimate the spatial relationship between MUA and the imaging signals, we computed correlation maps and then modeled the effects of distance from the electrode on the strength of the correlation. Example correlation maps are shown in Figure 5 calculated either with the MUA-predicted signal (top) or with the imaging signal from near the electrode (bottom), while the findings across all animals and runs are summarized in Figure 6. In each case, a significant difference in the relationship between correlation and distance was observed between the GCaMP and OIS-BOLD signals (p<0.001, likelihood ratio test). As above, we observe higher correlations with MUA when using the GCaMP signal. The OIS-BOLD signal shows greater improvements in correlation with band-pass filtering. In general, the drop off in correlation is flatter when using the OIS-BOLD signal compared to the GCaMP signal indicating less spatial specificity for MUA. When computing the correlation map using the time course near the electrode, as expected, we observe that the correlation is stronger at distance of 0 because the time course must be correlated with itself and the images contain spatial autocorrelation.

Figure 5.

Example spatial correlation maps. In the top row, maps were computed by taking the multi-unit activity (MUA), convolving with the relevant impulse response function (Fig. 4), and correlating this prediction against every pixel in the image. In the bottom row, maps were computed by taking the mean time course near the electrode (ETC) and correlating this with every pixel in the image. Electrode location is indicated on each image by a white circle.

Figure 6.

Summary of relationship between spatial correlation and distance from the electrode. The relationship was fitted by a linear mixed-effects model with a spline basis function using correlation maps calculated with either the MUA-predicted time course (top) or the mean time course near the electrode (bottom). Both high-pass (left) and band-pass (right) filtered data were considered. In all cases, significant differences were detected between the GCaMP and OISBOLD signals (p<0.001, likelihood ratio test). Shaded regions indicate the 95% confidence intervals of each model fit computed using bootstrapping.

Relationship between GCaMP and OIS-BOLD signal differs significantly across the brain

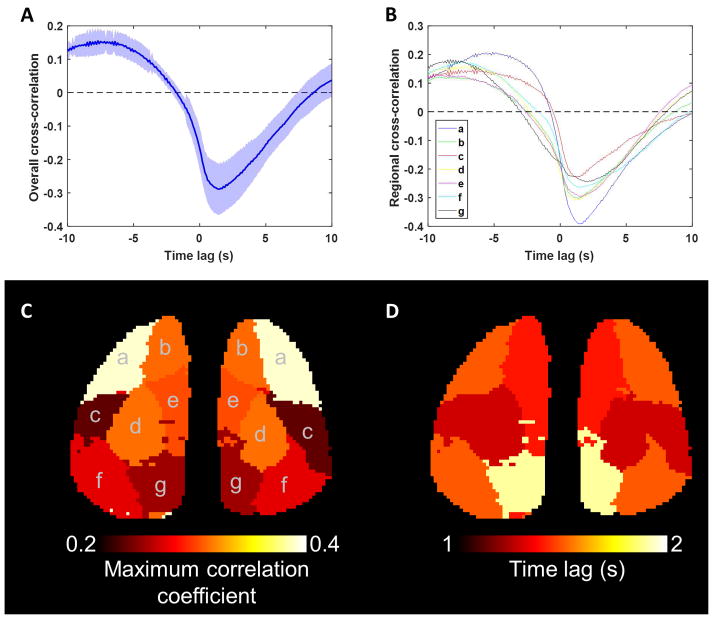
To test for regional differences in the hemodynamic response, we computed the cross-correlation function between the GCaMP and OIS-BOLD in each brain region and then tested whether a model that accounted for brain region provided a better explanation of the data compared to a model ignoring brain region. The mean cross-correlation function ignoring the effects of brain region is shown in the top-left panel of Figure 7. The maximum absolute correlation is 0.29 at a time lag of 1.5 s. However, when including fixed-effects for brain region we observed that significant improvements in describing the data compared to ignoring the effects of brain region, indicating that the HRF varies systematically across the mouse brain even when controlling for random effects. No significant improvements were observed by using 14 unilateral ROIs compared to 7 bilateral ROIs, and so the proceeding analyses were performed using the simpler, bilateral ROI model. The estimated cross-correlation functions for each of the 7 bilateral ROIs are plotted in the top-right panel of Figure 7, while the bottom panel of Figure 7 includes a map of the maximum correlation coefficient between the GCaMP and OIS-BOLD signals (left) and the time lag at which this maximum was observed (right). The range of delays varied from 1.3 to 1.9 seconds with the longer delays observed in posterior cortical regions.

Figure 7.

Summary of the relationship between calcium and hemodynamic signal as a function of brain region. Panel A shows the cross-correlation function between the GCaMP and OISBOLD resting-state signals assuming no differences across brain regions (mean ± 95% confidence interval, n=6 × 2 runs, t-test on intercept term of a linear mixed-effects model at each time point). Panel B shows the cross-correlation function for each of 7 bilateral ROIs, which explained the data significantly better than ignoring differences between regions (ROI predictors significantly improve model in two clusters from −5.1 to −0.3 s and from 0.6 to 3.3 s). Below are maps of maximum correlation between the signals (panel C), and the time lag at which the maximum occurred (panel D).

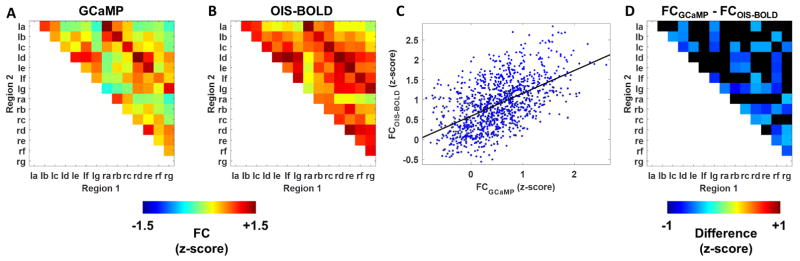
Functional connectivity measured by OIS-BOLD is highly correlated with, but also significantly different from, functional connectivity measured by GCaMP

The mean FC_GCaMP graph is shown in Figure 8A, as well as the mean FC_OIS-BOLD graph after correction Figure 8B. Example FC maps from one animal are included in Supplementary Figure 8. A scatter plot of FC measured by OIS-BOLD (FC_OIS-BOLD) versus FC measured simultaneously by GCaMP (FC_GCaMP) along with the model fit is shown in Figure 8C. The relationship is significant (p<0.001) with an estimated slope of 0.56 ± 0.023 and intercept of 0.54 ± 0.095 (mean ± standard error). However, 49 of the 91 edges in the correlation matrix were found to have statistically significant differences in the mean FC as estimated by the two modalities (p<0.05). The summary of these tests is shown in Figure 8D, with the magnitude of the difference displayed by color and edges that were tested but that did not reach significance shown in black. The differences in estimated FC generally increase in magnitude for longer-range connections (top-right corner of graph) with calcium imaging providing negative estimates of FC while hemodynamic imaging estimates these connections as near-zero. Four connections were estimated to be significantly greater by calcium imaging, and each of these was between left-right symmetric regions. This difference in left-right symmetry can also be observed in the spatial correlation maps (Fig. 5), where the correlation map is more symmetric when using the MUA-predicted signal compared to using the imaging time course near the electrode.

Figure 8.

Summary of the relationship between GCaMP and OIS-BOLD measurements of functional connectivity (FC). The first two panels are the mean FC graphs for computed using either the GCaMP (panel A) or OIS-BOLD (panel B) signal. In panel C is a plot of FC measured by OIS-BOLD versus FC measured by GCaMP (p<0.001, F-test). In panel D are differences between the two measurements with thresholded at a false discovery rate corrected q<0.05.

Discussion

Our work shows that both the resting-state calcium and hemodynamic signal are significantly correlated with spontaneous neuronal activity with both signals having the strongest correlation with spiking activity. The calcium signal is shown to possess higher SNR (Fig. 3) and greater spatial specificity (Fig. 6) compared to the hemodynamic signal, but the advantage in SNR can be reduced by temporal filtering. Furthermore, we show that the relationship between the calcium and hemodynamic signal varies significantly across the brain in a way that is systematic across animals. Differences in temporal lag between GCaMP and OIS-BOLD data ranged between 1.3 and 1.9 seconds, with posterior cortical regions exhibiting longer delays. Lastly, calcium- and hemodynamic-based measurements of connectivity are strongly correlated but with significant differences, which we hypothesize arises at least in part from this regional variation in the HRF.

Given the role of calcium in neurotransmitter release that follows generation of an action potential, it was expected that MUA was the best correlate of the calcium signal. However, our findings differ with some of the previous literature regarding what frequency bands in the electrophysiological recordings are the best correlates of the hemodynamic signal. Early work in this area proposed that LFPs were a stronger correlate of the BOLD signal (Logothetis et al., 2001; Niessing et al., 2005). This conclusion was based on the observation that change in the BOLD signal during a visual stimulus was better correlated to the change in LFP power as compared to the change in spike rate. Shmuel and Leopold implanted an electrode in the monkey visual cortex, and report correlation during spontaneous activity between the BOLD signal and both MUA and LFP but that this correlation is strongest in the gamma band of LFP (Shmuel and Leopold, 2008). Other studies point to an ultra-slow LFP basis for the resting state hemodynamic signal. He et al. compared networks obtained by BOLD fMRI and electrocorticography (ECoG) data collected in the same subjects but at different times. They found that ECoG networks computed with frequencies less than 0.5 Hz best correlated with the networks calculated by BOLD fMRI (He et al., 2008). In the rat auditory cortex, Pan et al. also showed that coherence between electrophysiology and the BOLD signal was greatest in this ultra-slow frequency band (Pan et al., 2013). On the other hand, a study by Mukamel et al. found like us that spiking activity was a strong correlate for the BOLD signal, with spiking activity slightly outperforming LFP for predicting the BOLD signal during a natural auditory stimulus (Mukamel et al., 2005). Several factors may contribute to the discrepancy between our finding and the previous literature. First, the approach to our study is to predict the hemodynamic signal from the electrophysiological data, which is a different approach from most (but not all) of the previous work that attempted to explain the change in the BOLD signal by the change in the electrophysiology signal. Second, differences may arise in part from the calculation of the LFP time courses, where some studies use band-limited power with slightly different forms of normalization, and others use the electrophysiological signal itself that has been filtered into the frequency band of interest. Finally, we cannot rule out the effects of anesthesia in explaining differences between our findings and previous literature, both on the underlying neuronal activity as well as on neurovascular coupling.

This work expands upon previous studies comparing the calcium and hemodynamic signals by investigating the relationship between the two signals as a function of brain region. In agreement with previous literature, the hemodynamic signal is significantly correlated with the calcium signal with a temporal lag (Du et al., 2014; Ma et al., 2016; Matsui et al., 2016), and furthermore, functional connectivity measured by the hemodynamic signal is correlated with connectivity measured by calcium (Matsui et al., 2016; Vazquez et al., 2014). Finally, our work appears to agree well with results from Ma et al. where it is possible to make reasonable comparisons, such as the strength of correlation between MUA and the uncorrected GCaMP signal and the shape of the HRF under anesthesia (Ma et al., 2016).

By demonstrating that the inclusion of brain region while modeling the relationship between GCaMP and OIS-BOLD provided a significantly better explanation of our data, we showed that the HRF varies systematically across the mouse cortex. At least another report has pointed to regional differences in the HRF, indicating significantly different neurovascular coupling between the brainstem, thalamus and cortex during whisker stimulation in the rat (Devonshire et al., 2012). It is possible that the differences between GCaMP and OIS-BOLD HRFs across the brain stem from differences in the neuronal populations being activated across the brain. Although we cannot discount this possibility, this mouse model targets a fairly homogenous population of pyramidal excitatory neurons across the cortex, which is the dominant population of cortical neurons (Chen et al., 2012). We observed correlated but significantly different estimates of functional connectivity, which we hypothesize arise from (1) global, largely non-neuronal fluctuations in the OIS-BOLD signal; and (2) the reported variation in the HRF that is consistent across animals. If validated, this regional variation may be of importance for human studies, as simulation experiments have already shown that uncorrelated variation in the HRF can make some network measures unstable (Smith et al., 2011). Systematic errors may be even less desirable, as they will produce bias and can affect even the simpler network measures like the correlation approach used here.

With this finding in mind, a question remains about how the effects of HRF variability can be controlled in human studies. Task- or stimulus-based imaging studies are able to account for this variability to some extent by including derivatives of the predicted hemodynamic responses in the model. These predictors provide the model with some flexibility to fit hemodynamic responses of slightly varied forms on a voxel-by-voxel basis. However, this approach is not feasible in resting state studies since we have no expectation for the underlying activity, prohibiting the design of a parametric model. Ultimately, we expect that the problem of HRF variability with respect to measurement of FC will need to be solved by improved modeling of the spontaneous BOLD signal. We recently used a machine learning approach to improve the spatial accuracy of activation maps computed from BOLD data in the rat olfactory bulb (Murphy et al., 2016). The results demonstrated that with the proper contextual features (particularly information about baseline blood volume), the BOLD signal can produce activation maps with significantly improved agreement with underlying neuronal activity compared to traditional parametric mapping. In a similar fashion, models that can transform the BOLD signal into a signal better correlated with spontaneous neuronal activity should improve FC estimation.

This work does have some limitations, which will be the subject of future investigations. First, the use of anesthesia was necessary because of the invasiveness of the experimental setup. As we more fully understand the relationship between electrophysiology and the calcium signal, electrophysiological recordings could become unnecessary and allow for imaging of behaving animals. Second, our method likely provides an underestimate for the association between the imaging signals and the underlying electrical activity. Given that we only recorded the hemodynamic signal at a single wavelength, we could not correct the GCaMP signal for the effects of the intrinsic signal that has been previously shown to improve this correlation (Ma et al., 2016). Recording intrinsic signal images (CBV-weighted) around the GCaMP emission band can be used for this purpose; however, our GCaMP IRF findings do not show typical CBV-weighted decreases suggesting that these contributions were not significant under our experimental conditions. Nonetheless, we cannot rule out at least some contamination of the GCaMP signal by the intrinsic signal, which if present would impact the estimated functional connectivity. Another potential limitation is that we only used the multi-unit activity to predict the imaging signals in this study. However, the results demonstrate that LFPs contribute to the signals to varying degrees, and the LFP time courses do have some independence from the MUA time course. Therefore, a prediction that includes all electrophysiological information should improve the correlation with the imaging signals. Finally, a mouse model was particularly useful for this study because of its widespread expression of the calcium indicator, but the shape of the OIS-BOLD signal does not exactly reflect the BOLD signal observed in humans or even larger animals. Using OIS-BOLD imaging in mice, it is common to detect only a decrease in signal intensity in response to neuronal activity instead of the typical increase in signal observed in BOLD fMRI or OIS-BOLD data in humans and larger animals (Belluscio and Katz, 2001; Drew and Feldman, 2009; Matsui et al., 2016). Therefore, neurovascular findings like those shown in this work should be confirmed in larger animals with physiological conditions more closely related to the human response.

In summary, we utilized the Thy1-GCaMP3 mouse model with simultaneous recordings of electrophysiology, calcium and optical intrinsic signals to investigate the relationship between spontaneous neuronal activity and imaging signals, and how this relationship varied across the mouse brain. Our results indicate that both the calcium and the hemodynamic resting-state signals are best predicted by spiking activity as compared to local field potentials. The SNR and the spatial specificity for reporting spiking activity was superior for GCaMP compared to intrinsic imaging, but this advantage was reduced by temporal bandpass filtering. Furthermore, we showed that the relationship between the calcium and hemodynamic signal varied across the brain systematically between animals. We hypothesis that this variation in turn contributed to the observed significant differences in functional connectivity as measured by calcium and hemodynamic signals. These findings highlight some of the strengths and weaknesses of using hemodynamic signals to map neuronal connectivity, and demonstrate the need for improved understanding of the fcMRI signal and how to properly model it.

Supplementary Material

1. Supplementary Figure 1.

Example GCaMP and simultaneously acquired OIS-BOLD images after preprocessing with temporal bandpass filtering.

10. Supplementary Figure 2.

Ten seconds of multi-unit activity recording showing detected spikes.

11. Supplementary Figure 3.

Group functional atlas computed with GCaMP imaging data is shown on the left. Following co-registration, time course data at each pixel were concatenated across animals and then regions of interest were estimated by k-means clustering with 8 clusters. The result is 7 roughly symmetric regions in each hemisphere. An analogous atlas constructed from OIS-BOLD data is shown on the right.

12. Supplementary Figure 4.

Example time course data from one experimental resting-state run showing only the first 30 seconds of data shown in Figure 2. Panel A shows the multi-unit activity measured in spikes per second in either 0.1 s windows (blue) or 1 s windows (red). Panel B shows the LFP spectrogram that is normalized by dividing the time course of each frequency by its own maximum value. Panel C shows the GCaMP (blue line, left y-axis) and OIS-BOLD (red line, right y-axis) imaging signals extracted from a region within 100 μm of the electrode excluding surface vasculature. Shaded region denotes areas where high periods of activity are present and similar responses to GCaMP and OIS-BOLD (negative) were generally observed.

13. Supplementary Figure 5.

Mean time courses in response to electrical stimulation of the forepaw including the rectified local field potential (LFP), multi-unit activity (MUA), GCaMP, and OISBOLD signals. The stimulus duration was 4 seconds indicated by the dashed red lines. The LFP signal was converted to z-scores for each run and rectified to reflect the amplitude of the signal. LFP was then binned to have the same temporal resolution as the imaging signals (10 Hz). An inset is also included showing the first 400 ms (2 pulses of stimulation) of the raw LFP traces. Imaging signals were computed as the mean time course within 100 μm of the electrode while excluding large surface vessels, and linearly detrended over the displayed temporal window to mitigate the effects of ongoing neuronal activity. In each case, the data from each animal and each trial were concatenated and then modeled at each time point using a mixed-effects model with a constant fixed-effect term and random intercepts for each animal. Shaded blue regions indicate the 95% confidence intervals, with 3 consecutive time points of p<0.05 considered significant. These data demonstrate robust electrophysiological responses to stimulation and significant changes in the imaging signals similar to those expected given the computed impulse response functions (Fig. 4).

14. Supplementary Figure 6.

Summary of correlation between spontaneous electrophysiology and imaging signals as a function of frequency band computed with the LFP power in each time window normalized to the total power in that window. Each panel shows the cross-correlation function computed by holding the electrophysiological signal stationary and shifting the imaging signal in a window of −10 to +10 s. The line and shaded regions represent the mean and standard error, respectively, across 6 animals (2 runs each) estimated by a linear mixed-effects model.

15. Supplementary Figure 7.

Example GCaMP and OIS-BOLD time courses for each animal including the time course predicted by the multi-unit activity and the measured signal. Data were temporally bandpass filtered from 0.01 to 0.1 Hz.

16. Supplementary Figure 8.

Example functional connectivity maps from one animal computed with simultaneously acquired GCaMP (top) or OIS-BOLD (bottom) images. Maps were computed by taking the mean time course in each atlas region, correlating it with the time course of every pixel in the image, and applying the Fisher r-to-z transformation.

Highlights.

• We acquired simultaneous electrophysiology and imaging in lightly anesthetized mice.

• Both calcium and hemodynamic signals are correlated with neuronal activity.

• Multi-unit activity was the best electrophysiological correlate of both signals.

• The hemodynamic versus calcium relationship varied significantly by brain region.

• Estimates of connectivity derived from two signals were correlated but different.