Abstract
Objective
To determine the circuit elements required to theoretically describe the stimulus waveforms generated by an implantable pulse generator (IPG) during clinical deep brain stimulation (DBS).
Methods
We experimentally interrogated the Medtronic Activa PC DBS IPG and defined an equivalent circuit model that accurately captured the output of the IPG. We then compared the detailed circuit model of the clinical stimulus waveforms to simplified representations commonly used in computational models of DBS. We quantified the errors associated with these simplifications using theoretical activation thresholds of myelinated axons in response to DBS.
Results
We found that the detailed IPG model generated substantial differences in activation thresholds compared to simplified models. These differences were largest for bipolar stimulation with long pulse widths. Average errors were ~3–24% for voltage-controlled stimulation and ~2–11% for current-controlled stimulation.
Conclusions
Our results demonstrate the importance of including basic circuit elements (e.g. blocking capacitors, lead wire resistance, electrode capacitance) in model analysis of DBS.
Significance
Computational models of DBS are now commonly used in academic research, industrial technology development, and in the selection of clinical stimulation parameters. Incorporating a realistic representation of the IPG output is necessary to improve the accuracy and utility of these clinical and scientific tools.
Keywords: Deep brain stimulation, Neuromodulation, Neurostimulation, Neural activation, Computational modeling, Parkinson’s disease
1. Introduction
Deep brain stimulation (DBS) is an established therapy to treat several neurological disorders (e.g. essential tremor, Parkinson’s disease, dystonia, obsessive-compulsive disorder) (Benabid et al., 1991; Greenberg et al., 2010; Obeso et al., 2001; Vidailhet et al., 2005) and its efficacy is being explored for a range of additional indications (e.g. epilepsy, treatment-resistant depression, neuropathic pain, Tourette syndrome) (Fisher et al., 2010; Holtzheimer, 2012; Lempka et al., 2017; Malone et al., 2009; Morrell and RNS System in Epilepsy Study Group, 2011; Schrock et al., 2015). The fundamental interaction of a DBS device with the brain is provided by the stimulus pulse. However, the technical details of the actual stimulus waveform used in clinical practice are poorly documented and typically ignored by DBS researchers. Instead idealized assumptions are commonly made on the definition of the stimulus amplitude and the shape of the stimulus waveform applied to the brain tissue. Unfortunately, these assumptions are too simplistic and represent an unrecognized source of error in scientific and clinical analyses attempting to correlate DBS patient outcome measures with stimulation parameter settings (Butson and McIntyre, 2007).
Limitations in the understanding of DBS pulses become especially relevant when attempting to use computational models to estimate the spread of stimulation. The last decade has seen a steady development of modeling technologies designed to characterize the electrical effects of DBS on individual patients (McIntyre et al., 2015). Such tools are now available to assist in the clinical programming of DBS devices (Frankemolle et al., 2010; Pourfar et al., 2015), and to identify specific axonal pathways that, when directly activated, correlate with therapeutic outcomes or side effects (Gunalan et al., 2017; Riva-Posse et al., 2017). However, as DBS research analyses become more specific, the tools necessary to evaluate possible correlations will likely need to become more precise. We believe that the fundamental stimulus waveform generated by a clinical implantable pulse generator (IPG) is one technical detail in need of reappraisal.
The goal of this study was to define the circuit elements (e.g. blocking capacitors, extension wire resistance, lead wire resistance) necessary to accurately represent the implanted DBS system. This circuit model could then be used to provide a more precise definition of the actual stimulus waveform used in clinical DBS research studies. In addition, a realistic model of the DBS IPG output could then be used as the input to volume conductor electric field models of DBS to facilitate more accurate predictions of axonal pathway activation.
2. Methods
2.1 Circuit models
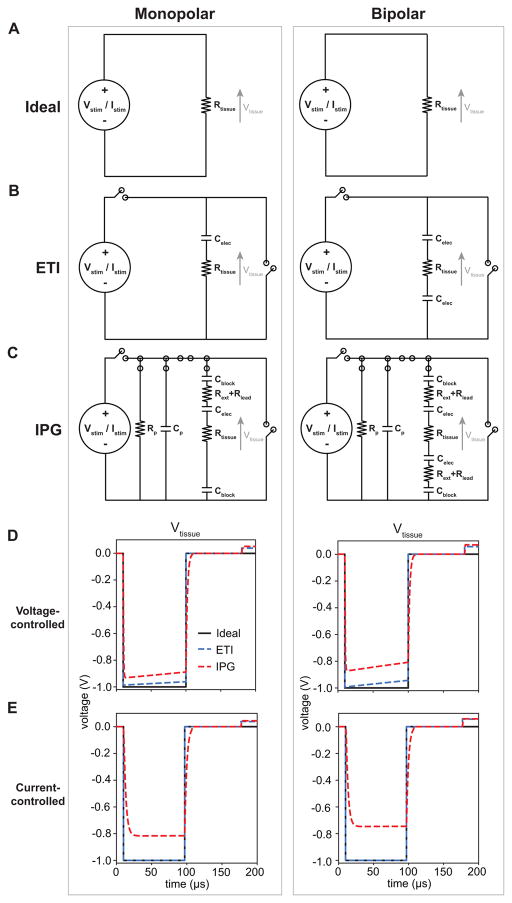
We considered multiple equivalent circuit models to represent the implanted DBS system (Fig. 1). The first model was an ideal model in which the applied pulse amplitude (i.e. Vstim or Istim) was directly applied to the tissue load, Rtissue (i.e. Vstim = Vtissue or Istim*Rtissue = Vtissue) (Fig. 1A). The second model represented the electrode-tissue interface (ETI) of the stimulating electrodes via a simple capacitor (Celec) (Fig. 1B) (Butson and McIntyre, 2005). The ETI model included two switches, one switch to apply the cathodic stimulus pulse and the second switch to allow for passive discharging. And the third model was designed to closely mimic the components of a clinical DBS system and the implantable pulse generator (IPG) (Fig. 1C). In addition to Celec, this IPG model included the blocking capacitors at the IPG outputs (Cblock) (Liu et al., 2008), the resistance of the metal lead extension wire (Rext) that connects the IPG to the lead wire, and the resistance of the lead wire (Rlead). The IPG model included a parasitic resistance (Rp) and a parasitic capacitance (Cp). The IPG model also included multiple switches (Gunalan et al., 2017). During the cathodic stimulus phase, the voltage/current source was connected to Rp, Cp, and the DBS system load. During the first 10 μs of the 80μs-interphase interval, the voltage/current source was disconnected from the circuit. During the last 70 μs of the interphase interval, Rp and Cp were also disconnected. During the passive discharge phase, the DBS system load was connected to ground and Rp and Cp were connected to each other. For the desired stimulation parameters, we simulated the tissue voltage generated for each circuit model for both voltage-controlled and current-controlled stimulation (Fig. 1D,E).
Figure 1.
DBS circuit models. A) Monopolar (left column) and bipolar (right column) circuit models of an ideal voltage-controlled or current-controlled stimulator in which the desired stimulus amplitude (Vstim or Istim) was applied directly across the tissue (Rtissue). B) Monopolar and bipolar circuit models that included the capacitance of the electrode-tissue interface (ETI) of DBS electrodes (Celec) and two switches to apply the cathodic pulse and for passive discharging. C) Monopolar and bipolar circuit models of an implantable pulse generator (IPG). These models included the blocking capacitors on the IPG outputs (Cblock), resistance of the DBS extension wires (Rext), resistance of the DBS lead wires (Rlead), and Celec. These models included a parasitic resistance (Rp) and a parasitic capacitance (Cp). The IPG models also included multiple switches to reproduce the output of the IPG (see Section 2.1). D) Computer simulations of the tissue voltages (Vtissue) for voltage-controlled stimulation for each circuit model using the following stimulation parameters: pulse amplitude (i.e. Vstim) = 1 V, pulse width = 90 μs, pulse frequency = 130 Hz, and impedance = 1 kΩ. E) Computer simulations of Vtissue for current-controlled stimulation for each circuit model using the following stimulation parameters: pulse amplitude (i.e. Istim) = 1 mA, pulse width = 90 μs, pulse frequency = 130 Hz, and impedance = 1 kΩ.
2.2 Bench recordings
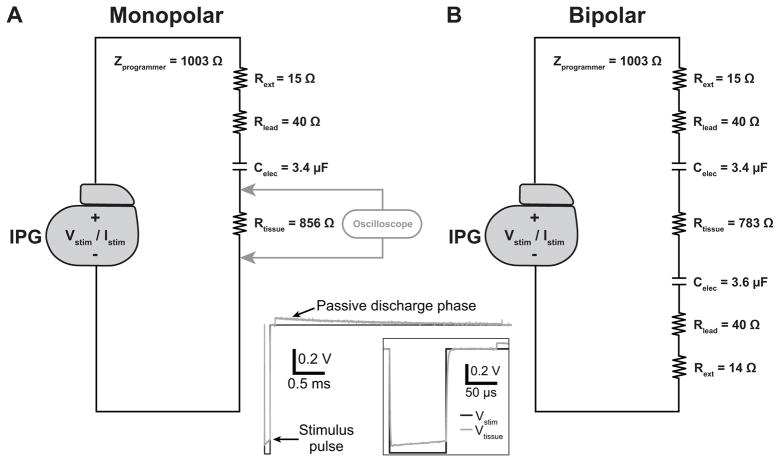
To characterize the output of a clinical IPG under different parameter settings, we recorded the output from an Activa® PC neurostimulator (Medtronic, Inc., Minneapolis, MN) for DBS applications across simple bench circuits representing an implanted DBS system. The stimulator output was saved to disk using an Agilent Technologies, Inc. MSO6014A mixed signal oscilloscope (Santa Clara, CA) with a sampling rate of 1 MHz. We obtained the stimulator output recorded across two different test circuits representing monopolar and bipolar stimulation from an implanted DBS system (Fig. 2). These test circuits included elements representing the following components: the resistance of the extension wire (14–15 Ω), the resistance of the lead wire (40 Ω), a 3.4 or 3.6 μF capacitor representing the electrode-tissue interface (ETI) (Butson and McIntyre, 2005), and a resistor representing the tissue impedance. The resistance of the lead extension and the lead wire were average resistance values directly measured from a DBS extension model 7483 and a DBS lead model 3387 (Medtronic, Inc.), respectively. Lastly, we manually selected resistance values to represent Rtissue to achieve the desired electrode impedance. We measured the overall bench circuit impedance using the built-in functionality of the IPG. The impedance values measured by the IPG were read via the hand-held N’Vision Clinician Programmer Model 8840 (Medtronic, Inc.). An Rtissue of 856 Ω and 783 Ω produced an overall electrode impedance of 1.0 kΩ for the monopolar and bipolar stimulation circuits, respectively.
Figure 2.
Circuits used in bench measurements of the implantable pulse generator (IPG) output. A) Circuit values used to measure the IPG output for a range of stimulation parameters for monopolar stimulation. B) Circuit values used to measure the IPG output for bipolar stimulation. In these circuits, Rext = resistance of a DBS extension wire, Rlead = resistance of a DBS lead wire, Celec = capacitance of the DBS electrode-tissue interface, and Rtissue = tissue resistance. For both circuits, the IPG programmer measured impedance values of 1 kΩ (Zprogrammer). These circuits were used to measure the IPG output for both voltage-controlled and current-controlled stimulation. The waveform at the bottom shows an example bench recording of Vtissue for monopolar voltage-controlled stimulation for pulse amplitude (i.e. Vstim) = 1 V, pulse width = 90 us, and pulse frequency = 130 Hz.
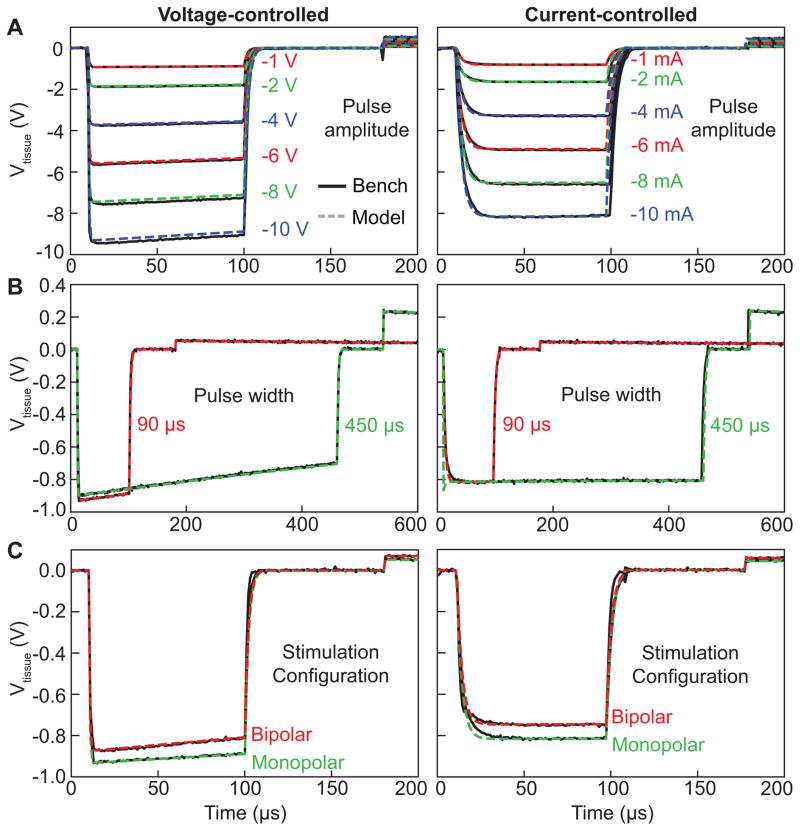
To thoroughly characterize the IPG output, we measured the stimulator output for a range of stimulation parameters (Fig 3). The IPG output was measured for both voltage-controlled and current-controlled stimulation modes. We also independently varied each of the stimulation parameters (pulse amplitude, pulse width, pulse frequency, stimulation configuration, and electrode impedance), while holding the other parameters constant. For the pulse amplitude, we measured the stimulator output at 1, 2, 4, 6, 8, and 10 V and 1, 2, 4, 6, 8, and 10 mA (pulse width of 90 μs, pulse frequency of 130 Hz, monopolar stimulation, electrode impedance of 1 kΩ) (Fig. 3A). For the pulse width, we measured the stimulator output at 90 and 450 μs (pulse amplitude of 1 V or 1 mA, pulse frequency of 130 Hz, monopolar stimulation, electrode impedance of 1 kΩ) (Fig. 3B). For the stimulation configuration, we measured monopolar and bipolar stimulation (pulse amplitude of 1 V or 1 mA, pulse width of 90 μs, pulse frequency of 130 Hz, electrode impedance of 1 kΩ) (Fig. 3C). For the pulse frequency, we measured the IPG output at 30, 130, and 250 Hz (pulse amplitude of 1 V or 1 mA, pulse width of 90 μs, monopolar stimulation, electrode impedance of 1 kΩ) (data not shown). And for the electrode impedance, we measured the IPG output at 0.5, 1.0, and 1.5 kΩ (pulse amplitude of 1 V or 1 mA, pulse width of 90 μs, pulse frequency of 130 Hz, monopolar stimulation) (data not shown).
Figure 3.
Implantable pulse generator (IPG) output. We measured the estimated tissue voltage (i.e. Vtissue in Fig. 1) for a range of pulse amplitudes (A), pulse widths (B), and stimulation configurations (C) for both voltage-controlled (left column) and current-controlled (right column) stimulation. The bench measurement (solid black line) and corresponding model simulation (dashed line) are shown for each set of stimulation parameters. Unless otherwise specified, we used the following default stimulation parameters: pulse amplitude = 1 V or 1 mA, pulse width = 90 μs, pulse frequency = 130 Hz, and stimulation configuration = monopolar.
2.3 Computer simulations of stimulator output
To model the IPG output, we defined computer models mimicking the bench recordings performed in Section 2.2. In these computer models, we included the same resistance and capacitance values that we used in the bench recordings. However, the Activa® PC neurostimulator includes 10 μF blocking capacitors at each output. Therefore, we also included two 10 μF capacitors to represent Cblock at each output of the IPG. We also included Rp and Cp of 20 kΩ and 3 nF for voltage-controlled stimulation and 20 kΩ and 4 nF for current-controlled stimulation (Fig. 1C). We estimated the values of Rp and Cp using a brute-force optimization algorithm in which we explored a wide range of possible values for Rp and Cp. We then determined the average resistance and capacitance values that produced the smallest differences between the model waveform and the corresponding bench recordings for each of the waveform parameters (i.e. pulse amplitude, pulse width, pulse frequency, stimulation configuration, impedance) that we tested in the bench recordings.
To accurately reproduce the IPG output, it was important to understand the output modes of the IPG. During the cathodic stimulus pulse, the IPG applied the selected pulse amplitude across the entire IPG circuit. At the end of the cathodic pulse, the circuit was placed in a “high-impedance” state that mimicked an open circuit for 80 μs to allow for more efficient neural excitation (van den Honert and Mortimer, 1979). At the end of this 80 μs interphase interval, residual charge in the IPG circuit was allowed to passively discharge. This passive discharge phase allowed for charge accumulated across the ETI capacitance and blocking capacitors to discharge. The duration of this passive discharge phase was dependent on the pulse frequency and was 16.5, 3.7, and 1.8 ms for pulse frequencies of 30, 130, and 250 Hz, respectively. At the end of the passive discharge phase, the IPG was placed in a “high-impedance” state until the start of the next cathodic stimulus pulse.
We performed numerical simulations of the appropriate circuit designs using custom scripts that solved the appropriate set of differential equations using forward Euler’s method with a time step of 1 μs. We calculated the corresponding tissue voltage (i.e. Vtissue) as a function of time for each circuit design and set of stimulation parameters (Fig. 3). Vtissue represented the input to our 3D finite element model (FEM) analysis (see Section 2.4).
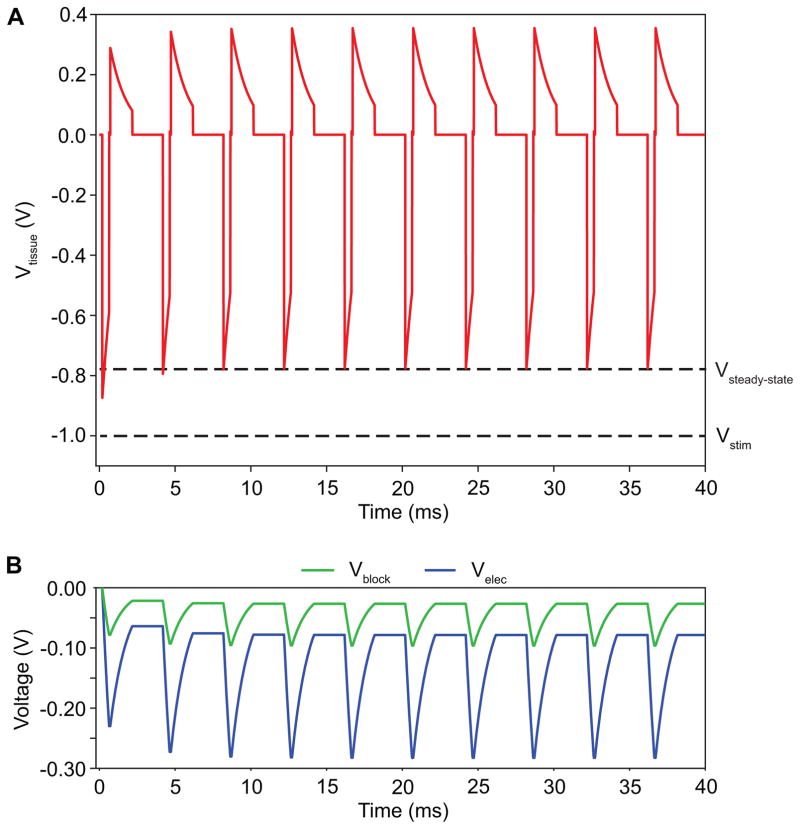
It is important to note, that because the IPG utilized a passive recharge phase, certain stimulation parameters (e.g. long pulse width and/or high pulse frequency) did not allow for the complete discharge of the charge accumulated across the ETI capacitance and blocking capacitors. Therefore, the charge accumulated across these capacitive elements continued to increase until a steady state was reached (Fig. 4). For voltage-controlled stimulation, this charge accumulation across the capacitive elements corresponded to a decrease in the peak amplitude of the tissue voltage (Vtissue) during the cathodic phase and an increase in the peak amplitude of the anodic phase. Therefore, we only analyzed model waveforms after the stimulator output had reached a steady-state (> 100 ms).
Figure 4.
Steady-state tissue voltage. Charge accumulation across the blocking capacitors and electrode capacitance can lead to time-dependent changes in the applied tissue voltage before a steady-state voltage (Vsteady-state) is achieved. Vstim is the pulse amplitude applied by the implantable pulse generator. The stimulus shown above had the following parameters: pulse amplitude = 1 V, pulse width = 450 μs, pulse frequency = 250 Hz, stimulation configuration = bipolar, impedance = 1 kΩ. A) The time-dependent tissue voltage (Vtissue). B) The time-dependent voltage across both blocking capacitors (Vblock) and both stimulation electrodes (Velec) for the bipolar stimulation.
2.4 Bioelectric field model
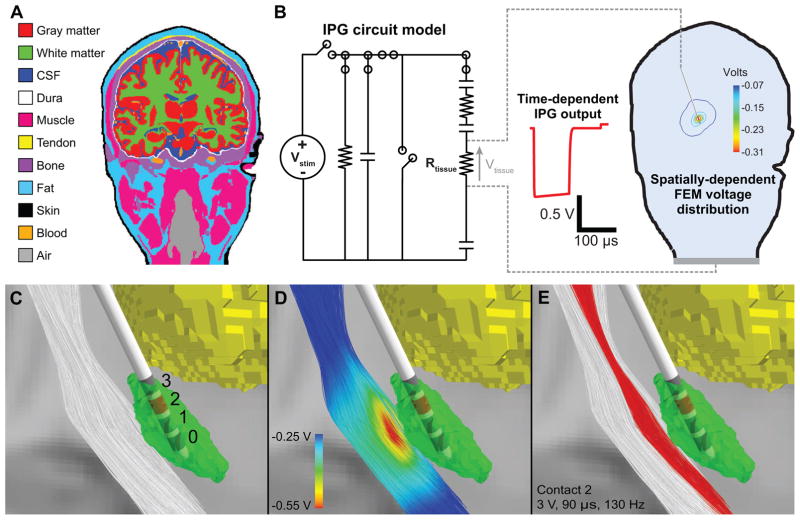
We used a 3D computer model of DBS to investigate how the different circuit models and corresponding differences in tissue voltage (i.e. Vtissue) affected the theoretical predictions of neural excitation. We used the time-dependent Vtissue waveform for each circuit model and set of stimulation parameters (see Section 2.3) as the input voltage applied to the stimulation electrodes in the FEM analysis. Therefore, we scaled the electrostatic FEM solutions by the appropriate model waveform and applied the resultant 3D voltages to the axon models (Fig. 5). We adopted the same methodology from our previous studies (Howell and McIntyre, 2017, 2016) and integrated a detailed single-subject atlas, termed MIDA (Iacono et al., 2015).
Figure 5.
Computational model of DBS. A) We created a 3-dimensional finite element model (FEM) of DBS using an anatomical model of a human head and neck. B) We used the circuit models to estimate the time dependence and the FEM to calculate the spatial dependence of the tissue voltage (Vtissue). C) The DBS model included 1000 descending corticofugal fibers and a DBS lead implanted in the subthalamic nucleus (STN). D) The voltage distribution generated by −3 V applied through contact 2 interpolated onto the corticofugal fibers. E) For the IPG model, the corticofugal fibers shown in red were activated by monopolar stimulation applied through contact 2 with the following parameters: pulse amplitude = 3 V, pulse width = 90 μs, pulse frequency = 130 Hz, and electrode impedance = 1 kΩ.
MIDA contains locations of 116 anatomical structures, which we combined into 12 electrically-equivalent classifications (Fig. 5A): white matter, gray matter, cerebrospinal fluid, muscle, bone, fat, tendon, air, intervertebral disc, dura, blood, and skin (Howell and McIntyre, 2017). We co-registered the MIDA to the MNI 152 standard space using a 12-parameter affine transformation. We used the inverse transformation to map a probabilistic atlas of the subthalamic nucleus (STN) (Keuken et al., 2013) from MNI space to MIDA space. We also used a 12-parameter affine transformation to co-register MIDA to the diffusion-weighted (DW) MR image of the healthy subject from the FMRIB Software Library (FSL) course data (Jenkinson et al., 2012). We then constructed a bioelectric field model from the MIDA that consisted of three domains: 1) a 0.5 mm thick encapsulation layer surrounding a Medtronic 3389 DBS electrode array placed in the right STN (Haberler et al., 2000; Moss et al., 2004), 2) a brain domain delineated by the outer boundaries of the encapsulation layer and the brain, and 3) a third domain delineated by the brain surface and the scalp.
We used the corresponding anatomical representations to define a conductivity tensor (Σ) for all elements of the tetrahedral mesh. We modeled the Σ’s within the parenchyma and cerebrospinal fluid of the brain as anisotropic. We derived the eigenvectors of these Σ’s from the fitted diffusion tensors of the DW image and we used the load-preservation approach (Howell and McIntyre, 2016) to calculate eigenvalues of Σ given an isotropic conductivity (σ) and eigenvalues of the diffusion tensors. Σ’s in all other regions, including the encapsulation layer, were isotropic. The σ’s for each tissue type were the measured conductivities at 1 kHz (Gabriel et al., 1996). The exceptions were the dura (0.03 S/m) (Struijk et al., 1993), air (1 × 10−12 S/m), and the encapsulation layer. The encapsulation layer conductivity was specified for each circuit model to produce an approximate overall impedance of 1 kΩ. For the Ideal and ETI models, the encapsulation conductivity was 0.09 S/m and 0.17 S/m for monopolar and bipolar stimulation, respectively. For the IPG model, the encapsulation conductivity was 0.11 S/m and 0.20 S/m for monopolar and bipolar stimulation, respectively.
We used the finite element method to solve Laplace’s equation for monopolar and bipolar electrode configurations. To model monopolar stimulation, we specified electrode 2 (Fig. 5C) as the cathode and insulated the outer boundary of the head except at the base of the neck which we set to ground. To model bipolar stimulation, we specified electrodes 2 and 3 as the cathode and anode, respectively, and insulated the entire outer boundary of the head. We treated inactive contacts as ideal conductors and modeled them using Robin boundary conditions that specified two conditions per contact: all potentials within the contact were equal in value, and the net current flow through the surface of the contact was 0 A. Neumann boundary conditions of 0 A/mm2 were used to model the electrode shaft and scalp surface (minus the neck) as perfect insulators. To estimate the tissue voltages generated by DBS, we scaled the electrostatic 3D spatial voltage distribution (from the FEM) by the time-dependent Vtissue (from the IPG circuit model) (Fig. 5B) (Gunalan et al., 2017; Howell and McIntyre, 2016). We then applied these time- and space-dependent tissue voltages to the axon models (Section 2.5) to determine the neural response to DBS.
2.5 Axon model
Experimental and theoretical data suggest that the primary effect of DBS is the generation of action potentials in axons (McIntyre et al., 2004; Ranck, 1975). Therefore, we took the trajectories of 1000 descending corticofugal axons that coursed through the internal capsule from a tractographic atlas (Meola et al., 2016) and mapped them to MIDA space (Howell and McIntyre, 2017) (Fig. 5C). We used each streamline to represent the trajectory of a multi-compartment cable axon model and to define the axonal coordinates in the volume conductor. The axon models had a diameter of 5.7 μm and were based on a previously-published mammalian axon model (McIntyre et al., 2002). To assess the direct axonal response to DBS, we applied the FEM voltage distributions (see Section 2.4) to the model axons. The position of an axonal compartment did not necessarily correspond to the location of a node within the FEM mesh. Therefore, we used linear interpolation to calculate the DBS-induced extracellular voltage for each axonal compartment. Because the FEM conductivities were linear, the voltage distributions generated by different stimulation parameters were scaled versions of the original FEM solutions with unit stimulation amplitudes. We used the extracellular mechanism within NEURON (Carnevale and Hines, 2005) to apply the scaled voltage distributions to each axon. For a given electrode configuration, pulse width, and pulse frequency we used a binary search algorithm to determine the threshold stimulus amplitude for action potential generation to within 0.01 V and 0.01 mA for voltage-controlled and current-controlled stimulation, respectively. We considered an axon to be activated when it responded with action potentials in a “one-to-one” fashion with the stimulus frequency. We performed the simulations in the NEURON (v7.3) simulation environment with a time step of 1 μs to match the time step we used to calculate the time-dependent Vtissue for each circuit model and set of DBS parameters (see Section 2.3).
3. Results
This study characterized the stimulus waveforms generated by a clinical DBS IPG and evaluated the impact of accurately representing these stimulus waveforms on computational estimates of axonal activation. Each DBS stimulus waveform consisted of a short duration cathodic stimulus phase (defined by the user-specified pulse width), followed by an 80 μs interphase interval, followed by a long duration passive recharge phase (Fig. 2). We found that the generic definition of stimulus amplitude in DBS studies is somewhat misleading. The actual magnitude of the cathodic phase of the stimulus pulse is actually ~5–20% less than the user-specified amplitude. The particular discrepancies, which are dependent upon the exact stimulation parameter settings, can be explicitly accounted for with a circuit model and appropriate selection of the circuit components inherent to the DBS system (Fig. 2).
We compared our DBS IPG circuit model to bench measurements from a clinical IPG. For both voltage-controlled and current-controlled stimulation, we tested stimulation parameters that were relevant to clinical applications of DBS: pulse amplitude (1–10 V and 1–10 mA), pulse width (90 and 450 μs), pulse frequency (30–250 Hz), stimulation configuration (monopolar and bipolar), and impedance (0.5–1.5 kΩ). Figure 3 shows that the IPG circuit model was able to accurately reproduce the time-dependent tissue voltages as a function of pulse amplitude, pulse width, and stimulation configuration. The IPG circuit model was also able to accurately reproduce the time-dependent tissue voltage as a function of pulse frequency and electrode impedance (data not shown).
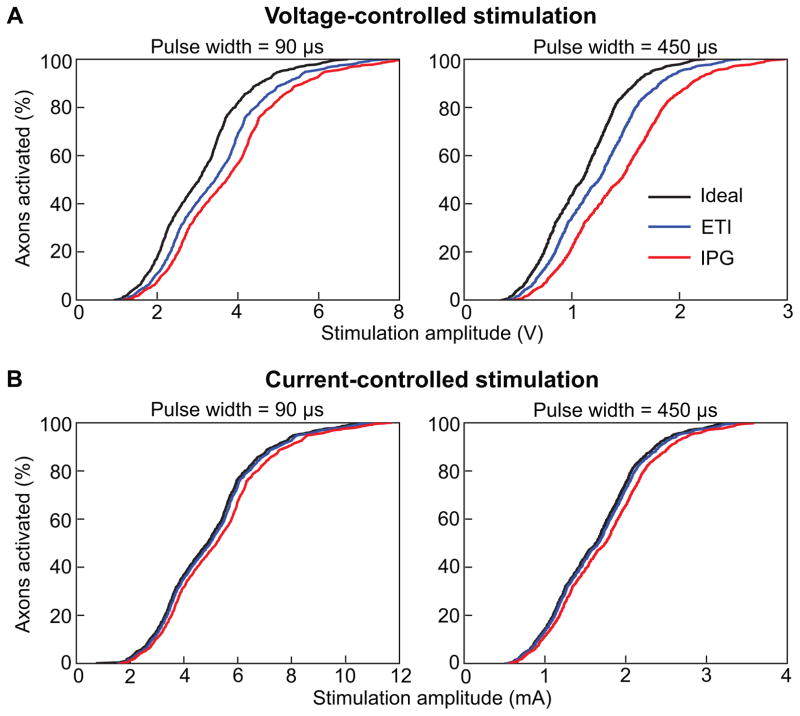
We then used the IPG circuit model to evaluate the errors associated with estimating axonal activation using typical simplifying assumptions on the DBS stimulus waveform. We used three circuit models (Ideal, ETI, and IPG) to investigate the role of different circuit elements on activation thresholds (Fig. 1). We applied the time-dependent Vtissue waveforms for each circuit type (see Section 2.3) to a 3D FEM (see Section 2.4) and multi-compartment axon models (see Section 2.5). For each circuit model, we calculated the activation thresholds for 1000 individual axons for both voltage-controlled and current-controlled stimulation. We estimated the activation thresholds for monopolar and bipolar stimulation using pulse widths of 90 and 450 μs and a pulse frequency of 130 Hz. We then calculated the percent error of the activation thresholds for each of the 1000 individual axons predicted for the Ideal and ETI models relative to the IPG model (e.g. percent error = (threshi,Ideal−threshi,IPG)/threshi,IPG × 100% where threshi,Ideal and threshi,IPG represent the activation thresholds for axon, i, for the Ideal and IPG models, respectively) (Table 1, Fig. 6). We observed the largest percent error for bipolar stimulation with a pulse width of 450 μs. For voltage-controlled stimulation, the average error was −20.2±0.3% and −7.7±0.3% for the Ideal and ETI models, respectively. For current-controlled stimulation, the average error was −10.6±0.4% and −9.1±0.3% for the Ideal and ETI models, respectively.
Table 1.
Average errors (± standard deviation) in activation thresholds between the circuit models.
| Stimulation configuration | Pulse width (μs) | Percent error (%) | ||
|---|---|---|---|---|
| Ideal v. IPG | ETI v. IPG | |||
| Voltage-controlled stimulation | Monopolar | 90 | 2.5 ± 0.4 | 4.5 ± 0.4 |
| 450 | −11.0 ± 0.3 | −3.3 ± 0.4 | ||
| Bipolar | 90 | −5.7 ± 0.4 | −2.8 ± 0.4 | |
| 450 | −20.2 ± 0.3 | −7.7 ± 0.3 | ||
| Monopolar (acute) | 90 | −18.6 ± 0.5 | −7.7 ± 0.1 | |
| 450 | −24.4 ± 0.4 | −13.8 ± 0.1 | ||
| Current-controlled stimulation | Monopolar | 90 | −2.1 ± 0.5 | −6.5 ± 0.4 |
| 450 | −8.5 ± 0.5 | −7.0 ± 0.4 | ||
| Bipolar | 90 | −8.4 ± 0.6 | −8.8 ± 0.4 | |
| 450 | −10.6 ± 0.4 | −9.1 ± 0.3 | ||
| Monopolar (acute) | 90 | −6.0 ± 0.4 | −4.5 ± 0.1 | |
| 450 | −6.8 ± 0.4 | −4.9 ± 0.2 | ||
Figure 6.
Percent error in activation thresholds for the 1000 corticofugal axons included in the DBS model. A) Boxplot of the percent errors in activation thresholds for voltage-controlled stimulation. B) Boxplot of the percent errors in activation thresholds for current-controlled stimulation. For both A and B, the two left columns represent the results for monopolar stimulation while the two right columns represent the results for bipolar stimulation. Activation thresholds were calculated for pulse widths of 90 μs and 450 μs for both monopolar and bipolar stimulation. For each set of stimulation parameters, percent errors were calculated for the Ideal and ETI models relative to the IPG model.
DBS electrode impedance typically increases during the first few weeks after implantation before stabilizing (Benabid et al., 1996; Lempka et al., 2009). Because stimulator programming procedures are commonly performed during this initial postoperative phase, we increased the encapsulation layer conductivity to 0.2 S/m to consider the effect of acute DBS electrode impedances on the model errors. To mimic the monopolar stimulation procedures that are commonly utilized during initial DBS programming (Volkmann et al., 2002), we estimated the activation thresholds for monopolar stimulation for both voltage-controlled and current-controlled stimulation. This acute DBS electrode impedance resulted in significant differences in axonal recruitment as a function of stimulation amplitude (Fig. 7). For voltage-controlled stimulation, the average percent error was −18.6±0.5% and −7.7±0.1% for a pulse width of 90 μs and −24.4±0.4% and −13.8±0.3% for a pulse width of 450 μs for the Ideal and ETI models, respectively. For current-controlled stimulation, the average error was −6.0±0.4% and −4.5±0.1% for a pulse width of 90 μs and −6.8±0.4% and −4.9±0.2% for a pulse width of 450 μs for the Ideal and ETI models, respectively.
Figure 7.
Axonal recruitment under acute DBS conditions. A) Percent of corticofugal axons activated as a function of stimulation amplitude for voltage-controlled stimulation with a pulse width of 90 μs (left plot) and 450 μs (right plot). B) Percent of corticofugal axons activated as a function of stimulation amplitude for current-controlled stimulation with a pulse width of 90 μs (left plot) and 450 μs (right plot). All simulations were performed for monopolar stimulation.
4. Discussion
The goal of this study was to characterize the details of the stimulus waveforms generated by clinical DBS devices. The substantial clinical growth in the use of DBS technology for a wide range of therapeutic applications is motivation for wide scale neurophysiological studies on the effects of electrical stimulation in the human brain. However, detailed investigations using clinical DBS devices, especially studies evaluating DBS mechanisms of action or modeling DBS systems, should at least be aware of the technical nuances of the IPG. These nuances become especially important in the context of patient-specific DBS models intended to estimate the spatial extent of activation or direct stimulation of individual axonal pathways in the brain (Fig. 5) (Gunalan et al., 2017). Given the substantial growth in the combined analysis of DBS clinical outcomes with DBS computer models and the increasing specificity of the analyses being performed, we propose that the precision of the DBS models used by the general research community needs to improve.
Improving the precision of DBS computer models is relevant not only for scientific study, but also clinical decision support. For example, DBS computer models have been used to improve patient outcomes (Frankemolle et al., 2010), decrease programming time (Butson et al., 2013; Pourfar et al., 2015), and a large scale clinical trial is currently underway to evaluate how nurses can use computer models to guide DBS programming in patients’ homes (NIH R01 NR014852). The use of DBS computer models will likely continue to evolve and expand as commercial stimulation systems incorporate additional features (e.g. independent current sources, increased number of electrodes, directional DBS arrays, novel stimulation waveforms) and expand to additional indications. As such, the accuracy of the models is crucial for their successful implementation as clinical decision support tools.
Model parameters are based on a judicious selection of several parameters. Some of these parameters can be characterized with a high degree of certainty (e.g. the stimulation waveform), while other parameters have inherent variability and uncertainty (e.g. electrical properties of the tissue surrounding DBS electrodes). Significant effort has been put forth to improve the volume conductor aspects of these models (Chaturvedi et al., 2010; Howell and McIntyre, 2017, 2016), but much less attention has been paid to the basic circuit elements (e.g. blocking capacitors, resistance of extension and lead wires) used to represent the DBS systems.
Under certain stimulation parameters, the results of this study suggest that the IPG circuit model did predict substantial differences in neural activation relative to more simplified circuit models (Table 1 and Figs. 6–7). We observed large differences in activation thresholds for the following stimulation conditions: bipolar stimulation, long pulse widths, and/or low tissue resistance. These situations corresponded to a relatively large amount of charge accumulation at the blocking capacitors and the capacitance of the electrode-tissue interface. Charge accumulation occurred because the commercial system utilized passive recharging that did not allow for sufficient charge dissipation during the anodic phase (Fig. 4). For voltage-controlled stimulation, it is also important to consider that the stimulator applies a set voltage across the entire IPG output. Therefore, the voltage drops across the resistance of the extension and lead wires alone can lead to a measurable reduction (~9% for a 1 kΩ impedance) in the voltages applied to the tissue.
For current clinical programming practices with 4-contact arrays, the model differences observed in this study may prove insignificant, especially for typical stimulation conditions (e.g. short pulse width, monopolar stimulation). However, there has been increasing scientific interest in quantifying the direct activation of specific axonal pathways surrounding the DBS electrode (Chaturvedi et al., 2010; Gunalan et al., 2017; Mahlknecht et al., 2017). From this scientific perspective, the model differences could become highly relevant, as behavioral effects associated with stimulating a specific pathway could be noted at low levels of percent activation. Therefore, research analyses attempting to draw correlations between (positive or negative) clinical effects and thresholds for pathway activation could easily be misguided by using reduced models.
The model errors observed in this study could also become directly clinically relevant if software packages are used in place of current clinical programming methods to prospectively define stimulation parameters for patients. To define optimal clinical settings, theoretical estimates of thresholds for major side effects would be a fundamental component in these model algorithms. This aspect would be especially true for patients with a small therapeutic window. These theoretical estimates could also prove valuable for DBS programming for emerging indications (e.g. treatment-resistant depression, post-stroke pain) (Lempka et al., 2017; Malone et al., 2009) that may require more complex programming procedures relative to standard indications. Furthermore, as commercial DBS systems begin to utilize leads with a higher number of electrodes (e.g. 8–32) (Kühn and Volkmann, 2017), it will become infeasible to use traditional programming methods to exhaustively search the nearly infinite parameter space within the context of standard clinical care. As such, the accuracy of the DBS model used in the programming software will likely play an important role in identifying the optimal stimulation settings.
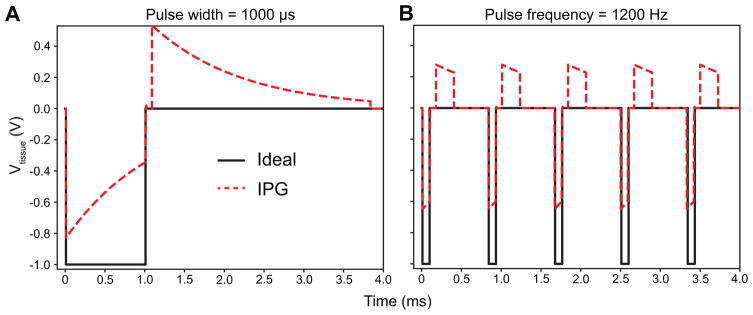
For this study, we only tested the range of stimulation parameters utilized in conventional DBS. However, we believe it is important to recognize that newer commercial systems and other neuromodulation therapies (e.g. spinal cord stimulation for chronic pain management) utilize stimulation parameters that can exacerbate the effects of charge accumulation across the electrode-tissue interface and blocking capacitors. For example, common commercial systems can apply stimulation with longer pulse widths (e.g. 1 ms) and higher pulse frequencies (e.g. 1.2 kHz). Figure 7 shows the theoretical steady-state Vtissue for a 1 ms pulse width (Fig. 8A) and a 1.2 kHz pulse frequency (Fig. 8B). These stimulation parameters lead to significant changes in both the cathodic stimulus and passive recharging phases.
Figure 8.
Tissue voltage (i.e. Vtissue in Fig. 1) generated for stimulation parameters that exacerbated the effects of charge accumulation at the blocking capacitors and electrode-tissue interface. A) Vtissue for an ideal stimulator (Fig. 1A) and a realistic IPG circuit model (Fig. 1C) for a long pulse width of 1000 μs (pulse amplitude = 1 V, pulse frequency = 130 Hz, stimulation configuration = bipolar, impedance = 1 kΩ). B) Vtissue for a high pulse frequency of 1200 Hz (pulse amplitude = 1 V, pulse width = 90 μs, stimulation configuration = bipolar, impedance = 1 kΩ).
Another important issue to consider is electrode impedance. Clinicians, scientists, and engineers use impedance measurements to interrogate a DBS system. For example, a high electrode impedance may indicate a lead wire fracture or a very low electrode impedance (<50 Ω) may indicate a short circuit (Butson et al., 2006). Clinical systems provide users with electrode impedance measurements, but it is not necessarily clear what these values represent. When interpreting electrode impedance, it is important to consider how a DBS system measures electrode impedance. For example, some commercial systems will measure the electrode impedance by applying a short-duration (~20 μs) current pulse while measuring the peak voltage generated during the pulse. Because this current pulse is short in duration, it is assumed that there is little voltage build up across any capacitance in the system and the measured voltage reflects the tissue resistance. Alternatively, the commercial neurostimulator utilized in this study measured impedance in a significantly different manner. To measure electrode impedance, this system applied a stimulus with a pulse amplitude of 0.7 V, pulse width of 80 μs, and a pulse frequency of 100 Hz. The system calculates the electrode impedance by measuring the current at 70 μs from the leading edge of the cathodic pulse (Gunalan et al., 2017). In our bench circuit (Fig. 2), the clinical programmer measured a 1 kΩ impedance for tissue resistances of 856 Ω and 783 Ω for monopolar and bipolar stimulation, respectively.
DBS models are typically parameterized so the FEM impedance matches the electrode impedance measured by the clinical system (Chaturvedi et al., 2010). For a 1 kΩ electrode impedance, the conductivities of the encapsulation layer and surrounding brain tissue would be assigned so that the FEM estimates a tissue impedance of 1 kΩ (i.e. Rtissue = 1 kΩ). However, this approach would lead to inaccuracies when using a 1 kΩ FEM to model a DBS electrode with a clinical impedance of 1 kΩ.
While our DBS IPG circuit model did an excellent job of mimicking the experimentally measured outputs, a few notable limitations should be acknowledged. The major limitation of our study was the focus on a single commercial neurostimulator, albeit the most commonly used clinical DBS device. However, the basic stimulator circuit design with blocking capacitors and passive charge recovery are common to clinical neurostimulation systems (Liu et al., 2008; Sooksood et al., 2009). Therefore, we believe our general approach can be extended to additional commercial DBS systems. Other limitations were that we used a bench circuit to mimic an electrochemical system and represented the electrode-tissue interface as a simple capacitor. The electrode-tissue interface consists of Faradaic and non-Faradaic impedances (Merrill et al., 2005). Some experimental evidence suggests Faradaic currents occur during DBS (Wei and Grill, 2009), while other studies suggest that DBS macroelectrodes can be approximated as ideally polarizable electrodes under standard clinical stimulation parameters (Howell et al., 2014). For our IPG circuit model, inclusion of a 2.5 kΩ resistance (Howell and McIntyre, 2016) in parallel with Celec produced negligible changes in the time-dependent Vtissue waveforms (data not shown). Nonetheless, we believe Faradaic currents are an important issue to consider in theoretical and experimental studies of DBS, especially at high pulse amplitudes and long pulse widths (Merrill et al., 2005). In this study, we utilized an electrostatic FEM in which we represented the electrical properties of the tissue as purely resistive. However, the capacitive properties of biological tissues could affect the spatiotemporal voltage distributions generated during DBS and the corresponding neural response. Previous studies have suggested that tissue capacitance has a negligible effect with standard DBS parameters, especially for voltage-controlled stimulation (Butson and McIntyre, 2005; Howell and McIntyre, 2016). However, for certain stimulation parameters (e.g. long pulse widths) and current-controlled stimulation, tissue capacitance could potentially increase the pulse amplitudes required for activation compared to electrostatic conditions (Butson and McIntyre, 2005). Finally, we used a single axonal pathway embedded within a highly detailed DBS volume conductor model to evaluate axonal thresholds (Howell and McIntyre, 2017). However, the relatively straight and simple internal capsule represents a “best case” scenario for the performance of reduced models to predict axonal activation (Gunalan et al., 2017).
5. Conclusion
Characterizing the neurophysiological effects of DBS starts with understanding the input signal to the brain. We examined which DBS circuit elements were necessary to accurately describe the time-dependent voltage waveforms applied to the tissue. Our results suggest that under certain stimulation conditions, such as low tissue impedance, long pulse widths, and bipolar/multipolar stimulation, that it is necessary to include basic circuit elements, such as blocking capacitors, lead wire resistance, and electrode capacitance, in the model analysis of DBS. Representation of these circuit elements is especially important when attempting to couple those model results to patient-specific experimental measurements.
Highlights.
The electrode-tissue interface and implantable pulse generator (IPG) circuitry affect the stimulus waveform applied to the brain.
Accurate representation of the IPG output significantly affects theoretical axonal activation.
Clinical decision support utilizing DBS models should include basic circuitry of the neurostimulator.
Acknowledgments
Technical assistance: We would like to thank Jim Buckett (Case Western Reserve University) for his assistance with stimulation circuit design and simulation.
Funding: This work was supported by the Louis Stokes Cleveland Veterans Affairs Medical Center, the National Institutes of Health (NIH R01 NS085188, NIH R01 MH102238, F32 NS096839, T32 GM007250, TL1 TR000441, and T32 EB004314), and the U.S. Department of Education (GAANN P200A100112). This work made use of the High Performance Computing Resource in the Core Facility for Advanced Research Computing at Case Western Reserve University.
Footnotes
Conflict of interest
CCM is a paid consultant for Boston Scientific Neuromodulation, and is a shareholder in the following companies: Surgical Information Sciences, Inc.; Autonomic Technologies, Inc.; Cardionomic, Inc.; Enspire DBS, Inc.; Neuros Medical, Inc. AGM has distribution rights to Cardionomic, Inc. and Enspire DBS, Inc., and is a paid consultant of St. Jude Medical.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Benabid AL, Pollak P, Gao D, Hoffmann D, Limousin P, Gay E, et al. Chronic electrical stimulation of the ventralis intermedius nucleus of the thalamus as a treatment of movement disorders. J Neurosurg. 1996;84:203–14. doi: 10.3171/jns.1996.84.2.0203. [DOI] [PubMed] [Google Scholar]
- Benabid AL, Pollak P, Gervason C, Hoffmann D, Gao DM, Hommel M, et al. Long-term suppression of tremor by chronic stimulation of the ventral intermediate thalamic nucleus. Lancet. 1991;337:403–6. doi: 10.1016/0140-6736(91)91175-T. [DOI] [PubMed] [Google Scholar]
- Butson CR, Maks CB, McIntyre CC. Sources and effects of electrode impedance during deep brain stimulation. Clin Neurophysiol. 2006;117:447–54. doi: 10.1016/j.clinph.2005.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butson CR, McIntyre CC. Differences among implanted pulse generator waveforms cause variations in the neural response to deep brain stimulation. Clin Neurophysiol. 2007;118:1889–94. doi: 10.1016/j.clinph.2007.05.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butson CR, McIntyre CC. Tissue and electrode capacitance reduce neural activation volumes during deep brain stimulation. Clin Neurophysiol. 2005;116:2490–500. doi: 10.1016/j.clinph.2005.06.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butson CR, Tamm G, Jain S, Fogal T, Krüger J. Evaluation of Interactive Visualization on Mobile Computing Platforms for Selection of Deep Brain Stimulation Parameters. IEEE Trans Vis Comput Graph. 2013;19:108–17. doi: 10.1109/TVCG.2012.92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carnevale NT, Hines ML. The NEURON Book. Cambridge: Cambridge University Press; 2005. [Google Scholar]
- Chaturvedi A, Butson CR, Lempka SF, Cooper SE, McIntyre CC. Patient-specific models of deep brain stimulation: Influence of field model complexity on neural activation predictions. Brain Stimul. 2010;3:65–77. doi: 10.1016/j.brs.2010.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher R, Salanova V, Witt T, Worth R, Henry T, Gross R, et al. Electrical stimulation of the anterior nucleus of thalamus for treatment of refractory epilepsy. Epilepsia. 2010;51:899–908. doi: 10.1111/j.1528-1167.2010.02536.x. [DOI] [PubMed] [Google Scholar]
- Frankemolle AMM, Wu J, Noecker AM, Voelcker-Rehage C, Ho JC, Vitek JL, et al. Reversing cognitive-motor impairments in Parkinson’s disease patients using a computational modelling approach to deep brain stimulation programming. Brain. 2010;133:746–61. doi: 10.1093/brain/awp315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabriel S, Lau RW, Gabriel C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys Med Biol. 1996;41:2271–93. doi: 10.1088/0031-9155/41/11/003. [DOI] [PubMed] [Google Scholar]
- Greenberg BD, Gabriels LA, Malone DA, Rezai AR, Friehs GM, Okun MS, et al. Deep brain stimulation of the ventral internal capsule/ventral striatum for obsessive-compulsive disorder: worldwide experience. Mol Psychiatry. 2010;15:64–79. doi: 10.1038/mp.2008.55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gunalan K, Chaturvedi A, Howell B, Duchin Y, Lempka SF, Patriat R, et al. Creating and parameterizing patient-specific deep brain stimulation pathway-activation models using the hyperdirect pathway as an example. PLoS One. 2017;12:e0176132. doi: 10.1371/journal.pone.0176132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haberler C, Alesch F, Mazal PR, Pilz P, Jellinger K, Pinter MM, et al. No Tissue Damage by Chronic Deep Brain Stimulation in Parkinson’s Disease. Ann Neurol. 2000;48:372–6. doi: 10.1002/1531-8249(200009)48. [DOI] [PubMed] [Google Scholar]
- Holtzheimer PE. Subcallosal Cingulate Deep Brain Stimulation for Treatment-Resistant Unipolar and Bipolar Depression. Arch Gen Psychiatry. 2012;69:150. doi: 10.1001/archgenpsychiatry.2011.1456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Honert C, Mortimer JT. The response of the myelinated nerve fiber to short duration biphasic stimulating currents. Ann Biomed Eng. 1979;7:117–25. doi: 10.1007/BF02363130. [DOI] [PubMed] [Google Scholar]
- Howell B, McIntyre CC. Role of Soft-Tissue Heterogeneity in Computational Models of Deep Brain Stimulation. Brain Stimul. 2017;10:46–50. doi: 10.1016/j.brs.2016.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howell B, McIntyre CC. Analyzing the tradeoff between electrical complexity and accuracy in patient-specific computational models of deep brain stimulation. J Neural Eng. 2016;13:36023. doi: 10.1088/1741-2560/13/3/036023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howell B, Naik S, Grill WM. Influences of Interpolation Error, Electrode Geometry, and the Electrode-Tissue Interface on Models of Electric Fields Produced by Deep Brain Stimulation. IEEE Trans Biomed Eng. 2014;61:297–307. doi: 10.1109/TBME.2013.2292025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iacono MI, Neufeld E, Akinnagbe E, Bower K, Wolf J, Oikonomidis IV, et al. MIDA: A Multimodal Imaging-Based Detailed Anatomical Model of the Human Head and Neck. PLoS One. 2015;10:e0124126. doi: 10.13099/ViP-MIDA-V1.0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M, Beckmann CF, Behrens TEJ, Woolrich MW, Smith SM. FSL. Neuroimage. 2012;62:782–90. doi: 10.1016/j.neuroimage.2011.09.015. [DOI] [PubMed] [Google Scholar]
- Keuken MC, Bazin P, Schäfer A, Neumann J, Turner R, Forstmann BU. Ultra-High 7T MRI of Structural Age-Related Changes of the Subthalamic Nucleus. J Neurosci. 2013;33:4896–900. doi: 10.1523/JNEUROSCI.3241-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kühn AA, Volkmann J. Innovations in deep brain stimulation methodology. Mov Disord. 2017;32:11–9. doi: 10.1002/mds.26703. [DOI] [PubMed] [Google Scholar]
- Lempka SF, Malone DA, Hu B, Baker KB, Wyant A, Ozinga JG, et al. Randomized clinical trial of deep brain stimulation for poststroke pain. Ann Neurol. 2017;81:653–63. doi: 10.1002/ana.24927. [DOI] [PubMed] [Google Scholar]
- Lempka SF, Miocinovic S, Johnson MD, Vitek JL, McIntyre CC. In vivo impedance spectroscopy of deep brain stimulation electrodes. J Neural Eng. 2009;6:46001. doi: 10.1088/1741-2560/6/4/046001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Demostheous A, Donaldson N. Five valuable functions of blocking capacitors in stimulators. 13th Annu. Conf. Int. Funct. Electr. Stimul. Soc; 2008. pp. 322–4. [Google Scholar]
- Mahlknecht P, Akram H, Georgiev D, Tripoliti E, Candelario J, Zacharia A, et al. Pyramidal Tract Activation Due to Subthalamic Deep Brain Stimulation in Parkinson’s Disease. Mov Disord. 2017;32:1174–82. doi: 10.1002/mds.27042. [DOI] [PubMed] [Google Scholar]
- Malone DA, Dougherty DD, Rezai AR, Carpenter LL, Friehs GM, Eskandar EN, et al. Deep Brain Stimulation of the Ventral Capsule/Ventral Striatum for Treatment-Resistant Depression. Biol Psychiatry. 2009;65:267–75. doi: 10.1016/j.biopsych.2008.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIntyre CC, Grill WM, Sherman DL, Thakor NV. Cellular Effects of Deep Brain Stimulation: Model-Based Analysis of Activation and Inhibition. J Neurophysiol. 2004;91:1457–69. doi: 10.1152/jn.00989.2003. [DOI] [PubMed] [Google Scholar]
- McIntyre CC, Richardson AG, Grill WM. Modeling the Excitability of Mammalian Nerve Fibers: Influence of Afterpotentials on the Recovery Cycle. J Neurophysiol. 2002;87:995–1006. doi: 10.1152/jn.00353.2001. [DOI] [PubMed] [Google Scholar]
- Meola A, Yeh F-C, Fellows-Mayle W, Weed J, Fernandez-Miranda JC. Human Connectome-Based Tractographic Atlas of the Brainstem Connections and Surgical Approaches. Neurosurgery. 2016;79:437–55. doi: 10.1227/NEU.0000000000001224. [DOI] [PubMed] [Google Scholar]
- Merrill DR, Bikson M, Jefferys JGR. Electrical stimulation of excitable tissue: design of efficacious and safe protocols. J Neurosci Methods. 2005;141:171–98. doi: 10.1016/j.jneumeth.2004.10.020. [DOI] [PubMed] [Google Scholar]
- Morrell MJ RNS System in Epilepsy Study Group. Responsive cortical stimulation for the treatment of medically intractable partial epilepsy. Neurology. 2011;77:1295–304. doi: 10.1212/WNL.0b013e3182302056. [DOI] [PubMed] [Google Scholar]
- Moss J, Ryder T, Aziz TZ, Graeber MB, Bain PG. Electron microscopy of tissue adherent to explanted electrodes in dystonia and Parkinson’s disease. Brain. 2004;127:2755–63. doi: 10.1093/brain/awh292. [DOI] [PubMed] [Google Scholar]
- Obeso JA, Olanow CW, Rodriguez-Oroz MC, Krack P, Kumar R, Lang AE. Deep-Brain Stimulation of the Subthalamic Nucleus or the Pars Interna of the Globus Pallidus in Parkinson’s Disease. N Engl J Med. 2001;345:956–63. doi: 10.1056/NEJMoa000827. [DOI] [PubMed] [Google Scholar]
- Pourfar MH, Mogilner AY, Farris S, Giroux M, Gillego M, Zhao Y, et al. Model-Based Deep Brain Stimulation Programming for Parkinson’s Disease: The GUIDE Pilot Study. Stereotact Funct Neurosurg. 2015;93:231–9. doi: 10.1159/000375172. [DOI] [PubMed] [Google Scholar]
- Ranck JB. Which elements are excited in electrical stimulation of mammalian central nervous system: A review. Brain Res. 1975;98:417–40. doi: 10.1016/0006-8993(75)90364-9. [DOI] [PubMed] [Google Scholar]
- Riva-Posse P, Choi KS, Holtzheimer PE, Crowell AL, Garlow SJ, Rajendra JK, et al. A connectomic approach for subcallosal cingulate deep brain stimulation surgery: prospective targeting in treatment-resistant depression. Mol Psychiatry. 2017:1–7. doi: 10.1038/mp.2017.59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrock LE, Mink JW, Woods DW, Porta M, Servello D, Visser-Vandewalle V, et al. Tourette syndrome deep brain stimulation: A review and updated recommendations. Mov Disord. 2015;30:448–71. doi: 10.1002/mds.26094. [DOI] [PubMed] [Google Scholar]
- Sooksood K, Stieglitz T, Ortmanns M. An experimental study on passive charge balancing. Adv Radio Sci. 2009;7:197–200. [Google Scholar]
- Struijk JJ, Holsheimer J, Barolat G, He J, Boom HBK. Paresthesia Thresholds in Spinal Cord Stimulation: A Comparison of Theoretical Results with Clinical Data. IEEE Trans Rehab Eng. 1993;1:101–108. [Google Scholar]
- Vidailhet M, Vercueil L, Houeto JL, Krystkowiak P, Benabid AL, Cornu P, et al. Bilateral Deep-Brain Stimulation of the Globus Pallidus in Primary Generalized Dystonia. N Engl J Med. 2005;352:459–67. doi: 10.1056/NEJMoa042187. [DOI] [PubMed] [Google Scholar]
- Volkmann J, Herzog J, Kopper F, Deuschl G. Introduction to the programming of deep brain stimulators. Mov Disord. 2002;17:S181–7. doi: 10.1002/mds.10162. [DOI] [PubMed] [Google Scholar]
- Wei XF, Grill WM. Impedance characteristics of deep brain stimulation electrodes in vitro and in vivo. J Neural Eng. 2009;6:46008. doi: 10.1088/1741-2560/6/4/046008. [DOI] [PMC free article] [PubMed] [Google Scholar]