Abstract
With the translation of metabolic MRI with hyperpolarized 13C agents into the clinic, imaging approaches will require large volumetric FOVs to support clinical applications. Parallel imaging techniques will be crucial to increasing volumetric scan coverage while minimizing RF requirements and temporal resolution. Calibrationless parallel imaging approaches are well-suited for this application because they eliminate the need to acquire coil profile maps or auto-calibration data. In this work, we explored the utility of a calibrationless parallel imaging method (SAKE) and corresponding sampling strategies to accelerate and undersample hyperpolarized 13C data using 3D blipped EPI acquisitions and multichannel receive coils, and demonstrated its application in a human study of [1-13C]pyruvate metabolism.
Keywords: Hyperpolarization, Parallel imaging, SAKE, Pyruvate, EPI, C13
1. Introduction
Dissolution dynamic nuclear polarization provides over a 10,000+ fold enhancement to nuclear spin polarization [1]. This huge increase in polarization allows 13C MRI to overcome sensitivity limitations, enabling non-invasive, real-time metabolic imaging of both the biodistribution of the injected substrate and its conversion into metabolic products. [1-13C]pyruvate has been the most widely studied molecule in both pre-clinical [2] and clinical [3,4] applications as it sits at the nexus of metabolism, simultaneously providing direct information on glycolysis (through conversion to lactate via lactate dehydrogenase) as well as pyruvate dehydrogenase activity via bicarbonate production and alanine transaminase activity via conversion to alanine.
To quantify this conversion, 5D data (3D spatial + 1D spectral + time) must be acquired to provide information throughout the entire volume, and the transient nature of the hyperpolarized magnetization leads to tradeoffs between spatial resolution, temporal resolution, and SNR. Frequency selective approaches using a spectral-spatial RF pulse to independently excite each metabolite [5] can help ameliorate the tradeoffs between spatial resolution and temporal resolution by removing the need for spectral encoding. This enables single-shot approaches with echoplanar or spiral readouts that would otherwise be unusable without a multiecho readout (e.g. EPSI [6] or IDEAL [7,8]).
While this is a tractable problem for pre-clinical applications, it becomes difficult to maintain adequate spatial and temporal resolution for many clinical research applications that require larger FOVs and longer scan times to maintain the same spatial resolution. This is an important point, as volumetric coverage will be crucial for clinical research when studying metastases and diffuse diseases, assessing treatment response, or when the disease location is not already known.
Parallel imaging can be employed to improve volumetric coverage of hyperpolarized 13C MRI through undersampling, reducing the total scan time and number of RF pulses needed for data acquisition. Image-based approaches such as SENSE [9] require a coil profile map as an input to the reconstruction. However, acquiring a sensitivity map directly from the 13C spins is an inefficient use of the hyperpolarization, and may cause artifacts if there is motion between the calibration scan and data acquisition. K-space based approaches, such as GRAPPA or SPIRiT [10,11], require autocalibration data from a fully sampled center of k-space. This typically comprises the central 24 × 24 or 30 × 30 region of k-space for 1H imaging, limiting the total acceleration. While this can be somewhat reduced for the comparatively small matrix sizes used for 13C acquisitions [12,13], a substantial subset of k-space must remain fully sampled because these techniques need a robust estimate of the weighting factors for synthesizing unacquired k-space points.
Alternatively, calibrationless parallel imaging techniques such as simultaneous autocalibrating and k-space estimation (SAKE [13,14]) are appealing because they obviate the need for either sensitivity maps or autocalibration data. Instead, the reconstruction is posed as a low-rank matrix completion problem and solved iteratively, potentially increasing the overall acceleration and providing more flexibility in sampling patterns. In this work, we explored the application of SAKE to accelerate and undersample hyperpolarized 13C data using a 3D blipped EPI acquisition (Fig. 1) with multichannel reception. Two different sampling patterns were explored over a range of undersampling factors in both numerical simulations and phantom experiments to assess their suitability for clinical applications, and the feasibility of this approach was demonstrated in an abdominal [1-13C]pyruvate imaging study with a healthy volunteer.
Fig. 1.
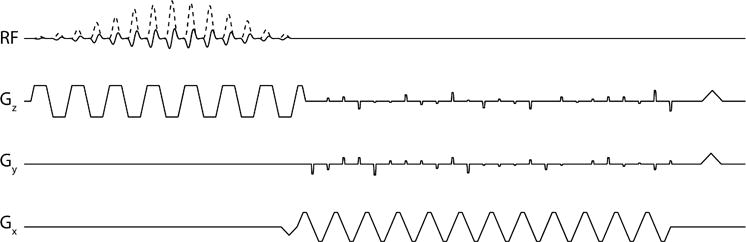
The 3D EPI pulse sequence used in this work. A singleband spectral-spatial RF pulse was used to selectively excite individual metabolites. Phase-encode gradients on the Y and Z-axis enable 3D imaging with an arbitrary blip pattern that is changed every TR.
2. Methods
2.1. Simulations
Numerical simulations were performed in MATLAB R2015b (The MathWorks Inc., Natick, MA). Two different sampling patterns were investigated: a center-out acquisition and a pseudorandom raster [15], with regular blips on one axis and pseudorandom blips on the other (Fig. 2). Here, undersampling is performed simultaneously in the two phase-encoding dimensions (ky–kz), while the through-slice readout dimension (kx) remains fully sampled. Sampling patterns were generated for undersampling factors R = 2–6 and were designed for a 48 × 48 × 48 matrix with 0.612 ms echo-spacing, with a 4 × 4 fully sampled center of k-space. The pseudorandom raster sampling patterns were generated with an echo train length (ETL) of 48 using a beta probability distribution in the pseudorandom (kz) dimension for each ky row. The center-out sampling patterns were generated from a variable-density Poisson disk pattern [11,16] with corner cutting and were designed with an ETL of 24 or 48. Since the fully sampled acquisitions assumed an ETL of 48, the ETL of 24 has an acceleration (or time-savings) of R/2.
Fig. 2.
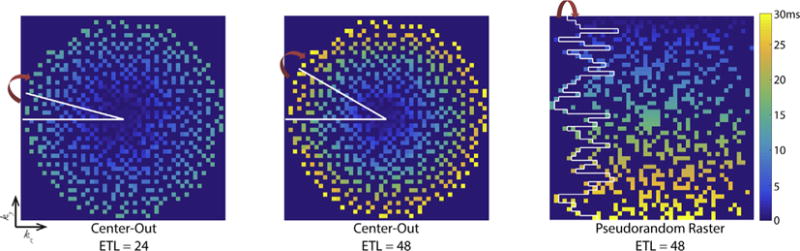
Representative sampling patterns (undersampling factor R = 4) used with the 3D EPI pulse sequence in this work. The center-out sampling patterns started at the center of k-space and encoded a wedge in ky-kz within each TR using a variable density Poisson disc distribution. The two center-out sampling patterns were identical aside from the echo train length. The pseudorandom raster sampling pattern started at ky,max and acquired a rectangular portion in ky-kz within each TR. The white lines denote the region in ky-kz encoded within a single TR.
T2* decay and chemical shift were included in an idealized signal model to quantify the effect of signal decay and bulk off-resonance on the reconstruction:
In this nomenclature, ρ(k) is the Fourier transform of the image at k-space point k and τn is the nth echo time (the product of the echo-spacing and the nth echo number). Here, we have assumed idealized sampling by subsampling k-space directly on a Cartesian grid. For each sampled point in k-space, off-resonance phase and T2* decay were applied. T2* values ranging from 10 ms to 50 ms and bulk off-resonance between 0 and 30 Hz were explored. This corresponds to a range of 120 Hz for conventional 1H MRI because of the fourfold difference in 1H and 13C gyromagnetic ratios. An 8-channel receive array was used in these simulations, with sensitivity profiles calculated based on the principle of reciprocity using the Biot-Savart Law in the quasi-static regime [17]. This setup was designed to match the receive array used in the phantom study described below.
Two different numerical phantoms were explored: one consisted of a uniform object with multiple signal voids comprising the entire FOV, and the other consisted of small circles of varying radii to mimic the sparse signal often seen in hyperpolarized studies (Fig. 3). Data were either zero-filled or reconstructed with SAKE using a 6 × 6 reconstruction window over 100 iterations. The appropriate window-normalized rank threshold (1.8 for the large phantom, 1.2 for the sparse phantom) was determined from the fully sampled data (Supporting Fig. 1), as it is closely related to the size of the object in the image domain [14]. The structural similarity (SSIM) index [18] between the numerical phantom and reconstructed images were calculated to assess reconstruction fidelity.
Fig. 3.
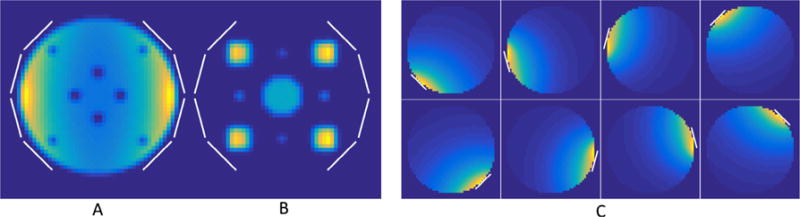
Numerical phantoms (A, B) and sensitivity profiles (C) of the eight channel receive array used in simulations, with the location of the elements of the receive array outlined in white. Undersampling was performed in-plane, with the through-plane direction being the fully encoded readout.
2.2. Phantom experiments
All data were acquired on a GE 3T scanner (MR750, Waukesha WI, USA) with clinical performance gradients (5 G/cm gradient strength, 20 G/cm/ms slew-rate). A 3D ramp-sampled, symmetric echo-planar imaging sequence with blip gradients on both Y and Z (Fig. 1) was used for data acquisition [19]. A bore-insertable clamshell coil was used for 13C RF transmit and an 8-channel coil comprised of two 4-element paddles [20] was used for reception.
For 13C phantom acquisitions, R = 6 sampling patterns were compared using an 18 cm diameter sphere filled with 3L of natural abundance ethylene glycol. To provide structure, a 60 mL, 3.5 cm diameter syringe filled with water was inserted vertically into the center of the sphere. A singleband spectral-spatial RF pulse (120 Hz FWHM passband, 600 Hz stopband) was used to selectively excite the central 13C ethylene glycol resonance. Scan parameters for the phantom acquisition were: FOV = 48.0 × 48.0 × 48.0 cm3, matrix = 48 × 48 × 48, TR = 62.5 ms, 7° flip angle, 5 min scan time. A fully sampled 3D stack-of-EPI acquisition was acquired as a reference. Data were acquired with a sagittal orientation, with the fully encoded readout perpendicular to the array. The total scan time of 5 min per sampling pattern was kept constant by increasing the number of averages for the undersampled acquisitions. A reference scan was acquired directly from the 13C phantom to correct for Nyquist ghost artifacts. The total acquisition time per average was 3 s for a fully sampled 3D volume, 1 s for the R = 6, ETL = 24 center-out sampling pattern, and 0.5 s for the R = 6, ETL = 48 center-out and pseudorandom raster sampling patterns.
2.3. Volunteer study
2.3.1. Sample preparation & polarization
Following an FDA IND and IRB approved protocol, 1.47 g of Good Manufacturing Practices (GMP) [1-13C]pyruvate (Sigma-Aldrich) and 15 mM electron paramagnetic agent (EPA) (AH111501, GE Healthcare) were prepared by a pharmacist the morning of the study. The sample was polarized using a 5T commercial polarizer (SPINlab, GE Healthcare) for 3 h before being rapidly dissolved with 130°C water and neutralized with NaOH and Tris buffer. The EPA was rapidly removed by filtration, and pH, pyruvate and EPA concentrations, polarization, and temperature were measured prior to injection. In parallel, the hyperpolarized solution was pulled into a syringe (Medrad Inc) through a 0.5 lm sterile filter and transported into the scanner for injection. The integrity of this filter was tested in agreement with manufacturer specifications prior to injection. After release by the pharmacist, a 0.43 mL/kg dose of ~250 mM pyruvate was injected at a rate of 5 mL/s, followed by a 20 mL saline flush, with the acquisition starting 10 s after the end of saline injection.
2.3.2. Imaging setup
A bore-insertable clamshell coil was used for 13C RF transmit and a 16-channel bilateral phased array (RAPID Biomedical, Rimpar, Germany) was used for 13C signal reception, functionally similar to the 8-channel array used in simulations and phantom studies, but with an extra row of coil elements in the readout (sagittal) direction to provide greater coverage. As with the phantom study, data were acquired with a sagittal orientation, with the fully encoded readout perpendicular to the array. These coils were placed anterior and posterior to the volunteer to provide coverage over the entire abdomen. For imaging, a singleband spectral-spatial RF pulse (130 Hz FWHM passband, 870 Hz stopband) was used to sequentially excite [1-13C]pyruvate, [1-13C]lactate (Δf = 390 Hz), [1-13C]alanine (Δf = 180 Hz), and 13C bicarbonate (Δf = 320 Hz). Scan parameters for the study were: FOV = 72.0 × 72.0 × 72.0 cm3, matrix = 48 × 48 × 48, TR/TE = 62.5/13.2 ms, 7° flip angle, echo-spacing = 0.416 ms, scan time per metabolite volume = 1.5 s. Data were acquired with an R = 4, ETL = 24 center-out sampling pattern. This represents a twofold time-savings compared to a fully sampled stack-of-EPI with ETL = 48. A total of 10 timeframes were acquired for each metabolite, yielding an effective temporal resolution of 6 s and a total scan time of 60 s. A reference scan was acquired on the 1H channel using the 13C waveform [19] to correct for inconsistencies between even and odd lines of k-space. Immediately following 13C imaging, a non-localized spectrum (θ = 60°, 5 kHz spectral bandwidth, 2048 points) was acquired with a 500 μs hard pulse to measure the relative metabolite frequencies. For anatomic reference, a 3D T1W SPGR was acquired with TR/TE = 4.3/1.9 ms, θ = 8°, FOV = 35 × 35 × 22 cm3, matrix size = 320 × 224 × 72.
2.3.3. Data processing
For phantom and volunteer datasets, phase coefficients from the reference scan were applied to the ramp-sampled data using the Orchestra Toolbox (GE Healthcare). The multichannel k-space data were pre-whitened [21] and subsequently reconstructed using SAKE on a slice-by-slice basis in the fully encoded (readout) dimension. For the phantom study, the structural similarity between the fully sampled 3D acquisition and the three accelerated sampling patterns was used to assess reconstruction fidelity. All 1H/13C overlay images were generated using SIVIC [22].
3. Results
The effects of T2* and off-resonance on the point spread function (PSF) for the fully-sampled center-out and pseudorandom raster sampling patterns can be seen in Fig. 4. The tradeoff between the center-out and pseudorandom raster yielded stark differences in the symmetry of the PSF (Fig. 4). Similar to a radial acquisition, the PSF is isotropic in the two blip dimensions (ky–kz) for the center-out sampling pattern. The PSF broadens as the T2* decreases, and is more pronounced for a longer echo train length and readout duration (Fig. 4B).
Fig. 4.
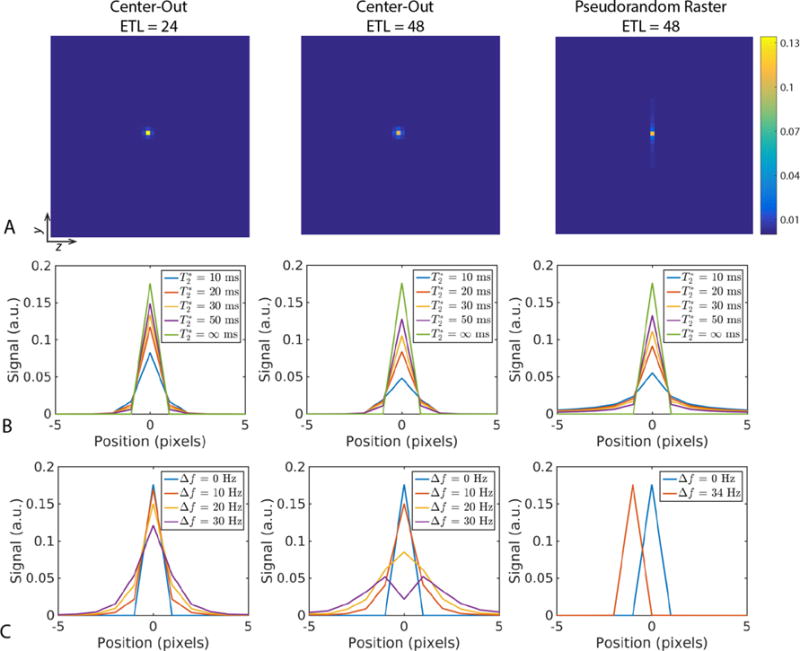
Point spread function (PSF) for the three sampling patterns explored in this work. A representative 2D PSF simulated with T2* = 30 ms and no off-resonance for each of the three sampling patterns (A) shows stark differences in symmetry. 1D line profiles in the y-dimension of the PSF as a function of T2* (B) shows that the two ETL = 48 sampling patterns are similarly sensitive to short T2* with respect to signal intensity. In contrast, the PSF as a function of off-resonance (C) highlights the robustness of the pseudorandom raster to bulk off-resonance, resulting in only a simple shift instead of blurring (broader PSF) for the center-out approach.
Similarly, the center-out ETL = 24 sampling pattern had an increased peak height compared to the pseudorandom raster, due to the shorter TE (Fig. 4B). In contrast, the pseudorandom raster had an anisotropic and highly directional PSF that is sharper in the pseudorandom blip dimension but broader in the regular blip (ky) dimension over all T2* values. However, this approach is much more robust to off-resonance, manifesting as a simple shift in the normal blip dimension instead of substantial broadening for the center-out approach (Fig. 4C). As with T2*, the degree of broadening for the center-out sampling scheme is more pronounced for a longer echo train length and larger chemical shift.
Numerical phantom simulation results for the three sampling patterns with different undersampling factors are shown in Fig. 5. While the pseudorandom raster had similar reconstruction fidelity to the center-out sampling patterns at low undersampling factors, its overall acceleration was limited, breaking down for R > 4 when the object comprises the majority of the FOV (Fig. 5A). For the sparse phantom (Fig. 5B), the overall SSIM is similar between the three sampling patterns. However, the pseudorandom raster sampling pattern has increased error at the center of the phantom due to residual undersampling artifacts, with decreased conspicuity and increased error for the smallest point sources. Conversely, the center-out approach allowed for more flexible sampling, including corner cutting and variable-density sampling. The error was highest at the boundary of the point sources that comprise the sparse phantom, and at the edge of the small signal voids within the large phantom, with the ETL of 48 sampling pattern having increased blurring and error at the object boundary. It is important to note that the hard rank threshold used in the reconstruction process will influence image quality (Supporting Fig. 1). Choosing too low of a threshold makes it difficult to separate the signal from the noise subspace, while too high of a threshold preserves the signal but results in an inability to remove undersampling artifacts.
Fig. 5.
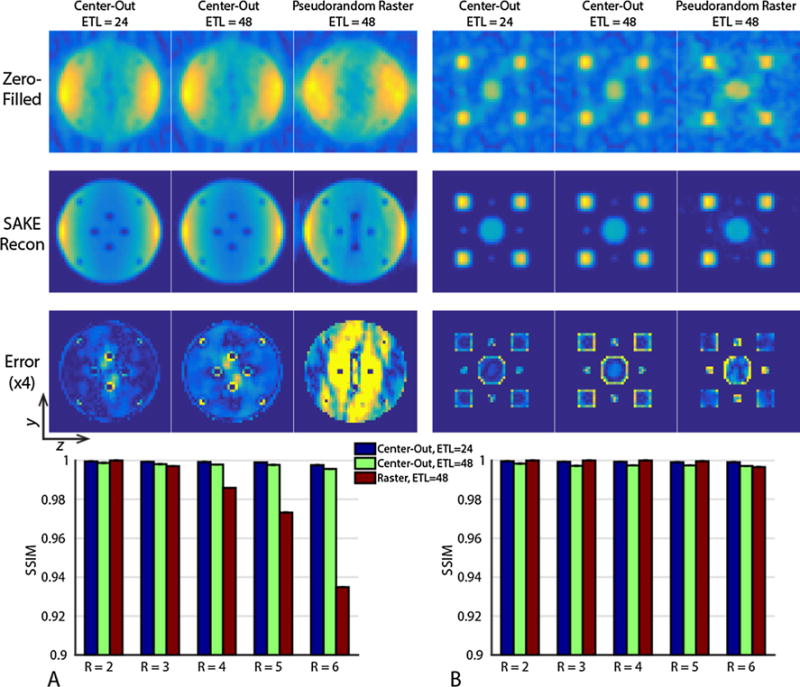
Numerical simulation results for a uniform object with multiple signal voids (A) and a sparse phantom with circles of varying radii (B) assuming T2* = 30 ms and acquired with R = 6 sampling patterns. While both the center-out and pseudorandom raster sampling patterns are able to reconstruct the sparse phantom (B), the raster approach breaks down when the object size approaches the FOV for higher undersampling factors (A). The two center-out sampling patterns have similar reconstruction fidelity as measured by SSIM. However, the center-out ETL = 48 sampling pattern has increased error at the object boundary, in agreement with the broader PSF. All images have been displayed with identical window and level.
The numerical simulations were corroborated by the thermal 13C ethylene glycol phantom studies in Fig. 6 with R = 6 sampling patterns. While the SSIM index was similar over the entire object for all three sampling patterns, subtle differences between the sampling patterns are evident. Similar to the numerical simulations, the pseudorandom raster sampling pattern has increased error and loss of signal at the center of the object, farthest from the receive array. Similarly, blurring was readily apparent at the ethylene-glycol/air boundary at the edge of the sphere for the center-out pattern with ETL = 48. In comparison, the center-out pattern with ETL = 24 provides a potential threefold reduction in scan time compared to the fully-sampled stack-of-EPI while yielding a beneficial tradeoff between blurring and signal loss, with less blurring compared to the center-out ETL = 48 sampling pattern and improved signal fidelity when compared to the pseudorandom raster sampling pattern.
Fig. 6.
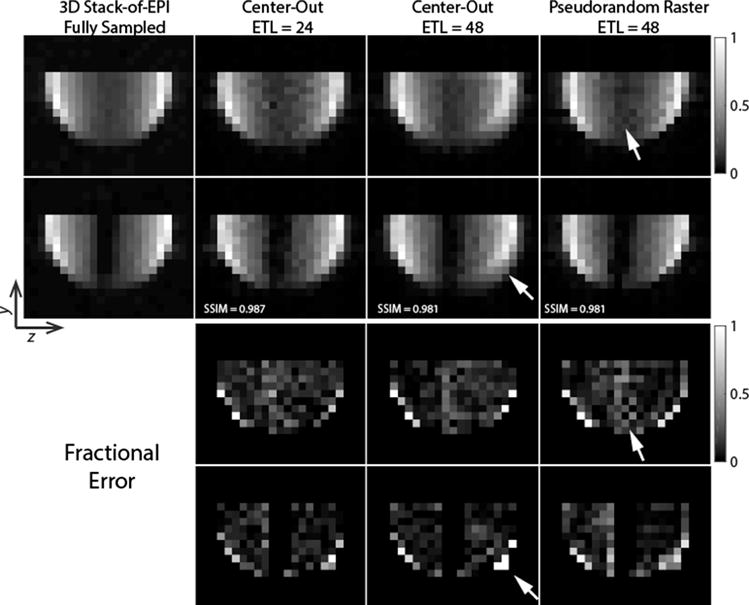
Thermal 13C ethylene glycol phantom data acquired using the three sampling patterns described in this work. Data were acquired with a sagittal orientation but have been reformatted axially to highlight the artifacts arising from the different sampling schemes. Two slices from the volume are shown, with the second containing a water filled syringe used to provide negative space at the center of the object. While SAKE can reconstruct the data from all three approaches, the center-out ETL = 24 acquisition provides a beneficial tradeoff between deleterious blurring (highlighted in the center-out ETL = 48) and reduced signal loss at the center of the object (highlighted in the pseudorandom raster).
The results from the healthy volunteer study showing the total signal (sum through time) for each metabolite can be seen in Fig. 7. For this study, the pyruvate injection began 55 s after the sample was dissolved, with a 45.1% back-calculated polarization. While there is no fully sampled dataset for comparison, there is good spatial agreement between the 1H anatomy and 13C data acquired with the R = 4, center-out ETL = 24 sampling pattern. Strong pyruvate signal is seen in the vasculature, kidneys, and heart, but the cardiac data lacks well-defined structure because cardiac gating was not employed. Lactate production is visible in the kidneys and other organs, while conversion to alanine is seen in smooth muscle and skeletal muscle close to the anterior array. Spectra acquired after imaging showed a center frequency offset of −3.7 Hz, resulting in minimal blurring due to a bulk receiver offset.
Fig. 7.
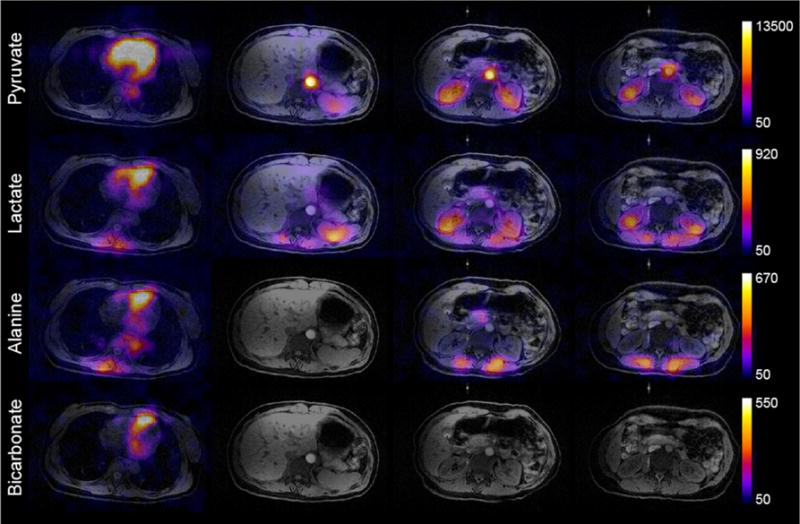
Area under the curve (sum through time) images demonstrate pyruvate uptake and metabolism in the heart and throughout the abdomen. Four representative slices (from the heart to the kidneys) within the active volume of the 13C abdominal array are shown. 13C data have been zero-filled fourfold for display. Colorbar scale is in arbitrary units.
4. Discussion
In this work, we explored the utility of calibrationless parallel imaging for hyperpolarized 13C imaging over a range of undersampling factors and sampling patterns. Based on the numerical simulations and phantom studies shown here, the best sampling pattern will be determined by the expected T2* and B0 inhomogeneity across the volume of interest. For well-shimmed applications, the center-out sampling pattern can potentially provide greater acceleration and a shorter TE. In these cases, the center-out, ETL of 24 sampling pattern can provide a beneficial tradeoff between reconstruction fidelity, PSF response and sensitivity to off-resonance, albeit with a time-savings of R/2 because of the reduced ETL. Care must be taken to avoid an extended readout in the presence of field inhomogeneity, as off-resonance will manifest as blurring for these radial-like sampling patterns [23,24]. Ultimately, the best sampling pattern will be determined by the T2* and B0 inhomogeneity expected throughout the volume.
The extent of the 13C transmitter and abdominal receive array in the sagittal dimension limited the spatial coverage in the volunteer study. While the encoding volume was 72 cm, signal was only received in the central 22 slices (33 cm). Nevertheless, these results demonstrate the utility of a volumetric imaging approach, as pyruvate uptake and metabolism through three enzymatic pathways was observed in multiple organs within a single injection. To our knowledge this is the first demonstration of pyruvate metabolism throughout the abdomen.
It is important to note that the performance of SAKE and other parallel imaging strategies depends on the orientation of the receive array with respect to the undersampled dimensions. Acceleration is only possible when there are variations in coil sensitivity, such as undersampling in the direction of the receive array, but not possible perpendicular to the array, where there is little-to-no variation in sensitivity between elements [25]. The performance of SAKE also depends on the choice of the window-normalized threshold, as shown above. While there was no fully sampled data for the volunteer study, the window-normalized threshold was chosen empirically. Choosing an optimal threshold in the absence of a fully sampled reference is beyond the scope of this project but will be investigated in future work.
In this approach, spectral-spatial excitation was used to selectively excite metabolites of interest. A bulk offset in the receive frequency can be readily corrected for by frequency demodulating the data. However, B0 field inhomogeneity throughout the volume of interest will impact the two sampling patterns differently. Spatially dependent blurring will occur in the center-out sampling pattern, whereas geometric distortion [26] will occur along the regular blip dimension for the pseudorandom raster. As shown in the numerical and phantom studies, reducing the ETL will mitigate artifacts by limiting the phase accrual due to this off-resonance, and in practice, the fourfold lower 13C gyromagnetic ratio also helps to reduce the sensitivity to off-resonance compared to 1H MRI. Incorporating a field map into the SAKE reconstruction will provide additional off-resonance correction, but is significantly more complex and will be explored in future work.
Blurring arising from T2*-related signal decay will ultimately limit the echo train length. Given that the in vivo T2* values are on the order of 20–100 ms at 3 T [27], readout durations on the order of 20–40 ms should be achievable without substantial resolution loss. While T2 has been reported to be substantially longer than T2* for 13C substrates [28,29], spin echo approaches [30,31] are problematic for hyperpolarized studies because miscalibration of the B1 power and inhomogeneity can lead to rapid RF decay from the refocusing pulses due to saturation at the edge of the coil [32].
Motion is also a concern with volumetric imaging. While 2D multislice approaches are more robust to motion, they will suffer from slice profile effects [33–35] due to unequal magnetization usage across the slice, confounding quantification when large flip angles are used or at the end of the imaging sequence. Acceleration will also be limited, as only one phase encode dimension can be undersampled [13]. As shown here, greater acceleration can be achieved with a 3D approach, and self-gating [36,37] can potentially be combined with the center-out acquisition to minimize motion-related artifacts.
An 8-channel bilateral coil was used for all numerical simulations and phantom studies, and center-out sampling patterns up to R = 6 were shown to yield reconstructed datasets with minimal error. Combining SAKE with compressed sensing [15,38] and the development of coils with more elements or better distributed geometries for 13C applications [39] may further improve image quality or provide greater acceleration, and will be explored in future work.
5. Conclusion
Parallel imaging approaches are crucial to increasing the scan coverage for human hyperpolarized 13C MR studies while minimizing the temporal resolution and RF requirements. The 3D EPI sequence developed in this manuscript provided a flexible acquisition that allows for arbitrary 2D undersampling patterns in the two phase-encode dimensions. Using a center-out sampling pattern, we demonstrated pyruvate uptake and metabolism in the heart and throughout the abdomen. This acquisition pattern yields a shorter TE and improved SNR while allowing a flexible tradeoff between time-savings, sensitivity to off-resonance, and reconstruction fidelity.
Supplementary Material
Acknowledgments
This work was supported by NIH grants R01EB017449, R01EB016741, R01CA183071, and P41EB013598.
Appendix A. Supplementary material
Supplementary data associated with this article can be found, in the online version, at https://doi.org/10.1016/j.jmr.2018.02.011.
References
- 1.Ardenkjær-Larsen JH, Fridlund B, Gram A, Hansson G, Hansson L, Lerche MH, Servin R, Thaning M, Golman K. Increase in signal-to-noise ratio of > 10,000 times in liquid-state NMR. Proc Natl Acad Sci USA. 2003;100:10158–10163. doi: 10.1073/pnas.1733835100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Albers MJ, Bok R, Chen AP, Cunningham CH, Zierhut ML, Zhang VY, Kohler SJ, Tropp J, Hurd RE, Yen YF, Nelson SJ, Vigneron DB, Kurhanewicz J. Hyperpolarized 13C lactate pyruvate, and alanine: noninvasive biomarkers for prostate cancer detection and grading. Cancer Res. 2008;68:8607–8615. doi: 10.1158/0008-5472.CAN-08-0749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Nelson SJ, Kurhanewicz J, Vigneron DB, Larson PEZ, Harzstark AL, Ferrone M, van Criekinge M, Chang JW, Bok R, Park I, Reed G, Carvajal L, Small EJ, Munster P, Weinberg VK, Ardenkjaer-Larsen JH, Chen AP, Hurd RE, Odegardstuen LI, Robb FJ, Tropp J, Murray JA. Metabolic imaging of patients with prostate cancer using hyperpolarized [1-13C]pyruvate. Sci Translat Med. 2013;5:198ra108. doi: 10.1126/scitranslmed.3006070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Cunningham CH, Lau JY, Chen AP, Geraghty BJ, Perks WJ, Roifman I, Wright GA, Connelly KA. Hyperpolarized 13C metabolic MRI of the human heart: initial experience. Circ Res. 2016 doi: 10.1161/CIRCRESAHA.116.309769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cunningham CH, Chen AP, Lustig M, Hargreaves BA, Lupo J, Xu D, Kurhanewicz J, Hurd RE, Pauly JM, Nelson SJ, Vigneron DB. Pulse sequence for dynamic volumetric imaging of hyperpolarized metabolic products. J Magn Reson. 2008;193:139–146. doi: 10.1016/j.jmr.2008.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cunningham CH, Chen AP, Albers MJ, Kurhanewicz J, Hurd RE, Yen YF, Pauly JM, Nelson SJ, Vigneron DB. Double spin-echo sequence for rapid spectroscopic imaging of hyperpolarized 13C. J Magn Reson. 2007;187:357–362. doi: 10.1016/j.jmr.2007.05.014. [DOI] [PubMed] [Google Scholar]
- 7.Reeder SB, Brittain JH, Grist TM, Yen YF. Least-squares chemical shift separation for 13C metabolic imaging. J Magn Reson Imag. 2007;26:1145–1152. doi: 10.1002/jmri.21089. [DOI] [PubMed] [Google Scholar]
- 8.Wiesinger F, Weidl E, Menzel MI, Janich MA, Khegai O, Glaser SJ, Haase A, Schwaiger M, Schulte RF. IDEAL spiral CSI for dynamic metabolic MR imaging of hyperpolarized [1-13C]pyruvate. Magn Reson Med. 2012;68:8–16. doi: 10.1002/mrm.23212. [DOI] [PubMed] [Google Scholar]
- 9.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42:952–962. [PubMed] [Google Scholar]
- 10.Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA) Magn Reson Med. 2002;47:1202–1210. doi: 10.1002/mrm.10171. [DOI] [PubMed] [Google Scholar]
- 11.Lustig M, Pauly JM. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magn Reson Med. 2010;64:457–471. doi: 10.1002/mrm.22428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Arunachalam A, Whitt D, Fish K, Giaquinto R, Piel J, Watkins R, Hancu I. Accelerated spectroscopic imaging of hyperpolarized C-13 pyruvate using SENSE parallel imaging. NMR Biomed. 2009;22:867–873. doi: 10.1002/nbm.1401. [DOI] [PubMed] [Google Scholar]
- 13.Feng Y, Gordon JW, Shin PJ, von Morze C, Lustig M, Larson PEZ, Ohliger MA, Carvajal L, Tropp J, Pauly JM, Vigneron DB. Development and testing of hyperpolarized 13C MR calibrationless parallel imaging. J Magn Reson. 2016;262:1–7. doi: 10.1016/j.jmr.2015.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Shin PJ, Larson PEZ, Ohliger MA, Elad M, Pauly JM, Vigneron DB, Lustig M. Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. Magn Reson Med. 2014;72:959–970. doi: 10.1002/mrm.24997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Geraghty BJ, Lau JYC, Chen AP, Cunningham CH. Accelerated 3D echo-planar imaging with compressed sensing for time-resolved hyperpolarized 13C studies. Magn Reson Med. 2016 doi: 10.1002/mrm.26125. https://doi.org/10.1002/mrm.26125. [DOI] [PubMed]
- 16.Vasanawala S, Murphy M, Alley M, Lai P, Keutzer K, Pauly J, Lustig M. Practical parallel imaging compressed sensing MRI: summary of two years of experience in accelerating body MRI of pediatric patients. 2011 IEEE International Symposium on Biomedical Imaging: From Nano to Macro. 2011:1039–1043. doi: 10.1109/ISBI.2011.5872579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ohliger MA, Larson PEZ, Bok RA, Shin P, Hu S, Tropp J, Robb F, Carvajal L, Nelson SJ, Kurhanewicz J, Vigneron DB. Combined parallel and partial Fourier MR reconstruction for accelerated 8-channel hyperpolarized carbon-13 in vivo magnetic resonance spectroscopic imaging (MRSI) J Magn Reson Imag. 2013;38 doi: 10.1002/jmri.23989. https://doi.org/10.1002/jmri.23989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhou W, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity, IEEE Trans. Image Process. 2004;13:600–612. doi: 10.1109/tip.2003.819861. [DOI] [PubMed] [Google Scholar]
- 19.Gordon JW, Vigneron DB, Larson PEZ. Development of a symmetric echo planar imaging framework for clinical translation of rapid dynamic hyperpolarized 13C imaging. Magn Reson Med. 2017;77:826–832. doi: 10.1002/mrm.26123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tropp J, Lupo JM, Chen A, Calderon P, McCune D, Grafendorfer T, Ozturk-Isik E, Larson PEZ, Hu S, Yen YF, Robb F, Bok R, Schulte R, Xu D, Hurd R, Vigneron D, Nelson S. Multi-channel metabolic imaging, with SENSE reconstruction, of hyperpolarized [1-13C]pyruvate in a live rat at 3.0 tesla on a clinical MR scanner. J Magn Reson. 2011;208:171–177. doi: 10.1016/j.jmr.2010.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kellman P, McVeigh ER. Image reconstruction in SNR units: a general method for SNR measurement. Magn Reson Med. 2005;54:1439–1447. doi: 10.1002/mrm.20713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Crane JC, Olson MP, Nelson SJ. SIVIC: open-source standards-based software for DICOM MR spectroscopy workflows. Int J Biomed Imag. 2013;2013:169526. doi: 10.1155/2013/169526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Noll DC, Pauly JM, Meyer CH, Nishimura DG, Macovskj A. Deblurring for non-2D fourier transform magnetic resonance imaging. Magn Reson Med. 1992;25:319–333. doi: 10.1002/mrm.1910250210. [DOI] [PubMed] [Google Scholar]
- 24.Smith TB, Nayak KS. MRI artifacts and correction strategies. Imag Med. 2010;2:445–457. [Google Scholar]
- 25.Deshmane A, Gulani V, Griswold MA, Seiberlich N. Parallel MR imaging. J Magn Reson Imag. 2012;36:55–72. doi: 10.1002/jmri.23639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jezzard P, Balaban RS. Correction for geometric distortion in echo planar images from B0 field variations. Magn Reson Med. 1995;34:65–73. doi: 10.1002/mrm.1910340111. [DOI] [PubMed] [Google Scholar]
- 27.Joe E, Lee H, Lee J, Yang S, Choi YS, Wang E, Song HT, Kim DH. An indirect method for in vivo T2 mapping of [1-13C]pyruvate using hyperpolarized 13C CSI. NMR Biomed. 2017 doi: 10.1002/nbm.3690. https://doi.org/10.1002/nbm.3690. [DOI] [PubMed]
- 28.Reed GD, von Morze C, Bok R, Koelsch BL, Van Criekinge M, Smith KJ, Shang H, Larson PE, Kurhanewicz J, Vigneron DB. High resolution 13C MRI with hyperpolarized urea: in vivo T2 mapping and 15N labeling effects. IEEE Trans Med Imag. 2014;33:362–371. doi: 10.1109/TMI.2013.2285120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kettunen MI, Hu DE, Witney TH, McLaughlin R, Gallagher FA, Bohndiek SE, Day SE, Brindle KM. Magnetization transfer measurements of exchange between hyperpolarized [1-13C]pyruvate and [1-13C]lactate in a murine lymphoma. Magn Reson Med. 2010;63:872–880. doi: 10.1002/mrm.22276. [DOI] [PubMed] [Google Scholar]
- 30.Busse RF, Hariharan H, Vu A, Brittain JH. Fast spin echo sequences with very long echo trains: design of variable refocusing flip angle schedules and generation of clinical T2 contrast. Magn Reson Med. 2006;55:1030–1037. doi: 10.1002/mrm.20863. [DOI] [PubMed] [Google Scholar]
- 31.Tamir JI, Uecker M, Chen W, Lai P, Alley MT, Vasanawala SS, Lustig M. T2 shuffling: sharp, multicontrast, volumetric fast spin-echo imaging. Magn Reson Med. 2017;77:180–195. doi: 10.1002/mrm.26102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Josan S, Yen YF, Hurd R, Pfefferbaum A, Spielman D, Mayer D. Application of double spin echo spiral chemical shift imaging to rapid metabolic mapping of hyperpolarized [1-13C]-pyruvate. J Magn Reson. 2011;209:332–336. doi: 10.1016/j.jmr.2011.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gordon JW, Milshteyn E, Marco-Rius I, Ohliger M, Vigneron DB, Larson PEZ. Mis-estimation and bias of hyperpolarized apparent diffusion coefficient measurements due to slice profile effects. Magn Reson Med. 2016 doi: 10.1002/mrm.26482. https://doi.org/10.1002/mrm.26482. [DOI] [PMC free article] [PubMed]
- 34.Miller GW, Altes TA, Brookeman JR, de Lange EE, Mugler JP., III Hyperpolarized 3He lung ventilation imaging with B 1-inhomogeneity correction in a single breath-hold scan. Magn Reson Mater Phys Biol Med. 2004;16:218–226. doi: 10.1007/s10334-003-0028-2. [DOI] [PubMed] [Google Scholar]
- 35.Deppe MH, Teh K, Parra-Robles J, Lee KJ, Wild JM. Slice profile effects in 2D slice-selective MRI of hyperpolarized nuclei. J Magn Reson. 2010;202:180–189. doi: 10.1016/j.jmr.2009.11.003. [DOI] [PubMed] [Google Scholar]
- 36.Brau ACS, Brittain JH. Generalized self-navigated motion detection technique: preliminary investigation in abdominal imaging. Magn Reson Med. 2006;55:263–270. doi: 10.1002/mrm.20785. [DOI] [PubMed] [Google Scholar]
- 37.Zaitsev M, Maclaren J, Herbst M. Motion artifacts in MRI: a complex problem with many partial solutions. J Magn Reson Imaging. 2015;42:887–901. doi: 10.1002/jmri.24850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wiens CN, Friesen-Waldner LJ, Wade TP, Sinclair KJ, McKenzie CA. Chemical shift encoded imaging of hyperpolarized 13C pyruvate. Magn Reson Med. 2015;74:1682–1689. doi: 10.1002/mrm.25532. [DOI] [PubMed] [Google Scholar]
- 39.Mareyam A, Carvajal L, Xu D, Gordon JW, Park I, Vigneron DB, Nelson SJ, Stockmann JP, Keil B, Wald LL. 31-Channel brain array for hyperpolarized 13C imaging at 3T. Proceedings of the 25th Annual Meeting of ISMRM; Honolulu, Hawaii. 2017; Abstract 1225. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


