Abstract
Background and aim
The practicability of computing dose calculation on cone beam CT (CBCT) has been widely investigated. In most clinical scenarios, the craniocaudal scanning length of CBCT is found to be inadequate for localization. This study aims to explore extended tomographic localization and adaptive dose calculation strategies using Hounsfield unit (HU) corrected CBCT image sets.
Materials and methods
Planning CT (pCT) images of the Rando phantom (T12-to-midthigh) were acquired with pelvic-protocol using Biograph CT-scanner. Similarly, half-fan CBCT were acquired with fixed parameters using Clinac2100C/D linear accelerator integrated with an on-board imager with 2-longitudinal positions of the table. For extended localization and dose calculation, two stitching strategies viz., one with “penumbral-overlap” (S1) and the other with “no-overlap” (S2) and a local HU-correction technique were performed using custom-developed MATLAB scripts. Fluence modulated treatment plans computed on pCT were mapped with stitched CBCT and the dosimetric analyses such as dose-profile comparison, 3D-gamma (γ) evaluation and dose-volume histogram (DVH) comparison were performed.
Results
Localizing scanning length of CBCT was extended by up to 15 cm and 16 cm in S1 and S2 strategies, respectively. Treatment plan mapping resulted in minor variations in the volumes of delineated structures and the beam centre co-ordinates. While the former showed maximum variations of −1.4% and −1.6%, the latter showed maximum of 1.4 mm and 2.7 mm differences in anteroposterior direction in S1 and S2 protocols, respectively. Dosimetric evaluations viz., dose profile and DVH comparisons were found to be in agreement with one another. In addition, γ-evaluation results showed superior pass-rates (≥98.5%) for both 3%/3 mm dose-difference (DD) and distance-to-agreement (DTA) and 2%/2 mm DD/DTA criteria with desirable dosimetric accuracy.
Conclusion
Cone beam tomographic stitching and local HU-correction strategies developed to facilitate extended localization and dose calculation enables routine adaptive re-planning while circumventing the need for repeated pCT.
Keywords: Cone beam computed tomography, Hounsfied unit, Rigid, Registration, Dose calculation, Adaptive radiotherapy
1. Background and aim
Linear accelerators integrated with kilovoltage (kV) on board imaging (OBI) system (sharing the same frame of reference) are widely used to facilitate online setup verification and correction during the course of radiotherapy.1, 2 The OBI system provides cone beam CT (CBCT) images of high spatial resolution with clinically appropriate field of view (FOV) for precise localization of bone and soft tissue boundaries.3, 4, 5 Several authors have reported the practicability of computing dose calculation on CBCT images while addressing HU inaccuracies with appropriate scatter rejection and HU correction strategies.6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 The off-centred detector panel arrangement in half-fan (HF) acquisition geometry of the OBI system limits the longitudinal coverage to a mere 16 cm with a maximum reconstruction diameter of 45 cm.17 However, in most clinical scenarios, the craniocaudal scanning length of CBCT is found to be inadequate for localizing the planning target volumes (PTV) with extended nodal coverage.18 In the present study, we propose to explore extended localization (EL) and a novel strategy for HU correction that is required for using CBCT in routine adaptive dose calculation (ADC) and evaluation.
2. Materials and methods
2.1. Image acquisition
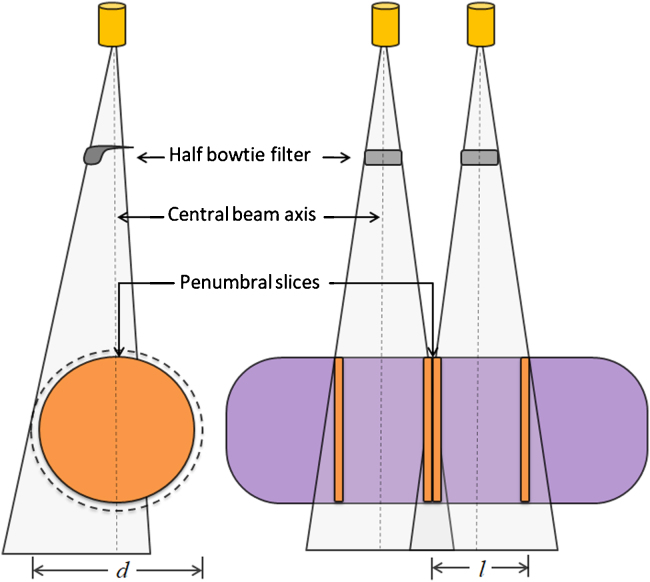
In our study, CBCT images of the Rando phantom (The Phantom Laboratory, NY) were acquired using OBI v1.6 system (Varian Medical Systems, Palo Alto, CA), with HF acquisition mode (body scan) with a half bow-tie filter (hBTF). In the HF acquisition geometry, the OBI system acquires 600–700 partially-covered projection images over a gantry rotation of 360° while the detector panel is off-centred to permit maximum FOV. To aid optimum baseline comparison with planning CT (pCT), CBCT images were acquired with fixed acquisition parameters viz., 125 kVp, 80 mA, 45 cm reconstruction diameter (d), 16 cm scanning length (l) and 2 mm slice thickness with 512 × 512 pixels resolution. Similarly, pCT images (T12 vertebrae to mid-thigh) were acquired with 120 kVp and 200 mA using Biograph True Point HD CT (Siemens Medical Systems, Germany). In our study, we developed two different stitching protocols to extend the longitudinal scanning length of CBCT, one with “penumbral overlap” and the other with “no overlap” (as illustrated in Fig. 1).
Fig. 1.
Schematic of HF-CBCT acquisition geometry without overlap (S2-protocol, n = 0) at penumbral region.
2.2. Stitching protocols
In order to overcome the HU difference at penumbral regions of CBCT, two consecutive HF-CBCT images were acquired with penumbral overlap (n) in the first strategy (S1), one at the isocentre, (i.e. at the first cone beam centre) where the couch longitudinal ‘Z’ is considered as ‘zero’ and the other with a couch shift “Z ± Δ” (where Δ = l–n). In the second strategy (S2), straightforward image stitching was performed without penumbral overlap (n = 0) in which Δ = l. In both cases, acquisition led to two distinct sets of DICOM images with unique identifiers (UIDs) viz., StudyInstanceUID, SeriesInstanceUID and FrameOfReferenceUID and respective TableTopLongitudinalPosition (TTLP), InstanceNumber (IN) and ImagePositionPatient (IPP), which uniquely identify every entity in the DICOM image. In our study, we developed a DICOM handling software using MATLAB scripts (MathWorks Inc., Natick, MA) for tomographic image stitching. The custom-developed stitching software can read the DICOM header of each series and identify the overlapping slices using corresponding TTLP and IN at the time of acquisition. Further, it performs HU averaging at the overlapping slices and rewrites the resultant series with the same UIDs.
2.3. Local HU correction
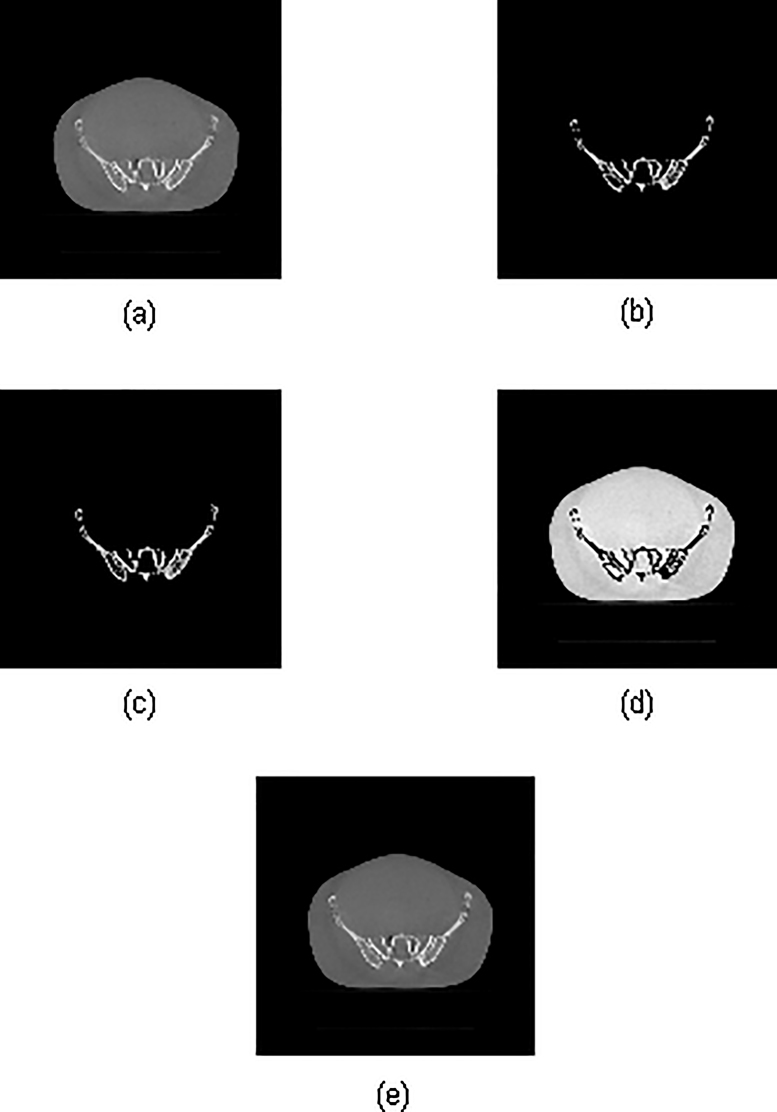
Accumulation of increased photon scatter in the flat-panel detector due to large cone angles in CBCT acquisition geometry leads to an increase in the HU values in reconstructed images. In this study, it was proposed to explore a new approach for local HU (HUL) correction in regions of high densities16, 19 using custom-developed MATLAB scripts. The purpose of this HUL technique was to perform accurate dose calculation on stitched CBCT (sCBCT) for use in routine adaptive radiotherapy (ART). Prior to performing HUL on the sCBCT, HU–electron density (eD) conversion calibration curves are generated for both reference pCT and CBCT using CATPhan (The Phantom Laboratory, NY) with fixed acquisition parameters. From these HU–eD calibration curves, the threshold HU is selected as the value beyond which the difference in HU is greater than 80. Furthermore, a correction co-efficient is calculated using known parameters viz., RescaleSlope, RescaleIntercept and HU difference for the constant eD values. The three-step correction strategy, illustrated in Fig. 2, first generates two distinct data sets viz., one with selected voxels of interest (VOI) having HU values greater than the set threshold corresponding to high-density regions (Fig. 2b) and the other with remaining voxels of original data set (Fig. 2d). A voxel-by-voxel HU correction is performed on the VOI of the former data set (Fig. 2c) and then fused with the latter and a new DICOM series that can be used for dose calculation is generated (Fig. 2e).
Fig. 2.
Local HU correction procedure using MATLAB: (a) original data set, (b) a new series with high density regions which fall beyond the set threshold HU. (c) HU corrected data set, (d) original data set with remaining voxels corresponding to low density regions. (e) HU corrected new DICOM series used for dose calculation comprises of data set (c) and (d).
2.4. Dose calculation
In our study, intensity modulated radiotherapy (IMRT) and volumetric modulated arc therapy (VMAT) treatment plans were generated on the pCT. To simulate actual workflow of CBCT-based ART procedure, setup verification CBCT images of the Rando phantom were acquired as stated above in the stitching protocols prior to the execution of treatment plans. Re-planning was performed with respect to the newly adapted contours that were mapped from pCT onto the respective sCBCT through rigid registration. Dosimetric analysis viz., dose profile comparison, 3D gamma evaluation and dose volume histogram (DVH) comparisons of IMRT and VMAT treatment plans generated on pCT and sCBCT were performed. For all the plans, the 3D gamma (γ) analysis was performed with both the standard γ criteria of 3% dose difference (DD) and 3 mm distance to agreement (DTA)20 and a stringent criteria of 2%/2 mm DD and DTA using commercial software VeriSoft (v6.2, PTW, Germany). Moreover, the dosimetric verification of treatment plans computed on pCT and independently re-optimized and re-calculated on both sCBCT image sets were analyzed using Octavius 1500 ion chamber array with 4D modular phantom (PTW, Germany).
3. Results
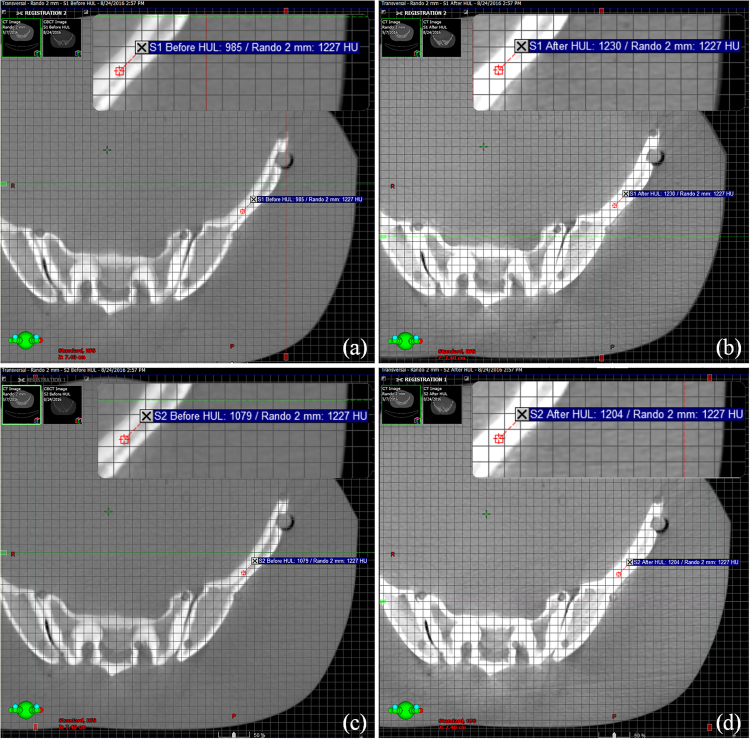
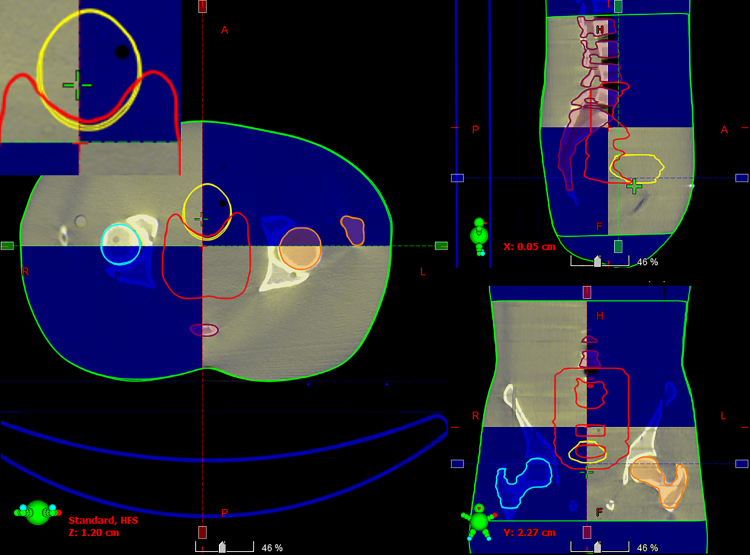
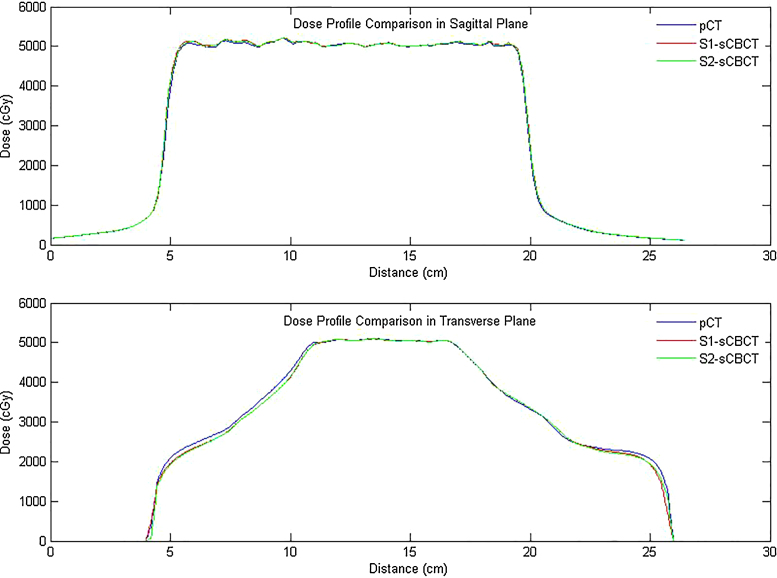
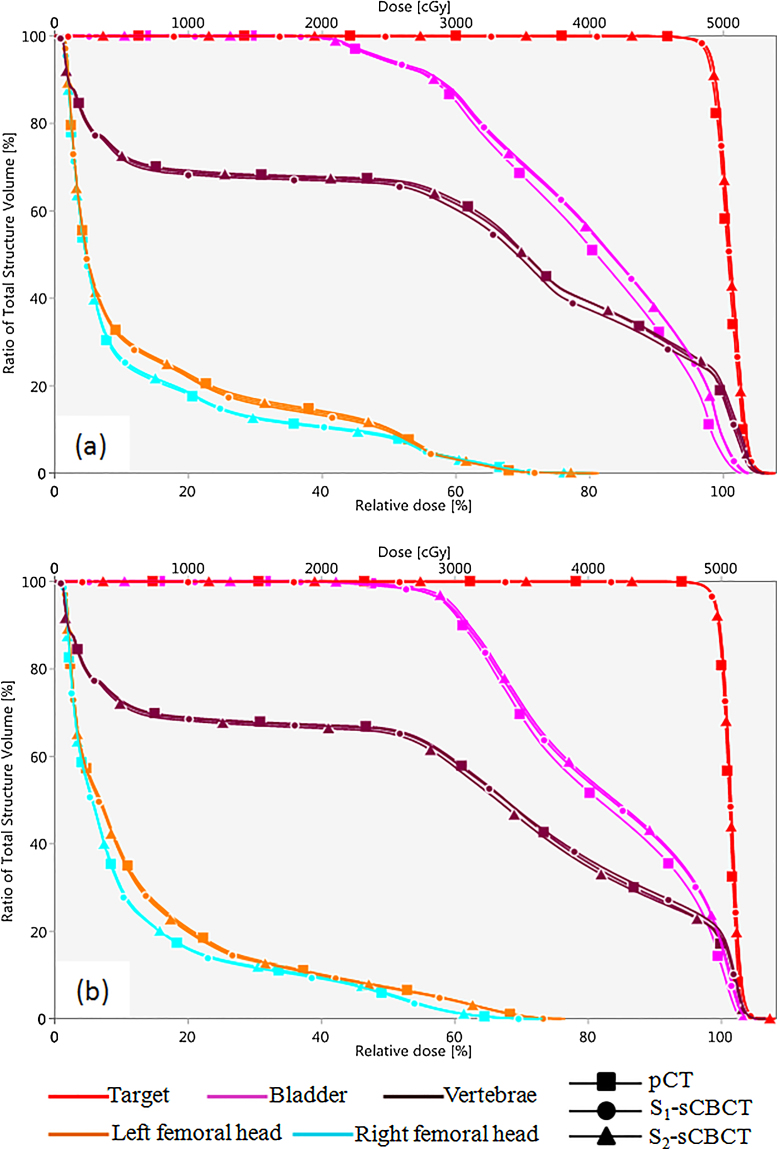
Two stitching strategies (S1 and S2) with consecutive HF-CBCT acquisitions resulting in maximum craniocaudal scanning lengths of 32 cm and 31 cm, respectively, were implemented. The scanning length of CBCT was extended by up to 16 cm in S2 when the couch shift ‘Δ’ was equal to ‘l’ of single HF-CBCT acquisition geometry. On the other hand, S1 protocol resulted in an extended scan length of 15 cm with an overlap (n = 1 cm) as previously described. Slice thickness and absolute scanning length of sCBCT from both strategies (S1 and S2) were found to be in good agreement with the expected value. HU values at a high density region before and after HUL correction for both image sets resulting from S1 and S2 in comparison with reference pCT are illustrated in Fig. 3. The HU values of sCBCT image sets presented in Fig. 3 obtained through rigid registration with pCT, showed a difference of ≥20% in the absence of HU correction. However, the HUL correction proposed in the present study is advantageous in reducing the HU difference down to ≤3%. Fig. 4 shows the rigid registration between pCT and S1–CBCT. The structures mapped from pCT to sCBCT resulted in minor variations in the volumes of all the five structures as listed in Table 1. The maximum variation of −1.6% was observed in the right femoral head corresponding to an absolute difference of 1.7 cc. The treatment plans computed on the pCT when mapped onto the registered sCBCT image sets resulted in small disparity in beam centre co-ordinates (X, Y, Z), as seen in Table 2. The maximum differences of 1.4 mm and 2.7 mm were observed in the anteroposterior direction of sCBCT images of S1 and S2, respectively. The possible causes of this variation could be due to a minor mismatch in registration, small differences in reconstruction diameter and the position of the centre of mass of target volume. The dosimetric analysis showed that the dose calculations of pCT-based IMRT and VMAT plans were in agreement with those computed on sCBCT for both strategies. Fig. 5 shows the dose profile comparison across the axial and sagittal plane of pCT and sCBCT image sets. The maximum difference in dose profile was found to be ≤−1.5%. However, both strategies showed a good match in the entire range of dose profile with respect to pCT, especially in the regions where the stitching was performed with and without penumbral overlap. Table 3 shows relative doses extracted from cumulative DVH data of IMRT and VMAT treatment plans computed on pCT and mapped on to the sCBCT (S1 and S2) image sets. In both cases, sCBCT-based dose calculation showed marginal difference in dose values for all the structures especially in the bladder (Table 3) for the entire range of dose in cumulative plan comparison DVH as illustrated in Fig. 6a and b. However, the dose calculation computed on sCBCT (S1 and S2) image sets demonstrated in the present study showed a good overall agreement with pCT. Further, the 3D γ-evaluation technique used in the study would serve as an effective quality assurance tool for comparing the pCT and sCBCT based treatment plans with high spatial resolution dose distributions generated in the Eclipse TPS. Fig. 7 shows the local gamma evaluation map of dual arc VMAT dose distribution computed on pCT and S1–CBCT image set for 2%/2 mm DD and DTA criteria. For both strategies, it was observed that the 3D γ-evaluation results showed superior pass rate with more than 98.5% dose pixels passing the standard and stringent γ-criteria as seen in Table 4 and found to be identical, which proves the potential of sCBCT image sets for use in ADC. Moreover, the quality assurance (QA) results of dosimetric plan verification performed using Octavius 1500 ion chamber array are reported in Table 5.
Fig. 3.
An example illustrating HU values at a high density region of registered image sets before and after HUL correction. (a) pCT versus S1–CBCT before correction, (b) pCT versus S1–CBCT after correction, (c) pCT versus S2–CBCT before correction, (d) pCT versus S2–CBCT after correction.
Fig. 4.
Rigid registration between pCT (shaded blue) and S1–CBCT showing optimal match with minor changes in the mapped structures.
Table 1.
Absolute and relative difference in contoured volumes mapped from reference pCT to sCBCT image sets.
| Contoured structures | Volume (cc) | Difference in sCBCT (cc/%) |
|
|---|---|---|---|
| S1 | S2 | ||
| Target | 440.3 | 1.5/−0.2 | 0.9/−0.1 |
| Bladder | 104.6 | 1.5/−1.4 | 1.4/−1.3 |
| Right femoral head | 105.2 | 0.7/−0.7 | 1.7/−1.6 |
| Left femoral head | 107.6 | 1.5/−1.4 | 1.3/−1.2 |
| Vertebrae | 354.7 | 2.2/−0.6 | 2.3/−0.03 |
Table 2.
Difference in beam centre co-ordinates (X, Y, Z) during plan transfer process.
| Image sets | Difference (mm) |
|
|---|---|---|
| IMRT | VMAT | |
| S1–CBCT (X, Y, Z) | (−0.1, 1.4, −1.2) | (−0.2, 1.1, −1.3) |
| S2–CBCT (X, Y, Z) | (−0.3, 2.7, −1.9) | (−0.3, 2.5, −2.0) |
Fig. 5.
Dose profile comparison between pCT and sCBCT (S1 & S2) image sets across the axial and sagittal planes.
Table 3.
Relative plan comparison DVH data of IMRT and VMAT treatment plans.
| Structure | IMRT |
VMAT |
||||
|---|---|---|---|---|---|---|
| pCT | S1–CBCT | S2–CBCT | pCT | S1–CBCT | S2–CBCT | |
| Target | ||||||
| V95% | 97.9 | 98.4 | 98.4 | 99.5 | 99.5 | 99.5 |
| V105% | 0.3 | 1.3 | 1.2 | 0.0 | 0.02 | 0.02 |
| Dmin% | 73.9 | 74.9 | 76.0 | 80.2 | 79.0 | 79.0 |
| Dmax% | 106.8 | 107.5 | 107.9 | 105.0 | 105.7 | 105.5 |
| Dmean% | 100.2 | 100.9 | 100.8 | 101.0 | 101.3 | 101.3 |
| Bladder | ||||||
| V35 Gy | 67.7 | 70.1 | 70.6 | 69.2 | 71.1 | 72.1 |
| V45 Gy | 33.0 | 37.2 | 37.6 | 38.8 | 41.5 | 42.1 |
| Dmin% | 33.7 | 31.6 | 33.6 | 38.3 | 35.4 | 37.8 |
| Dmax% | 102.6 | 103.7 | 103.9 | 104.5 | 105.4 | 105.5 |
| Dmean% | 78.7 | 80.2 | 80.5 | 81.4 | 82.4 | 82.8 |
| Femoral head (left) | ||||||
| V30 Gy | 3.5 | 3.1 | 3.3 | 4.2 | 4.2 | 4.0 |
| Dmin% | 1.3 | 1.3 | 1.3 | 1.2 | 1.3 | 1.3 |
| Dmax% | 81.5 | 81.3 | 80.7 | 76.0 | 76.6 | 76.2 |
| Dmean% | 14.0 | 13.9 | 13.6 | 13.7 | 13.5 | 13.4 |
| Femoral head (right) | ||||||
| V30 Gy | 3.4 | 3.3 | 3.1 | 1.3 | 1.4 | 1.5 |
| Dmin% | 1.3 | 1.3 | 1.3 | 1.2 | 1.2 | 1.2 |
| Dmax% | 79.3 | 79.6 | 80.5 | 72.9 | 73.2 | 73.5 |
| Dmean% | 12.1 | 12.1 | 12.2 | 11.7 | 11.6 | 11.8 |
| Vertebrae | ||||||
| Dmin% | 1.1 | 0.5 | 0.1 | 1.0 | 0.5 | 0.1 |
| Dmax% | 106.2 | 106.8 | 106.3 | 104.9 | 106.7 | 107.1 |
| Dmean% | 59.0 | 58.9 | 57.8 | 57.1 | 57.4 | 56.4 |
Fig. 6.
DVH comparison between pCT and sCBCT (S1 & S2) image sets. (a) 5-field IMRT plan and (b) dual arc VMAT plan.
Fig. 7.
3D gamma evaluation of VMAT plan using VeriSoft software: (a) dose distribution on pCT, (b) dose distribution on S1–CBCT, (c) 3D γ-evaluation results and (d) planar γ-distribution on isocentre plane.
Table 4.
3D γ-evaluation results of IMRT and VMAT treatment plans.
| γ-Criteria | Technique | Pass rate (%) |
|||
|---|---|---|---|---|---|
| IMRT |
VMAT |
||||
| S1–CBCT | S2–CBCT | S1–CBCT | S2–CBCT | ||
| 3%/3 mm DD/DTA | Global | 99.9 | 100.0 | 100.0 | 99.9 |
| Local | 99.8 | 99.8 | 99.8 | 99.7 | |
| 2%/2 mm DD/DTA | Global | 99.4 | 99.3 | 99.4 | 99.3 |
| Local | 98.9 | 98.8 | 99.1 | 99.0 | |
Table 5.
Dosimetric results of treatment plans computed on pCT and sCBCT image sets using Octavius 1500 ion chamber array.
| Image Sets | Central axis dose difference (%) |
γ-Evaluation pass rate (%) |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| IMRT | VMAT | IMRT |
VMAT |
|||||||
| 3% DD/3 mm DTA |
2% DD/2 mm DTA |
3% DD/3 mm DTA |
2% DD/2 mm DTA |
|||||||
| Local | Global | Local | Global | Local | Global | Local | Global | |||
| pCT | −1.12 | 0.27 | 88.6 | 96.5 | 69.6 | 87.1 | 95.1 | 99.2 | 80.3 | 93.4 |
| S1-CBCT | −1.01 | 0.43 | 89.5 | 96.8 | 71.6 | 88.2 | 93.8 | 99.2 | 78.8 | 93.8 |
| S2-CBCT | −1.16 | 0.60 | 89.9 | 96.9 | 71.7 | 88.2 | 94.5 | 99.2 | 79.4 | 93.9 |
4. Discussion
In this study, we successfully demonstrated that it is possible to perform extended localization and adaptive dose calculation using HU-corrected CBCT. Though a similar EL study primarily addressing the longitudinal coverage of CBCT has been reported by Zheng et al., it does not deal with HU correction or the potential use of EL for adaptive dose calculation.18 In the present study, we aimed to demonstrate the tomographic stitching protocols along with HU correction strategy with an intention to overcome the limitation encountered in ADC using CBCT. HF-CBCT geometry with hBTF was chosen as the standard acquisition protocol irrespective of the imaging site to ensure clinically appropriate reconstruction FOV (45 cm). On the other hand, in order to minimize the imaging dose, site specific acquisition and low dose imaging protocols must be followed for localization and setup verification except at specific intervals when CBCT-based ADC is desired for patients. Additionally, incorporation of automatic exposure control in the OBI system as recommended by Alaei and Spezi21 while acquiring CBCT could also be considered to reduce the imaging dose. Moreover, implementation of volumetric imaging dose reconstruction capabilities in TPS may allow the physician to assess the total dose delivered during the course that could help change or modify the fractionation regimen.
While the transfer of delineated volumes to CBCT from reference pCT through rigid registration resulted in minor variations for the Anthropomorphic phantom, major variations can be expected in the case of patient studies due to possible anatomical changes, setup error, misregistration errors and other influencing factors, such as couch sag, immobilization, intra-fraction organ displacement and respiratory movements. Hence, it is advisable to carefully validate the patient contours mapped from the reference standard when sCBCT-based ADC is desired. On the other hand, HU validation, eD calibration and correction for inaccurate HU values should also be performed prior to ADC. In our study, the marginal difference in dose profile and DVH (Fig. 5, Fig. 6) could be due to the allowed small variation in original HU values of large volume of low density regions, minor change in beam centre co-ordinates and reduction in structure volume resulting from contour mapping. This can be further improved by reducing the HU threshold down to the intermediate density when performing HUL and fine-tuning the structures mapped from pCT image set. Although Son et al., state that the γ-evaluation results of >95% pass rate with 3%/3 mm DD/DTA criteria is considered to be acceptable in quality assurance of dose matrix comparison,20 in the present study, sCBCT yielded superior pass rates of >98.5% even with stringent γ-criteria of 2%/2 mm DD/DTA (Table 4), confirming the potential of sCBCT for ART. Further, the sCBCT helps in avoiding repeated pCT during the treatment course and facilitates quick assessment of delivered dose. While this could reduce the patient dose, it can also help increase machine throughput and minimize the clinical time spent by physicians and physicists on each ART procedure. Furthermore, sCBCT-based ADC would enable quick re-planning and re-optimization strategy with desirable dosimetric accuracy. For CBCT-based ADC, it is recommended to compute treatment plans with asymmetric field aperture for PTV. For example, placing the beam centre at least about 6 cm from the superior border of PTV (>16 cm but less than ≤24 cm), while computing the treatment plan, provides the first HF-CBCT image set with an additional craniocaudal coverage of 2 cm since the present OBI system symmetrically fixes the collimator blade (i.e., Y1 and Y2) with respect to the planned beam centre. Hence, use of off-centred field placement, while missing the inferior portion of the PTV in the first acquisition, will be covered by the subsequent acquisition. While the first acquisition could be used for online setup correction, the sCBCT generated after the second acquisition will be useful for ADC. However, in the worst case scenario, where the length of the PTV is greater than 24 cm, it would be difficult to compute the treatment plan with the above said geometry. Hence, for such cases, the treatment plan can be computed with optimum field apertures, irrespective of the cone beam centre. During the online setup correction, it is suggested to position the patient with an intentional longitudinal shift (δ) with respect to the isocentre so as to attain the above recommended acquisition geometry. Eventually, the second acquisition employed to facilitate EL and ADC should have a couch longitudinal shift ‘Δ’ with respect to the centre of the first cone beam, irrespective of the isocentre. Care must be taken to ensure that the actual couch shift applied after CBCT registration is δ ± Δ (where ± indicates the direction of shift). The tomographic stitching techniques and HU correction strategy demonstrated in this study will enable CBCT-based ART for IMRT and VMAT delivery without the requirement of additional ART software and can be easily put into practice in radiotherapy clinics equipped with linear accelerators having integrated OBI facility.
5. Conclusion
Cone beam tomographic image stitching and local HU-correction strategies were developed in our study to facilitate extended localization of target and normal tissues and accurate dose calculation. This enables routine adaptive re-planning and re-optimization of treatment plans based on setup verification CBCT while circumventing the need for repeated planning CT that is a requisite for conventional adaptive radiotherapy.
Financial disclosure statement
None declared.
Conflict of interest
None declared.
Acknowledgement
I would like to thank Mr. Ebenezer Suman Babu, Lecturer in Radiation Physics, Department of Radiation Therapy, Christian Medical College, Vellore, India, for his help, suggestions and valuable discussions throughout this study.
Contributor Information
K Mohamathu Rafic, Email: raficmphy@gmail.com, raficmphy@cmcvellore.ac.in.
S Amalan, Email: amalans90@gmail.com.
B S Timothy Peace, Email: tim_peace@yahoo.co.in.
B Paul Ravindran, Email: paul@cmcvellore.ac.in.
References
- 1.Jaffray D.A., Drake D.G., Moreau M., Martinez A.A., Wong J.W. Int J Radiat Oncol Biol Phys. 1999;45:773. doi: 10.1016/s0360-3016(99)00118-2. [DOI] [PubMed] [Google Scholar]
- 2.Oelfke U., Tücking T., Nill S. Med Dosim. 2006;31:62. doi: 10.1016/j.meddos.2005.12.008. [DOI] [PubMed] [Google Scholar]
- 3.Jaffray D.A., Siewerdsen J.H. Med Phys. 2000;27:1311. doi: 10.1118/1.599009. [DOI] [PubMed] [Google Scholar]
- 4.Groh B.A., Siewerdsen J.H., Drake D.G., Wong J.W., Jaffray D.A. Med Phys. 2002;29:967. doi: 10.1118/1.1477234. [DOI] [PubMed] [Google Scholar]
- 5.Jaffray D.A., Siewerdsen J.H., Wong J.W., Martinez A.A. Int J Radiat Oncol Biol Phys. 2002;53:1337. doi: 10.1016/s0360-3016(02)02884-5. [DOI] [PubMed] [Google Scholar]
- 6.Paliwal B., Tewatia D., Orton N., Tome W., Basavatia A. Med Phys. 2006;33:2029. [Google Scholar]
- 7.Ding G.X., Duggan D.M., Coffey C.W. Radiother Oncol. 2007;85:116. doi: 10.1016/j.radonc.2007.06.015. [DOI] [PubMed] [Google Scholar]
- 8.Fu W., Yang Y., Yue N., Heron D., Huq M. Med Phys. 2007;34:2368. [Google Scholar]
- 9.van Zijtveld M., Dirkx M., Heijmen B. Radiother Oncol. 2007;85:195. doi: 10.1016/j.radonc.2007.08.010. [DOI] [PubMed] [Google Scholar]
- 10.Juh R., Back G., Ahn S., Kim J., Suh T. Med Phys. 2008;35:2647. [Google Scholar]
- 11.Richter A., Hu Q., Steglich D. Radiother Oncol. 2008;3:42. doi: 10.1186/1748-717X-3-42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hatton J., McCurdy B., Greer P.B. Phys Med Biol. 2009;54:N329. doi: 10.1088/0031-9155/54/15/N01. [DOI] [PubMed] [Google Scholar]
- 13.Poludniowski G.G., Evans P.M., Webb S. Int J Radiat Oncol. 2012;84:e109. doi: 10.1016/j.ijrobp.2012.02.019. [DOI] [PubMed] [Google Scholar]
- 14.Yoo S., Yin F.-F. Int J Radiat Oncol. 2006;66:1553. doi: 10.1016/j.ijrobp.2006.08.031. [DOI] [PubMed] [Google Scholar]
- 15.Dong H., Hammoud R., Li S., Chen Q., Guan H. Med Phys. 2006;33:2049. [Google Scholar]
- 16.Rafic M., Ravindran P. J Cancer Res Ther. 2015;11:690. doi: 10.4103/0973-1482.146087. [DOI] [PubMed] [Google Scholar]
- 17.Fave X., Yang J., Carvalho L. Med Phys. 2014;41:061906. doi: 10.1118/1.4875682. [DOI] [PubMed] [Google Scholar]
- 18.Zheng D., Lu J., Jefferson A. J Appl Clin Med Phys. 2012;13 doi: 10.1120/jacmp.v13i4.3796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Almatani T., Hugtenburg R.P., Lewis R.D., Barley S.E., Edwards M.A. Br J Radiol. 2016;89:20160443. doi: 10.1259/bjr.20160443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Son J., Baek T., Lee B. Radiol Oncol. 2015;49:307. doi: 10.1515/raon-2015-0021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Alaei P., Spezi E. Phys Med. 2015;31:647. doi: 10.1016/j.ejmp.2015.06.003. [DOI] [PubMed] [Google Scholar]