Single-shot dual-wavelength interferometric microscopy

Abstract

Interferometric microscopy (IM) can provide complex field information of the biological samples with high spatial and temporal resolution with virtually no photodamage. Measuring wavelength-dependent information in particular has a wide range of applications from cell and tissue refractometry to the cellular biophysical measurements. IM measurements at multiple wavelengths are typically associated with a loss in temporal resolution, field of view, stability, sensitivity, and may involve using expensive equipment such as tunable filters or spatial light modulators. Here, we present a novel and simple design for an interferometric microscope that provides single-shot off-axis interferometric measurements at two wavelengths by encoding the two spectral images at two orthogonal spatial frequencies that allows clean separation of information in the Fourier space with no resolution loss. We demonstrated accurate simultaneous quantification of polystyrene bead refractive indices at two wavelengths.

1. Introduction

Interferometric microscopy (IM) techniques provides complex field information for a wide variety of samples [1,2]. The label-free nature of these techniques makes them particularly suitable for studying biological samples in a minimally invasive way for an extended period of time. IM enables measurement of the quantitative phase over the field of view with high resolution in space and time. The measured phase represents the cumulative effect of the morphology and the refractive index (RI) distribution of the specimen in distorting the transmitted wavefront. This phase delay, in the case of eukaryotic cells, has been shown to be linked to the cellular dry mass [3], which provides a powerful tool for studying cellular processes such as cell division and growth over days or weeks [4]. When either of RI or morphology of the sample is known, one can measure the other without ambiguity. For instance, in the case of red blood cells (RBCs) in healthy individuals where cellular RI can be approximated with good precision, IM provides an accurate measurement of the morphology with nanometer precision [5]. Monitoring this morphology with sufficient temporal resolution enables measurement of the membrane fluctuations of RBCs that in turn provides a window to the cellular biomechanics [6,7]. Optical measurements of the biomechanical properties of RBCs have been used in studying the pathology of the diseases such as malaria [7] and sickle cell disease [8]. Similarly, a priori information about the sample morphology enables direct measurement of the refractive index from the quantitative phase information.

Early during the development of the interferometric techniques, it was realized that measurement of the phase delay at multiple wavelength can be a useful tool in studying cell and tissue refractometry or measuring concentrations of cellular proteins [9–11]. Additionally, IM measurements at a continuum spectrum in the visible range have been shown to provide tomographic measurement of the subcellular structures within the hematopoietic stem cells, while enabling an increase in the speed of the tomographic interferometric microscopy by orders of magnitude [12]. The sequential IM measurements of multiple wavelengths is either done through filter wheels [11], spatial light modulators [13,14], or tunable filters in combination with supercontinuum sources [15–17]. In the first case, the mechanical switching of the wavelength, sacrifices the temporal resolution, necessary for measurement of fast dynamics such as RBC fluctuation. In the case of acousto-optic tunable filters (AOTFs) or spatial light modulators, while they exhibit faster response time, the instrument cost is significantly higher. Color cameras have been suggested as an alternate way of simultaneous measurement of the phase information for multiple colors [18,19]. Because of the spectral ranges of the filters in the camera sensor are fixed by the manufacturer, color cameras compromise sensitivity of the IM measurements and reduce the flexibility in design for various applications. Stability of the interference is another factor that determines the sensitivity of the measurements and is maximized when reference and sample arms travel side by side [5,20]. Several designs for simultaneous measurements of two wavelengths has been suggested in non-common-path designs where the two colors travel different paths before interfering at the image plane limiting stability and sensitivity [9,21]. Two additional designs have been suggested to enable single-shot common-path measurements of multiple wavelengths by creating various degrees of tilting for different colors in an off-axis geometry [22,23]. Despite the stability advantage provided by common-path design, both designs have limitations in terms of the proximity of the two wavelengths or a compromise in the spatial resolution to avoid overlap of the information between two colors in the frequency domain. In this paper, we propose a new design to enable single-shot measurement of the complex field information without a decrease in the field of view, temporal or spatial resolution, or the measurement stability by using a monochrome camera. Next, we delineate the experimental setup and data analysis, and validate our instrument by measuring the dispersion of the polystyrene beads in the visible spectrum.

2. Experimental setup

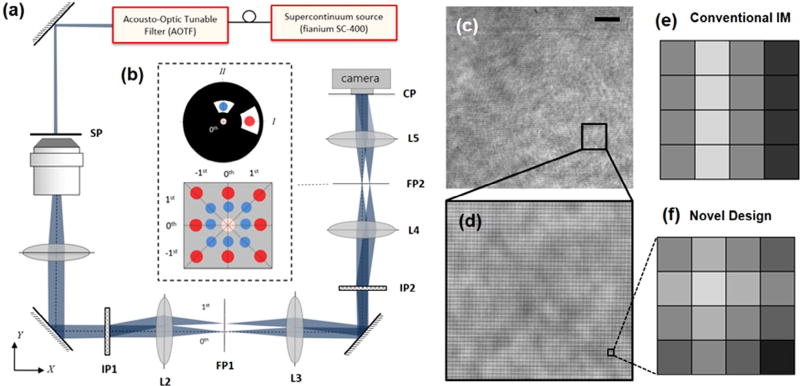
Fig. 1(a) shows the experimental setup of a dual-wavelength interferometric microscope that has been adapted from a diffraction phase microscope design [5]. The output of a super-continuum illumination source (Fianium WL SC 400-8) is used as an input to an acousto-optic tunable filter that allows for selection of up to 16 simultaneous band for illumination of the specimen. An objective (40×, NA = 0.65), in combination with a tube lens, is used to carry the sample information to the first image plane (IP1) where a diffraction grating (165 lines/mm) makes multiple copies of the beam in the y-direction. Using a 4-f imaging system, this image plane (IP1) is conjugated to the second image plane where a second diffraction grating is used to diffract the beam in the z-direction. The resulting diffraction pattern at the second Fourier plane is shown in Fig. 1(b). The non-diffracted beam of both colors overlaps at the center while the +1 and −1 beams have different distances from the optical axis based on the illumination wavelength. This distance in the physical Fourier plane could be simply calculated as f λ/Λ where Λ is the period of the grating, f is the focal length of the lens (L4), and λ is the wavelength of the corresponding beam. A physical filter is used in the Fourier plane to selectively pass only one color as the sample beam in each of the orthogonal directions. At the center, a pinhole (10 µm) is used to spatially filter the non-diffracted beam to create a reference for the interferometric measurement. Therefore, at the camera plane, the sample beams (each at different color) interfere with the corresponding reference beams such that two orthogonal fringe patterns overlap to form a non-conventional interference grid as shown in Fig. 1(c) and (d). The final interference pattern carries the information regarding the complex field sample information at both of the illumination wavelengths.

Fig. 1.

(a) Configuration of the experimental setup for single-shot dual-wavelength interferometric measurements. (b) The diffraction pattern caused by two orthogonally aligned gratings illuminated by two different wavelengths at the second Fourier plane (FP2). (c), (d) the non-conventional interference grid. (e), (f) fringe pattern at a single sample spot in conventional IM and novel designs, respectively. The scale bar is 10 µm.

3. Data analysis

Mathematically, the acquired interference pattern (I) shown in Fig. 1(c) can be described as,

$$I({\lambda }_1,{\lambda }_2)=I_0+\alpha ({\lambda }_1)\text{ cos}[\phi ({\lambda }_1)+{\mathit{\text{xq}}}_x]+\alpha ({\lambda }_2)\text{ cos}[\phi ({\lambda }_2)+{\mathit{\text{yq}}}_y]$$ (1)

where α and φ correspond to the amplitude and phase of the complex field of the sample, q_x and q_y are the fringe frequency determined by the diffraction angle of the two gratings in x and y directions, respectively, and I₀ is simply the sum of the intensity of the reference and sample beams. The Fourier transform of the fringe pattern can be written as,

$$I(k_x,k_y)=F\{I_0\}+F\{\alpha ({\lambda }_1)[\begin{array}{c}\hfill \text{cos}(\phi ({\lambda }_1))\text{ cos}({\mathit{\text{xq}}}_x)\hfill \\ \hfill -\text{sin}(\phi ({\lambda }_1))\text{ sin}({\mathit{\text{xq}}}_x)\hfill \end{array}\left]\right\}+F\{\alpha ({\lambda }_2)[\begin{array}{c}\hfill \text{cos}(\phi ({\lambda }_2))\text{ cos}({\mathit{\text{yq}}}_y)\hfill \\ \hfill -\text{sin}(\phi ({\lambda }_2))\text{ sin}({\mathit{\text{yq}}}_y)\hfill \end{array}\left]\right\}$$ (2)

Using the convolution theorem and applying the Fourier transform, we get

$$I(k_x,k_y)=F\{I_0\}+F\{\alpha ({\lambda }_1)\text{ exp}[\phi ({\lambda }_1)]\}\otimes \delta (k_x\pm q_x)+F\{\alpha ({\lambda }_2)\times \text{exp}[\phi ({\lambda }_2)]\}\otimes \delta (k_y\pm q_y)$$ (3)

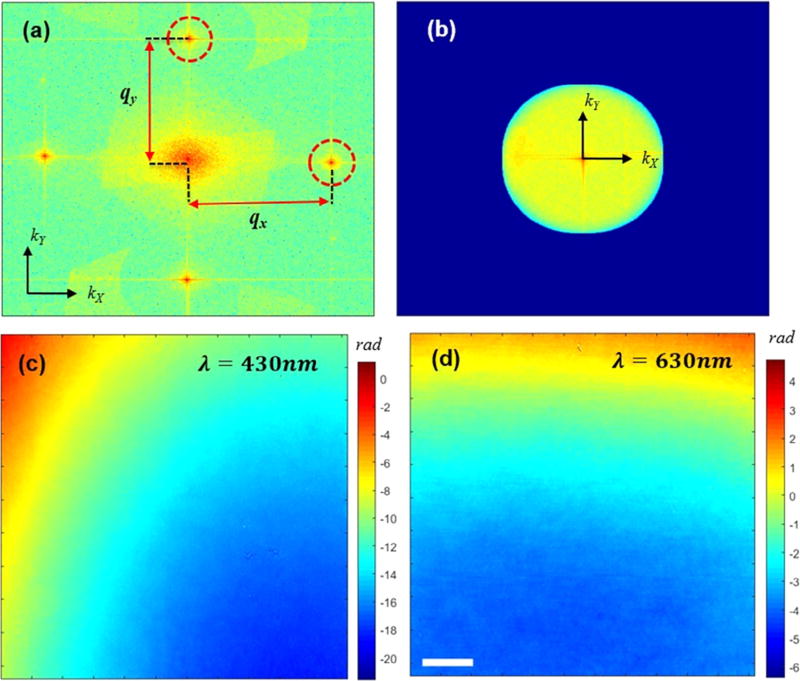
The Fourier transform of the phase shift for the first wavelength is shifted along the x-axis while the frequency information for the second wavelength is shifted along the y-axis. Fig. 2(a) shows the Fourier transform of sample-free interferogram where the shifted frequency of the sample can be identified in both k_x and k_y directions. The frequency information is subsequently cropped by a mask the size of which is determined by the numerical aperture of the imaging system. The masked information is then translated to the origin where applying inverse Fourier transform provides the complex field information for each of the two illumination colors. Fig. 2(c) and (d) show the measured phase maps corresponding to each wavelength for a sample-free interferogram, where the residue phase curvatures are resulted from the aberrations in the imaging system, and can be removed during post-processing.

Fig. 2.

(a) Fourier transform of the grid interference pattern. (b) Spatial frequency of the sample masked by the numerical aperture size in the Fourier space. (c), (d) background phase curvatures corresponding to λ = 430 nm and λ = 630 nm, respectively. The scale bar is 10 µm.

4. Experimental validation

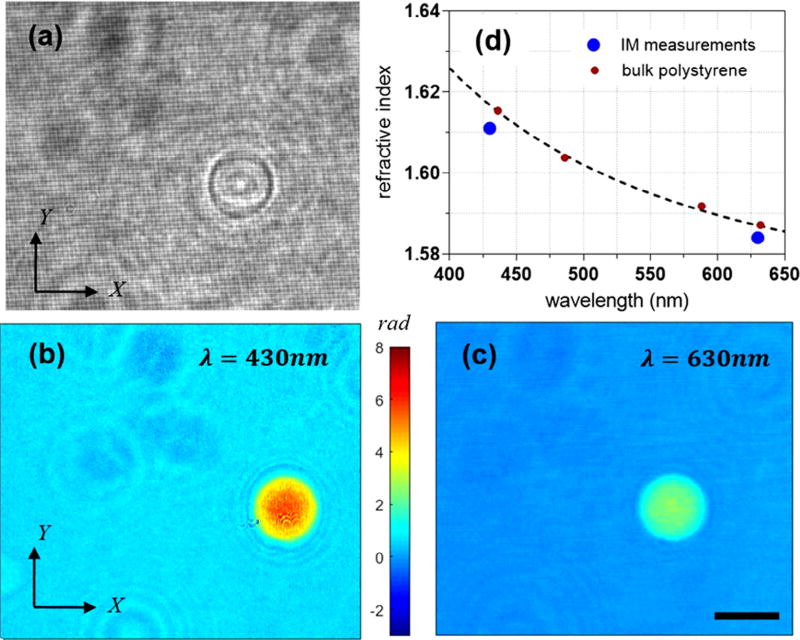
To validate the feasibility of our technique, we have measured the optical properties of polystyrene beads immersed in the refractive index matching oil (Cargill, 1.56). The sample was simultaneously illuminated by two colors, λ₁ = 430 nm and λ₂ = 630 nm. Fig. 3(a) shows the raw interference grid for this case. Applying the procedure outlined in the Section 3, one can calculate the complex field information for each of these two wavelengths. Fig. 3(b) and (c) shows the phase map for λ = 430 nm and λ = 630 nm, respectively. Since the thickness of the sample is exactly the same for both phase measurements, an increase in the wavelength is accompanied by a proportional decrease in the phase value, as seen in the phase maps. To calculate the refractive index of the sample, one needs to make certain assumption about the size and geometry of the sample. The diameter of the bead is specified to be approximately 10 µm by the manufacturer (Thermo Fisher Scientific). However, in each measurement, assuming a spherical geometry for the beads, one can calculate the diameter using the projected area of the bead as well. Once the diameter is known, we fit a spherical surface, to decouple the optical properties and geometry of the beads. Fig. 3(d) shows the calculated refractive indices corresponding to the two illumination wavelengths plotted against the dispersion of the bulk polystyrene from the literature [24]. An average value of refractive index was calculated for each color by measuring 10 beads; the corresponding standard deviation values were measured as 0.0017 and 0.0005 for λ = 430 nm and λ = 630 nm, respectively. The size of the dots in the graph then roughly represents the standard deviation of the average RI. There is a slight bias between our calculated values and that of the cited reference for bulk RI of the polystyrene, while the relative difference at both colors is quite consistent. At λ = 630 nm, for instance, we calculate the difference to be roughly 0.003. This discrepancy is rather small and may originate from error in our measurements and that of the reference. One potential error in our measurements includes over-estimation of the bead size due to the difficulty in locating the bead boundary due to diffraction effects.

Fig. 3.

(a) Grid interference pattern with a polystyrene bead in the field of view. (b), (c) Phase maps of a polystyrene bead at λ = 430 nm and λ = 630 nm, respectively. The scale bar is 10 µm. (d) The refractive index of the polystyrene bead compared to the polystyrene dispersion curve from the literature [24].

5. Discussion and outlook

In summary, we developed a new approach for single-shot interferometric microscopy to retrieve complex field information simultaneously at two illumination wavelengths via optimal use of camera pixels. To further elucidate this point, we show the fringe pattern at a specific sample point for conventional IM design and our new technique, in Fig. 1(e) and (f), respectively. To obtain the phase information of a sample point, the grating period has to be sampled with at least three camera pixels or more; in this case we show four pixels as an example. However, in conventional IM designs, this pattern is repeated in the vertical direction without providing any additional information. In our novel design, we are effectively using the same pixel area to sample two overlapping fringe patterns and thereby obtaining the field information for an additional color without a loss in the field of view. However, because of this overlap, there is a decrease in the fringe contrast in both horizontal and vertical directions that results in a drop in measurement sensitivity by a factor of $\sqrt{2}$ For a given camera and microscope objective, therefore, our design results in a more optical use of the camera pixels while maintaining speed, resolution, and stability advantage of the single-shot common-path designs. In this work, we have used 430 nm and 630 nm as the illumination wavelength to show the feasibility of the approach and the colors were physically blocked at the Fourier plane. These specific wavelengths are particularly useful in studying biophysical properties of the red blood cells where 430 nm represents a high absorption region whereas at 630 nm wavelength the scattering dominates with little to no absorption [25]. If one decides to have the illumination colors closer to one another, a physical block would become infeasible. Such a situation can be resolved by simply using a band-pass filter placed at the Fourier plane for each specific color Additionally, one may be able to add two more wavelengths to the design by projecting two oblique fringe patterns orthogonal to one another. In doing so, however, a more sophisticated diffraction grating needs to be implemented in addition to more elaborate filtering at the Fourier plane that adds additional cost. Whether this cost and additional effort is justified depends on whether there is a critical application that requires simultaneous interferometric measurements at more than two colors. The design of our microscope was mainly motivated by the need to study biophysical properties of the RBCs as a function of oxygen partial pressure of the medium. Since dispersion properties of the RBCs are more pronounced in the near-UV regime (e.g., 410 nm and 430 nm), this design allows for selection of any two wavelengths and measurement of fast dynamics, e.g., membrane fluctuations, without any compromise in the speed or resolution of the imaging system in a practical manner. The enhanced performance of this design should find applications in biophysical studies of many other cellular systems as well.