Suprathreshold fiber cluster statistics: leveraging white matter geometry to enhance tractography statistical analysis

Abstract

This work presents a suprathreshold fiber cluster (STFC) method that leverages the whole brain fiber geometry to enhance statistical group difference analyses. The proposed method consists of 1) a well-established study-specific data-driven tractography parcellation to obtain white matter tract parcels and 2) a newly proposed nonparametric, permutation-test-based STFC method to identify significant differences between study populations. The basic idea of our method is that a white matter parcel’s neighborhood (nearby parcels with similar white matter anatomy) can support the parcel’s statistical significance when correcting for multiple comparisons. We propose an adaptive parcel neighborhood strategy to allow suprathreshold fiber cluster formation that is robust to anatomically varying inter-parcel distances. The method is demonstrated by application to a multi-shell diffusion MRI dataset from 59 individuals, including 30 attention deficit hyperactivity disorder patients and 29 healthy controls. Evaluations are conducted using both synthetic and in-vivo data. The results indicate that the STFC method gives greater sensitivity in finding group differences in white matter tract parcels compared to several traditional multiple comparison correction methods.

1. Introduction

Diffusion magnetic resonance imaging (dMRI), which can probe the underlying microstructure of brain white matter (WM) in vivo, provides the only existing technique to study brain WM structures in a non-invasive way. With the growing popularity of dMRI, computational neuroimaging methods have been proposed to identify group WM differences for understanding brain neurological function in health and disease. Applications have included attention deficit hyperactivity disorder (ADHD) [93], autism [2], human aging [27], brain connectome modeling [47], and many more studies, as described in several reviews [97, 82, 3].

Traditional methods to study WM group differences rely on voxel-based image analysis techniques such as voxel-based morphometry (VBM) [4] and tract-based spatial statistics (TBSS) [87]. While these methods have been highly successful, several studies suggest that VBM and TBSS could be affected by highly-localized group differences [25, 46] and partial volume effects [7, 16]. An alternative can be using a region-wise WM atlas where regions are defined as WM tracts, which has been successfully applied in multiple studies [55, 45, 66, 26, 104, 90, 13]. However, using these voxel-based methods, accurate localization of between-population differences to specific WM tracts can be difficult to assess, especially since more than one tract may cross within a single voxel. Fixel-based analysis (FBA) that takes account of multiple fibers within a voxel has been proposed recently to enable enhanced whole-brain statistics [75, 76], showing the potential of incorporating information from multiple fiber populations into WM analyses.

In order to allow simultaneous analysis across multiple brain regions in neuroimaging, a hypothesis test (e.g. Student’s t-test) is normally used to identify local group differences, followed by multiple comparison correction (e.g. false discovery rate (FDR) [11] and Bonferroni [43] methods) for corrected statistical significance. Since these commonly used correction methods can be less sensitive in finding significance, voxel-based multiple comparison correction has been conducted in a cluster-thresholding manner that utilizes spatial neighborhoods to boost belief in extended voxel cluster areas [58]. Multiple studies have applied voxel-cluster-thresholding methods to find WM group differences [81, 72, 94, 75, 15].

An alternative approach for investigating differences in the brain’s WM uses tractography [9], which allows estimation of the trajectories of fiber tracts [102, 74] and thus measurement of microstructural WM properties of fiber pathways [40, 21]. A traditional tractography-based group difference analysis includes manual selection of anatomical tract(s) of interest (such as the corpus callosum [2] or multiple fiber tracts [71]) and then comparison of groups to find statistical differences in WM diffusion features (e.g. diffusion anisotropy), either using feature mean values [2, 23, 71] or along-tract measures [24, 36, 22, 71]. However, these studies are generally limited to a small number of selected tracts due to the requirement for extensive manual interpretation by trained experts.

Compared to the aforementioned studies that apply manual fiber tract selection methods, another strategy can efficiently identify multiple tracts in an automated fashion based on connected brain gray matter (GM) regions [101], anatomical priors [104], and/or WM anatomy (i.e. fiber geometric trajectory) [65]. Several groups have applied this strategy to study multiple tracts for identification of group WM differences [105, 103, 18, 84]. Nonetheless, in general each tract has been studied individually without any correction for multiple comparisons, preventing simultaneous analysis across multiple tracts. Recently, two research studies did perform simultaneous statistical analysis of multiple tracts using FDR for multiple comparison correction [100, 114]. Both works estimated direct fiber correspondences across subjects using fiber geometry. One work analyzed 30 major fiber tracts [100], while the other work performed a whole brain white matter statistical analysis [114]. These approaches demonstrated the potential of simultaneous multi-tract analysis. However, neither group investigated strategies for improving sensitivity during multiple comparison correction.

Another important approach for white matter analysis leverages a cortical parcellation to subdivide the white matter according to its cortical tract terminations and generates a structural connectome matrix that stores data such as fiber count. Statistical analyses of structural connectome matrices have employed FDR, Bonferroni, and permutation testing methods for correcting multiple comparisons [34, 48, 79, 47]. Cluster-formation methods that leverage cortical graph geometry have also been proposed for connectome matrix analysis [106]. However, there are challenges in the application of connectome-style analyses to dMRI [91] including anatomical variability of fiber tract terminations and cortical anatomy [8, 42, 96], spatial distortions [50], and reduced reproducibility due to the non-continuous nature of the matrix representation [56]. In contrast, white-matter-centric fiber analysis approaches can leverage information about the full course of a fiber tract, which is the anatomical basis for fiber tract definition [101], and empirical results indicate that white-matter-centric approaches benefit from low variability across subjects in terms of the WM parcellations that can be defined [109, 64, 19, 37].

In light of the above, we propose a suprathreshold fiber cluster (STFC) method to identify WM group differences using whole-brain tractography. For the first time, the proposed method leverages permutation testing and whole brain fiber geometry to enhance the statistical analysis of tractography. The method design is inspired by the idea that fiber tract parcels with similar WM anatomy, e.g. neighboring parcels, can support each other to obtain statistical significance. Important considerations in proposing such a method are the definition of the parcel neighborhood and the method for STFC formation using the parcel neighborhoods. This investigation extends our initial conference publication that demonstrated feasibility of STFC analysis [112] to 1) improve suprathreshold fiber cluster formation with anatomically varying inter-parcel distances and 2) improve robustness to parameter selection, an important goal in statistical neuroimaging analyses [89].

Our proposed method is based on a study-specific data-driven whole brain WM parcellation that finely divides all input tractography into many regions (a total of 1416 tract parcels in our study) and hence allows identification of potential local WM group differences from the whole brain. Recent research has shown the potential benefit of fine scale WM/GM parcellations to provide better group difference information compared to coarse-grained parcellations [39, 95, 111, 53]. In addition, we propose a fiber-cluster-thresholding-based multiple comparison correction to enable simultaneous analysis across the multiple tract parcels. Different from the voxel-cluster-thresholding approach [58, 89], our proposed method leverages fiber spatial neighborhoods that are defined according to the whole brain WM anatomy. To our knowledge, this work represents the first fiber-cluster-thresholding method to identify tractography-based group differences for whole brain analysis.

In the rest of this paper, we first describe our proposed method and then demonstrate its application to a multi-shell dMRI dataset from attention deficit hyperactivity disorder (ADHD) patients and healthy controls (HCs). A tract-specific study and a whole-brain WM study are conducted to illustrate the proposed method’s ability in both tract-of-interest and whole-brain tractography analyses.

2. Methods

2.1. Overview

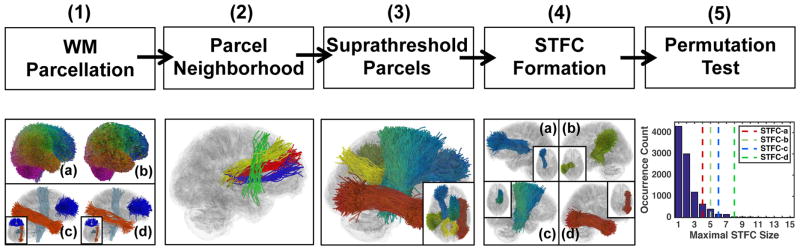
The proposed STFC method is designed to enhance statistical group difference analyses using whole-brain tractography. Figure 1 gives an overview of the proposed STFC method, including several steps: study-specific data-driven whole brain WM parcellation (Section 2.2), locally adaptive WM parcel neighborhood construction (Section 2.3), and computation of STFC statistics (Section 2.4) composed of suprathreshold parcel identification (Section 2.4.1), STFC formation (Section 2.4.2) and nonparametric, permutation-test-based group difference computation (Section 2.4.3). Overall, these steps enable identification of corresponding WM parcels in the whole brain of all subjects under study, followed by a statistical group difference analysis while correcting for multiple comparisons leveraging fiber geometry.

Figure 1.

Method overview: (1) WM Parcellation: (a) and (b) show the study-specific data-driven groupwise WM parcellation (atlas) and a subject-specific WM parcellation; (c) and (d) show several example atlas WM tract parcels and the corresponding subject-specific WM tract parcels (d); (2) Parcel Neighborhood: example neighbors of the red tract parcel include the yellow and the blue parcels but not the more distant green one with dissimilar WM anatomy to the others; (3) Suprathreshold Parcels: example fiber parcels that passed a parcel-level statistic test from the whole brain according to a quantitative parameter extracted from each parcel (the diffusion feature of return-to-the-origin probability (RTOP) was used in this study), computed using a Student’s t-test given a user-given threshold (uncorrected p-value = 0.05 is used in this study); (4) STFC Formation: example STFCs obtained using clique percolation (CP) to join neighboring parcels with uncorrected significance; (5) Permutation Test: example null distribution obtained from a non-parametric permutation test with summary statistic of maximal STFC size. For each STFC, its corrected significance is computed by comparing its STFC size (dashed lines) to the null distribution.

2.2. Data-driven WM Parcellation

A study-specific WM parcellation was first conducted using a well established data-driven pipeline to divide the whole brain tractography into multiple WM parcels according to the common WM anatomy from the whole population [63]. An open-source implementation of the WM parcellation pipeline is available online as the whitematteranalysis¹ software. Our recent research studies have shown high performance of the pipeline in WM parcellation [111, 108, 64, 109, 110]. Here, we provide a brief introduction of this WM parcellation pipeline.

First, we computed an unbiased groupwise whole brain tractography registration to align all subjects’ tractography into a common space (i.e. atlas space) [62]. The method performed an entropy-based registration in a multiscale manner based on the pairwise fiber trajectory distances (the popular mean closest point distance was used [54, 63]) across all subjects. An affine transform was first performed, followed by a b-spline transform, in a coarse-to-fine fashion. This enabled nonrigid deformations of the fibers for improvements in parcellation consistency across subjects. Registration was conducted in a symmetric manner by registering all subjects, including midsagittal plane reflected copies of the subjects. In this way, the registration could effectively perform tractography alignment across the midsagittal plane. This benefited the bilateral clustering for atlas generation, which is introduced in the following paragraph.

Next, we created a study-specific data-driven groupwise WM parcellation atlas using spectral embedding [63], as follows. Each fiber was first represented as a point in a space useful for clustering. This was achieved by performing spectral embedding based on pairwise fiber affinities across all subjects. Then fiber affinities were obtained by converting the pairwise fiber distances using a Gaussian-like kernel with sigma of 60 mm. Nystrom sampling [33] was performed to reduce the computations considering the large number of fiber pairs across subjects. Bilateral clustering that simultaneously segments fibers in both hemispheres was applied to improve parcellation robustness [63]. To achieve bilateral clustering, the fiber distance measurement used all fiber connections as well as their reflections through the midsagittal plane of the brain. In this study, a study-specific WM parcellation atlas consisting of a total of K=800 WM parcels, including both inter- and intra-hemispheric parcels, was generated from all subjects under study. K=800 was chosen to provide a good parcellation of the whole WM based on our recent study [64]. (Please see the video S1 included in the supplementary material for a visualization of each individual WM parcel within this atlas.)

Then, we applied the parcellation atlas to each individual subject to obtain a subject-specific WM parcellation [63]. The spectral embedding for each new fiber (already affine and non-rigid transformed) was calculated by comparison to the fibers stored in the atlas (the stored Nystrom sample) using the same fiber affinity as in the atlas generation. The subject-specific WM parcels were then obtained by assigning the fibers to their closest atlas parcel. Given the bilateral clustering of the atlas, the subject WM parcels were detected bilaterally. A hemisphere-based parcel separation was conducted, where bilateral (intra-hemispheric) parcels were separated into left and right hemisphere parcels.

After obtaining the hemisphere-based-separated parcels in all subjects, valid parcels were defined as the ones that were commonly detected in the population (shared structural connections). We identified the valid parcels using a nonparametric one-tailed sign test. For each parcel, the sign test was performed with the null hypothesis that there were no fibers in the parcel across all subjects (Bonferroni corrected at a significance level of 0.05). This method has been applied in multiple studies to identify valid white matter connections [34, 79, 111, 109]. In this study, we obtained a total of 1416 valid hemispheric and commissural parcels from the dataset under study. Parameters involved in the WM parcellation pipeline were set to the default values in the whitematteranalysis package.

2.3. WM Parcel Neighborhood Construction

The goal of constructing a parcel neighborhood is to identify nearby WM connections with similar WM anatomy. This will be further used to find neighboring WM parcels to form the STFCs (Section 2.4.2). The parcel neighborhood construction includes two steps of an inter-parcel distance computation and a locally adaptive neighborhood construction to adapt to local WM geometry.

The distance between parcels (p₁ and p₂) was computed as the mean of the pairwise fiber distances between parcels in the WM parcellation atlas (Section 2.2), i.e.

$$D(p_1,p_2)=\frac{{\sum }_{i=1}^I{\sum }_{j=1}^J{d}_{ij}}{IJ}$$ (1)

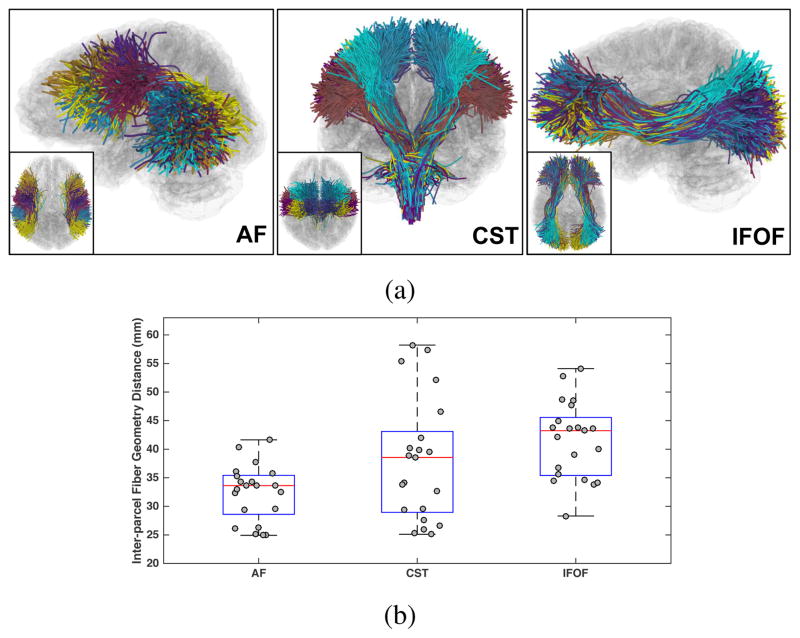
where d_{i j} is the fiber pair distance and I and J are the total numbers of fibers in the two parcels. We applied the mean closest point fiber distance [63], the same distance used in the spectral clustering WM parcellation, to measure d_{i j}. In this way, the distances D could capture the anatomical similarity between the parcels, with a low distance representing a high WM anatomy similarity and vice versa. Figure 2 shows the inter-parcel distances from several example fiber tracts.

Figure 2.

Inter-parcel distances across all parcel pairs in several example fiber tracts, including arcuate fasciculus (AF), corticospinal tracts (CST) and inferior fronto-occipital fasciculus (IFOF). (a) shows the WM parcels (colored differently) within each tract. These example fiber tracts were selected for visualization using expert knowledge following the anatomical hierarchy creation process using 3D Slicer as described in [64]. (b) shows that the inter-parcel distances in these tracts have different scales, e.g. the inter-parcel distances within the AF tract are in general lower than those within the IFOF tract, motivating our design of a locally adaptive neighborhood formation.

The strategy of constructing neighborhoods using locally surrounding information has been widely used in multiple fields, such as data mining [107, 28] and computer vision [73, 1] for its good performance in finding similar structures from data with heterogeneous distance scales. Here we propose to use this strategy to define WM parcel neighborhoods, considering that the inter-parcel distances in different anatomical WM structures are expected to have different scales (Figure 2b). We propose that the neighborhood of a WM parcel should be locally adaptive, where each parcel’s neighbors are decided considering its nearest parcels.

In machine learning, local neighborhood construction is often modeled as a graph-based problem. A robust method for “good” neighborhood selection is to use consensus information: first select the top T nearest neighbors for each node in the graph and then decide which neighbors should be retained to form a tight neighborhood where the nodes are highly similar to each other [107, 113, 73]. To apply this method to our data, we considered the WM parcels as graph nodes, where the internode distance was the inter-parcel distance (Eq. 1). For each individual parcel p, we first selected the top T nearest parcels, which we referred to as candidate neighbors. Then, among the T candidates, we considered the ones that formed the largest weakly connected sub-graph to be the neighborhood of p, as illustrated in Figure 3a. This ensured that all parcel neighbors had similar WM anatomy to each other while adapting to the different anatomical size scales. As a result, we could obtain a parcel neighborhood graph, where each node represented a WM parcel and an edge represented that two parcels were neighbors. Here, we note that compared to neighborhood construction using a strongly connected sub-graph that could be too strict in forming neighborhoods, a weakly connected sub-graph could reduce the possibility of missing potential neighbors. For example, in the CST shown in Figure 2a, in a weakly-connected-sub-graph-based way, the lateral brown cluster belonged to the neighborhood of the more superior blue cluster due to the cyan cluster between them, while using a strongly connected subgraph, such a neighborhood could be missed.

Figure 3.

Schema of (a) locally adaptive WM parcel neighborhood construction (Section 2.3) and (b) clique-percolation-based STFC formation (Section 2.4.2). (a) For an example parcel p₁ (blue circle), the top four nearest parcels p₂ to p₅ (under T = 4) are selected as candidates (orange circles). The candidates weakly (directly or indirectly) connect to each other (red edges) and thus are considered as the neighbors of p₁. (b) Here, we assume all parcels (colored circles) passed a parcel-level statistic test as the suprathreshold parcels (Section 2.4.1). Following the example in (a) with more parcels p₆ to p₉, there are one 4-clique ([p₁, p₃, p₄, p₅]) and three 3-cliques ([ p₁, p₂, p₃], [ p₄, p₅, p₉] and [ p₄, p₈, p₉]), which are 2-connected by sharing two common parcels (red edges). Therefore, they form an STFC of size 7 (under a parameter setting h = 2 that two parcel cliques are considered adjacent if they share at least two parcels). The parcels p₆ and p₇ do not form any cliques with the aforementioned parcels and thus are not considered as part of the formed STFC.

One benefit of the locally adaptive neighborhood construction was its robustness to parameter selection. The single needed parameter, T, could be chosen according to the WM anatomy of the parcels obtained from the whole brain parcellation, prior to any statistical analyses (see Section 3.2 for details). In all our statistical experiments (both on synthetic and real datasets) we used a single value of T = 4.

2.4. STFC Statistics Computation

Computation of the suprathreshold fiber cluster (STFC) statistics included the following steps: 1) identifying suprathreshold parcels that passed an uncorrected, parcel-level statistic test, 2) forming the suprathreshold parcels as STFCs given the obtained parcel neighborhoods, and 3) calculating the STFC statistics in a nonparametric permutation test while correcting for multiple comparisons.

2.4.1. Suprathreshold Parcel Identification

A suprathreshold parcel was defined as a WM parcel that passed a parcel-level statistic test at a predetermined primary threshold (analogous to suprathreshold voxel in the voxel-cluster-thresholding approach [58]). Specifically, to derive the parcel-level statistic, we performed a null hypothesis test that computed an uncorrected WM group significance (an uncorrected p-value) for each individual parcel. We set the primary threshold to p-value =0.05, i.e. the parcels with uncorrected p-values ≤ 0.05 were suprathreshold parcels. The suprathreshold parcel identification would be conducted in all runs in the permutation test (both correctly labeled and permuted data) (Section 2.4.3).

In the interest of the application to study ADHD, we applied a one-tailed Student’s t-test to compute the uncorrected p-values (see Section 3.1 for details). However, we note that the parcel-level statistics can be computed with many other statistical computation methods and/or other tract quantitative measures under the hypothesis of interest.

2.4.2. Clique-Percolation-Based STFC Formation

An STFC was defined as a fiber cluster of multiple neighboring suprathreshold parcels. Given the defined parcel neighborhood graph (Section 2.3) and the suprathreshold parcels that passed the parcel-level statistic test (Section 2.4.1), we applied clique percolation (CP) [68] to identify the STFCs. We chose CP due to its known good performance in identifying densely connected node clusters on a graph. Applying CP to our parcel neighborhood graph therefore enabled formation of STFCs consisting of WM parcels with highly similar WM anatomy.

In graph theory, CP is a popular method for detecting densely connected node clusters given known edges between nodes. It has been successfully used in a variety of applications, such as analyzing structural and functional brain connectivity [92], community detection in protein networks [51] and studying social networks [35]. In brief, given the neighborhood relationships among all nodes on a graph, CP first detects all cliques, i.e., fully connected subgraphs. A clique with k nodes is called a k-clique and two cliques are adjacent if they share at least h nodes. Then, a node cluster is calculated as the maximal union of cliques that could be reached from each other through a series of adjacent cliques.

Given the parcel neighborhood graph from all WM parcels (this was computed before statistical analysis (Section 2.3)), we first extracted a subgraph consisting of only the suprathreshold parcel nodes and edges. After that, CP was applied to identify all parcel cliques and then the adjacent parcel cliques as the STFCs, as illustrated in Figure 3b. The CP-based STFC formation had an advantage that the only parameter h to define clique adjacency could be determined according to the number of neighbor candidates T. In our experiments, given T = 4, we set h = 2 that made two parcel cliques adjacent if there were at least two shared parcels. Detailed explanations of parameter selections will be provided in Section 3.2. We note that the parameter selections of h and T were determined together before any statistical analyses.

2.4.3. STFC Statistics Using Nonparametric Permutation Test

STFC statistics were computed in a nonparametric permutation test to obtain a final significance of each STFC with correction for multiple comparisons. A nonparametric permutation test is used because it is conceptually simple, relies only on minimal assumptions, and allows multiple comparison correction for simultaneous analysis of multiple brain regions [44, 58]. In related work, we and other research groups have successfully applied a permutation test for identifying group WM statistic differences along single fiber tracts within certain WM regions [65, 94, 100]. In the proposed method, we uses a permutation test for a whole brain WM analysis. Our proposed STFC method determines a corrected significance for each STFC based on its STFC size, i.e. the number of WM parcels within each STFC, under the null hypothesis of no group difference in any parcel in this STFC. Similar to the suprathreshold voxel cluster test in [58], we used the maximal statistic, i.e. the maximal STFC size, as the summary statistic in the permutation test, where the maximal STFC size was computed in each permutation run to build the null distribution to provide family-wise error control of false positives.

Algorithm 1 shows the pseudocode of the overall STFC method. After performing the groupwise WM parcellation (line 1) and the locally adaptive neighborhood construction (line 2), we first produced a null distribution of the summary statistic across the permutation runs (N=10000 was used in all experiments) (lines 3.1 to 3.3). Then, for each STFC from the correctly labeled groups (i.e. the real data) (lines 4 to 6), we compared its STFC size to the null distribution to obtain a corrected significance of the STFC, as well as the corrected p-value of each parcel in the STFC (lines 7.1 to 7.3). The STFCs that had corrected significance values lower than or equal to a user-given significance level were considered to have statically significant group differences. We set the significance level to 0.05 in all statistical experiments in this study.

3. Evaluation Dataset, Experiments and Results

3.1. Dataset

We demonstrate the proposed method using a dataset from 59 individuals (30 ADHD, 7 females and 23 males; 29 HC, 10 females and 19 males) that were locally recruited from multiple sources including the Departments of Psychiatry and Neurology at a tertiary care university hospital, a community based health center, and through online advertisements. The two groups were matched for age (ADHD: 10.6±1.7 years; HC: 10.7±1.7 years; two-tailed t-test, p = 0.9) and socioeconomic status (SES) via household annual income (ADHD: 64.2 ±3.68 thousand dollars; HC: 78.6 ± 34.2 thousand dollars; two-tailed t-test, p-value = 0.2).

Algorithm 1.

Suprathreshold Fiber Cluster (STFC) Method

1:	Perform study-specific groupwise WM parcellation (Section 2.2)
2:	Build parcel neighborhood graph from all WM parcels (Section 2.3)
3:	for each permutation run in [1, N] do
3.1:	Randomly permute group labels of all subjects
3.2:	Identify suprathreshold parcels from the permuted data (uncorrected p-values ≤ 0.05) (Section 2.4.1)
3.3:	Extract all STFCs and record the maximal STFC size (Section 2.4.2)
4:	Calculate the histogram of the maximal STFC size to produce the null distribution
5:	Identify suprathreshold parcels in the correctly labeled data (uncorrected p-values ≤ 0.05) (Section 2.4.1)
6:	Extract all STFCs and compute their STFC sizes (Section 2.4.2)
7:	for each STFC s do
7.1:	Locate its STFC size in the histogram of the maximal STFC size
7.2:	Obtain number of permutations with the maximal STFC size larger than or equal to the size of STFC s as N(s)
7.3:	Compute the corrected significance value as (N(s) +1)/(N +1)

3.1.1. Data Preprocessing

High-resolution MR images were obtained on a Siemens 3T scanner at Boston Childrens Hospital, Boston, USA, with approval of the local ethics board. Multi-shell diffusion-weighted imaging (DWI) data were acquired using simultaneous multi-slice acquisition factor of 2 [83] at a spatial resolution of 2×2×2 mm³ with 70 gradient directions spread over the three b-value shells of 1000/2000/3000 s/mm². Additionally, T1- and T2-weighted images were acquired at a spatial resolution of 1 mm³ and 8 mm³ respectively.

A semi-automated quality control (using in-house developed Matlab scripts) was conducted on all datasets, and all gradient directions with a signal drop were removed. Brain masks for dMRI images were first obtained using BET [86], followed by manual inspection and correction in 3D Slicer² via SlicerDMRI³ [60]. Eddy current and head motion correction was performed using FSL FLIRT software [88]. Further, dMRI images were corrected for EPI distortions by registration (restricted to the phase-encode direction) to the T2-weighted images using ANTS [5]. All processed images were manually inspected to ensure high quality of the data sets.

3.1.2. Tractography, Diffusion Feature and Suprathreshold Parcel

Whole brain tractography was conducted using the unscented Kalman filter tractography method [77, 80], as implemented in the ukftractography⁴ package. Tractography was seeded 5 times per voxel, in all voxels within the brain mask. We employed a multi-fiber model, where each fiber is represented using a two-tensor bi-exponential model [78, 77]. This framework enables robust analytical estimation of fiber-specific diffusion propagator and microstructure measures, while simultaneously tracing the white matter tracts. Fibers that were longer than 40 mm were retained to avoid any bias towards implausible short fibers [38, 49, 52].

Return-to-the-origin probability (RTOP) was estimated using the bi-exponential model to provide a fiber-specific microstructure measure [77, 59]. RTOP estimates the probability of water molecules with zero net displacements during the diffusion time of the diffusion MRI scan. RTOP is known to be sensitive to the anisotropy of WM tissue and may increase pathophysiological specificity compared to traditional diffusion anisotropy measures, e.g. fractional anisotropy (FA) [67, 6]. The median of the RTOP values of all points in each WM parcel was measured, i.e. M_RTOP. The median value has been previously shown to provide a robust measure of the central tendency of diffusion properties in WM regions for group difference analysis [10, 99].

Studies in ADHD have widely suggested decreased diffusion anisotropy [41, 70, 57]. Therefore, we performed an one-tailed Student’s t-test under the null hypothesis H₀: μ_HC (M_RTOP) ≤ μ_ADHD(M_RTOP) to compute the parcel-level statistic for each individual WM parcel. The primary threshold to define suprathreshold parcels was set to p-value = 0.05, i.e., the parcels that had the uncorrected p-values ≤ 0.05.

3.1.3. Synthetic Dataset

A synthetic dataset with simulated true group difference was created to validate the proposed method. To simplify the assessment and tractography visualization, we created a realistic synthetic dataset in the corpus callosum (CC). The synthetic data was generated as follows. We identified a total of 34 CC parcels from the whole brain parcellation, as shown in Figure 4a. For each CC parcel, we added white Gaussian noise (signal-to-noise ratio at 1 [89]) to the actual measured features (i.e. RTOP) of all HC subjects. Repeating this process twice generated two synthetic groups of G1 and G2, each with 29 subjects. We then modified 15 CC parcels of interest to have true group difference by adding synthetic feature changes to the G2 subjects. For each of the 15 parcels, we decreased its group mean M_RTOP values in G2 (as a percent of its original feature mean) for a null hypothesis test: H₀: μ_G1(M_RTOP) ≤ μ_G2(M_RTOP). These 15 parcels were selected to form 3 different synthetic ground truth fiber clusters (with sizes of 4, 5 and 6, as shown in Figure 4b). This synthetic dataset will be used in two experiments to validate our method (Section 3.3) after we introduce the parameter decisions in the next subsection (Section 3.2)

Figure 4.

(a) All CC parcels (size of 34) obtained in the whole brain parcellation. (b) 15 CC parcels-of-interest with synthetic ground truth group differences. These parcels formed three fiber clusters from the genu (blue), body (green) and splenium (purple) sections of the CC, with sizes of 4, 5 and 6 respectively.

3.2. Parameter Selection According to Population Whole Brain WM Anatomy

We first performed an experiment for parameter selection. Our method has two parameters: 1) T that is the number of candidate neighbors per parcel (Section 2.3) for local neighborhood construction, and 2) h that is the number of shared parcels between cliques and defines clique adjacency (Section 2.4.3) to form STFCs. The two parameters together control if parcels with similar WM anatomy can be grouped into an STFC. We propose that reasonable settings of T and h are the ones that do not overly limit the size of potential STFCs that may be formed, while avoiding grouping parcels with dissimilar WM anatomy together.

To determine reasonable settings, we investigated how the two parameters affected fiber cluster (FC) formation according to the whole brain parcellation in the population. We note the experiment was conducted based on the whole brain fiber geometry and WM anatomy only, without using any measured diffusion data. Thus, the parameter selection was independent of any statistical analysis. Specifically, given certain settings of T and h, CP (under the given h) was applied directly to the full parcel neighborhood graph (under the given T ) of all WM parcels. This allowed us to detect all possible FCs that could be achieved from the whole brain. Here, we note that FCs were different from STFCs, since the STFCs were calculated based on a sub-neighborhood-graph consisting of only suprathreshold parcel nodes and edges (thus, an STFC was a subset of one of the FCs).

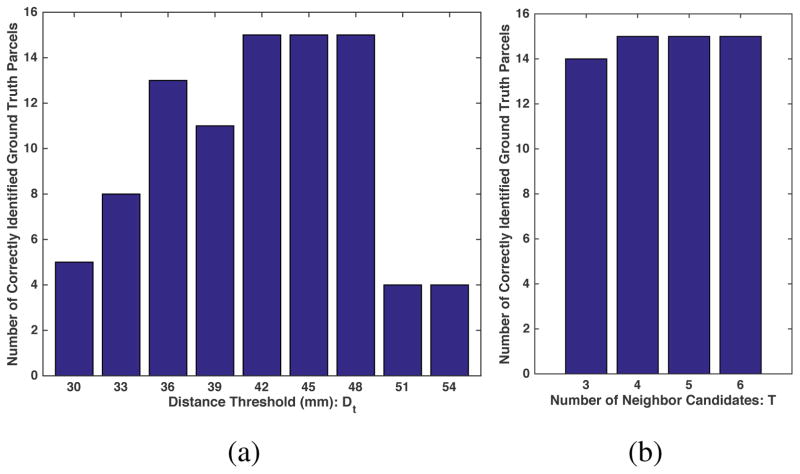
After obtaining all possible FCs under the given T and h, we investigated the largest FC (LFC), i.e. the FC that had the maximum number of parcels. Corresponding to the proposed criteria (introduced at the beginning of this section) for parameter selection, the most reasonable T and h were the settings resulting in the maximal LFC but without dissimilar WM anatomy. For quantitative comparisons, we computed the cluster size (number of parcels) and the maximum inter-parcel distance (D_max) for the LFC per setting, as shown in Table 1. Here, the experiments were conducted on a reasonable range of T between 3 to 6. While T ≤ 2 was too small to construct informative WM parcel neighborhoods, T ≥ 7 needed long computational time⁵ as extracting parcel cliques was a time-consuming process [68].

Table 1.

Quantitative assessments for selecting a reasonable h value given a certain T value include the cluster size and the maximum inter-parcel distance (D_max mm) for the largest fiber cluster (LFC) that formed with each setting. Note that given a certain T value (per column), the maximum possible parcel clique was a (T +1)-clique (see [68] for details) thus the maximum possible h was T (no two parcel cliques could share T +1 or more parcels). Therefore, no FCs formed when h > T. While a large h value (e.g. h = T ) tended to generate the most white-matter-constant FCs (a low D_max value), it was too strict when combining parcel cliques as FCs. Thus, it could overly limit the size of potential FCs that may be formed. For example, under h = T = 4, the LFC size was 6 (see Figure 5 for tract visualizations and comparisons across different h settings under T = 4), which meant that any FCs with sizes larger than 6 could not be identified. In this study, we set h = T – 2 (bold font per column) as a reasonable setting for a balance between a high WM anatomy consistency (a small D_max) and a high coverage of a local WM structure of fiber clusters (a large LFC size).

	T = 3		T = 4		T = 5		T = 6
	size	Dmax	size	Dmax	size	Dmax	size	Dmax
h = 1	18	66.2	64	90.4	433	142.3	604	144.7
h = 2	13	69.4	23	68.9	112	114.8	555	143.9
h = 3	5	48.7	8	59.0	15	51.5	56	94.0
h = 4	-	-	6	57.4	8	59.8	13	51.1
h = 5	-	-	-	-	6	58.9	7	59.8
h = 6	-	-	-	-	-	-	6	59.0

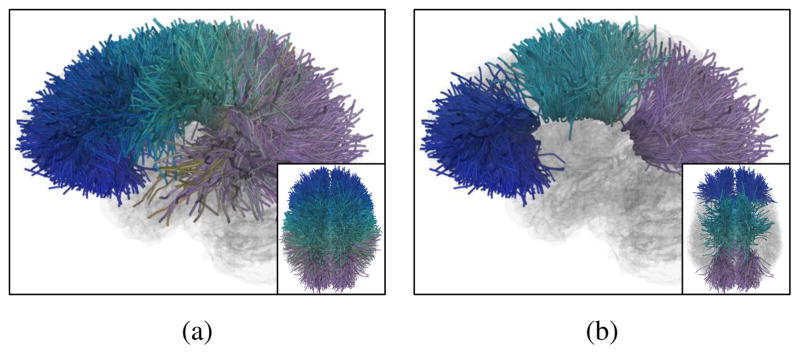
Experimental results indicate that given a certain T value, choosing h = T – 2 can balance between a high WM anatomy consistency (a small D_max) and a high coverage of a local WM structure of fiber clusters (a large LFC size), as illustrated in Table 1. For visual comparisons, Figure 5 displays the LFC obtained per h value, with T = 4 for an illustration. h = 2 (i.e. T – 2) generated the best result.

Figure 5.

Visual tract comparisons of the largest fiber cluster (LFC) obtained from the whole brain parcellation given different h values under T = 4. (a) to (d) were obtained from h =1 to 4, consisting of 64, 23, 8 and 6 WM parcels, respectively. h = 1 obtained a LFC with the most parcels; however the parcels were from different local WM regions including the temporal lobe and the cerebellum. h = 3 and 4 generated a LFC with only a small number of parcels, which provided a small coverage of the fiber connections from a local WM region. h = 2 generated a LFC with 23 parcels that were all from the corona radiata region, providing a visual confirmation of our choice of setting of h = T – 2.

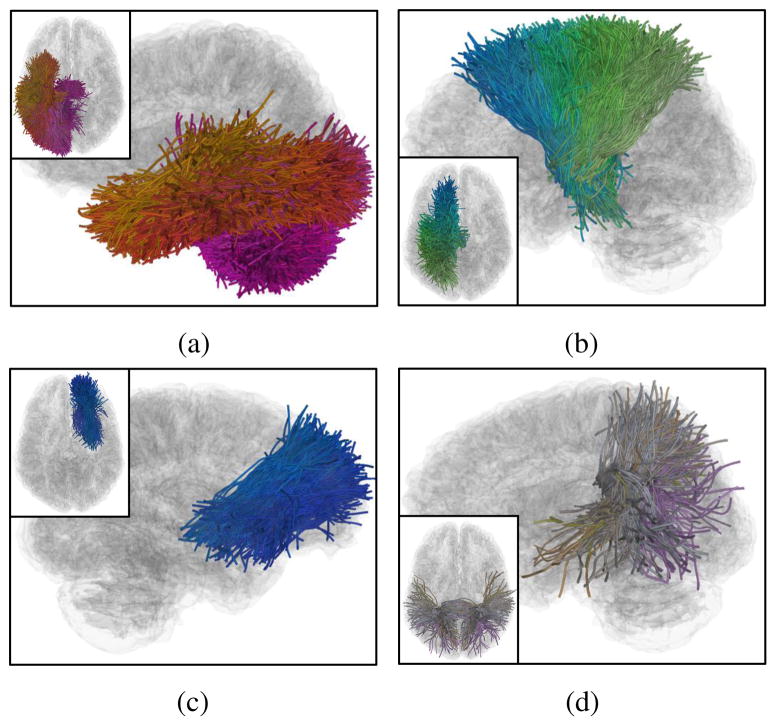
Under h = T – 2, we considered that T = 4 (across T ∈ [3,6]) was the most reasonable setting, which was used in all following experiments. This setting derived a maximal LFC (Figure 5b) for a high coverage of a local WM structure (cluster size 23) while the parcels within the LFC were highly white-matter-consistent (D_max = 68.9 mm). Given this setting, in Figure 6, we show several example FCs obtained in the whole brain parcellation and the inter-parcel distances per FC. The proposed STFC formation could identify FCs from different local WM structures that have different distance scales.

Figure 6.

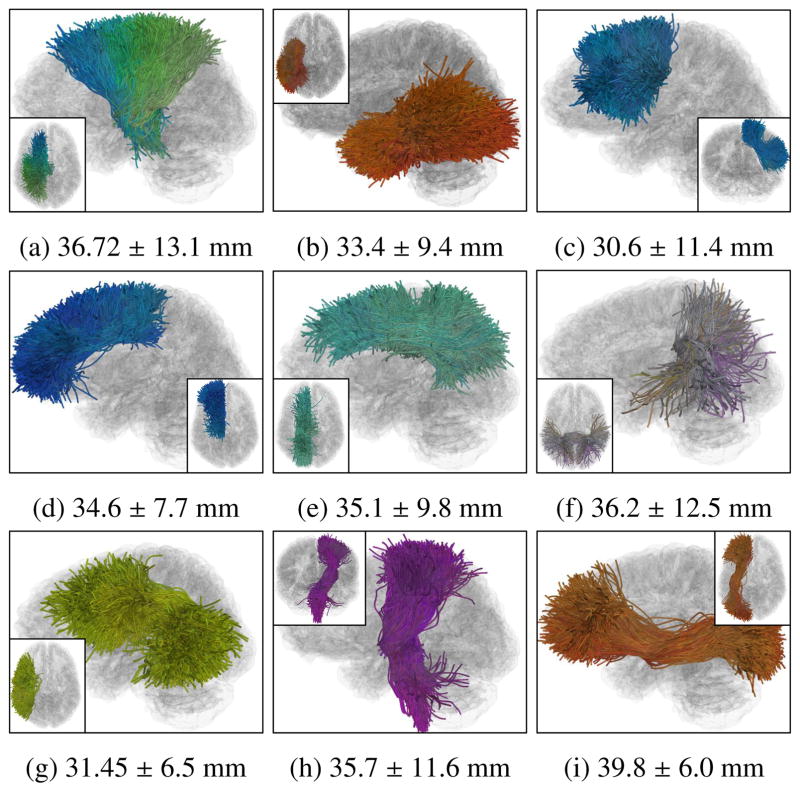
Visualizations of several example fiber clusters (FCs) obtained from the whole brain WM parcellation under the chosen parameter settings (T = 4 and h = 2), including the fiber connections belonging the local WM structures of (a) corona radiata (CR) (23 parcels), (b) inferior longitudinal fasciculus (ILF) (18 parcels), (c) frontal aslant tract (FAT) (14 parcels), (d) anterior cingulum (ACG) (11 parcels), (e) middle cingulum (MCG) (11 parcels), (f) posterior corpus callosum (CC) following the lateral paths to temporal lobes (6 parcels), (g) arcuate fasciculus (AF) (5 parcels), (h) corticalspinal tracts (CST) (5 parcels) and (i) inferior fronto-occipital fasciculus (IFOF) (5 parcels). Inter-parcel distances (mean ± standard deviation) within each of the FCs are displayed in the sub-captions. The proposed locally adaptive STFC formation was able to identify FCs from the different local WM structures that are expected to have different distance scales.

3.3. Synthetic Data Analysis

Given the chosen parameter settings, we first illustrate our STFC method on the synthetic data (Section 3.1.3) in the following two experiments.

3.3.1. Comparison of Multiple Comparison Correction Methods

We first compared the proposed STFC method with several multiple comparison correction methods using the synthetic datasets. The evaluation goal was to test if a method could correctly identify the parcels with true significance, even when the added change was small. To do this, we added synthetic feature changes to the ground truth parcels at different scales.

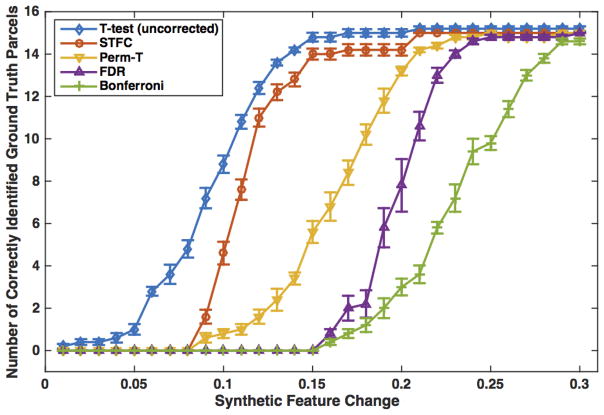
Comparisons were conducted among the uncorrected t-test, the proposed STFC method, a standard permutation test (Perm-T, N=10000) that used the minimal t-test-based p-value of all parcels for the summary statistic, and two traditional FDR (as applied in [100, 114]) and Bonferroni multiple comparison correction methods. The same significance level of α = 0.05 was used for all compared methods. Figure 7 displays the number of significantly different parcels that were correctly identified in each method. Here, we note that the four multiple comparison correction methods corrected for significance of the parcels that passed the initial uncorrected t-test. These were a subset of the ground truth parcels, i.e. the parcels with feature changes. (We note that in some experimental settings, the feature changes in the selected ground truth parcels were of small magnitude and therefore a subset of these parcels survived the initial t-test.) No false positives were detected by any of the compared methods.

Figure 7.

Comparison among different multiple comparison correction methods on the synthetic dataset: Number of correctly identified CC parcels per method, versus the level of synthetic group difference, is displayed. For each feature change scale (from 0.01 to 0.3), we reported the mean result from 10 randomly generated feature changes, with a quarter of the standard deviation displayed for better visualization.

3.3.2. Comparison of Locally Adaptive Neighborhood vs Global Distance Threshold

We then compared the proposed method to a simpler global-distance-threshold-based (GDTB) STFC formation approach as reported in our preliminary work [112]. Briefly, in GDTB, two parcels were considered as neighbors if their distance D (as in Eq. 1) was smaller than a user-given parcel distance threshold D_t, and neighboring suprathreshold parcels were joined to form STFCs.

The initially proposed GDTB method was relatively sensitive to the choice of distance threshold [112]; therefore we designed the current method to be highly robust to parameter selection. Here, we performed an experiment by varying the parameters of both methods to assess robustness of statistical findings in the synthetic data. Specifically, the GDTB approach has one parameter of the distance threshold D_t and the proposed approach has one parameter of the number of neighbor candidates T (given h = T – 2 as discussed in Section 3.2). The two methods were compared using a synthetic dataset with feature change at the level of 0.21, the minimum feature change to allow all ground truth parcels to be successfully detected by the initial t-test (Figure 7). Figure 8 shows the numbers of correctly identified parcels among those with feature changes given different parameter settings of the two methods. The proposed method was less sensitive to the parameter changes compared to the GDTB approach. The two STFC-based methods corrected for significance of the parcels that passed the initial uncorrected t-test. Therefore, no false positives were detected by the GDTB or the proposed method.

Figure 8.

Comparison between the proposed and a simpler global-distance-threshold-based (GDTB) STFC formations using the synthetic dataset: in GDTB (a), the numbers of correctly identified parcels were sensitive to the different distance threshold D_t values, while in the proposed method (b), the numbers of ground truth parcels that were correctly identified were similar across different T ∈ [3,6].

3.3.3. Receiver operating characteristic evaluations

We then performed a receiver operating characteristic (ROC) experiment to investigate potential false positives arising during the statistical analyses for the two STFC approaches: the GDTB method and the proposed method that uses a locally adaptive parcel neighborhood construction. We applied the alternative free-response ROC (AFROC) [17] method that has been used to measure the family-wise errors that could happen anywhere in the brain in the presence of multiple comparisons for neuroimage analyses [89, 75]. Specifically, in these studies the false positive rate (FPR) was computed using “noise-only” images as the probability of any false positives detected anywhere in the image, while the true positive rate (TPR) was computed using “signal+noise” images as the average fraction of true positives correctly detected.

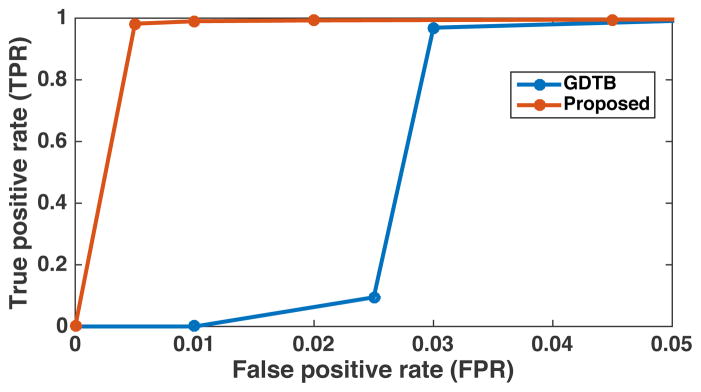
To perform an AFROC experiment using our tractography data, we extended the dataset from the previous experiment. We generated 1000 synthetic datasets, where each dataset was created by adding random Gaussian noise to the actual measured feature to create two synthetic groups (as described in Section 3.1.3). These were used as the “noise-only images” in our experiment. Then, for each synthetic dataset, we changed features of the ground truth parcels in the second synthetic group (as described in Section 3.1.3) at the level of 0.21 (as used in the above experiment). These were used as the “signal+noise images.” For the two compared STFC methods (i.e. GDTB and proposed), we varied the primary threshold (the uncorrected p-values from 0.01 to 0.1) to compute the ROC curves, as follows. At each threshold level, the FPR was computed as the probability of any false positive parcels detected anywhere across the 1000 synthetic datasets without feature changes (i.e. the “noise-only images”), and the TPR was computed as the average fraction of true positive parcels across the 1000 synthetic datasets after adding feature changes to the ground truth parcels (i.e. the “signal+noise images”). Similar to the studies from Smith and Nichols [89] and Raffelt et al. [75], we limited the ROC analysis to the FPR values smaller than 0.05 (FPR in excess of 0.05 is not of interest). We set the method parameters to D_t = 42 mm for the GDTB method and T = 4 for the proposed method, which were sufficient to detect all ground truth parcels in our previous experiment (Figure 8). Figure 9 shows the obtained ROC curves for the two compared STFC methods. The area under the curve (AUC) of the proposed method was 0.936 compared to that of 0.508 from the GDTB method, suggesting high sensitivity and specificity performances of the proposed method on these synthetic CC datasets.

Figure 9.

Receiver operating characteristic (ROC) curves obtained from the synthetic corpus callosum (CC) datasets using the alternative free-response ROC (AFROC) method for the two STFC methods: the global-distance-threshold-based (GDTB) method and the proposed method that uses a locally adaptive parcel neighborhood construction. The false positive rate (FPR) represents the probability of any false positive parcels detected anywhere across 1000 randomly generated synthetic datasets, and the true positive rate (TPR) is the average fraction of true positive parcels correctly detected across the 1000 datasets. The areas under the curve (AUCs) for the two methods are 0.936 and 0.508, respectively.

3.4. Real Data Analysis

Next, we show experimental results on the real data for a tract-specific study of the CC and a whole brain WM study.

3.4.1. Tract-specific Study of the Corpus Callosum

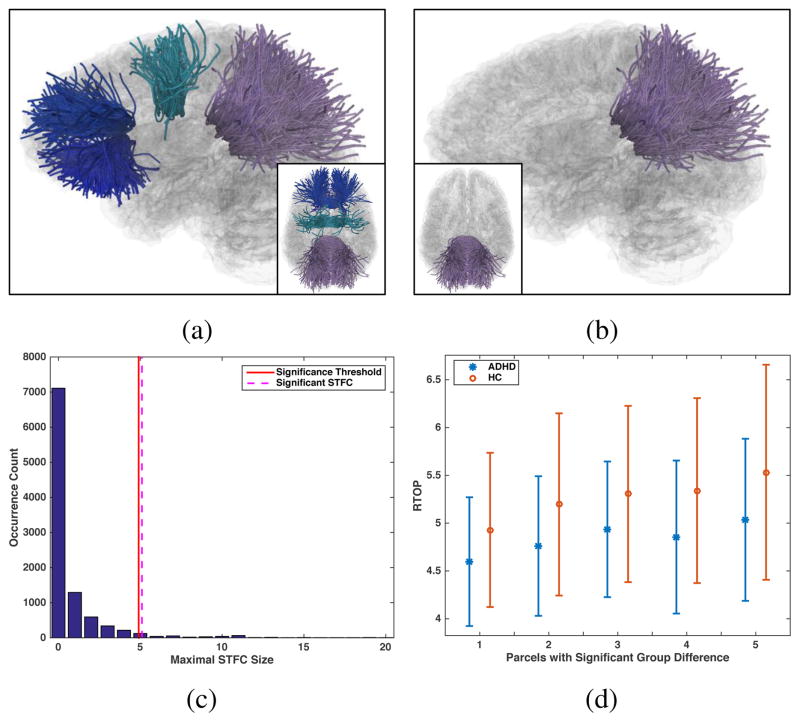
We first performed a tract-specific study to identify group differences specific to a local WM region. The CC tract was selected for a demonstration because it is one of the most commonly studied tracts in ADHD [14, 30, 69, 29]. Given the CC tract that consisted of a total of 34 parcels (Figure 4a), we first performed an one-tailed t-test with the null hypothesis H₀: μ_HC (M_RTOP) ≤ μ_ADHD(M_RTOP) to compute parcel-level statistics. 8 parcels passed the initial t-test with uncorrected p-values ≤ 0.05, as displayed in Figure 10a. Multiple comparison correction was then conducted using the STFC, the Perm-T, the FDR and the Bonferroni methods respectively, at a significance level of α=0.05. While no parcels survived the Perm-T, the FDR or the Bonferroni methods, a significant STFC of 5 parcels was identified using the proposed STFC method, as displayed in Figure 10b. (Please see the video S2 included in the supplementary material for a visualization of each individual WM parcel within the significant STFC.) The corrected significance value of the identified STFC was 0.046, as illustrated in Figure 10c. Comparisons of the group mean feature values (M_RTOP) of the 5 parcels are shown in Figure 10d.

Figure 10.

Real data experiment for tract-specific study of the corpus callosum: (a) 8 WM parcels passed the parcel-level statistic test, with uncorrected p-value ≤ 0.05; (b) The significant STFC consisting of 5 WM parcels from the splenium section of the CC; (c) Null distribution of the maximal STFC size from the permutation runs. Significance threshold of STFC size was 5, i.e. an STFC in the correctly labeled data with the size ≤ 5 would pass the significance level 0.05 as significant. The identified significant STFC had the size of 5, resulting in a corrected significance value of 0.046; (d) Comparison of M_RTOP values per identified parcel in the significant STFC, plotted in sorted order.

3.4.2. Whole Brain WM Study

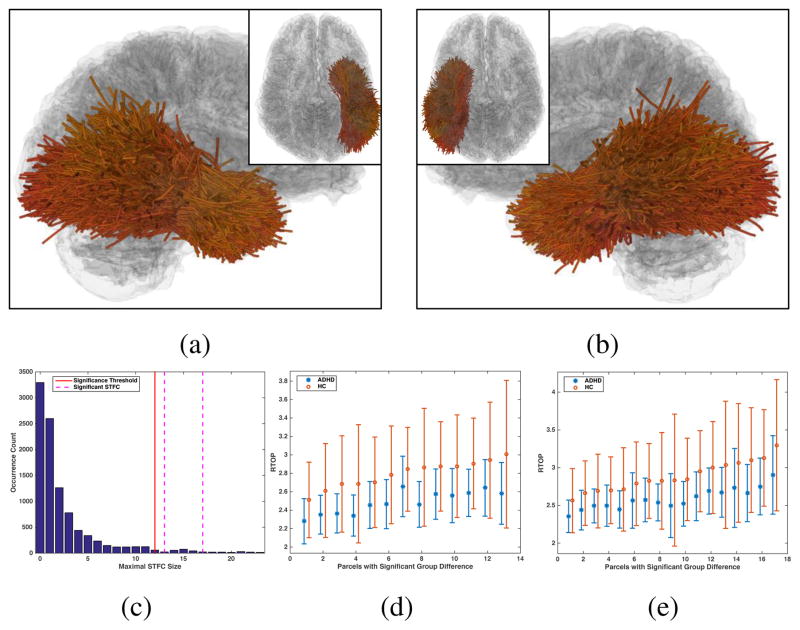
This experiment investigated potential WM alterations in the whole brain, without relying on a region-specific hypothesis. For the whole brain parcellation of a total of 1416 parcels (Section 2.2), 654 parcels had p-values smaller than 0.05 in the initial parcel-level t-test under the null hypothesis H₀: μ_HC (M_RTOP) ≤ μ_ADHD(M_RTOP). The same multiple comparison correction methods were applied as aforementioned. The FDR and the Bonferroni methods did not find any significantly different parcels between the groups. The Perm-T method identified one individual significant parcel (corrected p-value 0.0272) connecting the middle precentral gyrus to the supra-marginal and the superior-parietal gyri in the right hemisphere. Our method identified two significant STFCs of 13 and 17 WM parcels, which were located in the occipital and temporal lobes in both hemispheres as shown in Figures 11a and 11b. (Please see the video S3 included in the supplementary material for a visualization of each individual WM parcel within the significant STFCs.) The corrected significance values of the identified left and right hemisphere STFCs were p =0.035 and 0.015 respectively, as illustrated in Figure 11c. Comparisons of the group mean feature values (M_RTOP) of the parcels are given in Figures 11d and 11e.

Figure 11.

Real data experiment for the whole brain WM study: (a, b) The two significant STFCs consisting of 13 and 17 WM parcels respectively in the left and right occipital and temporal lobes; (c) Null distribution of the maximal STFC size obtained from the permutation runs. Significance threshold of STFC size was 12, i.e. an STFC in the correctly labeled data with the size ≥ 12 was considered as significant. The two significant STFCs had the sizes of 13 and 17, resulting in corrected significance values of 0.035 and 0.015 respectively. (d, e) Comparisons of M_RTOP values per identified parcel in the significance STFCs, plotted in sorted order.

4. Discussion

In this paper, we presented an STFC method that leverages the whole brain fiber geometry to enhance statistical analyses in identifying between-group white matter differences. We demonstrated the method’s performance with an application to a dataset of ADHD patients and healthy controls. We have several overall observations about the results, which are discussed below.

We demonstrated a high sensitivity and specificity of the proposed STFC method in identifying WM group differences while correcting for multiple comparisons. In the synthetic dataset with known group differences, results showed that the STFC method was more sensitive to detect the ground truth group differences when compared to three other multiple comparison correction methods (Figure 7). While the FDR and the Bonferroni methods could only find the significance when there were large differences (over 15% change of the group mean feature value), the two permutation-based approaches of the STFC and Perm-T could begin to detect the ground truth parcels after 9% feature changes (Figure 7). However, the STFC method could achieve a higher number of correctly identified parcels than the Perm-T method. The high sensitivity of the STFC method was also demonstrated by the experimental results on the real data analysis. In the tract-specific study, we identified a significant STFC of 5 WM parcels (Figure 10b), while no significance was found by the other three compared methods. In the whole brain WM study, two significant STFCs of a total of 30 WM parcels were identified using the STFC method (Figures 11a and 11b). Only one significant parcel was identified from the whole brain using the Perm-T method and no significance was detected using the FDR or Bonferroni methods. In addition, results from our AFROC experiment in the synthetic data analysis showed the proposed method’s high specificity, demonstrated by a high AUC value (0.936) obtained from the synthetic CC datasets (Figure 9).

The proposed method enabled a robust parameter selection, which was demonstrated from the following perspectives. First, reasonable parameter settings could be determined according to the whole brain fiber geometry in the population, prior to any statistical analyses (Section 3.2). Second, the proposed method was adaptive to the heterogeneous inter-parcel fiber distance scales in different WM structures (Figure 6). Third, the proposed method’s results demonstrated a low sensitivity to the changes of parameter settings (Figure 8).

Given the chosen parameters (T = 4 and h = 2), in the tract-specific study we found that the splenium could be most affected in the whole CC in ADHD. We used the median RTOP feature to explore potential changes in WM anisotropy in ADHD (Section 3.1). The feature comparison between the two groups showed significantly reduced median RTOP values in the ADHD individuals (Figure 10d), suggesting potentially reduced WM anisotropy in the splenium of the CC. This was consistent with the finding of altered splenium of the CC in ADHD in a review paper by Dougherty et al. [29], and with that of reduced anisotropy in this local CC region in dMRI-based studies [30, 69].

Regarding the experiments for the whole brain WM study, we identified WM regions with significant group differences in bilateral temporal and occipital lobes (Figures 11a and 11b). While previous studies have suggested these regions in either left [85, 20] or right [98, 61] hemispheres affected in ADHD, the alterations in both hemispheres have also been reported by recent studies [93, 31] similar to our analysis result. Our identified WM parcels had lower median RTOP values in the ADHD group when compared to the HC group, showing potentially reduced WM anisotropy in ADHD. Decreased WM anisotropy in the temporal and occipital lobes in ADHD has also been reported in multiple dMRI-based studies [20, 57]. The results related to the occipital and temporal lobes in our analyses are consistent with the findings in the existing literature in ADHD.

Potential future directions and limitations of the current work are as follows. First, similar to voxel-cluster-thresholding analyses, the proposed method aims to find large clusters of WM parcels with significance; thus it could potentially miss some significantly different parcels located in small neighborhoods, e.g. the one individual significant parcel identified in the standard permutation test (Perm-T). Second, it would be of interest to incorporate additional brain function and anatomy information, such as brain cortical parcellation from Freesurfer [32] or functional MRI data, to enable WM parcel neighborhood construction adaptively to not only local white matter anatomy but also brain functions. For example, only parcels connecting to the same Freesurfer cortical region could be considered as neighbors. Third, in our proposed method, we applied a parcel neighborhood construction to generate a binary neighborhood graph, followed by a CP-based fiber cluster formation, to identify STFCs adaptively to different inter-parcel distances. A further research direction could include applying a weighted-graph-based cluster formation method (e.g. the Lou-vain method [12]) on the pairwise parcel distance affinity D to reduce the number of parameters (e.g. the number of candidate neighbors T). Fourth, our previous work that applied the data-driven tractography parcellation method (Section 2.2) for a machine-learning-based classification task suggested that parcellation of the whole brain tractography into a large number of parcels tended to increase the classification performance [110]. Therefore, it would be of interest to investigate if a finer parcellation (in this study, we used a parcellation of 1416 parcels) could improve the statistical analysis by allowing the measurement of more locally specific WM changes.

5. Conclusion

In this paper, we have presented a novel suprathreshold fiber cluster (STFC) analysis to identify WM group differences using whole brain tractography. The proposed method leverages the whole brain fiber geometry to enhance statistical analyses of tractography while correcting for multiple comparisons to allow simultaneous analysis across the entire white matter. Experimental results suggest that our method in general is more sensitive for identifying WM group differences when compared to several traditional multiple comparison correction methods. The two real data demonstrations show that the proposed method can be generally applied in both hypothesis-driven tract-specific analysis and whole brain tractography analysis for between-population studies.