Identifying and characterizing systematic temporally-lagged BOLD artifacts

Abstract

Residual noise in the BOLD signal remains problematic for fMRI – particularly for techniques such as functional connectivity, where findings can be spuriously influenced by noise sources that can covary with individual differences. Many such potential noise sources – for instance, motion and respiration – can have a temporally lagged effect on the BOLD signal. Thus, here we present a tool for assessing residual lagged structure in the BOLD signal that is associated with nuisance signals, using a construction similar to a peri-event time histogram. Using this method, we find that framewise displacements – both large and very small – were followed by structured, prolonged, and global changes in the BOLD signal that depend on the magnitude of the preceding displacement and extend for tens of seconds. This residual lagged BOLD structure was consistent across datasets, and independently predicted considerable variance in the global cortical signal (as much as 30–40% in some subjects). Mean functional connectivity estimates varied similarly as a function of displacements occurring many seconds in the past, even after strict censoring. Similar patterns of residual lagged BOLD structure were apparent following respiratory fluctuations (which covaried with framewise displacements), implicating respiration as one likely mechanism underlying the displacement-linked structure observed. Global signal regression largely attenuates this artifactual structure. These findings suggest the need for caution in interpreting results of individual difference studies where noise sources might covary with the individual differences of interest, and highlight the need for further development of preprocessing techniques for mitigating such structure in a more nuanced and targeted manner.

1. INTRODUCTION

Analysis of BOLD data is predicated on the idea that the signals of interest can be separated from noise, so that reliable and meaningful conclusions about brain activity can be drawn. Accurate removal (i.e., “cleanup”) of non-random noise is particularly important for model-free, data-driven, techniques such as functional connectivity MRI (fcMRI) that seek to capture underlying structure in data. Because sources of residual noise can covary with individual differences of interest (e.g., Wilhelm, Trabert, & Roth, 2001; Siegel et al., 2016), these artifacts can produce spurious findings of group differences and may contribute to inconsistent results across studies when not properly addressed (Power et al., 2012; Satterthwaite et al., 2012; Van Dijk, Sabuncu, & Buckner, 2012; Deen & Pelphrey, 2012; Power et al., 2014; Tyszka, Kennedy, et al., 2014; Siegel et al., 2016; Satterthwaite et al., 2017). Understanding structured (e.g. non-random) residual noise is therefore critical both in order to assess how such noise might influence conclusions, and also to develop more effective cleanup methods.

But while preprocessing methods and recommendations are advancing at a remarkable rate, approaches for quantifying structured residual noise – a necessary first step before it can be addressed – are still largely lacking. It is widely known that many noise sources are not adequately modeled and removed from BOLD data (Birn, 2012; Uddin, 2017; Power et al., 2017a, 2017b) – in part because the mechanisms giving rise to fMRI noise are complex, often with temporally extended relationships between noise sources and effects. For instance, head motions can sometimes have effects on the BOLD signal that persist much longer in time than addressed by many existing preprocessing practices (Satterthwaite et al., 2013; Power et al., 2014; 2017; 2017a). Another example is respiration, which can produce structured noise at short timescales as chest movements modulate the magnetic field and at longer lags as the vasodilatory effects of changes in arterial CO₂ concentration (and concomitant changes in cerebral blood flow and volume) modulate the BOLD signal (Hu et al., 1995; Wise et al., 2004; Chang & Glover, 2009; Birn et al., 2006; 2008; 2014; Liu, Nalci, & Falahpour, 2017). Although methods for modeling and removing respiratory variance from fMRI datasets using respiratory belt recordings have been extensively developed (e.g., Glover, Li, & Ress, 2000; Birn et al., 2006, 2008; Chang & Glover, 2009; Falahpour, Refai, & Bodurka, 2013), such respiratory effects frequently remain unaddressed. These methods rely on models of respiration that are, like all models, imperfect, potentially leaving unmodeled respiration-related variance remaining in the data (Birn et al., 2006, 2008, 2012; Falahpour, Refai, & Bodurka, 2013; Power et al., 2017a) – and many existing datasets do not include respiratory belt recordings, precluding the use of these methods entirely.

Toward this end, here we present a new method for quantifying temporally extended noise artifact. Our approach is general and can be used to investigate temporally extended residual structured noise associated with any nuisance signal, and at any spatial scale. Here, we primarily focus on the framewise displacement trace (FD; an index of frame-to-frame head movement that is derived from image realignment estimates), for two reasons. First, it is available in all fMRI datasets, in contrast to physiological recordings (e.g., respiratory belt and pulse oximeter measurements) that are frequently unavailable and when collected are prone to acquisition difficulties and artifacts (Power et al., 2017a). Second, framewise displacements are likely to reflect numerous contributing sources and not only head motion per se (Power et al., 2012, 2014), and recent reports (Etzel, 2016; practiCALfMRI, 2016; Power, 2017; Power et al., 2017a) suggest that for multiband, high temporal resolution fMRI data, framewise displacements may partially index physiological noise – raising the possibility that framewise displacement traces might serve as a proxy or surrogate for assessing some effects of physiological noise in datasets even where those traces are unavailable. Here, we focus primarily on the global cortical (e.g., gray matter) BOLD signal, as many noise sources including motion and respiration can have widespread cortical effects (Wise et al., 2004; Satterthwaite et al., 2013; Power et al., 2014; 2017; 2017a).

Our general approach is to ask whether there is any common structure in the BOLD epochs immediately following all similar instances of the nuisance signal – specifically, following all framewise displacements within a particular range of values – using a construction similar to a peri-event time histogram. If there is any systematic covariance shared by BOLD epochs that follow similar displacements (within and/or across subjects), such a pattern reflects residual displacement-linked noise that should not be present in a perfect cleanup – regardless of the underlying sources of that noise. This is an extension of the logic of standard preprocessing, in which any relationship between the BOLD signal and a nuisance signal of no interest (typically, motion parameters) across the entire run is considered to be noise and removed in preprocessing (Friston et al., 1996).

Using this method, we find a characteristic pattern of structured BOLD artifact following even extremely small framewise displacements, including those that fall well within typical standards for data inclusion. These systematic FD-linked patterns of noise persist for temporally extended epochs – on the order of 20–30 seconds – following an initial displacement, with the magnitude of signal changes varying systematically according to the initial magnitude of displacement. This lagged BOLD structure seems to be impervious to many different methods of preprocessing, including some state of the art practices, and patterns are consistent across two independent datasets. This consistency allows us to model this artifact using one dataset and apply the model to individual FD traces in the other dataset, generating customized traces reflecting the cumulative effects of this artifact across each run. Using this approach, we find that the lagged BOLD structure following framewise displacements explains considerable variance in the global cortical BOLD signal. Importantly, global functional connectivity estimates also vary as a function of preceding framewise displacements. Disentangling the mechanisms underlying the observed residual noise is beyond the intended scope of this manuscript. However, physiological traces are available for a subset of scans analyzed, and exploratory analyses of these traces suggest the involvement of respiratory processes – because lagged BOLD structure is also apparent following respiratory (but not cardiac) fluctuations, and because respiratory and framewise displacement traces are themselves related. Removing a global BOLD signal during preprocessing minimizes the lagged structure following displacements, both in the BOLD signal and in functional connectivity. To allow others to examine their data in this manner, and to facilitate the development of preprocessing methods for addressing artifactual lagged structure, we have made a script available for use as a novel quality assessment tool for visualizing lagged structure associated with any nuisance measure.

2. METHODS

2.1. Datasets and data collection

We examined two fMRI datasets, one collected in-house at Indiana University (IU) and described here, and one publicly available from the Human Connectome Project (HCP; described in Smith et al., 2013). IU dataset acquisition parameters were chosen to be similar to Human Connectome Project (HCP) parameters, although there were slight differences (e.g. IU TR = 813 ms; HCP TR = 720 ms).

2.1.1. IU Dataset

Participants in this dataset included 25 high-functioning adults with an autism spectrum disorder (ASD; mean age 24.2; range 17–54; 6 female) and 29 age- and IQ-matched controls (NT; mean age 24.5; range 19-37; 5 female), recruited from the Bloomington, IN area. We have made a subset of this data publicly available as part of the Autism Brain Imaging Data Exchange II (ABIDE II) initiative (Di Martino et al., 2017). We excluded very little data a priori due to our interest in noise-associated BOLD structure, but we did exclude three ASD participants’ data due to consistently poor quality on all runs. In this report, we did not consider diagnosis and collapsed across groups, leaving a final sample of N=51 (41 male). All subjects provided written informed consent; all experimental procedures were approved by the Indiana University Institutional Review Board.

The study design consisted of two scanning sessions separated by approximately one week (mean 9.3 days between scan sessions, SD 6), with an optional third scanning session 201.6 days (approximately 6.7 months) later (SD 78.3 days). Each scanning session consisted of two approximately 16-minute resting state scans (interleaved with two scans where subjects watched videos, to be reported elsewhere). Subjects were instructed to move as little as possible and remain awake with eyes open. No visual stimulus was provided. Wakefulness was monitored via an MR-compatible video camera; scans in which participants fell asleep were excluded from analysis (6 scans total; 4 from 3 ASD participants and 2 from 1 NT participant). One additional scan was excluded due to a technical issue. The final sample analyzed included multiple scans for most participants (261 scans analyzed, mean 4.83 (SD 1.66) resting state runs per participant). Anatomical images were acquired after (session 1 and 2) or in between (session 3) resting state functional runs, during which participants watched a video in the scanner.

MRI images were acquired using a 3 Tesla whole-body MRI system (Magnetom Tim Trio, Siemens Medical Solutions, Natick, MA) with a 32-channel head receive array. Both raw and prescan-normalized images were acquired; raw images were used at all preprocessing stages and in all analyses unless specifically noted. During functional scans, T2*-weighted multiband echo planar imaging (EPI) data were acquired using the following parameters: TR/TE = 813/28 ms; 1200 volumes; flip angle = 60°; 3.4 mm isotropic voxels; 42 slices acquired with interleaved order covering the whole brain; multi-band acceleration factor of 3. Preceding the first functional scan, gradient-echo EPI images were acquired in opposite phase-encoding directions (10 images each with P-A and A-P phase encoding) with identical geometry to the EPI data (TR/TE = 1175/39.2 ms, flip angle = 60°) to be used to generate a fieldmap to correct EPI distortions, similar to the approach used by the Human Connectome Project (Smith et al., 2013). High-resolution T₁-weighted images of the whole brain (MPRAGE, .7 mm isotropic voxel size; TR/TE/TI = 2499/2.3/1000 ms) were acquired as anatomical references.

2.1.2. HCP Dataset

This dataset was comprised of a subset of 73 participants (34 male) from the “100 Unrelated Subjects” Public Data release of the Human Connectome Project (http://www.humanconnectome.org). Participant recruitment and consent is described in (Van Essen et al., 2013). In the current sample, participant age groups were as follows: 11 22-25 years, 27 26-30 years, 34 31-35 years, 1 36+ years. As for the IU dataset, very little data was excluded a priori, but we did exclude one subject with consistently poor data quality, leaving a final sample of N = 72 (33 male). MRI data acquisition and preprocessing is detailed in (Smith et al., 2013; Glasser et al., 2013) and briefly summarized here.

Subjects participated in four resting state scans across two sessions (2 scans per session), each approximately 15 minutes long (1200 TRs). In the current sample analyzed, 4/4 runs were available for 40 subjects and 2/4 runs were available for 33 subjects (due to an interrupted data download) for a total of 226 runs. Participants were instructed to remain awake with eyes open. MRI images were acquired using a customized 3 Tesla Siemens Skyra with 32-channel head coil. Parameters for T₂*-weighted resting state scans were as follows: TR/TE = 720/33.1 ms; 1200 volumes; flip angle = 52°; 2 mm isotropic voxels; 72 slices; multi-band acceleration factor of 8. High-resolution T1-weighted images of the whole brain were also acquired (MPRAGE, .7 mm isotropic voxel size; TR/TE/TI = 2400/2.14/1000 ms) as anatomical references.

2.2. MRI Data Preprocessing

2.2.1. IU Dataset

Data were preprocessed with an in-house pipeline using FEAT (v6.00) and MELODIC (v3.14) within FSL (v. 5.0.8; FMRIB’s Software Library, www.fmrib.ox.ac.uk/fsl), Advanced Normalization Tools (ANTs; v2.1.0) (Avants et al., 2011), and Matlab_R2014b.

Individual anatomical images were bias-corrected and skull-stripped using Advanced Normalization Tools (ANTs), and segmented into gray matter, white matter, and CSF partial volume estimates using FSL FAST. From 20 randomly selected anatomical images (10 NT; 10 ASD), a midspace template was constructed using ANTs’ buildtemplateparallel tool, and then skull-stripped. Composite (affine and diffeomorphic) transforms warping each individual anatomical image to this midspace template, and warping the midspace template to the Montreal Neurological Institute MNI152 1mm reference template, were obtained using ANTs.

The initial five volumes (~4 s) of each functional run were discarded to minimize magnetization equilibration effects. Framewise displacement traces for this raw (trimmed) data were computed using fsl_motion_outliers. Five parallel preprocessing streams were used to assess robustness of results: FIX, conventional GLM, conventional GLM including global signal regression (GSR), conventional GLM followed by mean cortical signal regression (equivalently, mean grayordinate time series regression or “MGTR”, following Burgess et al., 2016) in a second step (GLM+MGTR), and finally FIX followed by mean cortical signal regression in a second step (FIX+MGTR). Common preprocessing steps included rigid-body motion correction, field map-based geometric distortion correction, and non-brain removal, but not slice-timing correction (due to the fast TR; Smith et al., 2013). Initial preprocessing also included weak highpass temporal filtering (> 2000s FWHM) to remove slow drifts (as in Smith et al., 2013) but no spatial smoothing. Off-resonance geometric distortions in the EPI data were corrected using a fieldmap derived from two gradient-echo EPI images collected in opposite phase-encoding directions (P-A and A-P) using FSL topup (similar to Smith et al., 2013). The FIX and FIX+MGTR preprocessing streams employed FSL-FIX (Salimi-Khorshidi et al., 2014) and regressed out independent components classified as noise by a classifier trained on independent but similar data and validated on hand-classified functional runs. For the FIX preprocessing stream, these residuals were analyzed as the “cleaned” data. In conventional GLM, GSR, and GLM+MGTR preprocessing streams, nuisance signals were linearly regressed from the preprocessed data, and the residuals were analyzed as the cleaned data. In all 3 streams, nuisance signals included the mean time course for the eroded white matter and CSF masks, their temporal derivatives, as well as the 6 rigid-body motion parameters and their temporal derivatives. In GSR preprocessing only, nuisance signals also included two additional nuisance regressors: the global signal (the mean time course for the whole brain mask) and its derivative. In both the GLM+MGTR and FIX+MGTR preprocessing streams, the mean cortical signal (the mean BOLD signal across the individuals’ gray matter partial volume estimate obtained from FSL FAST) was regressed from the residuals (following conventional GLM or following FIX) in a second step (as in Burgess et al., 2016), and the resulting residuals were analyzed as the cleaned data.

Subsequent preprocessing steps were identical for each preprocessing stream. Registration of cleaned functional data occurred as follows. An affine transformation matrix registering the mean prescan-normalized functional image to each subject’s skull-stripped T₁-weighted anatomical image was obtained using Boundary-Based Registration (BBR) via epi_reg within FSL. (The mean prescan-normalized images yielded more accurate alignment than the raw functional images, due to the reduced contrast in fast-TR EPI data; see also Smith et al., 2013.). Next, each subject’s functional images were transformed to the MNI152 reference all in one step, using ANTS to apply a concatenation of this affine transformation matrix with the composite (affine+diffeomorphic) transforms mapping between the subject’s anatomical image, the midspace template, and the MNI152 reference.

For this dataset, we examined these residuals at two spatial scales. For most analyses, we analyzed the mean cortical BOLD signal, computed as the mean of the cleaned BOLD signal across the individuals’ gray matter partial volume estimate (obtained from FSL FAST). For functional connectivity analyses, we also obtained region of interest timeseries using the Harvard-Oxford Atlas distributed with FSL. Here, individual region of interest masks were created for each subject from the product of the individuals’ gray matter partial volume estimate and the region of interest mask (as in Tyszka, Kennedy, et al., 2014). The weighted mean signal across each individual region of interest mask was then extracted from the cleaned BOLD signal for each functional run. These time courses together formed the basis for all subsequent analyses.

2.2.2. HCP Dataset

Preprocessing for the HCP dataset is extensively described by Smith and colleagues (2013). We analyzed primarily the “Resting State fMRI FIX-Denoised” release, as well as the “minimal” preprocessing release (both as described in Smith et al., 2013; Glasser et al., 2013). We also conducted an additional preprocessing step, FIX+MGTR, by regressing out the mean cortical signal (and its derivative) from the FIX-denoised residuals in a second step (as described in Burgess et al., 2016). Framewise displacement traces based on the movement parameters distributed with the data were computed via in-house MATLAB scripts following Power and colleagues (2012).

As for IU data, we examined the resulting residuals at two spatial scales, mean cortical and ROI-level, as well as at a third finer scale of grayordinates (surface-based gray matter vertices; Glasser et al., 2013). ROI-level analyses used the parcellation introduced by Glasser and colleagues (2016). For mean cortical and ROI-level analyses, the time courses to be analyzed were extracted by computing the mean across the corresponding grayordinates.

For this dataset only, physiological recordings were available for some runs (N = 182), downloaded from the “900 Subjects Release” from the Human Connectome Project. Following Power et al., (2017a) the respiratory belt traces were preprocessed as-provided, without manual inspection for artifacts. The pulse oximeter traces were also preprocessed as-provided, without inspection, as they were not the primary focus of this project. Physiological records were preprocessed using the PNM (“Physiological Noise Modelling”) tool distributed with FSL (Brooks et al., 2008) to generate 34 physiological regressors: 32 RETROICOR-style regressors (Glover et al., 2000) including 8 cardiac regressors (up to 4^th order), 8 respiratory regressors (up to 4^th order), and 8 interaction regressors (up to 2^nd order), and as well as heart rate and respiration volume per time (Birn et al., 2006).

We also used PNM-generated regressors in one additional preprocessing method further detailed in Supplemental Methods.

2.3. Data Analysis

2.3.1. Overview

Our objective is to characterize structured patterns in the preprocessed BOLD signal following framewise displacements (or other nuisance measurements) of various magnitudes. To do this, we use an approach similar to a peri-event time histogram, and analyze a collection of time courses aligned by some shared event. But rather than aligning BOLD time courses based on an external stimulus presentation event, we instead consider framewise displacements as an “event” and examine the BOLD signal during the 65 time points that follow. Framewise displacements are measured continuously, and so one 1200 TR resting state run for one subject contains 1135 (1200-65) displacement “events” together with the immediately following 65 TR segments of the BOLD signal. We aggregate all such BOLD segments (within and across subjects) with similar displacements, and then ask whether the magnitude of initial displacement predicts any common pattern later in the BOLD segment. For example, we can ask whether there is any common structure in the BOLD signal 5, 20, or 30 time points following a displacement of approximately 0.4mm.

Our general approach can be applied to investigate BOLD time courses at any spatial scale. Here we primarily examine the mean of the preprocessed BOLD signal across the entire gray matter (cortical signal) across resting state scans, due to recent reports of prolonged consequences of larger framewise displacements that are largely global throughout the cortex (Satterthwaite et al., 2013; Power et al., 2014; 2017; 2017a). We also examine the preprocessed BOLD signal at each “grayordinate” (Glasser et al., 2013), to examine whether patterns observed are truly global.

Then, we examine individual subjects and individual runs. We begin by using this same general approach to aggregate the cortical BOLD signal for all scans within an individual, to ask whether the group-level structure observed is also visible within individual subjects. We then ask how well this lagged BOLD structure predicts the global cortical BOLD signal for a given scan. To do this, we use the pattern of lagged BOLD structure in one dataset as a model, apply that independent model to individual FD traces in the other dataset, and ask how much variance in the global cortical BOLD signal has been explained.

Next, we examine whether global functional connectivity estimates computed across short sliding windows also vary according to preceding displacements – specificially, whether functional connectivity might vary as a function of temporal distance from displacement and displacement magnitude. (For instance, whether functional connectivity computed across windows beginning 5 TRs after a ~0.4 mm displacement differed from functional connectivity computed across windows beginning 20 TRs later, and whether these FC estimates differed from FC estimates following ~0.2mm displacements.)

Finally, to gain some initial hints into the mechanisms underlying the patterns we observe, we also examined lagged structure associated with physiological recordings where available, for a subset of runs in the HCP dataset.

The details of each of these analyses are provided in the following sections.

2.3.2. Main approach

We first z-scored the mean cortical BOLD signal (GM signal) computed from the preprocessed BOLD data for every resting state scan. Next, we extracted all epochs of 66 TRs from this z-scored signal. We chose 66 TRs (~50 seconds) because based on prior reports, we expected displacement-linked effects on the BOLD signal to largely dissipate before then (Satterthwaite et al., 2013; Power et al., 2014; 2017; 2017a) and to limit computational demands.

For a single 1195 TR resting state scan, this yielded 1130 (1195-66-1) epochs. We excluded the initial epoch (corresponding to the first TR of each preprocessed scan, which has 0 displacement by definition), yielding 1129 epochs per 1195 TR scan (for IU data, and 1134 epochs for the 1200 TR scans in the HCP dataset). We then combined these epochs across subjects and across resting state scans (except when noted), resulting in 294669 epochs in total for the IU dataset and 256284 for HCP.

As described earlier, we conceptualized framewise displacement as an “event” and we were interested in whether similar displacements at the beginning of an epoch were linked with any structure later in the epoch. We defined similar displacement ranges as follows: 0-0.05 mm, 0.05-.1 mm, .1-.15 mm, .15-.2 mm, .2-.25 mm, .25-.3 mm, .3-.35 mm, .35-.4 mm, .4-.45 mm, .45-.5 mm, .5-.55 mm, .55-.7 mm, .7-.9 mm, .9-1.5 mm. Wider ranges for the larger displacements were chosen to increase sample sizes, which are listed in Supplemental Table 1. BOLD epochs beginning with displacements exceeding 1.5mm were rare (see Supplemental Table 1) and were excluded from analysis.

For each displacement range, we report the mean z-scored cortical BOLD signal across all the epochs that begin with a framewise displacement within that range. (For instance, for displacements of ~0.4mm, the mean signal across every timepoint that occurs 1 TR after a ~0.4mm displacement, the mean across every timepoint that occurs 2 TRs after a ~0.4mm displacement, and so on.) We note that an alternative approach is a finite impulse response analysis, as employed by Satterthwaite and colleagues (2013), which deconvolves closely spaced events (see also Birn et al., 2008, for a related approach). Our approach, in contrast, captures the natural statistics of displacements as they occur in the scanner. We also conducted this main analysis using medians rather than means, with no appreciable differences, so only means are reported here. We repeated this main cortical BOLD signal analysis for each preprocessing method considered and for each dataset.

We also conducted this main analysis at the fine spatial scale of grayordinates (corresponding to gray matter surface vertices; Glasser et al., 2013) using the HCP dataset. For 15,000 randomly selected cortical grayordinates, we repeated the main analysis using the preprocessed BOLD signal at that grayordinate rather than the mean cortical BOLD signal. To limit computational demands, this analysis (only) was restricted to the subset of 40 HCP subjects where all 4 runs were available.

We also conducted this main analysis at the individual subject level, using the mean cortical BOLD signal, and aggregating across all runs available for that subject. Due to the smaller sample sizes, we omitted displacement ranges that did not have at least 20 instances.

All analyses were conducted in TR space, but because TR differed slightly between IU and HCP datasets (813 ms vs. 720 ms), we present all results converted into seconds for easier comparison between datasets.

2.3.3. Alternative explanations

Because our main approach introduces some structure, we conducted a number of checks to ensure the patterns documented were not inadvertently introduced by our method or explained by other factors. These secondary analyses were all conducted using the mean cortical BOLD signal, for both datasets.

Check 1

We permuted the association between BOLD signal and FD traces, such that one subject’s BOLD data for a given run is associated with another subject’s FD trace for that same run, 1000 times, repeating the main analysis for each permutation. The expectation is that the average pattern across these iterations should not show any displacement-BOLD relationship.

Check 2

Our approach averages together potentially overlapping epochs, which could introduce additional autocorrelation above and beyond what is typical in fMRI data. Accordingly, we repeated the complete main analysis but only averaged over epochs that were at least 20 TRs apart, so that adjacent TRs are never directly averaged together. We conducted this analysis 20 times, to sample the data exhaustively. The expectation is that the average pattern observed across these iterations resembles the original pattern obtained in the main analysis.

Check 3

We conducted the original analysis upon epochs of FD traces rather than the BOLD signal. The expectation is that any structure observed in the FD traces is dissimilar to the patterns observed in the BOLD signal.

Check 4

We conducted the main analysis using 100 data-derived displacement ranges, each range including 1% of displacement magnitudes. Ranges are presented in Supplemental Figure 6. The expectation is that the pattern obtained resembles the primary pattern observed using the original displacement ranges, which would indicate that the pattern is not an artifact of displacement range choices.

2.3.4. Modeling the global cortical BOLD signal using lagged structure following displacements

We used the lagged BOLD structure following displacements in one dataset (i.e., either IU or HCP) as a model for independently predicting the mean cortical BOLD signal in the other dataset based on displacements alone. To do this, we first linearly interpolated the lagged patterns observed in each dataset from the native TR space to the TR space of the other dataset. 57 TRs post-displacement were available for both datasets (65 HCP TRs ≈ 57 IU TRS). Next, for a given FD trace, for the displacement magnitude at a given TR, we obtained the expected (based on the other dataset) lagged BOLD structure following that displacement for the next 57 TRs, and iteratively summed all such expected structure across the entire scan. We then used these resulting customized models of lagged post-displacement structure to predict the mean cortical BOLD signal for that same run. To establish a null distribution, for each scan, we conducted 1000 permutations in which we linked the mean cortical BOLD signal for that scan with customized models of lagged post-displacement structure from scans from different subjects and conducted the same regressions. We established empirical p-values for individual runs by comparing the actual R² obtained against the R² obtained by all permutations of that subject’s data against unrelated customized models. For comparison, we also conducted the same regressions and null distributions using raw FD traces rather than the customized models of lagged post-displacement structure.

We were also interested in how many TRs post-displacement the customized models should include to achieve the best predictions possible. To assess this, we varied the number of post-displacement TRs included in the model, t, from 1 to 57. For each such t we conducted the same regressions as above across all runs, predicting the global cortical signal as a function of customized lagged displacement models including t post-displacement TRs.

As above, we converted results to be a function of seconds post-displacement rather than TRs post-displacement, for clearer comparison across datasets.

2.3.5. Examining functional connectivity

We finally examined whether functional connectivity estimates differ as a function of time elapsed since displacement and the magnitude of that displacement. To do this, we used the z-scored mean preprocessed BOLD time courses computed across the 96 cortical ROIs of the Harvard-Oxford Atlas for the IU dataset and across the 360 cortical ROIs of the Glasser parcellation (Glasser et al., 2016) for the HCP dataset. We strictly censored all TRs with FD >= .2 mm. We then computed cortical functional connectivity as the fisher-z transformed pairwise correlations among segments of these ROI time series – specifically across short overlapping sliding windows of about 20 seconds (25 TRs for IU, 28 TRs for HCP). Sliding windows that were more than 50% censored were excluded entirely. Based on the results of the main analysis regarding the global nature of the patterns observed, we restricted our primary FC analysis to global FC levels (i.e., the mean computed across an entire FC matrix).

Our process was as follows: for a given scan and a given TR with an associated framewise displacement value, we compute global FC across a sequence of overlapping sliding windows spanning a total of around 54 seconds (66 windows for IU dataset, 75 for HCP). The first sliding window is taken entirely before the displacement in question. Windows are moved forward in time in 1 TR increments. For each displacement range, all such peri-displacement-event global FC window sequences were averaged first within subjects and then across subjects. Sample sizes for this analysis are listed in Supplemental Table 3.

To rule out alternative explanations, we also permuted the association between BOLD signal and FD traces, such that every subject’s BOLD data is associated with a different subject’s FD trace, repeating this FC analysis for each permutation. We conducted 500 such permutations for each dataset.

2.3.6. Structure associated with physiological recordings

To gain insights into potential mechanisms underlying the structure observed, we applied our main analytic method to examine structure associated with the physiological recordings that were available (for a subset of the HCP dataset only), with a more comprehensive examination beyond the intended scope of this manuscript. We examined 34 physiological regressors generated by FSL PNM based on these recordings. Regressors were z-scored and then used to define 14 percentile-based ranges, from the lowest to the highest values observed (across subjects), for each type of regressor. Note that we chose 14 ranges for consistency with prior analyses, but the pattern of results was similar across numerous range choices.

We examined these regressors in two ways. First, we repeated the main analysis, but instead of examining epochs of the BOLD signal as a function of displacement ranges, we examined BOLD epochs as a function of the ranges obtained for each of the nuisance signals examined. Second, to better understand relationships between displacement and each physiological regressor, we conducted an analogue of Check 3, except instead of examining epochs of FD traces as a function of displacement ranges, we examined epochs of each type of physiological trace as a function of those same displacement ranges.

3. RESULTS

3.1. Framewise displacements are followed by residual lagged structure in the global cortical BOLD signal

We found that a robust, temporally-extended relationship between framewise displacement and the mean cortical BOLD signal remains following many common preprocessing methods. Figure 1a (left) depicts this relationship within the IU dataset after FIX preprocessing. It presents the mean cortical BOLD signal taken across all epochs that begin with displacements within each of the ranges examined. The epochs that are combined for this analysis are taken from different times, different runs, and different individuals during a resting state protocol, and thus share nothing in common except initial framewise displacement magnitude. Although a perfect cleanup would eliminate any covariance between displacement and the later BOLD signal, it is evident from Figure 1a (left) that residual structure following displacement remains, and varies systematically with the severity of initial displacement.

Figure 1.

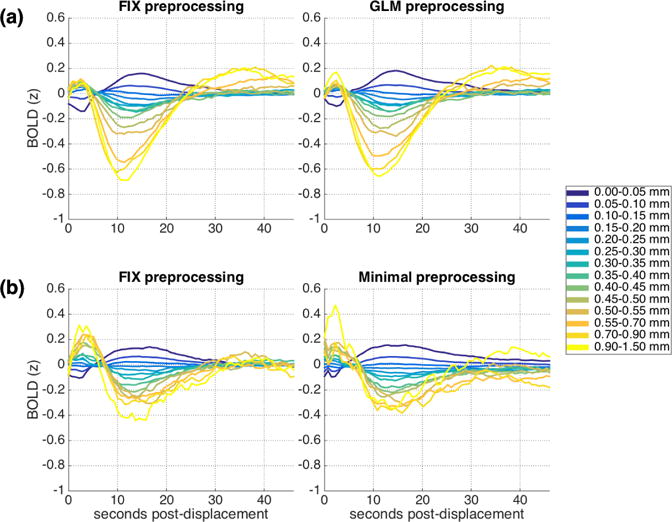
Mean cortical BOLD signal following framewise displacements of similar magnitudes. (a) IU dataset, FIX (left) and GLM (right) preprocessing. (b) HCP dataset, FIX (left) and Minimal (right) preprocessing. The BOLD signal for each run was z-scored before dividing into epochs, combining across runs and across subjects, and averaging. See also Supplemental Figure 3 for a version of Fig. 1a (right) conducted using slice time correction, and Supplemental Figure 4 for a version of Fig 1b (left) conducted in the WM and CSF.

Structure is evident in the BOLD epochs following most of the displacement ranges examined. Extrema are observed at around 2-3 seconds following the initial displacement and again after around 10-14 seconds. Peak amplitudes are largest for both extremes of the displacement ranges considered – for the very smallest displacements as well as for the larger displacements, and scale parametrically with displacement magnitude. Very small displacements are followed by an initial BOLD depression and a later BOLD elevation, while large displacements are followed by an initial BOLD elevation and later depression. For most displacement ranges, the BOLD signal returns to baseline around 25-30 seconds post-displacement. Supplemental Figure 1a presents the mean cortical BOLD signal along with 95% confidence intervals for each initial displacement range separately, for closer examination of the patterns and range of variability. Supplemental Figure 2a presents a censored version of Figure 1a, with all TRs with FD >= 0.2mm censored, indicating that the pattern is not driven by excessive motions occurring after the initial displacement.

3.2. The pattern of lagged structure following displacements is consistent across datasets and preprocessing streams

As Figure 1b (left; see also Supplemental Figure 1b) demonstrates, a very similar pattern of results is present when the same analyses are conducted using the HCP dataset (FIX preprocessing), despite differences in sites, populations, and protocols. Initial framewise displacements are associated with cortical BOLD signal elevations and depressions extending far after the initial displacement. Although there are some numerical differences across datasets in the amplitudes and temporal properties of the mean cortical BOLD signal for the different displacement ranges, the overarching structure is largely the same: two opposite-signed extrema separated by around 10 seconds and then an eventual return to baseline with amplitudes increasing systematically with displacement magnitude.

This pattern is not specific to just one commonly used preprocessing method. Figure 1a (right; see also Supplemental Fig. 1c) show the same analyses conducted using conventional GLM preprocessing in the IU dataset; Figure 1b (right; see also Supplemental Fig 1d) show the same analyses conducted using the minimal preprocessing release of the HCP dataset. In all cases, the patterns are largely the same.

3.3. The pattern is not accounted for by several alternative explanations

To establish that the pattern truly covaries with displacements rather than arising due to some other aspect of our analytic procedure, we conducted a number of checks. First (Check 1), we repeatedly permuted the association between the BOLD signal and framewise displacement traces, such that BOLD data from one subject was associated with framewise displacement from another subject. The results are presented in Figure 2a (IU FIX) and 2b (HCP FIX) and the characteristic structure observed in Figure 1 is absent.

Figure 2.

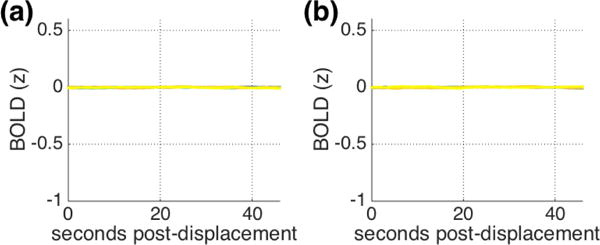
Mean patterns across 1000 permutations of BOLD-FD relationships in (a) IU and (b) HCP datasets with FIX preprocessing (Check 1). The structure observed in Figure 1 is absent. Note that the same 14 displacement ranges are plotted as in Figure 1 but cannot be visually distinguished.

Second, our analytic approach introduces autocorrelation above and beyond what is normally found in fMRI data, because it averages together all BOLD epochs for a given displacement range, which could include neighboring timepoints within a run. (For instance, if framewise displacements at TR 2 & 3 are equivalent for a given scan, the BOLD epoch from TR 2-67 and the epoch from TR 3-68 would be among the epochs averaged together.) To ensure that this additional autocorrelation is not driving our pattern of results, we conducted a downsampled version of the same analyses, in which we only averaged together epochs that were separated by at least 20 TRs (Check 2). We repeat this analysis 20 times, to fully sample the data, and present the average patterns across iterations in Supplemental Figure 5. The structure is highly similar to the original pattern of results, indicating this pattern is not driven by autocorrelation among neighboring data points.

Third, framewise displacement is of course measured continuously throughout the scan, and displacements at every time point (and not only at the onset of each epoch) have the potential to influence the BOLD signal. As our approach does not attempt to deconvolve adjacent displacement “events” (as in e.g. Satterthwaite et al., 2013), we must ask whether the pattern observed in the BOLD signal following displacement might be explained by similar systematic patterns in subsequent displacements. To do this (Check 3), we repeated the main analysis, but instead of examining epochs of the BOLD signal, we examined epochs of the FD trace itself. Figure 3 presents the mean FD trace for each displacement range. Larger initial displacements tend to be associated with somewhat larger displacements across the entire epoch, with remarkably similar patterns across datasets. However, the pattern observed in the FD traces is quite distinct from the pattern observed in the BOLD data. Although these ongoing displacements will surely contribute to the BOLD patterns observed, they are not sufficient to fully explain them.

Figure 3.

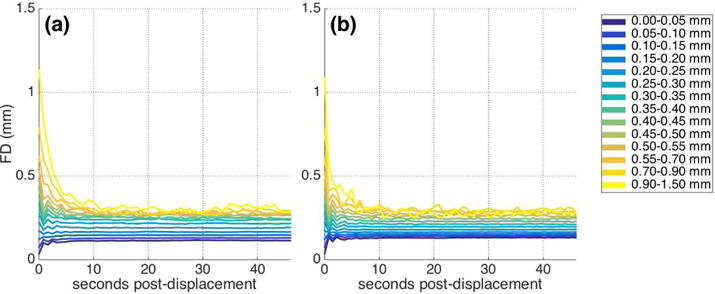
Main analysis performed using epochs of FD traces instead of BOLD signal (Check 3). Figure depicts mean FD across epochs following similar initial displacements for (a) IU and (b) HCP dataset with FIX preprocessing. Larger initial displacements tend to be associated with larger displacements throughout the epoch, but the structure differs from the pattern observed in the BOLD data.

Finally, in both datasets, sample sizes varied across displacement ranges. To ensure that the structure observed was not influenced by the base rates of displacements within each range, we repeated the same analyses using percentile-based displacement ranges. The results are presented in Figure 4 (left), in which each line plotted shows the mean pattern across each 1 percentile of displacement magnitudes for IU (4a) and HCP (4b) datasets using FIX preprocessing. (The displacement ranges are provided in Supp. Fig. 6). Similarity to the original pattern of results in Figure 1 is high, indicating that the pattern does not arise due to our original selection of displacement ranges, and similarity of the pattern across datasets is remarkable.

Figure 4.

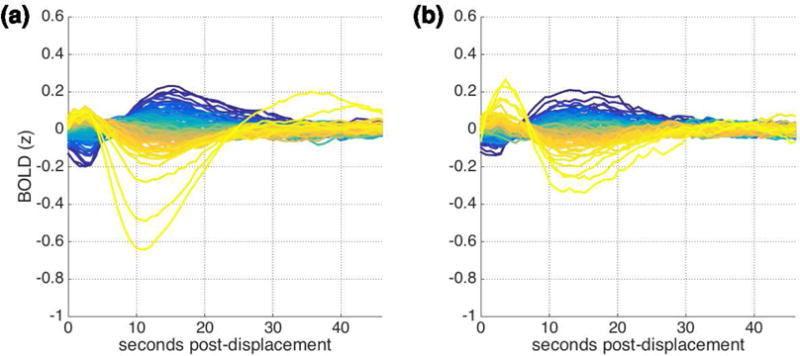
Mean cortical BOLD signal following data-derived displacement ranges, each corresponding to 1 percentile of displacements for (a) IU and (b) HCP datasets. Displacement ranges for each dataset are presented in Supplemental Figure 6; the smallest displacements are in blue while the largest displacements are in yellow.

3.4. The pattern is largely consistent across the whole cortex

We began with the mean cortical BOLD signal based on reports of temporally lagged effects of displacements that were widespread across the brain. To assess whether the specific patterns we observed in the mean cortical BOLD signal are accurately characterized as global patterns, we asked whether similar patterns were observable across the cortex at a finer scale. To do this, using the HCP dataset, we repeated the main analyses using the BOLD signal for a given grayordinate rather than the mean cortical BOLD signal. Figure 5 depicts the mean signal for each displacement range for a randomly selected subset of 15,000 cortical grayordinates, with the global pattern from Figure 1b (left) superimposed. It is clear from the figure both that the pattern is found at individual grayordinates and is largely homogeneous across grayordinates. Thus, the lagged BOLD structure we observe following displacements is indeed largely global.

Figure 5.

Main analysis performed at individual grayordinates for HCP data with FIX preprocessing. Each raster contains 15,000 rows; each row corresponds to one randomly-selected grayordinate and depicts the mean BOLD signal following similar framewise displacements at that grayordinate, from 0 to 46 seconds post-displacement. Each of the 14 rasters depicts the same 15,000 randomly selected cortical grayordinates in the same order. The mean cortical BOLD signal for each displacement range (previously presented in Fig. 1b, left) is superimposed in color. See also Supplemental Figure 7 for this same analysis repeated in white matter and CSF voxels.

3.5. The pattern is observed within many individual runs

The analyses conducted thus far have aggregated data together across subjects and runs. To ask whether displacements are followed by this lagged BOLD structure within individual subject data, we repeated the main analysis but aggregated together all runs available for a given subject. Figure 6 (Column 1) show the results of this analysis within several example subjects from both datasets. As is clear from the figure, the original pattern is observable within many – but not all – individual subjects, and some individual variability in peak onsets and amplitudes is apparent. To roughly quantify correspondence between the main analysis (aggregated across subjects) and individual subject analyses, we correlated patterns observed in individual subjects for each displacement range with the patterns observed in the main analysis re-run with that subject left out. Mean correlations within individual subjects ranged from r = −.17-.87 (mean .49; SD .25; one-sided t(50)=13.93, p << .0001, Cohen’s d = 1.95) for the IU dataset and from r = −.02-.86 (mean .37; SD .20; one-sided t(71)=15.38, p << 0.0001, Cohen’s d = 1.81) for the HCP dataset.

Figure 6.

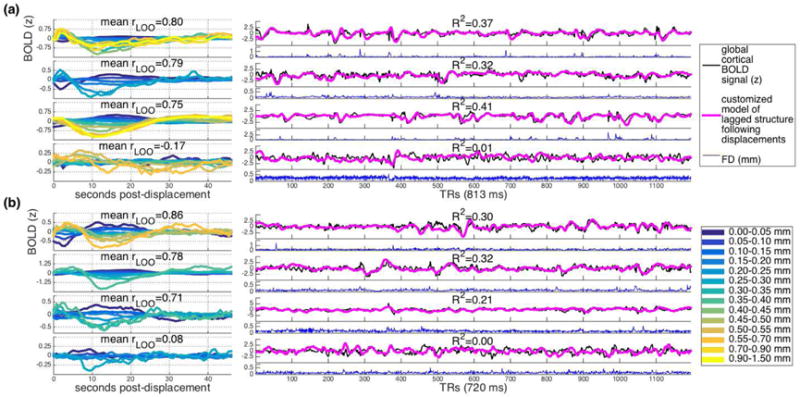
Example subject-level and run-level results for (a) IU and (b) HCP datasets with FIX preprocessing. Left: Pattern observed within individual subject data. Displacement ranges with fewer than 20 instances are omitted. Mean r_LOO is the mean of the correlations between this subject’s pattern as displayed here and the aggregate pattern for the remaining subjects, across all displacement ranges. Right: Global cortical signal (black), customized models of lagged structure following displacements (pink), and framewise displacement traces (blue) for one scan from the subject whose data is depicted at left. R² values refer to regressions independently predicting global cortical signal from lagged structure following displacements, for the scan depicted.

3.6. The pattern explains a considerable range of variance in the global cortical BOLD signal

The pattern we observe is global and found within many individual subjects’ aggregated data. This suggests that it could potentially be used to predict a non-negligible component of the mean cortical BOLD trace for an entire individual scan. To assess this, we used the main patterns for each displacement range (Fig. 1a & 1b, left) to a model the expected temporally extended BOLD structure for the epoch following a given framewise displacement. Then, we simply summed this predicted structure following each displacement in a given FD trace – in effect, convolving the pattern for each displacement range with each displacement trace – and z-scored the result. This process generated a customized model of the expected cumulative lagged BOLD structure following the unique displacements within each individual scan. Here, to ensure independence, we used the pattern observed in one dataset (interpolated to match sampling rates) to predict the lagged BOLD structure following FD traces in the other dataset – e.g. we use HCP BOLD data to predict the structure following IU FD traces, and vice versa.

Figure 6 (Column 2) shows these customized models of lagged structure following displacements for one scan from the example subjects depicted in Figure 6 (Column 1), along with the global cortical BOLD signal and framewise displacement trace. As can be seen in these examples, in many – but not all – cases, the customized model corresponds remarkably well with the global cortical signal. It is worth underscoring that these customized models are generated only as a function of framewise displacements. Thus, a sizeable component of the global cortical BOLD signal reflects noise that is linked with indices of displacement.

To quantify the correspondence between the global cortical BOLD signal and these customized models of lagged structure following displacements, we ran linear regressions predicting the global cortical BOLD signal for each run as a function of the customized model for that run. R² values ranged from 0 to .41 (mean .08; SD .08) for IU data, and from 0-.32 (mean .07, SD .07) for HCP data. Beta weights for customized models ranged from - 0.09 to 0.6 for IU data (mean .25, SD .14) and from −0.16 to .57 for HCP data (mean .2, SD .16), exceeding chance for both datasets (IU: one-sided t(260)=27.09, p << .0001, Cohen’s d = 1.7; HCP: t(221) = 19.5, p << .001, Cohen’s d = 1.31). And consistent with the previous section, for most but not all individual scans (70% for IU dataset; 58% for HCP dataset; α=0.05), the customized model explains more variance than expected by chance based on a permuted null distribution established by regressing out customized models for other subjects’ scans. For comparison, using raw FD traces (instead of the customized models) to predict the global cortical BOLD signal yielded negligibly small R^2 values (IU data: 0-.009, mean .0007, SD .001; HCP data: 0-.008, mean .0007, SD .001), smaller than for the customized model regressions (IU data: t(260) = 16.3, p << 0.0001, Cohen’s d = 1.41; HCP data: t(221) = 13.15, p << 0.0001, Cohen’s d = 1.24). Thus, for many runs, considerable variance in the global cortical BOLD signal can be explained as a function of displacement traces alone – and specifically as a function of the temporally extended structure following framewise displacements. (However, we do not suggest using these customized models for confound regression as an alternative preprocessing strategy; see Discussion.)

The next question that arises is how long following displacement needs to be modeled to achieve this level of prediction – in other words, for how long does the lagged structure following framewise displacements contribute to the global cortical signal? To answer this question, we varied the length of time post-displacement included in the model, and then repeated the same regressions as above. The results are presented in Figure 7. For both datasets, additional variance in the global cortical BOLD signal is explained as more time post-displacement is included in the customized lagged displacement models, up to about 20 seconds. These results further corroborate that framewise displacements are followed by temporally extended BOLD changes that contribute significantly to the global cortical BOLD signal.

Figure 7.

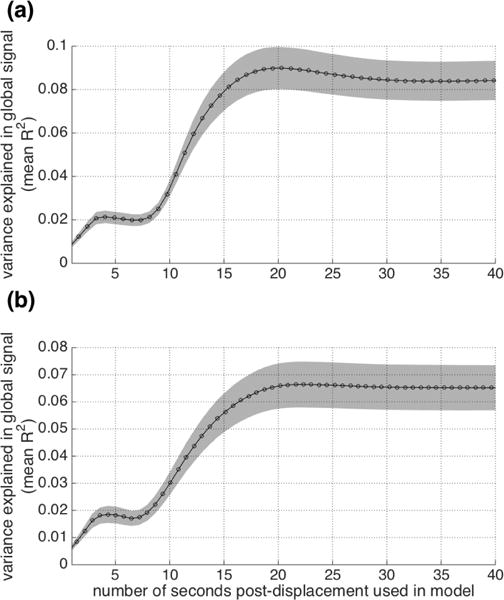
Predicting the global cortical BOLD signal as a function of customized models constructed from individual FD traces. Models vary in the length of time they include post-displacement (x axis). The y axis depicts the mean R² across all scans along with 95% confidence intervals of the mean (for visualization), for (a) IU and (b) HCP datasets with FIX preprocessing.

3.7. Functional connectivity estimates vary similarly

It is generally accepted that functional connectivity (FC) estimates can be influenced by large displacements in immediately preceding timepoints; this is the reason censoring/scrubbing (Power et al., 2012, 2014) is now a standard procedure. One implication of the current findings is that FC estimates may be influenced not only by immediately preceding large displacements, but also might vary as a function of displacements that are farther in the past and potentially smaller.

To examine this possibility, we estimated FC across short sliding windows and examined whether FC varied as a function of the magnitude of displacement events and the temporal distance between the displacement and the sliding window (e.g., whether a given displacement occurred at the end, beginning, or even before the beginning of a sliding window). We focused on global FC (the mean across an FC matrix) because the lagged residual BOLD structure observed was largely global (see Fig. 5), and we chose short sliding windows (~20 seconds, around half the duration of Fig. 1), in order to be able to detect any associated modulations in FC. Time series were censored at the strictest threshold in current use (0.2mm; Power et al., 2014; Ciric et al., 2017) before computing FC. We averaged together global FC for all sliding windows with the same temporal distance from displacement events of same range – for instance, for all sliding windows with onset 4 seconds following a ~0.5mm displacement – first within subjects and then across subjects. The question is whether global FC estimated across these sliding windows – which are combined together only on the basis of the displacement events in their vicinity – will be effectively uniform or instead might vary systematically.

Figure 8 presents the mean global FC across each sliding window for each displacement range for the IU (a) and HCP (b) datasets. For illustrative purposes, example mean functional connectivity matrices for the IU dataset are also presented in Figure 9. As these figures make clear, FC estimates vary according to the magnitude of displacement and the temporal distance between the sliding window and the displacement event. Displacement magnitude appears to be associated with a baseline shift, such that global FC in the vicinity of a larger displacement is consistently higher, across windows, than global FC calculated in the vicinity of a small displacement. Perhaps more importantly, for most displacement ranges, global FC levels vary across sliding windows – by as much as 17% and 35% for larger displacements in the IU and HCP datasets, respectively. These displacement-associated modulations are not limited to the largest displacements – for many displacement ranges, including some of the smallest, global FC can fluctuate 5% or more across sliding windows – and can take tens of seconds (or longer) before appearing to plateau.

Figure 8.

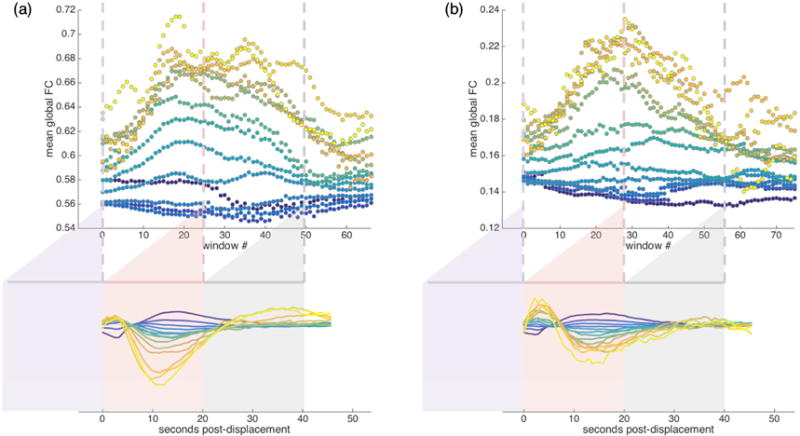
Mean global functional connectivity taken across sliding windows associated with displacements in a given range for (a) IU and (b) HCP datasets with FIX preprocessing. Sliding windows are approximately 20 seconds long; window 0 (purple) spans the ~20s immediately prior to displacements in a given range; each subsequent window advances forward in time by 1 TR. Global FC is the mean of the FC matrix for a sliding window. Strict censoring at FD >= 0.2mm was conducted before all FC estimates were computed. For each displacement range, all such peri-displacement-event global FC window sequences were averaged first within subjects and then across subjects. Three example windows are shown to illustrate how the FC is sampled from the BOLD data. Note that the number of ROIs differs between datasets: a relatively coarse parcellation of 96 ROIs for IU data (a) and more fine-grained parcellation of 360 ROIs for HCP data (b), and this is likely to contribute to differences in global functional connectivity baselines across the datasets. See Figure 9 for example mean functional connectivity matrices that correspond to the points plotted in Figure 8a.

Figure 9.

Example mean functional connectivity matrices corresponding to points plotted in Figure 8a, for IU dataset with FIX preprocessing, for each displacement range and for every 5th sliding window. Functional connectivity is computed across a ~20 second sliding window after strict censoring at FD >= 0.2mm; all corresponding FC matrices are averaged within subjects first and then the across-subject average is depicted here. For example, the upper left matrix depicts depicts functional connectivity computed across ~20 second sliding windows immediately prior to all displacements under 0.05mm, averaged first within subjects and then across subjects. See Figure 8 for further explanation of sliding window analysis.

To ensure that these modulations truly covary with framewise displacements, as before (see Figure 2), we repeatedly permuted the association between the BOLD signal and framewise displacement traces such that every individual’s BOLD data was linked with another individual’s framewise displacement trace, and conducted this same sliding window FC analysis. The mean results across permutations are presented in Figure 10 and the modulation of global FC levels across sliding windows observed in Figure 8 is absent (cf. Fig. 8a to 10a; Fig. 8b to 10b). Thus, FC estimates vary as a function of prior framewise displacements that occurred many seconds in the past.

Figure 10.

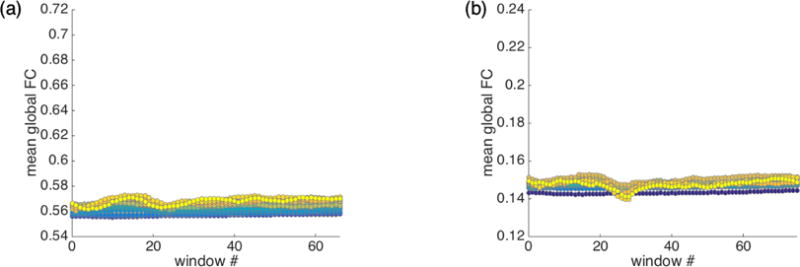
Mean global functional connectivity taken across sliding windows associated with displacements in a given range for (a) IU and (b) HCP datasets with FIX preprocessing, after 500 permutations of BOLD-FD relationships (see Methods). Strict censoring at FD >= 0.2mm is used. Plots are on the same scale as Figure 8; the structure observed in Figure 8 is absent here. (Although some structure is present due to complicated interactions between decreased sample sizes and increased censoring as displacements increase, patterns are substantially reduced relative to Figure 8.)

3.8. The patterns observed following displacements are related to respiration

We have found thus far that framewise displacements, especially very small and very large displacements, are followed by global modulations in the BOLD signal, and functional connectivity estimates fluctuate similarly. The next natural question pertains to the mechanisms that might produce such modulations. This question is beyond the original scope of this manuscript – because most datasets do not have physiological recordings, we focused on the framewise displacement traces that are available in all fMRI datasets. However, to gather some initial hints into the potential mechanisms contributing to these displacement-linked patterns in the BOLD signal, we conducted some exploratory analyses of the physiological recordings that are available for many runs in the HCP dataset, although we note that a full disentangling of contributing noise sources would need to be the topic of a different investigation.

To do this, we apply our main analytic method to examine the BOLD signal as a function of physiological regressors rather than framewise displacements, binning values of the regressor into 14 percentile-based ranges for consistency with prior analyses. We examined 34 physiological regressors generated by FSL PNM (“Physiological Noise Modelling” tool), including 32 RETROICOR-style regressors (Glover et al., 2000) modeling cardiac and respiratory frequencies and their interactions, as well as regressors reflecting heart rate and respiration volume per time (RVT; Birn et al., 2006). Some example regressors are presented in Supplemental Figure 8, for the same individuals whose data is presented in Figure 6. Again, a comprehensive examination of these noise sources and their interrelationships is beyond the intended scope of the current work, but we summarize some initial insights here (see also Supplemental Table 3 and Supplemental Figure 9-13).

Figure 11 presents lagged BOLD structure associated with two example physiological regressors – respiration volume per time (RVT; Fig. 11a) and heart rate (HR; Fig. 11b; lagged BOLD structure associated with all regressors examined is presented in Supplemental Figure 10 for the interested reader. In general, we found minimal lagged structure associated with any of the cardiac regressors and their interactions. To quantify the extent of structure apparent in the main analysis, we examined the absolute value of the peak amplitude observed for each range (i.e., the extreme value of the mean z-scored BOLD signal across the epochs beginning with nuisance values in each range). The largest such peak for any of the cardiac regressors and their interactions was 0.083 (Fig. 11b), with a mean largest peak of 0.032 across regressors (SD = 0.015), compared to 0.44 for the original displacement-based pattern observed (Fig. 1b). In contrast, considerably more lagged structure was associated with the respiratory regressors (mean largest peak 0.19, SD = 0.098), especially (but not exclusively) respiratory volume over time (Fig. 11a; see also Supplemental Figure 10 for lagged structure associated with other respiratory regressors). The lagged BOLD patterns associated with respiration are not the same as the lagged patterns associated with displacements, but their similar temporal and parametric properties are suggestive of the possibility that respiratory mechanisms may underlie some of the displacement-linked lagged structure in the BOLD signal (see also Supp. Fig. 9).

Figure 11.

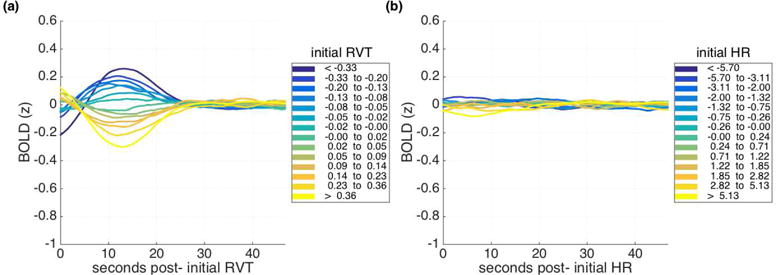
Mean cortical BOLD signal (a) following initial respiration volume per time (RVT) values of similar magnitudes and (b) initial heart rates (HR) of similar magnitudes, both for HCP dataset with FIX preprocessing.

If this is true, there must be a systematic relationship between respiratory traces and framewise displacements, examples of which have emerged recently in fast-TR datasets (Etzel, 2016; practiCALfMRI, 2016; Power, 2017; Power et al., 2017a). Mean cross-correlations between raw framewise displacement traces and the respiratory regressors, across lags from −21 to 21 TRs, were generally low: the largest mean cross-correlation across available runs (for any respiratory regressor and lag) was 0.1, with a mean across all regressors and lags of 0.00093 (SD = .015) (see also Supplemental Table 3). However, low similarity between nuisance traces spanning an entire run could obscure a more nuanced relationship between traces at smaller timescales. Toward that end, we used our method to examine epochs of the respiratory regressors as a function of the same initial framewise displacement ranges used in the prior analyses (similar to the earlier Check 3 analysis). As is evident in Figure 12, which depicts RVT as a function of initial framewise displacements, considerable structure is present. (Supplementary Figure 11 presents this same analysis for all physiological regressors examined). Very small displacements are followed by an increase in RVT, while larger displacements tend to precede a large decrease in the RVT trace. These patterns are suggestive of the possibility that the BOLD signal modulation following very small displacements (Fig. 1b) may be largely due to inspiration, while exhalation may play a role in the BOLD signal modulation following larger displacements.

Figure 12.

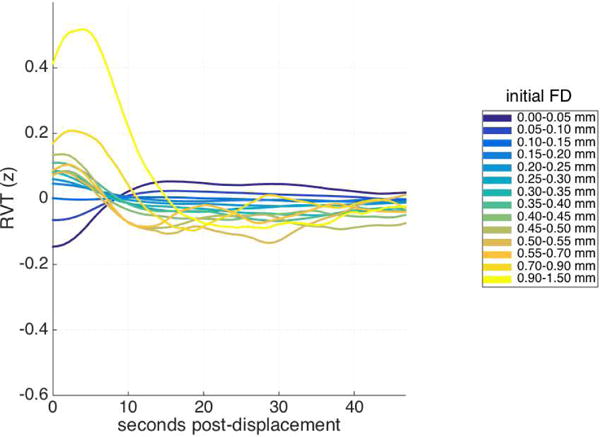
Mean Respiration Volume per Time (RVT) trace following framewise displacements of similar magnitudes, for HCP dataset with FIX preprocessing. Each RVT trace is z-scored before combining across runs and averaging.

However, regardless of the underlying sources of the lagged structure apparent in the BOLD signal, structure that covaries with a nuisance trace is likely to be an artifact. Thus in the next and final section we return to lagged structure following framewise displacements (which can be assessed in both datasets), and present one method for minimizing these artifactual patterns.

3.9. Removing a global signal attenuates lagged structure following displacements in the BOLD signal and modulation of functional connectivity estimates

The patterns of lagged BOLD structure following framewise displacements presented thus far are consistent across datasets and robust across a number of preprocessing methods. However, given that these patterns are widespread across the cortex (cf. Fig. 5), it might be expected that preprocessing with global signal regression would yield a different pattern of results. Figure 13 depicts the results of the primary analysis (Column 1; see also Fig. 1) and the functional connectivity analysis (Column 2; see also Fig. 8) conducted upon data that has been preprocessed with global signal regression. We employed three different methods of global signal regression: with the whole-brain signal (and its derivative) included within nuisance regression (IU data, Fig. 13a, top row) and with the mean cortical signal regressed out as a second step following conventional nuisance regression (IU data, Fig. 13a, second row) and following FIX denoising (IU data, Fig. 13a, third row, HCP data, Fig. 13b).

Figure 13.

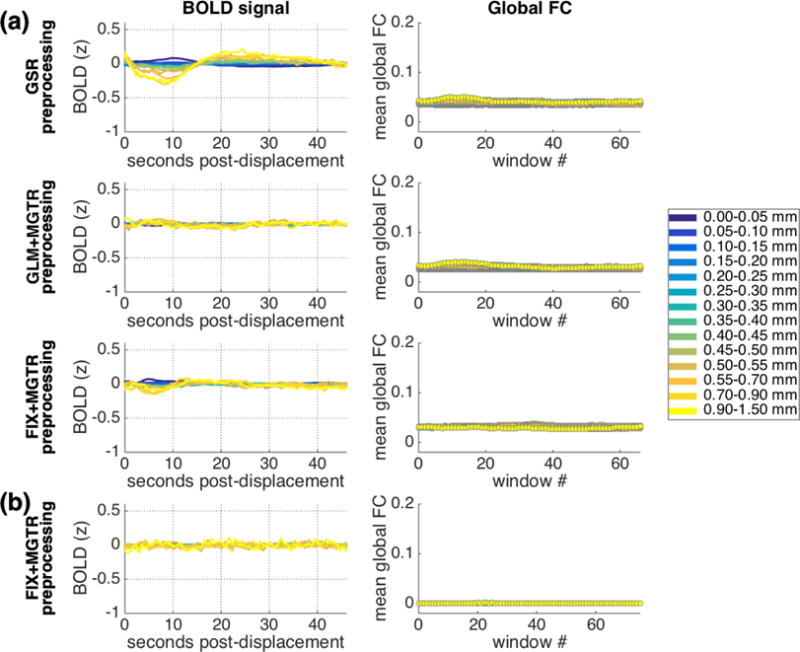
Results when a global signal is removed in preprocessing, either by including the mean whole-brain signal in nuisance regression (IU data: a, top row) or by regressing out the mean cortical BOLD signal in a second step following conventional GLM preprocessing (IU data: a, second row) and following FIX preprocessing (IU data: a, third row; HCP data: b). Column 1: Main pattern of lagged BOLD structure following framewise displacements. Column 2: Mean global functional connectivity taken across sliding windows associated with displacements in each range, after strict censoring. Window 0 spans the ~20s immediately prior to a given displacement, and each window slides forward in time in 1 TR increments. Differences in global functional connectivity baselines across rows are likely to arise due to differences in preprocessing methods (e.g., differences in ROI coarseness). Y-axis ranges for both columns were selected to be as comparable as possible to original analyses (Figure 1; Figure 8).

As is clear in Figure 13, global signal regression of all forms attenuates the lagged structure following framewise displacements in the BOLD signal (Column 1) and in functional connectivity estimates (Column 2) to different degrees, with the greatest improvement for mean cortical signal removal following FIX denoising. Thus, preprocessing methods that employ global signal regression – although controversial (Murphy et al., 2009; Saad et al., 2012; Birn, 2012; Gotts et al., 2013; Murphy & Fox, 2016; Power et al., 2017a; Liu et al., 2017; Power et al., 2017b; Satterthwaite et al., 2017) – considerably mitigate this artifact and its potential for spuriously influencing conclusions.

4. DISCUSSION

Here we introduce a tool for assessing data quality by visualizing residual lagged BOLD structure associated with nuisance signals of any kind. We use this tool to reveal that after numerous preprocessing methods, the global cortical BOLD signal contains residual lagged structure for 20-30 seconds following both large and small framewise displacements. This residual structure is robust: it is observable within many individuals’ data, consistent across independent datasets, and independently explains a considerable range of variance in the global cortical BOLD signal. Global functional connectivity estimates also vary as a function of displacements occurring many seconds in the past, even after very strict censoring. Exploratory investigations reveal that similar patterns of lagged BOLD structure follow respiratory fluctuations, which are in turn related to framewise displacements – suggesting respiration as one of the contributors to the residual displacement-linked noise we observe. Regardless of its underlying sources, though, lagged structure associated with a nuisance trace is likely to be artifactual; we find that global signal regression is one way to attenuate this residual lagged BOLD structure.

There are relatively few methods available for comparing effectiveness of different preprocessing methods and assessing their potential impact on results (see also Ciric et al., 2017; Power et al., 2015; Turner et al., 2015); our approach is robust and results are quick and easy to compute, requiring no additional preprocessing or extra information beyond that which is easily obtainable from all fMRI datasets. Toward this end, we have made a MATLAB script available at github.com/socialbrainlab/lag_patterns/. It takes as input an array of BOLD traces at any spatial scale (i.e., global or voxel-level) from any number of scans along with an array of corresponding nuisance traces (framewise displacement or any other nuisance measure sampled at the same rate) and generates the plots depicted in Figure 1. It can also be used to examine inter-relationships among nuisance traces, or, more generally, any time series. Numerous customization options are also available, allowing exploration of different displacement ranges and different epoch lengths. This tool allows researchers to evaluate how well lagged structure associated with any nuisance signal is eliminated in a given dataset (especially important for analyses where individual differences in nuisance factors could influence conclusions) and may facilitate further research into future alternative and ideally more nuanced approaches for removing residual structure. Importantly, this approach may also allow researchers to discover new patterns in their data, going beyond cross-correlations to reveal associations between timeseries at finer scales (c.f. Fig. 12). It is versatile and flexible: potential extensions include not only examining measures of additional noise sources but also exploring inter-relationships among network (or regional) timeseries during both resting and stimulus-evoked states, and potentially individual differences therein.

Using this approach as a discovery tool revealed seven key insights that build upon and extend the existing literature, which we enumerate in the next several paragraphs. We find that (1) lagged global BOLD structure follows framewise displacements. This is consistent with Satterthwaite and colleagues (2013), who documented that effects of larger displacements were widespread across the cortex (see also Power et al., 2014; 2017; 2017a) and that BOLD elevations occurred in the first seconds immediately following larger displacements (Figure 3a from Satterthwaite et al., 2013; note the origin in our figures corresponds to x = 1 in theirs) – as well as with Power and colleagues (2014; 2017; 2017a), who documented that the effects of displacements can persist more than 10 seconds post-displacement. We believe this is the first report that (2) even the smallest FD values – effectively, the absence of displacement – are associated with residual lagged BOLD structure. Further, (3) these patterns of lagged BOLD structure following displacements are so consistent across independent datasets that they can be used to independently predict the global cortical BOLD signal as a function of framewise displacement traces alone, explaining a considerable range of variance (up to 41%). This is consistent with reports that the global signal contains a substantial noise component (Chang, Cunningham, and Glover, 2009; for review see Liu et al., 2017), with variability in nuisance factors including displacement predicting variability in the global signal (Power et al., 2017a), but to our knowledge this is the first direct prediction of the global cortical signal itself using displacement traces – and specifically, by modeling the temporally lagged consequences following these displacements (note that prediction based on raw FD traces alone was unsuccessful). We also find that (4) prolonged displacement-linked structure is apparent in global functional connectivity estimates, consistent with Power and colleagues’ (2014) findings that displacements can influence functional connectivity within the 10s following a movement as well as with recent reports (Laumann et al., 2016) that fluctuations of functional connectivity estimates across subsamples can be linked with data quality measures across those subsamples.

We also conducted an exploratory examination of lagged BOLD structure associated with physiological traces where available. We found that (5) lagged global BOLD structure follows respiratory variations, captured most clearly (but not exclusively) by respiratory volume per time (RVT). RVT captures changes in the envelope of respiratory changes as well as breathing rate (Birn et al., 2006; 2008) and is thought to reflect changes in arterial CO₂ concentration, which has vasodilatory properties and influences the BOLD signal after a temporal lag, with largely global effects (Wise et al., 2004; Birn et al., 2006, 2008; Chang & Glover, 2009). Indeed, lagged BOLD signal modulations associated with RVT are sufficiently systematic that a respiratory response function (RRF) has been derived and can be used to explain a considerable proportion of variance in the global BOLD signal (Birn et al., 2008; Chang et al., 2009). In fact, we observed remarkable similarity between the RRF (which was derived using respiratory recordings and a cued breathing paradigm; Birn et al., 2008) and the main pattern of lagged residual structure we observed to be associated with displacements (which was obtained at rest from FD traces, without physiological recordings) – as well as between a time-shifted RRF and the pattern of lagged residual structure associated with RVT (see Supp. Fig. 9). It is also worth pointing out that the patterns observed following the smallest possible displacements (Fig. 1, dark blue) bear striking similarity to BOLD activity following the release of a breath hold (Magon et al., 2009) and several example epochs following isolated deep breaths show a global BOLD signal decrease and then increase (c.f. Fig. 6 in Power et al., 2017a) that appears similar to the pattern we document a few seconds after larger displacements – likewise hinting at respiratory involvement even prior to the analysis of physiological traces (see also Burgess et al., 2016).

The lagged patterns associated with respiration were not identical to those associated with displacements, and other noise sources are likely to contribute to the aggregate pattern as well. For instance, the effects of larger displacements on the BOLD signal are well-documented (e.g. Hajnal et al., 1994; Friston et al., 1996; Satterthwaite et al., 2013; Power et al., 2015; Caballero-Gaudes & Reynolds, 2017), and, as such, head movements per se are one probable contributor. However, the notable similarities between the displacement-linked and respiration-linked patterns suggests that respiratory fluctuations – which are sampled more frequently in the fast-TR fMRI datasets analyzed in this report (Power et al., 2014; Power, 2017; Burgess et al., 2016) – are among the sources of the displacement-linked noise we observed. These similarities are likely to arise in part because (6) displacement and respiratory traces are themselves related. Although this relationship was weak across the length of entire scans, at finer temporal scales, small and large displacements were associated with distinct respiratory patterns (c.f. Fig. 12): very small displacements preceded an increase in respiration volume per time, while large displacements preceded a decrease. Very recent reports (Etzel, 2016; practiCALfMRI, 2016; Power, 2017; Power et al., 2017a) have depicted relationships between framewise displacements and the envelope of respiratory oscillations in multiband, high temporal resolution fMRI data; our findings provide a systematic description of this phenomenon and its consequences.

Finally, whatever the underlying mechanisms, we find that (7) this lagged residual BOLD structure and the similar modulations in functional connectivity can both be largely attenuated by removing a global signal. This dovetails with our findings that the global signal has a considerable displacement-linked component (consistent with Satterthwaite et al., 2013; Power et al., 2017a) and is consistent with other reports indicating that global signal regression may best minimize the relationship between displacement and functional connectivity (Yan et al., 2013; Power et al., 2014, 2015, 2017b: Burgess et al., 2016; Ciric et al., 2017). We note that these findings are not intended as a critique of existing preprocessing methods – for instance, FIX was explicitly not designed to remove global signals (Salimi-Khorshidi et al., 2014) – but rather to point out that further cleanup of the signal is possible.

We highlight four key implications of our findings here. First, the residual lagged structure observed has potentially serious consequences for data-driven analysis techniques that examine BOLD timecourses across or within individuals (e.g. correlation-based methods). For functional connectivity analyses, we show modulations in global functional connectivity across sliding windows as a function of displacement magnitude and temporal distance since displacement. These modulations have the greatest potential to lead to spurious conclusions for group and individual difference analyses, and may be most serious when comparing groups and individuals whose displacement or respiratory characteristics (among other nuisance factors) might differ, such as in comparisons between clinical and control groups or across different ages and health-related measures (see also Deen & Pelphrey, 2012; Power et al., 2012, 2017b; Satterthwaite et al., 2012; Siegel et al., 2016; Wilhelm et al., 2001; Pecukonis et al., 2017; Satterthwaite et al., 2017). This residual lagged structure can also affect within-individual analyses, producing spurious modulations of dynamic functional connectivity across epochs that differ in displacement and/or respiratory characteristics (see also Laumann et al., 2016). For inter-subject correlation analyses (Hasson et al., 2004, 2009; Byrge, Dubois, et al., 2015), unique patterns of displacement and respiration across a scan are likely to artifactually decrease time course similarity across subjects, while similarities in displacement and respiration (potentially linked to stimulus properties) could artifactually increase BOLD timecourse similarity. It is important to underscore that the differences in nuisance factors that could spuriously influence such comparisons include their temporal characteristics and not just distributional characteristics: for instance, two subjects with identical distributions of framewise displacements that occur in a different order will present with distinct lagged BOLD structure following those displacements. This thus indicates the need to go beyond simply testing whether average displacements across a scan might differ between groups and individuals, and instead develop analysis and preprocessing strategies that mitigate these concerns.

Second, global signal regression remains a controversial preprocessing step (Murphy et al., 2009; Saad et al., 2012; Birn, 2012; Gotts et al., 2013; Murphy & Fox, 2016; Power et al., 2017a; Liu, Falci, & Falahpour, 2017; Satterthwaite et al., 2017), having costs as well as benefits (for extensive discussion, see Murphy & Fox, 2016; see also Satterthwaite et al., 2013; Ciric et al., 2017; Power et al., 2017a, 2017b), and individual researchers will need to weigh these tradeoffs in the light of their specific questions of interest. For these reasons, and echoing Power and colleagues (2017a), we explicitly refrain from recommending or not recommending global signal regression, although we do note that global signal regression was the only preprocessing method we examined that attenuated lagged displacement-linked residual structure (see also Power et al., 2017b). For the individual difference analyses that may be most susceptible to spurious conclusions arising from residual lagged BOLD structure, researchers might decide that the benefits of removing the global signal could outweigh the costs. When the global signal is retained, however, our results suggest caution is needed in interpreting results where differences in nuisance characteristics could covary with the individual differences of interest (see also Power et al., 2017a, 2017b; Siegel et al., 2016).

Third, research groups who are concerned about the costs of global signal regression for their specific questions might rely on censoring alone for artifact reduction. Although early reports (c.f. Fig. 8b in Power et al., 2014) demonstrated that censoring/scrubbing 10 seconds following displacements was necessary to minimize the effects on functional connectivity, in practice, censoring/scrubbing only the timepoint associated with displacement, or just a few timepoints afterward, is a much more common practice – probably because extensive censoring results in data loss beyond what many datasets can tolerate (see also Power et al., 2014). Our findings make clear that such frequently-used minimal censoring practices leave abundant residual lagged structure in the BOLD signal. Furthermore, very small displacements are generally considered indicative of high-quality data and are therefore not considered problematic. However, we show that residual lagged structure follows even these very small displacements – effectively, a lack of displacement – probably because such moments are likely to precede an increase in respiratory volume (c.f. Fig. 12) and its concomitant effects on the BOLD signal. Importantly, the magnitude of residual lagged structure following the very smallest displacements is comparable to that which follows 0.4 mm displacements (c.f. Fig. 1). Note also that 0.39mm has emerged as one of the data quality thresholds in common use; we emphasize here that displacements of 0-0.05mm are followed by comparable residual BOLD structure that also need to be addressed in some way. However, addressing this residual structure that follows both very small and larger displacements for over 20 seconds by using censoring/scrubbing alone is clearly not feasible due to unacceptable data loss, which again highlights the need for further development of methods that can address such residual lagged BOLD structure without entirely removing the global signal.

Fourth, while the current findings suggest respiration as one of the key mechanisms underlying the residual lagged structure we observed following displacements, this respiratory-linked structure was detectable without physiological recordings, due to the relationship observed between respiration and displacements. Thus, framewise displacements can – albeit imperfectly – index the lagged BOLD effects of physiological noise. This is important because, as noted, physiological recordings are not available for the majority of existing fMRI datasets, and when collected are often unusable due to acquisition problems and artifacts. But the lagged BOLD structure associated with respiration has the potential to spuriously influence research conclusions, so this structure needs to be quantified and addressed, regardless of whether physiological recordings are available. Nearly all techniques for cleaning up physiological noise without global signal regression rely on physiological recordings, so being able to use framewise displacement traces – which are always available – as a surrogate is an important step forward and may be key in the development of more targeted cleanup methods for existing datasets (although, for new acquisitions, obtaining and using physiological monitoring information would be preferable when possible).

The current findings, and particularly the implication of respiratory processes, seem to suggest that if respiratory variance is removed from the data, a qualitatively different pattern of lagged residual structure linked with displacements would emerge in the cleaned data, providing insights into noise sources. For instance, if the structure associated with the smallest displacements disappeared following respiratory cleanup, but the structure associated with larger displacements remained unchanged, one might conclude that residual structure linked with very small displacements was caused by respiration and that structure linked with large displacements might instead be caused by head movements. The problem with this logic hinges on a subtle point that Power and colleagues (2017a) have recently emphasized: the distinction between modeled and unmodeled variance associated with a given process. Despite extensive and continuing development of methods for modeling and remove respiratory variance, models of respiratory variance (like all models) are not perfect (Birn et al., 2006, 2008, 2012; Falahpour, Refai, & Bodurka, 2013; Power et al., 2017a), and this means that only modeled respiratory variance – and not all variance caused by respiratory processes – can be removed from the data. Unmodeled variance of respiratory and non-respiratory origin will remain in the data following respiratory cleanup, and without additional information, it is not possible to conclusively disentangle the origins of that residual noise.

With those caveats in mind, we did conduct a rigorous voxel-level respiratory cleanup upon the subset of HCP data with physiological recordings available (see Supplemental Methods). The results of the main analysis repeated upon this respiratory preprocessed data are included in Supplemental Figures 12 and 13. As is evident, the pattern of lagged residual structure is attenuated following respiratory cleanup, but qualitatively unchanged (note that Power and colleagues (2017a) also found residual “unwanted global variance time-locked to motion and respiration” after removing respiration volume per time and its convolution with the RRF from a different dataset). However, the conclusions that can be drawn from these results are limited due to the distinction just raised – and the strong similarity between the respiratory response function (Birn et al., 2008) and the main pattern of lagged residual structure following respiratory cleanup (Supplemental Figure 12b) remains suggestive of unmodeled respiratory variance remaining in the data. Without a targeted data acquisition designed to disentangle different noise contributions, discussions of mechanisms must remain speculative, but we believe that our analyses converge on the conclusion that framewise displacements can serve as an imperfect surrogate for assessing residual noise including that of probable respiratory origin.

We note that our approach captures lagged BOLD structure at the aggregate level (see also Satterthwaite et al., 2013), combining similar events across different epochs. An alternative approach is to consider events individually, because BOLD activity following individual displacements can be variable and idiosyncratic (Power et al., 2014, 2015). We believe both of these approaches are ultimately needed and provide complementary insights. Potential noise sources are of course occurring continuously throughout a scan, and because of their lagged effects on the BOLD signal, ongoing displacements and respiration will influence BOLD activity in a history-dependent manner. In other words, one contributor to the event-level variability observed by Power and colleagues (2014; 2015) following individual displacement events is likely to be preceding and subsequent variation in physiological factors and/or ongoing displacements.

As we have noted, our approach might facilitate the development of future cleanup methods that address this lagged residual variance in a more targeted manner, without entirely removing the global signal. However, it is important to emphasize that our customized models of lagged structure for individual scans (Fig. 6) are not sufficiently refined that they can be offered as an alternative preprocessing strategy without further development. Indeed, we attempted such an alternative cleanup, using these customized models as confound regressors, and found that the lagged residual structure was insufficiently mitigated. (We note in passing that this highlights one strength of our approach: examining residual structure pre- and post- cleanup to assess effectiveness). This initially counterintuitive finding arises in part from a combination of the event-level variability just discussed and our epoch-based modeling being used to model the length of an entire scan. Consider a scan, where, for instance, some of the displacement events are followed by the stereotyped lagged BOLD pattern we document, but the other displacement events are followed by idiosyncratic BOLD patterns. For such a scan, the subsequent customized models of lagged structure (e.g. pink lines in Fig. 6) may have little relationship with the BOLD data across the entire scan, and removing such a confound regressor from the data would have little effect, with the variance associated with both the stereotyped and idiosyncratic BOLD patterns remaining in the data alike. Nonetheless, with more sophisticated modeling, potentially at the individual subject level and using multiple confound regressors, it is possible that our approach could inform a future alternative to global signal regression.

Inter-relationships among potential fMRI noise sources are very complicated (see also Power et al., 2017a) but can also be informed by the current approach. An important direction for future research is a better understanding of these relationships and how they might vary within and across individuals, which might relate to individual differences in the response functions associated with physiological noise (Falahpour et al., 2013), as well as in the overall dominance of physiological noise in the BOLD signal (Birn et al., 2014). Furthermore, while a systematic deconstruction of noise factors is beyond the intended scope of the present work, another important future direction is to tease apart the distinct contributions of head movement per se, chest movement due to cardiac and respiratory cycles, changes in CO2 and cerebral blood flow and volume due to respiration, among other potential physiological noise sources, to the aggregate lagged structure we observe. Different preprocessing strategies (e.g. bandpass filtering, orders of preprocessing steps) also have the potential to differentially influence the contributions of these factors as well as the general appearance of artifactual structure across datasets. Finally, it is important to note that not all lagged structure in resting state fMRI data is artifactual: recent work has established non-artifactual physiological temporal lag structure at shorter timescales than examined here (Mitra et al. 2014, 2015, 2016; Matsui et al. 2016) that would not be expected to covary with displacements or other nuisance measures.

5. CONCLUSIONS

In sum, here we introduce a novel discovery and quality assessment tool. We use it to find that framewise displacements – even very small displacements – are followed by predictable changes in the global cortical BOLD signal that extend for tens of seconds and are likely to be at least partially the consequences of respiration. Regardless of its underlying sources, this residual lagged BOLD structure has the potential to spuriously influence conclusions of functional connectivity and other correlation-based analyses. Removing a global signal mitigates this risk. Our script is publicly available for use as a benchmark for comparing preprocessing methods within and across studies, and to encourage development of more targeted approaches for addressing these kinds of residual lagged structure. Ultimately, such methodological improvements in detecting and handling artifacts will enhance our ability to separate brain signal from noise (Uddin, 2017; Power et al., 2017b), allowing more accurate and confident measurement of variation in brain data and advancing the science of individual differences (see also Dubois & Adolphs, 2016).