The protonation states of GTP and GppNHp in Ras proteins

Abstract

The small GTPase Ras transmits signals in a variety of cellular signaling pathways, most prominently in cell proliferation. GTP hydrolysis in the active center of Ras acts as a prototype for many GTPases and is the key to the understanding of several diseases, including cancer. Therefore, Ras has been the focus of intense research over the last decades. A recent neutron diffraction crystal structure of Ras indicated a protonated γ-guanylyl imidodiphosphate (γ-GppNHp) group, which has put the protonation state of GTP in question. A possible protonation of GTP was not considered in previously published mechanistic studies. To determine the detailed prehydrolysis state of Ras, we calculated infrared and NMR spectra from quantum mechanics/molecular mechanics (QM/MM) simulations and compared them with those from previous studies. Furthermore, we measured infrared spectra of GTP and several GTP analogs bound to lipidated Ras on a membrane system under near-native conditions. Our findings unify results from previous studies and indicate a structural model confirming the hypothesis that γ-GTP is fully deprotonated in the prehydrolysis state of Ras.

Introduction

Ras GTPases are molecular switches that are turned on by nucleotide exchange from GDP to GTP and turned off by GTP hydrolysis (1). Whereas the first process is regulated by guanosine nucleotide exchange factors, the latter is accelerated by GTPase activating proteins (2). The importance of these signaling proteins is well-known, as about 20% of all human cancers show a mutation in Ras genes (3). Therefore, the molecular reactions of this significant protein have been investigated for more than 30 years with a variety of methods including NMR spectroscopy (4), X-ray structural analysis (2), infrared spectroscopy (5, 6), and many more (7–11). Especially computational approaches have elucidated many structural details of the molecular mechanisms and led to different well-founded models of how the GTPase reaction in Ras proteins is thought to take place (2, 12–16). A combination of infrared spectroscopy, NMR spectroscopy, and simulations led to the accepted hypothesis that in the prehydrolysis state the phosphate groups of GTP are fully deprotonated when bound to Ras (total charge −4) (17–20). Furthermore, besides GTP, several GTP analogs like GppNHp and GppCH₂p bound to Ras were investigated by ³¹P NMR (21–23). However, a recent work applying neutron diffraction on Ras·GppNHp crystals surprisingly revealed single protonation of γ-GppNHp (24) (Fig. 1). The authors argued that the measurement conditions of Ras·GppNHp at a pD of 8.4 resembles the situation of Ras·GTP under physiological conditions, providing a strong argument for a possible GTP protonation. Previous studies determined the pK_a of γ-GTP in Ras to be around 3 rather indirectly, using NMR spectroscopy over a broad pH range (25). As GTP was not investigated alone but bound to Ras, titration could also affect ionizable side chains of Ras, like aspartic or glutamic acid residues that are also present in the binding pocket. Also, the observed pK_a in NMR could be from the transition from mono- to di-protonated GTP. Yet several structural details of the neutron diffraction structure differ from the native Ras·GTP state, e.g. GppNHp instead of GTP was used, the solvent D₂O instead of H₂O was used, and the tightly packed crystal structure might deviate from the native situation (e.g. Tyr-32 of a neighboring protein was bound to γ-GppNHp). To overcome this problem, we immobilized semisynthetic lipidated N-Ras on a supported POPC membrane layer on top of a germanium crystal (26) and measured attenuated total reflection (ATR)³ Fourier transform infrared (FTIR) spectra of GTP, GppNHp, GppCH₂p, and GTPγS bound to Ras. We furthermore performed coupled quantum mechanics/molecular mechanics (QM/MM) simulations of GTP and its analogs with different protonation states bound to Ras and calculated infrared and NMR spectra of all protonation states. Our results show that the phosphate groups of both GTP and GppNHp are fully deprotonated both in solution and on a model membrane.

Figure 1.

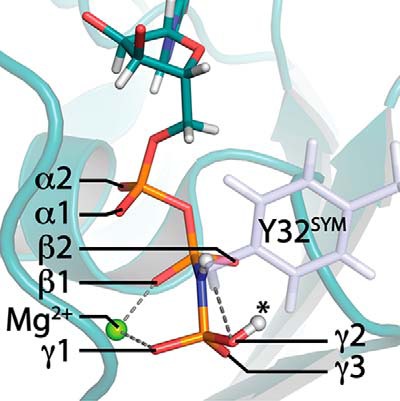
Neutron diffraction crystal structure of Ras with protonated γ-GppNHp. Observed deuterons of the triphosphate groups are depicted as white spheres (PDB ID: 4RSG). Tyr-32 of a neighboring symmetry cell is bound to γ-GppNHp and is depicted as blue sticks. The Mg²⁺ atom is depicted as a green sphere. Labels of α-,β-, and γ-oxygens were retained hereafter. Protonation at γ2 (asterisk) corresponds to experimental observation of γ-protonation.

Results

ATR-FTIR measurements of GTP bound to Ras on a model membrane

We immobilized semisynthetic full-length N-Ras on a POPC model membrane via its lipid anchors and performed exchange of the bound nucleotide from GDP to GTP (Fig. 2A). We compared the measured ATR-FTIR spectra to transmission FTIR spectra of the GTP hydrolysis reaction in Ras that were recorded previously by our group (20). The IR bands of GTP in this near-native setup are identical (Fig. 2B) for bands above 1000 cm⁻¹, allowing direct band assignment of the matching bands that were previously assigned via isotopic labeling (20). The asymmetrical phosphate stretching vibrations were recorded at 1263 cm⁻¹ (ν_AS PαO₂), 1219 cm⁻¹ (ν_AS PβO₂), 1160 cm⁻¹ (ν_AS PO₃γ1), and 1143 cm⁻¹ (ν_AS PO₃γ2). Absorbance changes of ATR-FTIR measurements were 100 times smaller compared with transmission FTIR experiments. Therefore, bands below 1000 cm⁻¹ that are mainly caused via symmetrical vibrations with smaller transition dipole moment, and therefore have smaller absorbance, could not be resolved using ATR-FTIR.

Figure 2.

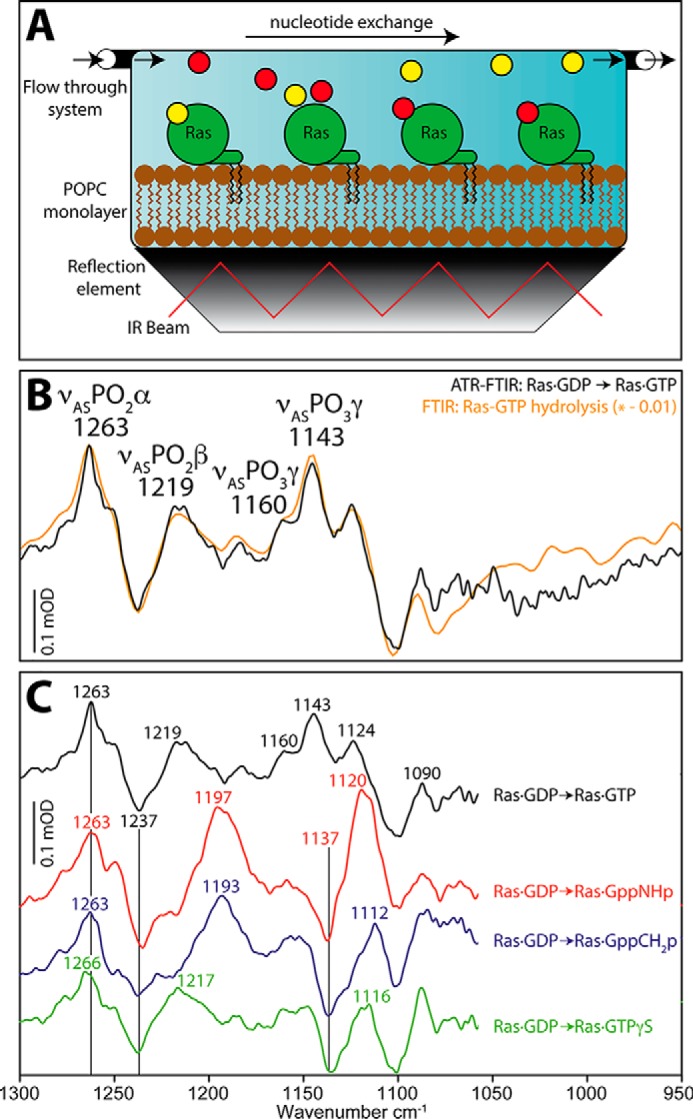
Infrared spectra of GTP, GppNHp, GppCH₂p, and GTPγS bound to Ras on a membrane system using ATR-FTIR measurements. A, lipidated N-Ras was immobilized on a POPC membrane in an ATR-FTIR setup. By buffer exchange in the flow-through system nucleotide exchange can be performed. B, comparison to previous transmission FTIR experiments with H-Ras (inverted, scaled by 0.01) show identical band positions. C, nucleotide exchange to GTP, GppNHp, GppCH₂p, and GTPγS in ATR-FTIR was performed with N-Ras·GDP background.

ATR-FTIR measurements of various GTP analogs bound to Ras on a model membrane

Further GTP analogs were bound to Ras on the POPC surface in the ATR-FTIR setup and their infrared absorption bands were recorded (Fig. 2C). The IR bands for Ras·GppNHp (Fig. 2C, red), Ras·GppCH₂p (Fig. 2C, blue), and Ras·GTPγS (Fig. 2C, green) were clearly resolved above 1000 cm⁻¹. Because the Ras·GDP background signal might create negative peaks that interfere with the nucleotide signals we also performed transmission FTIR experiments using Ras·NPEcgGppNHp and found the second γ-GTP vibration at 1128 cm⁻¹ to be masked by the neighboring β-GDP band at 1134 cm⁻¹ in the ATR-FTIR spectra (Fig. 3). The remaining bands exactly match the ATR-FTIR results, comparable with Ras·GTP.

Figure 3.

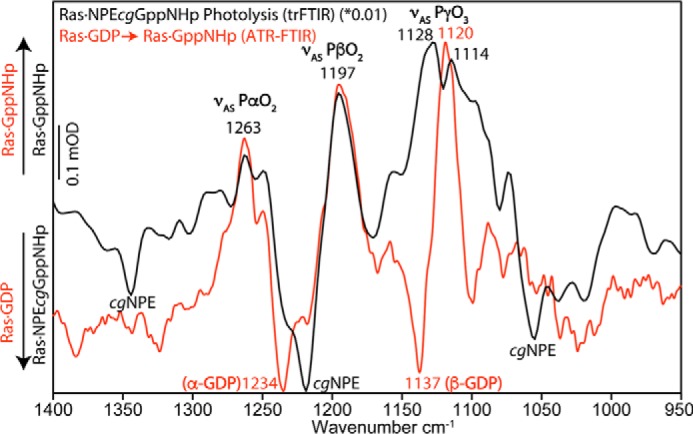
Comparison: Ras·GppNHp on ATR-FTIR and transmission-FTIR. To verify the ATR-FTIR experiments, we performed transmission FTIR experiments with photocaged GppNHp. Bands of α-GppNHp and β-GppNHp were identical, but γ-GppNHp showed two asymmetrical stretching vibrations instead of only one observed vibration in the ATR-FTIR measurements. Isotopic labeling assigned the negative band at 1137 cm⁻¹ to β-GDP. Therefore, the γ-GppNHp band at 1128 cm⁻¹ was superimposed by β-GDP in the ATR-FTIR measurements and reduced to a shoulder. Hence γ-GppNHp owns two asymmetrical stretching vibrations at 1128 cm⁻¹ and 1114 cm⁻¹.

Calculated ³¹P NMR signals match experimental NMR spectroscopy

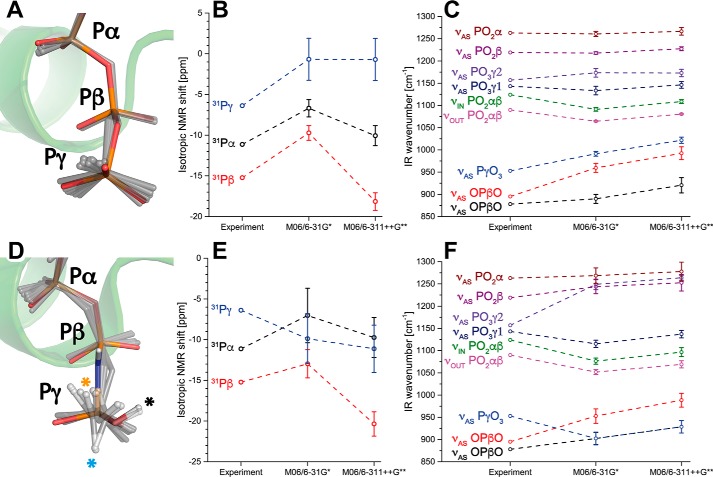
The protonation state of GTP was mainly investigated using NMR spectroscopy and infrared spectroscopy in the literature. Therefore we initially benchmarked our QM/MM calculations with previous NMR (21–23, 25) and infrared (20, 27) studies. When Kalbitzer and co-workers assigned the ³¹P NMR spectra of the α-, β-, and γ-phosphorous atoms of Ras·GTP it was surprising that the phosphorous atoms did not appear in an ascending or descending order, but the Pβ atom was the most shielded atom followed by the Pα and the Pβ atom, respectively (21). This even led to early incorrect assignments of NMR spectra (28) that were corrected when 2D NMR was performed (21). We calculated the ³¹P NMR shifts from an ensemble of molecular mechanics–molecular dynamics (MM-MD) simulations (15 snapshots, Fig. 4A) using QM/MM calculations and found the correct behavior for deprotonated GTP bound to Ras (Fig. 4B). Size of the basis set (6-31G*/6-311++G**) had an influence on the total numbers, but not on the order, of the NMR chemical shifts.

Figure 4.

NMR and infrared spectra for deprotonated and protonated GTP. A and D, geometries of (A) deprotonated and (D) γ-protonated GTP. Shown are the crystal structures of (A) Ras·GTP (1QRA.pdb) and (D) Ras·GppNHp (4RSG.pdb) in color and the dynamics of the substrate in the QM/MM optimized snapshots (gray sticks). The γ-GTP proton sampled the crystal structure (black asterisk), an O–Pγ–O–H torsion angle of 0° (orange asterisk) and 180° (cyan asterisk). B, calculated ³¹P NMR spectra match the experimental spectra for deprotonated GTP, with Pβ being most shielded, followed by Pα and Pγ, respectively. E, this was not the case for protonated GTP. C and F, the same applies for infrared spectra of deprotonated (C) and protonated (F) GTP. Therefore, GTP was most likely deprotonated in the experiments. Error bars depict the mean ± S.E. from each 15 independent calculations.

Calculated infrared spectra of GTP match experimental FTIR spectra

Next we calculated infrared spectra of Ras·GTP and compared them with experimental studies (20). Comparison of H-Ras and N-Ras is possible, because the active site is completely identical between the isoforms. We determined the quaternary structure of N-Ras on the POPC membrane and found dimer formation at the Helix4/Helix5 interface, leaving the active sites unperturbed by dimerization (26). Experimental vibrational difference spectra of GTP- and GDP-bound N-Ras and H-Ras are identical (Fig. 2B). The calculated spectra reproduced the experimental values well (Fig. 4C). The lack of major differences between the small (6-31G*) and large basis set (6-311++G**) indicate that the small basis set is appropriate for the system. It is notable that only GTP, Mg²⁺, and its coordinating water molecules were treated quantum chemically, which differs from previous studies (29, 30), but still the experimental values were matched by these cost-efficient simulations. After we have shown that both NMR and IR spectra can be reproduced via QM/MM calculations we protonated γ-GTP, conducted 100-ns MM-MD simulations and calculated IR and NMR spectra from QM/MM simulations.

Protonation of γ-GTP caused deviation from the experimental NMR and IR spectra

NMR and infrared spectra of γ2-protonated GTP (Fig. 1) were calculated from QM/MM simulations (15 snapshots, Fig. 4D) and are depicted in Fig. 4, E and F. The protonation γ2 corresponds to the protonation state that was proposed by the neutron diffraction crystal structure (24). The depicted structures that were obtained from QM/MM optimized snapshots of MD simulations (Fig. 4D, gray) show that the γ-GTP proton was flexible with a O–Pγ–O–H torsion angle comparable with the neutron diffraction structure, but also torsion angles of 0° and 180° were sampled. The O–Pγ–O–H torsion angle has a negligible torsion potential, meaning it is almost freely rotatable and the sampled proton positions did not cause significant deviations among the IR and NMR spectra. Therefore all positions were averaged and included in the standard deviation calculations. However, protonation caused significant changes in the NMR spectra compared with deprotonated GTP (Fig. 4E), resulting in permutation of the position of the ³¹Pα and ³¹Pβ chemical shift. Protonation of γ-GTP also altered the calculated IR spectrum (Fig. 4F) and caused large deviations from the experimental values. The upper ν_AS(PO₃)γ vibration was about 100 cm⁻¹ blue-shifted away from the experiment. The symmetrical γ-GTP vibration appeared strongly red-shifted and coupled to the asymmetrical OPO stretching vibration. Therefore the γ-GTP group was most likely fully deprotonated in the experiments.

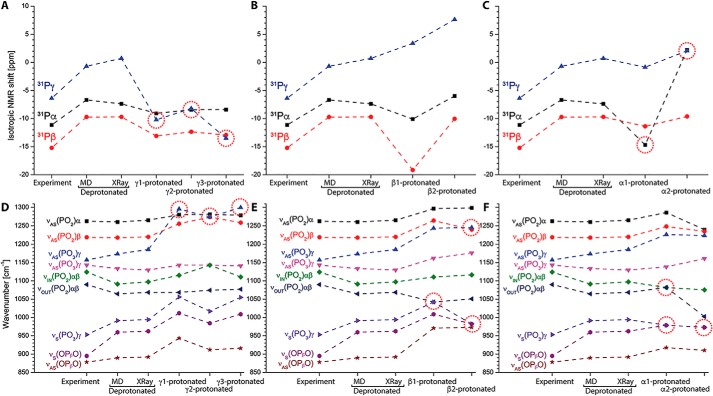
Calculation of α-, β-, γ-GTP protonation from crystal structures

We further calculated IR and NMR spectra directly from the corresponding crystal structures without prior MM-MD simulations to exclude artifacts from the molecular dynamics simulations. Calculations from crystal structures resulted in comparable values (Fig. 5). Then we protonated every terminal oxygen atom of GTP (α1, α2, β1, β2, γ1, γ2, γ3) to assess the effect on NMR and IR spectra from protonation on these sites. Protonation of γ-GTP always resulted in significant deviations of the NMR chemical shifts from the experimental values (Fig. 5A, red circles). Protonation on any γ-GTP oxygen perturbed even the correct order of the Pα, Pβ, and Pγ chemical shifts. Accordingly, the calculated IR spectra were perturbed and were shifted far from the experiment (Fig. 5D, red circles). Protonation of γ-GTP affected mainly NMR shifts and IR vibrations of the corresponding γ-GTP signals. Protonation of β-GTP caused less perturbation of the calculated IR and NMR signals; however both NMR (Fig. 5B) and IR spectra (Fig. 5E) deviated from the experiment when β-GTP was protonated. Protonation of α-GTP had large impact on both the Pα NMR signals (Fig. 5C) and the IR vibrations from α-GTP (Fig. 5F), resulting always in perturbation of the signals (Fig. 5, C and F, red circles). Therefore, protonation on any of those sites was probably not the case in the conducted experiments.

Figure 5.

NMR and IR spectra for GTP protonation on all possible sites. We calculated NMR and IR spectra for fully deprotonated phosphate groups and every possible protonation (γ1/γ2/γ3, β1/β2/, α1/α2; atom names match those in Fig. 1) of GTP bound to Ras (M06/6–31G*) from the crystal structure 1QRA.pdb. Results for deprotonated GTP and γ2 protonated GTP agree well to the values calculated from 15 QM/MM snapshots. Most significant deviations from experimental values are indicated by red circles. NMR spectra show significant deviations for γ protonation and α protonation. IR spectra show significant deviations for every kind of protonation, indicating fully deprotonated triphosphate was present in the experiments.

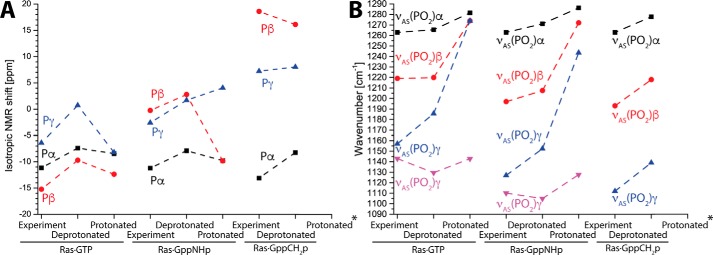
Calculation of GppNHp and GppCH₂p protonation

Similarly to Ras·GTP, we calculated Ras·GppNHp and Ras·GppCH₂p and the corresponding γ2-protonated nucleotides. The measured IR spectra from the ATR-FTIR experiments are complemented by previous ³¹P NMR experiments of Ras·GppNHp and Ras·GppCH₂p from the literature (22). Calculated NMR spectra of deprotonated Ras·GppNHp reproduce the experiment well, whereas γ2-protonation resulted in an incorrect order of the ³¹P shifts (Fig. 6A). Note that the ³¹Pα, ³¹Pβ, ³¹Pγ order was different for GTP and GppNHp, which was correctly calculated from the simulations. Protonation of Ras·GppNHp also resulted in perturbation of the IR spectra, although here the order of the individual vibrations was still reproduced. Calculation of Ras·GppCH₂p was only possible for deprotonated GppCH₂p, because the proton always dissociated from the nucleotide for the protonated calculations. However, both NMR and IR spectra were correctly reproduced (Fig. 6, A and B). Taking the results together, only deprotonated GppNHp and GppCH2p correctly reproduce the experiment.

Figure 6.

Calculation of GTP, GppNHp, and GppCH₂p protonation. A and B, we calculated protonated and deprotonated NMR (A) and IR spectra (B) of Ras·GTP, Ras·GppNHp, and Ras·GppCH₂p. The depicted γ protonations correspond to γ2 in Fig. 1 similarly to Ref. 24. Protonation always caused deviation from the experimental values. Protonated Ras·GppCH₂p always deprotonated during the calculations (asterisks).

Discussion

The protonation state of GTP, GppNHp, and GppCH₂p in the active center of Ras was determined using a combination of infrared spectroscopy and QM/MM calculations. The accuracy of the determined infrared vibrations is notable (1 cm⁻¹ corresponds to a P–O bond length alteration of 0.001 nm (31, 32)) and the impact of alterations down to single hydrogen bonds was shown various times in the literature (30, 33). The calculations were benchmarked against NMR spectra and infrared spectra from the literature (20, 21) and were found in excellent agreement when GTP was deprotonated. The small basis set M06/6-31G* was sufficient to reproduce the infrared experiments and the QM box only contained the nucleotide Mg²⁺ and its coordinating water molecules, enabling fast calculation of QM/MM spectra from a MM snapshot within 1 day on eight parallel central processing unit (CPU) cores. We calculated protonation of every phosphate group in GTP, including a protonation scheme that was suggested by neutron diffraction crystallography (24). The calculated NMR results of several protonations (γ1, γ3, α1, α2) contradicted the experimental findings, indicating these protonation states were not present in the NMR experiments. In addition, the calculated infrared spectra show large deviations upon protonation, also indicating that only the fully deprotonated GTP (charge −4) was present in the FTIR experiments. We further investigated this by measuring GTP and several GTP analogs bound to lipidated N-Ras on a POPC model membrane within an ATR-FTIR setup, which now resembled the in vivo situation. The spectra of Ras·GTP in solution (transmission FTIR (20)) matched exactly the spectra of lipidated Ras·GTP on a POPC membrane (ATR-FTIR) (Fig. 2). This is not surprising, because it was shown via Förster resonance energy transfer (FRET) measurements on a similar ATR-FTIR setup that N-Ras is organized in upright dimers or oligomers with no interaction of the nucleotide-binding pocket with the lipids (26). These measurements together with the QM/MM calculations now show that Ras·GTP bound on a lipid membrane does not carry any protons on any of its phosphate groups. Protonated GTP was not visible in the measured FTIR spectra, indicating its concentration in the present equilibrium is very low. We repeated the transmission FTIR measurements of GTP hydrolysis in H-Ras at pH 6 instead of pH 7.2 to increase the concentration of protonated GTP, but measured spectra were identical. This indicates that the pK_a for protonation of Ras-bound GTP is distinctly lower than 6. We furthermore calculated protonated GppNHp bound to Ras like in the neutron diffraction crystal structure and measured the nucleotide infrared spectra in solution (transmission FTIR) and bound on a lipid bilayer (ATR-FTIR). Our results show that GppNHp was also deprotonated. The different protonation state in the neutron diffraction crystal structure might be caused by the dense packing, which caused e.g. binding of a neighboring Tyr side chain to γ-GppNHp or the higher affinity for deuterons compared with protons because of the lower zero point energy of the deuterated species. The fact that both NMR and infrared spectra from different studies and our own measurements on a lipid surface could only be reproduced with both deprotonated GTP and deprotonated GppNHp is a strong argument that no protonation at the γ-phosphate group was present in the experiments. Our calculations now unify the results from different studies and transfer them to a structural model that confirms the hypothesis that γ-GTP is fully deprotonated in the prehydrolysis state of Ras.

Experimental procedures

Materials

The semisynthetic N-Ras protein used in the experiments was prepared as described elsewhere (34–37). 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) was purchased from Lipoid (Ludwigshafen, Germany). Synthesis of the P3–1-(2-nitrophenyl)-ethyl ester of GppNHp (NPEcgGppNHp) was performed in two steps from 2-nitro-phenylacetylhydrazone and GppNHp with subsequent purification via anion exchange chromatography (38). The compounds were characterized via mass spectrometry and NMR.

ATR-FTIR measurements

Preparation, lipid bilayer spreading, and protein immobilization were performed as described previously (26). Briefly, ATR germanium crystals (52 mm × 20 mm × 2 mm, Korth Kristalle, Altenholz, Germany) were cleaned, polished, and hydrophilized by dipping the crystal into concentrated sulfuric acid solution. Next the crystal was cleaned, dried, and treated with an air plasma. Lipid bilayers were prepared by spreading small vesicles onto the hydrophilic ATR crystal in the ATR flow-through system. Lipidated N-Ras in 20 mm Tris/HCl, pH 7.4, 5 mm MgCl₂, 1 mm DTT, 0.1 mm GDP was added to the buffer in a circulating flow-through system and slowly attached to the membrane (5, 36). Nucleotide exchange via Mg²⁺-chelation with EDTA was performed as described previously (26) with GDP background. ATR-FTIR measurements were performed with a Vertex 80v FTIR spectrometer (Bruker Optik, Ettlingen, Germany) at 293 K, with a spectral resolution of 4 cm⁻¹ and a scanner velocity of 80 kHz in the double-sided forward-backward mode of the spectrometer. The apodization function three-term Blackman-Harris was applied with a zero-filling factor of 4. Data evaluation was performed in OPUS (Bruker Optik). In Figs. 2 and 3, disappearing bands face downward and appearing bands face upward.

Transmission FTIR measurements

Prior to transmission FTIR measurements, nucleotide exchange to photocaged NPEcgGppNHp was performed as described previously (30). Samples were prepared between two CaF₂ windows, sealed and fixed in a metal cuvette, and mounted in the spectrometer (Vertex 80v, Bruker). After sample equilibration background spectra were taken (400 scans) and photolysis of the NPEcg compound was initiated with a laser flash at 308 nm with an LPX 240 XeCl excimer laser (Lambda Physics, Göttingen, Germany) (80 flashes within 160 ms; 100–200 millijoules/flash, 20-ns pulse duration). Data between 1800 and 950 cm⁻¹ were recorded with a liquid nitrogen–cooled mercury cadmium telluride (MCT) detector with a spectral resolution of 4 cm⁻¹ in the double-sided forward-backward data acquisition mode and a scanner speed of 120 kHz. The apodization function three-term Blackman-Harris was applied with a zero-filling factor of 4. Data of at least three independent measurements were averaged in OPUS. In Figs. 2 and 3, disappearing bands face downward and appearing bands face upward.

MD simulations

The structures of Ras·GTP (PDB ID: 1QRA (39)) and the neutron diffraction crystal structure with bound protonated GppNHp (PDB ID: 4RSG (24)) were prepared as starting structures for MD simulations in the Moby program suite (40). Structure preparation included dihedral, angle, and bond corrections according to the AMBER84 United Atom Forcefield (41), in case of protonated GTP followed by substitution of protonated GppNHp by protonated GTP. Ionizable residues were protonated according to local pK_a calculations in Moby with a total charge q = 0 (33). The starting structure was initially solvated in Moby following the Vedani algorithm (42) and then transferred to the GROMACS 2016 program suite (43–46) where full solvation with TIP4P waters and 154 mm NaCl in a cubic simulation cell (d = 7 nm) was performed. Simulations were conducted in the OPLS/AA forcefield (47) using parameters for deprotonated GTP (27) and singly protonated GTP (33). Coulomb interactions were calculated using particle mesh Ewald (0.9 nm) and a van der Waals cutoff of 1.5 nm was applied on a graphics processing unit (GPU)–accelerated work station. The systems were initially energy minimized using the conjugate gradient method and heated to 310 K using the Berendsen thermostat and barostat with a time step of 1 femtosecond for 25 picoseconds with restrained protein backbone positions, followed by a 100-ns MD simulation in several replica runs for deprotonated and protonated GTP. We applied a distance restraint for the hydrogen bond between α-GTP and the backbone of Ala-18 with default parameters for a hydrogen bond (r1 = 0.3; r2 = 0.4; k = 1000 kJ/mol*nm; ensemble averaging). Simulations without this restraint sometimes resulted in breaking of this hydrogen bond, yielding a distinctly different conformation of GTP compared with the X-ray structure. Calculated NMR and IR data of these snapshots deviated largely from the experiment, indicating this conformation is an artifact and this hydrogen bond has to be restrained to give correct results. Evaluation was performed using the GROMACS package. Pictures were created using PyMOL 1.7 (Schrödinger LLC, Portland, OR).

QM/MM calculations, IR and NMR spectra calculation

QM/MM calculations were performed using the ONIOM QM/MM method with electronic embedding (48–50) in Gaussian 09 (51). We performed two kinds of QM/MM calculations: on the one hand for the minimized crystal structures and on the other hand for 15 snapshots of equilibrated MD simulations (25 ns to 100 ns with 5-ns spacing). In this way we investigated both starting structures that are close to the experiment and ensembles that generate an estimate of the line-broadening in the infrared measurements. The QM area contained GTP, the Mg²⁺ ion, and its coordinating water molecules. The QM area was surrounded by two layers in a 1.5-nm radius a MM layer containing substructure-based all centers of the protein and the solvent within this radius around the QM box. This layer was surrounded by a fixed MM layer containing the remaining protein atoms (for details see Ref. 33). Nearest Na⁺/Cl⁻ ions were included in the MM layer to ensure a total charge of zero (GTP: q_QM = −2; q_MM = +2; GTPh: q_QM = −1; q_MM = +1; GppNHp: q_QM = −2; q_MM = +2; GppNHph: q_QM = −1; q_MM = +1, GppCH₂p: q_QM = −2; q_MM =+2; GppCH₂ph: q_QM = −1; q_MM = +1). Initially a QM single-point calculation was performed for the QM part with fixed MM centers in the Gaussian program with the functional M06 (52) and several basis sets (6–31G*/6–311++G**) (53). Merz-Singh-Kollman (ESP) partial charges were computed for the QM part and the geometry with updated charges was transferred to the Moby program suite where energy minimization for MM centers within 0.5 nm of the QM centers in the presence of all other centers was performed according to the Broyden-Fletcher-Goldfarb-Shanno algorithm (54, 55). We used this quasi-Newton method because the rather straightforward steepest descent algorithm failed to minimize the MM part properly. The updated coordinates were re-transferred to the Gaussian program where a full QM optimization was performed. This procedure was repeated two times for the MM, the QM, the MM, and the QM part. IR spectra calculation of the minimum structures was performed using normal mode analysis in the Gaussian program. No imaginary frequencies were observed for any calculation, even normal mode analysis of the MM part showed no imaginary frequencies, indicating both parts always reached a minimum. Infrared frequencies were scaled according to the Computational Chemistry Comparison and Benchmark Database (CCCBDB) of the National Institute of Standards and Technology (NIST) (M06/6–31G*: 0.95; M06/6–311++G**: 0.97). We investigated infrared frequencies between 850 and 1300 cm⁻¹ with considerable infrared intensities, namely the asymmetrical stretching vibrations of the α-GTP group (ν_AS PO₂ α), of the β-GTP group (ν_AS PO₂ β), the two asymmetrical stretching vibrations of the terminal PO₃ group (ν_AS PO₃ γ1/ν_AS PO₃ γ2), that appeared clearly separated because of the strong polarization toward the bound Mg²⁺ ion for the γ1 oxygen atom. Furthermore, we investigated the in-phase stretching vibration of α-GTP and β-GTP (ν_IN PO₂ αβ), the out-of-phase stretching vibration of the same group (ν_OUT PO₂ αβ), the symmetrical P–O₃ stretching vibration of γ-GTP (ν_S PγO₃), the symmetrical O–P_β–O backbone stretching vibration (ν_AS OP_βO) as well as its symmetrical vibration (ν_S OP_βO). The vibrational motions are depicted in Movie S1 for deprotonated GTP and Movie S2 for γ-protonated GTP. NMR spectra were calculated also from the obtained minimum structures using the Gauge-Independent Atomic Orbital (GIAO) method (56–60) implemented in Gaussian 09. To enable direct comparison with the experiments, the isotropic shielding tensors were standardized by subtracting the isotropic shielding tensors for phosphoric acid in aqueous solution as a standard, which were obtained via a QM calculation in water continuum environment (polarizable continuum model, ϵ = 78.3553) for both basis sets. A similar standardization was performed in the experiments (21, 61). The whole QM/MM calculation procedure for one snapshot with the small basis set was performed within 1 day on eight parallel central processing unit cores (AMD Opteron; 1.9 GHz).

Author contributions

D.M., K.G., and C.K. conceptualization; D.M. and C.K. data curation; D.M. software; D.M., J.G., and C.K. formal analysis; D.M., K.G., and C.K. funding acquisition; D.M., J.G., J.S., and C.K. investigation; D.M. visualization; D.M., J.G., and C.K. methodology; D.M. writing-original draft; D.M., K.G., and C.K. project administration; D.M., J.G., J.S., K.G., and C.K. writing-review and editing; J.G. and C.K. validation; K.G. resources; K.G. and C.K. supervision; J.S. chemical synthesis.