Dynamic Flexibility in Striatal-Cortical Circuits Supports Reinforcement Learning

Abstract

Complex learned behaviors must involve the integrated action of distributed brain circuits. Although the contributions of individual regions to learning have been extensively investigated, much less is known about how distributed brain networks orchestrate their activity over the course of learning. To address this gap, we used fMRI combined with tools from dynamic network neuroscience to obtain time-resolved descriptions of network coordination during reinforcement learning in humans. We found that learning to associate visual cues with reward involves dynamic changes in network coupling between the striatum and distributed brain regions, including visual, orbitofrontal, and ventromedial prefrontal cortex (n = 22; 13 females). Moreover, we found that this flexibility in striatal network coupling correlates with participants' learning rate and inverse temperature, two parameters derived from reinforcement learning models. Finally, we found that episodic learning, measured separately in the same participants at the same time, was related to dynamic connectivity in distinct brain networks. These results suggest that dynamic changes in striatal-centered networks provide a mechanism for information integration during reinforcement learning.

SIGNIFICANCE STATEMENT Learning from the outcomes of actions, referred to as reinforcement learning, is an essential part of life. The roles of individual brain regions in reinforcement learning have been well characterized in terms of updating values for actions or cues. Missing from this account, however, is an understanding of how different brain areas interact during learning to integrate sensory and value information. Here we characterize flexible striatal-cortical network dynamics that relate to reinforcement learning behavior.

Introduction

Learning from reinforcement is central to adaptive behavior and requires integration of sensory, motor, and reward information over time. Major progress has been made in understanding how individual brain regions support reinforcement learning. However, little is known about how these brain regions interact, how their interactions change over time, and how these dynamic network-level changes relate to successful learning.

In a reinforcement learning task, participants use feedback over many trials to associate choices with probable outcomes (O'Doherty et al., 2003; Frank et al., 2004; Shohamy et al., 2004). Computationally, this is captured by “model-free” learning algorithms, which provide a mechanistic framework for describing behavior (Sutton and Barto, 1998; Daw et al., 2005; Daw, 2011). These models account for neuronal signals underlying learning (Schultz et al., 1997; O'Doherty et al., 2003; Daw et al., 2006), demonstrating a role for the striatum and its dopaminergic inputs in updating reward predictions. However, to support reinforcement learning, the striatum must also integrate visual, motor, and reward information over time. Such a process is likely to involve coordination across a number of different circuits interconnected with the striatum.

The idea that the striatum serves an integrative role is not new (Kemp and Powell, 1971; Bogacz and Gurney, 2007; Hikosaka et al., 2014; Ding, 2015). The striatum is anatomically well positioned for integration: it receives input from many cortical areas and projects back to motor cortex (Alexander et al., 1986; Haber, 2003; Haber et al., 2006; Haber and Knutson, 2010). However, although the idea that the striatum serves such a role is theoretically appealing, it has been difficult to test empirically. Thus, it remains unknown how the striatum interacts with cortical regions representing sensory, motor, and value signals and how these network-level interactions reconfigure over the course of learning.

Here we aimed to address this gap, using the emerging field of dynamic network neuroscience (Kopell et al., 2014; Medaglia et al., 2015). This area of research has been spurred by the development of tools like multislice community detection (Mucha et al., 2010) that can infer activated circuits and their reconfiguration from neuroimaging data. These tools have been leveraged to understand the role of dynamic connectivity in motor learning (Bassett et al., 2011, 2013b; 2015). A key measure is an index of a brain region's tendency to communicate with different networks over time, known as “flexibility” (Bassett et al., 2011). Prior work has shown that flexibility across a number of brain regions predicts individual differences in acquisition speed on a simple motor task (Bassett et al., 2011), and it has been related to working memory performance (Braun et al., 2015). But its role in updating choice behavior based on reinforcement is not known.

We hypothesized that network dynamics, indexed by flexibility, support key processes underlying reinforcement learning; specifically, that reinforcement learning is associated with increases in dynamic coupling between the striatum and cortical regions processing visual and value information. We predicted that (1) reinforcement learning would involve increased flexible network coupling between the striatum and distributed brain circuits; and (2) that these circuit changes would be related to measurable changes in behavior, specifically learning performance (accuracy, within-subjects) as well as learning rate and inverse temperature, individual difference measures derived from reinforcement learning models.

Our final prediction concerned the relationship between flexibility and episodic memory for individual events. The rationale for testing episodic memory was twofold. First, it provided a comparison for time-on-task effects. Second, it was a question of interest given that little is known about how episodic memory is supported by brain networks. Given the extensive literature indicating that separate brain regions support episodic memory versus reinforcement learning (Knowlton et al., 1996; Myers et al., 2003; Foerde et al., 2013a; Doll et al., 2015), we predicted that (3) distinct medial temporal and prefrontal regions would exhibit a relationship between network flexibility and episodic memory.

Materials and Methods

To test these hypotheses, we used functional magnetic resonance imaging (fMRI) to measure changes in brain network structure while participants engaged in a reinforcement learning task (Fig. 1A). On each trial, participants were presented with a visual cue, made a choice indicated by a key press, and then received feedback. Participants had up to 4 s to respond to each trial, and feedback was shown for 2 s. We used a task for which behavior has been well described by reinforcement learning models (Foerde and Shohamy, 2011), and which is known from fMRI to involve the striatum (Foerde and Shohamy, 2011) and from patient studies to depend on it (Foerde et al., 2013a). The task also included trial-unique images presented during feedback, allowing us to test the role of network dynamics in episodic memory. Presentation of these images coincided with reinforcement, but they were incidental to the learning task (Fig. 1B).

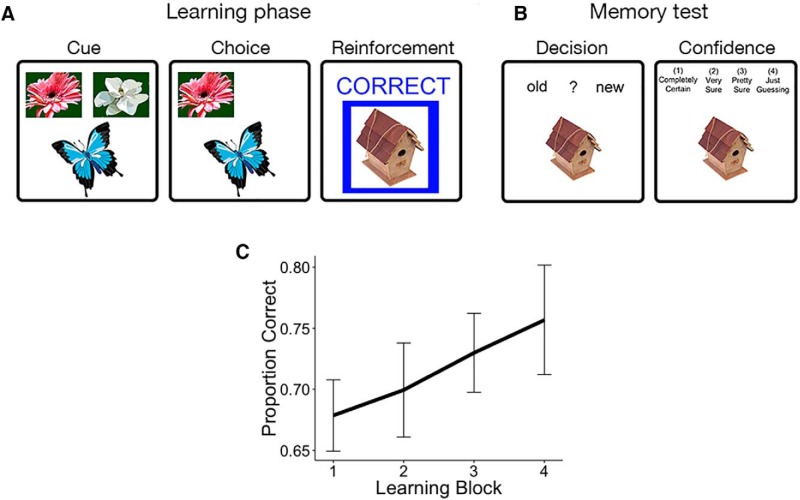
Figure 1.

Task design and learning performance. Participants performed a modified reinforcement learning task while undergoing fMRI (Foerde and Shohamy, 2011). A, Participants were instructed to associate each of four cues (butterflies) with one of two outcomes (flowers). Feedback was probabilistic, with positive feedback following the choice on 80% of correct trials and on 20% of incorrect trials. B, Each feedback event was presented with a unique image. Thirty minutes following the MRI scan, participants were given a surprise episodic memory test, testing recognition and confidence for images seen during the scan, intermixed with novel images. C, Average performance on the learning task improved linearly, suggesting continuous learning across all trials.

Experimental design.

Twenty-five healthy right-handed adults (age 24–30 years, mean = 27.7, SD = 2.0; 13 females) were recruited from the University of California Los Angeles and the surrounding community as the adult comparison sample in a developmental study of learning (Davidow et al., 2016). All participants provided informed consent in writing to participate in accordance with the UCLA Institutional Review Board, which approved all procedures. Individuals were paid for their participation. Participants reported no history of psychiatric or neurological disorders, or contraindications for MRI scanning. Three subjects were excluded from this analysis (2 for technical issues in behavioral data collection and 1 for an incidental neurological finding), leading to a final sample size of 22.

Task and behavioral analysis.

The probabilistic learning task administered to subjects undergoing an fMRI session has been previously described (Foerde and Shohamy, 2011; Foerde et al., 2013a,b; Davidow et al., 2016). Before scanning, participants completed a practice round of eight trials to become familiar with the task. On each trial, participants were presented with an image of one of the four butterflies along with two flowers, and asked to indicate which flower the butterfly was likely to feed from, using a left or right button press. The four learning blocks were followed by a test phase, in which subjects performed the same butterfly task without feedback for 32 trials. During the imaging session, individuals underwent an instrumental conditioning procedure, in which they learned to associate four cues with two possible outcomes. The cues were images of butterflies; the choices were images of flowers. They were then given feedback consisting of the words “Correct” or “Incorrect”. Presentation of feedback also included an image of an object unique to each trial, shown in random order for the purpose of subsequent memory testing. For each butterfly image, one flower represented the “optimal” choice, with a 0.8 probability of being correct, whereas the alternative flower had a 0.2 probability of being followed by correct feedback. Subjects performed four blocks of this probabilistic learning phase, each consisting of 30 trials. Feedback was presented for 2 s, and was followed by a randomly jittered intertrial interval.

For each trial in the learning phase, we recorded the feedback the participant actually received as well as whether the optimal choice was made, and we computed the percentage correct for each block based on the percentage of trials on which subjects made the optimal choice (regardless of actual feedback). These variables enable a characterization of learning as the proportion of optimal choices in each block, as well as that in the test phase. Using this information, we fit reinforcement learning models to subjects' decisions (Sutton and Barto, 1998; Daw, 2011), using a hierarchical Bayesian approach to pool uncertainty across subjects and aid in model identifiability.

Briefly, the expected value for a given choice at time t, Q_t, is updated based on the reinforcement outcome r_t via a prediction error δ_t:

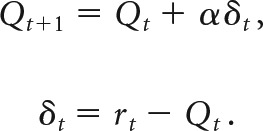The reinforcement learning models included two free parameters, α and β. The learning rate α is a parameter between 0 and 1 that measures the extent to which value is updated by feedback from a single trial. Higher α indicates more rapid updating based on few trials and lower α indicates slower updating based on more trials. Another parameter fit to each subject is the inverse temperature parameter β, which determines the probability of making a particular choice using a softmax function (Ishii et al., 2002; Daw, 2011), so that the probability of choosing choice 1 on trial t would be:

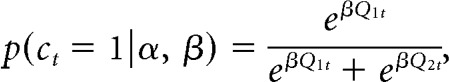where p(c_t = 1) refers to the probability of choice one and Q_1t is the value for this choice on trial t.

Reinforcement learning models of this form have known issues with identifiability (Gershman, 2016). To constrain the parameter space to reduce noise, we fit a hierarchical Bayesian model, which regularizes this estimation with empirical prior distributions on α and β (Daw, 2011):

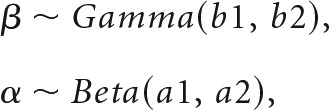where b1, a1, and a2 are shape parameters, and b2 is a scale parameter. By fitting prior parameters as part of the model, individual-level likelihood parameters are constrained by group average distributions. These group parameters were themselves regularized by weakly informative hyperprior distributions [Cauchy⁺ (0,5) in all cases]. Models were fit using Hamiltonian Markov Chain Monte Carlo in Stan (Carpenter et al., 2015). In addition to the benefit of constraining the parameter space, this approach produces a posterior distribution of all parameters, which incorporates uncertainty at both group and individual levels in parameter estimation, and also allows for the consideration of all plausible values of reinforcement learning (RL) parameters in subsequent analyses, rather than relying on point estimates or Gaussian assumptions.

Following the fMRI session (∼30 min), subjects were given a surprise memory test for the trial-unique object images presented during feedback in the learning phase. Subjects were presented with all 120 objects shown during the conditioning phase, along with an equal number of novel objects, and asked to judge the images as “old” or “new”. They were also asked to rate their confidence for each decision on a scale of 1–4 (1 being most confident; 4 indicating “guessing”). All responses rated 4 were excluded from our analyses (Foerde and Shohamy, 2011).

MRI acquisition and preprocessing.

MRI images were acquired on a 3 T Siemens Tim Trio scanner using a 12-channel head coil. For each block of the learning phase of the conditioning task, we acquired 200 interleaved T2*-weighted echoplanar (EPI) volumes with the following sequence parameters: TR = 2000 ms; TE = 30 ms; flip angle (FA) = 90°; array = 64 × 64; 34 slices; effective voxel resolution = 3 × 3 × 4 mm; FOV = 192 mm). A high-resolution T1-weighted MPRAGE image was acquired for registration purposes (TR = 2170 ms, TE = 4.33 ms, FA = 7°, array = 256 × 256, 160 slices, voxel resolution = 1 mm³, FOV = 256). In addition, as part of the original study for which these data were collected, two resting state scans were acquired; one before and one after the learning task. Resting state scans were acquired with identical sequence parameters to the EPI scans described above, except that each scan consisted of 154 images (308 s). We used these scans to test the specificity of our results to learning, and to demonstrate the reliability of our dynamic connectivity metric across multiple scans (see Dynamic network statistics: flexibility and allegiance).

Functional images were preprocessed using FSL's FMRI Expert Analysis Tool (FEAT; Smith et al., 2004). Images from each learning block were high-pass filtered at f > 0.008 Hz, spatially smoothed with a 5 mm FWHM Gaussian kernel, grand-mean scaled, and motion corrected to their median image using an affine transformation with tri-linear interpolation. The first three images were removed to account for saturation effects. Functional and anatomical images were skull-stripped using FSL's Brain Extraction Tool. Functional images from each block were coregistered to subject's anatomical images and nonlinearly transformed to a standard template (T1 Montreal Neurological Institute template, voxel dimensions 2 mm³) using FNIRT (Andersson et al., 2008). Following image registration, time courses were extracted for each block from 110 cortical and subcortical regions-of-interest (ROIs) segmented from FSL's Harvard-Oxford Atlas. Due to known effects of motion on measures of functional connectivity (Power et al., 2012; Satterthwaite et al., 2012), time courses were further preprocessed via a nuisance regression. This regression included the six translation and rotation parameters from the motion correction transformation, average CSF, white matter, and whole-brain time courses, as well as the first derivatives, squares, and squared derivatives of each of these confound predictors (Satterthwaite et al., 2013). Resting-state functional images underwent identical preprocessing steps.

Dynamic connectivity analysis.

To assess dynamic connectivity between the ROIs, time courses were further subdivided into sub-blocks of 25 TRs each. The selection of 25 TRs represents a compromise between the precision and range of frequencies sampled for each network, the number of networks per estimate of flexibility, and the number of flexibility measurements to compare to within-subject behavior. Smaller window sizes are more sensitive to short term-dynamics (including task-evoked changes) and also to individual differences in dynamic connectivity. In contrast, larger window sizes offer more precise estimates of connectivity and are more sensitive to inter regional variation (Telesford et al., 2016). Because we were interested in variation across time, regions, and subjects, we selected windows 25 TR (50 s) in duration, representing a middle ground between time windows that exhibit high levels of temporal and individual variability (∼25 s) and those that show high levels of interregional variability (∼75 s).

For each 25 TR sub-block, connectivity was quantified as the magnitude-squared coherence between each pair of ROIs at f = 0.06 − 0.12 Hz to later assess modularity over short time windows in a manner consistent with previous reports (Bassett et al., 2011, 2013b):

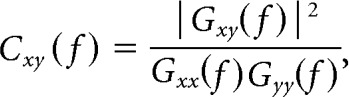where G_xy(f) is the cross-spectral density between regions x and y, and G_xx(f) and G_yy(f) are the autospectral densities of signals x and y, respectively. We thus created subject-specific 110 × 110 × 32 connectivity matrices for 110 regions and 8 time windows for each of the 4 learning blocks, containing coherence values ranging between 0 and 1. The frequency range of 0.06–0.12 Hz was chosen to approximate the frequency envelope of the hemodynamic response, allowing us to detect changes as slow as three cycles per window with a 2 s TR. We selected this frequency band based on previous work showing that high-frequency associations may not map on to task-evoked changes in connectivity (Sun et al., 2004). This observation follows if one assumes that the canonical hemodynamic response function serves as a low-pass filter of any high-frequency coupling. There is increasing reason to be suspicious of this assumption (Chen and Glover, 2015; Zhang et al., 2016), but the processes leading to interactions measured by high-frequency BOLD signals are not well understood. For this reason, we decided to follow previous studies of task-based flexibility (Bassett et al., 2011) by focusing on coupling in the frequency range associated with the canonical hemodynamic response.

Each connectivity matrix was treated as an unthresholded graph or network, in which each brain region is represented as a network node, and each functional connection between two brain regions is represented as a network edge (Bullmore and Sporns, 2009; Bullmore and Bassett, 2011). In the context of dynamic functional connectivity matrices, the network representation is a temporal network, which is an ensemble of graphs that are ordered in time (Holme and Saramäki, 2011). If the temporal network contains the same nodes in each graph, then the network is said to be a multilayer network where each layer represents a different time window (Kivelä et al., 2014). The study of topological structure in multilayer networks has been the topic of considerable study in recent years, and many graph metrics and statistics have been extended from the single-network representation to the multilayer network representation. Perhaps one of the single most powerful features of these extensions has been the definition of so-called identity links, a new type of edge that links one node in one time slice to itself in the next time slice. These identity links hard code node identity throughout time, and facilitate mathematical extensions and statistical inference in cases that had previously remained challenging.

Uncovering evolving circuits using multislice community detection.

To extract modules or communities from a single-network representation, one typically applies a community detection technique such as modularity maximization (Newman, 2004). However, these single-network algorithms do not allow for the linking of communities across time points, thus hampering statistically robust inference regarding the reconfiguration of communities as the system evolves (Mucha et al., 2010). In contrast, the multilayer approaches allow for the characterization of multilayer network modularity, with layers representing time windows. In this framework, each network node in the multilayer network is connected to itself in the preceding and following time windows to link networks in time. This enables us to solve the community-matching problem explicitly within the model (Mucha et al., 2010), and also facilitates the examination of module reconfiguration across multiple temporal resolutions of system dynamics (Bassett et al., 2013a). We thus constructed multilayer networks for each subject, allowing for the partitioning of each network into communities or modules whose identity is robustly tracked across time windows.

Although many statistics are available to the researcher to characterize network organization in temporal and multilayer networks, it is not entirely clear that all of these statistics are equally valuable in inferring neurophysiologically relevant processes and phenomena (Medaglia et al., 2015). Indeed, many of these statistics are difficult to interpret in the context of neuroimaging data, leading to confusion in the wider literature. A striking contrast to these difficulties lies in the graph-based notion of modularity or community structure (Newman, 2004), which describes the clustering of nodes into densely interconnected groups that are referred to as modules or communities (Porter et al., 2009; Fortunato, 2010). Recent and convergent evidence demonstrates that these modules can be extracted from rest and task-based fMRI data (Meunier et al., 2010; Cole et al., 2014), demonstrate strong correspondence to known cognitive systems (including default mode, frontoparietal, cingulo-opercular, salience, visual, auditory, motor, dorsal attention, ventral attention, and subcortical systems; Power et al., 2011; Yeo et al., 2011), and display non-trivial rearrangements during motor skill acquisition (Bassett et al., 2011, 2015) and memory processing (Braun et al., 2015). These studies support the utility of module-based analyses in the examination of higher order cognitive processes in functional neuroimaging data.

The partitioning of these multilayer networks into temporally linked communities was performed using a Louvain-like locally greedy algorithm for multilayer modularity optimization (Mucha et al., 2010). The multilayer modularity quality function is given by

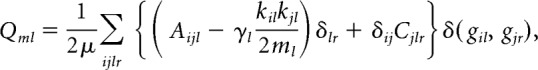where Q_ml is the multilayer modularity index. The adjacency matrix for each layer l consists of components A_ijl. The variable γ_l represents the resolution parameter for layer l, whereas C_jlr gives the coupling strength between node j at layers l and r (see next paragraph for details of fitting these two parameters). The variables g_il and g_jr correspond to the community labels for node i at layer l and node j at layer r, respectively; k_il is the connection strength (in this case, coherence) of node i in layer l; 2μ = Σ_jrκ_jr; the multilayer node strength κ_jl = k_jl + c_jl; and c_jl = Σ_rC_jlr. Finally, the function δ(g_il, g_jr,) refers to the Kronecker delta function, which equals 1 if g_il = g_jr, and 0 otherwise.

Resolution and coupling parameters (γ_l and C_jlr, respectively) were selected using a grid search formulated explicitly to optimize Q_ml relative to a temporal null model (Bassett et al., 2013a). The temporal null model we used is one in which the order of time windows in the multilayer network was permuted uniformly at random. Thus, we performed a grid search to identify the values of γ_l and C_jlr, which maximized Q_ml − Q_null, following Bassett et al. (2013a). We selected this objective function to maximize the distance between multislice modularity when temporal information is removed from the network. Grid searches are visualized in Figure. 2-1. To ensure statistical robustness, we repeated this grid search 10 times. To maximize the stability of resolution and coupling, each subject's parameters were treated as random effects, with the best estimate of resolution and coupling generated by averaging across-individual subject estimates. This is a similar approach to that taken in computational modeling of reinforcement learning, in which learning rate and temperature parameters are averaged to generate prediction error estimates (Daw, 2011). With this approach, we estimated the optimal resolution parameter γ to be 1.18 (SD = 0.61) and the coupling parameter C to be 1 (this was the optimal parameter for all subjects for all iterations). These values are quite similar to those chosen a priori (usually setting both parameters to unity) in previous reports (Bassett et al., 2011).

Finally, we note that maximization of the modularity quality function is NP-hard, and the Louvain-like locally greedy algorithm we employ is a computational heuristic with nondeterministic solutions. Due to the well known near-degeneracy of Q_ml (Good et al., 2010; Mucha et al., 2010; Bassett et al., 2013a), we repeated the multislice community detection algorithm 500 times using the resolution and coupling parameters estimated from the grid search procedure outlined above. This approach ensured an adequate sampling of the null distribution (Bassett et al., 2013a). Each repetition produced a hard partition of nodes into communities as a function of time window: that is, a community or module allegiance identity for each of the 110 brain regions in the multilayer network. We used these community labels to compute flexibility and module allegiance statistics.

Dynamic network statistics: flexibility and allegiance.

To characterize the dynamics of these temporal networks and their relation to learning, we computed the flexibility of each node, which measures the extent to which a region changed its community allegiance over time (Bassett et al., 2011). Intuitively, flexibility can be thought of as a measure of a region's tendency to communicate with different networks during learning. Flexibility is defined as the number of times a node displays a change in community assignment over time, divided by the number of possible changes (equal here to the number of time windows in a learning block minus 1). This was computed for each region in each block. In addition, average measures of flexibility were computed across the brain and across all blocks. We also computed the module allegiance of each ROI with respect to regions of the striatum during each learning block. Module allegiance is the proportion of time windows in which a pair of regions is assigned the same community label, and thus tracks which regions are most strongly coupled with each other at a given point in time. To obtain stable estimates, we averaged both flexibility and allegiance scores for each ROI over the 500 iterations of the multilayer community detection algorithm. To test the reliability of flexibility as a measure of dynamic connectivity, we calculated the correlation between flexibility averaged across the striatum (1) during the first resting state scan (before learning) and (2) during the second resting state scan (after learning).

We hypothesized that flexibility would be positively related to learning as measured by performance across blocks of the task. To examine the effect of flexibility on learning from feedback, we estimated a generalized mixed-effects model predicting optimally correct choices with flexibility estimates for each block with a logistic link function, using the maximum likelihood (ML) approximation implemented in the lme4 package (Bates et al., 2015). Thus, each participant's average flexibility in an a priori striatum ROI was calculated for each learning block and was used to predict the proportion of optimal choices in each block. The ROI included bilateral caudate, putamen, and nucleus accumbens regions from the Harvard-Oxford atlas. We included a random effect of subject, allowing for different effects of flexibility on learning for each subject, while constraining these effects with the group average. Average flexibility across sessions was included as a fixed effect in the model to ensure that our estimates represented within-subject learning effects. Additionally, to examine distinct effects in different striatal subregions, we included striatal ROI as a varying effect. The maximum likelihood estimate of the variance by region was 0, indicating that there is little variability across regions and not enough data to distinguish these small effects. To further explore differences in this effect across subregions of the striatum, we fit separate models for each subregion ROI, essentially assuming that this inter-regional variance is infinite. Even with this assumption, there were no significant differences between estimates for any pair of striatal regions. We also estimated this relationship between performance and whole-brain flexibility, which has been related to several cognitive functions in previous reports (Bassett et al., 2011; Braun et al., 2015). To rule out motion influences, we also included the block-level averages of the root mean squared relative displacement, a common output measure from motion correction preprocessing pipelines.

To provide appropriate posterior inference about the plausible parameter values indicated by our data, and to account for uncertainty about all parameters, we also fit a fully Bayesian extension of the ML approximation described above for the effect of striatal flexibility on learning performance. We used the “brms” package for fitting flexibility-performance models in the Stan language (Carpenter et al., 2015). These were similar to the likelihood approximation models, but included a covariance parameter for subject-level slopes and intercepts (which could not be fit by the above approximation), and weakly informative prior distributions to regularize parameter estimation:

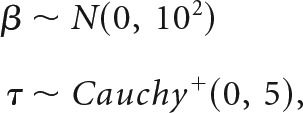where β represents the “fixed effects” parameters (slope and intercept), τ represents the “random effects” variance for subject-level estimates sampled from β, and Cauchy⁺ is a positive half-t distribution with 1 degree of freedom (Gelman, 2006). Similarly, we used an lkj prior with η = 2 for correlations between subject-level intercept and slope estimates (Lewandowski et al., 2009).

To examine the relationship between flexibility and parameters estimated from reinforcement learning models, we tested whether striatal flexibility was correlated with the learning rate α and inverse temperature β for each subject, using Spearman's correlation coefficient due to the non-Gaussian distribution of these parameters. We hypothesized that inverse temperature, which is tightly linked to overall optimal choice performance, would be positively correlated with flexibility in the striatum. Learning rate has a more complex relationship with performance on reinforcement learning tasks; different learning environments will afford distinct optimal learning rates. However, lower learning rates reflect wider temporal averaging, and are preferable once the correct choice is learned. In that sense, lower learning rates reflect more stable processing of sensory information indicating an optimal choice. Given the hypothesis that dynamic connectivity in the striatum underlies such processing, it is reasonable to suspect that lower learning rates would be associated with higher flexibility in this region. To account for joint uncertainty in these parameters at the group and subject level, correlations were computed over the full posterior distributions from the reinforcement-learning model. We computed correlations with flexibility in each subregion of the striatum, as well as with flexibility averaged across the striatum. To ensure that these associations were specific to network dynamics evoked during learning, rather than reflecting intrinsic network characteristics unrelated to task performance, we also calculated the correlation coefficient between both reinforcement learning parameters and the average flexibility in the striatum during the resting state scan acquired before the learning task.

Our hypothesis that dynamic connectivity in the striatum allows for the integration of sensory and value information during learning led us to predict that, as decisions are learned, the striatum should increase its tendency to couple with relevant sensory (in this case visual) areas and regions processing value, such as the vmPFC. To determine which regions changed coupling with the striatum during the course of the task, we fit mixed-effects models using learning block to predict log-transformed module allegiance. This analysis was computed first using the average of each ROI's allegiance across striatal subregions, and then separately for each subregion of the striatum. In both cases, this analysis was performed for each region of the brain, treating block as a factor so as to avoid assumptions about the linearity or direction of changes in allegiance. We controlled the false discovery rate across all ROI–striatum pairs.

To explore other regions exhibiting effects of dynamic connectivity on learning performance, we separately modeled the effect of flexibility in each brain region on reinforcement learning using the ML approximation implemented in the lme4 package. We applied a false discovery rate correction for multiple comparisons across regions (Benjamini and Hochberg, 1995). Whereas regions passing this threshold are reported, we also visualize the results using an exploratory uncorrected threshold of p < 0.05.

To explore the relationship between network dynamics and other forms of learning, we also regressed flexibility statistics from each ROI against subsequent memory scores for the trial-unique objects presented during feedback. If the effects of striatal flexibility were relatively selective to incremental learning, we expected to find no significant association even at an uncorrected threshold with memory in the regions comprising our striatal ROI. In addition, this provided an exploratory analysis to examine the regions in which network flexibility plays a potential role in episodic memory. Given a host of previous studies on multiple learning systems, we reasoned it might be possible to detect an effect of dynamic network coupling on episodic memory in regions traditionally associated with this form of learning.

Results

Reinforcement learning performance

Participants learned the correct response for each cue. The percentage of optimal responses increased continuously from 68% in the first block to 76% in the final block, on average. Using a mixed-effects logistic model, we observed a significant effect of block on learning performance, as measured by the proportion of optimal responses during each block [Fig. 1C; β = 0.28, SE = 0.11, p = 0.01 (Wald approximation); Bates et al., 2015]. We also fit reinforcement learning models (Sutton and Barto, 1998; Daw, 2011) to participants' trial-by-trial choice behavior, using hierarchical Bayesian models to aid estimation and pool information across subjects (Gershman, 2016).

We fit standard reinforcement learning parameters to subjects' choice data using a hierarchical Bayesian model. Fit was evaluated using the Widely Applicable Information Criterion, a measure of expected out-of-sample deviance (Watanabe, 2013; Vehtari et al., 2017). The full model fit better than a null model with no learning rate (WAIC difference = 894.2, SE = 47.4), as well as a model where a single learning rate (α) was estimated as fixed across all subjects (WAIC difference = 21.6, SE = 8.2). The average learning rate (α) was 0.41 with a SD of 0.14; the average inverse temperature (β) was 3.84, with a SD of 4.31. These α and β parameters provide a mechanistic probe of individual differences in learning, which allowed us to characterize the relationship between network dynamics and distinct sources of learning variability.

Flexibility in the striatum relates to reinforcement learning

To characterize spatial and temporal properties of dynamic brain networks during the task, we constructed dynamic functional connectivity networks for each subject in 50 s (25 TR) windows, and used a recently developed multislice community detection algorithm (Mucha et al., 2010) to partition each network into dynamic communities: groups of densely connected brain regions that evolve in time. Our analyses included 110 cortical and subcortical ROIs from the Harvard-Oxford atlas, including bilateral nucleus accumbens, caudate, and putamen subregions of the striatum. We computed a flexibility statistic for each learning block, which measures the proportion of changes in each region's allegiance to large-scale communities over time (Bassett et al., 2011). Overall, flexibility was highest in association cortex and subcortical areas, and lowest in primary sensory and motor regions (Fig. 2).

Figure 2.

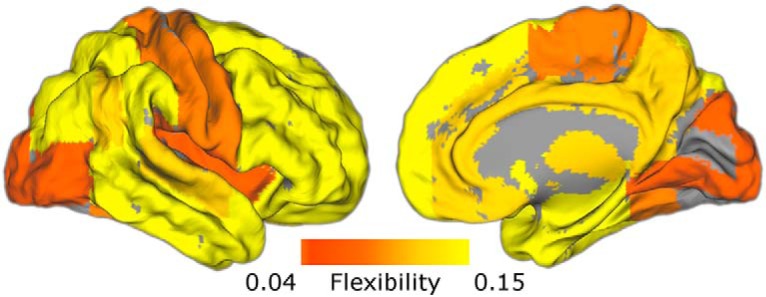
Spatial distribution of flexibility. Network flexibility was computed for each ROI in the Harvard-Oxford atlas. Here flexibility is averaged across learning blocks to visualize the spatial distribution. Flexibility is highest in subcortical regions and association cortex, and lowest in primary sensory areas. Figure 2-1 shows the grid search for selecting resolution and coupling parameters of the multislice community detection algorithm used when computing flexibility.

Figure 2-1

Two grid searches at distinct scales illustrating that our resolution and coupling parameters (1.18 and 1, respectively) fall at the peak of our optimization function, which is the difference between multi-slice modularity from our data and a null temporal model (Q_ml-Q_null, shown in A). We first used a wide grid to cover a larger range of potential parameters (left). The average peak of this search across subjects and iterations was used to select resolution and coupling terms for multi-slice community detection. To ensure that the large grid steps did not affect this selection, we repeated the search on a smaller scale (right). Our parameters are clearly within the optimum range on both grids. Panels B and C show the same grids for Q_ml (B) and Q_null (C). Q_ml and Q_null show similar changes with resolution and coupling due to their sensitivity to shared features such as network size and edge strength distribution (Good et al., 2010). Download Figure 2-1, TIF file ^{(8.6MB, tif)}

To test whether flexibility in the striatum's network coupling is related to learning performance, we fit a mixed-effects logistic regression (Bates et al., 2015) using average flexibility across the Harvard Oxford striatum ROIs during individual learning blocks to predict performance. Striatal flexibility computed for each block was significantly associated with the proportion of optimal responses [Fig. 3A; β = 9.45, SE = 2.75, p < 0.001 (Wald approximation); Bates et al., 2015]. This effect could not be distinguished statistically across subregions of the striatum (Fig. 3B). For appropriate posterior inference, we fit a Bayesian extension of this model (Carpenter et al., 2015) to generate a posterior 95% credible interval of (3.53, 14.99). To ensure that this approach reflected a within-subjects relationship between flexibility and learning, we included each subject's average flexibility across blocks in the model. This model produced similar results (β = 9.79, SE = 2.82, p = 0.0005), indicating that increases in dynamic striatal connectivity are associated with increased reinforcement-learning performance. Including average motion for each learning block in the model did not alter these results (β = 8.47, SE = 3.03, p = 0.005). We also recomputed coherence over 23- and 27-TR windows, and ran the multislice community detection algorithms to extract flexibility. The relationship between average flexibility and performance was similar across time windows (23 TR: effect = 8.38, SE = 2.55; 27 TR: effect = 6.52, SE = 3.67).

Figure 3.

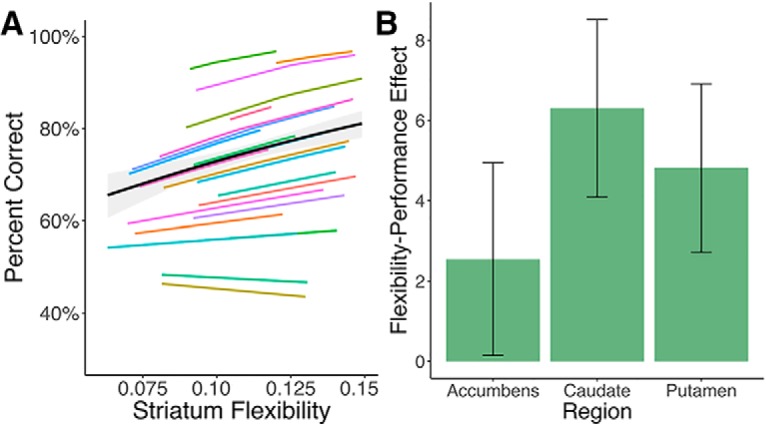
Flexibility in the striatum relates to learning performance within-subjects. A, Mixed-effects model fit for the association between network flexibility in an a priori striatum ROI and learning performance. The black line represents the fixed effect estimate and the gray band represents the 95% confidence interval for this estimate. Color lines are predictions based on subject-level random effects estimates of the flexibility–performance relationship. B, This effect was not distinguishable across regions of the striatum (bar plots and error bars represent estimates and SEs from separate mixed-effects models for each ROI).

Individual differences in reinforcement learning parameters correlate with striatal flexibility

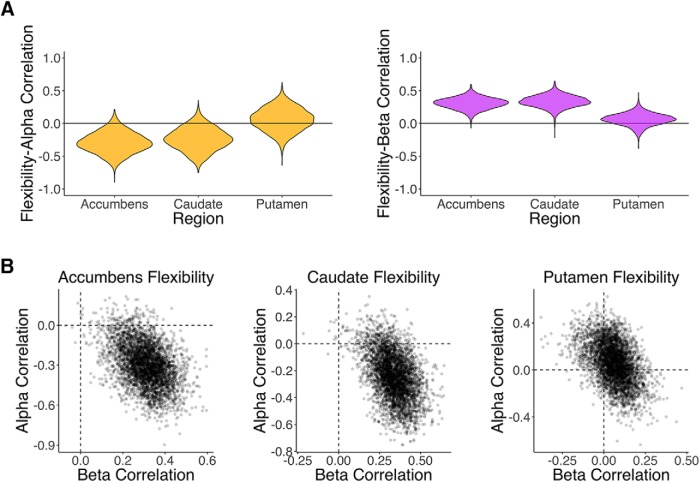
We next explored the relationship between flexibility and reinforcement learning model parameters, which account for individual differences in learning behavior. We were most interested in the learning rate α, which quantifies the extent to which individuals weigh feedback from single trials when updating the value of a choice (Sutton and Barto, 1998; Daw, 2011). Learning rate was negatively correlated with network flexibility in the nucleus accumbens [Spearman's correlation coefficient ρ = −0.29, p(ρ > 0) = 0.04; Fig. 4A, left] and to a lesser extent the caudate [ρ = −0.24, p(ρ > 0) = 0.09 Fig. 4A, left]; that is, participants with a lower learning rate (indicating more integration of value across multiple trials) had more flexibility in these regions. Inverse temperature was positively correlated with flexibility in the same regions [accumbens ρ = 0.30, p(ρ < 0) < 0.001; caudate ρ = 0.33, p(ρ < 0) = 0.002], indicating that subjects relying more on learned value overall showed more dynamic striatal connectivity (Fig. 4A, right). Averaging flexibility across all striatal regions, the correlation between learning rate and flexibility was ρ = −0.20 [p(ρ > 0) = 0.12] and the correlation between inverse temperature and flexibility was ρ = 0.27 [p(ρ < 0) = 0.007]. The effects of these two parameters were separable, as indicated by partial correlations and the joint posterior distribution (Fig. 4B).

Figure 4.

Flexibility in the striatum relates to reinforcement learning parameters across subjects. A, Violin plots showing posterior distributions of the correlation between parameters from RL models and flexibility in striatal regions. Left, Learning rate, which indexes reliance on single trials for updating value, is negatively correlated with flexibility in the nucleus accumbens and caudate. Right, Inverse temperature, which measures overall use of learned value, is positively correlated with flexibility in the same regions. B, Joint distributions of correlation between flexibility and reinforcement learning model parameters for striatal regions. Although there is some covariance between these correlations, the two effects are clearly separable. This is further supported by partial correlations, which did not substantially alter inference (accumbens-α ρ = −0.23, caudate-α ρ = −0.16, accumbens-β ρ = 0.23, caudate-β ρ = 0.28).

Finally, we sought to address the specificity and reliability of these results. We took advantage of resting state data obtained in the same individuals. We found that striatal flexibility as measured during the resting state scan, before learning, was not related to individual differences in learning parameters [learning rate: ρ = −0.01, p(ρ > 0) = 0.54; inverse temperature: ρ = 0.07, p(ρ < 0) = 0.21], indicating that these effects are specific to dynamic connectivity evoked by learning. Additionally, we assessed the reliability of this measure by comparing striatal flexibility measured during a resting-state scan before the learning task with that measured in a resting-state scan after learning. We found that flexibility was positively correlated across scans (r = 0.59, p = 0.004) indicating significant stability for this measure of striatal connectivity dynamics.

Together, these results demonstrate that reinforcement learning involves dynamic changes in network structure centered on the striatum. They also suggest that distinct sources of individual differences in learning, reliance on individual trial feedback and overall use of learned value, are related to differences in this dynamic striatal coupling. We next sought to examine which regions the striatum connects with during the task, and how such connections change over the course of learning.

Striatal allegiance with visual and value regions increases during learning

Although an increase in flexible striatal network coupling is associated with learning within and between individuals, this leaves open the critical question of which regions are involved in this process. To address this question we used a dynamic graph theory metric known as module allegiance, which measures the extent to which each pair of regions shares a common network during a given time window (Bassett et al., 2015). Using the community labels described above, we first estimated the allegiance between the striatal subregions and every other ROI in the brain for each time window, and then probed their relationship to learning.

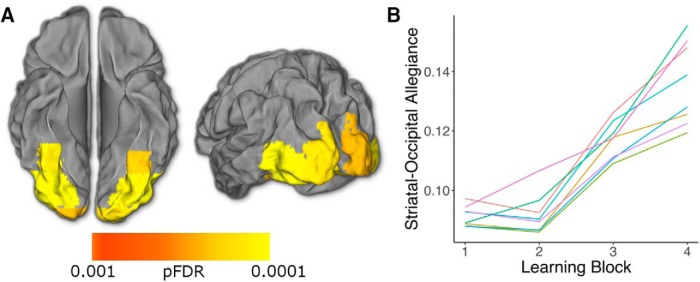
We found that overall, the nucleus accumbens and the caudate showed strongest connectivity with midline prefrontal, temporal, and retrosplenial structures, whereas the putamen exhibited its highest allegiance with motor cortices and insula (Fig. 5). To address the key question of which regions changed coupling with subregions of the striatum during learning, we ran whole-brain searches of separate mixed-effects ANOVAs for each region, predicting striatal allegiance with learning block. This analysis does not assume any shape or direction to these temporal changes. A number of regions of visual cortex showed an increase in striatal allegiance over the course of learning (all FDR p < 0.001; Fig. 6). Examining subregions of the striatum (correcting for multiple comparisons across allegiance of all ROIs with all striatal regions) revealed increases in visual coupling in the nucleus accumbens and putamen, as well as between the putamen and orbitofrontal and ventromedial prefrontal cortices, regions known for their role in value processing (Padoa-Schioppa and Assad, 2006; Fig. 6-1).

Figure 5.

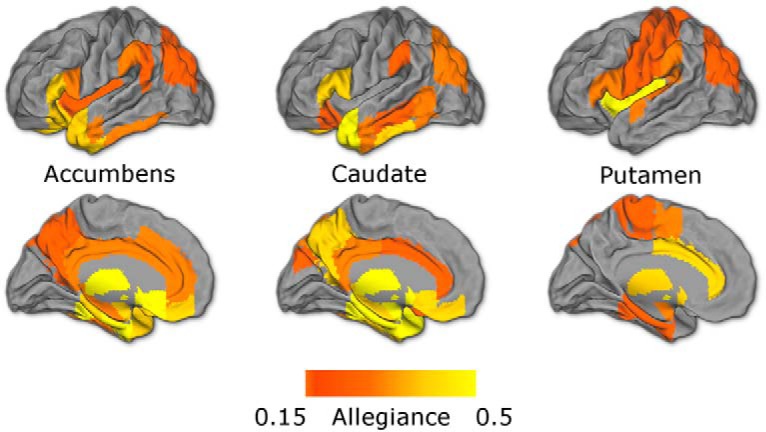
Module allegiance broken down by striatal region. Maps show regions in the 50th percentile of allegiance for each striatal ROI, averaged over all learning blocks. Consistent with anatomical and functional connectivity, the nucleus accumbens and caudate show stronger allegiance with midline frontal, temporal, and retrosplenial regions, whereas the putamen shows relatively stronger allegiance with motor regions.

Figure 6.

Allegiance between the striatum and visual cortex increases over the course of learning. A, Module allegiance between the striatum and a number of visual cortex ROIs changes over time (whole-brain corrected, p_FDR < 0.05). B, Average striatal allegiance increases in each of these visual ROIs (color lines represent the mean for each ROI passing FDR threshold across subjects and striatal regions). Allegiance is averaged across striatal subregions in both A and B. Figure 6-1 shows results presented by subregion.

Figure 6-1

Visual and value regions change allegiance with the striatum over the course of the task. A. Regions where time-dependent changes to striatal allegiance exceed a threshold of pFDR<0.05, corrected for all ROIs’ allegiance with all three striatal regions (109 x 3 comparisons). These results were generated using mixed-effects ANOVAs and contain no assumptions about the shape or direction of changes. B. Panel plot showing the change in allegiance over time for every pair passing the above threshold. Lines and bands represent and bands standard errors. As with average striatal allegiance, the nucleus accumbens and putamen increase coupling with visual regions during the task. In addition, the putamen exhibits an increase in coupling with the right orbitofrontal and ventromedial prefrontal cortex and a decrease in coupling with primary auditory cortex. No regions’ allegiance with the caudate survived correction for multiple comparisons. Abbreviations: Occ=Occipital, Temp=Temporal, Front=Frontal, and MTG=Middle Temporal Gyrus. Download Figure 6-1, TIF file ^{(44.7MB, tif)}

Flexibility relates to learning in a distributed set of brain regions

In a number of reports on dynamic networks, averaged whole-brain flexibility has been used as a marker of global processes and associated with cognition (Bassett et al., 2011; Braun et al., 2016). Indeed, we found that whole-brain flexibility related to learning performance within-subjects (β = 11.84, SE = 3.91, p < 0.005) and, to some extent, learning rate across subjects [ρ = −0.26, p(ρ > 0) = 0.07]. We were thus interested in regions outside of the striatum that exhibit dynamic connectivity related to learning.

We conducted the learning performance analysis for each of the 110 ROIs, in addition the analysis in the striatum reported above (Fig. 3). This analysis again revealed a significant effect of flexibility in striatal subregions (the right putamen and left caudate) surviving FDR correction. In addition, the whole-brain corrected results, presented in Figure 7, indicate that network flexibility in regions of the motor cortex, parietal lobe, and orbital frontal cortex [among others; see Table 1 and Fig. 7-1 for a full list and uncorrected map], are associated with reinforcement learning.

Figure 7.

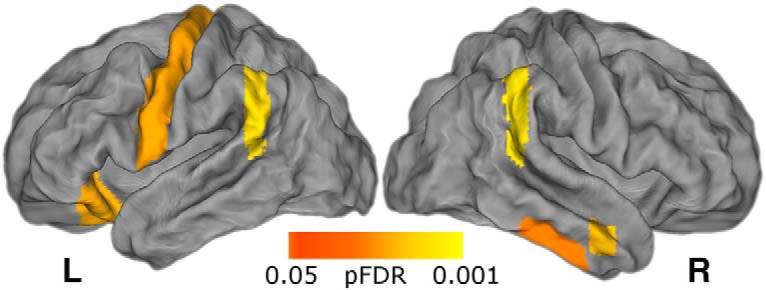
Flexibility in cortical regions is related to learning performance. Regions passing FDR correction following a univariate whole-brain analysis using the same mixed-effects model as the a priori striatum ROI. Regions passing this threshold include left motor cortex, bilateral parietal cortex, and right orbitofrontal cortex. See Table 1 and Figure 7-1 for a full list of regions and an exploratory uncorrected map.

Table 1.

List of regions showing a significant relationship between learning performance and flexibility after FDR correction

Harvard-Oxford region	Regression coefficient	p
Left caudate	5.93	0.003
Left orbitofrontal cortex	4.88	0.006
Left planum polare	10.97	0.000
Left precentral gyrus	4.79	0.006
Left supramarginal gyrus	5.38	0.003
Right inferior temporal gyrus, anterior	4.75	0.01
Right inferior temporal gyrus, posterior	4.66	0.01
Right supplemental motor cortex	8.54	0.0009
Right middle temporal gyrus	3.51	0.006
Right planum temporal	8.19	0.01
Right putamen	6.10	0.003
Right supramarginal gyrus	6.48	0.003

Figure 7-1

Exploratory uncorrected (p<0.05) results for whole-brain effect of network flexibility on reinforcement learning performance. Download Figure 7-1, TIF file ^{(25.6MB, tif)}

Flexibility in medial cortical regions is associated with episodic memory

Finally, our task also included trial-unique objects presented simultaneously with reinforcement, allowing us to measure subjects' episodic memory, a process thought to rely on distinct cognitive and neural mechanisms to feedback-based incremental learning. We tested whether network flexibility was associated with episodic memory for these trial-unique images, as assessed in a later surprise memory test (Fig. 1). Having a measure of episodic memory for the same trials in the same participants allowed us to determine whether striatal network dynamics are correlated with any form of learning, or whether these two forms of learning, occurring at the same time, are related to distinct network dynamics.

Behaviorally, participants' memory was better than chance (d′ = 0.93, t₍₂₁₎ = 7.27, p < 0.0001). Memory performance (“hits”) varied across learning blocks, allowing us to assess within-subject associations between network flexibility and behavior (Fig. 8A). Memory performance was not correlated with incremental learning performance [mixed-effects logistic regression: β = 0.41, SE = 0.51, p = 0.42 (Wald approximation)]. We tested the effect of flexibility on memory performance (proportion correct) in each of the 110 ROIs. A whole-brain FDR-corrected analysis revealed one region where flexibility was associated with episodic memory, the left paracingulate gyrus. An exploratory uncorrected analysis revealed regions in the medial prefrontal and medial temporal (parahippocampal) cortices where flexibility was associated with episodic memory (p < 0.05 uncorrected; Fig. 8B). None of the subregions from our a priori striatum ROI passed even this low threshold for an effect of flexibility on episodic memory.

Figure 8.

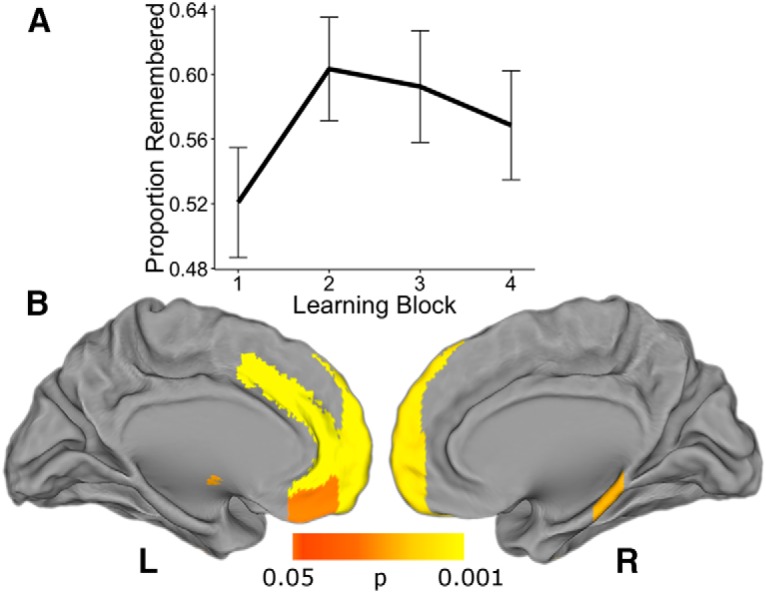
Network flexibility in medial prefrontal and parahippocampal cortex relates to episodic memory. An exploratory analysis showed effects of network flexibility on episodic memory performance in medial prefrontal and temporal lobes. A, Average memory (proportion remembered) across blocks. Participants' recollection accuracy varied across blocks. Line represents group average and bars represent SEs. B, A number of medial prefrontal regions as well as the right parahippocampal gyrus passed an exploratory uncorrected threshold of p < 0.05 for the effect of flexibility on subsequent episodic memory. The effect in the left paracingulate gyrus survived FDR correction.

Discussion

The current study reveals that reinforcement learning involves dynamic coordination of distributed brain regions, particularly interactions between the striatum and visual and value regions in the cortex. Increased dynamic connectivity between the striatum and large-scale circuits was associated with learning performance as well as with parameters from reinforcement learning models. Together, these findings suggest that network coordination centered on the striatum underlies the brain's ability to learn to associate values with sensory cues.

Our results indicate that during learning the striatum increases the extent to which it couples with diverse brain networks, specifically with regions processing value and relevant sensory information. This may represent the formation of efficient circuits for integrating and routing decision variables. Our reinforcement learning model findings are consistent with this idea. Striatal flexibility is negatively related to learning rate, suggesting that increased dynamic coupling with relevant cortical areas may lead to less trial-level weighting of prediction errors during learning. Flexibility in striatal circuits is also positively related to inverse temperature, indicating that this increased dynamic coupling is associated with stronger reliance on learned value during decision-making. Thus, our findings support a framework wherein network flexibility underlies information integration during learning.

Central to this interpretation is the finding that regions of the striatum increase connectivity with visual and orbitofrontal areas over the course of this task. If the striatum's role is in part to integrate motivational and sensory information in support of decisions, then such an increase is expected given that the relevant information on this task is the value of stimuli differentiated by their visual properties. The fact that bilateral primary auditory cortices are the only regions showing a significant decrease in connectivity with the striatum is also consistent with this explanation. It has been suggested that the striatum may serve to gate information coming in and out of the neocortex (Frank and Badre, 2012), and that this gating function may be related to a broad role for the striatum serving as a hub for controlling decisions (Shadlen and Shohamy, 2016). Reinforcement learning may be characterized in part by the dynamic formation of circuits linking areas processing sensory and value information to the striatum, and by the updating of these circuits via prediction error inputs from the midbrain, to ultimately control actions that reflect a decision. Although we focused primarily on the striatum, given its established importance in reinforcement learning, our whole-brain results suggest that the relationship between dynamic connectivity and learning is not localized to this region: it is plausible that a number of regions integrate information during learning via changes in dynamic connectivity patterns.

This framework offers clear and testable predictions for future studies. It suggests that flexibility will play a larger role in learning the more that learning depends on widespread information integration, and also that this process is specific to regions known to support the particular demands of learning in a given situation. For example, instrumental conditioning involving complex audiovisual stimuli (Kehoe and Gormezano, 1980) would be expected to associate more strongly with striatal flexibility than the task presented here and to involve increases in striatal interactions with auditory as well as visual cortex. Learning that relies on other forms of integration across time or space (Eichenbaum, 2000; Staresina and Davachi, 2009; Wimmer and Shohamy, 2012; Wimmer et al., 2012), is predicted to be associated with network flexibility in medial temporal and prefrontal regions.

There are a number of limitations to this report. First, given the static feedback probabilities, the relationship between network flexibility and learning performance could be affected by the time on task for each subject. This seems unlikely to fully explain the relationship because flexibility was related to multiple aspects of learning behavior and episodic memory, which was associated with network flexibility in a distinct set of brain regions, did not increase over time. Nonetheless, future studies incorporating reversal periods to dissociate time from performance will be important for addressing this issue. Another limitation is the hard-partitioning approach for network assignments provided by multislice community detection, which necessarily underemphasizes uncertainty about community labels. There have been very recent attempts to formalize probabilistic models of dynamic community structure (Durante et al., 2016; Palla et al., 2016), but most work examining dynamic networks in the brain have used deterministic community assignment (Bassett et al., 2011, 2015; Shine et al., 2016). More work is needed to develop and validate these probabilistic models and apply them to neuroscience data. Finally, although the spatial resolution of fMRI makes it an appealing method to characterize dynamic networks, studies using modalities with higher temporal resolution such as ECoG (Khambhati et al., 2016) and MEG (Siebenhühner et al., 2013) will be important for providing more fine-grained temporal information.

To summarize, we report a link between reinforcement learning and dynamic changes in networks centered on the striatum. Although most descriptions of reinforcement learning have focused on the role of individual regions, recent advances in network theory are beginning to make the role of dynamic communication between individual regions and broader networks in this process a tractable area of research (Bassett et al., 2011, 2015; Kopell et al., 2014; Braun et al., 2015). Here we show that incremental learning based on reinforcement is associated with dynamic changes in network structure, across time and across individuals. Our results suggest that the striatum's ability to dynamically alter connectivity with sensory and value-processing regions provides a mechanism for information integration during decision-making and that learning may be characterized by the formation of these dynamic circuits.