rpsftm: An R Package for Rank Preserving Structural Failure Time Models

Abstract

Treatment switching in a randomised controlled trial occurs when participants change from their randomised treatment to the other trial treatment during the study. Failure to account for treatment switching in the analysis (i.e. by performing a standard intention-to-treat analysis) can lead to biased estimates of treatment efficacy. The rank preserving structural failure time model (RPSFTM) is a method used to adjust for treatment switching in trials with survival outcomes. The RPSFTM is due to Robins and Tsiatis (1991) and has been developed by White et al. (1997, 1999).

The method is randomisation based and uses only the randomised treatment group, observed event times, and treatment history in order to estimate a causal treatment effect. The treatment effect, ψ, is estimated by balancing counter-factual event times (that would be observed if no treatment were received) between treatment groups. G-estimation is used to find the value of ψ such that a test statistic Z(ψ) = 0. This is usually the test statistic used in the intention-to-treat analysis, for example, the log rank test statistic.

We present an R package that implements the method of rpsftm.

Introduction

In a two-arm randomised controlled trial, participants are randomly allocated to receive one of two treatments or interventions. Ideally, all participants would fully receive their allocated treatment and no other treatment. However, in a recent review, 98 of 100 trials published in four high quality general medical journals reported some form of departure from randomised treatment (Dodd et al., 2012). When treatment is ‘all-or-nothing’ (for example, a surgical procedure), possible departures include not receiving the allocated treatment, receiving the other trial treatment, or receiving a non-trial treatment. When treatment is given over time (for example, a drug for HIV treatment), departures also occur over time, and often include starting a new treatment in response to a disease-related event.

This paper specifically focuses on the case of treatment switching over time, where participants may switch to receive the other trial treatment during the trial (Latimer et al., 2014). A common example is in a trial of active treatment versus placebo where placebo arm participants may start the active treatment in response to disease progression.

A randomised controlled trial with departures from randomised treatment is commonly analysed by intention-to-treat, in which departures from randomised treatment are ignored and all randomised participants are compared in the groups to which they were randomised (Higgins et al., 2011). This provides an unbiased comparison of two treatment policies, which accept that treatment may be changed, but does not compare the efficacies of the treatments themselves (White et al., 1999).

In order to compare the efficacies of the treatments, analysts often use per-protocol analysis, which censors participants when they depart from randomised treatment. However, this loses the advantage that randomisation produces comparable groups and instead introduces selection bias. Another possibility is to include treatment as a time-dependent variable in a Cox regression model. The issue with this method is that the estimate of treatment effect may not have a causal interpretation when switchers are prognostically different to non-switchers (Robins and Tsiatis, 1991).

There has therefore been strong interest in causal inference methods including marginal structural models (MSM) (i.e. inverse probability of censoring weighting (IPCW)) (Hernán et al., 2001) and instrumental-variable-type methods (White, 2005; Watkins et al., 2013).

The IPCW method is an extension of the per-protocol censoring approach, whereby the bias associated with censoring participants that depart from randomised treatment is removed by weighting the remaining non-switchers (Latimer et al., 2016). A model is formed for the probability of switching using baseline and time-dependent covariates. Time-varying weights are then obtained for each participant based on the inverse probability of not switching until a given time (Watkins et al., 2013). The method relies on data on prognostic factors for mortality that also affect the probability of switching being collected at both baseline and over time. This is called the ‘no unmeasured confounders’ assumption. Since this assumption is untestable, the method relies on good planning at the study design stage in order to collect information on all possible confounders. The method also has two potential issues: a) if many prognostic factors are included in the model to calculate weights the model may fail to converge, and b) if only a few participants switch then large weights are assigned to the remaining participants, which may result in biased analyses. The method has already been implemented in R in the package ipw and so is not considered further here.

Instead, this paper focuses on a popular causal method - the rank preserving structural failure time model (RPSFTM) (Robins and Tsiatis, 1991). In contrast to the IPCW method which requires potential confounders to be collected over time, the RPSFTM is randomisation based and only requires information on the randomised treatment group, observed event times, and treatment history in order to estimate a causal treatment effect. The method has been used, for example, in submissions to the UK’s National Institute for Health and Clinical Excellence whose Decision Support Unit commissioned a guidance document (Latimer and Abrams, 2014). The RPSFTM has been implemented in Stata (White et al., 2002) but not in R.

This paper describes the theory of the RPSFTM and presents a new implementation of the method in R, using data based on a trial in HIV infection.

Theory

RPSFTM method and assumptions

The RPSFTM uses a causal model to produce counter-factual event times (the time that would be observed if no treatment were received) in order to estimate a causal treatment effect. Let $T_i=T_i^{\text{off}}+T_i^{\text{on}}$ be the observed event time for participant i, where $T_i^{\text{off}}$ and $T_i^{\text{on}}$ represent the time spent off and on treatment, respectively. The T_i are related to the counter-factual event times, U_i, via the following causal model:

$$U_i=T_i^{\text{off}}+T_i^{\text{on}}\exp ({\psi }_0)$$ (1)

where exp(-ψ₀) is the acceleration factor associated with treatment and ψ₀ is the true causal parameter.

A grid search (g-estimation) procedure is used to estimate the treatment effect that balances the counter-factual event times across randomised treatment groups. To estimate the causal treatment effect, ψ, we assume that the U_i are independent of randomised treatment group R_i, i.e. if the groups are similar with respect to all other characteristics except treatment, the average event times should be the same in each group if no participant were treated. In general, this assumption is plausible in a randomised controlled trial.

A g-estimation procedure is used to find the value of ψ such that U_i is independent of R_i. For a range of ψ_s, the hypothesis ψ₀ = ψ is tested by computing U_i(ψ), subject to censoring, and calculating the test statistic Z(ψ). This is usually the same test statistic as for the intention-to-treat analysis, for example, the log rank test statistic to compare survival distributions between groups. In the rpsftm() function, the possible test options are the log rank, and the Wald test from a Cox or Weibull regression model. For the parametric Weibull test, the point estimate (ψ̂) is the value of ψ for which Z(ψ) = 0. For the non-parametric tests (log rank, Cox), ψ̂ is the value of ψ for which Z(ψ) crosses 0, since Z(ψ) is a step function. Confidence intervals are similarly found with the 100(1 − α)% confidence interval being the set {ψ : |Z(ψ)| < z_1−α/2}, where z_1−α/2 is the 1 − α/2 percentile of the standard normal distribution.

After finding ψ̂, an adjusted hazard ratio can be calculated. For example, by comparing counter-factual event times at ψ̂ in the control group to the observed event times in the experimental group we can estimate the treatment effect that would have been observed in the absence of switching (in the case where only the control group switch).

As well as assuming that the only difference between randomised groups is the treatment received, the RPSFTM also assumes a ’common treatment effect’. The common treatment effect assumption states that the treatment effect is the same for all participants (with respect to time spent on treatment) regardless of when treatment is received, which is implicit in equation (1).

Re-censoring

We assume that censoring occurs if participants survive to a specific calendar date (Robins and Tsiatis, 1991). Thus the potential censoring time C_i is known for all participants. The censoring indicators of the observed event times are initially carried over to the counter-factual event times. However, the uninformative censoring on the T_i scale may be informative on the U_i scale. Suppose we have two participants with the same U_i, one of whom receives the superior treatment. The participant receiving the superior treatment has their U_i extended so that they are censored whilst the other participant may observe the event.

In detail, C_i, the censoring times for the T_i, are transformed to C_i (1 − P_i + P_i exp(ψ)) when we work on the U_i scale, where P_i is a random variable, the proportion of time on treatment, $T_i^{\text{on}}/(T_i^{\text{on}}+T_i^{\text{off}}).$ This transformation of censoring times occurs by representing the censoring status in two equivalent ways: {C_i < T_i}, and re-scaling both sides {C_i (1 − P_i + P_i exp(ψ)) < T_i (1 − P_i + P_i exp(ψ)) = U_i}. We cannot assume the variable P_i is independent of U_i. For example, adherence to a protocolised treatment may depend on the underlying prognosis.

We can overcome this induced dependence by considering the sample space for P_i marginally over U_i and, optionally, conditioning on R_i. If we replace P_i with a function of its sample space then any dependency on U_i is thus removed. Any alternative transformed censoring times must be smaller than the original censoring times, else we may have to impute uncensored U_i values for censored T_i observations, which would be impossible. Hence taking the minimum value from the sample space for P_i meets both desiderata. If the sample space differs between arms, say switching is impossible in one arm, then this can be utilised to potentially observe more events with gains in efficiency.

Operationally, let C_i be the potential censoring time for participant i. A participant is then recensored at the minimum possible censoring time:

$$D_i^{*}(\psi )=\min (C_i,C_i\exp (\psi )).$$

If $D_i^{*}(\psi )<U_i(\psi ),$ then U_i is replaced by $D_i^{*}$ and the censoring indicator is replaced by 0. For treatment arms where switching does not occur, there can be no informative censoring and so re-censoring is not applied.

Sensitivity analysis

As previously mentioned, the RPSFTM has two assumptions:

1. The only difference between randomised groups is the treatment received.

2. The treatment effect is the same for all participants regardless of when treatment is received.

Whilst the first assumption is plausible in a randomised controlled trial, the latter may be unlikely to hold. For example, if control group participants can only switch at disease progression then the treatment benefit may be different in these participants compared to those randomised to the experimental treatment. The rpsftm() function allows for investigation of deviations from the common treatment effect assumption by featuring a treatment-effect modifier variable which means the treatment effect can be varied across participants. The assumption that defines the counter-factual treatment-free event times U_i is thus modified by multiplying ψ by some factor k_i > 0:

$$U_i=T_i^{\text{off}}+T_i^{\text{on}}\exp (k_i\psi ).$$

The value taken by k_i is derived from observed data and is left to the user to assign.

The package assumes that k_i is determined at baseline, and re-censoring is undertaken in a similar way by re-censoring at the minimum possible censoring time:

$$D_i^{*}(\psi )=\min (C_i,C_i\exp (k_i\psi )).$$

Again, if $D_i^{*}(\psi )<U_i(\psi ),$ then U_i is replaced by $D_i^{*}$ and the censoring indicator is replaced by 0. The case where k_i is observed post randomisation is equally valid in terms of defining U_i, but more complicated re-censoring may be required, taking the minimum value of $D_i^{*}$ over the sample space of k_i conditional on arm. This is not implemented in the package.

Using package rpsftm

The main function in the package rpsftm is of the same name, rpsftm(), which returns an object that has print, summary, and plot methods. The arguments to rpsftm() are given in table 1 below.

Table 1.

Arguments for the rpsftm() function

	rpsftm() arguments
formula	a formula with a minimal structure of Surv(time,status) ~rand(arm,rx) where arm is the randomised treatment arm rx is the proportion of time spent on treatment, taking values in [0, 1].
	Further terms can be added to the right hand side to adjust for covariates.
data	an optional data frame containing the variables
censor_time	variable or constant giving the time at which censoring would, or has occurred. This should be provided for all observations unlike standard Kaplan-Meier or Cox regression where it is only given for censored observations. If no value is given then re-censoring is not applied.
subset	an expression indicating which subset of the rows of data should be used in the fit. This can be a logical vector, a numeric vector indicating which observation numbers are to be included, or a character vector of row names to be included. All observations are included by default.
na.action	a missing-data filter function. This is applied to the model.frame after any subset argument has been used. Default is options()$na.action.
test	one of survdiff, coxph or survreg. Describes the test to be used in the estimating equation. Default is survdiff.
low_psi	the lower limit of the range to search for the causal parameter. Default is −1.
hi_psi	the upper limit of the range to search for the causal parameter. Default is 1.
alpha	the significance level used to calculate the confidence intervals. Default is 0.05.
treat_modifier	an optional variable that ψ is multiplied by on an participant observation level to give differing impact to treatment. Default is 1.
autoswitch	a logical to autodetect cases of no switching. Default is TRUE. If all observations in an arm have perfect compliance then re-censoring is not applied in that arm. If FALSE then re-censoring is applied regardless of perfect compliance.
n_eval_z	The number of points between hi_psi and low_psi at which to evaluate the Z-statistics in the estimating equation. Default is 100.

Example

The rpsftm function will be illustrated using a simulated dataset immdef taken from (White et al., 2002), based on a randomized controlled trial (Concorde Coordinating Committee, 1994). The trial compares two policies (immediate or deferred treatment) of zidovudine treatment in symptom free participants infected with HIV. The immediate treatment arm received treatment at randomisation whilst the deferred arm received treatment either at onset of AIDS related complex or AIDS (CDC group IV disease) or development of persistently low CD4 count. The endpoint considered here was time from study entry to progression to AIDS, or CDC group IV disease, or death.

Data

The immdef data frame has 1000 rows of 9 variables as described in table 2

Table 2.

Description of simulated data set

	immdef variables
id	participant ID number
def	indicator that the participant was assigned to the Deferred treatment arm
imm	indicator that the participant was assigned to the Immediate treatment arm
censyrs	censoring time, in years, corresponding to the close of study minus the time of entry for each participant
xo	an indicator that switching occurred
xoyrs	the time, in years, from entry to switching, or 0 for participants in the Immediate arm
prog	an indicator of disease progression (1), or censoring (0)
progyrs	time, in years, from entry to disease progression or censoring
entry	the time of entry into the study, measured in years from the date of randomisation

The first six observations are given below

 > library(rpsftm)
 > head(immdef)
   id def imm censyrs xo     xoyrs prog  progyrs entry
 1  1   0   1       3  0  0.000000    0 3.000000     0
 2  2   1   0       3  1  2.652797    0 3.000000     0
 3  3   0   1       3  0  0.000000    1 1.737838     0
 4  4   0   1       3  0  0.000000    1 2.166291     0
 5  5   1   0       3  1  2.122100    1 2.884646     0
 6  6   1   0       3  1  0.557392    0 3.000000     0

For example, participant 2 was randomised to the deferred arm, started treatment at 2.65 years and was censored at 3 years (the end of the study). Subject 3 was randomised to the immediate treatment arm and progressed (observed the event) at 1.74 years. Subject 5 was randomised to the deferred treatment arm, started treatment at 2.12 years and progressed at 2.88 years. The trial lasted 3 years with staggered entry over the first 1.5 years. The variable censyrs gives the time from entry to the end of the trial.

Intention-to-treat analysis

First, we estimate the effect of giving zidovudine ignoring any treatment changes during the trial. This is found by fitting an accelerated failure time model using the eha package:

> library(eha)
> itt_fit <- aftreg(Surv(progyrs, prog) ~ imm, data = immdef)
> itt_fit
Call:
aftreg(formula = Surv(progyrs, prog) ~ imm, data = immdef)

Covariate          W.mean          Coef   Time-Accn se(Coef) Wald p
imm	            0.510        -0.147       0.863    0.077  0.056

Baseline parameters:	
log(scale)	                  1.404	               0.062  0.000
log(shape)	                  0.392	               0.052  0.000
Baseline life expectancy:			
 
Events                    312
Total time at risk        1932.5
Max. log. likelihood      -855.14
LR test statistic         3.69
Degrees of freedom        1
Overall p-value           0.0548817

The intention-to-treat estimate is −0.147 which means that lifetime is used up exp(−0.147) = 0.863 times as fast when on zidovudine as when off zidovudine (or zidovudine extends lifetime by a factor of exp(0.147) = 1.16).

Fitting the RPSFTM

We now show how to use rpsftm with the immdef data. First, a variable rx for the proportion of time spent on treatment must be created:

rx <- with(immdef, 1-xoyrs/progyrs)

This sets rx to 1 in the immediate treatment arm (since no participants could switch to the deferred arm, and xoyrs=0 in such participants), 0 in the deferred arm participants that did not receive treatment (as xoyrs=progyrs in such participants) and 1-xoyrs/progyrs in the deferred arm participants that did receive treatment. Using the default options, the fitted model is

rpsftm_fit_lr <- rpsftm(formula=Surv(progyrs, prog) ~ rand(imm, rx),
                        data=immdef,
                        censor_time=censyrs)

The above formula fits an RPSFTM where progyrs is the observed event time, prog is the indicator of disease progression, imm is the randomised treatment group indicator, rx is the proportion of time spent on treatment and censyrs is the censoring time. The log rank test is used in finding the point estimate of ψ̂. Re-censoring is performed since the censor_time parameter is specified; if not specified then re-censoring would not be performed. After finding ψ̂, rpsftm refits the model at ψ̂ and produces a survdiff object of the counter-factual event times to be used in plotting Kaplan-Meier curves. The list of objects that the function returns is given in table 3.

Table 3.

Outputs from the rpsftm() function

	rpsftm() outputs
psi	the estimated parameter
fit	a survdiff object to produce Kaplan-Meier curves of the estimated counter-factual event times in each treatment arm using plot()
CI	a vector of the confidence interval around psi
Sstar	the (possibly) re-censored Surv() data using the estimate value of psi to give counterfactual untreated failure times.
rand	the rand() object used to specify the allocated and observed amount of treatment.
ans	the values from uniroot.all used to solve the estimating equation, but embedded within a list as per uniroot, with an extra element root_all, a vector of all roots found in the case of multiple solutions. The first element of root_all is subsequently used.
eval_z	a data frame with the Z-statistics from the estimating equation evaluated at a sequence of values of psi. Used to plot and check if the range of values to search for solution and limits of confidence intervals need to be modified. Further elements corresponding to either a survdiff, coxph, or survreg object. This will always include:
call	the R call object
formula	a formula representing any adjustments, strata or clusters - used for the update() function
terms	a more detailed representation of the model formula

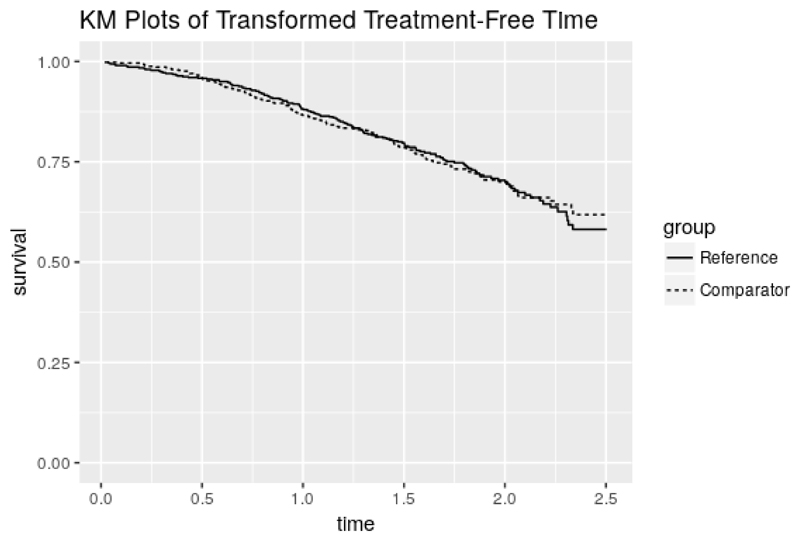
The point estimate and 95% confidence interval (CI) can be returned using rpsftm_fit_lr$psi and rpsftm_fit_lr$CI which gives ψ̂ = –0.181(–0.350, 0.002), slightly larger than in the intention-to-treat analysis. This means that lifetime is used up exp(–0.181) = 0.834 times as fast when on zidovudine as when off zidovudine, i.e. the time to progression to AIDS, or CDC group IV disease, or death is longer when on zidovudine (treatment is beneficial). However, the confidence interval contains zero, which suggests the treatment effect is non-significant. The function plot() produces Kaplan-Meier curves of the counter-factual event times in each group and can be used to check that the distributions are indeed the same at ψ̂ as shown in figure 1

Figure 1.

Output from plot(rpsftm_fit_lr)

We now provide examples of using the Cox regression model and the Weibull model in place of the log rank test. To use the Wald test from a Cox regression model, we specify test=coxph in the function parameters. Covariates can also be included in the estimation procedure by adding them to the right hand side of the formula. For example, baseline covariates that are included in the intention-to-treat analysis may also be incorporated into the estimation procedure of the RPSFTM. In the following example we add entry time as a covariate and use summary() to find the value of ψ̂ and its 95% CI.

> rpsftm_fit_cph <- rpsftm(formula=Surv(progyrs, prog) ~ rand(imm, rx) + entry,
+	                 data=immdef,
+	                 censor_time=censyrs,
+	                 test=coxph)
> summary(rpsftm_fit_cph)
   arm	 rx.Min.  rx.1st Qu. rx.Median	  rx.Mean rx.3rd Qu.   rx.Max.
1    0 0.0000000   0.0000000 0.0000000  0.1574062  0.2547779 0.9770941
2    1 1.0000000   1.0000000 1.0000000  1.0000000  1.0000000 1.0000000
   n= 1000, number of events= 286

         coef exp(coef) se(coef)      z Pr(>|z|)
entry  0.1235	 1.1315	  0.1487  0.831	   0.406

       exp(coef) exp(-coef) lower .95 upper .95
entry      1.131     0.8838    0.8454     1.514

Concordance= 0.514  (se = 0.018)
Rsquare= 0.001	(max possible= 0.976)

psi: -0.1811697
exp(psi): 0.8342938
Confidence Interval, psi -0.3496874 0.003370267
Confidence Interval, exp(psi)  0.7049084 1.003376

For the Weibull model we specify test=survreg in the function parameters. :

> rpsftm_fit_wb <- rpsftm(formula=Surv(progyrs, prog) ~ rand(imm, rx) + entry,
+	                 data=immdef,
+	                 censor_time=censyrs,
+	                 test=survreg)
> summary(rpsftm_fit_wb)
  arm	rx.Min. rx.1st Qu. rx.Median	rx.Mean rx.3rd Qu.	rx.Max.
1   0 0.0000000  0.0000000 0.0000000  0.1574062  0.2547779    0.9770941
2   1 1.0000000  1.0000000 1.0000000  1.0000000  1.0000000    1.0000000

Call:
rpsftm(formula = Surv(progyrs, prog) ~ rand(imm, rx) + entry,
    data = immdef, censor_time = censyrs, test = survreg)
              Value Std. Error	    z	     p
(Intercept)  1.3881	0.0857 16.197 5.34e-59
entry	    -0.0582	0.0906 -0.642 5.21e-01
Log(scale)  -0.4176	0.0568 -7.349 2.00e-13

Scale= 0.659

Weibull distribution
Loglik(model)= -759.8	Loglik(intercept only)= -760
Number of Newton-Raphson Iterations: 6
n= 1000


psi: -0.1811851
exp(psi): 0.8342809
Confidence Interval, psi -0.3501459 0.005170935
Confidence Interval, exp(psi)  0.7045852 1.005184

As we can see from the output for the Cox and Weibull models, the estimates of ψ are similar to the estimate obtained from using the log rank test. Both fitted models could be used as inputs to the plot() function, which produce figures very similar to figure 1.

As a sensitivity analysis we can investigate what would happen to the estimate of ψ if the treatment effect in the deferred treatment group was half of that in the immediate treatment group by setting k_i = 1 for participants in the latter group and k_i = 0.5 for participants in the former group.

> weight <- with(immdef, ifelse(imm==1, 1, 0.5))
> rpsftm(Surv(progyrs, prog) ~ rand(imm, rx), data = immdef, censor_time = censyrs,
+	treat_modifier = weight
+	)
 arm	rx.Min. rx.1st Qu. rx.Median   rx.Mean rx.3rd Qu.   rx.Max.
1  0  0.0000000  0.0000000 0.0000000 0.1574062  0.2547779 0.9770941
2  1  1.0000000  1.0000000 1.0000000 1.0000000  1.0000000 1.0000000
Call:
rpsftm(formula = Surv(progyrs, prog) ~ rand(imm, rx), data = immdef,
    censor_time = censyrs, treat_modifier = weight)

         N Observed Expected (O-E)^2/E (O-E)^2/V
.arm=0 500	157	 157  5.75e-07  1.22e-06
.arm=1 500      143      143  6.31e-07  1.22e-06

Chisq= 0  on 1 degrees of freedom, p= 0.999

psi: -0.1704745
exp(psi): 0.8432646

In this case the estimate of treatment effect is reduced slightly to −0.170 and lifetime is used up 0.843 times as fast when on treatment as when off treatment.

Trouble Shooting

There is no guarantee that unique solutions exist to the estimating equations for the estimate and confidence interval limits, or that we have searched a wide enough interval to find them if they do exist and are unique.

There are three instances where rpsftm will produce warning messages due to the search interval. The function first evaluates Z(ψ) at low_psi and hi_psi and will produce a warning message if Z(ψ) is the same sign at these two points and no root exists within the interval.

Warning messages:
1: In rpsftm(formula = Surv(progyrs, prog) ~ rand(imm, rx), data = immdef,  :

The starting interval (-1, -0.9) to search for a solution for psi 
gives values of the same sign (7.53, 6.88).
Try a wider interval. plot(obj$eval_z, type="s"), where obj is the output of rpsftm() 
2: In rpsftm(formula = Surv(progyrs, prog) ~ rand(imm, rx), data = immdef,  :
  Evaluation of the estimated values of psi failed. It is set to NA
3: In rpsftm(formula = Surv(progyrs, prog) ~ rand(imm, rx), data = immdef,  : 
  Evaluation of a limit of the Confidence Interval failed.  It is set to NA
4: In rpsftm(formula = Surv(progyrs, prog) ~ rand(imm, rx), data = immdef,  : 
  Evaluation of a limit of the Confidence Interval failed.  It is set to NA

This suggests widening the search interval via trial and error until a root for ψ can be found between low_psi and hi_psi. The second warning message occurs when uniroot.all, the function used to solve the estimating equation for ψ̂ and its 95% confidence interval limits, fails to find any one of these. It will set the value to NA and produce the following warning message

> rpsftm_fit <- rpsftm(formula=Surv(progyrs, prog) ~ rand(imm, rx),
+	               data=immdef,
+	               censor_time=censyrs,
+	               low_psi=-1,
+	               hi_psi=-0.1)
Warning message:
In rpsftm(formula = Surv(progyrs, prog) ~ rand(imm, rx), data = immdef,  :
  Evaluation of a limit of the Confidence Interval failed.  It is set to NA

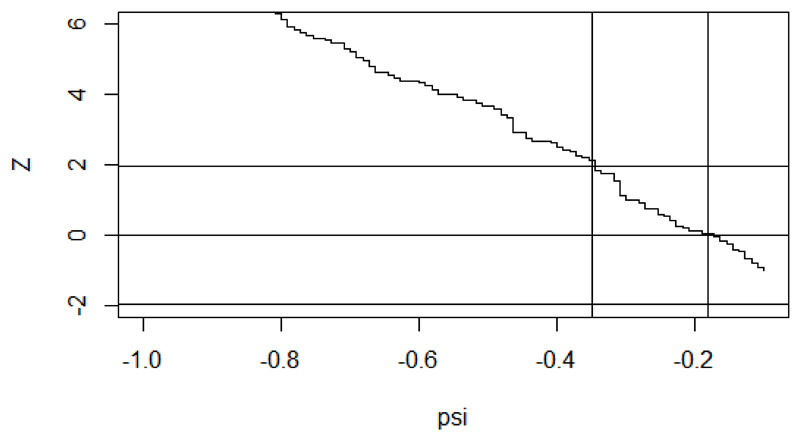
Investigation of a plot of Z(ψ) against ψ in figure 2 for a range of values of ψ could show why the function fails to find a root. The fitted object, rpsftm_fit, returns a data frame rpsftm_fit$eval_z with values of the Z-statistic evaluated at 100 points between the limits of the search interval. The data frame can be supplied as the argument to plot() to visualise the estimating equation.

Figure 2.

Plot of Z(ψ) against ψ to detect problems with the choice of search interval

plot(rpsftm_fit$eval_z, type="s", ylim=c(-2, 6))
abline(h=qnorm(c(0.025, 0.5, 0.975)))
abline(v=rpsftm_fit$psi)
abline(v=rpsftm_fit$CI)

In this case, we see that the search interval used was not wide enough to find the upper confidence limit. The third warning message occurs when multiple roots are found:

Warning message:
In root(0) : Multiple Roots found

In order to show what happens when multiple roots are found, a subset of the immdef dataset was created and is stored within the test area of rpsftm. Whilst the function uniroot.all will return multiple roots, the function rpsftm will only display the first root found by uniroot.all. A plot of Z(ψ) against ψ can be used to find the other roots.

The limits of the confidence intervals may not exist at all if Z(·) reaches an asymptote before it hits the required quantile of the standard normal distribution, in which case the limits should be reported as ± ∞. This scenario would be illustrated by a similar plot to figure 2.

Another possibility is for the coxph function to fail to converge. This occurs when the maximum likelihood estimate of a coefficient is infinity, e.g. if one of the treatment groups has no events. The coxph documentation states that the Wald statistic should be ignored in this case and therefore the rpsftm output should be taken with caution.

Limitations

As well as the potential computational issues highlighted in the previous section, the RPSFTM itself has some limitations. The method relies on the assumption that the treatment effect is the same for all participants regardless of when treatment is received. We have allowed for investigation of deviations from this assumption within the rpsftm() function by adding a treatment-effect modifier variable. Another possible limitation of the model is its requirement for only the total amount of time spent on/off treatment. In instances where participants can switch back and forth between treatments the model may be inefficient.

Conclusion

The intention is to fill a void in the methodology available to R users by providing this package and thus facilitate the adoption of newer methods in application to real data in future. The sensitivity analyses, which generalise the definition of the counter-factual treatment-free event times, are an original development.

Further developments to the package may include expanding the functionality to allow multi-armed studies with three or more arms. Such an extension would have at its core a set of g-estimating equations to solve, one for each element of the vector of ψ parameters. Defining the syntax to capture the multi-dimensional metric of time on treatments is challenging, as will be the numerical computational details when the g-estimating equations are step functions.