A Free Energy Barrier Caused by the Refolding of an Oligomeric Intermediate Controls the Lag Time of Amyloid Formation by hIAPP

Abstract

Transiently populated oligomers formed en route to amyloid fibrils may constitute the most toxic aggregates associated with many amyloid-associated diseases. Most nucleation theories used to describe amyloid aggregation predict low oligomer concentrations and do not take into account free energy costs that may be associated with structural rearrangements between the oligomer and fiber states. We have used isotope labeling and two-dimensional infrared spectroscopy to spectrally resolve an oligomeric intermediate during the aggregation of the human islet amyloid protein (hIAPP or amylin), the protein associated with type II diabetes. A structural rearrangement includes the F₂₃G₂₄A₂₅I₂₆L₂₇ region of hIAPP, which starts from a random coil structure, evolves into ordered β-sheet oligomers containing at least 5 strands, and then partially disorders in the fibril structure. The supercritical concentration is measured to be between 150 and 250 μM, which is the thermodynamic parameter that sets the free energy of the oligomers. A 3-state kinetic model fits the experimental data, but only if it includes a concentration independent free energy barrier >3 kcal/mol that represents the free energy cost of refolding the oligomeric intermediate into the structure of the amyloid fibril; i.e., “oligomer activation” is required. The barrier creates a transition state in the free energy landscape that slows fibril formation and creates a stable population of oligomers during the lag phase, even at concentrations below the supercritical concentration. Largely missing in current kinetic models is a link between structure and kinetics. Our experiments and modeling provide evidence that protein structural rearrangements during aggregation impact the populations and kinetics of toxic oligomeric species.

Graphical Abstract

INTRODUCTION

Amyloid diseases like Alzheimer’s, Parkinson’s, and type II diabetes are all associated with the formation of β-sheet rich amyloid fibrils and plaques.¹ Mounting evidence suggests that, for many amyloid diseases, prefibrillar intermediates or oligomeric assemblies are more toxic than mature plaques.^2,3 For this reason, it is important to characterize the structures, lifetimes, and populations of intermediate species along the aggregation pathway. Kinetics experiments are the most common method for studying transient species. By modeling the experimental aggregation kinetics, one retrieves the energetics of the free energy pathway that set the thermodynamic parameters responsible for driving the aggregation process.

Since the kinetics of fibril formation are almost always sigmoidal, amyloid fibril formation is commonly thought to be a nucleated polymerization phenomenon. Many variations of nucleation models have been proposed to explain the shape, lag time, and rise of the sigmoidal curve.^4–26 The key commonality between these models is a nucleation event in which a certain number of proteins (the critical nucleus size, n) assemble into an oligomer that, once formed, templates the addition of monomers to grow into a fibril.^4–26 Since the oligomer is an assembly of proteins, its free energy depends on concentration. Thus, in these models, it is the stability of the nucleus that largely dictates the kinetics, because the free energy of the nucleus sets the likelihood for fibril formation and thus the lag time of the sigmoidal kinetics.^4–7 Models often include fragmentation effects and secondary nucleation events to better match the steepness of the sigmoidal rise.^{6,7,9,16,19,20,22–26}

Missing from nucleated polymerization models of amyloid formation are free energy barriers that would be caused by structural changes of the oligomers, even though there is evidence that many amyloid oligomers or other intermediates have structures that differ from the parallel β-sheets of fibrils. α-Helical intermediates have been detected during the lag phase for amyloid formation in amyloid-β, α-synuclein, and human islet amyloid polypeptide (hIAPP, also known as amylin), by CD,^27–29 NMR^29,30 EPR,³¹ and fluorescence and neutron reflectometry³² studies. There is evidence for antiparallel β-sheet structure in intermediates of amyloid-β,³³ α-synuclein,³⁴ and the SH3 domain.^35,36 Cylindrin structures formed from fragments of αB-Crystallin have been crystallized.³⁷ While there is not yet an atomic structure for both an oligomer and fibril for a single amyloid protein, the structural properties of oligomers or other intermediates examined so far often do not resemble known structures of amyloid fibrils.^{27–31,33–37} Thus, it appears that many amyloid forming proteins and polypeptides must undergo a structural rearrangement in order to transition from an oligomeric state to the final state of the amyloid fibril. A structural rearrangement suggests a change in free energy. In other words, if the oligomers have a structure that differs from that of the fibrils, then there must be a free energy change associated with “refolding” the oligomeric protein structures into the structure of the fibril. We use the term “folding” to refer to protein secondary and tertiary changes analogous to those studied in the protein “folding” community, but in the context of an assembly of proteins with interprotein contacts.

In this manuscript we use pulse shaping 2D IR spectroscopy and ¹³C¹⁸O isotope labeling to investigate the structure of an intermediate in the aggregation pathway of hIAPP and model the kinetics of the evolving spectra to link the thermodynamics to the molecular structure. hIAPP is a 37-residue hormone which is cosecreted with insulin from pancreatic β -cells.³⁸ hIAPP normally plays a role in regulating metabolism,^39,40 but aggregates in type II diabetes.^41,42 The aggregation of hIAPP into amyloid plaques is correlated with the onset of type II diabetes, and cell viability studies have pointed to oligomeric intermediates as the toxic species.^2,3 We isotope label all 5 residues comprising the 23–27 FGAIL region of hIAPP, because it falls within the 20–29 SNNFGAILSS sequence that is crucial to the formation of amyloid plaques.^43,44 Mutations in this region slow or prohibit fibril formation.^45–47 Fragments of 20–29, or subsets of these residues, form amyloid plaques in vitro,^44,48,49 and natural variations among species correlate with the propensity of contracting type 2 diabetes.⁴³ Moreover, using single isotope labels, we previously observed interstrand couplings in this region that we assigned to an oligomeric intermediate.⁵⁰ The intermediate is not well-resolved from the fibrils without isotope labeling.⁵¹ The multiple labeling scheme used here creates 2D IR spectra that are also sensitive to dihedral angles, enabling the spectra to be simulated with model structures. Multiple labels also increase the signal strength,^52,53 allowing us to lower the polypeptide concentration, and thereby put bounds on the supercritical concentration of the oligomer. We find that the spectral kinetics can only be fit with a nucleated polymerization model when a concentration independent free energy barrier is included between the nucleus and fibril states. The free energy necessary to rearrange the structure of the oligomer into the structure of the fibril slows aggregation, lengthening the lag time, and stabilizing the population of oligomers. To deduce that a barrier exists, one needs to monitor the kinetics of both the oligomer and fibril. Thus, we provide experimental evidence that nucleated polymerization models should also include free energy barriers associated with structural rearrangements.

MATERIALS AND METHODS

A full description of the methods used is given in the SI, Materials and Methods. Briefly, ¹³C¹⁸O FGAIL labeled hIAPP and unlabeled hIAPP were synthesized using previously published methods.⁵⁴ hIAPP was dissolved in deuterated hexafluoroisopropanol (HFIP-d) in order to substitute exchangeable protons. Samples were lyophilized to remove HFIP-d prior to experiments. The addition of 20 mM phosphate D₂O buffer, pD 7, was used to initiate aggregation. Final peptide concentrations used for FGAIL labeled hIAPP were between 150 and 500 μM, and isotope dilution experiments were carried out using 20% FGAIL labeled peptide with a total hIAPP concentration of 500 μM. Rapid scan 2D IR spectra were collected as previously described.⁵⁵ Mass-action kinetic simulations were carried out using a modified version of the simplified nucleated autocatalytic polymerization model described by Hill,⁸ and detailed below. Spectral modeling was performed using the molecular snapshot approach.^56,57 Additional details are provided in the SI. 2D IR and kinetic simulations were carried out in MATLAB.

RESULTS

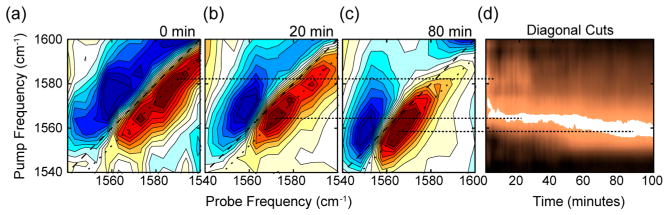
Rapid scan 2D IR spectroscopy, made possible by pulse shaping,^58–60 was used to monitor real-time aggregation kinetics in hIAPP samples with all five FGAIL residues ¹³C¹⁸O labeled. Figure 1 shows data collected at 500 μM concentration. Hundreds of 2D IR spectra were collected as a function of time. Three representative spectra are shown, focusing on the portion of the spectrum that arises from the isotope labeled FGAIL region. These three were chosen to represent the earliest, middle, and late stages of aggregation at T = 0, 20, and 80 min in Figures 1a, b, and c, respectively. The spectra differ in their frequencies and 2D lineshapes, which indicates that the couplings, and therefore the structure, of the FGAIL region is changing during the course of aggregation. Each spectrum consists of a fundamental (red) and overtone (blue) transition. At T = 0 (during the lag phase), the spectra are very broad along the diagonal, have an anharmonic shift (the difference in frequency between the two peaks along the ω_probe axis) of Δ = 25 cm⁻¹, and the frequency of the maximum absorption is near 1583 cm⁻¹, which are all consistent with the FGAIL sequence having a disordered structure typical of a random coil. At T = 20 min (later in the lag phase), the spectra are narrower, have a smaller anharmonic shift of Δ = 15 cm⁻¹, and a peak frequency of ω_probe = 1565 cm⁻¹. Reduced anharmonicity is associated with stronger coupling and more ordered β-sheet structures.⁶¹ At T = 80 min the anharmonic shift is Δ = 15 cm⁻¹, and the peak frequency even lower at ω_probe = 1558 cm⁻¹. The spectra at T = 20 and 80 min have frequency dependent anharmonic shifts. Spectral narrowing and <25 cm⁻¹ anharmonic shifts are signatures of exciton delocalization caused by coupling between multiple peptides, and so the spectra at T = 20 and 80 min must be of peptides associating into protein assemblies with defined structures. The frequency dependent anharmonicity and “Z-pattern” of the spectra is consistent with β-sheet structures.⁶² No fibrils are observed in TEM collected during the lag phase (Figure S1), and so we conclude that the 3-spectra correspond to disordered monomers, β-sheet oligomers, and the final amyloid fibrils, con s i s tent with our previous publi c a t i o ns on hIAPP.^{50,51,55,63–66}

Figure 1.

(a–c) 2D IR spectra of the isotopically labeled Amide-I vibrations of 0.5 mM FGAIL-labeled hIAPP in 20 mM phosphate buffer in the isotope labeled region at the indicted times after initiation of aggregation, and (d) as diagonal cuts through the fundamental transition in the 2D spectra as a function of time after initiation. Blue and red features correspond to negative and positive signals, respectively.

To more fully illustrate the changes in coupling as a function of aggregation time, we plot the diagonal cut through hundreds of the time dependent spectra, each normalized to the peak intensity, to create the kinetic plot shown in Figure 1d. Dashed lines illustrate the connection between the maximum of the peak frequency in the spectra in Figure 1a with the kinetic plot. Three distinct states are observed in the kinetics, each of which were represented by the 2D spectra in Figure 1a–c. The 1583 cm⁻¹ peak of the monomer shifts within 10 min to 1565 cm⁻¹, the peak of the oligomer, which remains for nearly an hour, until the spectrum transitions to 1558 cm⁻¹, the frequency of the fibril. The spectra no longer evolve after the third state, as determined by measurements made over 1 day later (see SI).

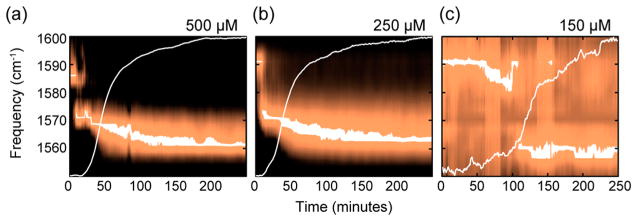
Figure 2 also shows the kinetics of the 500 μM data from Figure 1, along with kinetics collected at 250 and 150 μM concentrations. The maximum intensity for each probe wavelength is plotted rather than the diagonal cut, which gives higher signal-to-noise, and is why the frequencies are shifted a few cm⁻¹ from Figure 1. Superimposed on each plot is a trace of the intensity at 1620 cm⁻¹, which monitors the overall population of the β-sheets in the amyloid fibrils by signal from the 32 unlabeled ¹²C¹⁶O amino acids.⁶⁷ The 1620 cm⁻¹ signal is analogous to a thioflavin-T experiment, as we have previously demonstrated,⁵¹ which is why it exhibits a sigmoidal shape. The data at 250 μM (Figure 2b) exhibits the same three kinetic states observed at 500 μM. Note that the transition between the intermediate state and the final state in the 500 and 250 μM data occurs at about the half-rise time of the sigmoidal β-sheet trace. In other words, the intermediate oligomer is present throughout the lag phase. In contrast, the data at 150 μM only exhibit 2 of the 3-states; the monomers and the fibrils are observed, but not the oligomers. Thus, at 250 and 500 μM, we observe an intermediate FGAIL structure that is not observed experimentally at 150 μM. Based on our signal-to-noise, the intermediate state must be <5% of the total protein population, if present at all in the 150 μM data. Additional data is provided in the Supporting Information that demonstrates the experimental reproducibility, puts error bars on the frequencies, and tests the effects of interstrand and intrastrand couplings through isotope dilution experiments.

Figure 2.

Series of diagonal cuts through the hIAPP fundamental transition in the isotope labeled region of the 2D IR spectra collected at 500 (a), 250 (b) and 150 μM (c) concentration in 20 mM phosphate buffer as a function of time after initiation of aggregation. Trace of the amplitude of the unlabeled Amide-I band (1620 cm⁻¹) are overlaid for comparison with the time scale of fibril formation.

Structural Assignments and Simulations of 2D IR Spectra

In this section, we simulate 2D IR spectra for each of the 3 states that are consistent with known experimental data. In the next section, these spectra are combined with the kinetic model to reproduce the experimental data. To do so, we use an excitonic Hamiltonian that includes transition dipole coupling⁶⁸ and nearest neighbor couplings from the map of Jansen et al.,⁶⁹ diagonal disorder, and a homogeneous line width of 10 cm⁻¹ (fwhm). The Hamiltonian only includes the 5-residues in the FGAIL region, as the ¹³C¹⁸O labeled residues are effectively decoupled from the unlabeled residues in the rest of the protein.

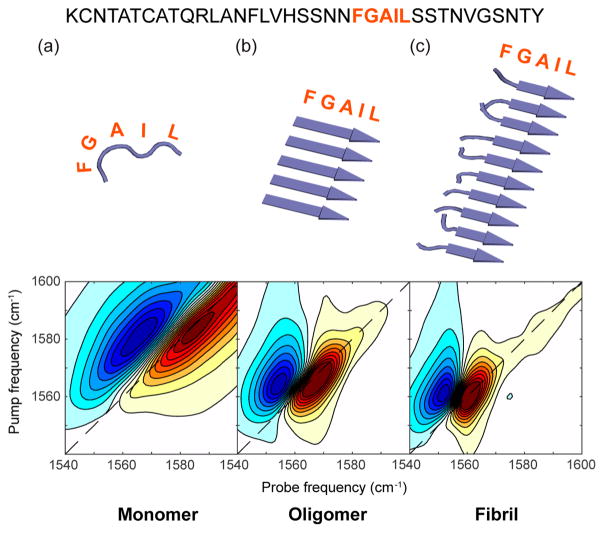
The modeled spectra and corresponding structures are shown in Figure 3, each of which match the experimental frequencies, line widths, and anharmonic shifts from Figure 1 to within a few wavenumbers. We modeled the T = 0 spectrum as a disordered monomer by creating 500 unique structures from a self-avoiding chain model and dihedral angles taken from the Top 500 database nonsecondary structure distribution.⁷⁰ Since the time resolution of 2D IR spectroscopy is about 1 ps, and we expect no protein structural dynamics to occur on that time scale, the ensemble averaged 2D IR spectrum is generated simply by calculating the spectrum for each individual structure and then summing.^56,57,71,72 Thus, the structure of the FGAIL segment of hIAPP during the first few minutes of aggregation is consistent with a highly disordered or random coil structure.

Figure 3.

Simulated 2D IR spectra generated using ensembles of structures and standard coupling models. (a) Random coil spectrum modeled using a self-avoiding poly peptide chain adhering to the Ramachandran distribution provided by the Top 500 database nonsecondary structure distribution.⁷⁰ (b) 5-Stranded β-sheet oligomer. (c) 10-Stranded β-sheet with disordered F and G residues to model the loop of hIAPP fibrils. The amylin sequence is shown above with the FGAIL residues highlighted.

The intermediate state at T = 20 min was simulated using a 5-stranded parallel β-sheet. All five FGAIL residues were modeled in a β-sheet conformation, consistent with previous single isotope labeled experiments that were consistent with inregister coupling.⁵⁰ β-Sheets with fewer than 5 strands are not consistent with the experimental data, but we cannot rule out β-sheets with more strands if there is a corresponding increase in structural disorder that creates diagonal and off-diagonal disorder in the vibrational Hamiltonian. The estimated oligomer size range overlaps with the size of oligomers detected by photochemcially induced cross-linking and by ion mobility mass spectroscopy.^73,74

The fibril state was simulated with residues F and G disordered and residues A, I, and L as part of a parallel β-sheet. This structure is consistent with the solid state NMR model for the hIAPP fibril with which previous 2D IR measurements and simulations were in agreement.^75,76 The F and G residues used the same self-avoiding chain model and dihedral angle distribution as for the monomer above. A fully ordered FGAIL region produces too low of a frequency. Additional details of the modeling are provided in the SI.

The simulations capture the essential features of the experimental 2D IR spectra. Thus, we conclude that the three states observed in the experiments are consistent with disordered monomers, an oligomeric nucleus in which the FGAIL region of at least 5 polypeptides that have assembled into an ordered β-sheet, and the fibril structure in which part of the FGAIL region adopts a disordered loop. We note that the negative couplings measured in our previous publication for the oligomer might be generated by structures other than the canonical parallel β-sheet modeled here, such as out of register parallel or perhaps antiparallel β-sheets.^77,78 Additional labeling schemes would be needed to test these possible structures.⁷⁸ Better agreement to experiment might also be obtained from molecular dynamics simulations of the structures and more sophisticated line shape theories.⁷² Regardless of the precise structure of the FGAIL β-sheet, the 2D IR spectra can only be explained by a well-ordered β-sheet, which is the most important finding for our conclusions regarding the free energy landscape. Below, we use the simulated spectra in conjunction with a mass action kinetic model to simulate the experimental kinetic plots.

Kinetic Model

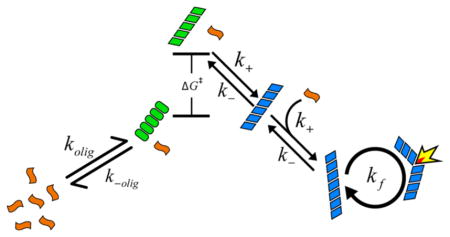
We now turn to modeling the population kinetics. We employ a nucleated polymerization mass action kinetic model, similar to others used by many researchers, ^{4–6,8,11,13,16,19,24,25} to describe the observed kinetics of monomer, oligomer, and fibril as a function of peptide concentration. Before presenting the equations that describe our model, we provide a graphical summary as an overview, given in Figure 4. In this model, monomeric peptides (orange) are allowed to form an oligomeric species of size n (green ovals). As a simplification, the peptides assemble in a concerted manner with forward and reverse rate constants of k_olig and k_−olig. To form fibrils, this oligomer must undergo a conformational change with a free energy cost of ΔG^‡ (green, parallelogram), after which it can accept an additional monomer and become “locked” into a fibril conformation (blue, parallelogram). Once locked, it can “seed” fibril growth by templating monomers with a bimolecular rate constant of k₊. Fibrils are allowed to fragment, generating additional ends for templating monomers, and thereby speeding up aggregation in an autocatalytic manner.^{6,7,9,19,22–26} Fragmentation is typically needed in aggregation models to account for the steepness of the sigmoidal curve, and is believed to result from mechanical instability of the fibrils.^19,79 In the case where the ΔG^‡ = 0, the above mechanism becomes equivalent to previous nucleation models.^8,13 Note that Figure 4 is drawn schematically; the relative free energies depend on concentration (as discussed later in Figure 6).

Figure 4.

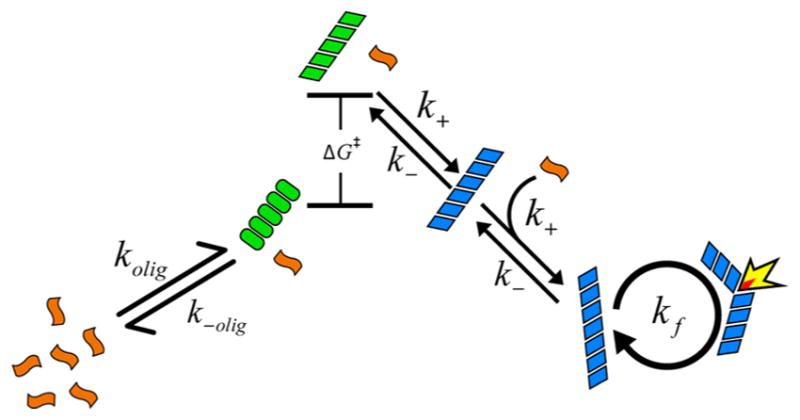
Cartoon summary of the kinetic model that best described the experimental observations. Monomers (orange) can form an oligomer (green ovals) that can undergo a conformational change into a fibril “seed” (green parallelograms) with free energy cost of ΔG^‡. The seeds grow into fibrils (blue) that can autocatalyze through a fragmentation mechanism.

Figure 6.

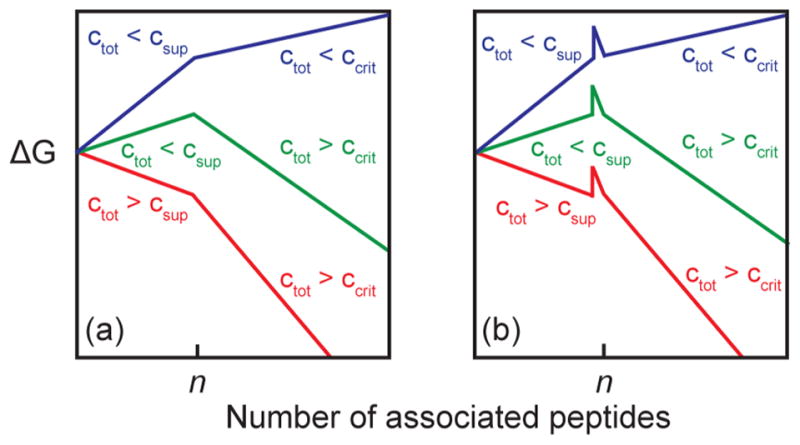
Schematic free energy diagrams for fibril growth in different concentration regimes for (a) classical nucleated fibril formation, and (b) nucleated fibril formation with a concentration independent free energy barrier incorporated between the nucleus and fibril states.

The starting point for deriving the kinetic model of Figure 4 comes from the following set of kinetic steps:

$$\begin{gathered} 2M\underset{k_{-\text{olig}}}{\overset{k_{+}}{\rightleftarrows }}{O}_2 \\ M+O_2\underset{k_{-\text{olig}}}{\overset{k_{+}}{\rightleftarrows }}{O}_3 \\ \cdots \\ M+O_{n-1}\underset{k_{-\text{olig}}}{\overset{k_{+}}{\rightleftarrows }}{O}_n \\ {O}_n\underset{k_{-a}}{\overset{k_a}{\rightleftarrows }}{O}_n^{‡} \\ M+O_n^{‡}\underset{k_{-}}{\overset{k_{+}}{\rightleftarrows }}{F}_{n+1} \\ M+F_{n+1}\underset{k_{-}}{\overset{k_{+}}{\rightleftarrows }}{F}_{n+2} \\ \cdots \end{gathered}$$ (1)

where monomers are M, “oligomers” are O_i where i ranges from 2 to n, “fibril” species are F_i with i ranging from n + 1 to ∞, and n is the critical nucleus size. The substantive difference between species defined as oligomeric versus fibrillar is the difference in stability provided by their respective dissociation rate constants (all of the forward second order reaction rate constants, k₊, are assumed to be equal). These stabilities can be conveniently quantified using the following definitions for the apparent equilibrium dissociation constants:

$$\begin{gathered} c_{\text{crit}}=\frac{k_{-}}{k_{+}} \\ {c}_{sup}=\frac{k_{-\text{olig}}}{k_{+}} \end{gathered}$$ (2)

where c_crit and c_sup are called the critical and supercritical concentrations, respectively.^4,13 The critical concentration is sometimes called the solubility, as it represents the maximum concentration of monomers that can exist in equilibrium with a very long fibril (because f_i ≅ f_i+1, where f_i represents the concentration of fibrils of size i).⁴ As the monomer cannot stably exist in excess of c_crit, all peptides present above this concentration will tend toward aggregation into a fibril, and thus the critical concentration gives the concentration above which fibrils become thermodynamically stable. A similar interpretation exists for the supercritical concentration and sets the concentration at which the oligomers become more stable than the monomer. Generally, c_crit < c_sup. Special significance is given to the species of size n, called the critical nucleus, or just nucleus, owing to it being the point at which the dissociation equilibrium constants change discontinuously. This can generate an extremum in concentration as a function of species size near n, leading to the nucleus often being interpreted as a “barrier” to aggregation. In the present model, a significant deviation from more conventional nucleated polymerization models is introduced in the form of an activated state, $c_n^{‡}=c_{n}exp(-\mathrm{\Delta }{G}^{‡}/RT)$, that the nucleus must visit prior to forming a fibrillar species. k_+a and k_−a are the forward and reverse rate constants for formation of the activated species. This additional reaction step may be approximately accounted for using the above activation barrier expression (detailed in SI). This process is similar in many respects to the “monomer activation” model^20,80,81 where the rate-limiting step of aggregation is posited to be a conformational change in the monomeric species before growth can occur,⁸² except that in the present case the conformational change is occurring for an n-mer rather than the monomer. Thus, we dub our scheme an “oligomer activation” model.

Since the reported 2D IR spectra only resolve three distinct states, we reduce the complexity of the kinetic model to 3-states with the following approximations: fast pre-equilibration of oligomers^8,13 that gives a concerted mechanism for formation of the nucleus, the extremum approximation for the nucleus c_n ≈ f _n+1,⁸ and the assumption that ${\sum }_{i=n+1}^{\infty }{f}_i\approx {\sum }_{i=n+2}^{\infty }{f}_i$. With these approximations, we arrive at the following coupled rate equations (detailed in SI):

$$\begin{gathered} \frac{\mathrm{d}{c}_1}{\mathrm{d}t}=n\left(k_{-\text{olig}}{c}_n-k_{+}\frac{c_1^n}{c_{sup}^{n-2}}\right)+(k_{-}-k_{+}{c}_1)f \\ \frac{\mathrm{d}{c}_n}{\mathrm{d}t}=k_{+}\frac{c_1^n}{c_{sup}^{n-2}}-k_{-\text{olig}}{c}_n-(k_{+}{c}_1-k_{-})c_n{e}^{-\mathrm{\Delta }{G}^{‡}/RT} \\ \frac{\mathrm{d}f}{\mathrm{d}t}=(k_{+}{c}_1-k_{-})c_n{e}^{-\mathrm{\Delta }{G}^{‡}/RT}+k_{-}(c_{\text{tot}}-c_1-n{c}_n) \end{gathered}$$ (3)

With this concerted mechanism for formation of the nucleus, c_n becomes representative of all oligomeric species and is referred to henceforth as the “oligomer”. The total peptide concentration is represented by c_tot and fibril species are collectively represented by f, which can only form by one of two mechanisms: conversion of an oligomer to a fibril, represented by the first term in the equation df/dt for, or by fragmentation, represented by the second term. Fragmentation allows fibrils to spontaneously disassociate, generating two new ends upon which monomers can attach. “Secondary nucleation” events, such as fragmentation, are well-known to be a cause of sigmoidal aggregation kinetics through autocatalysis,^5,6,19 and fragmentation has been invoked in the past to describe the kinetics of hIAPP aggregation.¹¹ A fragmentation rate of k₋ may be thought of as an upper limit approximation, and is the value used in the closed-form fragmentation model by Knowles et al.¹⁹ The free parameters in the model are n and ΔG^‡. Because we will not be matching absolute times with the experiment, k₊ is arbitrary and set to 1 everywhere. The reverse rate for fibril growth, k₋, is set using a previous experimental estimate of 100 nM for c_crit.⁸³ In order to set k_−olig, we estimate a value for c_sup based on the present 2D IR data. The signal from oligomers dominates during the lag phase at 250 μM, but are not detectable at 150 μM. As the 2D IR signal for a β-sheet oligomer should grow linearly or faster with the size of the sheet, nc_n < c₁ at 150 μM. Assuming detailed balance between monomers and oligomers is achieved during the lag phase, this implies that $c_{sup}>\sqrt[n-1]{n}{c}_1>c_1$. As only monomers are visible at 150 μM and the noise level is ~10%, monomers must represent at least 90% of the peptide present, making 135 μM the lower limit for the supercritical concentration. We choose 250 μM as an upper estimate for c_sup because oligomers dominate the signal during the lag phase at both 250 and 500 μM. Previous estimates for the size of the nucleus range from n = 3 to 20, so we have restricted our analysis to this range.^11,84 Finally, we note that the pre-equilibration approximation overestimates the rate at which monomers convert to oligomers since, for example, at c_tot = c_sup the initial slope of the monomer concentration is $\mathrm{d}c(0)/\mathrm{d}t=-n{k}_{+}{c}_{sup}^2$ while for the more general model in eq 1 the initial slope would be $-2k_{+}{c}_{sup}^2$. Nonetheless, this fact has little consequence for our interpretation, which focuses on the transition between oligomer and fibril.

Simulations of the Experimental Structural Kinetics

In the above sections, we have defined the dominant FGAIL structures populated during each of the 3-phases, created 2D IR spectra for each state, and outlined a kinetic model that is similar to previous models but contains an additional free energy barrier. In this section, we use these results to create kinetic plots for comparison to experiment and test the influence, if any, that a free energy barrier plays in the kinetics.

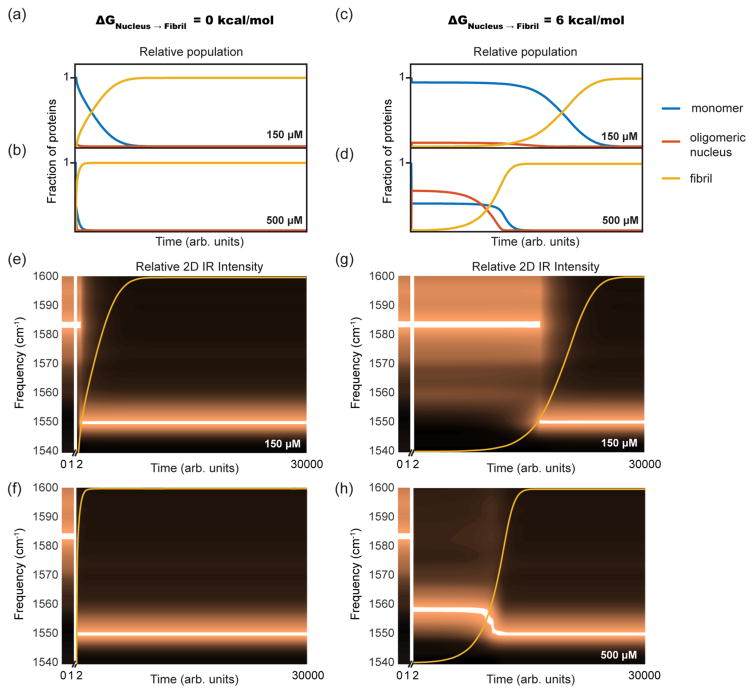
Shown in Figure 5a–d are the time-dependent mass fractions (i.e., populations) of monomers (blue), oligomers (red), and fibrils (yellow) as predicted from the kinetic model for initial protein concentrations of 150 and 500 μM with n = 10. Figure 5a,b presents results for ΔG^‡ = 0, and Figure 5c,d for ΔG^‡ = 6 kcal/mol. All the simulated kinetics begin with a fast phase wherein monomers quickly convert to oligomers, causing a rapid drop in the monomer concentration. Because the critical and supercritical concentrations set the relative free energies of the monomer, oligomer, and fibril (see eq 2), the mass fraction of monomers immediately following the initial fast equilibration phase depends on the total protein concentration, not the presence of a barrier. Thus, at the end of the fast phase, the monomer concentrations are the same in Figures 5a and 5c at 150 μM and Figures 5b and 5d at 500 μM. At 150 μM, the peptide concentration is smaller than the supercritical concentration, i.e., c_tot < c_sup, and thus the oligomers are less thermodynamically stable than the monomer. As a result, most of the protein remains monomeric and only a small fraction of proteins form oligomers. At 500 μM, the peptide concentration is higher than the supercritical concentration, i.e., c_tot > c_sup, and so the oligomer is stable relative to the monomer, and most of the monomer mass fraction converts into oligomers. Also seen in Figure 5 is that the mass fraction of oligomers decays concomitantly with the formation of the fibrils, regardless of concentration or ΔG^‡. At long times, when only the fibril state is significantly populated, the monomer concentration is nearly zero because the critical concentration is 100 nM.

Figure 5.

Results of kinetic modeling describing (a,b) mass fractions for monomer, oligomer, and fibril as a function of time at 150 μM and 500 μM concentrations with no free energy barrier between the nucleus and the fibril, and (c,d) when a 6 kcal/mol free energy barrier is present between the nucleus and fibril states. Panels (e–h) show the corresponding predicted 2D IR signal intensities produced by weighting the calculated 2D spectra for the monomer, oligomer, and fibril by the kinetic populations in panels (a–d). The parameters used in the plotted simulations were c_crit = 100 nM, c_sup = 250 μM, and n = 10.

While the initial concentrations of oligomers are solely set by the total protein concentration relative to the supercritical concentration, the kinetics and time-dependent mass fractions differ dramatically for the simulations with and without a barrier. Without a barrier (Figures 5a,b), the concentration of oligomers steadily drops during the lag phase. The steady loss occurs because, as oligomers of a critical nucleus n form, they are immediately available to begin templating monomers into a fibril, i.e., “seeding” fibril formation. With a barrier (Figures 5c,d), oligomers cannot seed fibril formation until they cross the barrier, corresponding to a structural refolding event, so that the concentration of seeds that template fibril formation is smaller than that of oligomers, set by the Boltzmann factor and the barrier height. Therefore, when a barrier is present, there are fewer seeds than oligomers, and so fibril formation is slower. As a result, the oligomer mass fraction is roughly constant during the lag phase in the simulations with a barrier (Figure 5c,d).

Notice also that the β-sheet kinetics are much more sigmoidal when a barrier is present. Powers showed, for a barrier free model, that fibril kinetics become more exponential and less sigmoidal when the initial peptide concentration exceeds the supercritical concentration.¹³ Our model does as well (See Figure S4), but also predicts that sigmoidal kinetics can still occur for c_tot > c_sup when a barrier is present. That result is another consequence of having fewer seeds than oligomers. Thus, with a barrier, it is possible to have both a large mass fraction of oligomers as well as sigmoidal kinetics, which is what we observe experimentally.

For comparison to experiment, Figures 5e–h show kinetic plots created by using the mass fractions from Figures 5a–d to weight algebraic sums of the simulated 2D IR spectra from Figure 3. The sums are then processed in a manner identical to the experimental data for comparison to Figure 1d and Figure 2. Superimposed on each plot, is the time-dependence of the fibril mass fraction. These plots illustrate that the experiments will appear as either two-state or three-state kinetics, depending on the initial conditions and the model. If the model has no barrier, ΔG^‡ = 0, then graphs approximating two-state kinetics will be observed regardless of initial conditions (Figure 5e,f). At 150 μM, the oligomer mass fraction will be difficult to measure experimentally, and so a step-transition is observed from monomer to fibril. At 500 μM, the mass fraction of the oligomer is large, but would only be observed transiently at the very beginning of the kinetics, because its population decays so quickly. Thus, without a barrier, we would expect to see kinetics that largely appear two-state from monomers to fibrils.

With a 6 kcal/mol barrier, two-state kinetics are still observed at 150 μM (Figure 5d) for a similar reason as the case without a barrier: the population of the oligomeric intermediate is much smaller than the monomers during the lag phase and the fibrils once they have formed. In contrast, three-state kinetics would be observed at 500 μM, with the oligomer having a distinct, strong absorbance throughout the lag phase. Thus, performing experiments at concentrations above the supercritical concentration produces 2D IR signals that can compete with the signals from the monomer and fibril species for oligomers with a free energy barrier, which is what we see experimentally.

Within the parameters of our model, the experimental data for hIAPP aggregation can only be explained by including a free energy barrier in the kinetic mechanism. The simulations with ΔG^‡ = 6 kcal/mol in Figure 5g,h very closely resemble the experimental data in Figure 2a and c (the 500 and 150 μM experimental data). Varying the constants in our model, we find that ΔG^‡ must be greater than 3 kcal/mol to create a population of oligomers that agrees with experiment. Oligomer nucleus sizes of n = 7 to 15 all produce spectra and kinetics in qualitative agreement with experiments. It is possible that nuclei of multiple sizes could participate in the aggregation process; our kinetic modeling suggests they would consist of 7 to 15 hIAPP peptides, though our model does not include ensembles that contain a distribution of sizes. If ΔG^‡ = 0, we cannot simulate sigmoidal curves that have both a significant lag time and an appreciable amount of oligomer mass fraction, nor do we observe sigmoidal kinetics for overall fibril aggregation at concentrations above c_sup, which we do observe experimentally. Since the data at 150 μM did not resolve an oligomeric intermediate, variables in the model can be adjusted to reproduce the relative lag time and sigmoidal kinetics for this concentration, but those variables do not produce a high enough mass fraction of oligomers to agree with experiments at higher concentrations. Thus, the experimental measurement of the oligomer concentration, even if only approximate, provides a very stringent condition for the modeling.

DISCUSSION

The 2D IR spectra of ¹³C¹⁸O labeled FGAIL in hIAPP clearly resolves a structure during the lag time that is neither the monomer nor fibril states. The data and simulations are consistent with an oligomeric species forming within the first few minutes that persists until the sigmoidal rise of the fibrils. From previous work on single-labeled FGAIL, we know that this intermediate is on-pathway to the fibril.⁵⁰ On- and off-pathway intermediates are usually difficult to discern from kinetics alone. In earlier work, we established that the intermediate was on-pathway using an I26P mutation to destabilize the FGAIL intermediate, which slowed fibril formation >10-fold. Macrocycles that promote β-sheet formation were also consistent with an on-pathway intermediate.

No fibrils are observed in TEM images collected during the lag phase (see SI). The kinetics and populations in the current study can only be modeled if an additional, concentration independent, free energy barrier is included between the oligomer and fibril state. Without an additional barrier, associated with structural rearrangement, the experimental data cannot be reproduced with regards to the duration of the lag phase, sigmoidal kinetics, the presence of appreciable oligomer concentrations, nor the stable population of oligomer. With a >3 kcal/mol barrier, very good agreement with experiment is found.

The inclusion of an explicit free energy barrier, representing an additional kinetic refolding step between the oligomer and fibril states, is not common for nucleation models. Figure 6a schematically illustrates the free energy landscape for a nucleated polymerization model that is the most common description for amyloid fibril formation, such as that of Powers and Powers.¹³ The x-axis is the number of associated polypeptides, which is 1 for the monomer, n for the critical size of the oligomeric nucleus, and n + 1 or greater for the fibril. The characteristics of these free energy surfaces depend on the protein concentration, c_tot. To compare the surfaces, they are calculated relative to the free energy of the monomers. As explained above (eq 2), if c_tot < c_sup, then it is thermodynamically unfavorable for oligomers to form. Likewise, if c_tot < c_sup, then it is unfavorable for fibrils to form. Thus, the relative values of c_sup and c_crit give rise to 3 scenarios for the free energy landscape. If c_tot is smaller than both c_sup and c_crit, then fibril formation is entirely uphill (blue curve). If c_tot is larger than both c_sup and c_crit, then it is entirely downhill for fibril formation (red curve). If c_tot lies in between c_sup and c_crit (green curve), the oligomers effectively serve as a transition state that is the barrier to refolding into the fibril conformation. Figure 6 schematically illustrates the scenarios.

According to the classical nucleation model, the free energy landscape for c_tot = 500 and 250 μM would be entirely downhill (red curve). Thus, formation of both the oligomers and fibrils is spontaneous, creating very fast kinetics and a low population of oligomers at these concentrations. The free energy landscape at c_tot = 150 μM would have an uphill oligomer and downhill fibril free energy (green curve). Because the oligomer is energetically uphill, only a small percentage of proteins will form oligomers (Figure 5a), and so the kinetics of fibril formation will be slow. Thus, in the nucleated polymerization model, it is not possible to generate high populations of oligomers for extended periods of time, because the oligomers are either unlikely to form or, if they do form quickly, they rapidly convert to fibrils. We could not fit our data with such a model.

To create a kinetic scheme that fits our data, we added a refolding barrier that is concentration independent, as shown schematically in Figure 6b. The idea is that the assembly of the n proteins into the oligomeric species is necessary, but not sufficient, for fibril formation. This free energy landscape reproduces our data. In our model, the barrier does not alter the free energy of the oligomers. Instead, it slows the formation of fibrils by kinetically trapping the oligomers, even when both the oligomers and fibrils are downhill (Figure 6b, red). At concentrations of c_tot > c_sup and a >3 kcal/mol barrier, sigmoidal kinetics can occur with long lag times and an easily measurable population of oligomers. At lower concentrations when c_tot < c_sup, the barrier still slows the kinetics of fibril formation, but does not increase the population of oligomers appreciably because they are already energetically uphill compared to the monomer. Models that postulate a free energy barrier between the monomer state and the oligomeric state, (e.g., “activated monomer” models),^20,80,81 would also not reproduce our data, because a monomer activation energy would not produce both long lag times and appreciable mass fractions of oligomers.

Because we observe an intermediate over a long period of time, we conclude that the oligomeric species observed experimentally does not have the correct structure to seed fibril formation, in agreement with the simulations. Rather, the oligomer must restructure prior to acting as a seed to template additional monomers, and the process of restructuring creates a free energy barrier.

The barrier simulated here, >3 kcal/mol, is in the range that one might expect for a moderately sized protein. The change in free energy associated with unfolding a globular protein like myoglobin is about 10.5 kcal/mol.^85,86 Similarly, the free energy of unfolding a leucine rich repeat domain (from the virulence factor Internalin B) containing seven short β-strands (each followed by a tight turn and an α-helix) is ca. 4 kcal/mol.⁸⁷ If the oligomer has n = 10 peptides, as we model, and if the only significant contacts between peptides are due to the observed FGAIL β-sheet, then there would be 50 hydrogen bonded residues contributing to the stability of the oligomer. It may not be necessary to completely unfold the intermediate prior to forming the fibril and so the complete unfolding of the intermediate may be higher than the free energy barrier determined here.

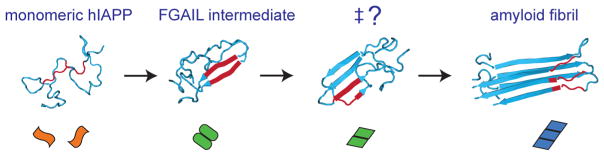
Structures consistent with our experimental results are shown in Figure 7, taken from a molecular dynamics simulation that used replica exchange to map the free energy landscape for a dimer of hIAPP,⁵⁰ and arranged into a postulated aggregation mechanism. The pathway starts with disordered peptides and ends in a fibril state with N- and C-terminal β-sheets. Also shown is a structure in which the FGAIL region forms a parallel β-sheet.^50,75 We also include in this pathway a structure taken from the MD simulations in which the FGAIL β-sheet is not fully formed nor are the fibril β-sheets (labeled “‡?”). A structure such as this (but containing more strands) may be on-pathway between the FGAIL intermediate and the fibril. It would presumably be higher in free energy than either the FGAIL intermediate or the fibrils, and therefore a transition state on the free energy surface. Other partially formed structures in the MD simulations are also consistent with a free energy transition state. To link the steps in this proposed aggregation mechanism with the kinetic model, we have added the shapes from Figure 4 to each of the structures (the structure of the fibril in Figure 7 is shown as a trimer for consistency with the kinetic model). As we noted above, the actual oligomers are much larger than a dimer and may contain other secondary and tertiary structures. The mechanism presented here is intended to provide a conceptual link between the kinetics and molecular structures that is self-consistent with the available experimental data. In essence, the oligomer needs to refold, and thus, the landscape should also include the free energy associated with this protein folding event.

Figure 7.

A schematic representation of the structural changes that occur during hIAPP aggregation. The structures of the monomer, intermediate, and potential transition state structure (‡?) were taken from a molecular dynamics simulation that used replica exchange to map the free energy landscape of a dimer of hIAPP.⁵⁰ The FGAIL sequence is colored red. The fibril structure uses the solid state NMR structure of Luca et al.⁷⁵ and is a trimer to be consistent with the kinetic model. Colored shapes from Figure 4 are assigned to each structure to illustrate the link to the kinetic model. Structures other than the one shown here might be consistent with forming the free energy transition state. We note that the experimental data is consistent with an oligomer that is at least pentameric.

The free energy cost of restructuring the oligomer should be independent of concentration, analogous to the refolding of a single complex protein. The barrier height might depend on oligomer size, which could be tested with kinetic models that allow for more than one oligomer nucleation size, n. A refolding barrier in the free energy landscape that is independent of concentration has implications for aggregation under physiological conditions, albeit in vivo conditions are much more heterogeneous and complex than our in vitro conditions. It has been estimated that the protein content of hIAPP in the β-cells of the islets of the pancreas may be as large as 500 μM to 5 mM.⁸⁸ If so, then the protein concentration would exceed the supercritical concentration, causing appreciable amounts of oligomers. The exact intracellular concentration of human amylin is not known, but the concentration of amylin is high in the intracellular environment of the β-cell and is likely to initially be high in the extracellular environment where it forms amyloid. Amylin is produced by the β-cells and is stored within the insulin secretory granule prior to release. Within the granule, amylin is located in the halo region (insulin occupies the dense core region) and its concentration within the granule in normal, nondiabetic subjects has been estimated to be between 500 μM to 5 mM,^39,88,89 although other compounds are present in the granule that are believed to inhibit aggregation.^39,89,90 Amylin is released to the extracellular space when the secretory granules fuse to the plasma membrane. Multiple vesicles release their contents simultaneously, which could create a spike in concentration. In vivo extracellular amyloid fibrils in humans and in animal models are initially deposited in the restricted confined space between pericapillary regions of the islet between the two basement membranes.^90,91 Thus, there will be an initial high local concentration released to a confinded space. High concentrations of amylin in vitro are clinically relevant as well. Amylin is deficient in both type 1 and type 2 diabetes patients and amylin analogs are a promising adjunct to insulin therapy.⁹² An improved understanding of amylin amyloid formation and aggregation at the concentrations used for storage of peptide therapeutics is required for the rational design of soluble amylin analogs for clinical applications.⁹²

Even if the soluble fraction of hIAPP is lower than the supercritical concentration, a free energy barrier associated with refolding extends the lifetimes and stabilizes the population of oligomers. If toxicity is caused by a structurally well-defined oligomer, then a long lifetime seems necessary, because the proteins need to diffuse to the cellular interface. Indeed, if oligomers were not long-lived, then they would be exceedingly difficult to be recognized by antibodies, which is not the case. Moreover, in our model, the oligomer has a distinct secondary and tertiary structure that might be targeted by small molecule therapeutics. Indeed, we have previously demonstrated that IAPP oligomers can be targeted with a rationally designed macrocyclic non-natural peptide.⁵⁰

SUMMARY AND CONCLUSIONS

The most common means for testing kinetic models for amyloid fibril formation, and thereby characterizing their free energy landscapes, is to perform a series of concentration dependent studies in which fibril formation is followed as a function of time, such as with Tht fluorescence assays. For simple free energy landscapes that correspond to classical nucleation-polymerization kinetic models, one can back out from these measurements the size of the nucleating species and the rate of fibril elongation. However, it is unlikely that Tht fluorescence alone has the necessary experimental information to constrain and test more sophisticated kinetic models corresponding to more complex free energy landscapes. In fact, as structural information about fibrils and oligomers becomes available, it is becoming increasingly apparent that there must be significant changes in the structures of some proteins during aggregation. These intermediate structures are of much interest, because they have been implicated as toxic species and it may be possible to inhibit their formation. Thus, models that unify structures and kinetics are needed. 2D IR spectroscopy probes both structure and kinetics, and thereby provides additional experimental observables to build such models. Our kinetic modeling demonstrates that a concentration independent free energy, associated with refolding, connecting the nucleus and fibril states is needed to produce a qualitatively accurate model of the experimental data, akin to the “monomer activation” model once used for describing actin filamentation, but applied to oligomers,^20,80,81 i.e., an “oligomer activation” model. The physical origin of this barrier is intuitively understood as a necessary structural rearrangement of the oligomer prior to adopting a structure that can elongate into a fibril by templating monomers. The structural free energy barrier is at least 3 kcal/mol and is attributed to the disruption of a ordered β-sheet formed by the FGAIL residues in the oligomers and refolding into the “disordered loop” of the fibril and probably includes other structure changes not measured here. An upper bound for the barrier height cannot be given, but a range of larger barriers can agree qualitatively with our experimental results. Beyond monomer activation models, the presence of a concentration independent, structurally associated free energy barrier at the boundary between oligomers and fibrils is a relatively unexplored approach in modeling nucleated amyloid fibril growth. Our results suggest that the thermodynamics of protein folding can alter the free energy landscape enough to modify the kinetics of amyloid formation. In addition, we show that working at concentrations above the supercritical concentration, a significant population of oligomers can be formed, thereby providing an experimentally tractable way to study their structures and properties as well as determine the free energy cost of refolding the oligomer into the structure of the fibril. Though we do not speculate as to whether our results extend to other amyloidogenic proteins, based on known structures of oligomers and fibrils, we anticipate that this concept might be applicable to many other amyloid forming proteins as well.