Transition Dipoles from 1D and 2D Infrared Spectroscopy Help Reveal the Secondary Structures of Proteins: Application to Amyloids

Abstract

Transition dipoles are an underutilized quantity for probing molecular structures. The transition dipole strengths in an extended system like a protein are modulated by the couplings and thus probe the structures. Here we measure the absolute transition dipole strengths of human and rat amylin in their solution, aggregated, membrane, and micelleular bound forms, using a combination of 1D and 2D infrared spectroscopy. We find that the vibrational modes of amyloid fibers made of human amylin can extend across as many as 12 amino acids, reflecting very ordered β-sheets in the most carefully prepared samples. Rat amylin has FTIR spectra that are nearly identical in solution, micelles, and membranes. We show that the transition dipoles of rat amylin are much larger when bound to micelles and membranes than when in solution, consistent with rat amylin adopting an α-helical structure. We interpret the transition dipole strengths as experimental measurements of the inverse participation ratio often calculated in theoretical studies. The structure of aggregating and membrane-bound proteins can be difficult to identify with existing techniques, especially during kinetics. These results demonstrate how absolute transition dipoles measured via our 1D/ 2D spectroscopy method can provide important structural information.

Graphical Abstract

INTRODUCTION

The aggregation mechanisms by which amyloid proteins misfold and assemble into long fibers is a perplexing issue. Ideally, one would continuously follow the structural changes associated with peptide or protein conformation throughout the process, from monomers, to oligomeric intermediates, and finally into the assembly of the fibers. Mapping the aggregation pathway in the presence of membrane bilayers or other protein constituents is also valuable for understanding cytotoxicity, because cytotoxicity may involve membrane permeation or binding to membrane proteins. However, the combination of structures, kinetics, aggregates, and membranes is a difficult set of circumstances for many experimental techniques. Infrared, both FTIR and 2D IR, spectroscopies are proving to be very useful in this regard.^1–7 They provide secondary structure information as a function of time and can be applied to soluble proteins as easily as membranes and aggregates.^1,8–14 Structural information can be refined with isotope labeling either site-specifically or in domains.^13–16 IR spectroscopy is providing new insights into amyloid fiber structures,^12,13 assembly process,^1,17 small molecules and peptide inhibition,^18–20 and membrane interactions.^2,9,11

Usually, the interpretation of an IR spectrum relies solely on frequencies. Tables can be found listing frequencies of various secondary structures and side chains.^21–23 The amide I mode, composed primarily of C═O stretch (~75%) but also of CN stretch (~10%) and NH in-plane bend (~10%), has a characteristic absorbance frequency based upon the local secondary structure.²¹ For instance, in water, the amide I band absorbs near 1645 cm⁻¹ for a random coil peptide, at 1635–1655 cm⁻¹ for an α-helical^15,16 peptide, and β-sheet peptides typically have a low frequency peak at 1620–1635 cm⁻¹ and a higher frequency band at 1670–1680 cm⁻¹, depending on if the β-sheet is parallel or antiparallel.²¹ It is important to note that these frequency ranges are compiled from empirical observations and that the frequency can vary by as much as 20 cm⁻¹, since it depends on the electrostatic environment and vibrational couplings for the specific structure at hand. For instance, transmembrane helices typically absorb 20 cm⁻¹ higher than soluble helical peptides. As a result, frequency assignments are oftentimes subjective.

In this Article, we exploit transition dipole strengths, which we think is an underutilized quantity in the identification and assignment of secondary structures. The transition dipole strength is the quantity responsible for the extinction coefficient, ε, that is central to Beers law according to A = ε × c × l, where A is absorbance, c is concentration, and l is path length. The extinction coefficient is related to the transition dipole strength, μ⃗, by ε = |μ⃗|². The carbonyl stretch of the amide I mode has a very large transition dipole strength as do many side chains.²² What is interesting about these quantities is that their strengths depend on secondary structure, because secondary structures like α-helices and β-sheets place the backbone carbonyl groups, for example, into tightly packed arrangements that create vibrational coupling between the amide I modes. This coupling causes a delocalization of the vibrational mode over multiple amide I units, which redistributes the oscillator strength and changes the transition dipole distribution.^24–26 While delocalization changes the transition dipole distribution, the sum of the transition dipole moments of the peptide does not change, due to Thomas–Reiche–Kuhn conservation laws, which is why the integrated area of an FTIR spectrum is constant.^27,28 In our text, when we refer to changes in transition dipole strengths, we mean changes in the distribution caused by delocalization. Thus, if one observes a change of transition dipole strength, then one knows that vibrational coupling has occurred, and quantification of the transition dipole strength can help identify secondary structures and provide a lower limit to the number of residues contributing to the structure.

Let us provide an example of how the transition dipole strength depends on structure. Consider the two acetone molecules in Figure 1 that are close enough in distance that the potential energy of one depends on the other, e.g., they are coupled. The transition dipoles of the normal modes are generated by vector sums of the local mode transition dipoles, μ⃗_± = (1/√2) × (μ⃗₁ ± μ⃗₂), as shown in Figure 1a. Because the transition dipoles are vectors, the sums weight the relative strengths of the normal modes. When the two modes are parallel, like in Figure 1b, then all of the transition dipole strength is apportioned into the symmetric stretch, μ⃗₊ = (2μ⃗/√2) for μ⃗₁ = μ⃗₂, and none in the antisymmetric stretch. Thus, the resulting extinction coefficient is ε₊ = 2|μ⃗|², which is twice as large as either of the original, local CO stretches. If the molecules happen to be antiparallel, then the vector sum will place all of the transition dipole intensity into the antisymmetric stretch.²⁴ In the more general case, both symmetric and antisymmetric modes will have a finite transition dipole strength, with one mode larger than the other. The coupling mechanism might be different (mechanical versus electronic), but the same principle applies to two carbonyl groups on the same molecule. The point of outlining this simple situation is that, unless the coupled modes are orthogonal to one another, the appearance of a transition dipole strength that is either larger or smaller than the individual modes indicates that coupling is occurring.

Figure 1.

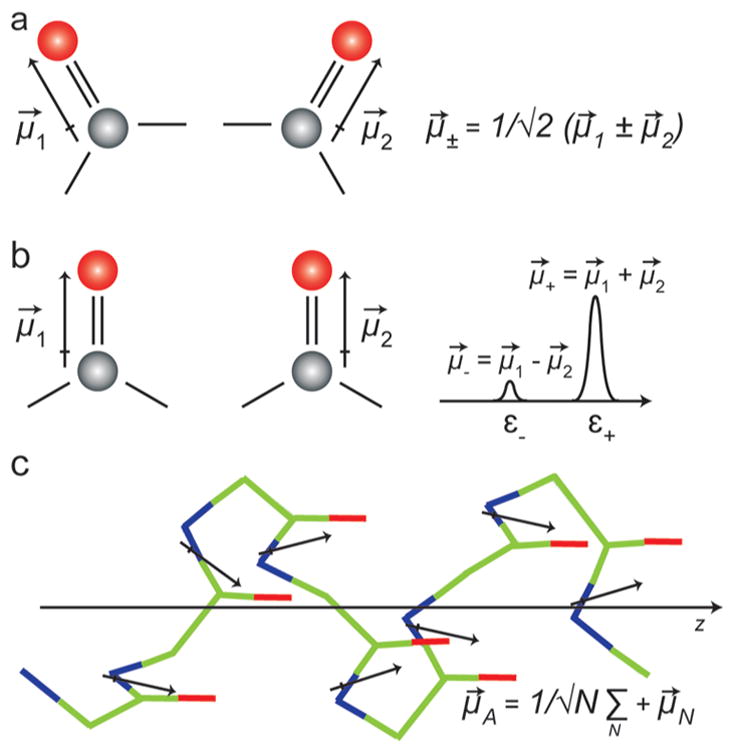
(a) Two coupled acetone molecules shown with their transition dipole moments. (b) Parallel vibrational modes in two nearby acetone molecules. The coupling between the two acetone molecules is dependent on the relative orientations and the distance between the two transition dipoles. Also shown is the associated linear absorption spectrum. (c) A model α-helix peptide in which the carbonyl groups are shown in red and the transition dipole moments are shown by the black arrows.

Now consider an α-helix versus a random coil. Like for the acetone molecules above, the normal modes are created from linear combinations of the local carbonyl (amide I) stretches (Figure 1c). The linear combination for the strongest mode in an α-helix is a sum of the coupling constants between the residues, μ⃗_A = 1/√N × Σμ⃗_n, which is referred to as the “A” mode in a perfect and infinitely long helix. The coupling constant between covalently bonded amide I modes (n and n + 1) is about 8 cm⁻¹, while the rest of the coupling constants are positive with the largest about +5 cm⁻¹ between hydrogen bonded residues (n and n + 3).^24,29 Thus, when the sum is performed to obtain the normal mode, the negative and positive coupling constants largely cancel one another. As a result, the frequency alone is often not enough to assign a spectrum an α-helix versus a random coil. It might help to measure other quantities such as line widths and anharmonic shifts. However, the vector addition of the amide I transition dipoles sum constructively, so that the transition dipole of an α-helix is equal to μ⃗_A = Nμ⃗/√N and ε_A = N|μ⃗|². Thus, the extinction coefficient of the A-mode could be as large as the helix is long, because all of the residues contribute to the normal mode in a perfect helix. In contrast, the extinction coefficient for a random coil is about the same as that for a single amino acid.²⁵ (More precisely, the oscillator strength of the local modes is also partitioned into the E-modes orthogonal to the helix axis and structural/environmental disorder prevents the normal mode from delocalizing along the entire helix. Also, random coils might be larger than unity if pieces are coupled.) Thus, measuring an extinction coefficient for a mode between 1635 and 1655 cm⁻¹ would be strong evidence for an α-helix even though this is a region in which random coils absorb. In conclusion, we believe that the transition dipole strength is a particularly useful quantity to measure when vibrational frequencies are otherwise inconclusive.

While transition dipoles would be very useful, it is often not possible to measure their strengths from FTIR spectroscopy because doing so requires knowing the concentration. Protein samples cannot always be prepared at precise concentrations, are not always homogeneous (like in aggregating or membrane systems), and in kinetics experiments the concentrations are constantly changing. Moreover, the integrated area of an FTIR spectrum is invariant under the redistribution of oscillator strengths. That is, for the same concentration, a random coil peptide of 30 residues has the same integrated area as a helix with 30 residues. Thus, in a helix folding experiment, the extinction coefficient will change (we recently estimated that it changes by a factor of 2.2), but the intensity of the FTIR spectrum is constant aside from a possible frequency shift and spectral narrowing.²⁵ Thus, even if the concentration is known, the spectra cannot usually be reliably decomposed into separate conformations, and therefore, the transition dipole strength(s) cannot be obtained.

In a previous paper, we described a method in which the relative amplitudes of FTIR and 2D IR spectra could be used to determine transition dipole strengths without prior knowledge of the concentration.²⁵ Additionally, a ratiometric method has been used to determine the surface enhancement from gold nanoparticle capping molecules in IR spectroscopy.³⁰ The essence of the approach uses the fact that an absorption spectrum scales as c × |μ⃗|² while a 2D IR spectrum scales as c × |μ⃗|⁴. Thus, by dividing the two, one gets the transition dipole strength independent of concentration. In our previous publication, we tested the approach on a model helical peptide. In this paper, we apply it to measure the transition dipole strengths associated with the human islet amyloid polypeptide (hIAPP or amylin) in its fiber state, and with rat amylin in solution, micelles, and membranes. Human amylin, the causative agent in type 2 diabetes misfolds, monomers form stacked columns with two parallel β-sheets connected by a flexible loop that runs along the fiber axis. There is considerable interest in understanding the structure of human amylin and how it forms fibers, especially in the presence of membranes, which catalyze fiber formation. In lipid membranes, it is thought that human amylin transitions through an α-helical intermediate en route to forming amyloid fibers. Rat amylin is a widely studied mutant of human amylin, whose sequence differs by only six residues. Rat amylin does not form amyloid fibers, and thus, it is often used as a model for human amylin micelle and membrane environments to which it binds but does not aggregate.^2,31–34 It is thought to also form an α-helical structure in the presence of membranes, as studied by NMR, EPR, and CD spectroscopies.^{31,32,35–38} The amide I frequencies of rat amylin in solution, micelle, and membrane are so similar that it is not enough to determine their structure by amide I frequency alone (the anharmonic shift of the amide I band in 2D IR spectra did resolve helix formation in kinetics experiments of human amylin on bilayers).² In addition, rat amylin in micelles and bilayers is probably not wholly α-helical. Instead, it is likely that the peptide adopts a partially folded structure, which will further complicate structural analysis using frequencies. In this manuscript, we aim to use 1D and 2D IR spectroscopy to measure the transition dipole strength of human amylin fibers and rat amylin in solution, micelles, and membranes in order to determine the delocalization of the amide I normal modes. The goal is to build a knowledge about the transition dipole strengths of amylin in these situations to which we can then apply to kinetic aggregation experiments and to provide baseline numbers for the magnitudes of transition dipoles of typical secondary structures.

MATERIALS AND METHODS

Amylin Peptide Synthesis

Human amylin is a 37-residue polypeptide with the sequence KCNTATCATQRLANF-LGHSSNNFGAILSSTNVGSNTY. Human and rat amylin share the same sequence, with the exception of six mutations: H19R, F23L, A25P, I26V, S29P, and S30P. Both peptides were prepared using standard FMOC solid phase peptide synthesis with a CEM Liberty 1 Microwave Peptide synthesizer. PAL-PEG-PS resin was used to ensure an amidated C-terminus. For hIAPP synthesis, a pseudoproline dipeptide was incorporated into residues 13–14 and 27–28 to facilitate the synthesis as described elsewhere.³⁹ For rIAPP synthesis, only the pseudoproline at 13–14 was used. Following synthesis, cleavage and deprotection was performed using standard trifluoroacetic acid (TFA) protocols, and 1,2-ethanedithiol was used as a scavenger. Crude peptide was dissolved in dimethyl sulfoxide (DMSO) at ~5 mg/mL overnight for the formation of a disulfide bond between Cys-2 and Cys-7. Both peptides were purified using reverse-phase high-performance liquid chromatography (HPLC, Jasco) with a C18 preparative column (Vydac). A two-buffer gradient was used; buffer A consisted of 100% water and 0.045% hydrocholoric acid (HCl) (v/v), and buffer B consisted of 80% acetonitrile and 0.045% HCl (v/v). The gradient was varied from 0 to 90% B over 90 min, and absorbance was monitored at 220 and 280 nm. The molecular weights of hIAPP and rIAPP were confirmed using MALDI-MS.

Lipid Preparation

For membrane studies, 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) and 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-(1′-rac-glycerol) (POPG) were purchased as chloroform solutions from Avanti Polar Lipids, Inc. The two lipid solutions were mixed at a molar ratio of 3:1. The mixture was dried under a gentle stream of nitrogen for 4 h and then lyophilized overnight. The dry film was rehydrated in D₂O at a concentration of 80 mM and subjected to five freeze–thaw cycles. The lipids were then sonicated at 40 °C for 30 min to form vesicles. For micelle experiments, n-dodecylphosphocholine (DPC) was purchased as a powder from Avanti Polar Lipids, Inc. DPC was dissolved in chloroform at 200 mM, dried under nitrogen, and lyophilized overnight. The dry film was rehydrated in 20 mM deuterated potassium phosphate buffer (d-PBS) with pH 7.4 to a final concentration of 200 mM. The lipids were sonicated at 40 °C for 1 h to form micelles.

Sample Preparation

All experiments were performed in deuterated solvents (D₂O and deuterated buffers), rather than water, to ensure that the amide I band was not obstructed by the strong water band in the same region. Purified peptides were dissolved in deuterated hexafluoroisopropanol (d-HFIP) to a final concentration of 1 mM. After 4 h of sonication, the peptides were completely deuterated in the amide II position. For hIAPP fiber preparation, aliquots of the stock solution were dried under a vacuum for 1 h to completely remove d-HFIP from the peptide. Once dry, the peptide film was reconstituted in d-PBS, pH 7.4, for final concentrations of 1, 1.5, 2.5, and 5 mM. Fiber initiation began upon addition of buffer, and fibers were allowed to form for 18 h before 2D IR spectra were collected. For rIAPP solution sample preparation, a 10 μL aliquot of the peptide stock solution was dried under a vacuum for 1 h to completely remove d-HFIP from the peptide. Once dry, the peptide film was reconstituted in 5 μL of d-PBS, pH 7.4, for a final concentration of 2 mM. For micelle sample preparation, a 10 μL aliquot of the peptide stock solution was dried under a vacuum for 1 h to completely remove d-HFIP from the peptide, and 5 μL of the 200 mM DPC solution was added to the dried peptide for a final concentration of rIAPP of 2 mM. For membrane sample preparation, a 10 μL aliquot of the peptide stock solution was dried under a vacuum for 1 h to completely remove d-HFIP from the peptide. Two μL of the 80 mM lipid solution was added to the dried peptide. An additional 3 μL of d-PBS was also added to give a final concentration of 2 mM rIAPP. All samples were then mixed and placed between two 2 mm thick CaF₂ windows separated by a 56 μm Teflon spacer. All samples were kept in a purge box until and during use. The fiber, solution, and membrane experiments were performed at 298 K, and the micelle experiments were performed at 303 K. To calculate the transition dipole strength of hIAPP and rIAPP under these conditions, two additional samples were necessary. A sample of pure d-PBS was prepared using the same sample cell as described above. Additionally, L-serine was dissolved in D₂O to a final OD of 0.39 for hIAPP samples and 0.26 for rIAPP samples. The OD of the sample is not critical, as long as it is known. In order to accurately calculate transition dipole strengths between samples, 2D IR spectra of peptide samples were averaged for 15 min to ensure complete purging of the spectrometer box in which the sample was measured. Immediately following a sample measurement, a 2D IR spectrum of L-serine was measured and averaged for 15 min and then a 2D IR spectrum of pure buffer was measured and averaged for 15 min. This process was repeated for each type of hIAPP and rIAPP sample.

Two-Dimensional Infrared Spectroscopy Measurements

The two-dimensional infrared (2D IR) spectroscopy setup consists of a home-built Ti-sapphire oscillator that seeds a Nd:YLF-pumped femtosecond regenerative amplifier, as described elsewhere.^14,40,41 The 800 nm output is sent to a home-built BBO-based optical parametric amplifier, and the generated signal and idler beams are overlapped spatially and temporally in a AgGaS₂ crystal for difference frequency mixing and 6 μm broad-band pulses are generated. The mid-IR light is split into pump and probe beams with a CaF₂ wedge. The pump beam passes through a Ge acousto-optic modulator (AOM) based pulse shaper and splits into two pulses. The pump and probe pulses are then focused onto the sample using parabolic mirrors. All spectra were recorded at T₂ = 0 ps, and all 2D IR spectra were normalized to the intensity of the amide I peak.

Transition Dipole Strength Calculations

Transition dipole strengths of hIAPP fibers and rIAPP in solution, micelle, and membrane were calculated using a combination of 1D and 2D spectroscopies, as described in detail elsewhere.²⁵ L-Serine, previously calculated to have a transition dipole strength of 0.2 D², was used as the calibrant molecule. Both linear and 2D IR spectra were collected simultaneously for all peptide samples, L-serine, and the buffer solution. A step-by-step outline of our method for calculating the transition dipole strengths from the data can be found in the Supporting Information. It is similar to that previously published, with one additional step explicitly outlined.

RESULTS

Transition Dipole Strength of Human IAPP Fibers

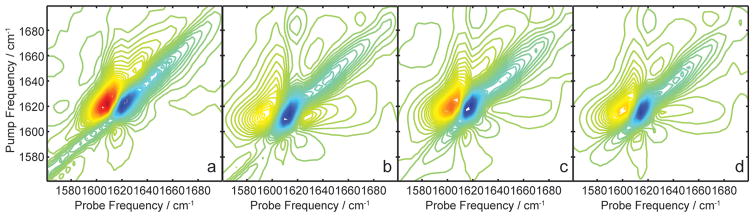
Steady-state 2D IR spectra were collected of human amylin at 1, 1.5, 2.5, and 5 mM. The 2D IR spectra of the human amylin samples are shown in Figure 2a–d, respectively. The spectra are typical for those published previously.^{1,12,26,42,43} They exhibit a sharp pair of diagonal peaks between 1615 and 1621 cm⁻¹, which are due to the amyloid β-sheets, and a broader pair of diagonal peaks with a maximum near 1642 cm⁻¹. These latter features are thought to reside from the disordered residues of the loop connecting the β-sheets and between the two cysteines that form a disulfide bond. These assignments are based primarily on the frequencies at which these features appear, since random coil residues absorb in a similar frequency range.

Figure 2.

(a) 2D IR spectrum of hIAPP fibers, 1 mM. (b) 2D IR spectrum of hIAPP fibers, 1.5 mM. (c) 2D IR spectrum of hIAPP fibers, 2.5 mM. (d) 2D IR spectrum of hIAPP fibers, 5 mM.

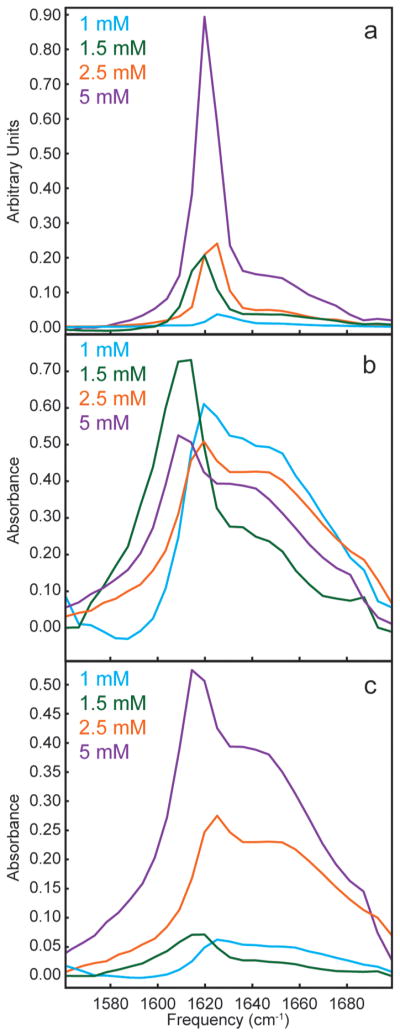
We determined the transition dipole strength for each of these samples using our previously published method, which is explicitly outlined in the Supporting Information. To do so, we need the linear absorption spectrum, the 2D IR spectrum, the absorption spectrum of the laser pulses, and a calibrant molecule with a known transition dipole strength. The probe pulse used in the 2D IR measurements provides the linear absorption and pulse spectrum. Figure 3 shows diagonal slices through 2D IR spectra as well as absorption spectra of hIAPP fibers at the four concentrations. The integrated area of the absorption spectra should scale with concentration according to Beer’s law, but the absorption spectra in Figure 3a do not follow the concentration trend.²⁴ Deviations are caused by inherent heterogeneity of mixing during sample preparation. The concentration varies within the same sample cell, which we know by measuring multiple spots (the laser beam is about 100 μm, while the sample spans about 3 mm, so many spectra can be collected for the same sample preparation). This scenario highlights another problem in measuring extinction coefficients from linear absorption, besides the ones mentioned in the Introduction. Nonetheless, for any chosen spot in the sample, we measure both a 1D and 2D IR spectrum with the same laser beam and thus can make a direct comparison.

Figure 3.

(a) Diagonal slices through 2D IR spectra of hIAPP fibers at 1 mM (cyan), 1.5 mM (green), 2.5 mM (orange), and 5 mM (purple). (b) Simultaneously measured absorbance spectra of hIAPP fibers at 1 mM (cyan), 1.5 mM (green), 2.5 mM (orange), and 5 mM (purple), normalized to their areas. (c) Absorbance spectra from part b, unnormalized for hIAPP fibers at 1 mM (cyan), 1.5 mM (green), 2.5 mM (orange), and 5 mM (purple).

Shown in Figure 3b are FTIR spectra normalized by their integrated areas. Normalization in this way removes the dependence on concentration. Clearly, the 2D IR intensities are not all equal, which immediately indicates that the transition dipole strengths vary from sample to sample. Moreover, notice that the β-sheet intensity at ~1620 cm⁻¹ is much larger than the random coil region near 1650 cm⁻¹. This indicates that the transition dipoles of the β-sheets are much larger than those of the random coil, which is qualitatively consistent with the Introduction. Table 1 lists the frequency of the β-sheet peak, the absorbance, the 2D maximum, and the calculated transition dipole intensity using our 1D/2D method (see the Supporting Information and ref 25) for each of the four samples. The transition dipole strengths range from 0.2 ± 0.01 to 1.5 ± 0.01 D². Figure 3c shows the non-normalized FTIR spectra of the four hIAPP samples.

Table 1.

Concentration, β-Sheet Frequency, Absorbance, Maximum of the 2D IR Diagonal Slice, and Calculated Transition Dipole Strengths of hIAPP Fibers

hIAPP fibers
concentration (mM)	frequency (cm−1)	absorbance	2D maximum (arb. units)	transition dipole strength (D2)
1	1621	0.067	0.037	0.2 ± 0.01
1.5	1614	0.071	0.207	0.5 ± 0.01
2.5	1618	0.275	0.245	0.36 ± 0.01
5	1615	0.525	0.914	0.76 ± 0.01

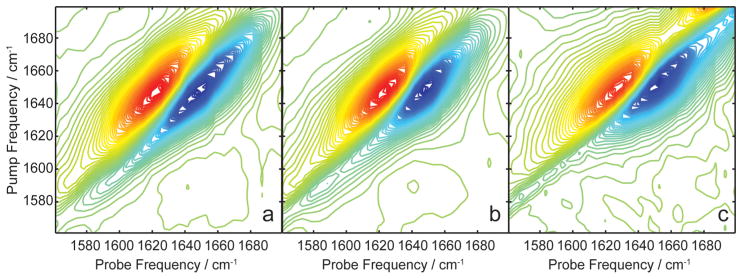
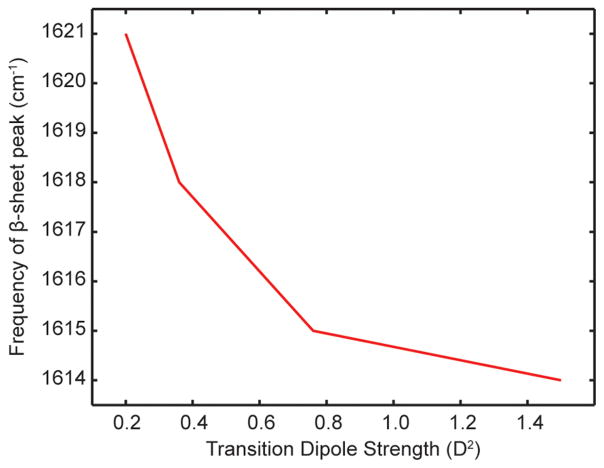
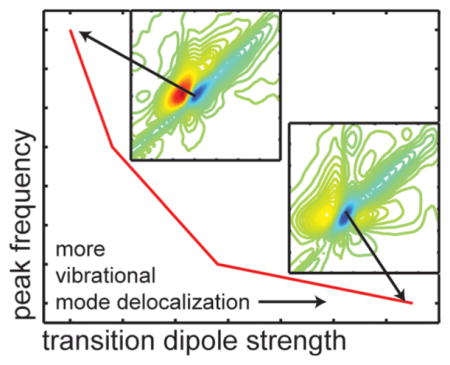
We note that there is a correlation between β-sheet frequency and transition dipole strength; the lower the frequency, the larger the transition dipole. Shown in Figure 4 are normalized 2D IR slices. The highest β-sheet mode absorbs at 1621 cm⁻¹, which also has the broadest 2D IR diagonal line width, the largest anharmonic shift (not shown), and the smallest transition dipole strength (0.2 ± 0.01 D²). In contrast, the lowest frequency β-sheet mode absorbs at 1614 cm⁻¹ and has the narrowest diagonal line width, the smallest anharmonic shift (not shown), and the largest transition dipole strength (1.5 ± 0.01 D²). The quantities are all related to the delocalization of the normal mode. We come back to this point in the Discussion.

Figure 4.

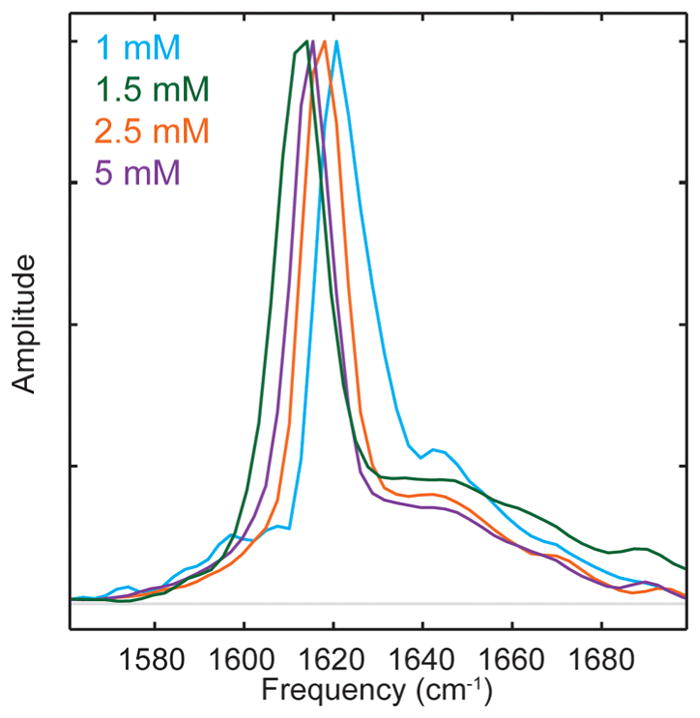
Normalized slices through the diagonal of 2D IR spectra of 1 mM (cyan), 1.5 mM (green), 2.5 mM (orange), and 5 mM (purple) hIAPP. The frequency of the β-sheet peak decreases with increasing transition dipole strength. In addition, the diagonal line widths narrow as the transition dipole strength increases.

Transition Dipole Strengths of Rat IAPP in Solution, Micelles, and Membranes

The 2D IR spectra of rat amylin in solution, micelles, and bilayers are shown in Figure 5. All spectra exhibit a broad peak along the diagonal near 1650 cm⁻¹ due to the amide I modes in the peptide and a small shoulder at 1591 cm⁻¹ from deuterated side chains, such as arginine, that are known to absorb in this region. Except for the ester stretch of the bilayer that begins to absorb at 1680 cm⁻¹, the three spectra are very similar to one another. The maximum absorbance between the samples differs by 2 cm⁻¹ or less, and there are slight differences in the antidiagonal line widths. The FTIR spectra (Figure 6b) are similar to one another as well. Using standard empirical assignments based on frequencies and line widths, one would probably conclude that amylin is random coil in all three environments.

Figure 5.

(a) 2D IR spectrum of rIAPP in solution. (b) 2D IR spectrum of rIAPP in micelles. (c) 2D IR spectrum of rIAPP in membranes. All slices are normalized to the amide I mode.

Figure 6.

(a) Diagonal slices through 2D IR spectra of rIAPP in solution (blue), micelles (magenta), and membranes (green). (b) Simultaneously measured absorbance spectra of rIAPP in solution (blue), micelles (magenta), and membranes (green).

Figure 6a shows diagonal slices through 2D IR spectra of rIAPP in solution, micelle, and membrane, and Figure 6b shows the simultaneously measured absorbance spectra. Once again, the absorption spectrum does not scale as expected based solely on concentration, because samples made from micelles and vesicles are often not spatially uniform. Thus, calculating transition dipole strengths from the absorption spectrum alone would be quite inaccurate. Following the same procedure as above for the fibers (and as outlined in the Supporting Information), the transition dipole strengths were calculated. The transition dipole of rIAPP in solution is |μ⃗|² = 0.15 ± 0.08 D² at 1650 cm⁻¹, which is the absorption maximum, in the micelle it is |μ⃗|² = 0.16 ± 0.06 D² at 1650 cm⁻¹, and in the membrane it is |μ⃗|² = 0.20 ± 0.07 D² at 1652 cm⁻¹. These values are compiled in Table 2. Notice that the transition dipole strength progressively increases from solution to micelle to bilayer. Moreover, the transition dipole intensity for a random coil peptide is |μ⃗|² = 0.12 ± 0.013 D^2.25 Thus, rat amylin is nearly entirely random coil in solution but progressively adopts a structure in micelles and bilayers that enables the vibrational modes to delocalize. Since the increase in the transition dipole strength occurs at 1650 cm⁻¹, we conclude that it is adopting α- helical character in micelles and bilayers, which is consistent with NMR studies.⁴⁴

Table 2.

Sample Type, Peak Frequency, and Transition Dipole Strength of the Three Types of rIAPP Samples^a

rIAPP
sample	frequency (cm−1)	transition dipole strength (D2)	percent random coil	calculated dipole strength (D2)
solution	1650	0.15 ± 0.08
micelle	1650	0.16 ± 0.06	0.67	0.55 ± 0.09
membrane	1652	0.20 ± 0.07	0.35	0.53 ± 0.08

^aThe scaling factors are calculated to scale the solution spectrum to the micelle spectrum and the solution spectrum to the membrane spectrum. They can be interpreted as the amount of random coil peptide in each sample. After subtracting the scaled solution spectrum from the pure micelle and pure membrane spectra, the transition dipole strength was calculated for the difference spectra and is the calculated dipole strength.

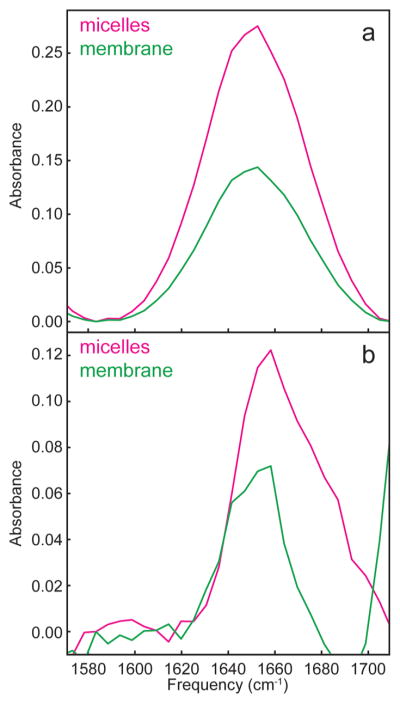
On the basis of our previous work, we know that soluble α-helices have a transition dipole strength of 0.26 D^2.25 Thus, in bilayers, rat IAPP might be largely helical. However, in all likelihood, rat IAPP will have both random coil and α-helical contributions to the structure. If so, then the measured |μ⃗|² value is an average of the random coil and α-helix transition dipoles, and thus represents a lower bound to the transition dipole strength of any helix that is present. To obtain the transition dipole strength of the helix alone, we repeat our calculation after first subtracting the random coil contribution to the spectra. To do so, we assume that, in solution, rIAPP is 100% random coil, which is consistent with its transition dipole strength although not entirely accurate according to molecular dynamics simulations.^45,46 We then subtracted the rIAPP absorption spectrum from the micelle and membrane absorption spectra scaled so that the frequency range between 1614 and 1620 cm⁻¹ went to baseline (Figure 7a). This region was selected because most helical membrane peptides do not absorb in this region.^21,47 The resulting difference spectrum is the absorption spectrum of the pure helix in the micelle and membrane samples (Figure 7b). The scaling factors were 0.67 and 0.35 for the micelles and membrane samples, respectively (Table 2), which are a measure of the percent random coil in each sample. Using these scaling factors, the 2D IR spectra are subtracted as well. Finally, the transition dipole strengths are calculated, as done above. Our procedure of subtracting the random coil follows our previous publication on soluble helices, and we discuss some of the caveats in the Supporting Information.²⁵ In the end, we obtain the transition dipole strength for what we believe to be the α-helix contribution to the structure, which is 0.55 D² in the micelles and 0.53 D² in the membrane. We note that the two are very similar to one another and that both are roughly twice as large as in the previously measured soluble α-helix, which are points that we discuss below.

Figure 7.

(a) Absorbance of rIAPP in solution scaled at 1614–1620 cm⁻¹ to the absorbance of rIAPP in a micelle (magenta). Scaling the rIAPP in solution to rIAPP in a micelle over that frequency range gives a scaling factor of 0.67. Absorbance of rIAPP in solution scaled at 1614–1620 cm⁻¹ to absorbance of rIAPP in a membrane (green). Scaling the rIAPP in solution to rIAPP in a membrane over that frequency range gives a scaling factor of 0.35. (b) The absorbance of the scaled (to micelle spectrum) rIAPP in solution spectrum subtracted from the pure rIAPP in solution trace (magenta). The absorbance of the scaled (to membrane spectrum) rIAPP in solution spectrum subtracted from the pure rIAPP in solution trace (green).

DISCUSSION

Interpretation of Transition Dipole Strengths and Participation Ratios

The transition dipole strength is a measure of the number of residues over which excitons are delocalized. A single peptide unit, as modeled by N-methylacetamide (NMA), has a transition dipole strength of |μ⃗|² = 0.12 D^2.25 We consider this value to be equivalent to an uncoupled amide I mode, which is the same value we found for a denatured soluble peptide. Thus, transition dipole strengths greater than 0.12 D² indicate a peptide has adopted a structure with vibrational coupling large enough to delocalize the amide I vibrational modes. The largest transition dipole measured here was for the 1.5 mM sample of hIAPP, which had |μ⃗|² = 1.5 ± 0.01 D², indicating that the amide I mode is delocalized over ~12 amino acids. We discuss the structural implications of this observation below, but the first conclusion from our study is that the amide I vibrational modes can delocalize across an enormous distance.

There are several factors that determine the degree of vibrational delocalization, and hence the transition dipole strengths. First, there is the structure that sets the coupling constants. To the best of our knowledge, amylin always assumes parallel β-sheets, and thus, the coupling strengths should be approximately invariant from sample to sample. The coupling constants in perfect parallel β-sheets have been calculated to be as large as 20 cm⁻¹, which is the primary driver for delocalization.⁴⁸ Ultimately, the size of the β-sheet determines the number of residues that can participate in a β-sheet vibrational mode, which in the case of amylin is about 20 residues.⁴⁹ Second, there is structural disorder. Structural variations, such as fraying that typically occurs at the edges of β-sheets and the ends of α-helices, alter the coupling constants.²⁶ This effect is often called “off-diagonal disorder” and usually localizes the vibrational modes. Third, frequency variations caused by the surrounding environment, such as residues exposed to water, will also localize the vibrational modes even if the secondary structure is not altered. This effect is usually called “diagonal disorder” because it changes the diagonal elements of an excitonic Hamiltonian. In essence, the degree of delocalization is a competition between coupling strength and disorder.

In calculations of vibrational normal modes, one often computes the inverse participation ratio, defined as

$${\text{IPR}}_{\alpha }\equiv {(\sum _j{U_{\alpha ,j}}^4)}^{-1}$$ (1)

where U_α,j is the jth element of the eigenvector associated with the αth amide I normal mode. The participation ratio is a measure of the number of local vibrations, in our case the amide I modes from each residue, that contribute to the normal mode. For example, Cho used the inverse participation ratio to understand the delocalization of the amide I normal a modes across the strands of a simulated β-hairpin turn⁵⁰ and a multistranded β-sheet.⁵¹ The participation ratio is calculated using the eigenvectors of the normal modes, whose coefficients are determined by the competition between coupling and disorder, as discussed above. A participation ratio can be computed from an eigenvector, but one cannot uniquely back calculate an eigenvector from a participation ratio. For example, IPR_α = 1 means that the normal mode is localized on one amino acid or one peptide strand, while IPR_α = 5 is created when the normal mode is delocalized over five amino acids or five strands.

The experimental transition dipole strengths measured here are closely related to the participation ratio. The transition dipole of the normal mode is created by the vector sum of the local amide I modes, weighted by the coefficients of the eigenstates

$$\overrightarrow{\mu }=\sum _i{c}_i{\overrightarrow{\mu }}_i$$ (2)

where μ⃗ is the transition dipole of the normal mode, c_i is the weighted coefficient of the eigenstates, and μ⃗_i is the local amide I mode. The main difference between the transition dipole strengths and the participation ratio is the vector nature of the transition dipoles. Thus, the orientations of the local modes will alter the transition dipoles but not the participation ratio, although they may indirectly influence the participation ratio through the couplings (e.g., transition dipole coupling depends on orientations). For a given secondary structure with known coupling constants and transition dipoles, the interpretation of the transition dipole strength can include orientations, which we discuss below. Nonetheless, to a first-order approximation, we can interpret the transition dipole strengths as an experimental measure of the participation ratio by simply dividing the transition dipole strength by that of the local modes, knowing that the calculated participation ratio is a lower bound for the reasons given above. With these concepts in mind, we now turn to the interpretation of the experimental data.

Structural Disorder and Polymorphs in Amyloid Fibers

As discussed above, to a first approximation, the transition dipole strength can be considered a measure of the number of residues over which the vibrational modes are delocalized, for which we use the transition dipole strength of NMA, |μ⃗|² = 0.12 D², as the standard for a single peptide unit. In the 1 mM hIAPP fiber sample, the transition dipole strength was measured to be 0.20 ± 0.01 D², which indicates that the amide I vibrational modes were delocalized over nearly two amino acids. The 2 mM sample had a transition dipole strength of 0.36 ± 0.01 D², which is 3 times that of NMA, revealing that the excitons were delocalized over three residues in the β-sheet. The 5 mM sample had a transition dipole strength of 0.76 ± 0.01 D², corresponding to delocalization over ~6 amino acids. The largest transition dipole strength of 1.5 ± 0.01 D² was observed in the 1.5 mM sample, which corresponds to delocalization over ~12 amino acids. Thus, the extent of delocalization is enormous.

For the fibers, we note that the transition dipole strength is anticorrelated to the frequency of the β-sheet mode; the larger the transition dipole strength, the lower the amide I frequency, as illustrated in Figure 4 and Table 1. The smallest transition dipole strength had a β-sheet mode at 1621 cm⁻¹, while the largest was at 1614 cm⁻¹. This experimental observation is in agreement with prior experimental simulations.^48,50,52 Simulations by Cho and co-workers showed that the amide I frequency of parallel and antiparallel sheets depended largely on the number of strands over which the vibrational modes were delocalized and to a lesser extent over the number of residues in each strand (because interstrand coupling is stronger than intrastrand coupling, e.g., 10 cm⁻¹ versus 1 cm⁻¹).⁵¹ Cho did not report absolute transition dipole strengths, but they scale approximately linearly with the number of strands in the β-sheet. Thus, we conclude that the largest transition dipole strength measured here corresponds to vibrational modes that are delocalized over 12 strands in the amyloid β-sheets of the fibers.

We believe that the transition dipole strength is a better measure of delocalization than the frequency itself. Shown in Figure 8 is a plot of the measured β-sheet frequency versus the transition dipole strength. Notice that the frequency appears to be reaching an asymptote at 1614 cm⁻¹. The simulations by Cho also predicted asymptotic behavior.⁵¹ Notice that the dipole strengths increase by a factor of 7.5, while the frequency only changes by 7 cm⁻¹. Thus, the frequency is not as sensitive as the transition dipole strength. Moreover, interpretation of the frequency requires knowledge about the environment electrostatics. For instance, β-sheets exposed to water versus buried inside hydrophobic amyloid fibers will certainly have different frequencies even if they are the same size. In contrast, the transition dipole strength of the amide I mode is quite insensitive to its environment or whether it is hydrogen bonded, and thus provides an accurate reference point.^53,54 While solvation and hydrogen bonding do not change the transition dipole strength of the amide I mode considerably, non-Condon effects are present for other modes such as the OH stretch in water.⁵⁵

Figure 8.

Measured β-sheet peak frequency in the four hIAPP fiber samples versus the transition dipole strength measured in each sample.

Why do fibers formed at different concentrations exhibit different transition dipole strengths, and why is there seemingly no correlation between the two? One explanation might be polymorphs which are now being recognized as a common phenomenon of amyloids. Polymorphs are variations in amyloid fiber structure that occur for identical monomers.^56–59 They can differ in the arrangement of the side chains or in the tertiary structure. It is thought that the preparation conditions are responsible for dictating which polymorph forms. Our results might be explained by the conversion of one polymorph into another. However, there is evidence for Aβ that, once a polymorph forms, it is kinetically trapped and does not interconvert into another.⁵⁷ That result may not hold true for amylin, since we have observed an interconversion between fiber structures in a peptide inhibition study.⁶⁰ It might be possible to determine if the samples formed from the different concentrations form polymorphs, but it would be difficult because polymorphs typically exhibit very similar transmission electron microscope images, CD spectra, and ThT binding.

Another possible explanation for the results is simply the heterogeneity of the sample preparation procedure. Variations from sample to sample can occur when drying the d-HFIP from the peptide. While care was taken to ensure the peptide samples were dried completely of d-HFIP, the process of lyophilizing d-HFIP could have promoted different structures of hIAPP to form. The rate of drying was not controlled, and thus, the sample preparation procedure could have been somewhat varied.

Rat IAPP in Membrane Bilayers Is α-Helical-Like in Micelles but More Structurally Ordered

As discussed above, the extent of delocalization is determined by a competition between the strength of the coupling and the magnitude of the disorder. Disorder can localize the vibrational modes without altering the secondary structure, such as would occur by the frequency shifts caused by solvation. As such, the transition dipoles measured here provide lower bounds to the number of amino acids involved in the secondary structure. This statement is most obvious in the context of the amyloid fibers discussed above for which we found at most 12 strands participating in the vibrational modes even though the fibers are formed from hundreds of peptide β-strands. In the case of the helices, which are formed from a single polypeptide, it provides a lower limit to the length of the helix. Considering that the transition dipoles of the helices in the micelle and bilayer were calculated to be 0.16 ± 0.06 and 0.20 ± 0.07 D² and that the transition dipole is oriented 38° from the helix axis,⁶¹ there must be ~7.4 residues, or two complete helix turns, participating in the measured vibrational mode. According to NMR data on rat IAPP in micelles, residues Ala-5 to Ser-23 are helical.³² In comparison, in our original report using this methodology, for a soluble α-helix, we measured |μ⃗|² = 0.26 D² and concluded that the vibrations spanned 3.5 residues, or one complete helix turn. Thus, the increase of the transition dipole strength from 0.15 to 0.53 D² is not a reflection of the length of the helix but instead indicates that the helices themselves are becoming more rigid.

In NMR studies, micelles are often used as approximations to bilayers to study membrane peptides because micelles rotate fast enough that high-resolution NMR spectroscopy can be used rather than solid-state NMR. However, micelles can perturb the peptide structure by causing curvature or not being a good model for a membrane. The first step toward determining how much α-helix secondary structure is in the samples of rIAPP in micelles and membranes was to scale the absorbance of rIAPP in solution (assumed to be 100% random coil) to the absorbance of rIAPP in micelles and membranes. The scaling factor between the solution and micelle traces was 0.67, and the scaling factor between the solution and membrane traces was 0.35. This means that 67% of rIAPP in micelles is random coil and 35% of rIAPP in membranes is random coil, corresponding to ~25 and ~13 residues, respectively. After subtracting the solution spectrum from the micelle and membrane spectra, the final transition dipole strength of the α-helix content in rIAPP in micelles was 0.55 D², and the transition dipole strength of rIAPP in membrane was 0.53 D². Comparing those values to NMA, the transition dipole strength of the α-helix in micelles is ~4.6 times larger, and the transition dipole strength of the α-helix in membrane is ~4.4 times larger. The transition dipole moment of the amide I mode is oriented 38° relative to the helix axis.⁶² The measure of delocalization can then be calculated as 4.6 cos⁻²(38°) for rIAPP in micelles, meaning that excitons delocalize over ~7.4 residues, or two complete turns. Exciton delocalization for rIAPP in membranes spans ~7.1 residues, or just less than two complete turns. This is in agreement with previous work that estimated two α-helix turns for the extent of exciton delocalization.⁶¹ On the basis of previous work suggesting that the N-terminus of rIAPP adopts an α-helix on a micelle and the work presented here that shows that exciton delocalization spans ~7 residues, it is likely that the α-helix in rIAPP on micelles and membranes spans residues ~8–16. This region is adjacent to the disordered residues between Cys-2 and Cys-7 but before what is considered the turn region in hIAPP. The sequence in the region is identical to that of hIAPP, and thus may provide insight into intermediates in the pathway for hIAPP to disrupt cell membranes.

CONCLUSIONS

To conclude, we have shown that measuring the transition dipole strength is a useful way to determine secondary structures of proteins that otherwise could not be accurately determined. In the case of hIAPP fiber structure, we have shown that this technique can identify polymorphs of the same peptide that would not be definitively revealed on the basis of the β-sheet frequency alone. We show that hIAPP forms fibers with vibrational mode delocalization that varies from 2 to 12 residues, depending on the concentration of the peptide monomers that sets the rate of fiber formation. The faster the fibers form, the more internal disorder, and the weaker the transition dipole strength. We have also shown that the transition dipole strength of rIAPP varies depending on if it is in solution, micelles, or membrane bilayers. In micelles and membranes, vibrational modes delocalize over two helix turns, most likely segregated to the N-terminus of the peptide, in agreement with NMR measurements of rat amylin. Transition dipole strengths are especially interesting to interpret in excitonic systems in which the local modes are all the same, because they are directly related to the extent of structure formation and provide an experimental measure of the participation ratio. This method could also be used in kinetically evolving samples, such as protein folding and the aggregation of amyloid proteins. One outstanding question regarding amyloid aggregation is the nature of structural intermediates and identifying these independent of the monomer and fibers. If a transition dipole strength larger than that of a random coil is observed during the kinetics, it would be strong evidence for a transient oligomeric species.