Photoresponse of graphene field-effect-transistor with n-type Si depletion layer gate

Abstract

Graphene/semiconductor Schottky junctions are an emerging field for high-performance optoelectronic devices. This study investigates not only the steady state but also the transient photoresponse of graphene field-effect transistor (G-FET) of which gate bias is applied through the Schottky barrier formed at an n-type Si/graphene interface with a thin oxide layer, where the oxide thickness is sufficiently thin for tunneling of the charge carrier. To analyze the photoresponse, we formulate the charge accumulation process at the n-Si/graphene interface, where the tunneling process through the SiO_x layer to graphene occurs along with recombination of the accumulated holes and the electrons in the graphene at the surface states on the SiO_x layer. Numerical calculations show good qualitative agreement with the experimentally obtained results for the photoresponse of G-FET.

Introduction

Graphene is anticipated for use in high-performance electronic devices because of its extraordinary carrier transport property with single-atomic-layer thickness¹. A graphene/semiconductor heterojunction is an emerging field of recent optoelectronic devices because of their low light absorption of graphene of 2.3%², which is appropriate for high-performance transparent electrodes of optoelectronic devices such as photosensors and photovoltaic applications^3–13. In such applications, the charge carrier transport through the graphene/semiconductor heterojunction is crucially important to assess the device performance. Generally, a graphene contact to the doped semiconductor substrates is described as a Schottky contact, which is useful in high-performance optoelectronics and photovoltaic devices^4,10,13–21. In addition, the presence of the thin tunnel barrier at graphene/semiconductor interface modifies the current-voltage characteristics of the junction. In the case of a metal/Si Schottky junction with a 2–10-nm-thick oxide layer at the interface, which is sufficiently thin for tunneling of charge carriers, the open circuit voltage and short circuit current under light irradiation are strongly suppressed because the photogenerated carriers recombine at the interface states in the thin oxide followed by tunneling^22,23. Photoresponse similar to the ideal Schottky diode is observed only in a reverse bias regime. Similar characteristics were observed for a graphene-Si Schottky contact^{11,13–15,18,20}. In this case, both the trap state at the interface and the unique density of states of graphene should be considered for detailed analyses, where the energy position of Fermi level of graphene can be modulated by the field effect through the oxide layer.

The transfer characteristics of graphene field-effect transistor (G-FET) are governed by the induced charge carrier density by application of the gate voltage. For a graphene/doped Si junction with thin oxide layer at reverse bias, the induced charge carrier in graphene should be balanced to that of Si depletion layer induced by the reverse bias corresponding to the gate bias. Under light irradiation, the excess charge carrier generated in the depletion layer by light irradiation is accumulated at the Si/oxide interface because of the presence of the thin oxide layer, which increases the charge carrier density in the graphene and which consequently increases the drain current of the G-FET. This effect can be used to amplify the photoresponse of the graphene/Si Schottky junction, where the photoresponse appears on the drain current of G-FET¹¹. Although detailed analysis of current–voltage characteristics of the graphene/Si Schottky junction with thin oxide layer has been conducted¹⁴, detailed analysis of the G-FET with the Si Schottky junction with the thin oxide gate remains an open subject.

This study investigates not only the steady state but also the transient photoresponse of G-FET of which gate bias is applied through the Schottky barrier formed at the n-type Si/graphene interface with a thin oxide layer, where the oxide thickness is sufficiently thin to tunnel the charge carrier. To analyze the photoresponse, we formulate the charge accumulation process at n-Si/graphene Schottky interface, where the tunneling process through the SiO_x layer is considered in addition to the recombination of the accumulated holes and the electrons in the graphene at the surface states on SiO_x layer.

Results and Discussion

Figure 1a presents a schematic illustration of the G-FET, where the depletion layer formed at the n-Si/graphene Schottky contact with thin SiO_x layer acts as the insulating layer of the gate. All processes were performed in air, so that the channel part of the graphene is contacted to the Si surface through a 2–5 nm thick native oxide layer, which is sufficiently thin to tunnel the charge carrier^22,23. As depicted schematically in Fig. 1b, the Schottky junction is formed at the interface between the Si and graphene, where the depletion layer at Si is developed at the positive gate bias (V_GS) corresponding to the reverse bias of the Si/graphene Schottky junction.

Figure 1.

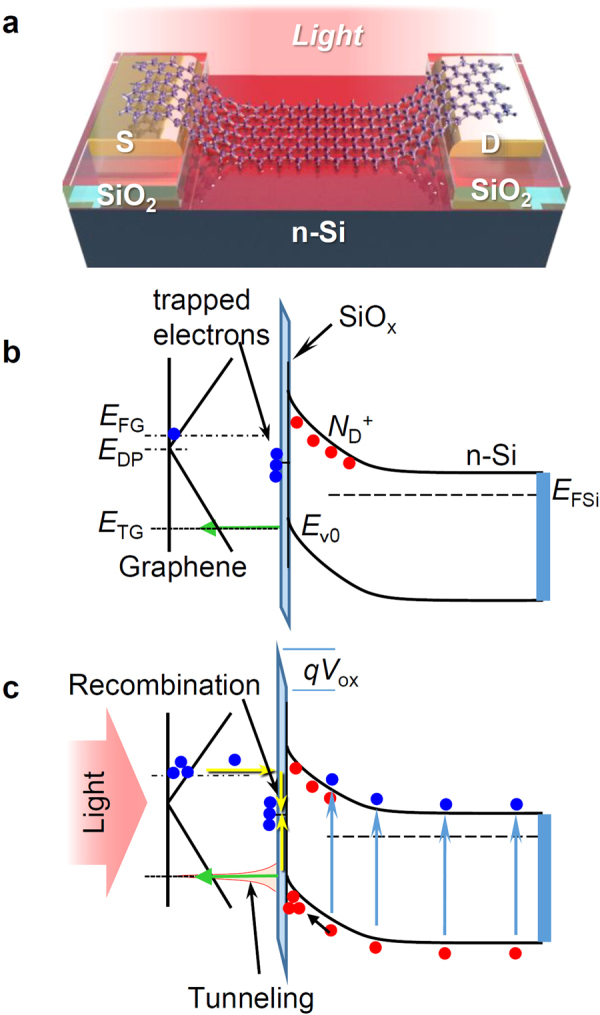
Model of G-FET with Si depletion layer gate. (a) Schematic of G-FET with Si depletion layer gate with thin SiO_x layer at the interface and energy band profiles at Graphene/n-Si contact under reverse bias (b) in a dark condition and (c) under light irradiation.

At V_GS > 0, the photoinduced hole–electron pair at the depletion layer is separated by the build-in potential, as presented schematically in Fig. 1c. For the light source used in this study, we used a light emitting diode (LED) with 623 nm wavelength. The absorption coefficient of Si to 623 nm light is ~3000 cm⁻¹, so that the penetration depth of the 623 nm light is ~3 μm, which is much greater than the depletion layer thickness. Consequently, the hole–electron pair is generated throughout the depletion layer. The photo-excited electrons at the depletion region drift to the back gate electrode that is positively biased. The holes at the depletion region also drift toward the graphene channel. Thus, the either direct or trap controlled recombination of photogenerated hole and electron in the depletion region is suppressed. For an ideal Schottky junction, the holes are swept out to the graphene without restriction. However, under the presence of the thin SiO_x, the holes are accumulated at the interface, followed by tunneling to the graphene, which closely resembles the inversion layer at MOS interface for n-type semiconductor. In this case, the electrons are induced in the graphene as the counter charge of the accumulated holes at the interface, which engenders the Fermi level shift of graphene. Additionally, one must consider recombination of the photogenerated holes and electrons in the graphene through the recombination center at SiO_x. Consequently, the output current (I_DS) of the G-FET is increased by light irradiation depending on the accumulated holes at the Si/SiO₂ interface. Similar concept of the trap controlled band modification for the enhancement of photosensitivity has been reported in organic photodiodes^24–28.

Based on the model described above, we will formulate the light-intensity dependence of I_DS, which is determined by the carrier density of graphene n_G. For simplicity, we assume that the recombination life-times of both of electrons and holes are the same to match τ_R of the Shockley–Read–Hall (SRH) recombination model²⁹. Furthermore, we assume that the intrinsic carrier density is negligibly small. Therefore, the resultant rate equation of accumulated holes, p_Si, at the Si/SiO₂ interface can be expressed as

$$\frac{d{p}_{Si}}{dt}=-\frac{p_{Si}}{{\tau }_T}-\frac{1}{{\tau }_R}\frac{n_G{p}_{Si}}{n_G+p_{Si}}+g,$$ 1

where the first and second terms at right respectively correspond to the direct tunneling of the accumulated holes into graphene through the thin SiO_x and the SRH recombination of the accumulated holes and the electrons in graphene at SiO_x. Also, τ_T⁻¹ stands for the tunneling probability of the accumulated holes, τ_R⁻¹ expresses the recombination rate of the accumulated holes and the electrons in graphene at SiO_x, and g denotes the photo-generation rate of holes in the depletion layer. The density of electrons in graphene at Fermi level E_FG is known to be^1,30–32.

$$n_G={(E_{FG}-E_{DP})}^2/\pi {\hslash }^2{v_F}^2,$$ 2

where E_DP is the energy position of the charge neutral point, the Dirac point, $\mathrm{\hslash }$ is Planck’s constant, and v_F represents the Fermi velocity of charge carriers in graphene (~10⁸ cm/s). The tunneling probability τ_T⁻¹ of holes into graphene is proportional to the graphene density D_G(E_TG) as final states for tunneling, where E_TG is the energy position for hole tunneling. The graphene density at energy E is

$$D_G(E-E_{DP})=2(E-E_{DP})/\pi {\hslash }^2{v_F}^2,$$ 3

which is also crucially important for ascertaining E_FG − E_DP . At V_GS higher than that at the gate voltage corresponding to the Dirac point (V_Dirac) under the dark condition, the excess V_GS (=V_GS − V_Dirac) is applied for development of the depletion layer, so that one can assume E_FG ~ E_DP . At this condition, the energy state for tunneling of accumulated holes into graphene, which corresponds to the energy position of valence band top of Si at the SiO₂/Si interface, is defined as E_v0. To clarify the tunneling process under light irradiation, we investigate the relation between E_TG and E_v0, where we consider the Fermi level shift of graphene ΔE_FG = E_FG − E_DP and the additional potential drop at the thin SiO_x, ΔV_OX, because of n_G as the counter charge of accumulated holes induced by photoexcitation, p_Si. The relation between E_TG and E_v0 under the light irradiation is given as

$$E_{TG}-E_{DP}=E_{v0}+q\mathrm{\Delta }{V}_{OX}-\mathrm{\Delta }{E}_{FG}\approx E_{v0}+q\mathrm{\Delta }{V}_{OX}-\sqrt{\pi {\hslash }^2{v_F}^2{n}_G}.$$ 4

Using the combination of Eqs (3) and (4), one can ascertain the density of states of graphene at energy of tunneling hole expressed as

$$D_G(E_{TG}-E_{DP})=2{(\pi {\hslash }^2{v_F}^2)}^{-1}(E_{v0}+q\mathrm{\Delta }{V}_{OX}-\mathrm{\Delta }{E}_{FG})\approx 2{(\pi {\hslash }^2{v_F}^2)}^{-1}(E_{v0}+q^2{n}_G/C_{OX}-\sqrt{\pi {\hslash }^2{v_F}^2{n}_G}),$$ 5

where we assume that n_G at dark is negligible. In this case, one can expect n_G ~ p_Si. As described above, tunneling probability τ_Τ⁻¹ is proportional to the final density of states as

$${\tau }_T^{-1}\approx \alpha D_G(E_{TG})=2\alpha {(\pi {\hslash }^2{v}_F^2)}^{-1}(E_{v0}+q^2{n}_G/C_{OX}-\sqrt{\pi {\hslash }^2{v}_F^2{n}_G}),\approx 2\alpha {(\pi {\hslash }^2{v}_F^2)}^{-1}\left(E_{v0}+q^{2}p{}_{Si}/C_{OX}-\sqrt{\pi {\hslash }^2{v}_F^2{p}_{Si}}\right)$$ 6

where α is the constant for proportional factor including the transmittance of tunneling electrons through the thin SiO₂. Inserting this equation to Eq. (1) with n_G ~ p_Si and grouping p_Si terms, one obtains

$$\frac{d{p}_{Si}}{dt}\approx -2\alpha {(\pi {\hslash }^2{v_F}^2)}^{-1}{p}_{Si}(E_{v0}+q^2{p}_{Si}/C_{OX}-\sqrt{\pi {\hslash }^2{v_F}^2{p}_{Si}})-\frac{p_{Si}}{{\tau }_R}+g=-{\beta }_1{p}_{Si}-{\beta }_2{p_{Si}}^2+{\beta }_3{p_{Si}}^{3/2}+g,$$ 7

where ${\beta }_1=2\alpha {(\pi {\hslash }^2{v_F}^2)}^{-1}{E}_{v0}+{\tau }_R^{-1}$, ${\beta }_2=2\alpha {(\pi {\hslash }^2{v_F}^2)}^{-1}{q}^2/C_{OX}$ and ${\beta }_3=2\alpha {(\sqrt{\pi }\hslash v_F)}^{-1}$. At weak light intensity, the contribution of β₁ term is dominant, where the tunneling process and the recombination at SiO_x are the main causes. The light intensity (corresponding to g) dependence of p_Si should be expressed as g^θ with θ = 1 at the steady state, i.e., dp_Si/dt = 0. For the case in which β₂ originating from the voltage across the thin oxide layer is dominant at stronger light intensity, θ is approx. 0.5. As presented in Fig. S1 in Supplementary Information, the numerically calculated light-intensity dependence of p_Si shows power law dependence with two slopes. It is noteworthy that n_G ~ p_Si. Thereby, one can expect that the light-intensity dependence of I_DS shows power law dependence of g^θ with θ < 1.

To investigate the depletion layer at the junction, the capacitance–voltage (C_G–V_GS) characteristics of the Schottky junction were investigated with or without light irradiation, where the measured capacitance C_G is a series capacitance consisting of a quantum capacitance of graphene C_Q, the thin native oxide layer C_OX, and the depletion layer at the Si/SiO_x interface, C_D. As presented in Fig. 2a and b, at V_GS < −0.5 V corresponding to the accumulation condition for MOS junction, the gate capacitance C_G decreases with increasing V_GS because of the decrease of C_Q^33,34. The maximum capacitance of C_G⁻¹ = C_ox⁻¹ + C_Q⁻¹ at V_GS < −1 V is greater than 0.65 μF/cm². The SiO_x layer thickness is estimated as 5 nm or less. The corresponding band diagram is portrayed in Fig. S2 in Supplementary Information. To clarify the light irradiation effect on C_G, the C_G difference between the dark and the light conditions, ΔC_G, is shown against V_GS in Fig. 2c. At V_GS < −0.5 V, ΔC_G shows no marked light-intensity dependence.

Figure 2.

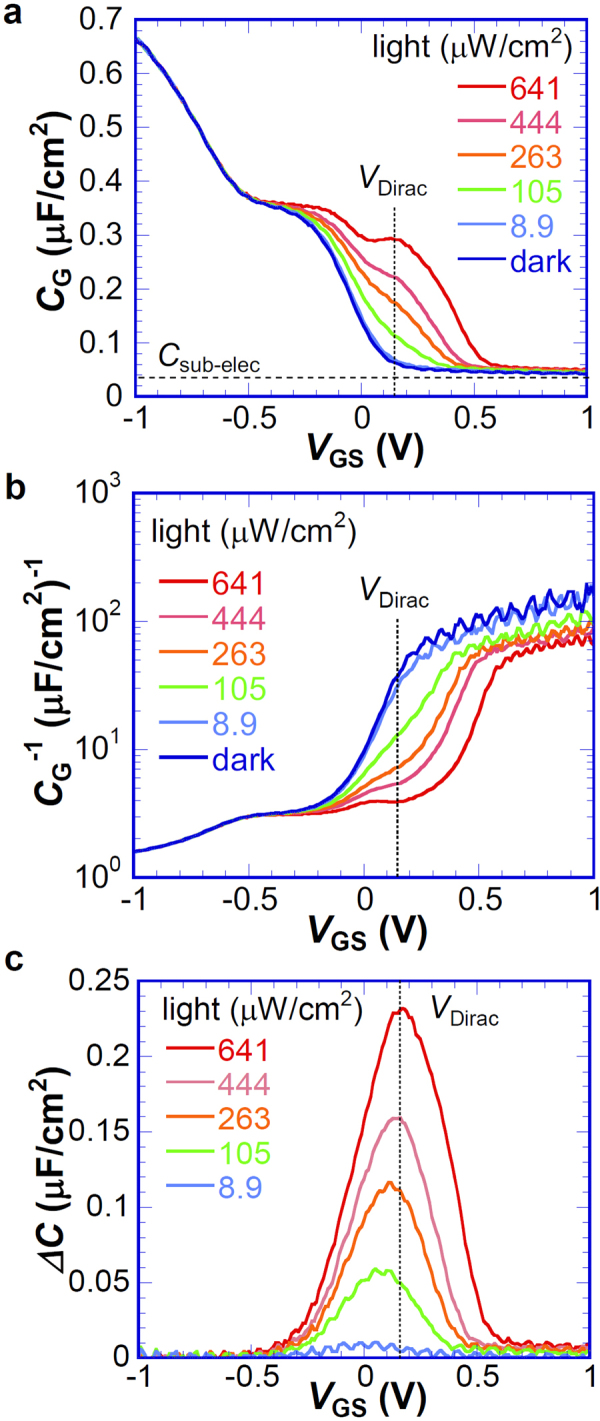
C-V characteristics under light irradiation. (a) V_GS dependence of C_G under various light intensities, (b) V_GS dependence of C_G⁻¹ under various light intensities, and (c) V_GS dependence of ΔC_G under various light intensities. V_Dirac in the figure corresponds to the charge neutral point.

At V_GS ~ −0.5 V, the V_GS dependence of C_G becomes weaker; C_G depends slightly on the light intensity. This slight dependence implies that this bias region corresponds to the transition from accumulation to weak depletion of Si²⁹ (Fig. S2b to S2c), which results in the appearance of C_D. This C_D induces the decrease of the applied voltage dependence of the Fermi level shift of the graphene, which gives rise to the weaker V_G dependence of C_Q. Under light irradiation, the depletion layer thickness decreases because of the photogenerated charge in Si (Fig. S2g), which causes the increase of C_D and the accumulation of photogenerated holes at the SiO_x/Si interface, resulting in the increase of voltage applied to SiO_X: V_OX. Further application of V_GS increases the depletion region thickness at Si and therefore decreases C_G in the dark condition in addition to the decrease of C_Q. Under light irradiation, C_G at −0.5 < V_GS < 0.5 V increases concomitantly with increasing light intensity, which indicates a decrease of the depletion region by light irradiation. At V_GS > 0.5 V, C_G decreases to capacitance originated from the stray capacitance because the electrode pads were connected in parallel.

Figure 3a presents the gate bias voltage V_GS dependence of the current passing through the Schottky junction I_G equivalent to the gate leak current of G-FET under conditions of various light intensities from dark condition to 641 μW/cm², where both the source and drain of the G-FET were connected to ground. At V_GS > 0, corresponding to reverse bias for the Schottky junction, I_G in the dark is well blocked (<0.1 nA) by the Schottky barrier. Under the light irradiation, I_G increases concomitantly with increasing light intensity to 63 nA at 641 μW/cm². In this region, the photo-excited electrons are swept out through the depletion layer of n-Si, whereas the photo-excited holes are tunneled to the graphene through SiO_x layer or recombined at the graphene-Si interface at the thin SiO_x layer, as presented in Fig. 1c. I_G at −0.5 V < V_GS < 0.2 V under light illumination is suppressed, unlike the common Schottky junction behavior. This behavior is commonly observed at the Schottky junction of lightly doped n-Si with thin SiO_x layer^22,23. It originated mainly from the presence of thin SiO_x layer at the interface, resulting in the increase of the direct carrier recombination of the photogenerated carriers at the depletion layer of n-Si¹⁴.

Figure 3.

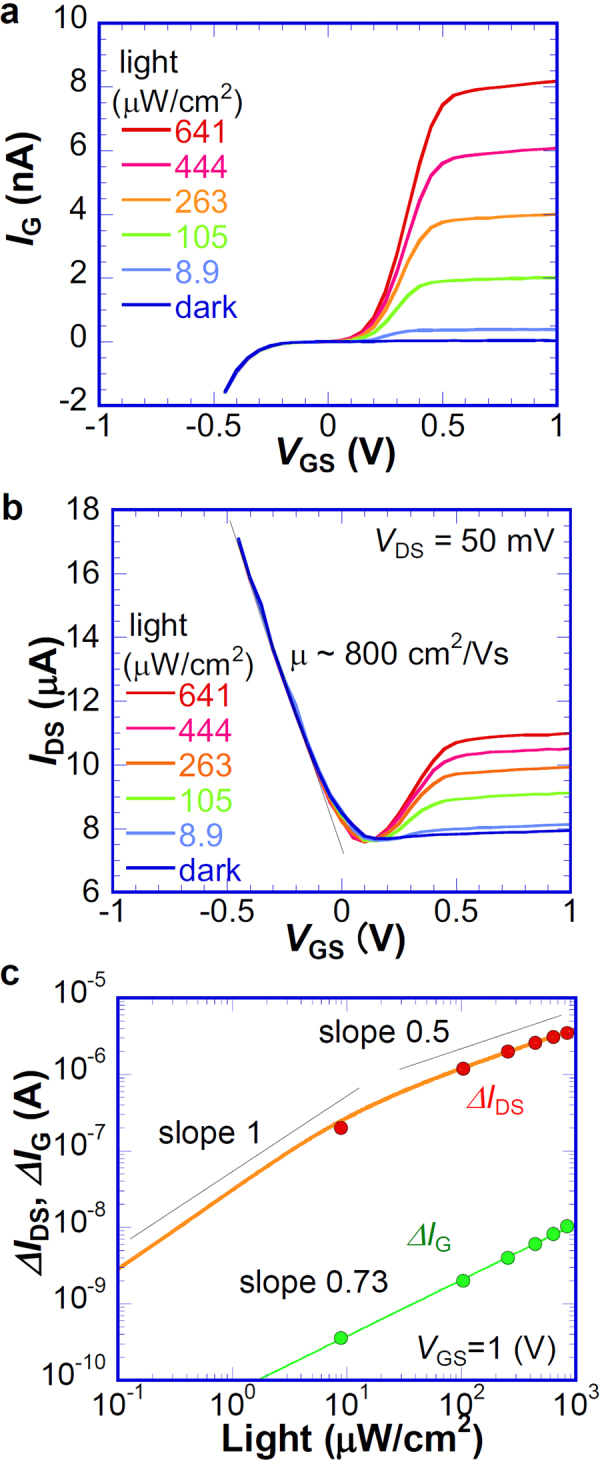
Steady state electrical characteristics under light irradiation. (a) V_GS dependence of I_G corresponding to the current passing through the graphene/n-Si junction under various light intensities. (b) V_GS dependence of I_DS under various light intensities measured at V_DS = 50 mV. (c) Light-intensity dependence of ΔI_G and ΔI_DS at V_DS = 50 mV and V_G = 1 V. The solid curve shown in the figure is the numerically calculated curve ΔI_DS shown in Fig. S1.

The transfer characteristics of the G-FET under an illumination condition are presented in Fig. 3b, which is very similar to the case for conventional G-FETs¹ at V_G < V_Dirac. The drain current I_DS at V_G > V_Dirac in a dark condition remains almost constant, which implies that E_FG ~ E_DP, as assumed in the numerical calculations. Under light irradiation, I_DS increases concomitantly with increasing light intensity of 8–11 μA with saturation behavior at higher V_GS, where V_Dirac (V_GS ~ 0.15 V) is the bias voltage for the charge neutrality point of G-FET determined at minimum I_DS. The I_DS difference between the dark-current and photo-current, ΔI_DS, is 3 μA at 641 μW/cm², which is 2–3 orders of magnitude larger than that of ΔI_G depicted in Fig. 3a, indicating that the direct contribution of gate leak current to I_DS is negligible.

Based on the band model depicted in Fig. 1b and c, I_DS is governed by the accumulated holes at SiO_x/Si interface, even under light irradiation, as described earlier. The ionized donor (positively charged) in the depletion layer gives limited impact to I_DS at V_GS > V_Dirac under light irradiation because of the slight increase of I_DS in dark conditions. The light-intensity dependence of the saturated I_DS under light irradiation at V_G > V_Dirac indicates that the charge carrier density in graphene is determined by the accumulated photo-excited excess hole at the interface, where the density of the accumulated photo-excited excess hole is regulated by the recombination rate of excess holes through the thin SiO_x barrier, as described above. The field effect mobility of hole in graphene was estimated as 800 cm²V⁻¹s⁻¹ from C_G of around V_GS = −0.5 V.

Figure 3c presents the light-intensity dependences of ΔI_G and ΔI_DS, both showing power law dependence of the light intensity. The light-intensity dependence of ΔI_G can be fitted by one slope of 0.73. By contrast, the light-intensity dependence of ΔI_DS comprises two slopes as predicted theoretically earlier. The experimental data are well fitted to the numerically calculated result shown in Fig. S1, as indicated by the solid curve in Fig. 3c. For the numerical calculations, v_F = 0.8 × 10⁶ m/s, τ_R = 18 ms, E_vo = 0.05 eV, α = 2 × 10⁻³⁴, SiO_x thickness = 5 nm are used. The actual p_si, which is proportional to ΔI_DS, is unknown. For that reason, the vertical axis was adjusted with an arbitrary ratio of ΔI_DS/p_si. From a practical perspective for the photosensor, the ΔI_DS is 2–3 orders of magnitude larger than ΔI_G. This photocurrent amplification of G-FET with the Si Schottky gate gives rise to easier measurement of the light intensity than the simple graphene/Si Schottky diode, where the noise equivalent power (NEP) of the G-FET obtained at 8.9 μW/cm² is 7 × 10⁻¹⁴ W/Hz^1/2 (corresponding specific detectivity: 1 × 10¹¹ Jones).

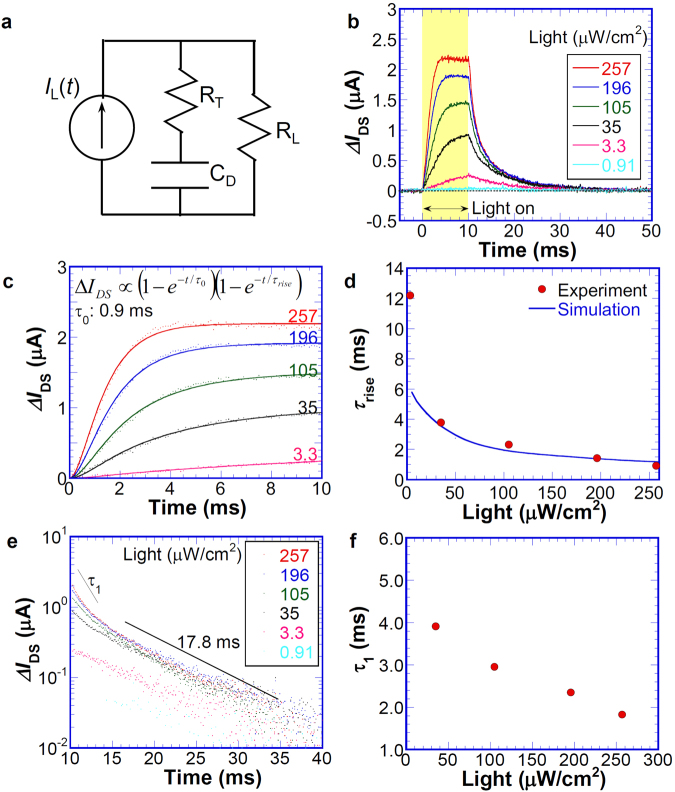
Transient response of G-FET is important for practical applications. The photoresponse time of the Schottky diode is usually explained by the simplified model with junction capacitance C_D, internal series resistance R_T, and load resistance R_L, as portrayed schematically in Fig. 4a, where the photo-generated current I_L is a current source determined by the light intensity. In our device structure, R_L and R_T consist of contact resistance, tunnel resistance, and resistance of the Si substrate. Based on the simplified model presented here, the time constant for rise time, τ₀, is defined simply by C_DR_T, expressed as $I_L\left[1-\exp (-t/{\tau }_0)\right]$. In addition to this time constant, one must consider the time for hole accumulation at the Si/SiO₂ interface, which induces the time dependence of I_L determined by Eq. 7. Figure S3 presents the transient response of numerically calculated p_Si corresponding to I_L under various light intensities, where the used parameters are the same for those of light-intensity dependence in a steady state. The calculated data are well fitted by $1-\exp (-t/{\tau }_{rise})$ with a different time constant, τ_rise, which depends on the light intensity. Consequently, one can expect that the transient photoresponse at light-on is given as the product of $\left[1-\exp (-t/{\tau }_{rise})\right]\left[1-\exp (-t/{\tau }_0)\right]$.

Figure 4.

Transient photoresponse. (a) Equivalent circuit of the Schottky photodiode. (b) Typical transient photoresponse ΔI_DS of G-FET with n-type Si depletion layer gate under various light intensities at V_DS = 50 mV and V_G = 1 V. (c) Transient response of ΔI_DS at light-on under various light intensities. Solid lines are fitting curves. (d) Light-intensity dependence of the time constant τ_rise obtained from the fitting for light-on. (e) Semi-log plot of transient response of ΔI_DS at light-off with various light intensities. (f) Light-intensity dependence of the time constant τ₁ for light-off.

Figure 4b presents the transient photoresponse of I_DS on the G-FET, where the light intensity was varied from 0.91 to 257 μW/cm². As might be readily apparent, the response time at light-on τ_rise decreases concomitantly with increasing light intensity, which is consistent with the calculated results based on the proposed model shown in Fig. S3, where the higher light intensity causes the faster charge accumulation at the interface. To investigate the transience time, we fitted the transient response at light-on with the function expressed as $\left[1-\exp (-t/{\tau }_{rise})\right]$ $\left[1-\exp (-t/{\tau }_0)\right]$. As portrayed in Fig. 4c, the experimental data are well fitted as we expected, where τ₀ determined from C_DR_T was fixed. Note that the lowest photoresponse obtained at 0.91 μW/cm² is quite noisy and close to the dark signal, so that we could not obtain the reliable fitting curve. The experimentally obtained results were not fitted well by the simple exponential function. The time constant τ_rise obtained from the fitting clearly depends on the light intensity: it decreases from 12.5 to 1.6 ms with increasing light intensity, as portrayed in Fig. 4d. The solid line represents τ_rise obtained from the numerically calculated results presented in Fig. S3b, which well reproduces the experimentally obtained results indicating that the hole accumulation process at the interface accelerates the photoresponse time at higher light intensity, as we proposed. Note that the low power region around 3.3 μW/cm² could not be well reproduced based on our simplified model. This is most likely that the contribution of recombination process becomes more dominant at low carrier density. This is a subject for further study.

The transient responses for the light-off condition were described by a double exponential function, as portrayed in Fig. 4e. At t > 3 ms, the decay can be expressed by τ_f = 17.8 ms for all light intensities, mainly because of the recombination time constant τ_R (see Eqs 1 and 7) for excess holes at the interface. For the numerical calculations presented above, τ_R = 18 ms was used. At t < 3 ms, the time constant τ₁ at this region depends on the light intensity, as depicted in Fig. 4f. Time constant τ₁ closely resembles τ_rise, as portrayed in Fig. 4d, which implies that the tunneling process of accumulated holes at the interface mainly contributes to the high decay rate. Results show that the proposed analysis can explain the experimentally obtained results qualitatively.

Conclusions

We demonstrated a photosensor consisting of G-FET with gate bias applied through the Schottky barrier formed at an n-Si/graphene interface, where a thin SiO_x barrier of ~5 nm is present at the interface. The photocurrent amplification of G-FET with the Si Schottky gate gives rise to easier measurement of light intensity than the simple graphene/Si Schottky diode, where the noise equivalent power (NEP) of the G-FET obtained at 8.9 μW/cm² is 7 × 10⁻¹⁴ W/Hz^1/2. This amplification function is useful for practical applications. To analyze the photoresponse, we formulated the charge accumulation process at the n-Si/graphene interface, where the tunneling process through the SiO_x layer was considered in addition to the recombination of the accumulated holes and the electrons in the graphene at the surface states on SiO_x layer. The accumulated holes induce the Fermi level shift of graphene, which produces variation of the tunneling probability. The analytical framework proposed here is well described by the experimentally obtained results for both steady states and transient states. Moreover, it provides an effective means of analyzing charge carrier transport through the grapheme-based heterostructure through a thin tunneling barrier, which represents one path to achieving ultrathin opto-electronic devices in the future.

Methods

The device fabrication process was the following. First, metal electrodes consisting of Cr/Au (5 nm/30 nm) as a source and drain electrodes were fabricated on a Si substrate with a 300 nm-thick SiO₂ layer using conventional photolithography processing. The resistivity of the n-type Si substrate used in this experiment is 8 Ωcm. Unlike common back-gate G-FETs, we removed the SiO₂ layer (300 nm thick) between the electrodes using buffered HF. All processes were performed in air, so that the channel part of the graphene is contacted to the Si surface through a 2–5 nm thick native oxide layer. Subsequently, after a monolayer graphene was transferred onto the substrate using polymethyl methacrylate, it was trimmed using oxygen plasma etching to form the G-FET channel, where the graphene was synthesized using low-pressure chemical vapor deposition at 1000 °C using Cu foil as catalyst^35,36. The channel length and width are, respectively, 70 and 100 μm.

Author Contributions

S.K. and S.A. conceived and designed the experiments, led the research, and wrote the paper. K.T. and T.A. contributed to analysis of the data. All authors discussed the results and assisted in manuscript preparation.

Competing Interests

The authors declare no competing interests.