IMPROVING THE EFFICIENCY OF BIOMARKER IDENTIFICATION USING BIOLOGICAL KNOWLEDGE

Abstract

Identifying and validating biomarkers from high-throughput gene expression data is important for understanding and treating cancer. Typically, we identify candidate biomarkers as features that are differentially expressed between two or more classes of samples. Many feature selection metrics rely on ranking by some measure of differential expression. However, interpreting these results is difficult due to the large variety of existing algorithms and metrics, each of which may produce different results. Consequently, a feature ranking metric may work well on some datasets but perform considerably worse on others. We propose a method to choose an optimal feature ranking metric on an individual dataset basis. A metric is optimal if, for a particular dataset, it favorably ranks features that are known to be relevant biomarkers. Extensive knowledge of biomarker candidates is available in public databases and literature. Using this knowledge, we can choose a ranking metric that produces the most biologically meaningful results. In this paper, we first describe a framework for assessing the ability of a ranking metric to detect known relevant biomarkers. We then apply this method to clinical renal cancer microarray data to choose an optimal metric and identify several candidate biomarkers.

1. Introduction

The subjective nature of traditional medical techniques limits the accuracy of cancer subtype classification and, subsequently, the effectiveness of therapy. Clinicians visually examine cancer specimens to determine their subtypes before proposing treatment regimens. However, cancers with similar characteristics may behave very differently despite similar treatment conditions [1]. Because cancer is the result of genetic anomalies, emerging diagnostic research has primarily focused on genetic and proteomic expression. This research generally involves the use of high throughput technology (e.g. microarrays and mass spectrometry) to generate large amounts of genetic and proteomic expression data. We typically reduce this data using one of many analysis algorithms with the goal of identifying a subset of features (corresponding to genes or proteins) with high predictive accuracy [2-4]. We hope that these feature subsets will both enhance our understanding of the biological mechanisms as well as provide us with an accurate diagnostic system. When validated, we call these differentially expressed features biomarkers. Unfortunately, even the selection of a ranking metric is subjective, as different metrics may identify different subsets of features [5]. Feature ranking affects both the efficiency of identifying relevant genes and the accuracy of subsequent predictive models. We address this issue by presenting a method that uses existing biological knowledge to identify the best feature ranking metric for a particular gene expression dataset. The optimal metric maximizes the probability of correctly ranking differentially expressed and previously validated genes.

Despite numerous feature selection studies, there is still a lack of clinically validated and proven biomarkers for most cancers. Thus, the use of “correct” genes as knowledge for algorithm selection is subjective and we should choose these genes carefully. Sources of biological knowledge are abundant, but vary in terms of reliability. We consider a knowledge source to be reliable if genes (or the corresponding expressed proteins) from that source have been clinically validated as differentially expressed. The majority of knowledge is contained in the literature and roughly falls into four levels of reliability, adapted from a review of post-analysis validation methods by Chuaqui et al. [6]:

1. No biological validation. As the lowest level of reliability, this includes studies that develop feature selection algorithms and present the selected list of genes without a stringent interpretation of the biological results.

2. In silico validation. Also known as computational validation, these studies compare their feature selection results to the results of other studies. They may also identify Gene Ontology (GO) categories that are statistically overrepresented as a result of feature selection.

3. Same-sample validation. These studies validate their microarray experiments by performing additional assays on the same samples from which their microarrays were derived. These assays typically include quantitative real-time PCR (qRT-PCR) or northern analysis and serve to validate the technical reliability of the microarrays.

4. Independent or clinical validation. As the highest level of reliability, these studies validate the results of their microarray experiments using independent biological samples, usually from a clinical source. Independent validation ensures that the selected features are not a result of over-fitting. These validations often take the form of qRT-PCR and in situ hybridization (ISH) for RNA products, or immunohistochemistry (IHC) and western analysis for protein products.

Despite frequent disagreement between qRT-PCR and microarray results, qRT- PCR is the most common method for validation of differentially expressed genes. Genes with large fold-change in microarray data are consistently correlated with qRT-PCR while those with smaller fold change are more susceptible to technical variability [7]. The detection of differentially expressed genes is generally reproducible across several microarray platforms [8]. However, in light of a recent study illustrating the pervasiveness of technical artifacts in microarray data [9], we only consider a knowledge source reliable if it falls into category three or four.

Investigators have attempted to improve feature selection by using biological knowledge. Their knowledge sources often fall into category two of reliability, in silico validation, and include Gene Ontology and pathway databases, published literature, microarray repositories, and sequence information. Generally, these studies identify genes that cluster or correlate with genes from the knowledge sources [10-12]. Another study developed a theoretical framework to compare feature ranking metrics in the presence of control features [13]. However, this study also neglected to focus on the reliability of the control features. Indeed, the wealth of available information in the form of gene and protein interactions, functional annotation, and genetic and pathways can improve the results of data analysis [14]. Furthermore, microarray data analysis has shifted from purely data driven methods to methods that use additional knowledge, even in the feature selection process [14].

We develop a method to quantify the efficiency of detecting biomarkers by feature ranking. This method maximizes the biological relevance of feature ranking by choosing the best metric from a population of metrics. The chosen ranking metric is optimal with respect to knowledge obtained from reliable sources. We test the effectiveness of our method using clinical gene expression data. Results indicate that the choice of ranking metric significantly affects feature ranking, which, in turn, affects the efficiency of discovering and validating novel biomarkers.

2. Methods

2.1. Modeling Knowledge in Feature Selection

Throughout this paper, the term ‘feature set’ denotes a group of one or more features or genes that act in concert. A ‘sample’ refers to measurements of a feature set from a single microarray or molecular profile. The entire microarray sample contains l features while a feature set may contain p features (where p<<l). We represent samples for feature set i as jointly distributed random vectors, ${\overrightarrow{X}}^i\in {\Re }^p$, and labels, Yⁱ ∈ {0,1} . The class label, Y , indicates the clinical source of the microarray sample. In most cancer problems, Y = 1 indicates, for example, samples measured from patients with cancer and Y = 0 indicates samples from patients with no cancer. For a microarray dataset with N samples, feature set i for a particular dataset is the vector ${\overrightarrow{d}}_i=((y_1^i,{\stackrel{‒}{x}}_1^i),(y_2^i,{\stackrel{‒}{x}}_2^i),\dots ,(y_N^i,{\stackrel{‒}{x}}_N^i))$ from the random variable D , which represents all feature sets in a dataset. Each feature set is associated with a relevance variable, r_i , from the random variable R ∈ {0,1}. r_irepresents the biological relevance of the feature set and the reliability of the knowledge source. D and R are jointly distributed.

For each feature set, we assign a score that represents the predictive ability of that feature set:

$$A=h(\overrightarrow{D},\theta )$$ (1)

where $A\in \Re$ is a random variable and θ is a meta-parameter that characterizes the scoring function, or ranking metric. Although θ may represent the space of all ranking methods, we use a reduced set of wrapper- based methods in our simulations. Specifically, we use a support vector machine (SVM) classifier with the linear and radial basis kernels and estimate the classification accuracy of biomarkers using the 0.632 bootstrap [5, 15]. The SVM classifier depends on a cost parameter, C , which determines the penalty of misclassification. The radial basis kernel depends on , which is proportional to the complexity of the classifier. For the radial basis kernel, the pair of parameters, (C, γ ) , represents θ . We discretely vary C and γ over the log scale range of 0.1 to 10³ and 0.01 to 10⁵, respectively. For the linear kernel, only the single parameter, C , represents θ . We vary this parameter over the log scale range of 0.01 to 10².

In practice, a gene expression dataset will have N samples, each with l features. We separately examine m ( m can be different from l and include, for example, all pairs, triplets, or a subset of feature combinations) feature sets, corresponding to {d₁, d₂ ,..., d_m} and {r₁, r₂, ..., r_m}. From the mapping defined in eq. 1, we compute the set of values {α₁,α₂,...,α_m} where each α is an observation from A . Using a simple selection method, we can then conclude that the best feature sets and potential biomarkers are in the set

$$G=\{i:{\alpha }_i<\tau \}$$ (2)

where τ is a threshold.

We want to choose a θ that produces the most biologically relevant ranking of the m feature sets, {d₁, d₂ , ..., d_m}, with respect to a given set of knowledge. Assuming that lower scores are better, the best θ assigns scores such that α_i < α_j for r_i = 1 and r_j = 0 , i.e., feature set i is known to be more relevant than feature set j for this particular dataset. Although we may never know the relevance of all features in a dataset, we may infer from literature that the k feature sets, G_k = {g₁, g₂, ..., g_k } , are relevant, where k << m . This implies that the elements of the set{α_i:i∈G_k} should generally be smaller than those of {α_j:j∉G_k}. If the knowledge is reliable, we want to choose a θ that maximizes the probability that the score of a feature set from G_k probability is less than that of a feature set that is not from G_k . Explicitly, this

$$P({\alpha }_i<{\alpha }_j\mid \theta )$$ (3)

for i ∈ G_k and j ∉ G_k. The estimated optimal ranking method is

$$\widehat{\theta }=\arg {\max }_{\theta }P({\alpha }_i<{\alpha }_j\mid \theta ),$$ (4)

keeping in mind that $\widehat{\theta }$ is only optimal, or maximizes the probability, with respect to the given knowledge set. For m feature sets, k of which are in our knowledge set, G_k , we can empirically approximate the probability of eq. 3 with

$$P({\alpha }_i<{\alpha }_j\mid \theta )=\frac{1}{k(m-k)}\sum _{i\in G_k}\sum _{j\notin G}I({\alpha }_i<{\alpha }_j)$$ (5)

where I (x) evaluates to one when x is true and zero when x is false. Eq. 5 is equivalent to computing the area under an ROC curve (AUC) for classifying feature sets as either relevant or irrelevant [13].

2.2. Iteratively Updating Knowledge

It may be difficult to compile a comprehensive list of knowledge from literature and independent validation. Consequently, we can expect that some feature sets that are not in our knowledge set,j∉G_k, are, in fact, relevant biomarkers. If V is the set of all relevant biomarkers, regardless of whether their relevance is known, we define the knowledge update function, S , as

$$G_{k+1}=S_{\widehat{\theta }}\left(G_k\right)=\{\{G_k,\arg {\min }_i{\alpha }_i\}:i\in V,i\notin G_k\}.$$ (6)

This function adds to G_k a relevant biomarker with the best rank according to the estimated optimal metric, $\widehat{\theta }$. Of course, a feature set is known to be in the set V only after performing a validation procedure such as qRT-PCR.

If we know all feature sets in V , we can quantify any improvement in efficiency due to optimization of the ranking metric. Using bootstrap resampling, we randomly and repeatedly partition the feature sets in V into a group of known relevant feature sets (training) and a group of unknown relevant feature sets (testing). If there are K elements in V , we randomly select K elements with replacement, resulting in K * (K * <K) unique elements for the testing set. We use the group of K - K * known relevant feature sets to optimize the ranking metric, then iteratively detect feature sets from the unknown set of K * features and update our knowledge using eq. 6. Every validation test requires a finite amount of time and resources. Plotting the fraction of correctly validated biomarkers (y-axis) vs. total validation time (x- axis), reveals that higher detection efficiency corresponds to a larger area under this curve. This curve is similar to a ROC curve, so we also call the area under this curve the AUC. We repeat this bootstrap sampling of feature sets 100 times in order to compute the significance of the differences among three conditions: optimal metric selection, sub-optimal metric selection, and sub-optimal initial knowledge. For the sub-optimal metric selection condition, we use correct initial knowledge selected from V via bootstrap, but use a modified equation to choose $\widehat{\theta }$ with median AUC:

$$\widehat{\theta }=\arg media{n}_{\theta }P({\alpha }_i<{\alpha }_j\mid \theta ).$$ (7)

Selection of a ranking metric with median AUC represents the common practice of arbitrarily selecting a metric with no regard for biological relevance and efficiency. This median AUC algorithm also serves as a reference point for assessing the potential improvement of efficiency when using the optimal algorithm.

For the sub-optimal initial knowledge condition, we begin the simulation with incorrect knowledge selected via bootstrap and use eq. 4 to optimize the ranking algorithm before updating the current knowledge set. We expect the average AUC of the optimal selection condition to be higher than that of both of the sub-optimal conditions. Figure 1 illustrates this process.

Figure 1.

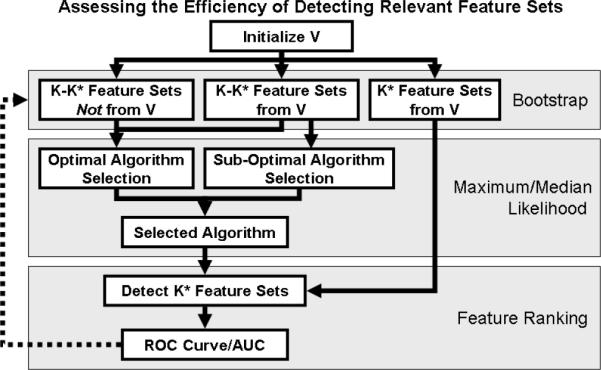
Quantifying the efficiency of detecting relevant feature sets. For clinical data, we define V as the set of K known differentially expressed feature sets. Using bootstrap cross validation, we partition V into K* and K-K* samples. K* is the number of unique samples after sampling from V K times with replacement. We optimize the ranking algorithm using K-K* feature sets and assess the algorithm's efficiency in detecting the remaining K* feature sets. For each of the three conditions— optimal metric selection, sub-optimal metric selection, and sub-optimal initial knowledge—we perform this bootstrap sampling 100 times in order to compute the significance of any differences between mean AUC values.

To determine whether the optimization procedure is over-fitting to the knowledge set, we conduct additional tests using randomly selected knowledge sets. If over-fitting is occurring, results of the optimal, suboptimal, and suboptimal knowledge tests for randomly selected knowledge should be similar to those of the true knowledge set.

2.3. Microarray Data Analysis and qRT-PCR Validation

We examine two clinical case studies using renal tumor microarray datasets. The first dataset, from a study by Schuetz et al., uses Affymetrix microarrays (HG-Focus, 8793 probesets) to profile samples from three subtypes of renal tumors: 13 clear cell (CC) renal cell carcinoma (RCC), 4 chromophobe (CHR) RCC, and 3 oncocytoma (ONC, benign) [2]. The second dataset, from a study by Jones et al., uses a different model of Affymetrix microarrays (HG-U133A, 22283 probesets reduced to 8793 that are common to HG-Focus) to examine similar renal tumor subtypes with 32 CC, 6 CHR, and 12 ONC samples [16]. We are interested in biomarkers that differentiate the CC class from the combined group of ONC and CHR.

Using literature, we identify genes that have been validated (via qRT-PCR or IHC) as differentially expressed between the CC and ONC/CHR subtypes. We then validate an additional 94 genes using qRT-PCR (using RNA from 34 CC and 18 CHR tissue samples). These 94 genes were selected by a renal cancer pathologist based on his knowledge and previous research. Only some of the 94 genes assayed with qRT-PCR are differentially expressed as assessed by a linear SVM with classification error estimated using 0.632 bootstrap. Genes measured with qRT-PCR are categorized as differentially expressed if the estimated classification error is less than 10%. Using the set of knowledge from both literature and qRT-PCR validation, we examine the efficiency of detecting these biomarkers by optimizing the ranking metric under various conditions, as illustrated in figure 1.

3. Results and Discussion

As described in the methods, we identify five genes from literature that are differentially expressed between the CC and ONC/CHR renal tumor subtypes (table 1). Each of these genes had been validated using either qRT-PCR or IHC. Additionally, we validate several other potential biomarkers using qRT-PCR and select genes with estimated classification errors of less than 10% (table 2).

Table 1.

Genes validated as differentially expressed between CC and ONC/CHR renal rumor subtypes from various knowledge sources.

Gene Symbol	Knowledge Source	Validation Method
CA9	Chen et al., Clin Cancer Res, 2005	qRT-PCR
CLCNKB	Chen et al., Clin Cancer Res, 2005	qRT-PCR
DEFB1	Schuetz et al., J Mol Diagn, 2004	qRT-PCR, IHC
LRP2	Schuetz et al., J Mol Diagn, 2004	qRT-PCR, IHC
PVALB	Chen et al., Clin Cancer Res, 2005	qRT-PCR

Table 2.

Genes that we validated with qRT-PCR. These genes have estimated classification errors of less than 10% as assessed by a linear SVM classifier using 0.632 bootstrap estimation.

Gene Symbol	Error	Gene Svmbol	Error
STC1	2.43E-05	COX5A	0.0394058
SLC25A4	0.00186696	BAG1	0.0548365
CFTR	0.00279081	LY6E	0.0596081
PDHA1	0.0133316	CD99	0.0600892
PFKM	0.0279739	AKAP12	0.0624445
NNMT	0.0289622	ACAT1	0.0687972
CP	0.0300157	SPTBN2	0.077287
CFB	0.0387219	GOT1	0.0784855

Combining all knowledge from both literature and qRT-PCR validation, we examine the effect of optimizing the feature ranking metric using the method illustrated in figure 1. Box plots of the 100 iterations for each of the three tests indicate that optimal selection outperforms sub-optimal selection (figure 2, left column). The comparison of optimal to suboptimal metrics may seem to always favor the optimal metric. However, the optimal metric is not always a simple linear classifier. In fact, during the iterative gene detection process, θ changes frequently as V is updated. Moreover, suboptimal selection may represent the common practice of arbitrarily selecting ranking metrics with no regard to their potential disadvantages for particular datasets. The box plots represent the median and quartiles of the AUC values for each of the 100 iterations. Correspondingly, the ROC curves also indicate that the optimal selection method improves the efficiency of biomarker detection (figure 2, right column).

Figure 2.

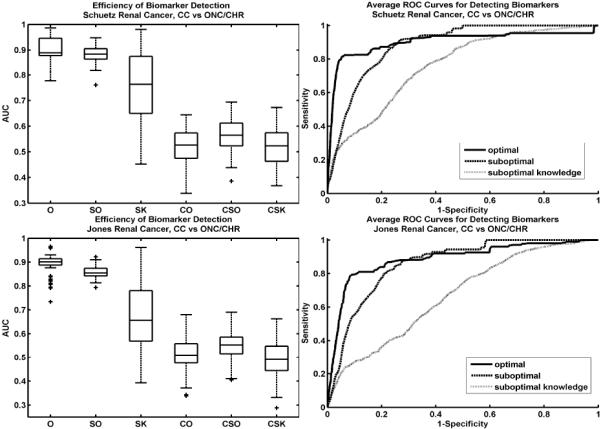
Box plots of AUC areas over 100 iterations for each test (left). AUCs for the optimal test (O) are higher than both the sub-optimal (SO) and sub-optimal knowledge (SK) tests (differences are statistically significant with p-values very close to 0). The control tests, using randomly selected knowledge indicate that optimizing the ranking metric does not over-fit (CO=control optimal, CSO=control suboptimal, CSK=control suboptimal knowledge). Average ROC curves for each test, illustrate the differences in biomarker detection efficiency (right). The ROC for the optimal metric test (solid line) indicates more accurate biomarker detection for both the Schuetz (top row) and Jones (bottom row) renal cancer datasets.

For the Schuetz data (figure 2, top row), the performance difference between the optimal and suboptimal ranking metrics seems small according to the box plots. However, the ROC curve of the optimal metric initially rises much more quickly compared to that of the suboptimal. The region of low specificity boosts the performance of the suboptimal metric. However, this region should be neglected when assessing performance since the number of false positives at this point is very high. Validation procedures would likely consider only the biomarkers detected in the high specificity region. Results are similar for the Jones data (figure 2, bottom row).

The high variance of the suboptimal initial knowledge condition indicates that optimization of the ranking metric is sensitive to the initial conditions. Some of the randomly selected initial knowledge may, in fact, be differentially expressed, resulting in good performance. However, these random initial knowledge sets are more likely to be irrelevant. Thus, box plots for this condition illustrate this mixture of knowledge quality. These results stress the importance of the quality of biomarker knowledge.

The control tests using random knowledge sets for V show that our method does not over-fit to the knowledge (figure 2, box plots CO, CSO, and CSK). None of the algorithms considered in our space of θ are able to favorably rank these randomly selected genes. AUCs of these control tests are close to 0.5 as expected for random classification.

Using all knowledge from literature and the first round of qRT-PCR, we optimize the ranking metric and select the top genes that have not been previously validated and that have estimated classification errors of less than 5% (table 3). We can link a few of these genes directly to previous literature pertaining to renal cancer. For example, CXCR4 has been linked to kidney cancer. Using qRT-PCR, Schrader et al. shows that this gene is over-expressed in kidney cancer tissue compared to normal kidney tissue [17]. IGFBP3 and KLF10 has also been linked to renal cell carcinoma [18, 19]. Validation of these genes using qRT-PCR may yield additional knowledge to iteratively refine the biomarker selection process. However, since we want to primarily focus on the methodology here, we reserve the actual validation of these results for a future study.

Table 3.

Proposed list of genes for further qRT-PCR validation.

Gene Symbol	Error	Gene Symbol	Error
ACLY	0	PCCB	0.03274
CXCR4	0.013907	TMSB10	0.034201
C4A /// C4B	0.0187	HCLS1	0.034415
FLNA	0.019903	ACTA2	0.039398
PMP22	0.023798	IGFBP3	0.040989
PFKFB3	0.026506	NFKBIA	0.042332
KLF10	0.027801	CD44	0.049095
PRG1	0.03003	IER3	0.049571
LGALS1	0.030617

4. Conclusion

We have shown that biomarker identification by feature ranking benefits from knowledge integration at key points. Using this knowledge—whether from clinical observations, laboratory experiments, or existing literature—we can intelligently choose an optimal ranking metric for a specific gene expression dataset. The use of an optimal metric for ranking and identifying novel biomarkers reduces the number of false discoveries, increases the number of true discoveries, reduces the required time for validation, and increases the overall efficiency of the process.

The results of our simulations indicate that knowledge integration improves biomarker selection for clinical microarray data. Although this study assumes independent gene expression, the method is general and we can use it to rank combinatorial gene expression data as well. Furthermore, we test this method using only a limited set of wrapper-based feature ranking metrics. However, it is easily expandable to encompass a variety of metrics, including the commonly used filter methods such as t-tests and fold change. We hope that the proposed method will impact biomarker identification practices and improve the effectiveness of resulting clinical applications.