Abstract
Purpose
To compare the performance of OKULIX ray-tracing software with SRK-T and Hoffer Q formula in intraocular lens (IOL) power calculation in patients presenting with cataract.
Methods
In this prospective study, 104 eyes of 104 patients with cataract who underwent phacoemulsification and IOL implantation were recruited. Three IOL brands were used and for all eyes, IOL power calculation was performed using SRK-T, Hoffer Q formula and also OKULIX ray-tracing software. For all patients, axial length and keratometry data was obtained with IOLMaster 500 device and IOL power was determined using Hoffer Q and SRK-T formula. The IOL powers were also calculated using the OKULIX ray-tracing software combined with CASIA AS-OCT and IOLMaster 500 device. Optically measured axial length of eyes were inserted to OKULIX software from IOLMaster 500 device, and anterior and posterior tomographic and corneal pachymetry data was imported from CASIA AS-OCT into the OKULIX.
The performance of each calculation methods was measured by subtracting the predicted postoperative refraction from the postoperative manifest refraction spherical equivalent (MRSE). For each of the 3 methods, the mean absolute prediction error was determined, too.
Results
The mean value absolute prediction error by OKULIX, SRK-T and Hoffer Q formulas, respectively, were 0.42 (±0.03), 0.36 (±0.02) and 0.37 (±0.02). The mean absolute prediction error by OKULIX had no significant difference between three IOL groups (P = 0.96), and it was confirmed that there was no meaningful statistically difference in mean absolute prediction error between the OKULIX, SRK-T and Hoffer Q formula. (P = 0.25). Also in each group of implanted IOLs, all three formulas worked with the same accuracy. The prediction error using OKULIX were within ±0.50 diopter in 63.5% of eyes and within ±1.00 diopter in 94.2% of eyes.
Conclusion
OKULIX ray-tracing IOL power measurements provides reliable and satisfactory postoperative results, which are comparable to other 3rd generation formulas of SRK-T and Hoffer Q.
Keywords: Ray-tracing, IOL power calculation, OKULIX
Introduction
Accurate intraocular lens (IOL) power determination is an important factor to achieve the ideal uncorrected distance visual acuity and patient satisfaction after cataract surgery.
In the past, IOL power calculations have been performed with analytical formulas based on Gaussian optics,1, 2, 3, 4, 5, 6 which is an approximation in which the sine function in Snell's law is approximated by the argument: sin(α) ≃ α.7
Gaussian optics is so called paraxial optics or thin lens method because this is valid for paraxial rays only, so it is a poor approximation of the real pseudophakic human eye.8
In the 1980, regression formulas were mostly used because of their simplicity to use like; Sanders, Retzlaff, Kraff (SRK) I and II. In the 1990s, these formulas were replaced by more accurate, newer formulas like; Haigis, Hoffer Q, SRK-T, Holladay 1, 2 and Oslen. Most of the advances in these new generation formulas concerned improved methods of estimating the effective lens position (ELP).
Despite these advancing new formulas and precision surgical improved equipment and techniques, refractive surprise after uneventful cataract surgery is still a challenge, especially in eyes with abnormal axial length (short or long axial length)9, 10 previous corneal refractive surgery or corneal pathologies like keratoconus.11
Ray-tracing, the gold standard in lens and optical system design, is a straightforward and promising approach in IOL power calculation.8, 12 Indeed the only method in which the prediction error can be kept as small as necessary is numerical tracing.13 This calculation does not contain any approximation.8
It has been shown that the optics of pseudophakic eye can be accurately described using exact ray-tracing technique.14
OKULIX (Tomey Corporation) is a numerical ray-tracing software, which is developed at the University of Mainz, Germany, and has been explained in detail by Preussner et al.8, 13, 15 It is able to determine the monochromatic optical capacities of pseudophakic, human eye.12 In this technique, single light rays limited only by pupillary size are evaluated. Rays undergo different refractions on different surfaces, where the refractive index changes (intravitreal, lens, aqueous humor, and cornea). The shape of surface is mainly described by their central curvature radii.8 Axial length, IOL curvature radii, IOL central thickness, asphericity and refractive index, as well as corneal topography measurements [anterior/posterior corneal keratometric values and central corneal thickness (CCT)], are also used in OKULIX software for more precise IOL power calculation.
Anterior segment optical coherence tomography (AS-OCT) can measure the entire shape of anterior/posterior corneal surfaces with a near-infrared light.16 It has been found that AS-OCT based topography and CCT data agree well with conventional pachymetric measurements.17, 18 These data can be transferred to OKULIX software for IOL calculations. The curvature, central thickness, refractive index, and the asphericity of the target IOL were retrieved from a database in the software.
The aim of this study was to determine the performance of the IOL power calculation using OKULIX, in cataractous eyes by comparing its prediction error with other routine formulas; Hoffer Q19 and SRK-T.20
Methods
This prospective study included 104 eyes of 104 Iranian patients (55 male and 49 female, mean age 60.91 ± 14.90 years; range from 6 to 81 years) candidate for cataract surgery and IOL implantation from January 2015 to April 2016.
Our predetermined exclusion criteria were eyes with axial length higher than 26 mm or less than 21 mm or measured with contact applanation or immersion ultrasound A-scan, cases with preoperative or postoperative astigmatism greater than 2 diopters, keratoconus, previous trauma or surgery (such as laser refractive surgery and corneal transplantation). Eyes with complicated cataract surgery (such as posterior capsule tear with or without vitreous loss, anterior capsule extended tear, sulcus or anterior chamber positioned IOL, corneal suturing) were excluded, too. Because of compounding (correlation) of data with bilateral eyes, we have included only one eye from each bilateral cataract surgery.
Preoperative examination
For all patients, axial length and keratometry data was obtained with IOLMaster 500 device (Carl Zeiss Meditec AG, Jena, Germany), and IOL power was measured using Hoffer Q and SRK-T formulas.19, 20 These two formulas were included in IOLMaster 500 device and IOLs A-constant for SRK-T formula and personalized anterior chamber depth (PACD) for Hoffer Q formula were optimized from User Group Laser Interference Biometry (ULIB) online table (as of Oct 31, 2016) available at: www.ocusoft.de. Target refraction was set to zero.
The IOL powers were also calculated using the OKULIX ray-tracing software combined with CASIA AS-OCT (SS-1000, TOMEY Corp). This device is a non-contact, three dimensional system based on the principle of Swept Source OCT. Its scanning speed is 30,000 A-scan/second with radial scan direction (16 images) and 512 lines A-scan per image sampling. The anterior and posterior tomographic and corneal pachymetry data was imported into the OKULIX. The predicted postoperative refraction was chosen for best focus for the default pupil diameter of 2.5 mm. Optically measured axial length of eyes were inserted to OKULIX software from IOLMaster 500 device. Target refraction was set to zero too.
IOLs brands which were implanted are alphabetically listed below:
-
1
Alcon; Acrysoft IQ: SN60WF
-
2
Bausch and Lomb: enVista MX60
-
3
HOYA: NY-60/250/251 isert.
Surgical technique
All cataract surgeries were done by the same surgeon (M.G.). The cataract was removed by phacoemulsification through clear cornea 3.2 mm incision, under topical or general anesthesia. An acrylic monofocal hydrophobic IOL was implanted in the capsular bag. Four surgeries were complicated with posterior capsular tear and vitreous loss, and these eyes were excluded from the study.
Postoperative examination
All the patients were examined postoperatively at 1 day, 1 week, and 1 month. Postoperative final manifest refraction spherical equivalent (MRSE) was obtained at 3 month after surgery.
Statistical analysis
The prediction error was calculated by subtracting the predicted postoperative refraction from the postoperative MRSE. For each of the 3 methods, the arithmetic mean prediction error as well as mean absolute prediction error was determined. We also calculated the percentage of eyes within ±0.5 and ±1.0 diopter of prediction error for every method, too.
Statistically, the analysis was performed using the one-way analysis of variance (ANOVA) and repeated measures ANOVA test for parametric data and the Friedman's test for non-parametric data. The SPSS software Statistics version 20 (IBM, Chicago, IL, USA) was used, and P-value below 0.05 was considered a statistically significant difference.
The study protocol adhered to the tenets of the Declaration of Helsinki and was approved by the ethics committee. All patients provided written informed consent.
Results
The mean power of implanted IOL was +20.71 ± 3.00 diopter and ranged from +9.50 to +29.5 diopter.
The optically measured axial length of operated eyes ranged from 21.13 to 25.04 mm and mean axial length was 23.22 ± 0.97 mm.
The mean power of implanted IOLs and the mean axial length of eyes in all three IOL groups were not statistically different (P = 0.22 and P = 0.71, respectively).
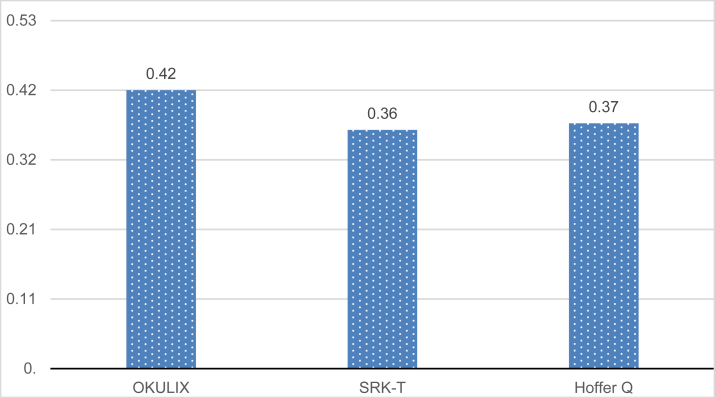
The mean absolute prediction error of OKULIX, SRK-T, and Hoffer methods of IOL power calculation for each brand of IOL, and generally is shown in Table 1 and Fig. 1, respectively.
Table 1.
Mean absolute prediction error (MAPE) of three formulas in each intraocular lens (IOL) brands.
| IOL brand formula | HOYA: NY-60/250/251 MAPE ± SE |
Bausch & Lomb: enVista MX60 MAPE ± SE |
Alcon: SN60WF MAPE ± SE |
P-value |
|---|---|---|---|---|
| OKULIX | 0.43 ± 0.07 | 0.43 ± 0.05 | 0.41 ± 0.05 | 0.96 |
| SRK-T | 0.34 ± 0.03 | 0.32 ± 0.04 | 0.40 ± 0.05 | 0.44 |
| Hoffer Q | 0.33 ± 0.03 | 0.39 ± 0.04 | 0.41 ± 0.06 | 0.50 |
| P-value | 0.26 | 0.30 | 0.99 |
IOL: Intraocular lens.
MAPE: Mean absolute prediction error.
SE: standard error.
Fig. 1.
Mean absolute prediction error (MAPE) of each intraocular lens (IOL) power calculation formula, generally (without considering the kind of IOL brand) P = 0.25.
There was no statistical difference in mean absolute prediction error of OKULIX, SRK-T or Hoffer Q formula for each kind of implanted IOL brand (P-values: 0.96, 0.44 and 0.50, respectively) [Table 1].
It was shown that in HOYA: NY-60/250/251, Bausch and Lomb: enVista MX60 or Alcon; Acrysoft IQ: SN60WF groups, there was no statistically significant difference in mean absolute prediction error of all three used formula (P-values: 0.26, 0.30 and 0.99, respectively) [Table 1].
Without considering the type of IOL brand implanted in operated eyes, it was confirmed that there was no meaningful statistical difference in mean absolute prediction error between the OKULIX, SRK-T and Hoffer Q formula (P = 0.25) [Fig. 1].
In other words, all of these three formulas work with the same accuracy generally or separately in each group of IOLs.
The frequency of percentage of eyes within ±0.50 diopter, and within ±1.00 diopter of IOL power prediction error is shown in Table 2.
Table 2.
The frequency of eyes within ±0.50 and ±1.00 diopter prediction error of intraocular lens (IOL) power calculation in each formula group.
| Percentage of eyes within ±0.5 diopter of IOL power prediction error | Percentage of eyes within ±1.00 diopter of IOL power prediction error | |
|---|---|---|
| OKULIX | 63.5% | 94.2% |
| SRK-T | 70.2% | 97.1% |
| Hoffer Q | 76.9% | 95.2% |
| P-value | 0.06 | 0.53 |
IOL: Intraocular lens.
The Friedman test demonstrated that the percentage of eyes within ±0.50 diopter of IOL power prediction error was not statistically different between the IOL power formulas (P = 0.06) [Table 2].
This test also demonstrated that the percentage of eyes within ±1.00 diopter of IOL power prediction error was not statistically different between IOL power formulas (P = 0.53) [Table 2].
Discussion
There are two main methods for IOL power calculation in cataract surgery: the thin-lens formula and newer method, ray-tracing based calculations.12
Ray-tracing approach regards a lens as original thick lens with thickness and surface. If the surface data, thickness, and refractive index of each lens are known, optical rays can be traced from object to macula or vice versa. In this method, exact Snell's law is used to calculate the trace of optical rays passing through each surface. In the more complex and accurate individual ray-tracing approach, not only are the surface radii, refractive indices, thickness data of optical pathway lenses included, but also detailed anterior/posterior topography and pachymetric data, and physical properties of desired IOL is imported and taken into account for calculations.12
There are several advantages of the exact ray-tracing method in IOL power calculation rather than conventional formulas:
-
1
The ray-tracing method uses exact Snell's law, which adopts no assumption in the calculation.12 There, it can provide the real simulation of the human eye.8, 21
-
2
The ray-tracing calculation using corneal topography may be more accurate in corneal power calculation because more detailed corneal surface data are imported into the ray-tracing software.21
-
3
It has been shown that ray-tracing based IOL power calculations accuracy in normal cataractous eyes was unaffected by corneal asphericity.22
OKULIX is a program package which calculates single rays exactly and suited for IOL calculation.8, 10, 15, 23, 24 Axial length is entered to this software from ultrasonic or optical measurement devices, which will be changed to optical axial length in this program.
The OKULIX program package includes a compilation of the mostly implanted IOL of the market leaders. For the calculation inside this software, the IOL is physically characterized by curvature radii, the refractive index, the asphericity and the central thickness, which makes the calculation more accurate than conventional formula.23
Like other formulas, OKULIX ray-tracing software require an estimation of the distance at which the principle plane of the IOL will be placed behind the cornea after surgery (known as estimated lens position, or ELP). For more accurate estimation of ELP, OKULIX software uses an algorithm which contains axial length, manufactures IOL parameters and mean postoperative anterior chamber depth values of IOL-type; extracted from A-constant SRK-T formula.25 When position and thickness of the crystalline lens are known from measurements, these data can be used in OKULIX to further improve the accuracy of ELP.
Topographic and pachymetric data can be transferred to OKULIX software from variety of measurement devices like Haag-Streit-Lenstar, Oculus Pentacam, Tracy iTrace, Zimer Galilei G6 or Tomey CASIA OCT topography (as it used in our study).
Exploitation of this topography actually measured data, by OKULIX makes IOL power calculation more accurately in cases of IOL power calculation for Toric IOLs or after corneal refractive surgery.26, 27
In this prospective case series study, we have shown the performance of OKULIX software ray-tracing IOL power calculation was not significantly different compared with the other two routine and reliable IOL power calculation formulas, SRK-T and Hoffer Q.
In current study, three brands of posterior chamber IOLs; HOYA: NY-60/250/251, isert, Bausch and Lomb: enVista MX60 and Alcon; Acrysoft IQ: SN60WF were used in cataractous eyes, with no statistically significant different mean IOL power and axial length values between these lenses (P = 0.22 and P = 0.71, respectively).
It has been shown that the Hoffer Q performed best for axial lengths less than 21.00 and the SRK-T for axial lengths of 27.00 mm or longer.24 The accuracy and mean absolute prediction error of OKULIX ray-tracing software had no difference in all IOLs, like the other SRK-T and Hoffer Q formula. On the other hand, we have shown that in each group of implanted IOLs, all three formulas worked with the same accuracy.
Our research also reported that the percentage of eyes within ±0.50 and ±1.00 diopter of IOL power prediction error was statistically the same between the three methods of IOL power calculation. These results agreed with the results of the study conducted by Preussner et al. for comparing the accuracy of OKULIX and other calculation formulae in large patient collectives, including eyes with extreme axial lengths.25
In summary, we concluded that the new ray-tracing based IOL power calculation software OKULIX can be considered an accurate and reliable method of IOL power calculation in routine practice, especially considering its stable accuracy in different brands of IOLs and variable axial length of operated eyes.
The limitations of our study were the small sample size, limited range of axial length that did not include very short or very long eyes, and not including the Toric or multifocal IOLs. Considering the cost and dependency of OKULIX software to other measuring tools like IOLMaster and topographic devices, this method of IOL power calculation does not seem to be convenient, nor cost benefit, especially regarding that there is no superiority in its accuracy, compared to the other routine accessible formulas like SRK-T or Hoffer Q.
The accuracy, reliability, and prediction error of OKULIX IOL power calculation method should be evaluated in more challenging IOL power calculations issues like after laser corneal refractive surgery, post-radial keratotomies, keratoconus eyes, or other corneal pathologies that make accurate, unsurprising IOL power calculation difficult.
Acknowledgments
Authors are thankful to Mr. Hassanzadeh, who helped us in data analysis and final conclusion.
Footnotes
Financial disclosure: None of the authors has a financial or proprietary interest in any material or method mentioned.
Conflict of interest: None.
Peer review under responsibility of the Iranian Society of Ophthalmology.
References
- 1.Barret G.D. An improved universal theoretical formula for intraocular lens power prediction. J Cataract Refract Surg. 1993;19(6):713–720. doi: 10.1016/s0886-3350(13)80339-2. [DOI] [PubMed] [Google Scholar]
- 2.Frings A., Hold V., Steinwender G., El-Shabrawi Y., Ardjomand N. Use of true net power in intraocular lens power calculations in eyes with prior myopic laser refractive surgery. Int Ophthalmol. 2014;34(5):1091–1096. doi: 10.1007/s10792-014-9916-x. [DOI] [PubMed] [Google Scholar]
- 3.Olsen T., Corydon L., Gimbel H. Intraocular lens power calculation with an improved anterior chamber depth prediction algorithm. J Cataract Refract Surg. 1995;21:313–319. doi: 10.1016/s0886-3350(13)80140-x. [DOI] [PubMed] [Google Scholar]
- 4.Haigis W. Challenges and approaches in modern biometry and IOL calculation. Saudi J Ophthalmol. 2012;26(1):7–12. doi: 10.1016/j.sjopt.2011.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Camps V.J., Piñero D.P., de Fez D., Mateo V. Minimizing the IOL power error induced by keratometric power. Optom Vis Sci. 2013;90(7):639–649. doi: 10.1097/OPX.0b013e3182972f50. [DOI] [PubMed] [Google Scholar]
- 6.Oslen T. Theoretical approach to intraocular lens calculation using Gaussian optics. J Cataract Refract Surg. 1987;13(2):141–145. doi: 10.1016/s0886-3350(87)80128-1. [DOI] [PubMed] [Google Scholar]
- 7.Einighammer J., Oltrup T., Bende T., Jean B. Calculating intraocular lens geometry by real ray tracing. J Refract Surg. 2007;23(4):393–404. doi: 10.3928/1081-597X-20070401-12. [DOI] [PubMed] [Google Scholar]
- 8.Preussner P.R., Wahl J., Lahdo H., Dick B., Findl O. Ray tracing for intraocular lens calculation. J Cataract Refract Surg. 2002;28(8):1412–1419. doi: 10.1016/s0886-3350(01)01346-3. [DOI] [PubMed] [Google Scholar]
- 9.Shammas H.J. 1st ed. Slack; Thorofare, NJ: 2004. Intraocular Lens Power Calculations; pp. 15–24. [Google Scholar]
- 10.Preussner P.R., Olsen T., Hoffmann P., Findl O. Intraocular lens calculation accuracy limits in normal eyes. J Cataract Refract Surg. 2008;34(5):802–808. doi: 10.1016/j.jcrs.2008.01.015. [DOI] [PubMed] [Google Scholar]
- 11.Gimbel H.V., Sun R. Accuracy and predictability of intraocular lens power calculation after laser in situ keratomileusis. J Cataract Refract Surg. 2001;27(4):571–576. doi: 10.1016/s0886-3350(00)00795-1. [DOI] [PubMed] [Google Scholar]
- 12.Jin H., Rabsilber T., Ehmer A. Comparison of ray-tracing method and thin-lens formula in intraocular lens power calculations. J Cataract Refract Surg. 2009;35(4):650–662. doi: 10.1016/j.jcrs.2008.12.015. [DOI] [PubMed] [Google Scholar]
- 13.Preussner P.R., Wahl J. Konsistente numberische Berechnung der Optik des pseudophaken Auges. Ophthalmologe. 2000;97:126–141. doi: 10.1007/s003470050023. [DOI] [PubMed] [Google Scholar]
- 14.Oslen T., Funding M. Ray-tracing analysis of intraocular lens power in situ. J Cataract Refract Surg. 2012;38:641–647. doi: 10.1016/j.jcrs.2011.10.035. [DOI] [PubMed] [Google Scholar]
- 15.Preussner P.R., Wahl J., Lahdo H., Findl O. Consistent IOL-calculation. Ophthalmologe. 2001;98:300–304. doi: 10.1007/s003470170166. [DOI] [PubMed] [Google Scholar]
- 16.Salim S. The role of anterior segment optical coherence tomography in glaucoma. J Ophthalmol. 2012;2012:476801. doi: 10.1155/2012/476801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tang M., Li Y., Avila M., Huang D. Measuring total corneal power before and after laser in situ keratomileusis with high-speed optical coherence tomography. J Cataract Refract Surg. 2006;32:1843–1850. doi: 10.1016/j.jcrs.2006.04.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Nakagawa T., Maeda N., Higashiura R., Hori Y., Inoue T., Nishida K. Corneal topographic analysis in patients with kerato-conus using 3-dimensional anterior segment optical coherence tomography. J Cataract Refract Surg. 2011;37:1871–1878. doi: 10.1016/j.jcrs.2011.05.027. [DOI] [PubMed] [Google Scholar]
- 19.Hoffer K.J. The Hoffer Q formula: a comparison of theoretic and regression formulas'. J Cataract Refract Surg. 1993;19(6):700–712. doi: 10.1016/s0886-3350(13)80338-0. [DOI] [PubMed] [Google Scholar]
- 20.Retzlasff A., Sanders D.R., Kraff M.C. Development of SRK/T intraocular lens implant power calculation formula. J Cataract Refract Surg. 1990;16(3):333–340. doi: 10.1016/s0886-3350(13)80705-5. [DOI] [PubMed] [Google Scholar]
- 21.Preussner P.R., Wahl J., Weitzel D. Topography-based intraocular lens power selection. J Cataract Refract Surg. 2005;31:525–533. doi: 10.1016/j.jcrs.2004.09.016. [DOI] [PubMed] [Google Scholar]
- 22.Mine K., Otani S., Mori Y. [Comparison of intraocular lens power calculation OKULIX using topographic data and ray tracing method with the SRK/T formula] Atarashii Ganka. 2011;28(1):131–134. [Japanese] [Google Scholar]
- 23.Hoffmann P.C., Wahl J., Hütz W.W., Preußner P.R. A ray tracing approach to calculate toric intraocular lenses. J Refract Surg. 2013;29(6):402–408. doi: 10.3928/1081597X-20130515-04. [DOI] [PubMed] [Google Scholar]
- 24.Aristodemou P., Knox Cartwright N.E., Sparrow J.M., Johnston R.L. Formula choice: Hoffer Q, Holladay 1, or SRK/T and refractive outcomes in 8108 eyes after cataract surgery with biometry by partial coherence interferometry. J Cataract Refract Surg. 2011;37(1):63–71. doi: 10.1016/j.jcrs.2010.07.032. [DOI] [PubMed] [Google Scholar]
- 25.Preussner P.R., Hoffmann P., Petermeier K. Comparison between ray tracing and 3rd-generation IOL calculation formulae. Klin Monbl Augenheilkd. 2009;226(2):83–89. doi: 10.1055/s-2008-1027966. [DOI] [PubMed] [Google Scholar]
- 26.Rabsilber T.M., Reuland A.J., Holzer M.P., Auffarth G.U. Intraocular lens power calculation using ray tracing following excimer laser surgery. Eye (Lond) 2007;21(6):697–701. doi: 10.1038/sj.eye.6702300. [DOI] [PubMed] [Google Scholar]
- 27.Saiki M., Negishi K., Kato K., Torii H., Dogru M., Tsubota K. Ray tracing for intraocular lens power calculation after corneal excimer laser surgery. Jpn J Ophthalmol. 2014;58(3):267–281. doi: 10.1007/s10384-014-0304-x. [DOI] [PubMed] [Google Scholar]