Update on the State of the Science for Analytical Methods for Gene-Environment Interactions

Abstract

The analysis of gene-environment interaction (G×E) may hold the key for further understanding the etiology of many complex traits. The current availability of high-volume genetic data, the wide range in types of environmental data that can be measured, and the formation of consortiums of multiple studies provide new opportunities to identify G×E but also new analytical challenges. In this article, we summarize several statistical approaches that can be used to test for G×E in a genome-wide association study. These include traditional models of G×E in a case-control or quantitative trait study as well as alternative approaches that can provide substantially greater power. The latest methods for analyzing G×E with gene sets and with data in a consortium setting are summarized, as are issues that arise due to the complexity of environmental data. We provide some speculation on why detecting G×E in a genome-wide association study has thus far been difficult. We conclude with a description of software programs that can be used to implement most of the methods described in the paper.

Gene-environment interaction (G×E) can be defined broadly as the interplay between a gene and an environmental factor as they affect some trait. For example, epidemiologists may be interested in studying how genetic susceptibility might predispose subgroups of the population to enhanced effects of an environmental exposure. Alternatively, geneticists may be interested in studying how exposure to an environmental fact may stimulate the expression of a gene and lead to disease.

In the first article in this series, McAllister et al. (1) provide a broad overview of the state of the science related to G×E. In this article, we summarize the latest statistical methods available for analysis of G×E. We address many of the practical questions that statisticians face as they try to uncover G×Es for complex traits, and we summarize some of the latest approaches to address these issues (Table 1).

Table 1.

Challenges and Potential Solutions in the Analysis of Gene-Environment Interactions, Based on Issues Raised at the Workshop “Current Challenges and New Opportunities for Gene-Environment Interaction Studies of Complex Diseases,” United States, October 2014

Challenges	Old Approach	Solutions/New Approach	Section Heading
Interaction can be dependent on scale	Only multiplicative scale considered	Consider evaluating interaction on both additive and multiplicative scales	Models of G×E
SNP-based analyses can lack power	Single-step analysis subject to multiple comparisons burden due to large number of SNPs considered at once	Conduct more efficient 2-step tests	Detecting interactions in a GWAS
	Single-variant approach agnostic to biological information	Conduct gene-based/set-based tests	G×E with gene sets
	Individual studies report results independently	Conduct meta-analysis across studies/cohorts	G×E analysis in a consortium setting
	Only homogeneous populations considered, typically of European decent	Consider admixture analysis, if appropriate	G×E analysis in a consortium setting
Exposure measurement can be inconsistent and imperfect	Individual studies independently determine method of exposure measurement	Work towards common core of exposures and definitions	The complexity of exposure
	Employ easiest measurement method for largest study sample possible	Prioritize improving precision of measurements	Why haven't many G×Es been identified?
Software is not available to conduct efficient G×E analysis	Individual analysts tweak existing software to generate limited G×E results	Implement new software designed for high-volume G×E analyses using novel methods	Available software for analysis of G×E

Abbreviations: GWAS, genome-wide association study; G×E, gene-environment interaction; SNP, single nucleotide polymorphism.

MODELS OF G×E

Basic models

Consider a study of a disease outcome (D), environmental factor (E), and genetic factor (G), with data also collected on a set of potential confounders (C). Exposure E can represent an exogenous environmental variable (e.g., air pollution), personal exposure (e.g., smoking), or other personal characteristic (e.g., sex). Although a single genetic locus may be of interest, most studies now genotype a large number (e.g., 1 million) of single nucleotide polymorphisms (SNPs) on each study subject. Each locus may be coded as G = 0, 1, or 2 for the number of minor alleles, or dominant, recessive, or codominant coding can be used. Additional untyped SNP genotypes are now routinely imputed based on the 1,000 Genomes (2) or Haplotype Reference Consortium (3) panels.

For a case-control study, logistic regression is typically used to model G×E, with the form (model 1):

$$\begin{array}{c}\mathrm{Logit}(\mathrm{Pr}\left(\mathrm{D}=1|\mathrm{G},\mathrm{E},\mathbf{C}\right)={\mathrm{\beta }}_0+{\mathrm{\beta }}_{\mathrm{G}}{\mathrm{G}+\mathrm{\beta }}_{\mathrm{E}}\mathrm{E}\hfill \\ +{\mathrm{\beta }}_{\mathrm{G}\times \mathrm{E}}\mathrm{G}\times \mathrm{E}+{\mathbf{\beta }}_{\mathbf{C}}\mathbf{C}.\hfill \end{array}$$ (1)

Compared to an unexposed noncarrier (E = 0, G = 0), OR_G = exp(β_G) measures the “main effect” of G (E = 0, G = 1) and OR_E = exp(β_E) measures the main effect of E (E = 1, G = 0). The corresponding odds ratio when E = 1 and G = 1 is exp(β_G)exp(β_E)exp(β_G×E), and so the “interaction odds ratio” is OR_G×E = exp(β_G×E) and measures the departure from the multiplicative effects of the corresponding main effects. Note that the choice of coding system (e.g., E = 1 for obese, E = 0 for nonobese) is arbitrary and has no impact on the significance of the interaction test. However, the coding system is important for interpretation of β_G, β_E, and β_G×E, in that the magnitude and/or direction of these effects can change when shifting the coding of G and/or E (4).

The G×E model (model 1) builds on the typical model (model 2) that does not consider G×E:

$$\mathrm{Logit}\left(\mathrm{Pr}\left(\mathrm{D}=1|\mathrm{G},\mathbf{C}\right)\right)={\mathrm{\mu }}_0{+\mathrm{\mu }}_{\mathrm{G}}\mathrm{G}+{\mathbf{\mu }}_{\mathbf{C}}\mathbf{C},$$ (2)

where E may be included in C. Here OR_G = exp(μ_G) measures the “marginal odds ratio” of G, interpreted as averaging (or marginalizing) over the exposure-specific effects of G.

For the simplest situation of a binary exposure, binary G, and no covariates, Web Figure 1 (available at https://academic.oup.com/aje) shows how cell counts from two 2 × 2 tables can be used to compute the interaction and marginal effects described above. In the context of a cohort study, one could replace models 1 and 2 with log-linear models to estimate relative risks RR_G, RR_E, and RR_G×E (5), or with proportional hazards models to estimate hazard rate ratios for time-to-disease data (6). For a quantitative outcome, linear regression is typically used (see below).

Interpretations of interaction parameters

Interpretation of G×E depends on the underlying scale on which G×E effects are modeled. The classical result of Prentice and Pyke (7) ensures that estimates of (β_G, β_E, β_G×E, β_C) obtained from model 1 are valid and efficient under case-control sampling. Most commonly, interaction in epidemiology refers to the departure from multiplicative effects described above.

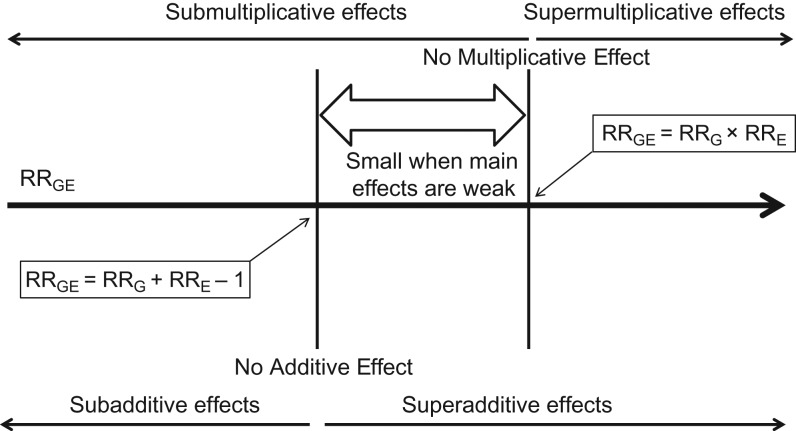
Another form of interaction that is not commonly assessed is the departure from additivity on the absolute risk scale. The additive effect is defined as G×E_ADD = RR_G × RR_E × RR_G×E − RR_G − RR_E + 1 for a relative risk model, with analogous form for an odds ratio model. Departure from additivity implies that absolute risk reduction associated with removal of one risk factor depends on the levels of another and vice versa. As such, the model has direct relevance for evaluation of public health impact of risk-factor intervention (8). Furthermore, many mechanistic forms of interactions, such as under the sufficient-component cause model (8, 9) and various modern extensions (10), have been shown to yield superadditive effects (G×E_ADD > 0).

It is useful to understand the relationships between different models for interactions (Figure 1). A supermultiplicative G×E (RR_G×E > 1) automatically implies the effects of G and E are superadditive. Conversely, a superadditive G×E can correspond to either sub- or super-multiplicative effects of G and E. In absence of a main effect of G and/or E, the additive and multiplicative models coincide. Thus for G and/or E with weak main effects, which is often the case for common SNPs, models may be hard to distinguish without large sample size. Recent studies conducted to explore genome-wide association study (GWAS) results suggest that the multiplicative model often provides reasonable approximation of G×E joint effects on disease risks (11–14). However, although the multiplicative model may be the “accepted” analysis approach, superadditive effects have been reported (15), demonstrating that investigation of interactions both scales can be informative for understanding joint G and E effects.

Figure 1.

Comparison of additive and multiplicative models for the joint effects of gene (G) and environment (E). Assuming binary G and binary E, the joint-effect relative risk RR_GE = RR_G × RR_E × RR_G×E—relative risk for G = 1 and E = 1 compared with G = 0 and E = 0—is shown under the additive and multiplicative models. Under the 2 different models, the RR_GE is determined by underlying main-effect relative risks (RR_G and RR_E), that is, relative-risk associated with one factor (e.g., G = 1 vs G = 0) while the other factor is fixed at baseline (e.g., E = 0) in 2 different functional forms. Throughout, it is assumed that G = 1 and E = 1 correspond to higher-risk categories than G = 0 and E = 0 (RR_G > 1 and RR_E > 1).

Mechanistic interpretation of statistical interaction is difficult because of its dependence on scale. However, certain forms of scale-invariant interactions can provide important mechanistic insights. In a “pure interaction” model when the effect of G is present only in the presence/absence of E (corresponding to β_G = β_E = 0 in model 1), interaction would be evident irrespective of scale. Genetic markers of acetylation in the N-acetyltransferase 2 gene (NAT2) have been associated with bladder cancer only among smokers (16). Another form of invariant interaction is the qualitative interaction where the presence of one risk factor may reverse the effect of another.

DETECTING INTERACTIONS IN A GWAS

Basic tests: G×E and the 2-df test

In context of model 1, detection of multiplicative interaction is based simply on the test of the null hypothesis that β_G×E = 0, and a Wald, Score, or likelihood ratio test may be applied. The same type of test is used if conditional logistic, log-linear, or Cox regression are used for analysis. Standard GWAS screens for marginal G effects are based on the test of H₀: μ_G = 0 from model 2. A 2-degrees-of-freedom (df) procedure based on model 1 (17) or a combination of models 1 and 2 (18) can be used to test the joint null H₀: β_G = β_G×E = 0. For many models, 2-df tests have better power to detect genes than either the marginal G or 1-df G×E test alone (17).

Regardless of the specific test, one should carefully consider potential confounders C, G×C, and E×C interactions, because G×E effects can themselves be confounded by other interactions (19). Some potential confounders seem like obvious choices for inclusion in the model—for example, principal components to adjust for ancestry. Others require more judgment, such as whether or not to adjust for body mass index (BMI) in a study of gene-diet interaction. While BMI may seem like an obvious confounder, it may also be a mediator of dietary effects, and including BMI, G × BMI, and diet × BMI as adjustments may reduce the ability to detect G × diet signals.

In a GWAS, both G and E are each typically coded using a single trend variable, yielding a 1-df test of interaction. However, the effect of E can often be specified as categorical, ordinal, or continuous form depending on the nature of the underlying measurements. It may be desirable to code a complex exposure using a flexible model to avoid bias in the test for interaction due to model misspecification (20). This will translate to a multi-df test of interaction, which can reduce power and should be avoided if a single trend variable can be justified.

Testing for additive interaction can be numerically complex due to constraints required to guarantee risk estimates are bounded between 0 and 1 for all risk-factor combinations. For rare diseases and categorical risk factors, the additive model can be specified in the form of a general logistic regression model where the interaction term is specified by a nonlinear function of the main effects (21).

Case-only and empirical Bayes approaches

Piegorsch et al. (22) showed that for binary (G, E), the parameter β_G×E in model 1 can be estimated by using data from cases only (Web Figure 2). To allow for nonbinary G and/or E, and adjustment for confounders, one can adopt a polytomous logistic model for case-only analysis, as in model 3:

$$\mathrm{Logit}\mathrm{P}\left(\mathrm{G}=\mathrm{g}|\mathrm{E},\mathbf{C},\mathrm{D}=1\right)={\mathrm{\gamma }}_{\mathrm{g}}+{\mathrm{\gamma }}_{\mathrm{g}\mathrm{E}}\mathrm{E}+{\mathbf{\gamma }}_{\mathbf{gc}}^{\mathbf{T}}\mathbf{C}\mathrm{g}=1,2$$ (3)

where each parameter quantifies the effect of a heterozygous (g = 1) or homozygous (g = 2) carrier of a risk allele compared with a homozygous noncarrier (g = 0). Under the assumption of gene-environment (G-E) independence conditional on C, the test of H₀: γ_1E = γ_2E = 0 is a valid test of multiplicative interaction. One often desires a test of trend across G = 0, 1, and 2, which can be accomplished in model 3 by setting γ_1E = γ_E and γ_2E = 2γ_E and testing H₀: γ_E = 0. A limitation of case-only analysis is that one cannot estimate main effects β_G and β_E, and thus cannot retrieve the subgroup effects of genotype across exposure strata (e.g., OR_DG|E=1 and OR_DG|E=0). Alternative “case-only” approaches that use controls to estimate main effects have been proposed (23, 24).

If the G-E independence assumption is violated, estimates derived from case-only analysis will be biased (25), either toward or away from the null depending on directions of the G-E association and G×E. To reduce bias but retain some efficiency of the G-E independence assumption, an empirical Bayes (EB) strategy has been proposed (26). In the simple case of a binary G and E, the EB estimator ${\hat{\mathrm{\beta }}}_{\mathrm{E}\mathrm{B}}$ is constructed using estimates from models 1 and 3:

$$\begin{array}{c}{\hat{\mathrm{\beta }}}_{\mathrm{E}\mathrm{B}}={\hat{\mathrm{\gamma }}}_{\mathrm{g}\mathrm{E}}+K({\hat{\mathrm{\beta }}}_{\mathrm{G}\mathrm{x}\mathrm{E}}-{\hat{\mathrm{\gamma }}}_{\mathrm{g}\mathrm{E}})\hfill \\ \mathrm{where}K={\hat{\mathrm{\theta }}}_{\mathrm{g}\mathrm{E}}^2/({\hat{\mathrm{\sigma }}}_{\mathrm{G}\times \mathrm{E}}^2+{\hat{\mathrm{\theta }}}_{\mathrm{g}\mathrm{E}}^2)\hfill \end{array}$$ (4)

The intuitive explanation behind the EB estimator is that if there is G-E independence in the population (i.e., θ_gE = 0), γ_gE and β_G×E will be approximately equal, and one should favor the case-only estimate ${\hat{\mathrm{\gamma }}}_{\mathrm{g}\mathrm{E}}$ for its increased efficiency. On the other hand, if the data provide evidence of G-E dependence ${(\hat{\mathrm{\theta }}}_{\mathrm{g}\mathrm{E}}>0)$ or if the variance of ${\hat{\mathrm{\beta }}}_{\mathrm{G}\times \mathrm{E}}$ is small $({\hat{\mathrm{\sigma }}}_{\mathrm{G}\times \mathrm{E}}^2\to 0)$, larger weight is assigned to ${\hat{\mathrm{\beta }}}_{\mathrm{G}\times \mathrm{E}}$.

Chen et al. (27) provided a more general EB framework, which is implemented in the CGEN software package (28). Li and Conti (29) developed a Bayes model averaging framework, where the weights in Equation 4 are defined by posterior probabilities. Both EB and Bayes model averaging approaches often provide greater power than a standard case-control test, while providing improved (although not perfect) control of type I error compared with a case-only test in the presence of population G-E association (26) (Web Appendix 1).

Efficient 2-step tests

Several “2-step” approaches have been proposed to improve the efficiency of G×E analysis while controlling type I error, both for disease (30–35) and quantitative (36, 37) traits. All of these methods use the following general approach:

• Step 1 screen: For all M (e.g., 1 million) SNPs, compute screening test statistic T₁ and corresponding P value p₁.

• Step 2 test: Prioritize SNPs based on p₁ (e.g., conduct step 2 only on m SNPs with p₁ < 0.05), and compute G×E test statistic T₂ with corresponding P value p₂. Power is increased by the need to adjust in step 2 for only m < M tests.

A key requirement for validity of any 2-step procedure is that T₁ and T₂ must be independent. In a case-control study, two types of step-1 screening tests have been proposed: 1) test of marginal D versus G (DG) association (33), based on model 2; and 2) test of E versus G (EG) association (35), based on model 3 applied to the combined case-control sample. The step-2 test is based on β_G×E from model 1. It has been shown that tests of μ_G = 0 and γ_gE = 0 (in the combined sample) are independent of the test of β_G×E = 0, and so either is a valid screening statistic (38). In the presence of G×E, one can typically expect nonzero values of both μ_G and γ_gE, making either the DG or EG screening statistic useful for identifying those SNPs that are most likely to be involved in a G×E. Three additional 2-step methods have been proposed including H2 (34), Cocktail (32), and EDGE (31), each of which use the DG and EG screening statistics in combination to further improve efficiency. Both standard tests and 2-step methods are implemented in the GxEScan software program (39).

G×E analysis for quantitative measures

Quantitative trait analyses in plant and animal models have clearly identified the importance of G×Es, in some cases having profound impact on phenotypes such as longevity in Drosphila (40) or flowering time in Arabiaopsis (41). In humans, Winkler et al. (42) identified 15 loci showing evidence for age-dependent genetic effects on BMI, 4 of which were not identified previously. A recent analysis suggests that estimates of heritability for quantitative traits can be substantially underestimated when interaction effects are not modeled (43). For a quantitative outcome Y, a linear model of the form of model 5:

$${Y=\mathrm{\beta }}_0{+\mathrm{\beta }}_{\mathrm{G}}{\mathrm{G}+\mathrm{\beta }}_{\mathrm{E}}{\mathrm{E}+\mathrm{\beta }}_{\mathrm{G}\times \mathrm{E}}\mathrm{G}\times \mathrm{E}+{\mathbf{\beta }}_{\mathbf{C}}\mathbf{C}+\mathrm{\epsilon }$$ (5)

is often adopted. As for any such regression model, failure to satisfy basic model assumptions (e.g., linearity, normality of residuals ε) can lead to inflated type I error or reduced power. As for a disease trait, G×E can induce a marginal G effect, here a difference in mean Y across G. This information can be used efficiently in a 2-df joint test of G and G×E (17, 44–46), or to construct a 2-step procedure that screens on marginal G association (37). It has also been shown that G×E induces a difference in the variance of Y across G (36, 37, 47). This variance-heterogeneity information can also be used to develop valid testing procedures that are more powerful than standard tests of G×E or marginal G effects (37, 47). Standard and 2-step testing procedures are implemented in GxEScan (39).

Which analysis should you choose for GWAS?

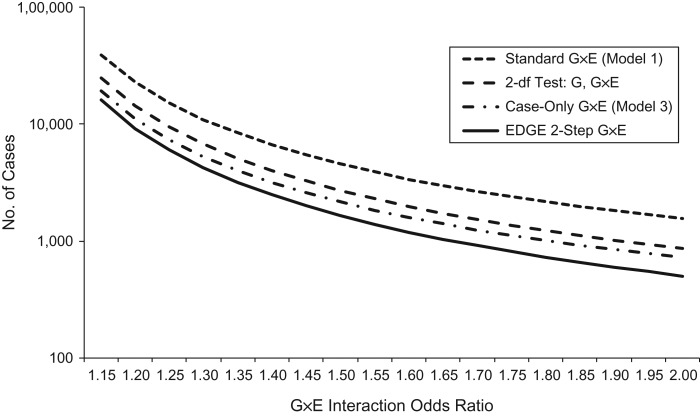
There have obviously been many statistical approaches developed for testing G×E. Perhaps the most natural is the standard test of β_G×E from model 1 or model 5, as this is a simple extension of the kind of model used for marginal G analysis. However, case-only, EB, 2-df, and 2-step procedures can offer improvements in efficiency and should be considered. As an example, Figure 2 shows that the case-only, 2-df, and 2-step EDGE approaches can require substantially lower sample sizes to achieve 80% power for detecting G×E compared with the standard (model 1) G×E test. While this example is representative, the efficiency of various approaches relative to one another varies depending on the underlying true model (31, 32).

Figure 2.

Required sample size (n) versus gene-environment interaction (G×E) effect size (OR_G×E) to achieve 80% power using 4 different analysis methods, assuming an equal number of controls (except for the case-only analysis). The underlying model assumes that G has minor allele frequency 30% and additive (0–2) genotype coding, E is binary with prevalence 40%, and neither G nor E has a main effect on disease risk (β_G = β_E = 0.0, model 1). The calculations also assume a scan of 1 million single nucleotide polymorphisms and an overall type I error rate of 0.05, yielding significance threshold for a single interaction of single nucleotide polymorphism × E of 5 × 10⁻⁸. For example, when OR_G×E = 1.5, a case-control study would require n = 4,557 cases using a standard test of β_G×E = 0 from model 1. The same power can be achieved with n = 2,716 cases by using a 2-df joint test of G and G×E, n = 2,160 by using a case-only analysis, or with only n = 1,654 by using the 2-step EDGE (31) approach. QUANTO (83), modified to accommodate the EDGE method, was used for computations.

G×E WITH GENE SETS

Set-based methods for G×E have emerged for detecting G×E effects within biologically defined sets, such as variants mapping to a particular pathway. A set-based G×E test is a single global test of interaction between an entire set of variants and the exposure of interest, rather than multiple individual tests, one per variant. The idea behind set-based methods is that accumulating multiple weak signals—possibly undetectable in isolation—across a set of variants may result in a detectable overall G×E signal. For rare variants, set-based methods are indispensable because the power to detect G×E with any single mutation is exceedingly small. Additional issues in rare-variant × E interaction analyses are provided in the online supplement (Web Appendix 2).

Methods for testing set-based G×E effects can be broadly classified into 3 categories: burden-type (BT) tests, variance component (VC) tests, and a combination of both. For BT tests, G×E testing uses a “G” defined as a weighted risk score computed on the gene set. The weight can be informed by DG and/or EG screening statistics (48, 49), analogous to 2-step approaches for single SNPs. The VC approach is based on the assumption that G×E effects are random and follow an arbitrary distribution with mean 0 and variance τ². Testing G×E can be accomplished using a score test of H₀: τ² = 0 (50) or using a regression model of genotypic and phenotypic similarity (51, 52). BT tests perform better when many variants in the set are causal and have effects in the same direction. In contrast, VC tests are more powerful when there is heterogeneity in magnitude and direction of effects. To potentially improve power across a range of underlying scenarios, hybrid methods that combine BT and VC tests have been proposed (53–55). Set-based analogs of the 2-df joint test of G and G×E have also been developed (56, 57). The BT, VC, and hybrid methods are implemented in the MiST-I software program (55).

THE COMPLEXITY OF EXPOSURE

A significant challenge in G×E analysis is the complexity of the environmental data (58). First, environmental exposures are heterogeneous in their type (e.g., continuous or discrete). Second, measurement modalities (e.g., community-level vs. home-level assessment of air pollution) can differ vastly in their measurement-error characteristics (59, 60), which in turn affects bias in estimates and power to detect effects. Third, exposures and their biological effects can vary considerably from the period before conception through adulthood. This has implications in estimation of effect sizes and interpretation. Fourth, exposures are often spatially, temporally, and/or culturally dependent. For example, air pollution levels can vary significantly between rural and urban settings and across decades (61, 62), and racial/ethnic-specific differences in exposure to phthalates (63) and air pollution (64) have been reported. Fifth, multiple environmental exposures can be highly correlated with one another (58, 65–68), making it difficult to identify the independent influence of a single exposure. Additional issues arise related to emerging exposome-type measurements (69).

G×E ANALYSIS IN A CONSORTIUM SETTING

For standard GWAS of marginal genetic effects, achieving sufficient sample size commonly requires merging data from multiple cohorts across a consortium. Due to ethical and data protection constraints, it is usually not possible to share individual level data (to perform a so-called mega-analysis), and the solution has been to perform meta-analysis of cohort-specific analyses. In brief, each study performs the same analysis (e.g., application of model 1), perhaps with some cohort-specific adjustment covariates if necessary.

Recent work has shown that meta-analysis of G×E is asymptotically similar to mega-analysis (70, 71). However, there are some important considerations. First, for a binary E, a consortium may choose to perform stratified analysis. Here the goal is to estimate the marginal G effect separately within the exposed and unexposed, and test for G×E based on heterogeneity across E strata (72–74). Advantages of this stratified approach are that standard software for marginal G effects can be used, and one obtains stratified estimates and tests of G effects naturally. However, the stratified approach obviously does not extend to continuous E. Additionally, one may be tempted to overinterpret P values of G effects within each stratum, rather than being guided by the overall test of G×E that forms the basis for the primary analysis (4).

The distribution of exposure will almost certainly vary across studies in a consortium for reasons described above. For a continuous exposure, differences in distribution across cohorts are unlikely to affect the estimate of the G×E effect if the interaction effect is mostly linear (i.e., its direction and magnitude do not differ across the exposure range). In fact, such heterogeneity can lead to more precise estimates and greater power to detect G×E (Web Figure 3). If G×E effects are nonlinear (e.g., increased genotypic risks occur only above some threshold of ozone exposure), meta-analysis becomes more complicated and may have low power. Fundamental differences in how exposures are assessed across studies (e.g., different questionnaire items or satellite versus ground-based measurement of air pollution) may make it impossible to analyze G×E for some E in a consortium setting.

The inclusion of diverse and/or admixed populations in a consortium may increase power to detect G×E. Diverse populations can increase both genomic variation and the range of environmental exposures (75, 76). Diverse populations with varying levels of linkage disequilibrium are beneficial for fine mapping of G×Es to identify truly causal variation. In admixed populations, local patterns of genetic ancestry can be used to perform ancestry × E interaction analyses to increase power of discovery over traditional G×E analysis (77).

WHY HAVEN'T MANY G×Es BEEN IDENTIFIED?

While some G×Es have been reported (46, 78, 79), detecting and replicating them has been a challenge. A key reason may be low statistical power or, equivalently, the need for large sample sizes in order to detect interaction effects of moderate magnitude (Figure 2). Analysis (or reanalysis) in the largest possible samples (perhaps in a consortium setting), using the most efficient methods may lead to the identification of additional G×Es.

Measurement error of G and/or E will reduce the effective sample size and adversely affect our ability to detect G×E. The causal locus G is often not directly measured, and we rely on linkage disequilibrium between G and one or more measured marker loci. While linkage disequilibrium is generally high (e.g., R² > 0.8), it can vary substantially across the genome and across racial/ethnic groups. Difficulties in accurately measuring E as described above can lead to limited correlation between the observed and true E values. For example, dietary measures assessed from food frequency questionnaires commonly have low correlation with those assayed via a 24-hour dietary record (e.g., R² < 0.5). Obtaining more precise measures of G (e.g., direct sequencing) and E (e.g., repeat measurements or biomarkers of exposure) may be more cost-effective for improving power of G×E analysis than simply increasing sample size (80).

Of course, we cannot rule out the possibility that a G×E does not exist, or is not that important, for a particular phenotype. For example, common genetic variants are likely to have occurred in the more distant past, and over time selection pressure may have weeded out variants with large G×E effects, leaving little detectable interaction in a current study. As another example, G×E may be important for a specific rare variant and rare exposure, but the amount of disease risk attributable to the G×E will likely be negligible and nearly impossible to detect. Alternatives to omnibus G×E tests, including stratified analyses (81), may be more effective for uncovering the genetic and environmental architecture of complex traits.

AVAILABLE SOFTWARE FOR ANALYSIS OF G×E

As is true in many areas of research, the most efficient methods of statistical analysis may not get wide use unless they are implemented in available software. For smaller-scale analyses (e.g., analysis of single variants or a set of candidate genes), popular statistical software such as SAS (SAS Institute, Inc., Cary, North Carolina) or STATA (StataCorp LP, College Station, Texas) can be used for G×E analyses. However, these programs do not scale well to genome-wide analyses or more complex models. In the sections above, we cited 3 software programs specifically designed for high-volume G×E analyses using novel and efficient methods (28, 39, 82). Additionally, many of the papers we cite include links to software programs that implement the corresponding methods. As we continue to move into a more high-volume, “-omics” driven research environment, it is essential that there be a strong focus on developing efficient software tools that implement evolving approaches.

DISCUSSION

G×E analysis may hold the key to further understanding many complex traits. In recent years, more efficient methods for GWAS scans have been developed. These open the door to the analysis (or reanalysis) of existing resources to learn more about the range of genetic and environmental factors that affect a given trait. Modern methods for assessing exposure provide new opportunities but also new challenges for the detection of G×Es. Consortium-based studies or very large cohorts will likely be required to achieve adequate power for the analysis of G×E. The study of an admixed population, either alone or as part of a consortium, may increase power for detecting G×E and will certainly broaden the public-health relevance of any findings. The evolving availability of new -omics technologies will provide us with rich data resources for discovering G×Es and translating them into predictive/diagnostic models. Methods and software development for the analysis of G×E will need to keep pace in order efficiently use these exciting new data resources.