Modeling gene-wise dependencies improves the identification of drug response biomarkers in cancer studies

Abstract

Motivation

In recent years, vast advances in biomedical technologies and comprehensive sequencing have revealed the genomic landscape of common forms of human cancer in unprecedented detail. The broad heterogeneity of the disease calls for rapid development of personalized therapies. Translating the readily available genomic data into useful knowledge that can be applied in the clinic remains a challenge. Computational methods are needed to aid these efforts by robustly analyzing genome-scale data from distinct experimental platforms for prioritization of targets and treatments.

Results

We propose a novel, biologically motivated, Bayesian multitask approach, which explicitly models gene-centric dependencies across multiple and distinct genomic platforms. We introduce a gene-wise prior and present a fully Bayesian formulation of a group factor analysis model. In supervised prediction applications, our multitask approach leverages similarities in response profiles of groups of drugs that are more likely to be related to true biological signal, which leads to more robust performance and improved generalization ability. We evaluate the performance of our method on molecularly characterized collections of cell lines profiled against two compound panels, namely the Cancer Cell Line Encyclopedia and the Cancer Therapeutics Response Portal. We demonstrate that accounting for the gene-centric dependencies enables leveraging information from multi-omic input data and improves prediction and feature selection performance. We further demonstrate the applicability of our method in an unsupervised dimensionality reduction application by inferring genes essential to tumorigenesis in the pancreatic ductal adenocarcinoma and lung adenocarcinoma patient cohorts from The Cancer Genome Atlas.

Availability and Implementation

The code for this work is available at https://github.com/olganikolova/gbgfa

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

A fundamental problem in computational cancer biology is to predict drug response in a new sample from its genomic make up and further identify a subset of genes most predictive of drug response (signature). From an application stand point, this problem is important because it can help identify subpopulations of patients that are responsive to a particular therapy and suggest novel treatment targets and pathways for co-treatment with existing regimens. Cancer is a vastly heterogeneous disease. Studies in solid tumors have shown that heterogeneity in response to therapies is partially determined by molecular differences between tumors (Collisson et al., 2011). Stratification of drugs to tumor subtypes in which they are selectively effective is shown to improve treatment outcomes (Druker et al., 2001; Lynch et al., 2004; Slamon et al., 2001). Thus, ability to predict therapeutic efficacy from molecular data is critical.

Recent advances in biomedical and sequencing technologies have revealed the genomic landscape of common forms of human cancer in unprecedented detail. Of the genes that are able to promote or ‘drive’ tumorigenesis when altered, for most cancers, it is believed that there exist a small number of ‘mountains’ (genes altered at high frequencies across the population), and a much larger number of ‘hills’ (much less frequently altered genes). For example, in pancreatic ductal adenocarcinoma, alteration frequencies decrease at nearly exponential rate for the top five most frequently mutated genes from 96 to 8% (Biankin et al., 2013). While mountains are relatively easy to statistically identify their number ($\approx$140) is believed to be reaching saturation (Vogelstein et al., 2013), and identifying the more prevalent driver events altered at lower frequencies is much more challenging. To make matters worse, the rate of mutation in normal cells is indicated to vary by $\approx$100-fold genome-wide (Michaelson et al., 2012). This challenging mutational profile of the cancer genome calls for approaches that can integrate data from different genomic platforms to more reliably prioritize driver genes with lower alteration frequencies.

1.1 Previous work

Various computational methods have been applied to tackle both the prediction (predict drug responses from genomic data) and variable selection (identify genomic features associated with drug sensitivity or resistance) questions. The use of multivariate linear regression, based on least squares formulation, has been extensive because it is readily amendable to regularization, which accounts for model complexity and introduces sparsity (Tibshirani, 1996; Zou and Hastie, 2003). While regularized regression methods like Elastic Net have been widely used in cancer studies (Barretina et al., 2013; Garnett et al., 2013), they do not allow for flexible integration of genomic features coming from distinct platforms, possibly with very different underlying distributions (e.g. copy number variation and RNA-sequencing count data). Canonical correlation analysis (CCA) is a technique that allows for such data integration. CCA finds a lower dimensional representation of two sets of multidimensional variables in which they are maximally correlated by solving a generalized eigenvalue problem (Hotteling, 1936; Ray et al., 2014; Sun et al., 2011; Tucker, 1958). Further, regularized CCA extensions have also been proposed (Sun et al., 2011; Witten et al., 2009), but these approaches remain limited to two input sets (views). To overcome this limitation, the multiple CCA model has been proposed (Witten and Tibshirani, 2009). A fully Bayesian formulation of group factor analysis (BGFA) has also been proposed, which extends beyond two views (Klami et al., 2013) and simultaneously learns the structure of the model. However, in all of the above described methods, measurements of the same gene’s genomic aberrations (e.g. gene expression and copy number) are assumed to be independent from one another. A handful of methods attempt to explicitly model such dependencies by introducing very specific regulatory assumptions (Vaske et al., 2010; Wang et al., 2013). For example, in PARADIGM, a directed causal relationship is postulated to encode the central dogma as well as biological pathway information (Vaske et al., 2010). Alternatively, Wang et al. (2013) adopted a strong regulatory assumption for the role of methylation and their approach is not applicable to studies where methylation data are not available.

1.2 Contributions

We investigate the applicability of the BGFA approach to the cancer biology problems that we set out to solve. We further propose a novel, biologically driven re-parametrization of BGFA, which explicitly models gene-centric dependencies in multi-omic readouts collected for the same genes. Our modified model favors genes that carry information in multiple measurement platforms, where we will more likely see a real biological effect. We extend the fully Bayesian formulation presented in the work of Klami et al. (2013) by introducing a gene-wise prior into a group factor analysis model that learns a lower-dimensional latent representation of the data via shared and private components across input datasets (views). We derive a variational approximation inference algorithm that casts and solves multiple learning tasks simultaneously as one, a property also known as multitask. The multitask property of our approach enables us to leverage similarities in the response profiles of groups of drugs that are more likely to correspond to true biological effects as opposed to experimental noise and off-target effects, which improves generalization ability of the results. Multitask approaches have been shown to improve predictive performance as compared to their single-task counterparts (Gönen and Margolin, 2014; Tsoumakas et al., 2010).

2 Materials

To evaluate the proposed model, we use four different cancer datasets. We first analyze genomically characterized cell lines profiled against two panels of drugs in the Cancer Cell Line Encyclopedia (CCLE) (Barretina et al., 2013) and the Cancer Therapeutics Response Portal (CTRP) (Seashore-Ludlow et al., 2015) studies. We then consider genomically characterized patient samples from the The Cancer Genome Atlas (TCGA) pancreatic ductal adenocarcinoma (PAAD) and lung adenocarcinoma (LUAD) cohorts (Hoadley et al., 2014).

2.1 Cell lines for comparative performance analysis

2.1.1 CCLE

Hybrid-capture sequencing mutation data for 1651 genes and Affymetrix messenger RNA (mRNA) expression data for 18 897 genes were collected in 504 cell lines profiled with 24 compounds (Barretina et al., 2013). Filtering missing values by rows (cell lines) and columns (drugs) in the response matrix and by columns (genes) in feature matrices is necessary to produce complete (fully observed) data. This procedure yielded 18 969 unique genes in 267 cell lines. Drug response in this dataset is given by the half-maximal inhibitory concentration (IC₅₀), which indicates the drug concentration needed to achieve 50% cell death.

2.1.2 CTRP

An expanded set of 886 CCLE cell lines were profiled with a total of 545 compounds (Seashore-Ludlow et al., 2015). Even though overall only $\approx 20\%$ of the response matrix data was missing, filtering the response matrix by rows or columns resulted in an empty set. To generate a complete response matrix, we considered all cell lines for which at most $T\%$ of compound data was missing, where T varied from 20 to 10 in increments of 0.1 (Supplementary Fig. S1). In this study, we chose to analyze performance using a matrix of 409 cell lines × 98 drugs ($T=15.3\%$). Combining hybrid-capture mutation and mRNA gene expression data with the response matrix, after filtering missing data, yielded 18 969 genes and 409 cell lines. Drug response in this dataset is reported using the area under the drug dose–response curve (AUC).

2.2 Cell lines for feature type analysis

In addition to the data described in Section 2.1, CCLE copy number variation and OncoMap mutation were obtained and analyzed as described above (Barretina et al., 2013). Ten combinations of the four feature matrices were considered as input datasets in addition to the single feature type views.

2.3 Compounds with known targets and biomarkers

A list of CCLE compounds with known biomarkers of drug response was compiled from previously published studies (Supplementary Table 1). The biomarkers for many of the CTRP compounds are not known and we considered their targets as a proxy instead (Supplementary Table 2). This list was obtained from the CTRP portal (Seashore-Ludlow et al., 2015).

2.4 Patient data

2.4.1 PAAD

PAAD RNA-seq transcript data (178 samples × 20 501 genes) and mutation data (144 samples × 11 520 genes) were obtained from the TCGA data portal (https://tcga-data.nci.nih.gov/docs/publications/tcga/, date accessed: March 15, 2015). Combining these data and filtering missing values yielded 21 132 unique genes and 132 patients.

2.4.2 LUAD

Platform corrected LUAD RNA-seq transcript data (412 samples × 20 501 genes) and mutation data (236 samples × 15 637 genes) was obtained from Synapse (https://www.synapse.org/#!Synapse:syn395683) as part of the Pan-Cancer 12 TCGA data (Hoadley et al., 2014). Combining these data as described above yielded 20 608 unique genes and 165 patients.

3 Methods

3.1 Notation and preliminaries

We consider M different sets of measurements ${\mathcal{X}}_1,\hspace{0.17em}{\mathcal{X}}_2,\hspace{0.17em}\dots ,\hspace{0.17em}{\mathcal{X}}_M$ which we will interchangeably call ‘views’. For each view ${\mathcal{X}}_m$ with D_m features and N observations, we assume an independently and identically distributed sample ${\mathbf{X}}_m=\{x_{m,n,d_m}\in {\mathcal{X}}_m|m\in [1\dots M],n\in [1\dots N],d_m\in [1,D_m]\}$, where m, n and d_m index the views, observations and features, respectively. The different views usually correspond to measurements from either different technical platforms or quantifications of different biological characteristics, such as gene expression, copy number variation, mutation or cell viability in response to drug treatment. Views can include overlapping sets of features (genes). A feature-wise (gene-wise) prior $\mathit{\gamma }\in {ℝ}^{G\times 1}$ is defined over the set of G unique features across all views. The learning algorithm proceeds to generate the data points of all M views by projecting their latent representations in a shared space $\mathbf{Y}\in {ℝ}^{K\times N}$ with K hidden components using view-specific projection matrices ${\mathbf{W}}_m\in {ℝ}^{D_m\times K}$ and the feature-wise prior $\mathit{\gamma }$ (Fig. 1). We use $\mathcal{N}(\mathit{\mu },\mathbf{\Sigma })$ to denote the normal distribution with mean vector $\mathit{\mu }$ and covariance matrix $\mathbf{\Sigma }$ and $\mathcal{G}(\alpha ,\beta )$ to denote the Gamma distribution with shape α and scale β hyperparameters. Finally, we use $\langle ·\rangle$ to denote the expectation.

Fig. 1.

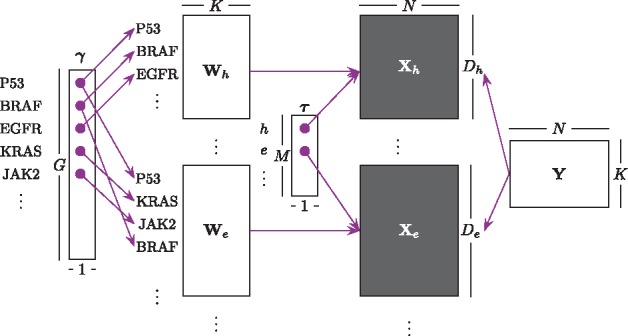
Algorithm workflow illustrating a matrix representation of GBGFA and dimensionality of each variable and prior, where h and e denote mutation and gene expression, respectively

3.2 Gene-wise prior Bayesian group factor analysis (GBGFA) model

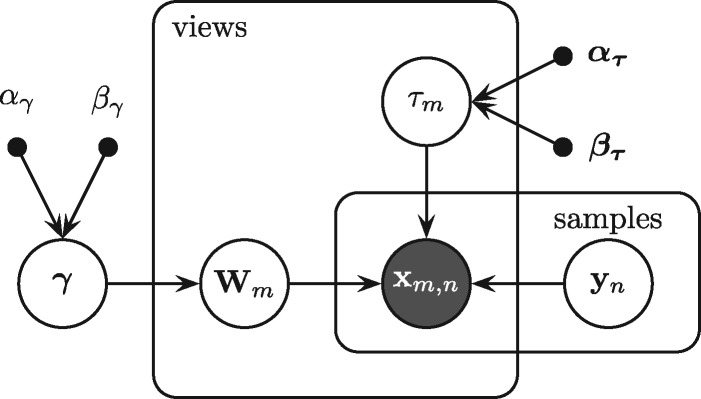
Figure 2 shows the graphical representation of GBGFA. Its joint likelihood is given by:

$$\begin{array}{l}p({\mathbf{W}}_1,\dots ,{\mathbf{W}}_M,{\mathbf{X}}_1,\dots ,{\mathbf{X}}_M,\mathbf{Y},\mathit{\gamma },\mathit{\tau })=\\ p(\mathit{\gamma })\prod _{m=1}^M(p({\mathbf{W}}_m|\mathit{\gamma })p({\tau }_m))\\ \prod _{n=1}^N(p({\mathbf{y}}_n)p({\mathbf{x}}_{m,n}|{\mathbf{W}}_m,{\mathbf{y}}_n,{\tau }_m)),\end{array}$$

where

Fig. 2.

Graphical representation of GBGFA model

$$\begin{array}{l}{\mathit{x}}_{m,n}|{\mathbf{W}}_m,{\mathit{y}}_n,{\tau }_m\sim \mathcal{N}({\mathit{x}}_{m,n}; {\mathbf{W}}_m{\mathit{y}}_n,{\tau }_m^{-1}\mathbf{I})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall (m,n),\\ {\mathit{w}}_{m,d_m}|{\gamma }_g\sim \mathcal{N}({\mathit{w}}_{m,d_m}; \mathbf{0},{\gamma }_g^{-1}\mathbf{I})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall (m,d_m),\\ {\gamma }_g\sim \mathcal{G}({\gamma }_g; {\alpha }_{\gamma },{\beta }_{\gamma })\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall g,\\ {\tau }_m\sim \mathcal{G}({\tau }_m; {\alpha }_{\tau },{\beta }_{\tau })\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall m,\\ {\mathit{y}}_n\sim \mathcal{N}({\mathit{y}}_n; \mathbf{0},\mathbf{I})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall n.\end{array}$$

3.2.1 Inference

We present a deterministic variational approximation inference algorithm, which leads to closed-form update equations due to the conjugate priors. We approximate the full posterior using the following distribution and its factorization:

$$\begin{array}{l}p({\mathbf{W}}_1,\dots ,{\mathbf{W}}_M,\mathbf{Y},\mathit{\gamma },\mathit{\tau }|{\mathbf{X}}_1,\dots ,{\mathbf{X}}_M)\approx \\ q({\mathbf{W}}_1,\dots ,{\mathbf{W}}_M,\mathbf{Y},\mathit{\gamma },\mathit{\tau })=\\ q({\mathbf{W}}_1)\dots q({\mathbf{W}}_M)q(\mathbf{Y})q(\mathit{\gamma })q(\mathit{\tau })\end{array}$$

where each factor is defined to be from the family of its respective full conditional distribution. Recall that G denotes the total number of unique features across all views. Then, the approximating distribution factorizes as follows:

$$\begin{array}{l}q(\mathit{\tau })=\prod _{m=1}^M\mathcal{G}({\tau }_m; a_{{\tau }_m},b_{{\tau }_m}),\\ q(\mathit{\gamma })=\prod _{g=1}^G\mathcal{G}({\gamma }_g; a_{{\gamma }_g},b_{{\gamma }_g}),\\ q(\mathbf{Y})=\prod _{n=1}^N\mathcal{N}({\mathit{y}}_n; \mathbf{0},\mathbf{I}),\\ q({\mathbf{W}}_m)=\prod _{d_m=1}^{D_m}\mathcal{N}({\mathit{w}}_{m,d_m}; {\mathit{\mu }}_{{\mathit{w}}_{m,d_m}},{\mathbf{\Sigma }}_{{\mathit{w}}_{m,d_m}}).\end{array}$$

Minimizing the Kullback–Leibler divergence between the posterior $p({\mathbf{W}}_1,\dots ,{\mathbf{W}}_M,\mathbf{Y},\mathit{\gamma },\mathit{\tau }|{\mathbf{X}}_1,\dots ,{\mathbf{X}}_M)$ and the approximate posterior $q({\mathbf{W}}_1,\dots ,{\mathbf{W}}_M,\mathbf{Y},\mathit{\gamma },\mathit{\tau })$ distributions is equivalent to maximizing the following lower bound derived using Jensen’s inequality:

$$\begin{array}{l}\hspace{0.17em}\text{log}\hspace{0.17em}p(\mathbf{Y}|{\mathbf{X}}_1,\dots ,{\mathbf{X}}_M)\ge \\ \langle \hspace{0.17em}\text{log}\hspace{0.17em}p({\mathbf{W}}_1,\dots ,{\mathbf{W}}_M,\mathbf{Y},\mathit{\gamma },\mathit{\tau }|{\mathbf{X}}_1,\dots ,{\mathbf{X}}_M)\rangle -\\ \langle \hspace{0.17em}\text{log}\hspace{0.17em}q({\mathbf{W}}_1,\dots ,{\mathbf{W}}_M,\mathbf{Y},\mathit{\gamma },\mathit{\tau })\rangle =\ell (q).\end{array}$$

The algorithm optimizes the lower bound $\ell (q)$ by updating each term of the bound until convergence. Let $V_g\le M$ be the number of views in which the feature with index g in $\mathit{\gamma }$ appears. Let also $\xi (g,i)$ be a many-to-one mapping function which returns the row d_m in projection matrix ${\mathbf{W}}_i$ of the feature with index g in $\mathit{\gamma }$. Then the approximate posterior distribution for the feature-wise prior is given as follows:

$$\begin{array}{l}{a}_{{\gamma }_g}={\alpha }_{\gamma }+\frac{V_g}{M}K,\\ b_{{\gamma }_g}={\beta }_{\gamma }+{\displaystyle \sum _{i=1}^{V_g}\frac{1}{2}\left({\mathit{w}}_{\xi (g,i)}{}^{\mathrm{\top }}{\mathit{w}}_{\xi (g,i)}+\text{tr}\left({\Sigma }_{{\mathit{w}}_{\xi (g,i)}}\right)\right)},\end{array}$$

where $\langle {\gamma }_g\rangle =a_{{\gamma }_g}/b_{{\gamma }_g}$. The noise precision parameters update is given by:

$$\begin{array}{l}{a}_{{\tau }_m}={\alpha }_{\tau }+\frac{N{D}_m}{2},\\ b_{{\tau }_m}={\beta }_{\tau }+\frac{1}{2}{\displaystyle \sum _{d_m=1}^{D_m}{\displaystyle \sum _{n=1}^N{x}_{m,d_m,n}^2}}\\ +\frac{1}{2}\text{tr}[\langle W_m{}^{\mathrm{\top }}{W}_m\rangle \langle Y{Y}^{\mathrm{\top }}\rangle ]-\text{tr}[\langle W_m\rangle \langle Y\rangle X_m{}^{\mathrm{\top }}].\end{array}$$

The latent variable’s approximate posterior can be updated as follows:

$$\begin{array}{l}\langle Y\rangle ={\displaystyle \sum _{m=1}^M\langle {\tau }_m\rangle }{\Sigma }_Y{\langle W_m\rangle }^{\mathrm{\top }}{X}_m,\\ {\Sigma }_Y={\left(I+{\displaystyle \sum _{m=1}^M\langle {\tau }_m\rangle \langle W_m{}^{\mathrm{\top }}{W}_m\rangle }\right)}^{-1},\end{array}$$

where

$$\langle W_m{}^{\mathrm{\top }}{W}_m\rangle ={\displaystyle \sum _{d_m=1}^{D_m}\left({\mathit{w}}_{m,d_m}{}^{\mathrm{\top }}{\mathit{w}}_{m,d_m}+{\Sigma }_{{\mathit{w}}_{m,d_m}}\right)}.$$

For each pair $(m,d_m)$, let $\varphi (m,d_m)$ denote a many-to-one mapping function, which returns the index g in the prior vector γ of the feature in row d_m of the projection matrix ${\mathbf{W}}_m$. Then, projections are updated as follows:

$$\begin{array}{l}\langle {\mathit{w}}_{m,d_m}\rangle ={\mathit{x}}_{m,d_m}\langle {\mathbf{Y}}^{\mathrm{\top }}\rangle {\mathbf{\Sigma }}_{{\mathit{w}}_{m,d_m}}\langle {\tau }_m\rangle ,\\ {\mathbf{\Sigma }}_{{\mathit{w}}_{m,d_m}}={(\langle {\gamma }_{\varphi (m,d_m)}\rangle \mathbf{I}+\langle {\tau }_m\rangle \langle \mathbf{Y}{\mathbf{Y}}^{\mathrm{\top }}\rangle )}^{-1},\end{array}$$

and ${\langle {\mathbf{W}}_m\rangle }^{\mathrm{\top }}=[{\mathit{\mu }}_{{\mathit{w}}_{m,1}},{\mathit{\mu }}_{{\mathit{w}}_{m,2}},\dots ,{\mathit{\mu }}_{{\mathit{w}}_{m,D_m}}]$. The lower bound is given in the Supplementary Materials.

3.2.2 Prediction

Suppose that we wish to predict views ${\mathbf{X}}_{i_1},{\mathbf{X}}_{i_2},\dots ,{\mathbf{X}}_{i_L}$, where $i_l\in \{1\dots M\},L<M$ given the views ${\mathbf{X}}_{j_1},{\mathbf{X}}_{j_2},\dots ,{\mathbf{X}}_{j_{M-L}}$ where $\left\{{\mathbf{X}}_i\right\}$ and $\left\{{\mathbf{X}}_j\right\}$ are mutually exclusive and $\{i_1,i_2,\dots i_L\}$$\cup \{j_1,j_2,\dots ,j_{M-L}\}$$\equiv \{1,2,\dots ,M\}$. That is, we are now interested in the predictive distribution $p({\mathbf{X}}_{i_1},{\mathbf{X}}_{i_2},\dots ,{\mathbf{X}}_{i_L}|{\mathbf{X}}_{j_1},{\mathbf{X}}_{j_2},\dots ,{\mathbf{X}}_{j_{M-L}})$. This distribution cannot be computed in closed form but can be derived using expectations from the variational approximation:

$$\begin{array}{l}\langle {\mathbf{X}}_{i_1},{\mathbf{X}}_{i_2},\dots ,{\mathbf{X}}_{i_L}|{\mathbf{X}}_{j_1},{\mathbf{X}}_{j_2},\dots ,{\mathbf{X}}_{j_{M-L}}\rangle =\\ \prod _{i=i_1}^{i_L}{\langle {\mathbf{W}}_i\mathbf{Y}\rangle }_{q({\mathbf{W}}_{i_1},{\mathbf{W}}_{i_2},\dots ,{\mathbf{W}}_{i_L})q(\mathbf{Y}|{\mathbf{W}}_{j_1},{\mathbf{W}}_{j_2},\dots ,{\mathbf{W}}_{j_{M-L}})}=\\ \prod _{i=i_1}^{i_L}\langle {\mathbf{W}}_i\rangle \prod _{j=j_1}^{j_{M-L}}\langle {\mathit{\tau }}_j\rangle {\Sigma }_j\langle {\mathbf{W}}_j^{\mathrm{\top }}\rangle {\mathbf{X}}_j\end{array}$$

where ${\Sigma }_j={(\mathbf{I}+\langle {\mathit{\tau }}_j\rangle \langle {\mathbf{W}}_j^{\mathrm{\top }}{\mathbf{W}}_j\rangle )}^{-1}$.

3.3 Comparison algorithms

We compare the performance of our proposed model to Elastic Net and BGFA. Elastic Net is a regularized linear regression with L₁ and L₂ penalties, which does continuous shrinkage, automatic variable selection and is able to select groups of correlated variables (Zou and Hastie, 2003). BGFA is a Bayesian formulation of generic factor analysis model with a specific group-wise sparsity prior, which generalizes the CCA model originally introduced by Hotteling (1936) and limited to exactly two views. This model is also known as ‘inter-battery factor analysis’ (Browne, 1979). Comprehensive overview of both methods is given in the Supplementary Materials.

4 Experimental results

We evaluate the predictive performance of our proposed model in cell lines profiled with the CCLE and CTRP drug panels. We perform feature selection to analyze the model’s ability to recapitulate known drug targets and response biomarkers. We compare the performance of GBGFA with that of Elastic Net (Zou and Hastie, 2003) and BGFA (Klami et al., 2013). Finally, we illustrate our model’s applicability in an unsupervised setting by applying GBGFA to TCGA PAAD and LUAD patient cohorts.

4.1 Predictive performance evaluation

To evaluate the predictive accuracy of the proposed model, we perform 5-fold cross-validation using data from CCLE and CTRP. For each dataset, we partition the data into five mutually exclusive subsets, each containing a nearly equal number of cell lines. Each of the five data subsets is used for testing of the model trained on the remaining four subsets. To achieve robust measurements, we report the average result of 10 random fold splits for each dataset. We calculate the proportion of variance explained (POV) to compare the three methods, i.e. $\text{POV}=1-\text{NRMSE}$,

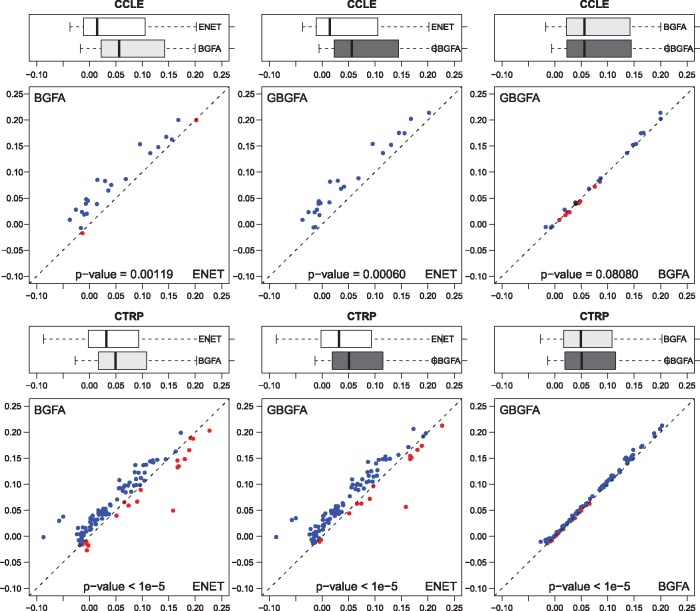
$\text{NRMSE}=\sqrt{\frac{{(\mathit{v}-\widehat{\text{v}})}^{\mathrm{\top }}(\mathit{v}-\widehat{\text{v}})}{{(\mathit{v}-\mathit{1}{\mathit{1}}^{\mathrm{\top }}\mathit{v}/N)}^{\mathrm{\top }}(\mathit{v}-\mathit{1}{\mathit{1}}^{\mathrm{\top }}\mathit{v}/N)}}$, where NRMSE is the normalized root mean square error, and $\mathit{v}$ and $\widehat{\mathit{v}}$ denote the observed and predicted values. The results of these experiments are summarized in Figure 3. The top and bottom rows correspond to the CCLE and the CTRP panels, respectively. Columns 1 through 3 illustrate pairwise method comparisons. Average values of 10 random data splits into training and testing sets for 5-fold cross-validation are reported. The boxplots illustrate the average proportion of variance explained for all drugs and the dot plots show results for individual drugs. Paired t-test P-value is also reported for each comparison.

Fig. 3.

Cross-validation results of drug response prediction. The top and bottom rows correspond to the CCLE and the CTRP panels, respectively. Columns 1 through 3 present the pairwise comparison of BGFA and Elastic Net, GBGFA and Elastic Net, and GBGFA and BGFA, respectively. The boxplots illustrate the average POV over all drugs and the dot-plots show POV for individual drugs

We use the $\text{glmnet}$ package to run Elastic Net (Friedman et al., 2010) and the CCAGFA package to run BGFA (Klami et al., 2013). When training Elastic Net, a tuning grid is used to optimize the α and λ parameters such that tested values are from $\{{10}^{-5},{10}^{-4},\dots ,{10}^0\}$ for α and $\{e^{-5},e^{-4},\dots ,e^0\}$ for λ. For GBGFA and BGFA, the best model is picked of 50 random restarts with hyperparameters ${\alpha }_{\gamma }={\beta }_{\gamma }={\alpha }_{\tau }={\beta }_{\tau }=1$e-14 and K = 50.

4.2 Prediction as a function of input data size

We further evaluate how decreasing the number of observations affects predictive performance. This question is important because most clinical trials have limited size patient cohorts, and this experiment allows us to investigate method performance in clinically relevant scenarios. For this purpose, for each of the 10 random splits into five partitions, we subset the training set in each experiment by selecting at random 75, 50 and 25% of the input cell lines. The results of these experiments are shown in Supplementary Figures S2 and S3 for CCLE and CTRP, respectively.

4.3 Prediction as a function of input feature type

We analyze the relative importance of each molecular feature type in the accuracy of predictions derived from GBGFA. For each of the two drug panels, CCLE and CTRP, and each random data split, we considered the input feature types gene expression (e), copy number (c), mutation measured by OncoMap (o), and mutation measured by hybrid-capture sequencing (h), and their respective combinations, with the corresponding POV as response. We fitted a random effects model using the lme4 R package (Bates et al., 2015) and calculated the percent variance explained by each factor and the residual. All non-zero factors are reported in Figure 4.

Fig. 4.

Analysis of predictive performance as a function of input data feature type

4.4 Feature selection performance evaluation

We evaluate our model’s ability to recapitulate known drug biomarkers (CCLE) and drug targets (CTRP) on a subset of compounds for which the targets or biomarkers are known (Supplementary Tables 1 and 2). For each drug panel, we learn models using combinations of input data comprised of gene expression (e), copy number (c), OncoMap mutation (o), and hybrid-capture sequencing mutation (h) data. We then perform feature selection by computing gene-centric scores.

In BGFA and GBGFA, for each drug i and view m, gene scores ${\mathit{s}}_{\mathit{i},\mathit{m}}$ are computed as the product of the view-specific projection matrix and the drug response vector ${\mathit{s}}_{\mathit{i},\mathit{m}}={\mathbf{W}}_{\mathbf{m}}{\mathit{w}}_{\mathit{i},\mathit{dr}}$ and standardized. An overall gene score for each drug i and gene g is computed by optimizing the absolute value of view-specific standardized gene scores $s_{i,g}^{*}={\text{argmax}}_{\forall m}\left|s_{i,m,g}\right|$. In Elastic Net, no standardization within views is required as different views are concatenated into a single input matrix and normalized together in the pre-processing step. To ensure fair comparison with BGFA and GBGFA in terms of total number of genes ranked, we similarly compute a gene-centric score by optimizing the absolute value of all available feature type weights per gene.

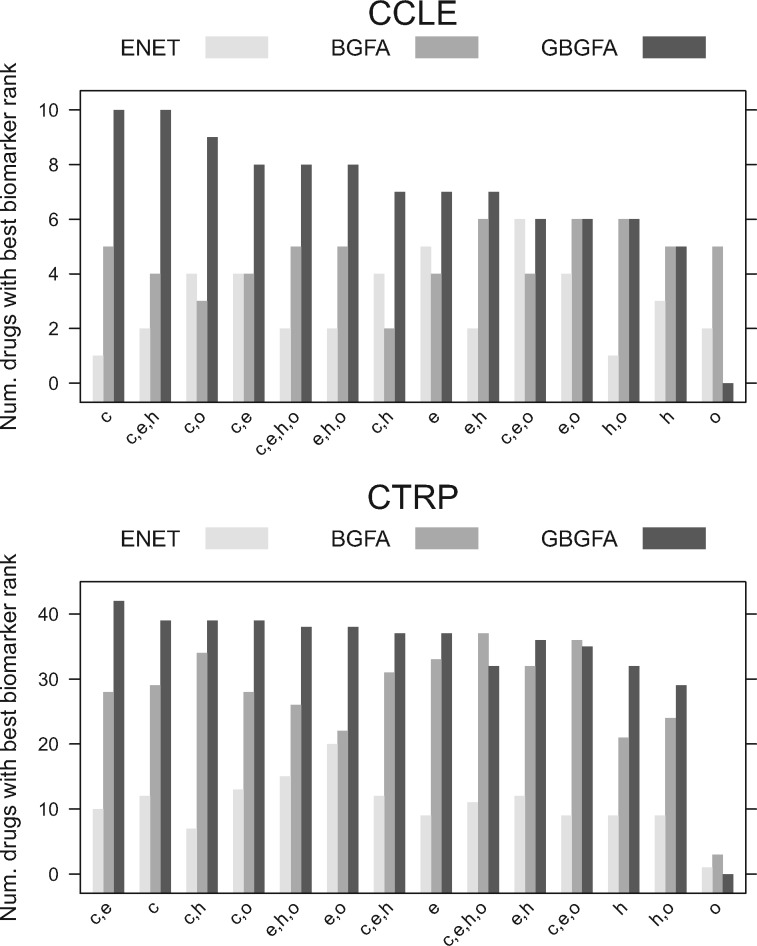
The computed gene scores are used to rank genes in decreasing order of importance (the first rank being the most relevant). We then consider how well each method ranks the biomarker or target of each compound across all input sets. Figure 5 summarizes the results: each bar corresponds to the performance of a given method on a given input dataset. Bar height indicates the number of drugs for which a given method scored better than all others. A total of 16 CCLE and 80 CTRP drugs had known biomarkers and targets, respectively.

Fig. 5.

Feature selection results for CCLE compounds (top) with known biomarkers and CTRP compounds (bottom) with known targets

4.5 Unsupervised learning in TCGA patient cohorts

We performed an exploratory analysis of TCGA PAAD and LUAD patient cohorts to illustrate the applicability of our model in an unsupervised scenario. For each cohort we train GBGFA on the mutation and gene expression data for all patients. We consider the overlapping genes between the mutation and expression sets (N  > 11 000) and compute gene-centric scores s_g for each gene g as the sum over hidden components of the product of expression and mutation weights, i.e. $s_g={\sum }_{k=1}^{K=200}{\prod }_{m=1}^2{\mathit{w}}_{m,g,k}$, where K is the number of hidden components of the learned model. We use the scores to rank genes and consider the top and bottom 100 genes ($<1\%$). We filter the selected genes by comparing their expression levels. A gene was deemed dysregulated if it was over- or under-expressed in samples carrying a mutation in that gene, as compared to the wild type samples (P <  0.05).

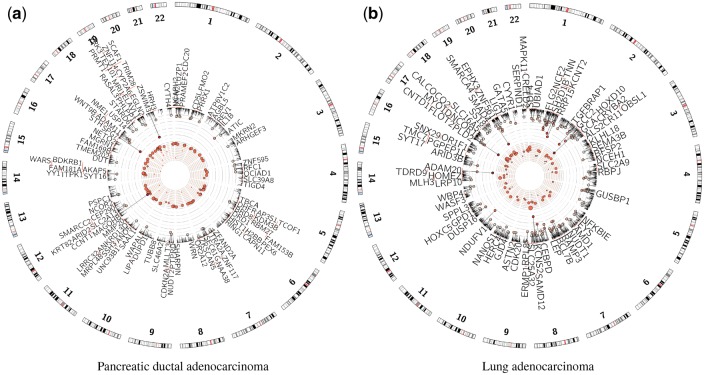
We performed functional annotation and pathway enrichment analysis of the identified genes using the gProfileR package version 0.5.3 with FDR as the multiple test correction method (Reimand et al., 2011), which integrates data from the Gene Ontology (Ashburner et al., 2000), Corum (Ruepp et al., 2009), KEGG (Kanehisa et al., 2013), and REACTOME (Croft et al., 2013) databases. These results are summarized in Supplementary Tables 3 and 4. The prioritized and dysregulated genes are shown in Figure 6.

Fig. 6.

Circos plots of TCGA data analysis results. Predicted essential genes are shown after learning models using gene expression (inner track) and mutation (outer track) data

5 Discussion

Predictive performance: We compared the predictive performance of GBGFA, BGFA and Elastic Net using 5-fold cross-validation. We reported the average POV on results from 10 random splits of the data into training and testing sets. The results are summarized in Figure 3 and the mean NRMSE and variance for each drug and test case are shown in Supplementary Tables 5 and 6. This comparison revealed that in CCLE, BGFA performed significantly better than Elastic Net (P = 0.0012); GBGFA improved upon Elastic Net even further (P = 0.0006). In CTRP, GBGFA performed significantly better than both Elastic Net and BGFA (P <1e-5). Our observations indicate that the integration of a gene-wise prior improved predictive performance as compared to Elastic Net and BGFA.

Predictive performance as a function of input data size: We next analyzed how decreasing the size of training input data affects predictive performance by observing 75, 50 and 25% of the complete input data for each random split. This analysis revealed that both GBGFA and BGFA tend to do better than Elastic Net as the input data size decreases (Supplementary Figs. S2 and S3). In CCLE, GBGFA achieved lower prediction error for more drugs than BGFA in the 100, 75 and 25% cases and tied in the 50% case (Supplementary Fig. S2, bottom row). In CTRP, GBGFA performed statistically better than BGFA (P$\le$3e-5) in all four cases (Supplementary Fig. S3, bottom row). Thus, we show consistent predictive performance improvement even when the sample size decreases.

Predictive performance as a function of input feature type: Finally, we analyzed predictive performance as a function of the input data feature type (Fig. 4). This analysis revealed that, consistent with previous studies, the majority of the variance, namely 84.5% in CCLE and 90.13% in CTRP, was explained by gene expression (Jang et al., 2014; Yuan et al., 2014). However, our results show that additional 15.3% in CCLE and 8.53% of the variance were captured by the combination of gene expression and copy number; in CTRP, a cumulative 9.62% of variance was explained by combinations of input feature matrices. In both CCLE and CTRP, $<1\%$ was attributed to the residual. We thus believe that the integration of the gene-wise prior allows us to leverage information in the combinations of molecular feature types that may otherwise not be used.

Feature selection: We compared the ability to recapitulate known drug targets and biomarkers of GBGFA, BGFA and Elastic Net in the same two drug panels, CCLE and CTRP. In CCLE, biomarkers for 16 of the total 24 drugs were compiled (Supplementary Table 1), while in CTRP, we used targets as a proxy to biomarkers instead. Of the 98 drugs considered, 80 had known targets (Supplementary Table 2). The three methods were compared on each input dataset and for each compound (Fig. 5). Our results indicate that GBGFA ranked CCLE biomarkers better than both other methods in 9 out of 14 cases, as compared to 1 for BGFA and none for Elastic Net. In the remaining four cases, we observed one tie with Elastic Net and three ties with BGFA. When ranking CTRP targets, GBGFA outranked BGFA and Elastic Net, respectively, by 11:3:0 with no observed ties. The overall relatively better performance of the two Bayesian methods as compared to Elastic Net in CTRP could be due to the multitask property that both GBGFA and BGFA employ and the ability to borrow information across compounds with similar response profiles could become more advantageous in larger drug panels (Gönen and Margolin, 2014). The overall superior performance of GBGFA over BGFA illustrates that the gene-wise prior captures relevant biological information and aids the model’s ability to better rank essential genes for drug response biomarkers.

Unsupervised learning: We applied our model in an unsupervised scenario to prioritize genes essential for the tumorigenesis of PAAD and LUAD in TCGA patient data. Figure 6 illustrates the predicted essential genes, based on gene expression and mutation data, in their respective physical locations on the chromosome. While somatic mutations in the KRAS oncogene and tumor suppressors, TP53, CDKN2A, SMAD4 are signature genomic events in PAAD, very little is known about additional genomic events that occur at lower frequencies and how these genes might reveal important pathways that impinge on pancreatic cancer progression. Our analysis identified the PBAF (Polybromo- and BAF containing complex) chromatin-remodeling complex, chromosomal organization and modifying enzymes (KDM3B, HIST1H2BB, PRMT1, NCOR2, SMARCC2, ARID2 and BRD8), a component of the polycomb repressive complex (RING1) and folate metabolism (DHFR) as important genes in the epigenetic etiology of PAAD (Locasale, 2013; Sanchez et al., 2012; Satijn and Otte, 1999; Wilson and Roberts, 2011 ). MicroRNAs are key regulators of oncogenesis and analysis of prioritized genes, which were mutated in at least three patients, identified a potentially important role for miR-30d, reduced expression of which is associated with poor prognosis in PAAD (Jamieson et al., 2012). In addition, high serum levels of IL-1B are associated with poor prognosis and can predict the efficacy of gemcitabine in patients with advanced pancreatic cancer (Mitsunaga et al., 2013).

When applied to the LUAD cohort, this analysis identified known tumor suppressors (SMAD4 and SMARCA4) (Medina et al., 2008; Orvis et al., 2014). Mutations and/or loss of heterozygosity (LOH) in these genes are common somatic events in the progression of LUAD which can also dictate response to therapeutics (Haeger et al., 2016). Massively parallel sequencing efforts on LUAD have recently identified RBM10 as a recurrent somatic mutation in non-small cell lung carcinoma (NSCLC) (Imielinski et al., 2012). RBPJ is implicated in the NOTCH mediated generation and maintenance of Kras (G12V)-driven NSCLC (Maraver et al., 2012), and hypermethylation of the GATA5 promoter correlates with clinicopathological parameters in lung cancer (Guo et al., 2004).

6 Conclusions and future work

We developed a novel Bayesian formulation of group factor analysis model with gene-centric prior to explicitly model the dependencies between genomic alterations of the same gene. Future work will extend our model to integrate prior information on functional (e.g. pathway) relationships between genes, as incorporation of such information has been demonstrated to be beneficial for drug sensitivity prediction (Costello et al., 2014; Jang et al., 2015). We are exploring modeling information from molecular pathway databases via a hierarchical prior over genes. We are also working on model extensions to enable learning in the presence of missing values.

Our current results show that the GBGFA model enables leveraging information from combinations of genomic data which improves the predictive performance and feature selection as compared to Elastic Net and BGFA. It also identifies biologically relevant genes for both PAAD and LUAD and should prove to be broadly applicable as an analytical tool for the covariate structure of biological data with high dimensionality and complexity.