Abstract
Motivation
Genome-wide association studies (GWAS) have played an important role in identifying genetic variants underlying human complex traits. However, its success is hindered by weak effect at causal variants and presence of noise at non-causal variants. In an effort to overcome these difficulties, a previous study proposed a regularized regression method that penalizes on the difference of signal strength between two consecutive single-nucleotide polymorphisms (SNPs).
Results
We provide a generalization to the afore-mentioned method so that more adjacent SNPs can be incorporated. The choice of optimal number of SNPs is studied. Simulation studies indicate that when consecutive SNPs have similar absolute coefficients our method performs better than using LASSO penalty. In other situations, our method is still comparable to using LASSO penalty. The practical utility of the proposed method is demonstrated by applying it to Genetic Analysis Workshop 16 rheumatoid arthritis GWAS data.
Availability and implementation
An implementation of the proposed method is provided in R package MWLasso.
1 Introduction
Genome-wide association studies (GWAS) is a powerful tool in the identification of genetic factors for complex diseases. It has been found by numerous studies that many complex diseases are associated with genetic variants among populations (Welter et al., 2014). However these identified variants explain only a small fraction of the heritability for most complex traits (Eichler et al., 2010; Lee et al., 2011; Manolio et al., 2009; Zuk et al., 2012). Hence there is a need for improved statistical methods. In this report we present a method for GWAS that scans the genome with a moving-window.
Usually, GWAS depends on single SNP (single nucleotide polymorphism) analysis by testing the association between each SNP and the trait of interest. Depending on the type of the trait, one can use linear regression or logistic regression. However, such single SNP analysis has limitations. A stringent significance level needs to be used in order to account for multiple testings. Genetic information in neighboring SNPs, such as the extent of linkage disequilibrium (LD), is not used which results in loss of power and excess of false discoveries.
From a statistical point of view, identifying SNPs associated with a trait is a variable selection problem in a sparse, high-dimensional model setting. Genetic variants underlying the trait are deemed to be rare in comparison with the vast number of SNPs that are genotyped. Variable selection is a classical problem in statistics. Traditional methods include the well-known forward, backward, or stepwise selection. Unfortunately these methods do not work properly for high-dimensional problems because the number of predictors is much larger than the sample size.
Recently regularized regression methods have become more and more popular for variable selection. In LASSO (least absolute shrinkage and selection operator) (Tibshirani, 1996), L1-norm is imposed as a penalty for the regression coefficients. LASSO can return sparse coefficient estimates and has been widely applied in variable selection. However, LASSO does not handle the correlation between predictors in a way meaningful in the context of GWAS. If the predictors are highly correlated, LASSO will tend to select few of the predictors and omit the others. In GWAS, SNPs in close genomic proximity tend to show high correlation due to LD. So LASSO will select few SNPs in a group of important ones and omit the rest.
Elastic net (Zou and Hastie, 2005) is an alternative regularized regression method. The penalty is imposed as a linear combination of LASSO penalty and the penalty used in the ridge regression (Hoerl and Kennard, 1970). An advantage of the ridged regression is that there is an explicit expression for the coefficient estimates. However, there is no sparse property on these estimates as none of them will be exactly equal to 0. By incorporating the LASSO penalty the elastic net regression method is able to achieve sparse coefficient estimates while handling the correlations among predictors properly.
Both LASSO and elastic net are convex regularized problems. Their coefficient estimates are biased as they are shrunken towards zero. Recently several non-convex regularized regression methods are developed. For instance, bridge regression (Fu, 1998), SCAD (Fan and Li, 2001) and MCP (Zhang, 2010). These methods can reduce the shrinkage effect and hence the bias in the regression coefficients.
In GWAS, there is a natural sequential structure for the SNPs. SNPs are located sequentially on the genome with known base-pair location. We note that none of the methods mentioned above takes into account such valuable information on predictors, i.e. SNPs in the current context.
If the SNPs can be separated into different groups, then the group LASSO (Yuan and Lin, 2006) seems to be a reasonable choice. The group LASSO imposes the L2-norm penalty on predictors in the same group and the L1-norm penalty on groups. Therefore, predictors from the same group will be selected or not selected collectively while predictors within a group are not forced to be sparse. Along the same idea, there are other group selection methods in high-dimensional models, such as group MCP and group bridge (Huang et al., 2012). These non-convex group selection methods are natural extensions of MCP and bridge regression. However application of these group selection methods to GWAS is not straightforward. Due to LD it is not obvious how to group SNPs. One approach might be to group SNPs based on gene definition and ignore cross-gene correlation. In this report we are interested in methods that can take advantage of the SNP structure without the need to group the SNPs in advance. One possible candidate method might be fused LASSO (Tibshirani et al., 2005).
Fused LASSO employs a smoothing penalty on the difference between the coefficients estimates of two consecutive features so that their effect sizes are close to each other. It can be used in variable selection and signal denoising for both 1-dimensional and 2-dimensional signals. It appears to be appealing for GWAS because two adjacent SNPs are expected to have similar effect size. However, the score of SNP depends on the choice of reference allele. For instance, genotypes aa, aA and AA can be scored as 0, 1 and 2, or equivalently as 2, 1 and 0, depending on whether allele a or allele A is chosen to be the reference allele for genotype scoring. Obviously, these two different ways of scoring yielding two effect sizes that are of opposite sign. Therefore, fused LASSO is not suitable for GWAS.
To smooth effect size at two consecutive SNPs SMCP (Liu et al., 2013) combines the MCP penalty with a smoothing penalty. This smoothing penalty is invariant to the choice of the reference allele for genotype scoring. In this report, we extend SMCP by introducing a moving-window regression. The smoothing penalty works over more than two SNPs while SMCP only smoothes two adjacent SNPs.
This report is organized as follows. We elaborate the details of the proposed method including the optimization algorithms to minimize the loss function. This method is developed for both continuous traits and binary traits. Simulation studies are described and the results are presented. Finally, the method is applied to a Genetic Analysis Workshop (GAW) 16 rheumatoid arthritis data.
2 Model
Let p be the number of SNPs and n the total number of subjects. The SNPs are indexed in their chromosomal order. The genotype score of subject i at SNP j is denoted by xij. Let nj be the number of subjects whose genotype at SNP j is non-missing and Θj the set of indices of such subjects. That is, . Genotype scores are normalized as usual such that and . The phenotype of subject i is denoted by yi.
The loss function, denoted by , is defined through a set of marginal models, one for each SNP. Here is a vector of regression coefficients. The main advantage of using marginal models is that it is very convenient to handle missing genotypes. If all SNPs were included simultaneously in a joint model, the missing genotypes would need to be imputed in the first place. Using marginal models obviates such a need.
Define the (quadratic) loss function by
| (1) |
where . For case-control designs, the trait y is dichotomous, and the βj in the quadratic loss function can still be interpreted as the effect size of SNP j (Liu et al., 2013), with a slight loss of power compared to logistic regression.
SMCP (Liu et al., 2013) imposed the following MCP penalty for SNP selection
Here λ is the penalty parameter, γ is the regularization parameter which controls concavity and . It approaches the LASSO penalty as and approaches the hard-thresholding as . So the LASSO penalty is a limiting case of the MCP penalty.
Let denote the Pearson correlation coefficient between genotype scores at SNPs j and j + 1 computed from subjects whose genotypes are non-missing at both SNPs. SMCP enforces the effect size of two adjacent SNPs to be similar by using the following smoothing penalty
where measures the strength of LD and η is a tuning parameter. The objective function of SMCP is
The penalty is responsible for SNP selection while the penalty is responsible for smoothing the effects of neighboring SNPs.
The smoothing penalty involves only two SNPs. In the context of GWAS, the effect of LD may well extend beyond two adjacent SNPs. Based on this consideration, we replace by a penalty that involves d consecutive SNPs, where the value of d is determined by data and can be larger than 2. To this end, we consider a moving window of size d that scans all SNPs from the beginning to the end. For SNPs in the same window, they are considered to be close enough and are expected to have similar strength of effects. Therefore, their effect size in terms of |β| are expected to be similar. Let Ws denote the set of SNP indices in the sth moving window. The total number of Ws is : . We define the following smoothing penalty for :
where the weight is defined as .
As for the penalty responsible for SNP selection, we choose the LASSO penalty instead of MCP. This is because the LASSO penalty is easier to deal with and it is a limiting case of MCP. The LASSO penalty is defined as:
So our objective function is defined as:
| (2) |
We also consider the following (logistic) loss function for dichotomous traits:
where and . Replacing the quadratic loss in (2) by leads to the objective function for dichotomous traits. This objective function is denoted by .
3 Computing algorithm
As in other high dimensional problems, a major challenge in estimating the model parameters is to find out a computational feasible way to optimize the objective function or . LAR (least angle regression) has been proposed as a feasible computation method for LASSO (Efron et al., 2004). Coordinate descent algorithm has been applied for both LASSO and elastic net (Friedman et al., 2010b) and some non-convex problems such as SCAD and MCP (Breheny and Huang, 2011). Block coordinate descent algorithm can be applied to grouped LASSO (Foygel and Drton, 2010; Friedman et al., 2010a). For fused LASSO, the coordinate descent algorithm diverges. Alternative direction method of multipliers (ADMM) (Wahlberg et al., 2012) and majorization-minimization (MM) algorithm (Chen et al., 2012) can be applied to minimize the objective function for fused LASSO. For SMCP, the coordinate descent algorithm is appropriate and there is an explicit solution in updating each βj (Liu et al., 2013). For the proposed moving-window regression, the coordinate descent algorithm is applicable. Details are described below.
3.1 Continuous traits
Given current values , βj is updated by the minimizer of which is defined as
where
It is straightforward to verify that
where C represents a term free of βj,
and
The minimizer of is the same as that of over βj, which is
We note that Pj and Qj are free of . They can be computed once in advance. The coordinate descent algorithm proceeds as Algorithm 1.
Algorithm 1.
Coordinate Descent Method for Continuous Traits
Compute Pj, Qj, for t = 0
Input the initial values
repeat
fordo
Fix
Compute Rj
Update
end for
until converges
The convergence of the coordinate descent algorithm can be shown as follows: the objective function can be written in the form of . Here f0 is the summation of the loss function and the smoothing penalty, while . Since is a regular function and is separable, the coordinate descent algorithm will converge to a stationary point, which should be a local minimal point of the objective function (Tseng, 2001).
3.2 Dichotomous traits
For dichotomous traits, we can use the quadratic loss function and hence apply Algorithm 1 described in the previous subsection. Now we introduce the coordinate descent method for the logistic loss function that applies only to dichotomous traits.
In the marginal logistic regression which tests the strength of association between the jth SNP and the phenotype, we define αj as the coefficient for the constant effect and βj as the coefficient for the SNP effect. Let and . The coordinate descent algorithm to minimize the depends on iteratively reweighted least squares. We use the following quadratic approximation to :
where
So the ‘working’ objective function is
The optimization problem is transformed to minimize an iteratively reweighted penalized linear squared function. Note that in this function, the intercept terms can not be omitted. This is different from the case of continuous traits discussed earlier. To ease computation burden, we fixed the values of at their respective estimates computed from their marginal logistic regressions. The optimization of is conducted with respect to only as follows.
Given current values , βj is updated by the minimizer of which is given by
where C is a term free of βj,
and Pj and Rj are defined in the same way as in the case of continuous traits. The minimizer of is
To summarize, the coordinate descent algorithm proceeds as Algorithm 2.
Algorithm 2.
Coordinate Descent Method for Dichotomous Traits
Estimate from the marginal logistic regressions. These values are then fixed.
Input the initial values
Compute zij, wij,
Compute Pj, Qj,
repeat
repeat
fordo
Fix
Compute Rj
Update
end for
until converges
Update zij and wij by using the current estimates
Update Pj, Qj,
until converges
Such algorithm can be considered as two nested loops: the outer loop is to update the quadratic approximation by using the current parameters , while the inner loop is to run the coordinate descent algorithm on the penalized weighted quadratic function.
Note that in this case Qj needs to be updated in each iteration. This is because now Qj depends on βj through zi.
3.3 Selection of tuning parameters λ and η
There are various ways for determining the value for tuning parameters. Common methods include AIC, BIC and cross-validation. These methods are intended to measure the prediction ability of the covariates. In GWAS, it is very likely that the covariates, i.e. the genotypes of disease-causing variants, are not directly observed although they are expected to be in LD with the observed SNPs. Furthermore, the goal of GWAS is to identify associated SNPs rather than prediction. Most importantly, the loss functions considered in this report are both marginal. Given these considerations, AIC, BIC and cross-validation are not suitable for the proposed method. A bisection method has been used to search for the values of tuning parameters (Liu et al., 2013; Wu et al., 2009). We use the same method here. This method needs a specification of a number of SNPs to be selected upfront. Let m denote this number. The tuning parameters are then determined so that the number of SNPs is no less than m (while keeping it as close to m as possible).
We begin by re-parameterizing the tuning parameters λ and η as follows: . To proceed, γ2 is fixed at 0.05. This is the value used for SMCP (Liu et al., 2013). The value of γ1 is determined by the bisection method. Let be the largest value of γ1 under which at least one SNP is selected. It is known that . Since γ1 cannot be zero, the lower bound of γ1 is set to be . We set . The bisection method involves an iterative process. Set and . We compute . Let be the number of selected SNPs under γ1. If , replace by . Otherwise, if , replace by . Repeat the process until . As a result, we are able to select the value of tuning parameters λ and η.
3.4 Selection of tuning parameter d
The window size d controls the number of SNPs to be included in a window. When d = 0, the penalty for the moving-window model is equivalent to the LASSO penalty. When d = 2, the smoothing penalty reduces to the one used in SMCP. Here we apply the empirical mean of the absolute value of lag- autocorrelations to select d. Let
s(d) is expected to be a non-increasing function of d. If so, its largest value occurs at d = 2. For any given value ρ which is not too small but is less than s(2), there would be a value such that . The value of d is determined by . Technically, the value of ρ is restricted to be no smaller than ρl, which is equal to for a small value . The value of ρ is pre-specified. In the simulation study, we will try and 0.15. In the empirical study to be reported later, we use and 0.4.
Since d takes only integer values, it should be pretty fast to select its value. If necessary, this procedure can be sped up by using a bisection method. Starting with and , set d = 2 as dl. s(d) are evaluated at . The smallest d that satisfies is denoted by du. Then we apply the bisection method. We set . If , replace du by dmid. Otherwise if , replace dl by dmid. As a result, we will find out the largest d such that faster.
4 Simulation
In the simulation study, we use part of the real genotype data from the rheumatoid arthritis (RA) study that were made available through Genetic Analysis Workshop (GAW) 16 (Amos et al., 2009). Only the trait values are simulated. In the next section, this data will be analyzed in whole for association with the observed trait.
There are 2062 subjects. 400 subjects are randomly selected. 5000 consecutive genotypes are selected from chromosome 6 arbitrarily. The reason they are consecutive is to maintain their LD structure. The genotypes are standardized in advance such that and . The continuous trait y is generated from the linear model:
| (3) |
where is a vector of SNP scores of subject i, is the vector of genetic effects for these SNPs. is the random residual sampled from a normal distribution with mean 0 and variance 1. The elements of are all 0, except that = (-0.3, 0.2, -0.25, 0.2, -0.6, 0.7, -0.5, 0.1, -0.5, 0.3, -0.6, 0.2) and = (0.25, -0.4, 0.2, -0.1, -0.25, 0.3, -0.4, -0.4, 0.15, 0.3, -0.4, 0.4, -0.5, 0.2, -0.3, 0.16, 0.36, -0.2, 0.1). That is, the number of truly non-zero βs is 31.
For the dichotomous trait, the systematic component for the logistic regression model is the same as that for the continuous trait. In particular, the dichotomous trait yi for subject i is generated from the Bernoulli distribution with probability yi = 1 given by , where is set to equal 0.
For the continuous trait, we used the marginal quadratic loss. For dichotomous trait, both the quadratic loss and the logistic loss were used.
To assess and compare the performance of different methods, we use recall and precision. Both measurements are derived from the number of true positives (TPs), the number of false positives (FPs) and the number of false negatives (FNs) as follows:
They measure the magnitude of TP relative to FP and FN, respectively. Both values are in the range with larger values indicative of better performance. PPV and TPR are also known as precision and recall, respectively.
The tuning parameter is fixed at 0.05. After several trials, the tuning parameter is chosen such that the number of selected SNPs (i.e. those with non-zero coefficients) is m = 45. The size d of the moving-window is determined for and 0.2 (see section ‘Selection of tuning parameter d’). The corresponding values of d are and 15, respectively. Simulation results based on 100 simulation replicates are shown in Table 1.
Table 1.
Positive predictive value and true positive rate over 100 replicates in mean (standard deviation)
| Continuous trait | Binary traita | Binary traitb | |
|---|---|---|---|
| Positive predictive value | |||
| LASSO | 0.4460(0.0423) | 0.4312(0.0399) | 0.4313(0.0400) |
| d=2 | 0.6024(0.0453) | 0.4940(0.0561) | 0.5787(0.0536) |
| d=4 | 0.6611(0.0349) | 0.5612(0.0526) | 0.6399(0.0392) |
| d=6 | 0.6790(0.0229) | 0.6352(0.0429) | 0.6753(0.0260) |
| d=10 | 0.6779(0.0247) | 0.6498(0.0441) | 0.6756(0.0275) |
| d=15 | 0.6649(0.0421) | 0.6378(0.0520) | 0.6580(0.0440) |
| True positive rate | |||
| LASSO | 0.6477(0.0618) | 0.6261(0.0580) | 0.6261(0.0580) |
| d=2 | 0.8745(0.0658) | 0.7171(0.0812) | 0.8400(0.0778) |
| d=4 | 0.9597(0.0507) | 0.8145(0.0764) | 0.9293(0.0570) |
| d=6 | 0.9887(0.0332) | 0.9223(0.0624) | 0.9803(0.0378) |
| d=10 | 0.9855(0.0424) | 0.9432(0.0640) | 0.9809(0.0399) |
| d=15 | 0.9652(0.0611) | 0.9258(0.0755) | 0.9551(0.0638) |
Note: The number of truly non-zero βs is 31. Truly non-zero βs are consecutive. ‘LASSO’ refers to LASSO penalty.
Binary trait with quadratic loss.
Binary trait with logistic loss.
First of all, there is indeed a performance improvement as more SNPs are included in the smoothing window. From LASSO penalty (i.e. d = 1) to the moving-window method with d = 6, both TPR and PPV are increasing for both the continuous trait and the binary trait with either quadratic loss or logistic loss. For the binary trait, this trend continues up to d = 10. After d = 6 the performance for the continuous trait starts to decrease. The same is also true for the binary trait for d > 10. This phenomenon is probably due to over-smoothing. Overall, d = 6 seems to be a suitable choice of the moving window size for this data.
At d = 6, the PPV for continuous trait is increased by 52%, compared to LASSO penalty (from 0.446 to 0.679) and by 12% compared to the case of d = 2 (from 0.6024 to 0.679). The TPR also increases 52 and 12%, respectively, compared to LASSO penalty (from 0.6477 to 0.9887) and the case of d = 2 (from 0.8745 to 0.9887).
For the binary trait with quadratic loss, at d = 6 the PPV increases 47 and 29%, respectively, compared to LASSO penalty (from 0.4312 to 0.6352) and the case of d = 2 (from 0.4940 to 0.6352) while the TPR is increased by 47 and 29%, respectively. For the binary trait with logistic loss, the PPV in increased by 57 and 17%, respectively, compared to LASSO penalty and the case of d = 2 while the TPR is increased by 57 and 17%, respectively, as well. The performance with logistic loss is better than the performance with quadratic loss in terms of both PPV and TPR. The downside of the logistic loss is that it involves more computation time.
Next, we consider a simulation study in which neighbouring SNPs do not have similar coefficients in the true model. The genotypes are the same as the previous simulation study. The elements of are all 0, except that = (-0.8, 0.4, -0.4, 1.2, -0.8). The number of truly non-zero βs is 5. Unlike the previous simulation study, the truly non-zero βs are not consecutive. β1524 and β1530 will be smoothed only if , while β2400 and β2403 will be smoothed only if . The tuning parameter is fixed at 0.05. The tuning parameter is chosen such that the number of selected SNPs (i.e. those with non-zero coefficients) is m = 7. Simulation results based on 100 simulation replicates are shown in Table 2.
Table 2.
Positive predictive value and true positive rate over 100 replicates in mean (standard deviation)
| Continuous trait | Binary traita | Binary traitb | |
|---|---|---|---|
| Positive predictive value | |||
| LASSO | 0.5557(0.1283) | 0.5786(0.1258) | 0.5786(0.1258) |
| d=2 | 0.5557(0.1283) | 0.5743(0.1251) | 0.5736(0.1254) |
| d=4 | 0.5343(0.1229) | 0.5586(0.1302) | 0.5593(0.1296) |
| d=6 | 0.5357(0.1241) | 0.5600(0.1246) | 0.5571(0.1227) |
| d=10 | 0.5314(0.1285) | 0.5586(0.1237) | 0.5571(0.1243) |
| d=15 | 0.5343(0.1278) | 0.5586(0.1237) | 0.5571(0.1227) |
| True positive rate | |||
| LASSO | 0.778(0.1796) | 0.810(0.1761) | 0.810(0.1761) |
| d=2 | 0.778(0.1796) | 0.804(0.1752) | 0.802(0.1764) |
| d=4 | 0.748(0.1720) | 0.782(0.1822) | 0.782(0.1822) |
| d=6 | 0.750(0.1738) | 0.784(0.1745) | 0.780(0.1717) |
| d=10 | 0.744(0.1800) | 0.782(0.1731) | 0.780(0.1741) |
| d=15 | 0.748(0.1789) | 0.782(0.1731) | 0.780(0.1717) |
Note: The number of truly non-zero βs is 5. Truly non-zero βs are not consecutive. ‘LASSO’ refers to LASSO penalty.
Binary trait with quadratic loss.
Binary trait with logistic loss.
In this simulation study, the assumption that neighboring SNPs have similar |β| values is not true. From LASSO penalty to the moving-window method with d = 4, both TPR and PPV decrease slightly for both the continuous trait and the binary trait with either quadratic loss or logistic loss. For the continuous trait, the PPV decreased from 0.5557 (LASSO penalty) to 0.5343 (d = 4). The TPR decreased from 0.778 (LASSO penalty) to 0.748 (d = 4), respectively. After d = 4, the PPV and TPR remain stable up to d = 15, for both the continuous trait and the binary trait with either quadratic loss or logistic loss. The differences in the PPV and TPR are not significant, suggesting that the moving-window method performs no worse than using LASSO penalty even when neighboring SNPs do not have similar |β| values.
5 Empirical study of GAW 16 rheumatoid arthritis data
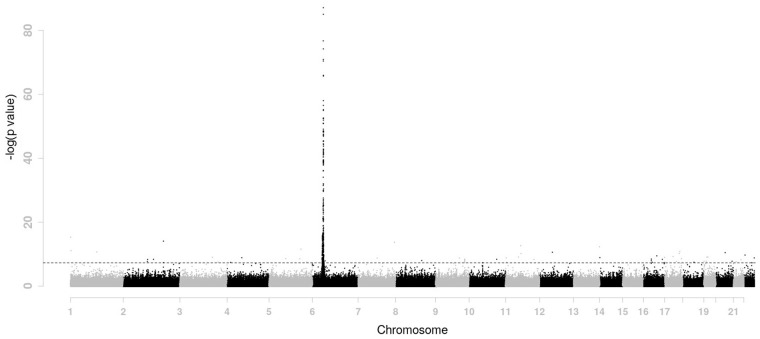
Rheumatoid arthritis is a complex human disorder with a prevalence ranging from around 0.8% in Caucasians to 10% in some native American groups (Amos et al., 2009). Several studies showed that rheumatoid arthritis was associated with genetic markers (Huizinga et al., 2005; Silman and Pearson, 2002). GAW 16 data are from the North American Rheumatoid Arthritis Consortium (NARAC). It is the initial batch of the whole genome association data for the NARAC cases (N = 868) and controls (N = 1194) after removing duplicated and contaminated samples. There are 531 689 SNPs across 22 autosomes. The phenotype y is binary, where y = 0 for controls and y = 1 for cases. The SNP scores were standardized in advance. We first did a regular genome wide association study in which each SNP was tested for association individually. Their negative log p-value computed from a simple logistic regression were presented in Figure 1. A strong association signal is present on chromosome 6. We apply LASSO penalty and the proposed moving-window method for the purpose of selecting SNPs and compare their results.
Fig. 1.
P values (-transformed) across the genome for the GAW 16 data. P = is indicated by the horizontal dashed line
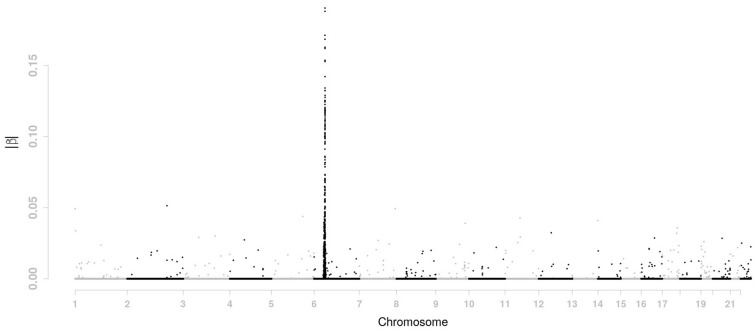
For LASSO penalty, the tuning parameter λ is 0.0516 and η is 0 in order to choose m = 800 SNPs. The 800 SNPs chosen by LASSO penalty are identical to the 800 SNPs which are most strongly correlated with the phenotype in the marginal regression shown in Figure 1. The estimated βs are presented in Figure 2. Most of the selected SNPs are located on chromosome 6. On all other chromosomes, there are few non-zero βs.
Fig. 2.
Estimated value of |β| across the genome for the GAW 16 data using LASSO penalty
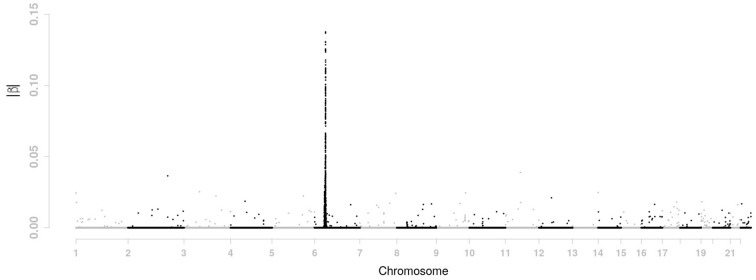
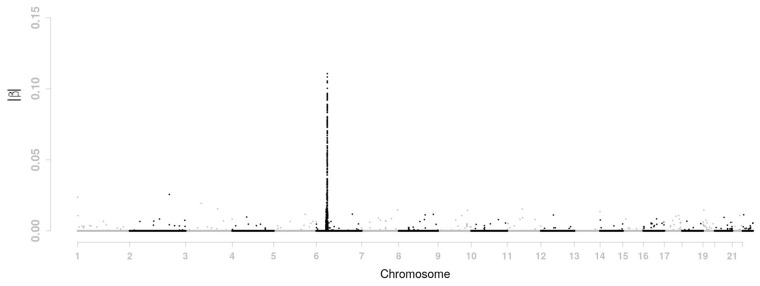
Here is what we did with the proposed moving-window method. Simulation study in the previous section suggest is an appropriate choice for the GAW 16 data. In the simulation study only chromosome 6 data were used to determine the size d of the moving-window and we got d = 6 for . Now we use data from all chromosome to determine d. The value for d is turned out to be again 6 given that and . In addition, we also considered the case of ρ = 0.4. This is also a value of ρ considered in the simulation study where the corresponding d was 2. Interestingly, the value of d for ρ = 0.4 remains 2 when data from all genomes are used. The tuning parameter is set at 0.05 and the tuning parameter was chosen such that the number of selected SNPs (i.e. those whose βs are not equal to 0) is 800. When d = 2, the tuning parameters are and . When d = 6, we have and . The estimated βs for these two situations are presented in Figures 3 and 4, respectively.
Fig. 3.
Estimated value of |β| across the genome for the GAW 16 data using moving-window regression with d = 2
Fig. 4.
Estimated value of |β| across the genome for the GAW 16 data using moving-window regression with d = 6
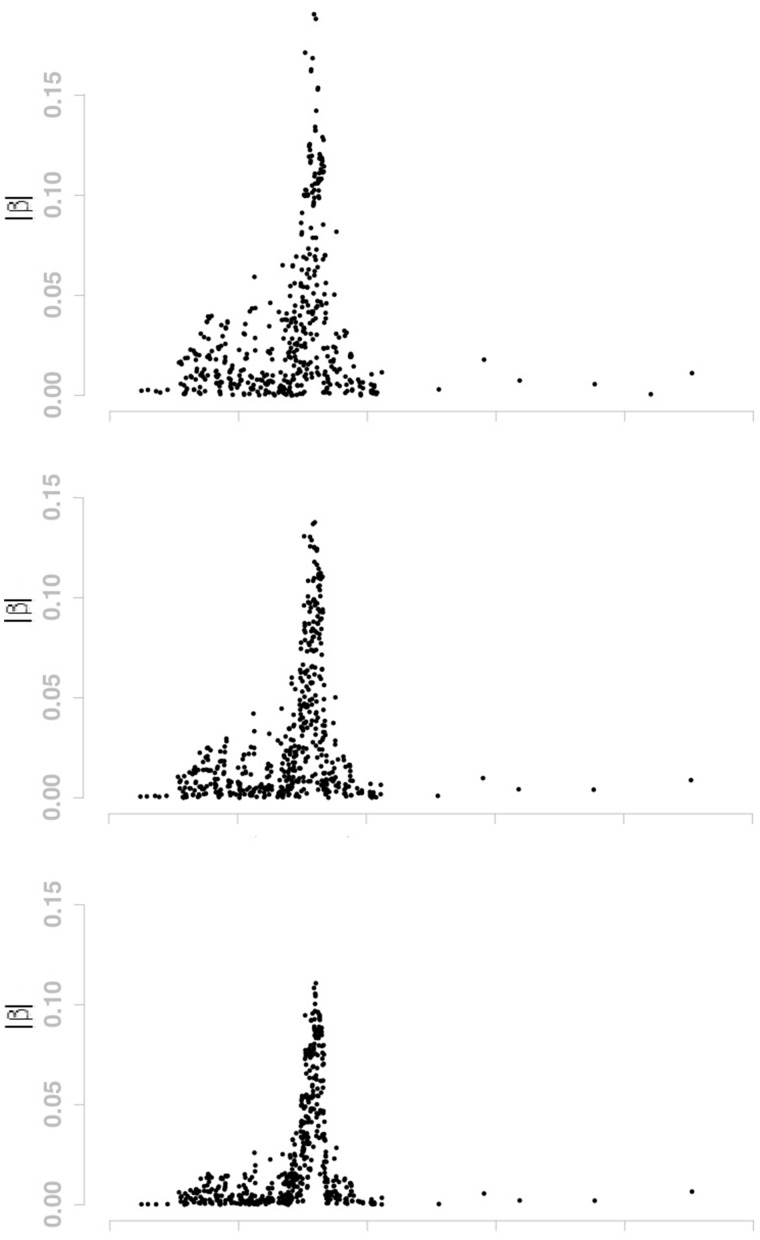
There is a shrinkage effect on the estimates of |β|s. For LASSO penalty, the max value of |β|s is about 0.19. It becomes 0.14 and 0.11 for d = 2 and d = 6, respectively. Such effect comes from the smoothing penalty. As window size d increases, the effect of the smoothing penalty becomes stronger. The moving-window regression model also has a clustering effect. It tends to choose adjacent SNPs with high LD together. For instance, as d increases from 0 (i.e. LASSO penalty), 2, to 6, more and more selected SNPs are located on chromosome 6. The number of selected SNPs is 489 for LASSO penalty, 513 for the case of d = 2 and 540 for d = 6. In order to show the shrinkage effect and clustering effect more clearly, the β estimates on part of chromosome 6 are displayed in Figure 5 for LASSO penalty, d = 2, and d = 6.
Fig. 5.
Estimated values of |β| on part of chromosome 6 for the GAW 16 data. From top to bottom: (1) LASSO penalty; (2) Moving-window regression with d = 2; (3) Moving-window regression with d = 6
6 Discussion
We have proposed a penalized moving-window regression method that incorporates adjacent LD information in genome-wide association studies. This method is an extension to the SMCP method in that the smoothing penalty considers more than two SNPs. By including more SNPs in a smoothing window, it is expected that valuable LD information among neighboring SNPs can be better utilized. For dense SNPs typically seen in nowadays association studies, LD information captured by two SNPs may be rather limited. Indeed, our simulation has demonstrated that including more than two SNPs in a moving-window does improve the precision and recall rate of association studies. The proposed moving-window regression also has a clustering effect in which SNPs in LD tend to be selected together. The simulation study also confirms the intuition that including too many SNPs has a negative effect on the performance of the proposed method as true signals tend to be smoothed out while false signals tend to be picked up.
Kim et al. (2014) proposed a hypothesis testing approach related to penalized regression called TLP-SG. The penalized regression shrinks the difference of s only if the difference is relatively small as compared to a tuning parameter τ. Thus, it avoids severely biasing the coefficient estimate towards zero by shrinking it towards a null coefficient. In the moving-window method, the strength of the smoothing penalty is controlled by . Thus, |β|s are smoothed only if there exist high correlations. A possible future work is to apply the moving-window method on hypothesis testing (Kim et al., 2014).
We also described two coordinate descend algorithms for the proposed method: one for quadratic loss and the other for logistic loss. To enhance the computation speed, explicit expressions for updating parameter estimates are given for each step of the algorithm.
We have used a constant window size d across the genome in order to achieve computation efficiency. In theory, it is possible to make d adaptive to local features of genetic structure such as the density of SNPs and the strength of LD at the cost of extra computation time.
We note that is proportional to the sample variance of the |β|s that are in window Ws. So the smoothing penalty can be regarded as a measure of variation in |β|s that are in Ws but with pair-wise weights .
The proposed method has been implemented in a freely available R package named MWLasso.
Acknowledgements
We would like to thank Associate Editor Dr. John Hancock and three anonymous reviewers for their valuable suggestions. The GAW 16 was supported by NIH grant R01 GM031575 from the National Institute of General Medical Sciences.
Conflict of Interest: none declared.
References
- Amos C.I. et al. (2009) Data for genetic analysis workshop 16 problem 1, association analysis of rheumatoid arthritis data BMC Proc., 3, S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breheny P., Huang J. (2011) Coordinate descent algorithms for nonconvex penalized regression, with applications to biological feature selection. Ann. Appl. Stat., 5, 232–253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X. et al. (2012). A two-graph guided multi-task lasso approach for eqtl mapping. In: International Conference on Artificial Intelligence and Statistics, pp. 208–217.
- Efron B. et al. (2004) Least angle regression. Ann. Stat., 32, 407–499. [Google Scholar]
- Eichler E.E. et al. (2010) Missing heritability and strategies for finding the underlying causes of complex disease. Nat. Rev. Genet., 11, 446–450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J., Li R. (2001) Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc., 96, 1348–1360. [Google Scholar]
- Foygel R., Drton M. (2010). Exact block-wise optimization in group lasso and sparse group lasso for linear regression. arXiv preprint arXiv: 1010.3320.
- Friedman J. et al. (2010a). A note on the group lasso and a sparse group lasso. arXiv preprint arXiv: 1001.0736.
- Friedman J. et al. (2010b) Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw., 33, 1–22. [PMC free article] [PubMed] [Google Scholar]
- Fu W.J. (1998) Penalized regressions: the bridge versus the lasso. J. Comput. Graph. Stat., 7, 397–416. [Google Scholar]
- Hoerl A.E., Kennard R.W. (1970) Ridge regression: Biased estimation for nonorthogonal problems. Technometrics, 12, 55–67. [Google Scholar]
- Huang J. et al. (2012) A selective review of group selection in high-dimensional models. Stat. Sci. Rev. J. Inst. Math. Stat., 27, 481–499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huizinga T.W. et al. (2005) Refining the complex rheumatoid arthritis phenotype based on specificity of the hla–drb1 shared epitope for antibodies to citrullinated proteins. Arthritis Rheum., 52, 3433–3438. [DOI] [PubMed] [Google Scholar]
- Kim S. et al. (2014) Penalized regression approaches to testing for quantitative trait-rare variant association. Front. Genet., 5, 121.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S.H. et al. (2011) Estimating missing heritability for disease from genome-wide association studies. Am. J. Hum. Genet., 88, 294–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J. et al. (2013) Accounting for linkage disequilibrium in genome-wide association studies: a penalized regression method. Stat. Interface, 6, 99–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manolio T. et al. (2009) Finding the missing heritability of complex diseases. Nature, 461, 747–753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silman A.J., Pearson J.E. (2002) Epidemiology and genetics of rheumatoid arthritis. Arthritis Res., 4, S265–S272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R. (1996) Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Methodological), 58, 267–288. [Google Scholar]
- Tibshirani R. et al. (2005) Sparsity and smoothness via the fused lasso. J. R. Stat. Soc. Ser. B (Statistical Methodology), 67, 91–108. [Google Scholar]
- Tseng P. (2001) Convergence of a block coordinate descent method for nondifferentiable minimization. J. Optim. Theory Appl., 109, 475–494. [Google Scholar]
- Wahlberg B. et al. (2012). An admm algorithm for a class of total variation regularized estimation problems. arXiv preprint arXiv: 1203.1828.
- Welter D. et al. (2014) The NHGRI GWAS Catalog, a curated resource of SNP-trait associations. Nucleic Acids Res., 42, D1001–D1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu T.T. et al. (2009) Genome-wide association analysis by lasso penalized logistic regression. Bioinformatics, 25, 714–721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan M., Lin Y. (2006) Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Ser. B (Stat. Methodol.), 68, 49–67. [Google Scholar]
- Zhang C.-H. (2010) Nearly unbiased variable selection under minimax concave penalty. Ann. Stat., 38, 894–942. [Google Scholar]
- Zou H., Hastie T. (2005) Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B (Stat. Methodol.), 67, 301–320. [Google Scholar]
- Zuk O., Hechter E.. et al. (2012) The mystery of missing heritability: genetic interactions create phantom heritability. Proc. Natl. Acad. Sci. USA, 109, 1193–1198. [DOI] [PMC free article] [PubMed] [Google Scholar]