Potential for Bias When Estimating Critical Windows for Air Pollution in Children’s Health

Abstract

Evidence supports an association between maternal exposure to air pollution during pregnancy and children’s health outcomes. Recent interest has focused on identifying critical windows of vulnerability. An analysis based on a distributed lag model (DLM) can yield estimates of a critical window that are different from those from an analysis that regresses the outcome on each of the 3 trimester-average exposures (TAEs). Using a simulation study, we assessed bias in estimates of critical windows obtained using 3 regression approaches: 1) 3 separate models to estimate the association with each of the 3 TAEs; 2) a single model to jointly estimate the association between the outcome and all 3 TAEs; and 3) a DLM. We used weekly fine-particulate-matter exposure data for 238 births in a birth cohort in and around Boston, Massachusetts, and a simulated outcome and time-varying exposure effect. Estimates using separate models for each TAE were biased and identified incorrect windows. This bias arose from seasonal trends in particulate matter that induced correlation between TAEs. Including all TAEs in a single model reduced bias. DLM produced unbiased estimates and added flexibility to identify windows. Analysis of body mass index z score and fat mass in the same cohort highlighted inconsistent estimates from the 3 methods.

There is a growing body of epidemiologic and experimental evidence that supports an association between maternal exposures to air pollution and both birth and children’s health outcomes, including decreased birth weight and increased risk of preterm birth and childhood wheeze (1–8). Because prenatal development occurs through a multiple-event process starting in early gestation (9), it is hypothesized that the association between maternal exposure to air pollution and children’s health outcomes may vary throughout pregnancy. In particular, there may be critical windows during which there is an increased association between prenatal exposure and a future health outcome (10–12). However, different statistical approaches to estimate the association between exposure over the course of pregnancy and future health outcomes can result in substantially different estimates of the exposure effect and can identify different critical windows.

With regards to air pollution and child health, the most commonly used approach to estimate the association between maternal exposures during pregnancy and a future health outcome is to regress the outcome on each trimester average exposure (TAE) separately in 3 regression models. Several recent papers reviewed numerous studies that have taken this approach to estimate the association between maternal exposures to fine particulate matter (having an aerodynamic diameter of ≤2.5 μm (PM_2.5)) and children’s health outcomes (3, 13, 14). The use of TAEs is particularly appealing because it is easy to implement and interpret. Further, it is convenient given that pregnancy is typically 9 months long and easily broken down into intervals of 3 months. However, biological changes do not cleanly follow 3-month intervals, and the potential for windows to span multiple trimesters or to exist in periods shorter or longer than 3 months must be considered.

Several recent studies have proposed data-driven methods, such as distributed lag models (DLMs), to estimate the association between maternal exposure to PM_2.5 and children’s health outcomes (15–19). The DLM framework was originally developed for time-series analysis where an outcome observed on a given day is regressed on exposures over a previous time period to estimate how the effect of exposure on 1 day is distributed over the subsequent time period (20, 21). When applied to maternal exposure during pregnancy, the DLM regresses a child’s health outcome on exposure measured at regular intervals, such as daily or weekly, throughout the pregnancy. In this setting, the DLM estimates the time-varying association between a time-varying exposure and an outcome observed at a single time. DLMs are often constrained so that the exposure effect varies smoothly over time using a parametric model (such as a quadratic function of time), splines, Bayesian priors, or other penalization approach (21, 22), but they are not constrained to correspond with clinically defined trimesters. Hence the class of DLMs is a data-driven approach to identifying critical windows and is likely to identify critical windows that would be missed by traditional regression approaches.

This work was motivated by analyses of data from a Boston-area prebirth cohort designed to identify critical windows of air pollution exposures on multiple children’s health outcomes. Preliminary analyses of the relationship between weekly PM_2.5 exposure and several children’s health outcomes showed that the results were sensitive to the analysis method used and different conclusions would be reached with different methods. In the present work, we compared statistical approaches to estimating the association between maternal exposure to air pollution during pregnancy and children’s health outcomes in both a simulation study and data analysis. The approaches are: 1) a model with a single TAE without controlling for exposures in the other 2 trimesters; 2) a model containing all TAEs in a single regression model; and 3) a DLM. The simulation study is designed to illustrate and quantify the bias in the estimated time-varying exposure effects using these methods under 6 realistic scenarios. We then illustrated the sensitivity of estimates obtained from the methods by estimating the relationship between PM_2.5 and each of body mass index z score (BMIz) and fat mass in the same cohort as a case study.

METHODS

Data

We used data from the Asthma Coalition on Community, Environment, and Social Stress (ACCESS) project (23). ACCESS is a prospective, longitudinal study originally funded to recruit n = 500 mother-child pairs between August 2002 and January 2007. The women were at least 18 years of age, spoke English or Spanish, and received prenatal care at one of 2 hospitals in the Boston, Massachusetts, area or at affiliated community health centers.

Between 3 and 6 (mean = 3.95; standard deviation, 0.67) years of age, child weight and height were measured using a calibrated scale. BMIz was derived based on 2000 Centers for Disease Control and Prevention reference data (24), based on the sex of the child and age at measurement. Fat mass was determined based on bipolar bioelectrical impedance assessed using the BIM4 bioimpedance analyzer (Impedimed, Queensland, Australia) (25).

Maternal exposures to PM_2.5 were estimated based on residential address using a hybrid land-use regression model that incorporated satellite-derived aerosol optical depth measures (26). Each mother was assigned an average PM_2.5 exposure value for each week of pregnancy based on the predicted values at her address of residence. We limited our analysis to full-term births (at least 37 weeks’ gestation) and to exposures during the first 37 weeks of pregnancy, for which we had complete exposure data for all full-term births.

Statistical methods

We estimated the association between weekly PM_2.5 exposure over the first 37 weeks of pregnancy and 2 outcomes, BMIz and fat mass, using linear regression. To compare the estimates under different modeling assumptions, we employed different regression approaches.

Separate TAE

The “separate TAE” approach uses separate regression models to estimate the association between each of the TAEs and the outcome. The model to estimate the association between the jth TAE (TAE_j for j = 1,2,3) and the outcome (Y) for individual $i=1,\dots ,n$ is

$$Y_i={\mathrm{\beta }}_j^S+{\mathrm{\alpha }}_j^S\mathrm{TA}{\mathrm{E}}_{ij}+z_i^T{\mathrm{\gamma }}_j^S+{ϵ}_{ij}^S,$$ (1)

where $z_i$ is a vector of baseline covariates, ${\mathrm{\beta }}_j^S$, ${\mathrm{\alpha }}_j^S$, and ${\mathrm{\gamma }}_j^S$ are unknown regression coefficients, and ${ϵ}_{ij}^S$ are independent and identically distributed mean zero residuals. We fitted this model separately for each TAE, j = 1,2,3. Each model estimates the association between 1 TAE and the outcome without controlling for the other 2 TAEs. The regression coefficient ${\mathrm{\alpha }}_j^S$ represents the cumulative effect over trimester j.

Joint TAE

The “joint TAE” approach estimates the association between all TAEs and the outcome in a single regression model. The joint TAE model is

$${\mathit{Y}}_i={\mathrm{\beta }}_0^J+{\mathrm{\alpha }}_1^J{\mathrm{TAE}}_{i1}+{\mathrm{\alpha }}_2^J{\mathrm{TAE}}_{i2}+{\mathrm{\alpha }}_3^J{\mathrm{TAE}}_{i3}+{\mathrm{z}}_i^T{\mathrm{\gamma }}^J+{ϵ}_i^J.$$ (2)

Using this approach, ${\mathrm{\alpha }}_j^J$ represents the cumulative effect over trimester j adjusted for the other 2 TAEs.

Distributed lag model

The DLM assumes that the association between exposure and outcome varies smoothly over time. The DLM takes the form

$${\mathit{Y}}_i={\mathrm{\beta }}_0^D+\sum _{t=1}^{37}{\mathrm{\alpha }}_t^D{\mathrm{PM}}_{it}+{\mathrm{z}}_i^T{\mathrm{\gamma }}^D+{ϵ}_i^D,$$ (3)

where ${\mathrm{\alpha }}_t^D$ is the regression coefficient for week t. While any of several models for the functional form of ${\mathrm{\alpha }}_t^D$ as a function of t can be employed (17–19, 27), we modeled ${\mathrm{\alpha }}_t^D=\mathrm{\alpha }(t)$ as a natural cubic spline. The model controls for the exposure in every other week but makes the assumption that the association between exposure and outcome varies smoothly across weeks. Fitting this model requires the specification of the degrees of freedom of the natural splines. We selected degrees of freedom by letting it range from 3 to 20 and selecting the best-fitting model using generalized cross-validation (28).

The DLM estimates the weekly association between exposure and outcome. The 2 TAE-based models estimate the cumulative exposure effect over each trimester. To make the models comparable, we divided the estimated regression coefficient from the joint and separate TAE approaches by the number of weeks in a given trimester. This results in an estimate of the weekly association between exposure and outcome.

Simulation study

We compared the methods in a simulation study designed to evaluate the bias in each method under 6 plausible patterns for the time-varying exposure effect. This included an exposure effect in 1 trimester only, exposure effect in multiple trimesters, constant exposure effect over the whole pregnancy, and no exposure effect.

For the simulation study we used the observed PM_2.5 exposures from the 238 births in the ACCESS data for which there were complete exposure data (up to 37 weeks). Using the real exposure from the ACCESS data ensured realistic seasonal trends and autocorrelation among the weekly exposures.

We simulated the outcomes from a DLM following equation 3. The week-specific exposure effects were constructed to vary smoothly over time using B-splines, and the outcome is Gaussian with variance 100. This gave an average signal-to-noise ratio of about 1:5 across the 6 scenarios. The simulation assumed that no other covariates affect the outcome. In order to isolate the impact of the choice of model, and not any additional residual confounding, there were no seasonal trends in the simulation other than those that can be fully explained by the observed PM_2.5 exposures. Additional details on the simulation are provided in Web Appendix 1 (available at https://academic.oup.com/aje).

We compared the performance of the regression approaches in 6 simulated scenarios. These scenarios are specified to have: exposure effect in a critical window that aligns with clinically defined trimesters (scenarios 1 and 2); exposure effect in a critical window that does not align with clinically defined trimesters (scenarios 3 and 4); a constant exposure effect across all 37 weeks (scenario 5); and no exposure effect (scenario 6). For each scenario, we simulated 1,000 data sets and analyzed each data set with all of the regression approaches.

Analysis of the association between PM_2.5 and BMIz and fat mass

We applied the approaches to estimate the association between maternal exposure to PM_2.5 during pregnancy and child BMIz and fat mass in the ACCESS cohort, both overall and stratified by sex.

We controlled for potential confounding variables: maternal age at enrollment, maternal prepregnancy body mass index, child age at measurement of BMIz and fat mass, an indicator for mother self-reported race (African-American, Hispanic, non-Hispanic White), and an indicator for mother’s highest level of education less than a high school diploma. In addition, we included indicators for missing race, educational level, maternal body mass index, season of birth, and child’s sex.

RESULTS

Correlation in the TAEs

There were 238 mother-child pairs for which there were complete data on exposure through 37 weeks’ gestation and BMIz. Complete information including fat mass was available for 224 of those children. Table 1 shows the average and standard deviation of the TAEs as well as the correlation between the TAEs for PM_2.5 among the 238 births. The mean exposure was fairly constant across trimesters, ranging from 10.65 μg/m³ to 10.81 μg/m³. The standard deviations range from 1.52 to 1.87. The TAEs are correlated. TAE₁ and TAE₃ are positively correlated with each other (Pearson correlation, 0.67). On the other hand, TAE₂ is negatively correlated with both TAE₁ and TAE₃ (correlations of −0.34 and −0.39, respectively).

Table 1.

Summary of Trimester Average Exposures for 238 Mother-Child Pairs Using Data From the Asthma Coalition on Community, Environment, and Social Stress in Boston, Massachusetts, 2002–2009^a

	PM2.5 in μg/m3, Mean (SD)	Correlation With
		TAE1	TAE2	TAE3
TAE1	10.81 (1.87)	1.00	−0.34	0.67
TAE2	10.69 (1.52)	−0.34	1.00	−0.39
TAE3	10.65 (1.83)	0.67	−0.39	1.00

Abbreviations: PM_2.5, particulate matter having an aerodynamic diameter of ≤2.5 μm; SD, standard deviation; TAE, trimester average exposure.

^a The table shows the mean values and standard deviations of the TAE for each trimester and the Pearson correlation between TAEs.

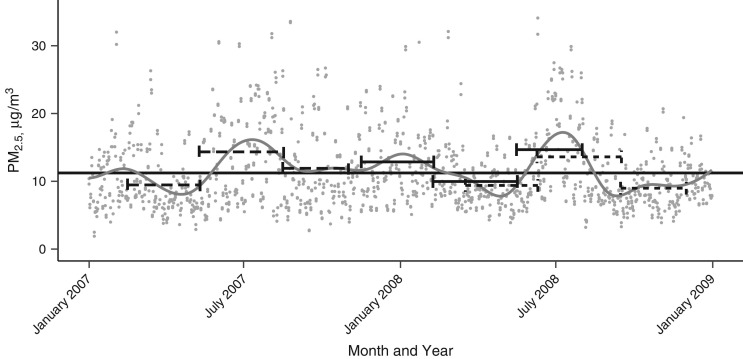
Figure 1 illustrates that this correlation structure arises from seasonal trends in PM_2.5. The figure shows PM_2.5 levels in Suffolk County, Massachusetts, in 2007 and 2008, as an example, with a smoothed trend line. The horizontal lines span the first, second, and third trimesters for hypothetical births. The height of the lines shows levels of the TAEs for each hypothetical birth. For each of the hypothetical births, the TAEs show an oscillating up-down-up or down-up-down pattern. This pattern results in the positive correlation between TAE₁ and TAE₃ and negative correlation between TAE₂ and the other 2 TAEs.

Figure 1.

Illustration of how seasonal patterns in particulate matter having an aerodynamic diameter of ≤2.5 μm (PM_2.5) result in the correlation between trimester average exposures (TAEs) in Suffolk County, Massachusetts, 2007 and 2009. The gray dots are PM_2.5 values, and the gray line is the smoothed trend. The horizontal line segments illustrate the TAEs for hypothetical births (each line type—solid, long dash, and short dash—is a different birth). The horizontal line segments are vertically aligned to the TAE and each span 1 trimester.

Simulation study

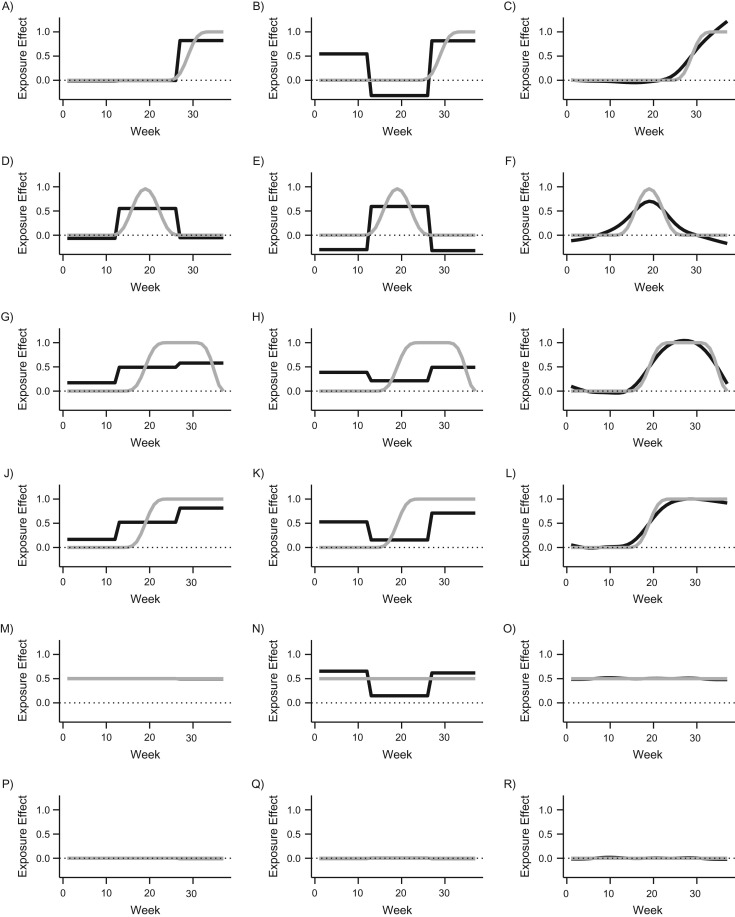
Figure 2 shows results from the simulation study. In scenarios 1 and 2, we simulated situations where there was an exposure effect in 1 trimester only (in trimester 3 for scenario 1 and in trimester 2 for scenario 2). For the trimester where there was a true exposure effect, all methods yield an unbiased effect estimate. Additionally, joint TAE and DLM both resulted in unbiased estimates in the trimesters where there was no exposure effect. However, estimates from the separate TAE approach were biased in the trimesters where there was no true exposure effect. Specifically, estimates in scenario 1 from the separate TAE approach were positively biased in TAE₁ and negatively biased in TAE₂. In scenario 2, the estimates using the separate TAE approach were negatively biased for both TAE₁ and TAE₃. Hence, when there was a true exposure effect in only 1 trimester, both joint TAE model and DLM were unbiased, but the separate TAE approach was biased.

Figure 2.

Results from the simulation study comparing the joint trimester average exposure (TAE), separate TAE, and distributed lag model (DLM) approaches. A) Joint TAE and scenario 1; B) separate TAE and scenario 1; C) DLM and scenario 1; D) joint TAE and scenario 2; E) separate TAE and scenario 2; F) DLM and scenario 2; G) joint TAE and scenario 3; H) separate TAE and scenario 3; I) DLM and scenario 3; J) joint TAE and scenario 4; K) separate TAE and scenario 4; L) DLM and scenario 4; M) joint TAE and scenario 5; N) separate TAE and scenario 5; O) DLM and scenario 5; P) joint TAE and scenario 6; Q) separate TAE and scenario 6; and R) DLM and scenario 6. The estimated DLM functions were constructed with natural splines with the degrees of freedom selected with generalized cross-validation. The gray lines show the simulated true exposure effects for each week. The black lines are the mean estimated weekly exposure effects over 1,000 simulated data sets.

In scenarios 3 and 4, the critical windows did not align with clinically defined trimesters. For scenario 3, the window spanned parts of the second and third trimester while for scenario 4 the window was the entire second half of pregnancy. In both scenarios 3 and 4, the separate TAE approach was biased. The estimated exposure effect in the first trimester was larger than the exposure effect in the second trimester, despite a true exposure effect in the second trimester but no true exposure effect in the first trimester.

For both scenarios 3 and 4, the DLM model resulted in unbiased estimates. The joint TAE model correctly identified that the largest exposure effect was in the third trimester and the smallest was in the first trimester, but the estimates were slightly biased for each trimester.

In scenario 5, there was a constant exposure effect over the entire 37 weeks of gestation. Both the DLM and the joint TAE model were unbiased. The separate TAE model was again biased, showing positively biased estimates in the first and third trimester and a negative bias in the second trimester.

Finally, in scenario 6, there was no exposure effect. All methods were unbiased. This is the only scenario for which the separate TAE model was unbiased. Additional results for the cumulative effect are shown in Web Table 1.

Analysis of the association between PM_2.5 and BMIz

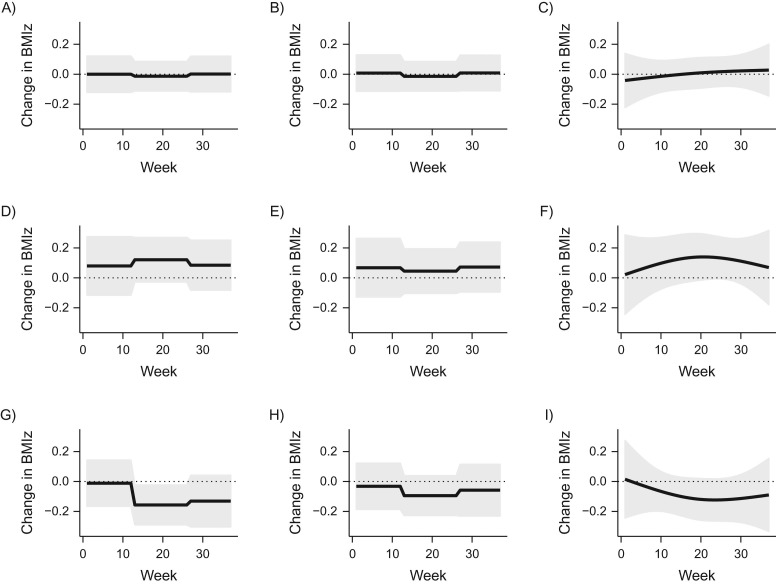
Figure 3 shows the estimated association between maternal PM_2.5 exposure and BMIz, both overall and stratified by sex. The analysis includes 238 births (108 girls and 130 boys). All regression models in the data analysis adjusted for the potential confounders previously described.

Figure 3.

Results from the analysis of the association between particulate matter having an aerodynamic diameter of ≤2.5 μm (PM_2.5) and body mass index z score (BMIz) in data from the Asthma Coalition on Community, Environment, and Social Stress in the area of Boston, Massachusetts, 2002–2009. The estimates are for all children (n = 238), boys only (n = 130), and girls only (n = 108), each using methods from among joint trimester average exposure (TAE), separate TAE, and distributed lag model (DLM). A) Joint TAE; B) separate TAE; C) DLM; D) joint TAE for boys; E) separate TAE for boys; F) DLM for boys; G) joint TAE for girls; H) separate TAE for girls; I) DLM for girls. For each estimate using DLM, there were 3 degrees of freedom. All estimates were adjusted for maternal race, maternal age, maternal prepregnancy body mass index, maternal educational level, and age of the child when BMIz was measured. The overall estimate was adjusted for child sex. The thick lines show the estimated values, and the gray ribbons show the 95% pointwise confidence intervals.

In the overall analysis, the methods all estimated only a small association between time-varying exposure and outcome. None of the methods identified a critical window.

For the boy-specific analysis, the joint TAE and DLM approaches intensified the largest association between exposure and outcome during the second trimester. However, the separate TAE model estimated the smallest association during the second trimester. Hence, while the joint TAE and DLM suggested that there may be a critical window around the second trimester, the separate TAE provided the contradictory result that there was a decreased association between exposure and outcome during that same period.

For the girl-specific analysis, the methods all identified a negative association between exposure in the second and third trimesters and the outcome. The separate TAE model estimated a smaller association than the other 2 methods, but the general pattern was consistent across all methods.

Analysis of the association between PM_2.5 and fat mass

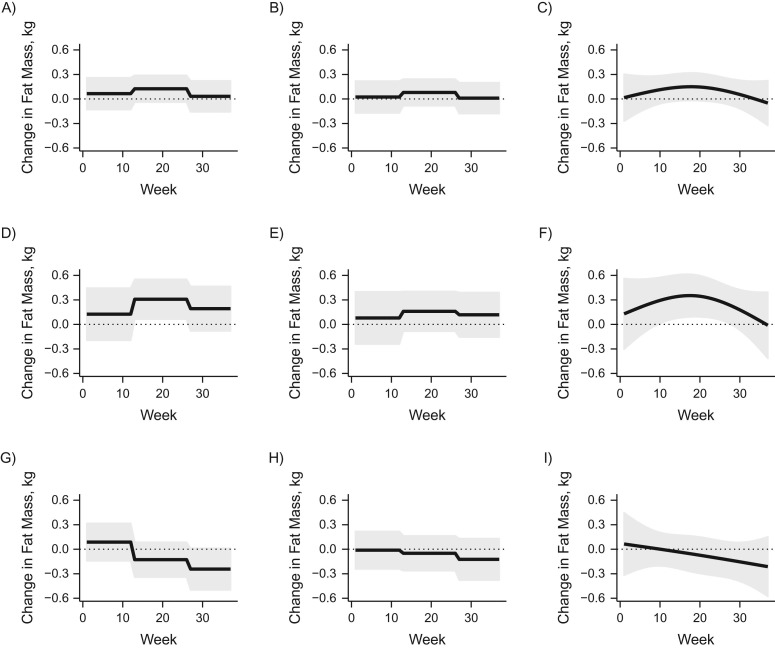
Figure 4 shows the overall and sex-specific estimates of the association between maternal PM_2.5 exposure and fat mass as well as 95% pointwise confidence bands. The analysis included 224 births (94 girls and 130 boys). All estimates were adjusted for the potential confounders previously described.

Figure 4.

Results from the analysis of the association between fine particulate matter (PM_2.5) and fat mass (kg) in data from the Asthma Coalition on Community, Environment, and Social Stress in the area of Boston, Massachusetts, 2002–2009. The estimates are for all children (n = 224), boys only (n = 130), and girls only (n = 94), each using methods from among joint trimester average exposure (TAE), separate TAE, and distributed lag model (DLM). A) Joint TAE; B) separate TAE; C) DLM; D) joint TAE for boys; E) separate TAE for boys; F) DLM for boys; G) joint TAE for girls; H) separate TAE for girls; I) DLM for girls. For each estimate using DLM, there were 3 degrees of freedom. All estimates were adjusted for maternal race, maternal age, maternal prepregnancy body mass index, maternal educational level, and age of the child when fat mass was measured. The overall estimate was adjusted for child sex. The thick lines show the estimated values, and the gray ribbons show the 95% pointwise confidence intervals.

The methods estimated similar overall trends. For both the overall analysis and the boy-specific analysis, the methods all estimated the that largest association was in the second trimester. For the girl-specific analysis, the methods all estimated a decreasing trend with the largest association in the first trimester and a negative association in the third trimester. However, the methods differed in terms of magnitude and significance. Only the joint TAE and the DLM approaches found a significant association for boys in the second trimester. In large part, the lack of significance in the separate TAE model was due to a smaller point estimate. Web Table 2 shows the cumulative and trimester-specific estimates using each method.

DISCUSSION

Many studies have estimated the association between maternal exposure to PM_2.5 during pregnancy and outcomes at birth or in children’s health. Ambient air pollution exposure data can be observed daily. The potential to leverage the high temporal resolution of exposure data to define biologically relevant critical windows is only beginning to be appreciated. Use of TAEs to estimate the exposure effect, with or without controlling for exposure in other trimesters, is a popular method of choice (3, 13, 14). Several other recent studies have estimated the association using DLMs (15–19, 29). We have shown through a simulation study and in a real-data analysis that these approaches can result in substantially different estimates of the association between exposure and outcome, particularly with respect to the ranking of the trimester-specific effect sizes.

The results of the simulation study highlighted that estimating the effect of an exposure during a given window without controlling for exposures in other time windows (the separate TAE approach) can result in biased estimates. Adjusting for exposure during other time periods (joint TAE or DLM) reduced this bias. In several cases (simulation scenarios 3 and 4), the estimates with the separate TAE approach failed to rank the trimesters correctly by the strength of their association with the outcome (Figure 2H and 2K). We demonstrated that this bias could be eliminated when employing a DLM.

Bias in the trimester-specific effect estimates arose due to seasonal trends in air pollution exposures that result in correlation between TAEs (Table 1 and Figure 1). When one estimates the association between the TAEs and the outcome without controlling for other TAEs, the other TAEs act as unmeasured confounders if they are also associated with the outcome. For example, in simulation scenario 1, TAE₃ was positively associated with both the outcome and TAE₁. When estimating the association between TAE₁ and the outcome without controlling for TAE₃, the estimated exposure effect of TAE₁ was positively biased. In reality, season and other factors that are predictive of seasonal trends in air pollution are the confounding factors.

When the true critical window is 1 or more trimesters (simulation scenarios 1 and 2), the joint TAE and DLM approaches were unbiased. Hence, controlling for exposure during the other trimesters eliminates this bias. However, when the critical window did not align with the trimester boundaries (simulation scenarios 3 and 4), both the joint TAE model and the separate TAE model were misspecified. In this situation, the DLM was the only unbiased approach tested here.

The analysis of the ACCESS cohort further highlights the sensitivity of results to the method of analysis. For the analysis of BMIz, the joint TAE and DLM analysis found the greatest association between PM_2.5 and BMIz in the second trimester for boys. However, the separate TAE approach found the weakest association during that same time period (Figure 3E). For fat mass, the joint TAE and DLM found a statistically significant window for boys during the second trimester. However, the separate TAE approach found a weaker association during that period and no statistical significance (Figure 4E). In both analyses, correlation between TAEs resulted in estimates from the separate TAE approach that were compressed toward the null relative to the estimates obtained with the other methods. Sex differences may result for a number of reasons. The prenatal developmental process is not homogeneous across sexes, and sensitive stages of development during which the neonate is vulnerable may occur during different time periods for boys and girls. This may result in a different pattern and strength of association between exposure and outcome between the sexes.

In light of these results, we recommend using the DLM approach when the air pollution exposures are measured at a sufficiently fine temporal resolution to apply the method (e.g., daily or weekly). Both the joint TAE and DLM approaches adjust for exposure during different periods of gestation and reduce the bias incurred by the separate TAE approach. The joint TAE model was unbiased when the exposure was associated with the outcome only in critical windows that align with clinically defined trimesters or is constant. When the critical window did not align with trimesters, the joint TAE estimates were slightly biased but showed a pattern generally consistent with the true exposure effect.

The DLM model is the most flexible model tested here. In all simulation scenarios, the DLM model performed well. DLM has the added advantage of not prespecifying a critical window, which itself can introduce bias. The flexibility of the DLM is better able to capture peaks in the time-varying exposure effect and can evaluate the effect of acute changes in exposure that would be muted by averaging over a 3-month window. Furthermore, the DLM was the only method with unbiased estimates of the cumulative effect (Web Table 1). The results also showed that none of the methods will identify an association when there is not a true association at any time during pregnancy.

The simulated data contained no residual seasonal effects that were not explained by the exposure. Hence, further adjusting for seasonality will not sufficiently control for confounding in the separate TAE model. However, it is important to note that in real-data analyses, seasonal trends may confound the exposure effect through other pathways. It is therefore important to adjust for seasonal trends in practice even when controlling for exposures over other time periods.

We are not the first to note that correlation between TAEs can bias trimester-specific effect estimates. Motivated by correlation between TAEs, Slama et al. (30) presented results for both the separate TAE and joint TAE models to estimate the effect of PM_2.5 and nitrogen dioxide (NO₂) on birth weight. Several results were statistically significant with the separate TAE model but not with the joint TAE model. Bell et al. (31) also addressed this issue by removing the correlation between TAEs via regression (32–33). This approach uses exposure variables: 1) TAE₁; 2) residuals from regressing TAE₂ on TAE₁; and 3) residuals from regressing TAE₃ on TAE₁ and TAE₂ (which is then repeated after permuting the order of the TAEs). The effect of the first method is the same as the TAE₁ effect estimated with the separate TAE approach. The estimate of third method is the same as the estimated TAE₃ effect in the joint TAE approach. Hence, this can be viewed as an alternative version of the separate TAE and joint TAE approaches. Another approach suggested within a causal inference framework is to use an imperfect negative control such postbirth exposure (34).

A notable limitation of this work is that we investigated the correlation structure among trimester-specific exposures to PM_2.5 in the Boston area of Massachusetts. Seasonal patterns and the resulting correlation between TAEs may be different for different air pollutants and weather exposures or for other locations. Another limitation is that the DLM model requires selection of a tuning parameter. Here, we used generalized cross-validation, which can result in oversmoothed DLMs when the signal-to-noise ratio is small (see simulation scenario 2). However, the correct window was still identified. When there is more data or a larger signal-to-noise ratio, the tuning is more accurate. The natural spline basis used to constrain the DLM in this work is one of several formulations of the DLM. Other approaches include parametric models, Bayesian priors, other penalization approaches, or a cross-basis for nonlinear effects (35–37). Although they are not explored in this paper, it is important to note that these other formulations also properly adjust for exposure throughout pregnancy and can be expected to eliminate the bias observed with TAE models in this paper. Finally, the simulation study presented here focused solely on bias due to seasonal trends in exposure and isolated this from other potential sources of bias, such as from additional residual confounding. We did not investigate whether any of the methods are more or less prone to confounding by other factors. That issue deserves separate investigation.

When interest focuses on the association between maternal exposure to air pollution during pregnancy and birth or children’s health outcomes, the separate TAE model, arguably the most commonly used approach, can result in biased estimates of the exposure effect. The DLM yields unbiased estimates and adds flexibility to identify windows that do not correspond to a clinically defined trimester. When one uses TAEs, the joint TAE model should be used. DLM is preferred to using TAEs when possible.

Abbreviations

ACCESS

Asthma Coalition on Community, Environment, and Social Stress

BMIz

body mass index z score

DLM

distributed lag model

PM_2.5

particulate matter having an aerodynamic diameter of ≤2.5 μm

TAE

trimester average exposure