Abstract
Motivation
Nucleosome positioning plays important roles in many eukaryotic intranuclear processes, such as transcriptional regulation and chromatin structure formation. The investigations of nucleosome positioning rules provide a deeper understanding of these intracellular processes.
Results
Nucleosome positioning prediction was performed using a model consisting of three types of variables characterizing a DNA sequence—the number of five-nucleotide sequences, the number of three-nucleotide combinations in one period of a helix, and mono- and di-nucleotide distributions in DNA fragments. Using recently proposed stringent benchmark datasets with low biases for Saccharomyces cerevisiae, Homo sapiens, Caenorhabditis elegans and Drosophila melanogaster, the present model was shown to have a better prediction performance than the recently proposed predictors. This model was able to display the common and organism-dependent factors that affect nucleosome forming and inhibiting sequences as well. Therefore, the predictors developed here can accurately predict nucleosome positioning and help determine the key factors influencing this process.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Nucleosomes are the basic units of eukaryotic chromatin, and each one is formed by 147 DNA base pair (bp) sequences wrapped tightly around a histone octamer. The precise nucleosome formation and its inhibitory effects on promoters (Choi and Kim, 2009; Jiang and Pugh, 2009; Tirosh and Barkai, 2008), enhancers (Andreu-Vieyra et al., 2011; He et al., 2010; Maston et al., 2012; McPherson et al., 1996) and insulators (Bi et al., 2004; Takagi et al., 2012) play crucial roles in the precise regulation of transcription (West et al., 2014). The precise nucleosome positioning facilitates DNA replication, DNA repair, and RNA splicing (Berbenetz et al., 2010; Chen et al., 2010, 2014a; Schwartz et al., 2009; Yasuda et al., 2005). Therefore, the elucidation of nucleosome positioning steps may allow an in-depth understanding of various biological processes.
Recently, high-resolution genome-wide nucleosome maps were obtained for several model organisms (Lee et al., 2007; Mavrich et al., 2008a,b; Schones et al., 2008; Segal et al., 2006). In contrast to this, the determinant factors of the nucleosome positioning remained unclear. However, with the increase in the availability of high-quality experimental datasets, various computational methods and tools for the prediction of nucleosome positioning were proposed (reviewed in Teif, 2015), providing valuable insights and allowing the mechanisms determining nucleosome positioning to be unveiled. Furthermore, the construction of the accurate predictors can lead to the possibility of the analysis of single nucleotide polymorphism and gene mutation effects on this process.
Many of these predictors were constructed based on the information about the frequencies and distributions of the combinations of polynucleotide sequences as feature vectors (Field et al., 2008; Ioshikhes et al., 2006; Kaplan et al., 2009; Ogawa et al., 2010; Peckham et al., 2007; Segal et al., 2006; Struhl and Segal, 2013; Yi et al., 2012; Zhang et al., 2012). Sequence-dependent mechanical properties, such as sequence-dependent geometry and DNA fragment flexibility, were also considered for the characterization of nucleosome forming and inhibiting sequences (Chen et al., 2012a, 2015; Freeman et al., 2014; Goñi et al., 2008; Guo et al., 2014; Isami et al., 2015; Nikolaou et al., 2010; Tahir and Hayat, 2016; Tolstorukov et al., 2008; Stolz and Bishop, 2010; Yuan and Liu, 2008). Furthermore, a powerful web-server called Pse-in-One (Liu et al., 2015a) was developed, where all existing feature vectors for DNA/RNA and protein/peptide sequences can be generated (see references cited in Chen and Lin 2015), together with the generation of the feature vectors for the sequences defined by users themselves.
For human (Homo sapiens), worm (Caenorhabditis elegans) and fly (Drosophila melanogaster) genomes, Guo et al. (2014) constructed the stringent benchmark datasets of nucleosome forming and inhibiting sequences with low similarities, in order to examine the performance of nucleosome position predictors. Additionally, predictors iNuc-PseKNC and iNuc-PseSTNC (we call iNuc-Pse predictors) were proposed, and they were shown to have better success rates in the prediction of nucleosome positioning than any of the previously developed predictors (Guo et al., 2014; Tahir and Hayat, 2016). Furthermore, for yeast (Saccharomyces cerevisiae) genomes, Chen et al. (2015) constructed a stringent benchmark dataset using the same methodology as Guo et al. (2014), and predicted the nucleosome positioning in yeast genome based on the deformation energies of DNA fragments.
In order for iNuc-Pse predictors to show the best prediction performance for nucleosome positioning in different organisms, different sets of parameter values must be used (Guo et al., 2014; Tahir and Hayat, 2016). The sequence predicted as the nucleosome forming sequence in one organism may be predicted as the nucleosome inhibiting sequence in another organism. This shows that the function of any given DNA sequence in assisting or inhibiting nucleosome formation depends on the investigated organism. However, no key factors and criteria affecting this process could be elucidated using this predictor, because iNuc-Pse predictors are based on support vector machine. Additionally, based on these datasets, some common short motif nucleosome forming and inhibiting sequences were found (Giancarlo et al., 2015). However, the nucleosome positioning cannot be predicted sufficiently well using only these motives.
In this study, a novel nucleosome positioning predictor was developed based on the linear regression model, consisting of three types of variables with different fragment length scales—the number of five-nucleotide sequences, the number of three-nucleotide combinations in one period of helix, and mono- and di-nucleotides distributions in whole DNA fragments. This predictor exhibited better prediction performance than the recently developed iNuc-Pse predictors for the same benchmark datasets of human and fly genomes and displayed common and organism-dependent key factors of nucleosome positioning explicitly.
A series of recent publications (Jia et al., 2015, 2016; Lin et al., 2014, Liu et al., 2016; Qiu et al., 2014, 2016a; Xiao et al., 2015) demonstrated, in compliance with Chou’s five-step rule (Chou, 2011) that, in order to establish a useful sequence-based statistical predictor for a biological system, the following five guidelines should be observed: (i) how to construct or select a valid benchmark dataset to train and test the predictor; (ii) how to represent the biological sequence samples by catching their key features associated with the target to be predicted; (iii) how to introduce or develop a powerful algorithm to operate the prediction; (iv) how to properly perform cross-validation tests to objectively evaluate the anticipated accuracy; and (v) how to establish a user-friendly web-server for the predictor that is accessible to the public. Below, these steps are further explained.
2 Materials and methods
2.1 Benchmark datasets of nucleosome forming and inhibiting sequences
The stringent benchmark datasets of nucleosome forming and inhibiting sequences with low biases constructed by Guo et al. (2014) and Chen et al. (2015) were used for the evaluation of the performance of the proposed predictor. These datasets involved human (H.sapiens: 2273 forming sequences and 2300 inhibiting sequences of 147 bp), worm (C.elegans: 2567 forming sequences and 2608 inhibiting sequences of 147 bp), fly (D.melanogaster: 2900 forming sequences and 2850 inhibiting sequences of 147 bp) (Guo et al., 2014) and yeast (S.cerevisiae: 1880 forming sequences and 1740 inhibiting sequences of 150 bp) (Chen et al., 2015).
In these datasets, none of the sequences has >80% pairwise sequence identity with any other sequence. Note that the benchmark datasets used in previous studies were expected to contain many redundant, highly similar sequences, and these biased datasets lacked statistical representativeness (Chou, 2011), and the predictors may have yielded misleading results if trained and tested using these biased datasets. Therefore, only the low-biased datasets, proposed by Guo et al. (2014) and Chen et al. (2015) were employed in this study.
2.2 Model predicting nucleosome positioning 1: three-length scales model
In order to predict whether a given 147-bp DNA sequence of human, worm, and fly genomes is involved in the formation or the inhibition of formation of nucleosome, the model included three types of variables: (i) the number of five-nucleotide sequences, (ii) the number of three-nucleotide combinations in one period of a double helix and (iii) mono- and di-nucleotide distributions in DNA fragments. The model was named three length scales (3LS), and it belongs to a class of general PseKNC-based predictors (Guo et al., 2014; Liu et al., 2015a).
The model is described by the following equations:
| (1) |
| (2) |
| (3) |
| (4) |
and
| (5) |
Here, Qseq is defined as a value of a given sequence, and when Q > Qc = 0.5, this sequence was considered a nucleosome forming sequence, while it was predicted as an inhibiting sequence otherwise. are defined as follows:
defines the number of adenine (A) or thymine (T) nucleotides in ith region of the given DNA sequence. Here, region 1 occupies the central 11 bp fragment of the given 147-bp DNA, the regions for 1 < i < 8 occupy 2 10-bp fragments (20 bp) at (i-1)th nearest neighbor of first region, and eighth region occupies the remaining 16-bp fragment (Fig. 1a).
Fig. 1.
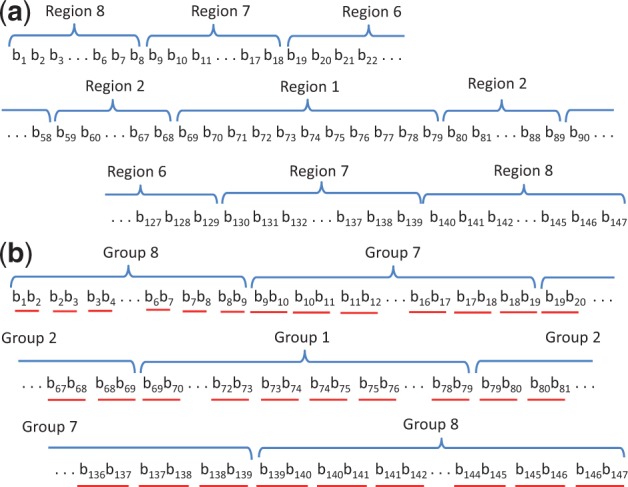
Nucleotide regions and groups analyzed in each 147-bp DNA sequence. (a) Each nucleotide belongs to a specific region. (b) Each dinucleotide pair belongs to a specific group. bn indicates the nth base of nucleotide, and dinucleotide pairs are underlined red
defines the sum of the number of each type of successive dinucleotide sequence and its complementary sequence, named Di-seq and Di-seq*, in the i’th group of the dinucleotide series of a given DNA sequence. Here, first group consists of 10 dinucleotides at the central region of a given 146-dinucleotide series, i’th groups for 1 < i’ < 8 consist of 20 dinucleotides between (5 ± (10 × (i’-2)+1))th to (5 ± 10 × (i’-1))th dinucleotide from the center of a given 146 dinucleotide series, and eight group contains the remaining 16 dinucleotides (Fig. 1b).
) defines the sum of the number of each type of combination of 3-nucleotide set (3-nuc) that consists of a nucleotide, the second nucleotide located downstream at the distance j, and the third nucleotide located at the distance k in downstream sequence (j < k), together with the number of the complementary nucleotide combinations (3-nuc*) in the given DNA sequence. Here, 5 < k <11 cases were considered.
(5-seq or 5-seq*) defines the sum of the number of each type of successive five-nucleotide sequence (5-seq) and that of the complementary sequence (5-seq*) in the given DNA sequence.
The coefficients M (), D (), T (), and P () provide the weight of the contributions of to Qseq and Q0 as a constant value. They are organism-dependent values, which reveal the common and organism-specific characteristics of nucleosome forming and inhibiting sequences.
2.3 Variable selection in 3LS model
In order to obtain high prediction performances, the 3LS model should contain only the appropriate variables of. The coefficients M (), D (), T () and P () of the appropriate variables should be given as finite values, while the values of redundant variables should be given as zero. The appropriate variables were chosen by the stepwise forward selection method (Efroymson, 1960). Here, in order to avoid multicollinearity (Farrar and Glauber, 1967), the variance inflation factors of all chosen variables were kept below 10 (10.5 for fly genomes, since the prediction performance of the model increased drastically in comparison with the case when 10.0 was used) (O’brien, 2007). The model consists of the linear combination of, instead of that of , since this allows a better prediction performance.
2.4 Model predicting nucleosome positioning 2: tri-nucleotide sequence model
For the prediction of nucleosome positioning, a simpler model than 3LS, named Tri-nucleotide sequence (TNS) model was introduced:
where is defined by the sum of the number of each type of successive TNS and that of the complementary sequence in a given DNA sequence. The coefficient R () provide the weight of the contributions of to Qseq and Q0 as a constant value. This simple model allows a very high accuracy of the nucleosome positioning prediction for yeast genome.
2.5 Evaluations of the quality of prediction
The prediction quality of the present model was evaluated using the jackknife test (Lachenbruch and Mickey, 1968) and relative operating characteristic (ROC) curve. These methods were generally employed for the evaluation of the quality of several previously developed predictors (Chen et al., 2012b, 2013; Chen and Li, 2013, Chou et al., 2012; Esmaeili et al., 2010; Gupta et al., 2013; Mei, 2012, Mohabatkar et al., 2011, 2013) and iNuc-Pse predictors (Guo et al., 2014; Tahir and Hayat, 2016).
Here, N+, N−, N+−, and N−+ were defined as the total number of nucleosome forming sequences, nucleosome inhibiting sequences, nucleosome forming sequences incorrectly predicted as nucleosome inhibiting sequences, and nucleosome inhibiting sequences incorrectly predicted as nucleosome forming sequences. Using the jackknife test, the following metrics were obtained:
where Sn, Sp, Acc and MCC stand for sensitivity, specificity, accuracy, and Mathew’s correlation coefficient, respectively. Note that Sn and (1 − Sp) represent true positive rate (TPR) and false positive rate (FPR), respectively. The conventional formulations of the four metrics are not quite intuitive and it may be difficult for many experimental scientists to understand them, particularly MCC. Fortunately, the more intuitive expressions, presented in this paper, can be derived using the symbols defined in a signal peptide study (Chou, 2001), and elaborated in other studies (Chen et al., 2013; Xu et al., 2013).
The ROC curve can be obtained as the trajectory of TPR–FPR two-dimensional surface for the change in Qc. The area surrounded by TPR = 0, FPR = 0, and ROC curve, called AUROC, was used to estimate the performances of predictors, where AUROC = 0.5 is equivalent to a random prediction, and AUROC = 1 indicates perfect prediction.
Note that the following three cross-validation methods are often used to examine the effectiveness of a predictor in practical applications: independent dataset test, subsampling test, and jackknife test (Chou and Zhang, 1995). However, of the three, the jackknife test is deemed the least arbitrary one (most objective) that can always yield a unique result for a given benchmark dataset (Chou, 2011), and therefore, it has been increasingly used for the investigations of the accuracy of various predictors (e.g. Dehzangi et al., 2015; Kabir and Hayat, 2016; and references cited in Chou, 2011). Accordingly, the jackknife test was also adopted here for the examination of the quality of the present predictor.
2.6 Construction of nucleosome positioning predictor
Based on the 3LS and TNS models, the nucleosome positioning predictors for each organism were constructed. The predictors for human, worm and fly genomes were assumed to consist of the appropriately chosen variables. The coefficients of these chosen variables were determined by the multiple regression analysis, using benchmark datasets for each organism, and the explanatory variables were given by the chosen for 3LS model, and for TNS model, and the objective variables were given as 1 for nucleosome forming sequences and 0 otherwise.
3 results
3.1 Variable selection for 3LS model using human, worm and fly sequences
Variables , involved in the construction of the nucleosome positioning predictors in 3LS model were chosen by stepwise forward selection method. Here, 403, 392 and 325 variables were chosen for human, worm and fly genomes, respectively (Supplementary Table S1).
3.2 Prediction quality for human, worm and fly genomes
Using the jackknife cross-validation tests, Sn, Sp, ACC and MCC of 3LS model based predictor were evaluated for human, worm, and fly genome benchmark datasets (Table 1). The obtained ACCs of the investigated predictor for these datasets (≈ 0.9001, ≈ 0.8786 and ≈ 0.8341, respectively) were shown to be higher than those obtained by iNuc-PseKNC (Guo et al., 2014) for all organisms, and higher than those obtained by iNuc-PseSTNC (Tahir and Hayat, 2016) for human and fly genomes. The higher AUROC values were obtained as well (≈ 0.9588, ≈ 0.9505 and ≈ 0.9147 for human, worm, and fly datasets, respectively), compared with those obtained by iNuc-PseKNC (≈ 0.925, ≈ 0.935 and ≈ 0.874) (Guo et al., 2014) (Fig. 2). Thus, we expected that 3LS model-based predictor with appropriate coefficients (Supplementary Table S2a) can predict the nucleosome positioning more accurately than the recent iNuc-Pse predictors for human and fly genomes.
Table 1.
The prediction quality of 3LS model-based predictor measured using jackknife tests
| Human | Worm | Fly | |
|---|---|---|---|
| ACC | 0.9001 (0.8627a, 0.8760b) | 0.8786 (0.8690a, 0.8862b) | 0.8341 (0.7997a, 0.8167b) |
| Sn | 0.9169 (0.8786a, 0.8931b) | 0.8654 (0.9030a), 0.9162b) | 0.8407 (0.7831a, 0.7976b) |
| Sp | 0.8835 (0.8470a, 0.8591b) | 0.8921 (0.8355 a, 0.8666b) | 0.8274 (0.8165a, 0.8361b) |
| MCC | 0.8006 (0.73a, 0.75b) | 0.7576 (0.74 a, 0.77b) | 0.6682 (0.60a, 0.63b) |
Sn, sensitivity; Sp, specificity; Acc, accuracy; MCC, Mathew’s correlation coefficient.
Values in brackets are those obtained using iNuc-PseKNCa and iNuc-PseSTNCb.
Fig. 2.
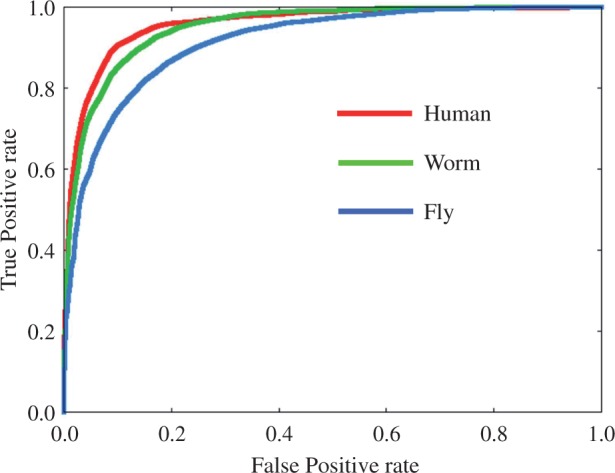
ROC curves obtained with the jackknife tests using human, worm, and fly genome datasets (Color version of this figure is available at Bioinformatics online.)
3.3 TNS model for yeast genome
The quality of TNS model-based predictor was expected to be lower than that of 3LS model based. ACCs of TNS model were shown to be ≈ 0.8167, ≈ 0.8394 and ≈ 0.7082 for human, worm, and fly genomes, respectively. However, TNS model based predictor exhibited perfect nucleosome positioning prediction (ACC = 1.0) for the benchmark yeast genome dataset, presented in Chen et al. (2015). For the same benchmark dataset, the predictor based on DNA deformation energy (Chen et al., 2015) had ACC of ≈ 0.981. Moreover, we confirmed that the predictor based on the nearest neighbor algorithm (Yi et al., 2012) had ACC of ≈ 0.9906 for the same benchmark dataset. These predictors can perform sufficiently well in predicting nucleosome positioning for yeast genome. However, we expected that TNS model-based predictor with appropriate coefficients (Supplementary Table S2b) is able to predict the nucleosome positioning more precisely than these recent predictors.
4 Discussion
3LS model-based predictor can predict nucleosome positioning in human and fly genomes more accurately than the recently proposed nucleosome position predictors can. Additionally, the predictor defined here can display the details of organism-dependent key factors for the determination of nucleosome forming and inhibiting sequences.
The chosen in 3LS model differed greatly between human, worm, and fly genomes (Supplementary Table S1). This indicates there are many organism-dependent differences in the features contributing to the nucleosome formation. The coefficients of these variables, M (), D (), T () and P (), and constant value Q0, obtained by multiple regression analysis, clearly showed organism-dependent specificities (Supplementary Table S2). These differences are presented in the following examples:
(i) In 3LS models of these genomes that contained common variables, their coefficients’ signs often differed between the organisms.
(ii) There were only six variables with the same signs of their coefficients between these organisms, and these were:
T(0, 1, 6, = CTT or 0, 5, 6, = AAG) > 0,
T(0, 1, 10, = TTG or 0, 9, 10, = CAA) > 0,
P(TTTTT or AAAAA) < 0,
P(GCTTC or GAAGC) > 0,
P(GTGTC or GACAC) > 0 and
P(GGATC or GATCC) >0
Poly(dA-dT) sequences, such as AAAAA sequence, are known as physically rigid sequences (Brunkner et al., 1995; Nelson et al., 1987; Packer et al., 2000). Therefore, the sequences containing these motives inhibit the nucleosome formation in the genomes of several organisms, which was confirmed by experimental evidence and the use of different nucleosome positioning predictors (Bi et al., 2004; Giancarlo et al., 2015; Kunkel and Martinson, 1981; Yi et al., 2012), which is consistent with the results presented here. The sequences with high GC content were reported to have a nucleosome-forming tendency (Tillo and Hughes, 2009). However, considering the results of the recent studies, 30–50% nucleotides found in the nucleosome forming sequences are A or T nucleotides located at the appropriate positions (Giancarlo et al., 2015; Ioshikhes et al., 2006; Ogawa et al., 2010; Ohyama 2001; Satchwell et al., 1986; Segal et al., 2006), which seems to agree with the results obtained in this study.
(iii) When only the six variables described above were chosen in 3LS model based predictor, ACCs for human, worm, and fly genomes were ACC ≈ 0.7525, ≈ 0.7716 and 0.6438, respectively, which is much lower than the values obtained using the model with suitable variables. However, even when these variables were removed from the 3LS model based predictor with suitable variables, the decrease in ACCs for human, worm and fly genomes was not considerable, and the obtained ACC values were ≈ 0.8974, ≈ 0.8730 and ≈ 0.8290, respectively. This indicates that the organism-specific sequence patterns dominantly contribute to the determination of nucleosome forming abilities.
(iv) The weight of the contribution of the set for each k is defined as Wk= [Number of chosen]/[Number of chosen variables] (Table 2). The obtained Wk values were different for different organisms, e.g. W5 ∼ 0.074, 0.112, 0.080 (k = 5 as the smallest k) and W10 ∼ 0.159, 0.115, 0.151 (k = 10 as the largest k) were obtained for human, worm, and fly genomes, respectively. This indicates that the length scale of nucleotide combinations required for the characterization of nucleosome forming sequences depends on the organism analyzed.
Table 2.
Weights of the contributions of (0, j, k, = 3-nuc or 0, k − j, k, = 3-nuc*) for each k (Wk) and (i’ | Di-seq or Di-seq*) for the positions near and far from the dyad position (Wnear and Wfar)
| Human | Worm | Fly | |
|---|---|---|---|
| W5 | 0.074441687 | 0.112244898 | 0.08 |
| W6 | 0.094292804 | 0.068877551 | 0.089230769 |
| W7 | 0.069478908 | 0.073979592 | 0.098461538 |
| W8 | 0.11662531 | 0.114795918 | 0.083076923 |
| W9 | 0.1191067 | 0.135204082 | 0.12 |
| W10 | 0.158808933 | 0.114795918 | 0.150769231 |
| Wnear | 0.027295285 | 0.025510204 | 0.027692308 |
| Wfar | 0.027295285 | 0.015306122 | 0.006153846 |
(v) The weight of the contribution of the set (i’ | Di-seq or Di-seq*) near and far from the center of sequence (dyad position) was defined as Wnear = [Number of chosen (i’ | Di-seq or Di-seq*) near and far from the center of sequence (dyad position) was defined as Wnear = [Number of chosen)]/[Number of chosen variables] and Wfar = [Number of chosen]/[Number of chosen variables] (Table 2). Wnear values were similar values in the datasets for the 3 investigated organisms. The values of Wfar, ≈ 0.027, 0.015 and 0.006, were obtained for human, worm, and fly genomes, respectively, where Wfar for fly was shown to be ∼1/2 of that for worm and ∼1/4 for human. This suggests that the contribution of the sequences far from the dyad position to the nucleosome formation depends on the organism type.
Using the TNS model-based predictor, the obtained ACC values of nucleosome position predictions for human, worm, and fly genomes were much lower than those obtained using 3LS model-based predictor. while ACC = 1 was obtained for yeast genome. This clearly demonstrates organism-dependent characteristics of nucleosome forming and inhibiting sequences, showing that the nucleosome positioning is much more easily predicted in yeast than in higher organisms.
The predictors developed here can predict nucleosome positioning in human, fly and yeast genomes with higher accuracy than the recently proposed predictors and can determine the key factors influencing this positioning in human, worm, fly and yeast genomes. In contrast to the recently proposed iNuc-Pse predictors, 3LS model-based predictor developed in this study is based on the following sequence properties as well: (i) Combinations of nucleotides located further away than those considered by iNuc-Pse predictors; (ii) More detailed distributions of A, T and dinucleotide sequences in a DNA fragment than those in iNuc-Pse predictors. These properties most likely contribute to the exhibited improved performance of the predictor proposed here in comparison with the iNuc-Pse predictors.
However, the variable selections and the formalization of the model can be improved, and further modifications are needed for this predictor to perform better than the recent ones. Recent studies suggested that sequence-dependent geometry and flexibility of each DNA fragment may play important roles in the determination of its nucleosome forming ability (Chen et al., 2012a, 2015; Freeman et al., 2014; Goñi et al., 2008; Guo et al., 2014; Isami et al., 2015; Nikolaou et al., 2010; Stolz and Bishop, 2010; Tolstorukov et al., 2008; Yuan and Liu, 2008). Furthermore, the nucleosome forming ability of each sequence may change with intracellular and environmental conditions (Andreu-Vieyra et al., 2011; He et al., 2010; Maston et al., 2012; McPherson et al., 1996; Struhl and Segal, 2013; Zhang et al., 2012). Because of this, the predictors should be modified in the future by considering these physical and chemical influences.
Additionally, as demonstrated in a series of recent publications (e.g. Chen et al., 2014b, 2016; Jia et al., 2015; Lin et al., 2014; Liu et al., 2015b; Qiu et al., 2016b), during the development of new prediction methods, user-friendly and publicly accessible web-servers can significantly enhance the impacts of these tools (Chou, 2015). Therefore, the future efforts will include providing a web-server for the use of the prediction method presented here.
Supplementary Material
Acknowledgements
The author is grateful to N. Sakamoto, S. Isami, T. Kameda, H. Nishimori, H. Yanagihara and H. Wakaki for their fruitful discussion.
Funding
This work was partially supported by the Japan Agency for Medical Research and Development (AMED); and the Grant-in-Aid for Scientific Research on Innovative Areas ‘Initiative for High-Dimensional Data-Driven Science through Deepening of Sparse Modeling’ (grant numbers 4503, 26120525) of MEXT of Japan.
Conflict of Interest: None declared.
References
- Andreu-Vieyra C. et al. (2011) Dynamic nucleosome-depleted regions at androgen receptor enhancers in the absence of ligand in prostate cancer cells. Mol. Cell. Biol., 31, 4648–4662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berbenetz N.M. et al. (2010) Diversity of eukaryotic DNA replication origins revealed by genome-wide analysis of chromatin structure. PLoS Genet., 6, e1001092.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bi X. et al. (2004) Formation of boundaries of transcriptionally silent chromatin by nucleosome-excluding structures. Mol. Cell. Biol., 24, 2118–2131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brukner I. et al. (1995) Sequence-dependent bending propensity of DNA as revealed by DNase I: parameters for trinucleotides. EMBO J., 14, 1812.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L. et al. (2012a) Predicting anatomical therapeutic chemical (ATC) classification of drugs by integrating chemical-chemical interactions and similarities. PloS One, 7, e35254.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W. et al. (2010) The organization of nucleosomes around splice sites. Nucleic Acids Res., 38, 2788–2798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W. et al. (2012b) iNuc-PhysChem: a sequence-based predictor for identifying nucleosomes via physicochemical properties. PloS One, 7, e47843.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W. et al. (2013) iRSpot-PseDNC: identify recombination spots with pseudo dinucleotide composition. Nucleic Acids Res., 41, e68.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W. et al. (2014a) iSS-PseDNC: identifying splicing sites using pseudo dinucleotide composition. BioMed Res. Int., 2014, 623149.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W. et al. (2014b) iTIS-PseTNC: a sequence-based predictor for identifying translation initiation site in human genes using pseudo trinucleotide composition. Anal. Biochem., 462, 76–83. 2014, [DOI] [PubMed] [Google Scholar]
- Chen W. et al. (2015) Using deformation energy to analyze nucleosome positioning in genomes. Genomics, 107, 69–75. [DOI] [PubMed] [Google Scholar]
- Chen W., Lin H. (2015) Pseudo nucleotide composition or PseKNC: an effective formulation for analyzing genomic sequences. Mol. Biosyst., 11, 2620–2634. [DOI] [PubMed] [Google Scholar]
- Chen W. et al. (2016) iRNA-PseU: Identifying RNA pseudouridine sites. Mol. Ther. Nucleic Acids, 5, e332.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y.K., Li K.B. (2013) Predicting membrane protein types by incorporating protein topology, domains, signal peptides, and physicochemical properties into the general form of Chou’s pseudo amino acid composition. J. Theor. Biol., 318, 1–12. [DOI] [PubMed] [Google Scholar]
- Choi J.K., Kim Y.J. (2009) Intrinsic variability of gene expression encoded in nucleosome positioning sequences. Nat. Genet., 41, 498–503. [DOI] [PubMed] [Google Scholar]
- Chou K.C., Zhang C.T. (1995) Prediction of protein structural classes. Crit. Rev. Biochem. Mol. Biol., 30, 275–349. [DOI] [PubMed] [Google Scholar]
- Chou K.C. (2001) Prediction of protein signal sequences and their cleavage sites. Proteins, 42, 136–139. [DOI] [PubMed] [Google Scholar]
- Chou K.C. (2011) Some remarks on protein attribute prediction and pseudo amino acid composition. J. Theor. Biol., 273, 236–247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chou K.C. (2015) Impacts of bioinformatics to medicinal chemistry. Med. Chem., 11, 218–234. [DOI] [PubMed] [Google Scholar]
- Chou K.C. et al. (2012) iLoc-Hum: using the accumulation-label scale to predict subcellular locations of human proteins with both single and multiple sites. Mol. BioSyst, 8, 629–641. [DOI] [PubMed] [Google Scholar]
- Dehzangi A. et al. (2015) Gram-positive and Gram-negative protein subcellular localization by incorporating evolutionary-based descriptors into Chou's general PseAAC. J. Theor. Biol., 364, 284–294. [DOI] [PubMed] [Google Scholar]
- Efroymson M.A. (1960) Multiple regression analysis In Ralston A., Wilf H.S. (eds.), Mathematical Methods for Digital Computers. Wiley, New York. [Google Scholar]
- Esmaeili M. et al. (2010) Using the concept of Chou's pseudo amino acid composition for risk type prediction of human papillomaviruses. J. Theor. Biol., 263, 203–209. [DOI] [PubMed] [Google Scholar]
- Farrar D.E., Glauber R.R. (1967) Multicollinearity in regression analysis: the problem revisited. Rev. Econ. Stat., 49, 92–107. [Google Scholar]
- Field Y. et al. (2008) Distinct modes of regulation by chromatin encoded through nucleosome positioning signals. PLoS Comput. Biol., 4, e1000216.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeman G.S. et al. (2014) DNA shape dominates sequence affinity in nucleosome formation. Phys. Rev. Lett., 113, 168101.. [DOI] [PubMed] [Google Scholar]
- Giancarlo R. et al. (2015) Epigenomic k-mer dictionaries: shedding light on how sequence composition influences in vivo nucleosome positioning. Bioinformatics, 31, 2939–2946. [DOI] [PubMed] [Google Scholar]
- Goñi J.R. et al. (2008) DNAlive: a tool for the physical analysis of DNA at the genomic scale. Bioinformatics, 24, 1731–1732. [DOI] [PubMed] [Google Scholar]
- Guo S.H. et al. (2014) iNuc-PseKNC: a sequence-based predictor for predicting nucleosome positioning in genomes with pseudo k-tuple nucleotide composition. Bioinformatics, 30, 1522–1529. [DOI] [PubMed] [Google Scholar]
- Gupta M.K. et al. (2013) An alignment-free method to find similarity among protein sequences via the general form of Chou’s pseudo amino acid composition. SAR QSAR Environ. Res., 24, 597–609. [DOI] [PubMed] [Google Scholar]
- He H.H. et al. (2010) Nucleosome dynamics define transcriptional enhancers. Nat. Genet., 42, 343–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ioshikhes I.P. et al. (2006) Nucleosome positions predicted through comparative genomics. Nat. Genet., 38, 1210–1215. [DOI] [PubMed] [Google Scholar]
- Isami S. et al. (2015) Simple elastic network models for exhaustive analysis of long double-stranded DNA dynamics with sequence geometry dependence. PloS One, 10, e0143760.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia J. et al. (2015) iPPI-Esml: an ensemble classifier for identifying the interactions of proteins by incorporating their physicochemical properties and wavelet transforms into PseAAC. J. Theor. Biol., 377, 47–56. [DOI] [PubMed] [Google Scholar]
- Jia J. et al. (2016) iCar-PseCp: identify carbonylation sites in proteins by Monto Carlo sampling and incorporating sequence coupled effects into general PseAAC. Oncotarget, 7, 34558–34570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang C., Pugh B.F. (2009) Nucleosome positioning and gene regulation: advances through genomics. Nat. Rev. Genet., 10, 161–172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kabir M., Hayat M. (2016) iRSpot-GAEnsC: identifing recombination spots via ensemble classifier and extending the concept of Chou's PseAAC to formulate DNA samples. Mol. Genet. Genomics, 291, 285–296. [DOI] [PubMed] [Google Scholar]
- Kaplan N. et al. (2009) The DNA-encoded nucleosome organization of a eukaryotic genome. Nature, 458, 362–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kunkel G.R., Martinson H.G. (1981) Nucleosomes will not form on double-stranded RNA or over poly(dA)-poly(dT) tracts in recombinant DNA. Nucleic Acids Res, 9, 6869–6888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lachenbruch P.A., Mickey M.R. (1968) Estimation of error rates in discriminant analysis. Technometrics, 10, 1–11. [Google Scholar]
- Lee W. et al. (2007) A high-resolution atlas of nucleosome occupancy in yeast. Nat. Genet., 39, 1235–1244. [DOI] [PubMed] [Google Scholar]
- Lin H. et al. (2014) iPro54-PseKNC: a sequence-based predictor for identifying sigma-54 promoters in prokaryote with pseudo k-tuple nucleotide composition. Nucleic Acids Res., 42, 12961–12972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu B. et al. (2015a) Pse-in-One: a web server for generating various modes of pseudo components of DNA, RNA, and protein sequences. Nucleic Acids Res., 43, W65–W71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu B. et al. (2016) iEnhancer-2L: a two-layer predictor for identifying enhancers and their strength by pseudo k-tuple nucleotide composition. Bioinformatics, 32, 362–389. [DOI] [PubMed] [Google Scholar]
- Liu Z. et al. (2015b) iDNA-Methyl: Identifying DNA methylation sites via pseudo trinucleotide composition. Anal. Biochem., 474, 69–77. [DOI] [PubMed] [Google Scholar]
- Maston G.A. et al. (2012) Characterization of enhancer function from genome-wide analyses. Annu. Rev. Genomics Hum. Genet., 13, 29–57. [DOI] [PubMed] [Google Scholar]
- Mavrich T.N. et al. (2008) A barrier nucleosome model for statistical positioning of nucleosomes throughout the yeast genome. Genome Res., 18, 1073–1083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mavrich T.N. et al. (2008) Nucleosome organization in the Drosophila genome. Nature, 453, 358–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McPherson C.E. et al. (1996) Nucleosome positioning properties of the albumin transcriptional enhancer. Nucleic Acids Res., 24, 397–404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mei S. (2012) Predicting plant protein subcellular multi-localization by Chou’s PseAAC formulation based multi-label homolog knowledge transfer learning. J. Theor. Biol., 310, 80–87. [DOI] [PubMed] [Google Scholar]
- Mohabatkar H. et al. (2011) Prediction of GABA A receptor proteins using the concept of Chou's pseudo-amino acid composition and support vector machine. J. Theor. Biol., 281, 18–23. [DOI] [PubMed] [Google Scholar]
- Mohabatkar H. et al. (2013) Prediction of allergenic proteins by means of the concept of Chou's pseudo amino acid composition and a machine learning approach. Med. Chem., 9, 133–137. [DOI] [PubMed] [Google Scholar]
- Nelson H.C. et al. (1987) The structure of an oligo (dA)· oligo (dT) tract and its biological implications. Nature, 330, 221–226. [DOI] [PubMed] [Google Scholar]
- Nikolaou C. et al. (2010) Structural constraints revealed in consistent nucleosome positions in the genome of S. cerevisiae. Epigenet. Chromatin, 3, 1.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’brien R.M. (2007) A caution regarding rules of thumb for variance inflation factors. Qual. Quant., 41, 673–690. [Google Scholar]
- Ogawa R. et al. (2010) Computational prediction of nucleosome positioning by calculating the relative fragment frequency index of nucleosomal sequences. FEBS Lett., 584, 1498–1502. [DOI] [PubMed] [Google Scholar]
- Ohyama T. (2001) Intrinsic DNA bends: an organizer of local chromatin structure for transcription. Bioessays, 23, 708–715. [DOI] [PubMed] [Google Scholar]
- Packer M.J. et al. (2000) Sequence-dependent DNA structure: tetranucleotide conformational maps. J. Mol. Biol., 295, 85–103. [DOI] [PubMed] [Google Scholar]
- Peckham H.E. et al. (2007) Nucleosome positioning signals in genomic DNA. Genome Res., 17, 1170–1177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiu W.R. et al. (2014) iRSpot-TNCPseAAC: Identify recombination spots with trinucleotide composition and pseudo amino acid components. Int. J. Mol. Sci., 15, 1746–1766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiu W.R. et al. (2016a) iHyd-PseCp: Identify hydroxyproline and hydroxylysine in proteins by incorporating sequence-coupled effects into general PseAAC. Oncotarget, 7, 44310–44321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiu W.R. et al. (2016b) iPTM-mLys: identifying multiple lysine PTM sites and their different types. Bioinformatics, doi: 10.1093/bioinformatics/btw380. [DOI] [PubMed] [Google Scholar]
- Satchwell S.C. et al. (1986) Sequence periodicities in chicken nucleosome core DNA. J. Mol. Biol, 191, 659–675. [DOI] [PubMed] [Google Scholar]
- Schones D.E. et al. (2008) Dynamic regulation of nucleosome positioning in the human genome. Cell, 132, 887–898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz S. et al. (2009) Chromatin organization marks exon-intron structure. Nat. Struct. Mol. Biol., 16, 990–995. [DOI] [PubMed] [Google Scholar]
- Segal E. et al. (2006) A genomic code for nucleosome positioning. Nature, 442, 772–778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stolz R.C., Bishop T.C. (2010) ICM Web: the interactive chromatin modeling web server. Nucleic Acids Res., 38, W254–W261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Struhl K., Segal E. (2013) Determinants of nucleosome positioning. Nat. Struct. Mol. Biol., 20, 267–273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tahir M., Hayat M. (2016) iNuc-STNC: a sequence-based predictor for identification of nucleosome positioning in genomes by extending the concept of SAAC and Chou's PseAAC. Mol. Biosyst., 12, 2587–2593. [DOI] [PubMed] [Google Scholar]
- Takagi H. et al. (2012) Nucleosome exclusion from the interspecies-conserved central AT-rich region of the Ars insulator. J. Biochem., 151, 75–87. [DOI] [PubMed] [Google Scholar]
- Teif V.B. (2015) Nucleosome positioning: resources and tools online. Brief. Bioinf., bbv086.. [DOI] [PubMed] [Google Scholar]
- Tillo D., Hughes T.R. (2009) G+C content dominates intrinsic nucleosome occupancy. BMC Bioinformatics, 10, 442.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tirosh I., Barkai N. (2008) Two strategies for gene regulation by promoter nucleosomes. Genome Res., 18, 1084–1091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tolstorukov M.Y. et al. (2008) nuScore: a web-interface for nucleosome positioning predictions. Bioinformatics, 24, 1456–1458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- West J.A. et al. (2014) Nucleosomal occupancy changes locally over key regulatory regions during cell differentiation and reprogramming. Nat. Commun., 5, 4719.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao X. et al. (2015) iDrug-Target: predicting the interactions between drug compounds and target proteins in cellular networking via the benchmark dataset optimization approach. J. Biomol. Struct. Dyn., 33, 2221–2233. [DOI] [PubMed] [Google Scholar]
- Xu Y. et al. (2013) iSNO-PseAAC: predict cysteine S-nitrosylation sites in proteins by incorporating position specific amino acid propensity into pseudo amino acid composition. PLoS One, 8, e55844.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yasuda T. et al. (2005) Nucleosomal structure of undamaged DNA regions suppresses the non-specific DNA binding of the XPC complex. DNA Repair, 4, 389–395. [DOI] [PubMed] [Google Scholar]
- Yi X.F. et al. (2012) Nucleosome positioning based on the sequence word composition. Protein Pept. Lett., 19, 79–90. [DOI] [PubMed] [Google Scholar]
- Yuan G.C., Liu J.S. (2008) Genomic sequence is highly predictive of local nucleosome depletion. PLoS Comput. Biol., 4, e13.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z. et al. (2012) Prediction of nucleosome positioning using the dinucleotide absolute frequency of DNA fragment. match, 68, 639. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


