NetProphet 2.0: mapping transcription factor networks by exploiting scalable data resources

Abstract

Motivation

Cells process information, in part, through transcription factor (TF) networks, which control the rates at which individual genes produce their products. A TF network map is a graph that indicates which TFs bind and directly regulate each gene. Previous work has described network mapping algorithms that rely exclusively on gene expression data and ‘integrative’ algorithms that exploit a wide range of data sources including chromatin immunoprecipitation sequencing (ChIP-seq) of many TFs, genome-wide chromatin marks, and binding specificities for many TFs determined in vitro. However, such resources are available only for a few major model systems and cannot be easily replicated for new organisms or cell types.

Results

We present NetProphet 2.0, a ‘data light’ algorithm for TF network mapping, and show that it is more accurate at identifying direct targets of TFs than other, similarly data light algorithms. In particular, it improves on the accuracy of NetProphet 1.0, which used only gene expression data, by exploiting three principles. First, combining multiple approaches to network mapping from expression data can improve accuracy relative to the constituent approaches. Second, TFs with similar DNA binding domains bind similar sets of target genes. Third, even a noisy, preliminary network map can be used to infer DNA binding specificities from promoter sequences and these inferred specificities can be used to further improve the accuracy of the network map.

Availability and implementation

Source code and comprehensive documentation are freely available at https://github.com/yiming-kang/NetProphet_2.0.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

A TF network map is a directed graph comprising nodes that represent genes and the proteins they encode and edges that link the TFs to their direct, functional targets. Developing effective methods for mapping TF networks genome-wide is a long-standing goal in genomics (Harbison et al., 2004; Hu et al., 2007) and computational biology (Faith et al., 2007; Margolin et al., 2006); see (Brent, 2016) for a recent review. TF network maps encode basic knowledge about the biochemical functions of molecules, much like metabolic network maps. They are thus a key part the encyclopedic knowledge that enables research and development. In addition, a TF network map is an essential input to at least two downstream applications. The first is TF activity inference. A TF network map links TFs with the target genes that they have the potential to bind and regulate, given the right circumstances, external signals, or developmental context. TF activity inference uses such a map to quantitatively model how much influence each TF is exerting on each target in a given context (Boorsma et al., 2008; Boulesteix and Strimmer, 2005; Kao et al., 2004; Tran et al., 2005). Unlike ordinary regression of target RNA levels against TF RNA levels, this approach treats TF activity levels as latent variables that are not necessarily proportional to TF RNA levels. A second application is transcriptome engineering, in which the goal is to modify the transcriptional regulatory network of a cell in a way that drives it into an expression state associated with some desirable behavior (Michael et al., 2016). The most common application of transcriptome engineering to date has been aimed at driving mammalian cells of one type (e.g. stem cells) into the transcriptional state associated with another cell type (e.g. liver cells) (Cahan et al., 2014; D'Alessio et al., 2015; Heinaniemi et al., 2013; Rackham et al., 2016).

Previous approaches to TF network mapping can be loosely categorized into those that rely exclusively on gene expression data (‘expression only’) and those that integrate a wide range of data types, including chromatin immunoprecipitation sequencing (ChIP-seq) of many TFs, genome-wide chromatin marks, and binding specificities for many TFs determined in vitro (‘integrative’). The data required for integrative approaches are available only for major model systems, principally Saccharomyces cerevisiae (yeast), Drosophila melanogaster (fly) (Marbach et al., 2012b) and the mammalian cell lines that have been the focus of the ENCODE project (Brent, 2016). Such resources are unlikely to become available soon for most other organisms and cell types. Even for fly and mammalian cell lines only a small fraction of the TFs encoded in the genome have been successfully subjected to ChIP-seq. Furthermore, most of the genes whose regulatory regions are bound by a TF show no evidence of being functionally regulated by that TF (Cusanovich et al., 2014; Gitter et al., 2009).

Gene expression data, by contrast, can be obtained from low cost, reliable and easily scalable experiments. Expression-only approaches to network inference have had notable successes on bacterial networks (Faith et al., 2007; Ghanbari et al., 2015; Greenfield et al., 2010; Haury et al., 2012; Huynh-Thu et al., 2010; Lam et al., 2016). More recently the NetProphet algorithm, which directly compares expression profiles from TF-knockout strains and wild-type strains, has been shown to give good results on single-cell eukaryotes (Brent, 2016; Haynes et al., 2013). There is evidence to suggest that when NetProphet is applied to yeast (Saccharomyces cerevisiae) it identifies bound genes more accurately than existing yeast ChIP-chip data (Haynes et al., 2013). Unlike ChIP-chip, however, all of the targets NetProphet identifies for a TF are functionally regulated by that TF. However, the accuracy of this approach on animal networks, which are much more complex than that of yeast, has never been demonstrated.

Here, we report on a second-generation ‘data light’ TF-network mapping algorithm called NetProphet 2.0. Our approach requires only data that can be generated from low-cost, reliable and easily scalable experimental methods. NetProphet 2.0 relies on three fundamental ideas. First, combining several expression-based network algorithms that use different types of models can yield better results than using either one alone—the ‘wisdom of the crowds’ idea (Marbach et al., 2012a). Second, TFs with similar DNA binding domains (in terms of amino acid sequence) tend to bind similar sets of target genes. Third, even an imperfect network map can be used to infer models of each TF’s DNA binding preferences from the promoter sequences of its putative targets and these models can be used to further refine the network. We describe the modules of NetProphet 2.0, show that each module contributes to its overall accuracy on both yeast and fly, and show that its overall accuracy improves on that of earlier data light methods, which rely only on gene expression data.

2 Results

2.1 Overview of analysis steps in NetProphet 2.0

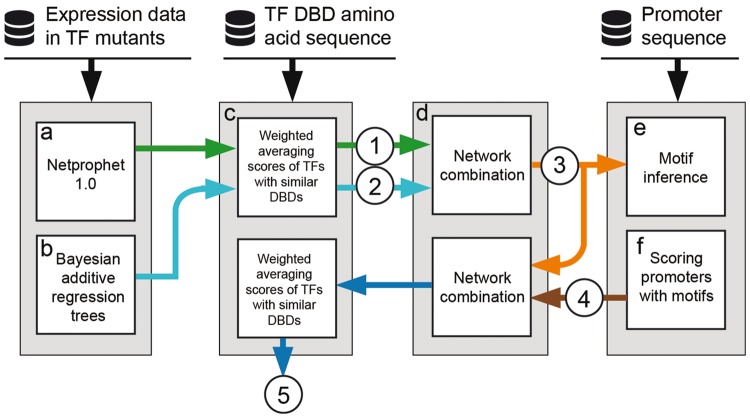
NetProphet 2.0 comprises six computational modules (Fig. 1), five of which take advantage of information obtained from gene expression profiling or genome sequencing. The output of each module is a map, represented as a score matrix with rows corresponding to TFs and columns corresponding to all genes, each of which is a potential target. The score vector (row) for a TF represents the strength of evidence that the TF regulates each potential target gene. A discrete graph structure can always be constructed by including only edges whose scores exceed a chosen threshold.

Fig. 1.

Overview of the NetProphet 2.0 pipeline. Database icons: input data sources. Rectangles: computational modules. Circles: network maps

Module A (Fig. 1a) is NetProphet 1.0, as previously described (Haynes et al., 2013). It constructs a map from gene expression profiles and performs best when the data include expression profiles of single TF perturbation strains. Module B (Fig. 1b) constructs an independent network map from the same gene expression data by using a machine learning algorithm called Bayesian Additive Regression Trees (BART) (Chipman et al., 2010). For each gene, Module B trains a separate BART model to predict the RNA level of that gene as a function of the RNA levels of all TFs. It then simulates the effect of varying each TF’s RNA level on the predicted RNA level of the target, holding the levels of all other TFs constant. Each TF’s level is varied between its minimum and maximum observed levels. The difference between the two predicted target gene expression levels is used as the score of the TF-target pair. Intuitively, the more a gene is predicted to change as a result of changing the level of a TF, the more likely it is to be a direct target of that TF.

Although Module B (BART) and Module A (NetProphet 1.0) use the same gene expression data, they do so in very different ways. NetProphet 1.0 relies primarily on the direct comparison of a gene’s expression after genetic perturbation of a TF to its expression in unperturbed, wild-type cells. Secondarily, it uses sparse linear regression of each gene’s RNA level against the RNA levels of the TFs. BART does not explicitly compare expression of a gene before and after an experimental TF perturbation. Instead, it uses a non-linear, non-parametric regression model based on random forests to predict the effects of a TF perturbation on the expression of a gene.

Module C (Fig. 1c) capitalizes on the fact that TFs with similar DNA binding domains (DBDs) tend to bind similar sets of target genes (Weirauch et al., 2014). It replaces the score matrix row for each TF by a weighted average of rows for other TFs with similar DBDs. Each row is weighted according to how similar the DBD of its TF is to the DBD of the row being replaced (see Methods & Supplementary Fig. S1). The predicted amino acid sequence of the DBD can be obtained from automated annotation of the genome sequence. The outputs of modules A and B are independently passed through Module C. They are then combined into a single score matrix by Module D (Fig. 1d), which uses quantile normalization to make the score distributions of the two networks comparable (see Methods).

Modules E and F (Fig. 1e, f) make use of the target genes’ promoter sequences to further refine the network map. Module E infers the DNA-binding specificity (motif) of each TF by identifying motifs whose presence in a promoter best distinguishes high scoring (likely) target genes from low scoring (unlikely) target genes (see Methods). Module F scans the inferred motif for each TF over the promoters of all genes and computes a score reflecting the strength of evidence that the TF binds the promoter. If no significant motif is found for a TF then its score vector remains unchanged after Module F. The resulting score matrix is then combined with the input score matrix by using module D again. In a final step, the combined matrix is passed through module C again.

In the following sections, we evaluate the contribution of each successive module to the overall accuracy of NetProphet 2.0. Finally, we compare the accuracy of the complete system to that of some previous systems for mapping TF networks from gene expression data.

2.2 Input data and benchmarking standards

We collected input data and benchmarking data for both yeast and fly. The gene expression data we used as inputs came from two sources. The first is a recently published yeast dataset, which contains 1487 samples including 265 TF knockout strains and 1219 knockouts of non-TF-encoding genes (Kemmeren et al., 2014). The second is a fly dataset, which contains 200 samples including 23 TF knockdown lines and 84 knockdowns of non-TF-encoding genes (Bonke et al., 2013). To evaluate the accuracy of the inferred network maps, we compared them to both ChIP-based binding data and motif-based binding potential. However, we do not assume that either of these networks is the correct network we are aiming to learn. Indeed, we know that most genes whose promoters are bound by a TF according to ChIP data show no evidence of being functionally regulated by that TF (Cusanovich et al., 2014; Gitter et al., 2009). However, a TF’s direct, functional targets are likely to be a subset of the genes whose promoters are bound by that TF. In other words, binding is necessary, but not sufficient, for direct regulation. Because our predicted targets are based on evidence of functional regulation from gene expression data, those predicted targets that are also bound by the TF are likely to be its direct, functional targets.

For each species, we constructed two benchmark networks whose edges connect TFs to the genes whose promoters they bind (but do not necessarily regulate). The first is based on ChIP-chip/seq data, which assesses the physical binding locations of the TFs. For yeast, we compiled ChIP data from TNET (Babu et al., 2004) and YEASTRACT (Abdulrehman et al., 2011), which contains ∼30 000 interactions for 184 TFs. For fly, we compiled ChIP data from FlyNet (Marbach et al., 2012b) and seven other ChIP-chip/seq studies, which together contain ∼180 000 interactions for 82 TFs. The second benchmark is a motif network constructed by scoring the promoters using position weight matrix (PWM) models of the DNA binding specificity of each TF. These models are derived from protein binding microarray (PBM) data collected in UNIPROBE database (Gordân et al., 2011; Robasky and Bulyk, 2011), which are completely independent of both gene expression and ChIP experiments. PWM models are available for 150 yeast TFs and 98 fruit fly TFs.

2.3 Exploiting similarity between DNA binding domains improves accuracy

Previously, we showed that NetProphet 1.0 (Module A) performed well on yeast by using an older gene expression dataset (Hu et al., 2007). Here, our first step is to determine its accuracy on a new yeast dataset and on the fruit fly. We evaluated the percentage of the top ranked edges that were supported by the ChIP network (Fig. 2A, C) or by the known-PWM network (Fig. 2B, D). In all cases, the predicted networks scored much better than randomly generated networks (gray shading), except for the PWM evaluation of the fly network when the number of predicted targets exceeded ∼25 per TF encoded in the genome (24 225 total). The Kemmeren yeast dataset yielded better results than those previously obtained using the smaller Hu dataset (Supplementary Fig. S2). Module C (weighted averaging) improved the evaluations against ChIP data except that it was neutral for large fly networks (Fig. 2). It slightly hurt the PWM evaluation of the smaller yeast networks, but it was otherwise neutral.

Fig. 2.

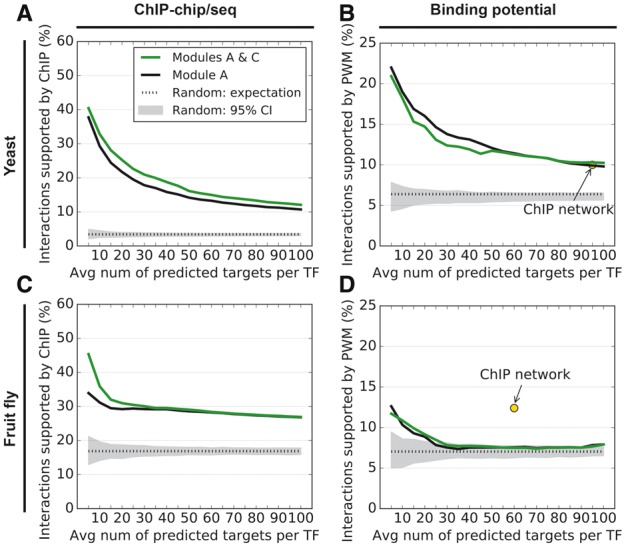
(A) Accuracy of NetProphet 1.0 on yeast before weighted averaging (black line) or after weighted averaging (green line). Horizontal axis: number of top ranked edges included in the network per TF encoded in the genome. E.g. since there are 320 TFs in the yeast genome, ‘10’ on the horizontal axis corresponds to a network with 3200 edges. Vertical axis: percentage of edges supported by ChIP data. Dotted line: expected accuracy of random networks. Gray area: 95% confidence interval for randomly selected networks. (B) Same as A for PWM support. The point labeled ‘ChIP network’ indicates the number of ChIP-supported edges and the fraction of those edges that also have PWM support. (C) Same as A for the fly data. (D) Same as B for the fly data, except that the vertical axis shows support by conserved PWM hits only

2.4 NetProphet 1.0 works on the fly network

Comparing the results for yeast and fly, it is apparent that the fly networks received slightly more support than the yeast network from ChIP data but less support from PWM data. In fact, the PWM support for fly networks with more than 25 edges per TF encoded in the genome does not significantly exceed the support for random networks. That is probably because the number of fly expression profiles in which a single TF has been knocked down represents 10-fold fewer TFs than for yeast (23 versus 265) and the number of expression profiles from non-TF knockdowns is also much smaller (84 versus 1219). The number of known fly PWMs against which to evaluate is also smaller (98 versus 150). Another difference is that the yeast ChIP network was supported by PWM evidence at the same rate as the similar-sized networks predicted by NetProphet 1.0. The fly ChIP network, by contrast, was supported at a much higher rate than similar-sized networks predicted by NetProphet 1.0. That may be the result of the smaller expression dataset for fly and because the fly ChIP data are more recent than the yeast data, so the ChIP methodology may have matured in the interim.

2.5 Combining with Bayesian Additive Regression Trees improves accuracy

Module B uses Bayesian Additive Regression Trees (BART), which provides an alternative approach to making use of the gene expression data. As weighted averaging (Module C) improved the accuracy of the NetProphet 1.0 output, we applied it to the BART output (Fig. 1, Network 2), which it also improved (Supplementary Fig. S3). Finally, we tried combining the two resulting networks (Fig. 1, Network 3). The effects of processing through these modules on accuracy are shown in Figure 3. NetProphet 1.0 with weighted averaging (Modules A & C, green) generally performed better than BART with weighted averaging (Modules B & C, cyan), except that BART significantly outperformed in PWM support on yeast (Fig. 3B). Remarkably, combining the two networks (Modules A-D) performed as well as the better of the two on the yeast ChIP and PWM metrics (Fig. 3A, B) and significantly better than either network on fly (Fig. 3C, D). This is consistent with the previously reported ‘Wisdom of Crowds’ effect in TF network mapping (Marbach et al., 2012a).

Fig. 3.

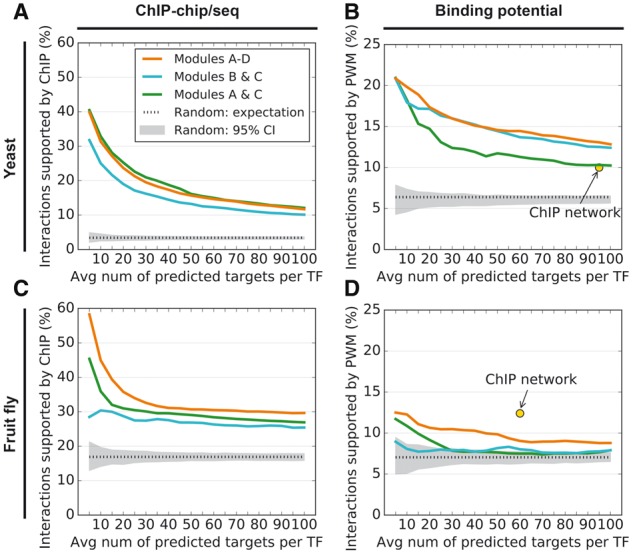
(A) Accuracy of NetProphet 1.0 on yeast after weighted averaging (Modules A & C, green line), BART after weighted averaging (Modules B & C, cyan line) and the combination of the two (Modules A–D, orange line). Horizontal axis: number of top ranked edges included in the network per TF encoded in the genome. Vertical axis: Percentage of included edges that are supported by ChIP data. Dotted line: Expected accuracy of random networks. Gray area: 95% confidence interval for random networks. (B) Same as A for PWM support. The point labeled ‘ChIP network’ indicates the number of ChIP-supported edges and the fraction of those edges that also have PWM support. (C) Same as A for the fly data. (D) Same as B for the fly data, except that the vertical axis shows support by conserved PWM hits only

2.6 Inferring TF binding preferences from promoter sequence improves accuracy

We hypothesized that knowing the DNA binding specificities of the TFs would enable us to improve on the accuracy of the maps output by Modules A–D. To test that hypothesis, we scanned the known yeast and fly PWMs across the promoter sequences of all genes in the genome, producing a binding potential score for each TF at each promoter (see Methods). This score matrix was then combined with the score matrix output by Modules A–D (Fig. 1, Network 3) by using Module D again. The resulting maps were evaluated as before (Fig. 4, purple dashed lines). For the evaluation by PWM support, using known PWMs constitutes ‘peeking’ at the evaluation standard, so it would have been worrisome if performance had not improved. For the evaluation by ChIP support, using known PWMs provided a small but consistent accuracy improvement, except for mid-sized fly networks, where it had no effect. The fact that this helped the yeast results more than the fly results is not surprising, since the promoter regions in yeast are much smaller and a much higher fraction of yeast TFs have known PWMs (46.9% versus 10.1%).

Fig. 4.

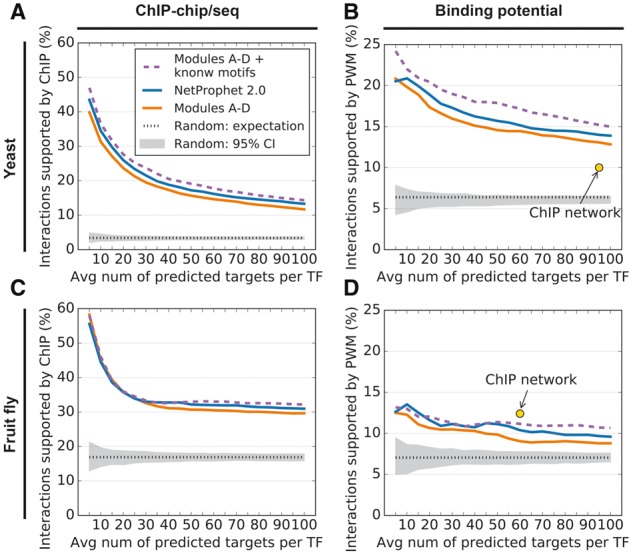
(A) Accuracy of Modules A–D [Combination of NetProphet 1.0 and BART after weighted averaging (orange line)], Modules A–D with known yeast PWM motifs (dashed purple line) and Modules A–F (NetProphet 2.0). Horizontal axis: number of top ranked edges included in the network per TF encoded in the genome. Vertical axis: Percentage of included edges that are supported by ChIP data. Dotted line: Expected accuracy of random networks. Gray area: 95% confidence interval for random networks. (B) Same as A for PWM support. The point labeled ‘ChIP network’ indicates the number of ChIP-supported edges and the fraction of those edges that also have PWM support. (C) Same as A for the fly data. (D) Same as B for the fly data, except that the vertical axis shows support by conserved PWM hits only

The known PWMs used above were obtained from protein binding microarray experiments. However, we hypothesized that we could infer PWMs using only gene expression and genome sequence data, thereby avoiding the need for additional experiments. Thus, we applied the FIRE motif inference algorithm (Elemento et al., 2007) to the score vector of each TF after Modules A–D. FIRE attempts to find a motif whose presence in a promoter best discriminates between high and low scoring target genes. We then used the inferred motifs to score the promoter of each gene just as we had with the known PWMs. These scores were combined with the output of Modules A-D, except that the scores for TFs for which FIRE could not identify a high confidence motif were left unchanged. The resulting accuracy improvement (Fig. 4, blue line) was approximately half of that obtained from the known motifs. Importantly, this approach does not require any additional experiments, making it suitable for application to non-model systems.

Next, we directly compared the motifs inferred by Module E to the known motifs. For each TF with a known PWM, we calculated the Spearman correlation between the scores assigned to each promoter by the inferred and known PWMs (Fig. 5, blue bars). As a randomized baseline distribution, we calculated the median of the correlations between each inferred PWM and all other known PWMs (Fig. 5, orange bars). For yeast, 37.9% of the inferred PWMs correlated with the corresponding known PWMs at levels significantly above the baseline distribution. In the fly data, the baseline distribution showed much higher correlations than in the yeast data. This is probably because 42% of all known fly PWMs belong to the Homeodomain family, whose members share a preference for binding motifs containing ATTA (Hughes, 2011). Additionally, there were only 2 fly TFs whose inferred PWM scores had a correlation of >0.5 with their known PWM score (as compared to 25 in yeast). This may reflect the larger size of the fly promoters, the smaller amount of gene expression data available for fly, and/or a greater tendency for gene regulation in the fly to be determined by combinatorial logic, rather than by independently active binding sites. Although few of the inferred fly PWMs showed a statistically significant degree of similarity with their known counterparts, the use of the PWM inference module results in a small but noticeable increase in overall accuracy.

Fig. 5.

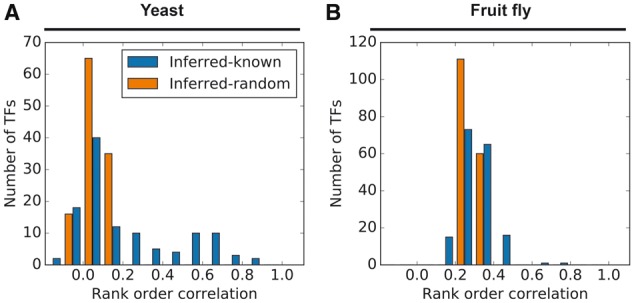
Relationships between inferred and known PWMs. Blue bars: distribution of rank order correlations between binding potential scores assigned to each promoter by inferred PWMs and known PWMs. Orange bars: distribution of the medians of rank order correlations between each inferred PWM and the known PWMs for all other TFs. (A) Yeast. (B) Fruit fly

2.7 NetProphet 2.0 improves on previous network mapping methods

For several years, algorithms for mapping TF networks from gene expression data were compared in a series of community evaluation projects known as DREAM [Dialog on Reverse-Engineering Assessment and Methods; (Marbach et al., 2012a)]. In a previous publication, we compared NetProphet 1.0 to several of the best performing algorithms from DREAM on a set of yeast expression profiles (Haynes et al., 2013). The comparison algorithms were Inferelator (Greenfield et al., 2010) and GENIE3 (Huynh-Thu et al., 2010). Here, we compare NetProphet 2.0 to those same algorithms plus two others: CLR (Faith et al., 2007) and TIGRESS (Haury et al., 2012), on a new set of yeast expression profiles and a set of fly expression profiles. We also compare to Aracne (Margolin et al., 2006) on the fly data; in our hands, Aracne could not be run on the 1487 yeast samples. We also compare to using the squared Spearman correlation coefficient between the expression of each TF and each target gene as the TF-target score, the method used in the FlyNet paper (Marbach et al., 2012b).

To evaluate NetProphet and the six other algorithms, we ran them all on the same sets of expression profiles used throughout this paper and selected the top scoring interactions from the output of each algorithm. The number of top scoring interactions selected was ten per TF encoded in the genome—i.e. 3200 for yeast and 9690 for fly. It is important to note that NetProphet 2.0 requires an annotated genome sequence as input, whereas the other algorithms use only the gene expression data. Therefore, we are not evaluating algorithms designed for exactly the same tasks. However, they can all be viewed as special cases of algorithms designed to infer direct, functional TF networks from data that can be produced by low-cost, reliable, scalable methods.

The results of the comparison showed that NetProphet 2.0 was more accurate than the other algorithms as evaluated by the yeast ChIP benchmark and by the fly ChIP and PWM benchmarks (Fig. 6). GENIE3 was slightly more accurate than NetProphet 2.0 on the yeast PWM benchmark. When comparing predictions to known interactions that are supported by both ChIP and PWM data, NetProphet 2.0 was substantially more accurate than all of the comparison algorithms. This is significant because ChIP hits that coincide with PWM hits are more likely to be functional than those that do not (Cusanovich et al., 2014; Van Nostrand and Kim, 2013).

Fig. 6.

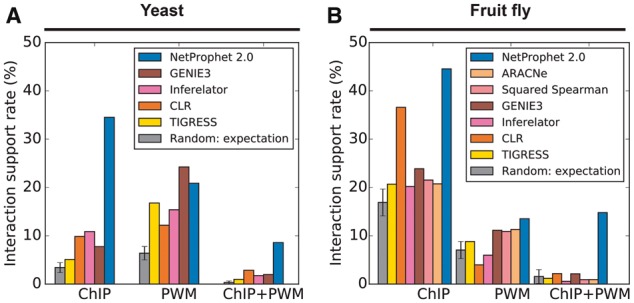
Comparison between NetProphet 2.0 and other leading expression-based mapping algorithms. (A) Yeast. (B) Fruit fly

3 Materials and methods

3.1 Download and preparation of datasets

See Supplementary Material.

3.2 Evaluation

3.2.1 ChIP support

We used the ChIP benchmarks to assess the mapping accuracy of our algorithm. These network maps are binary matrices in which ones represent positive ChIP interactions. Based on a certain stringency level, the top L interactions predicted by NetProphet 2.0 modules were evaluated against ChIP interactions. The mapping accuracy, termed as ChIP support rate, is the fraction of these predicted top interactions supported by ChIP evidence. The network size is based on all predicted edges above a given stringency, while the ChIP support rate is based on the edges whose TFs have ChIP data. We evaluated the accuracies of the mapped networks of different sizes as we varied the stringency levels.

3.2.2 PWM support

The PWM score matrix for yeast was binarized using a threshold for each TF. The threshold was the greatest binding potential score that was exceeded by at least 10% of the ChIP-supported interactions of that TF. We calculated the PWM-support rates using this binary matrix, just as we did for the ChIP binary matrix.

3.3 Weighted averaging

3.3.1 Calculation of weighting function & threshold

We used a four-step process to characterize the relationship between the similarities of DBDs and the similarities of known PWMs. First, for each yeast TF, we obtained the sequences of any DBDs found within it as well as the PWM associated with it from the CIS-BP data base (Weirauch et al., 2014). We then aligned the DBDs of each TF to the DBDs of each other TF by using Clustal Omega (v1.2.1) (Sievers et al., 2014) and used the percent identity (PID) to quantify the similarity between the two DBDs. If there were multiple DBDs within a TF all pairs of DBDs were aligned and the largest percent identity was used. Second, we aligned the PWM of each TF to that of each other TF by using Tomtom (v4.9.1) (Gupta et al., 2007) and used the E value output from Tomtom as a measure of the similarity between the two PWMs. Third, for the TF pairs whose DBD similarity scores fall in a certain range, we calculated the fraction of the corresponding PWM pairs that are similar (Tomtom E value < 1). Finally, we fit a logistic function to model the relationship between the percent identities of DBDs and the fraction of significantly similar PWMs:

$$w(d)=\frac{0.9}{1+e^{-0.1(d-40)}}$$ (1)

where d is the percent identity of a pair of DBDs (Supplementary Fig. S1). The fraction of similar PWMs can also be seen as the probability of a pair of TFs at a given DBD-similarity level binding to similar DNA sequences.

3.3.2 Use of weighting function

To implement Module C, we calculated the PID between each pair of DBDs to predict the probability that the DBDs bind significantly similar sequences, according to the logistic model. For each TF i, this probability was used as a weighting factor for each other TF with PID  > = 50%; for TFs with PID < 50%, the weighting was 0. Row i was then replaced by the weighted sum of all rows:

$${S\mathrm{\text{'}}}_i=\sum _{k}w\left(d_{k,i}\right)S_k$$ (2)

where $S_i^{\text{'}}$ is the updated row of edge scores of TF i to all genes, $d_k{,}_i$ is the percent identity score between the DBD’s of TF k and TF i, and w(·) is the weighting factor calculated using the logistic function.

3.4 Bayesian Additive Regression Trees

We used the BART model trained for each target gene to predict the effects of varying each TF’s level on the level of the target gene. Specifically, we varied the RNA level of each TF between its minimum and maximum observed levels while keeping the levels of other TFs constant. The edge score of TF i to target j in the BART network map is the difference between the predicted level of target j in the two simulations, one with TF i at its maximum observed level and the other with TF i at its minimum observed level. BART package implemented in R was used [v0.3-1.3, https://cran.r-project.org/package=BayesTree (Chipman et al., 2010)].

3.5 Quantile combination of network maps

Since the network maps output by various modules have different score distributions, we used quantile normalization (Module D) to combine score matrices. One matrix is designated as the reference and the other as the auxiliary. The scores in the auxiliary matrix are modified to have the same distribution as the reference matrix before averaging with the corresponding entries of the reference matrix. Formally, if $S_{i,j}^{ref}$ is the score for TF i as a regulator of gene j in the reference matrix and $S_{i,j}^{aux}$ is the score for TF i as a regulator of gene j in the auxiliary matrix:

$$S_{i,j}=\frac{1}{2}(S_{i,j}^{ref}+F_{ref}^{-1}(F_{aux}\left(S_{i,j}^{aux}\right)\left)\right)$$ (3)

where $F_{ref}$ and $F_{aux}$ are the empirical cumulative distribution functions of the reference and auxiliary matrices, respectively. For combining the NetProphet-derived (Fig. 1, Network 1) and BART-derived (Fig. 1, Network 2) matrices, the former is designated as the reference. This approach was chosen over other quantile normalization methods empirically, because it gave better results.

3.6 PWM inference and promoter scoring

3.6.1 PWM inference

Module E uses an algorithm called FIRE (Elemento et al., 2007) to infer a motif for each TF based on its score vector and the promoter sequences of all genes. For each TF, Module E divides the range of target scores into 20 bins, each spanning 1/20th of the range. For each gene, the bin number corresponding to its score as a target of the TF is input to FIRE, along with the sequence of its promoter region. We used 7 as the k-mer seed size, 20/20 as the robustness threshold, and default parameters for other criteria. If more than one motif passed the criteria for a TF, we only considered the best one, according to FIRE.

3.6.2 Promoter scoring

Semantically, the motifs output by FIRE are patterns specifying which nucleotides are possible at each position of a binding site. However, these can be converted to PWMs by assigning each of the possible nucleotides at each position the same probability and assigning each impossible nucleotide probability zero. For example, if the motif specified is {A, T}{G}{G, C, T}, A or T in the first position would have probability 1/2, G in the second position would have probability 1, and G, C or T in the third position would have probability 1/3. With this interpretation, Module F uses the FIMO program (Grant et al., 2011) to score the binding potentials by scanning the inferred motifs over the promoters. The TF-promoter binding potential was calculated as the maximum of two scores: (1) the log odds of the most significant binding site, (2) the sum of log odds of all significant (P < 0.05) binding sites. Subsequently, we used Module D again to combine this binding potential matrix (the auxiliary matrix; Fig. 1, Network 4) with the input to Module E (the reference matrix; Fig. 1, Network 3). The rows of TFs for which we could not infer a motif were left unchanged.

3.7 Other algorithms to which NetProphet 2.0 is compared

3.7.1 TIGRESS

Trustful Inference of Gene REgulation using Stability Selection (TIGRESS) uses stability selection to sample the expression data and scores the TF-target interaction as the frequency of each TF being chosen in LARS for each target gene (Haury et al., 2012). We used its MATLAB implementation (v2.1) downloaded from http://cbio.mines-paristech.fr/∼ahaury/svn/dream5/html/index.html. We modified the code so that the TFs could be indexed at any position in the comprehensive gene list.

3.7.2 CLR

Context likelihood of relatedness (CLR) estimates the likelihood of the mutual information (MI) by contrasting the MI calculated using the RNA levels of each TF-target pair across all samples with the null model, given the local network context (Faith et al., 2007). We used minet (v3.30.0, R/Bioconductor package) downloaded from https://www.bioconductor.org/packages/release/bioc/html/minet.html to build MI matrix and infer CLR network.

3.7.3 Inferelator pipeline

The Inferelator pipeline in DREAM4 (Greenfield et al., 2010) is a mixture model that consists of median corrected Z-score, mutual information (CLR) and LASSO regression coefficient (Inferelator 1.0). The source code was downloaded from

https://github.com/smidget/Network-Inference-Workspace/tree/master/algorithms/inferelator-pipeline. We wrote a script to pipeline Inferelator modules according to the provided pseudo-code.

3.7.4 GENIE3

GEne Network Inference with Ensemble of trees (GENIE3) uses random forests that estimate how much the expression level of each TF contributes to explaining the level of each target gene (Huynh-Thu et al., 2010). We used the Python implementation downloaded from http://www.montefiore.ulg.ac.be/∼huynh-thu/software.html.

3.7.5 ARACNE

ARACNE (Algorithm for Reconstruction of Accurate Cellular Networks) is an approach based on mutual information and the data processing inequality (Margolin et al., 2006). We downloaded ARACNE from http://califano.c2b2.columbia.edu/aracne/.

4 Discussion

NetProphet 2.0 is designed around the principle of using only data that can be obtained with robust, predictable and scalable experimental methods. Specifically, it requires only gene expression data after TF perturbation and genome sequence with automated annotation. It makes use of three fundamental ideas. First, combining the results of distinct approaches to mapping networks from gene expression data can significantly improve accuracy (Marbach et al., 2012a). Second, similar DNA binding domains bind similar sets of promoters (Weirauch et al., 2014). Third, even a noisy, imperfect network can be used to infer useful binding motifs from promoter sequences. By combining these three ideas, NetProphet 2.0 significantly outperforms NetProphet 1.0 and a range of other expression-based algorithms, as assessed by measured binding locations and by binding potentials. The fraction of predicted interactions that are supported by both ChIP and PWM substantially exceeds that of the other algorithms tested (Fig. 6).

There are many possible ways to implement the ideas behind NetProphet 2.0. For example, there are other non-parametric regression algorithms that could substitute for or supplement BART. Fused regression (Lam et al., 2016) is a possible alternative to our weighted averaging approach for exploiting the similarities between DNA binding domains. There are also many software packages for inferring TF binding motifs, which could be substituted for FIRE. Implementations using these alternative components, which are beyond the scope of this paper, have the potential to improve accuracy in the future.

NetProphet’s ‘data light’ approach stands in contrast to the ‘integrative’ approach, which has also been applied to mapping the fly TF network (Marbach et al., 2012b). In that study, a network was constructed by using all available data sources, including the same TF-ChIP and PWM datasets that we used only for validation. Because these two data sources were used as inputs, they could not also be used for validation of the integrative network. As a result, it is not possible to directly compare the accuracy of the two approaches on genome-scale networks. The integrative model also used ChIP of a wide range of chromatin marks as input. Thus, applying it to a new organism or cell type would require a data generation effort beyond what can currently be done in a single lab. Integrative network construction is feasible for a few model systems that have been targeted for exhaustive data generation by large consortia. When the integrative approach is feasible, NetProphet 2.0 can be used to process the available gene expression data in place of methods such as the Spearman correlation of expression profiles (Marbach et al., 2012b). In addition, NetProphet 2.0 can integrate binding specificity models determined by methods such as yeast one hybrid (Fuxman Bass et al., 2016), high throughput SELEX (Jolma et al., 2013) and protein binding microarrays (Weirauch et al., 2014), for any TFs for which they are available. An interesting intermediate between data-light and integrative approaches would be to combine NetProphet 2.0 with TF binding locations that are predicted from TF binding specificity, conservation and cell-type specific DNA accessibility data, but not requiring ChIP-seq of individual TFs (Cuellar-Partida et al., 2012; Zhong et al., 2013). There has also been recent progress in formal frameworks for integration of prior knowledge into expression-based network mapping (Ghanbari et al., 2015; Lam et al., 2016).

TF-target interactions predicted by NetProphet 2.0 are supported by binding potential (PWMs derived from protein-binding microarray experiments) at a significantly higher rate than the interactions predicted by existing yeast ChIP-chip data (Fig. 4B). The ChIP-seq data on the fly genome are much more recent than the yeast data (Clough et al., 2014; Georlette et al., 2007; Hadzic et al., 2015; Ikmi et al., 2014; Liu et al., 2009; Marbach et al., 2012b; Page et al., 2005; Teleman et al., 2008). When networks of similar size (number of targets per TF) are compared, the fly ChIP edges are supported by PWMs at a slightly higher rate than the NetProphet 2.0 predictions (Fig. 4D). However, the NetProphet 2.0 edges that score among the top 14 535 (∼15 targets per TF) are supported by strong binding potential at a rate comparable to those of the larger ChIP network. For practical purposes, it is also important to keep in mind that the ChIP data come at a much higher cost than the NetProphet 2.0 predictions, take much longer to generate, and are plagued by the uncertain success of individual ChIP-seq experiments. Furthermore, existing evidence suggests that only a very small fraction of ChIP-supported interactions are functional, in the sense that the expression of the gene whose promoter is bound changes when the TF is perturbed [typically < 10% (Cusanovich et al., 2014; Gitter et al., 2009); reviewed in Brent (2016)]. Since NetProphet 2.0 is primarily an expression-based method, all its predictions are supported by expression data and hence are likely to be functional. Thus, NetProphet 2.0 provides an attractive alternative to TF ChIP, especially for experimental systems that are unlikely to benefit from an ENCODE-style undertaking to systematically ChIP a large number of TFs.

NetProphet 2.0 is the first algorithm that has been shown to be effective on an animal genome without requiring any data beyond gene expression after TF perturbations and genome sequence. While the steps from bacteria to yeast and yeast to fly were significant (Haynes et al., 2013; Marbach et al., 2012b), the step from a compact invertebrate genome such as that of the fly to mammalian genomes will also be challenging. The primary challenges include limited data availability, large, poorly defined promoters, and long-range enhancers. The data limitation will probably be removed over the next few years, now that CAS9 has made deleting TFs in mammalian systems much easier. The problem of defining enhancers and identifying their target genes may also be alleviated before long. One source of data that will likely prove useful is the expression of enhancer RNAs, which can highlight active enhancers and the genes whose expression correlates with enhancer activity (Andersson et al., 2014; Core et al., 2008; Danko et al., 2015). Data on three-dimensional chromosome conformation from rapidly improving, sequencing based methods will also prove useful. We expect that these new data sources will make it possible to test, validate and apply NetProphet 2.0 to mammalian systems in the near future.

Funding

This work was supported in part by NIH T32 training grant HG000045 (National Human Genome Research Institute) and R01 grants AI087794 (National Institute for Allergy and Infectious Disease) and GM100452 (National Institute of General Medical Sciences).

Conflict of Interest: none declared.