Mechanisms to protect the privacy of families when using the transmission disequilibrium test in genome-wide association studies

Abstract

Motivation

Inappropriate disclosure of human genomes may put the privacy of study subjects and of their family members at risk. Existing privacy-preserving mechanisms for Genome-Wide Association Studies (GWAS) mainly focus on protecting individual information in case–control studies. Protecting privacy in family-based studies is more difficult. The transmission disequilibrium test (TDT) is a powerful family-based association test employed in many rare disease studies. It gathers information about families (most frequently involving parents, affected children and their siblings). It is important to develop privacy-preserving approaches to disclose TDT statistics with a guarantee that the risk of family ‘re-identification’ stays below a pre-specified risk threshold. ‘Re-identification’ in this context means that an attacker can infer that the presence of a family in a study.

Methods

In the context of protecting family-level privacy, we developed and evaluated a suite of differentially private (DP) mechanisms for TDT. They include Laplace mechanisms based on the TDT test statistic, P-values, projected P-values and exponential mechanisms based on the TDT test statistic and the shortest Hamming distance (SHD) score.

Results

Using simulation studies with a small cohort and a large one, we showed that that the exponential mechanism based on the SHD score preserves the highest utility and privacy among all proposed DP methods. We provide a guideline on applying our DP TDT in a real dataset in analyzing Kawasaki disease with 187 families and 906 SNPs. There are some limitations, including: (1) the performance of our implementation is slow for real-time results generation and (2) handling missing data is still challenging.

Availability and implementation

The software dpTDT is available in https://github.com/mwgrassgreen/dpTDT.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

The continuous progress in genome technologies is rapidly reducing the cost of human genome sequencing (online source), and has produced massive human genome data (Clarke, 2012; Church, 2005). For example, the US government’s Precision Medicine Initiative (Collins and Varmus, 2015) aims at developing treatments tailored to a person’s genetic profile from a cohort of one million volunteers. Extensive collection of genome data and the development of advanced analysis techniques increase the probability of using human genome data for clinical diagnosis and treatments, but it also leads to many privacy challenges. Many studies (Craig 2011; Gymrek, 2013; Homer, 2008; Gutmann, et al., 2012, Wang, 2009) demonstrated the vulnerability of exposing human genome data without protection. For example, Lin et al. (2004) shows that as few as 75 independent SNPs can be used to uniquely identify an individual. Given genome data without explicit identifiers, it is possible to infer personal information (Gymrek, 2013; Sweeney, 2013). Even aggregated genome statistics can be used to recover sensitive personal information (Homer, 2008; Wang, 2009) and many recent attack models use allele frequencies (or absence/presence information such as particular variants) to reveal an individual’s membership in case or control groups (Clayton, 2010; Homer, 2008; Jacobs, 2009; Sankararaman, 2009; Visscher and Hill, 2009). That is, an attacker can discover that a particular person of interest, from whom the attacker has gathered genetic information, participated in a study. This is problematic when the participants do not want to disclose their participation in a study. For example, in certain studies in which the ‘controls’ are individuals with a particular diagnosis receiving standard-of-care and the ‘cases’ are individuals with the same diagnosis receiving a new type of treatment, it is possible to infer whether a person of interest participated in the study (i.e. the person has the diagnosis) and whether she was in the case or control group when the attacker gets information about allele frequencies. For this reason it is important to develop secure and privacy-preserving methods (Chen, 2017; Wang, 2016; Zhang, 2015) to protect genome studies against emerging attacks (Humbert, 2013; Malin and Sweeney, 2001, 2004).

Differential privacy (DP) (Dwork, 2006) provides a rigorous framework to protect the genome database in the information disclosure phase. They introduce perturbations (i.e. noise) that make re-identification of targeted individuals as difficult as disclosers want (the higher the risk, the less noise is introduced and vice-versa). DP (Dwork, 2006) provides provable quantification of the privacy risk associated with disclosed information. Yu (2010) studied a DP-based logistic regression method to detect SNP associations in GWAS. A DP-based genomic data dissemination model was proposed in Wang (2014). In Johnson and Shmatikov (2013), a DP mechanism was developed to protect the outcome of chi-square test outcomes in GWAS. Uhler (2013) improved previous methodology to allow privacy-protecting release of the $K$ most relevant SNPs. Yu (2014) demonstrated better performance in terms of privacy and utility tradeoffs, and presented formal proofs (Yu, 2014; Yu and Ji, 2014).

However, these current privacy-preserving mechanisms in GWAS only focus on case–control studies. As far as we know, none of the work in GWAS considers protecting privacy in family-based studies. Since the data are recorded and structured in the unit of a family in these studies, it is possible that an attacker may infringe the privacy of the whole family instead of that of just one individual. Hence, to avoid this, we need a reliable method to protect privacy at the family level. This paper focuses on protecting family privacy for transmission disequilibrium test (TDT) in GWAS.

The TDT is primarily designed to account for population stratification and detect potential Mendelian inconsistencies. It measures the over-transmission of an allele from heterozygous parents to an affected offspring (Spielman, 1993). It takes into account the family structure allowing for investigating heritability questions especially powerfully in the rare diseases such as Kawasaki disease, which cannot be addressed in the case–control studies (Ott, 2011). TDT has been successfully applied to whole exome sequencing studies in autism (Levin-Decanini, 2013) and Kashin-Beck disease (Yang, 2014).

To protect privacy in TDT, we consider that an attacker might violate the privacy of the entire family to figure out whether one family participates in the study, and not just an individual of the family. To protect family level privacy, we develop and analyze differentially private (DP) mechanisms for TDT based on test statistics, P-values and the shortest Hamming distance (SHD) scores. This is a non-trivial extension from individual privacy-protection methods because we need to preserve the family structure while introducing the perturbation. Under the DP framework, we define the neighbor datasets by replacing single family with other valid types to protect the privacy of trios (mother, father and one child) used in TDT. We carefully manipulate the sensitivity of the statistics to guarantee privacy while maximizing the utility. We develop both exact and approximate algorithms to get SHD scores for TDT. To maintain both privacy and utility (the usefulness of the method and a former definition is in the section ‘Results’), our DP methods on TDT is preferable to be applied in a large cohort with sufficient number of families. We give an illustration to apply our methods in a real GWAS study dataset for the Kawasaki disease. On a proper cohort size, our proposed DP mechanisms based on SHD score can preserve higher privacy and better utility than other proposed methods for TDT in GWAS.

1.1 Transmission disequilibrium test

TDT is a family-based association test for linkage disequilibrium (LD). It tests at a marker locus for the LD in two alleles and as well as more alleles from the genotypes of trio families (two parents with one affected child) or other types of families (Spielman, 1993). In GWAS, we do not apply TDT only in one locus but in hundreds, thousands even hundreds of thousands loci. The process might reveal sensitive patient information and therefore we are proposing a private version of TDT to protect family information. Our analysis focuses on applying TDT to SNPs (considering two alleles) from trio families. Other extension work can be found in the ‘Discussion’ section.

In on SNP, TDT determines whether two alleles, $W$ and $w$, have equal probability of being transmitted from the parents to their child. Let $b$ be the number of the $Ws$ transmitted when $w$ is not transmitted and $c$ be the number of $w\text{'}s$ transmitted when $W$ is not transmitted. For example, in a family with genotype configuration $WW\times Ww\to WW$, one parent $WW$ transmits one $W$ to the child ($b=1)$ while $w$ is non-transmitted from neither of the parents ($c=0)$. All possible parent genotypes are enumerated in the Appendix (Supplementary Table S1). Suppose there are N independent trio-families in our study. In Table 1 we gather the allele transmission (and non-transmission) information from these N families and give the numbers of families in each type of $\left(b,c\right)$.

Table 1.

Number of Trio-families in one SNP

$\left(b,c\right)$ in one family	$\left(\mathrm{1,0}\right)$	$\left(\mathrm{0,1}\right)$	$\left(\mathrm{1,1}\right)$	$\left(\mathrm{2,0}\right)$	$\left(\mathrm{0,2}\right)$	$\left(\mathrm{0,0}\right)$
# of families	$n_1$	$n_2$	$n_3$	$n_4$	$n_5$	$n_6$

From Table 1, we get in one SNP from N trio-families,

$$\begin{array}{l}b=n_1\times 1+n_2\times 0+n_3\times 1+n_4\times 2+n_5\times 0+n_6\times 0;\\ c=n_1\times 0+n_2\times 1+n_3\times 1+n_4\times 0+n_5\times 2+n_6\times 0;\\ N=n_1+n_2+n_3+n_4+n_5+n_6.\end{array}$$

Table 2 summarizes allele transmission in N trio-families. The TDT statistic in one SNP is based on

$$T:=T\left(b,c\right)=\frac{(b-s{)}^2}{s}+\frac{(c-s{)}^2}{s}=\frac{(b-c{)}^2}{b+c},\mathrm{ }\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{ }s=\frac{b+c}{2}.$$ (1)

In the concern of privacy, we include the families with homozygous parents $b=c=0$. We define $T=0/0=0$. Under the null hypothesis that there is no linkage disequilibrium and the independence assumption among families, the counts $b$ and $c$ have binomial distribution with size $b$+c and probability 0.5 and thus the test statistic $T$ in (1) approximately obeys a ${\chi }^2$-distribution with one degree of freedom (Spielman, 1993). Under the alternative hypothesis, the counts $b$ and $c$ become unbalanced so the hypothesis is rejected for large values of $T$. Since both $(n_1,\dots ,n_6)$ and $(b,c)$ are both sufficient statistics for TDT, we can represent the dataset by either one of them. The exact algorithm in the Section 2.2 is based on the representation of $(n_1,\dots ,n_6)$. In the other parts of this article we consider the dataset based on $(b,c)$. We define the dataset in one SNP by $\mathcal{D}:\hspace{0.5em}=\left\{\right(b,c):b+c\le 2N,b,c\in \mathbb{N}\}$ where $\mathbb{N}$ is the set of nonnegative integers. In the studying of family-based association in GWAS, we apply TDT for each SNP. For $M$ SNPs, we represent the dataset $D$ by $(\left(b_{1 }, c_1\right), \cdots ,\left(b_{M }, c_M\right))$ and the data space is ${\mathcal{D}}^M$.

Table 2.

TDT contingency table from $N$ trio-families in one SNP

	Non-transmitted allele
Transmitted allele	$\mathrm{W}$	$\mathrm{w}$	Total
$\mathrm{W}$	$\mathrm{a}$	$\mathrm{b}$	$\mathrm{a}+\mathrm{b}$
$\mathrm{w}$	$\mathrm{c}$	$\mathrm{d}$	$\mathrm{c}+\mathrm{d}$
Total	$\mathrm{a}+\mathrm{c}$	$\mathrm{b}+\mathrm{d}$	2$\mathrm{N}$

Now the family information is summarized in $(b,c)$ pairs. From one pair, one can infer possible family genotypes and thus it leaves a potential risk for an attacker to identify families. In the framework of DP, Figure 1 illustrates the workflow for private data access from DP TDT. We take the query as to get the top $K$ significant SNPs. The data owner first calculates the statistics $T_i$’s for each SNP and next applies a DP mechanism (Laplace or exponential mechanism) to perturb the original $T_i$’s. Based on the perturbed responses, the data owner reports to the data user the top $K$ most significant SNPs. Our DP TDT is developed to protect the privacy of outcomes of data analyses. Instead of exposing the data to end users, we can hide them behind a query interface (for example, by providing results of certain statistical tests). It has been shown that repeated queries can lead to information leakage (Shringarpure and Bustamante, 2015). Our model is developed to protect such information leakage using the principled differential private criteria (Dwork, 2006).

Fig. 1.

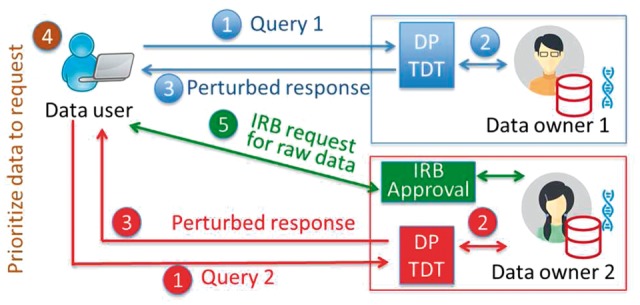
A workflow for privacy-protecting data access from DP TDT. (1) A data user sends queries to different datasets. (2) Data owners compute the true results based on the query. (3) Instead of returning the true results, data owners return perturbed, DP TDT results. (4) The data user compares the utility among different datasets to prioritize requests for data. (5) The data user files a data access application to obtain participant-level data

1.2 Differential privacy model

Differential privacy (Dwork, 2006) provides guarantees on the privacy of whole database against any arbitrary external attacks. In practice, there are two main mechanisms (randomized functions) satisfying the differential privacy definition (in Definition 1). One is the Laplace mechanism (Dwork, 2006), which adds Laplace noise to the original output. The Laplace parameter depends on the sensitivity of the output in Definition 2. The other one is the exponential mechanism (McSherry and Talwar, 2007), which first assigns a score to each pair $(data, its output)$. Then, the mechanism samples original outputs from an exponential distribution based on the score and the sensitivity of the score function (in Definition 2).

Definition 1:

(Differential Privacy (Dwork, 2006)) A randomized mechanism $\mathcal{M}$ is $\epsilon$-differentially private if, for all datasets $D$ and $D\mathrm{\prime }$ which differ on at most one family and for any measurable subset $S\subset range\left(\mathcal{M}\right)$,

$$\frac{\mathbb{P}\left(\mathcal{M}\right(D)\in S)}{\mathbb{P}\left(\mathcal{M}\right(D^{\text{'}})\in S)}\le e^{\epsilon }.$$ (2)

In Definition 1, $D$ and $D^{\text{'}}$ are called the neighbors and denoted $D\sim D\text{'}$. In our case, the dataset $D$ gathers family information (in terms of $(b,c)$ pairs defined in Section 1.1). Note that the exchange of two families may affect TDT on several SNPs so we protect privacy in each SNP. Parameter $\epsilon$ is called the privacy budget. When $\epsilon$ is small, the probabilities in the numerator and denominator in (2) are similar and when $\epsilon =0$, they are identical. If a mechanism $\mathcal{M}$ controls the probability ratio in (2) under $\epsilon$, we say $\mathcal{M}$ protects the privacy of$\mathrm{ }D$ under $\epsilon$-differentially privacy. $\epsilon$ is the budget that has to pay for the level of privacy. In other words, the privacy budget $\mathrm{\epsilon }$ can be imagined as a pre-defined limit of information disclosure. We provide a short sketch on its relationship with the probabilities of type I and type II errors in any statistical test in the Appendix, within the section ‘How privacy budgets affect probabilities of type I and type II errors’.

Definition 2:

(Sensitivity for the Laplace Mechanism (Dwork, 2006)) The sensitivity of a function $f:{\mathcal{D}}^M\to {\mathbb{R}}^M$ in the Laplace Mechanism is the smallest number $S\left(f\right)$ such that

$$\parallel f\left(D\right)-f\left(D^{\mathrm{\prime }}\right){\parallel }_1\le S\left(f\right),$$

for all neighbors$D\sim D^{\mathrm{\prime }},\mathrm{ }and\mathrm{ }D,D^{\mathrm{\prime }}\in {\mathcal{D}}^M.$

Definition 3:

(Sensitivity for Exponential Mechanism (McSherry and Talwar, 2007)) The sensitivity of a score function $q:{\mathcal{D}}^M\times \{1,\mathrm{ }\dots ,\mathrm{ }\mathrm{M}\}\to \mathbb{R}$ in the exponential mechanism is the smallest number $S\left(q\right)$ such that

$$\left|q\right(D,r)-q(D\mathrm{\prime },r\left)\right|\le S\left(q\right),$$

for all neighbors $D\sim D^{\text{'}}, and D,D^{\text{'}}\in {\mathcal{D}}^M$and $r \in \{1,\mathrm{ }\dots ,\mathrm{ }\mathrm{M}\}$ is the index of the SNP.

Definition 4:

(Laplace Mechanism (Dwork, 2006)) Releasing $\left(f\right(D)+noise)$ where $noise$ has $Laplace\left(S\right(f)/\epsilon )$ distribution is an $\epsilon$-differentially private mechanism satisfying Definition 1, where $f$ is a function of data, $Laplace(\mathrm{\lambda }=S(f)/\epsilon )$ has density $\frac{1}{2\lambda }\text{exp}(-\frac{\left|x\right|}{\lambda })$, and $S\left(f\right)$ is the sensitivity of $f$ from Definition 2.

Definition 5:

(Exponential Mechanism (McSherry and Talwar, 2007)) Let $q:{\mathcal{D}}^M\times \{1,\mathrm{ }\dots ,\mathrm{ }\mathrm{M}\}\to \mathbb{R}$ be a function assigning a score to the pair $(D,r)$ where $D\in {\mathcal{D}}^M$ and $r \in \{1,\mathrm{ }\dots ,\mathrm{ }\mathrm{M}\}$ is the SNP index associated with $D$. Choose $r$ from the mechanism ${\mathcal{M}}_q^{\epsilon }$ that has distribution

$$\mathbb{P}\left({\mathcal{M}}_q^{\epsilon }\left(D\right)=r\right)=\frac{\exp \left(\frac{\epsilon q\left(D,r\right)}{2S\left(q\right)}\right)}{\sum _{s\in \{1,\mathrm{ }\dots ,\mathrm{ }\mathrm{M}\}}\exp \left(\frac{\epsilon q\left(D,s\right)}{2S\left(q\right)}\right)},$$

where $S\left(q\right)$ is the sensitivity of $q$ from Definition 3. Releasing ${\mathcal{M}}_q^{\epsilon }$ is an $\epsilon$-differential privacy mechanism according to Definition 1.

Different from the Laplace mechanism, which directly adds noise on the original output, the exponential mechanism perturbs the probability of the outcomes by assigning scores to the original outputs such that the ones with high scores have higher probability to be sampled.

2 Materials and methods

In GWAS, we are often interested in a small number of significant SNPs. In this study, our goal is to answer the query about top$K$ most significant SNPs based on a privacy-preserving TDT algorithm to avoid an attacker violating family information. Releasing differentially private top $K$ significant SNPs has been considered in Bhaskar (2010). In GWAS case–control studies, there are several differentially private approaches. Uhler (2013) analyzed private allelic test and develop Laplace and exponential mechanisms based on the test statistics and P-values. Johnson and Shmatikov (2013) took another approach based on Shortest Hamming Distance (SHD). Yu (2014), Yu and Ji (2014) and Simmons and Berger (2016) extended and improved the SHD method in the allelic test. These previous works are in the case–control studies to protect individuals’ privacy. To the best of our knowledge, we are the first to analyze differentially private TDT to protect the privacy of families.

Different from protecing individual information, to protect family privacy in TDT, the algorithms and computation are more involved. Under the framework of DP, we start our analysis from defining neighbor families. Suppose there are $\mathrm{N}$ trio-families and $\mathrm{M}$ SNPs. We define two neighbor datasets $\mathrm{D}$, ${\mathrm{D}}^{\mathrm{\prime }}$ by exchanging the genotypes of exact one trio-family. For example, suppose in one SNP, in $\mathrm{D}$ there is one family with $\mathrm{W}\mathrm{W}\hspace{0.5em}\times \hspace{0.5em}\mathrm{W}\mathrm{w}\to \mathrm{W}\mathrm{W}$ ($(\mathrm{b},\mathrm{c})=\left(\mathrm{1,0}\right)$) and now in ${\mathrm{D}}^{\mathrm{\prime }}\mathrm{ }$it changes to $\mathrm{W}\mathrm{W}\hspace{0.5em}\times \hspace{0.5em}\mathrm{W}\mathrm{w}\to \mathrm{W}\mathrm{w}$ ($({\mathrm{b}}^{\mathrm{\prime }},{\mathrm{c}}^{\mathrm{\prime }})=\left(\mathrm{0,1}\right)$) while $\mathrm{D}$ and ${\mathrm{D}}^{\mathrm{\prime }}$ are consistent in all other families. In this case, changing from $\mathrm{D}$ to ${\mathrm{D}}^{\mathrm{\prime }}$ gives a moving direction ${\displaystyle \overrightarrow{\mathrm{v}}}:=(\mathrm{\Delta }\mathrm{b},\mathrm{\Delta }\mathrm{c})=({\mathrm{b}}^{\mathrm{\prime }}-\mathrm{b},{\mathrm{c}}^{\mathrm{\prime }}-\mathrm{c})=(-\mathrm{1,1})$. Considering all the family genotypes, we obtain 18 valid moving directions between two neighbor families as illustrated in Figure 2. Compared to neighbor individuals in the case–control studies, neighbor families have more moving directions making the privacy-protection algorithms much harder to develop. Details to obtain in the valid moving directions are listed in the Appendix.

Fig. 2.

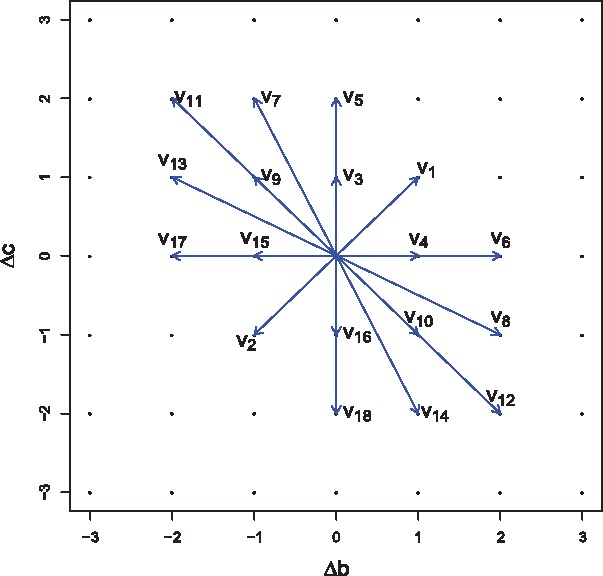
Moving directions ${\displaystyle \overrightarrow{\mathit{v}}}=(\mathbf{\Delta }\mathit{b},\mathbf{\Delta }\mathit{c})$ among all neighbor families

2.1 Differentially private mechanisms based on the ${\mathit{\chi }}^2-\mathbf{t}\mathbf{e}\mathbf{s}\mathbf{t} \mathbf{s}\mathbf{t}\mathbf{a}\mathbf{t}\mathbf{i}\mathbf{s}\mathbf{t}\mathbf{i}\mathbf{c}\mathbf{s} \mathbf{a}\mathbf{n}\mathbf{d} \mathit{P}$-values

With well-defined neighbor families, we perform sensitivity analysis (proofs in Appendix) on the TDT test statistics and P-values, which is the key element in applying Laplace and exponential mechanisms under the framework of DP.

Theorem 1:

For one SNP, the sensitivity of the TDT statistic $T$ in (1) for $N$ trio-families is $8(N-1)/N$ given a fixed $N$ with $N\ge 2$.

Adding Laplace noise from distribution $Laplace\left(8\right(\mathrm{N}\hspace{0.5em}-\hspace{0.5em}1)/(\epsilon N\left)\right)$ to $T$ achieves $\epsilon$-differential privacy. We also consider releasing differentially private$p$-values, without perturbing the test statistics first.

Theorem 2:

In one SNP, the sensitivity of $p$-value of ${\chi }^2$-statistics with one degree of freedom for TDT is $F_{{\chi }_1^2}\left(4\right)(\approx 0.954)$ when $N\ge 4$, where $F_{{\chi }_1^2}(\cdot )$ is the cumulative density function for a ${\chi }^2$ distribution with one degree of freedom.

From Theorem 2, we can see that the sensitivity of $P$-value (which is nearly 1) is quite large which may result in the perturbed outputs useless. Since in GWAS what we really concern are the SNPs in small P-values, following (Uhler, 2013), we consider a projected $p$-value of TDT test statistic $t$, defined by

$$P\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}{\mathrm{e}}_{\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{j}}\left(t\right)=\mathrm{m}\mathrm{i}\mathrm{n}\left\{p\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}\right(t),p^{\mathrm{*}}\},$$ (4)

where $p^{\mathrm{*}}$ is a predefined threshold.

Theorem 3:

In one SNP, the sensitivity of the projected $P$-value defined in (4) is $|1-F_{{{\chi }_1}^2}((t^{\mathrm{*}}-4{)}^2/t^{\mathrm{*}})-p^{\mathrm{*}}|$ for a predefined threshold $p^{\mathrm{*}}$, and $t^{\mathrm{*}}$ is the quantile such that $F_{{\chi }_1^2}\left(t^{\mathrm{*}}\right)=1-p^{\mathrm{*}}$ when $N\ge 2$.

From our analysis, the most sensitive case for the test statistic corresponds to $\left(\mathrm{b},\mathrm{c}\right)=\left(\mathrm{0,2}\hspace{0.5em}\mathrm{N}\right) or (2N, 0)$where$\mathrm{ }\mathrm{b}$ and $\mathrm{c}$ has the largest difference, while the case for the $p$-value corresponds to $\left(\mathrm{b},\mathrm{c}\right)=\left(2,2\right)$ where$\mathrm{ }\mathrm{b}$ and $\mathrm{c}$ has the smallest difference, which agrees with the finding in Uhler (2013) in allele-frequency test. To releasing top $K$ significant SNPs based on test statistics and$P$-values, we adapt the procedures in Bhaskar (2010) and summarize the Algorithms 1–2.

Algorithm 1:

$\mathrm{\epsilon }$-Differentially Private Algorithm for Releasing the $\mathrm{K}$ Most Significant SNPs Using the Laplace Mechanism.

Input: The number $\mathrm{K}$ of significant SNPs to release, the data function $\mathrm{f}\mathrm{ }$(${\mathrm{\chi }}^2$ statistics or $P$-values) for all $\mathrm{M}$ SNPs, the sensitivity of the data function $\mathrm{S}\left(\mathrm{f}\right)$, privacy budget $\mathrm{\epsilon }$.

Output: Top $\mathrm{K}$ most significant SNPs after adding noise.

1. Let ${\mathrm{f}}_{\mathrm{i}}$ be the data function for $\mathrm{i}$-th SNP.

2. Add independent Laplace noise with parameter $\mathrm{\lambda }\hspace{0.5em}=\hspace{0.5em}2\hspace{0.5em}\mathrm{K}\mathrm{ }\mathrm{S}\left(\mathrm{f}\right)/\mathrm{\epsilon }$ to ${\mathrm{f}}_{\mathrm{i}}$ for $\mathrm{M}$ SNPs.

3. Pick the top $\mathrm{K}$ significant SNPs based on the noisy$\mathrm{ }{\mathrm{f}}_{\mathrm{i}}$’s.

Algorithm 2:

The $\mathrm{\epsilon }$-Differentially Private Algorithm for Releasing the $\mathrm{K}$ Most Significant SNPs Using the Exponential Mechanism.

Input: The number $\mathrm{K}$ of significant SNPs to release, the score function $\mathrm{q}$ (${\mathrm{\chi }}^2$ statistics or Hamming distance score) for all $\mathrm{M}$ SNPs, the sensitivity of the score function $\mathrm{S}\left(\mathrm{q}\right)$, privacy budget $\mathrm{\epsilon }$.

Output: $\mathrm{K}$ noisy significant SNPs.

1. Let $\mathcal{S}=\mathcal{\varnothing }$ and ${\mathrm{q}}_{\mathrm{i}}=\hspace{0.5em}$the score of $\mathrm{i}$-th SNP.

2. For each $\mathrm{i}\in \{1,\dots ,\mathrm{M}\}$, set the weight ${\mathrm{w}}_{\mathrm{i}}=\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{\mathrm{\epsilon }{\mathrm{q}}_{\mathrm{i}}}{2\mathrm{K}\mathrm{S}\left(\mathrm{q}\right)}\right)$ and ${\mathrm{p}}_{\mathrm{i}}=\frac{{\mathrm{w}}_{\mathrm{i}}}{{\sum }_{\mathrm{i}\hspace{0.5em}=\hspace{0.5em}1}^{\mathrm{M}}{\mathrm{w}}_{\mathrm{i}}}$ the probability for sampling $\mathrm{i}$-th SNP.

3. Sample $\mathrm{k}$ elements independently from $\{1,\dots ,\mathrm{M}\}$ with probabilities $\{{\mathrm{p}}_1,\dots ,{\mathrm{p}}_{\mathrm{M}}\}$ without replacement. Add SNP${\mathrm{ }}_{\mathrm{k}}$ to $\mathcal{S}$ and set ${\mathrm{q}}_{\mathrm{k}}=-\mathrm{\infty }$.

4. Repeat step 2, 3 until the size of $\mathcal{S}$ reaches $\mathrm{K}$.

2.2 Differential privacy based on the shortest hamming distance score

Previous works (Johnson and Shmatikov, 2013; Simmons and Berger, 2016; Yu, 2010, 2014) show the DP mechanism based on the SHD score perform well in the case–control studies. We would like to develop and analyze this method to protect family’s privacy in conducting TDT. The formal definition of SHD score in one SNP is in Definition 6. Johnson and Shmatikov (2013) showed that the sensitivity of the SHD score is 1. The SHD basically counts how many steps by moving the $(b,c)$ pair among neighbor families such that the associated test statistic from being significant to being non-significant or vice versa, where the significance is defined by the test statistic is greater than or equal some predefined threshold $c^{\mathrm{*}}>0$. Since we are more concerned on the significant SNPs, we assign positive steps for the SNPs from being significant to being non-significant and negative steps for the SNPs from being non-significant to being significant. In this way, more significant SNPs obtain higher scores while non-significant SNPs get lower scores. In the exponential mechanism, the SNPs with higher scores have larger probabilities to be sampled.

Definition 6:

(The SHD score (Johnson and Shmatikov, 2013)) Given a predefined threshold $c^{\mathrm{*}}>0$, the SHD score for $i$-th data $D_i:=(b_i, c_i)$, $i=1, \dots , M,$ is

$$d_{SH}\left(D_i,i\right)=\left\{\begin{array}{l}0,\mathrm{ }\mathrm{i}\mathrm{f}\mathrm{ }{T}_i\ge {\mathrm{c}}^{\mathrm{*}}\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{ }\exists \mathrm{ }{D_i}^{\mathrm{\prime }},T_i\mathrm{\prime }<{\mathrm{c}}^{\mathrm{*}}\\ 1+\underset{D\sim D\mathrm{\prime }}{\mathrm{m}\mathrm{i}\mathrm{n}}{d}_{SH}\left(D_i\mathrm{\prime },i\right),\mathrm{i}\mathrm{f}\mathrm{ }{T}_i\ge {\mathrm{c}}^{\mathrm{*}}\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{ }\nexists \mathrm{ }{D_i}^{\mathrm{\prime }},T_i\mathrm{\prime }<{\mathrm{c}}^{\mathrm{*}}\mathrm{ }\\ -1+\underset{D\sim D^{\mathrm{\prime }}}{\mathrm{m}\mathrm{a}\mathrm{x}}{d}_{SH}\left({D_i}^{\mathrm{\prime }},i\right),\mathrm{ }\mathrm{i}\mathrm{f}\mathrm{ }{T}_i<{\mathrm{c}}^{\mathrm{*}}\end{array}\right.$$

where$\mathrm{ }{T_i\mathrm{ }(T}_i\mathrm{\prime })$ is the test statistic associated with $D_i\mathrm{ }\left({D_i}^{\mathrm{\prime }}\right)$ and $D_i\mathrm{\hspace{0.17em}}\sim \mathrm{\hspace{0.17em}}{D_i}^{\mathrm{\prime }}$ in ${\mathcal{D}}^M$. For $i\mathrm{\hspace{0.17em}}\notin \{1,\dots M\}$, setting $d_{SH}\left(D_i,i\right)=-\hspace{0.5em}\mathrm{\infty }$.

To get the SHD score in case–control studies, early work (Johnson and Shmatikov, 2013; Yu, 2014) showed that it is a computational intensive task. Based on the minor allele frequencies using the iDASH healthcare privacy protection challenge data, Yu and Ji (2014) speeded up the computation by assuming that the control group is known. Later on, Simmons and Berger (2016) further improved the algorithm through a convex analysis and relaxed the constraint about knowing the control cohort.

The key to get the SHD score for TDT is to analyze how to move $\left(\mathrm{b},\mathrm{c}\right)$ pair among neighbor families affects the change of the test statistic $\mathrm{T}=\hspace{0.5em}\frac{(\mathrm{b}\hspace{0.5em}-\hspace{0.5em}\mathrm{c}{)}^2}{\mathrm{b}\hspace{0.5em}+\hspace{0.5em}\mathrm{c}}$. Different from the allelic test statistic, the contour of $\mathrm{T}$ in TDT is not a straight line but a parabola, therefore, the change of $\mathrm{T}$ is no longer a constant. Hence, we have to take into account the starting point of $\left(\mathrm{b},\mathrm{c}\right)$ and the ending point along every move. Besides this, in TDT, there are 18 possible moving directions as shown in Figure 2, which makes the computation more challenging in our case. We develop two algorithms to calculate SHD score in private TDT: one is the exact algorithm (Algorithm 3) and the other is the approximation algorithm (Algorithm 4). In the exact algorithm, we take (${\mathrm{n}}_1,\dots ,{\mathrm{n}}_6$) the family numbers in each genotype (defined in Table 1) as the input. We construct a graph of nodes from all possible (${\mathrm{n}}_1,\dots ,n_6$)’s with fixed total family number and connected nodes from neighbor families. The brute force searching shortest distance in the graph gives the SHD score. We show that our exact algorithm gives exact SHD score (in Definition 6) in Theorem 4 with the proof in Appendix. The brute force searching (based on dynamic programming) is slow in the large cohort studies. To tackle its computation issue, we develop an approximate version of SHD for TDT, which may not have a guaranteed sensitivity but can be computed efficiently. In the approximation algorithm, we relax the constraint on the fixed total family number and only search the shortest distance path in the domain of $\left(\mathrm{b},\mathrm{c}\right)$. If initial$\hspace{0.17em}T$ from the dataset is significant (non-significant), we move $\left(\mathrm{b},\mathrm{c}\right)$ in each step along the one of 18 possible moving direction in the largest (smallest) non-normalized directional gradient until the significance status of$\hspace{0.17em}T$ is just altered. Figure 3 depicts the SHD scores from the approximation algorithm for 10 families in one SNP.

Fig. 3.

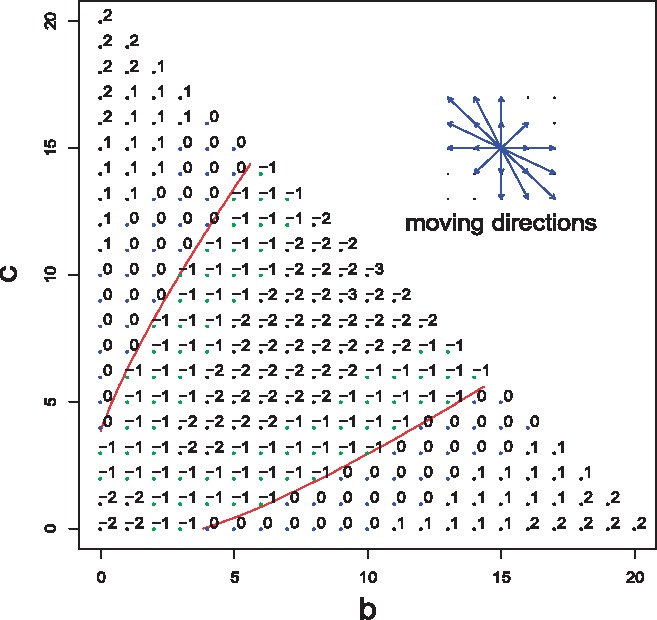
The SHD scores for the points in ${\mathcal{D}}^1$ from 10 families in one SNP. The red curves are from ${\mathit{T}=\mathit{c}}^{\mathbf{*}},$ where ${\mathit{c}}^{\mathbf{*}}=95\mathbf{\%}{-\mathbf{q}\mathbf{u}\mathbf{a}\mathbf{n}\mathbf{t}\mathbf{i}\mathbf{l}\mathbf{e} \mathbf{o}\mathbf{f} \mathbf{\chi }}_1^2$. The points above the upper curve and below the lower curve are significant and the points between two curves and in boundaries are non-significant. The labels aside the points are their SHD scores from Algorithm 4

Theorem 4:

Algorithm 3 outputs exactly the SHD score (in Definition 6).

Algorithm 3:

Exact Algorithm to calculate the SHD score in one SNP.

Input: Information regarding one SNP and the threshold $c^{\mathrm{*}}$ for $T$.

Output: The SHD score in one SNP.

1. Compute ($n_1,\dots ,n_6$) defined in Table 1.

2. Construct a graph of nodes as $\{\left(n_1^{\text{'}},\dots ,n_6^{\text{'}}\right):\sum n_i=\sum n_i\text{'}\}$ where two nodes are connected if $\sum \left|n_i-n_i^{\text{'}}\right|=2$.

3. Compute $T={\left(n_1+2n_4-n_2-2n_5\right)}^2/(n_1+n_2+2n_3+2n_4+2n_5)$ for all the nodes.

4. Find nodes which have a) $T>c^{*}$ and b) a neighbor with $T\le c^{*}$. Put them in a set $S.$

5. If $(n_1,\dots ,n_6$) has $T>c^{*}$, compute its shortest distance to $S$ and take it as its score; otherwise compute the distance and then use 1–distance as the score. Dijkstra algorithm solves this.

Algorithm 4:

Approximation Algorithm to calculate the SHD score in one SNP.

Input: Information regarding one SNP and the threshold $c^{\mathrm{*}}$ for $T_i$.

Output: The SHD score in one SNP.

1. Get $\left(b_i,c_i\right)$ for $T_i$.

2. If $T_i<c^{\mathrm{*}}$, move $\left(b_i,c_i\right)$to the direction among the valid moving directions in the domain that maximizes the non-normalized directional gradient until $T_i$ is just above or equals $c^{\mathrm{*}}$ then $d_{SH}(\left(b_i,c_i\right), i)=-\left(\#\mathrm{ }\mathrm{o}\mathrm{f}\mathrm{ }\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}\mathrm{s}\right)$; if $T_i\ge c^{\mathrm{*}}$, move $\left(b_i,c_i\right)$to the direction among the valid moving directions in the domain that minimizing the non-normalized directional gradient until $T_i$ is below $c^{\mathrm{*}}$ then $d_{SH}(\left(b_i,c_i\right), i)=\left(\#\mathrm{ }\mathrm{o}\mathrm{f}\mathrm{ }\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}\mathrm{s}\right)-1$.

3 Results

We are often interested in a few most significant SNPs. In most real datasets, there is a gap between the extremely significant SNPs and other SNPs in terms of P-value. This makes it possible to apply a DP mechanism to maintain both utility and privacy. Under the DP framework, we would like to apply the $\mathrm{\epsilon }$-differential privacy mechanisms we analyzed in the previous section to protect the privacy of releasing top $K$ most significant SNPs in TDT. We quantify the utility by the accuracy defined by the proportion of the reported top $K$ significant SNPs that are correctly selected, i.e. $|\mathrm{A}\cap \mathrm{B}|/\left|\mathrm{A}\right|$ where $\mathrm{A}$ is the set of true top $K$ significant SNPs and $\mathrm{B}$ is the set reported from a DP mechanism.

In a DP mechanism, there is always a tradeoff among the family size $N$ in TDT, the privacy budget $\epsilon$ and the accuracy. Without the concern of privacy, the family number determines the power of the TDT; larger family number gives more statistically powerful of TDT thus returns more accurate significant SNPs. Privacy budget $\epsilon$ controls the level of privacy protection (from Definition 1); smaller$\hspace{0.17em}\epsilon$ provides stronger privacy protection. An $\epsilon$-DP mechanism perturbs the TDT results by adding noise (e.g. in the Laplace mechanism or resampling the results in the exponential mechanism). Under a certain $\epsilon$, applying DP mechanisms on a dataset of a large family size can lead to a more accurate result, otherwise on a dataset of a very small family size could make the result useless. The number of most significant SNPs to release also plays an important role in privacy and utility. Suppose the total number of SNPs we are concerned is $M=10\hspace{0.17em}000$ and 10 SNPs are extremely significant. To release top $K\le 10$, a well-designed DP mechanism can give an almost perfect result under a given privacy budget, but to choose a much larger $K$, perturbation could reduce the gap between extremely SNPs and others, and therefore making these DP mechanisms un-useful. We can see this from Algorithms 1–2. A large $K$ leads larger variances (in the Laplace noise) in the Laplace mechanism and smaller weights on the significant SNPs in the exponential mechanism. Hence, given a dataset, under a fixed family size, to maintain both accuracy and privacy under the framework of DP, how powerful of the TDT test can achieve and how much privacy of the dataset can support (i.e. how many top significant SNPs to release) are essentially determined by the data. We would like to demonstrate these points and investigate the performance of our propose DP mechanisms in TDT under various settings in the simulation studies and give a guideline for real practices.

3.1 Simulation studies

In the simulation studies, we compare various DP mechanisms for TDT in a small cohort and a large cohort. We investigate how the parameters $(N,\hspace{0.17em}M,\hspace{0.17em}K,\epsilon )$ affect the accuracy in the simulated two cohorts, where $N$ is the family number, $M$ is the total SNPs number in the study, $K$ is number of selected top significant SNPs to release, and $\epsilon$ is the privacy budget.

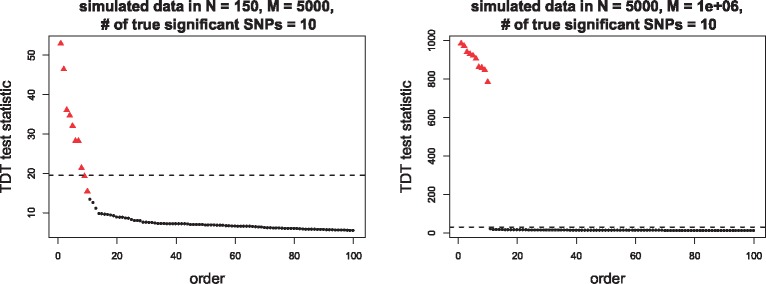
To generate the simulated cohorts, suppose there are true 10 significant SNPs associated with some disease of interest. In the small cohort, we set family number $N=150$ and the SNPs number $M=5000$ and in the large cohort, we set $N=5000$, $M={10}^6$. To generate the test statistic for $i$-th SNP, we first generate $S_i:=b_i+c_i$, the sum of the $\left(b_i,c_i\right)$ pair, uniformly sampled from discrete integers from 0 to $2N$. Given $S_i$, we generate $b_i$ from Binomial distribution with size $S_i$ and probability 0.5 then set ${c_i=S}_i-b_i$. From $\left(b_i,c_i\right)$’s, the corresponding test statistics $T_i$’s have approximately ${\chi }_1^2$ distribution, which simulate the case that there is no linkage disequilibrium in those SNPs. To get the SNPs with linkage disequilibrium, we select the SNPs with top $K=10\hspace{0.17em}{S}_i$’s and regenerate their $\left(b_i,c_i\right)$ pairs, where $b_i$ is from Binomial distribution with size $S_i\hspace{0.17em}$and probability 0.65, then ${c_i=S}_i-b_i$. In this way, these 10 SNPs are significantly greater than the others. To apply the exact algorithm in Algorithm 3, since its input is the family numbers in each genotype, given $\left(b_i,c_i\right)$ for the $i$-th SNP, we generate a random combination of $n$’s that satisfy the equations in section 1.1. We plot the top 100 largest test statistics from two cohorts in Figure 4. In our setting, the true significant SNPs are the top 10 largest test statistics, indicated by triangles in the figure. Comparing two cohorts in Figure 4, under the Bonferroni correction as$\hspace{0.17em}100\left(1-0.05/M\right)\%$-quantile of ${\chi }_1^2$ distribution, even without adding any perturbation from a DP mechanism, from the small cohort, we can only select 8 true significant SNPs above the threshold, while in the large cohort, the true 10 significant SNPs are dramatically greater the non-significant SNPs and can be picked accurately. We can expect if we would like to ask for the top 10 SNPs from the small cohort, the released results under DP cannot have much accuracy, but from the large cohort, a well-designed DP mechanism can maintain both the privacy and accuracy.

Fig. 4.

Top 100 largest TDT test statistics in the simulated data. The left panel is from a small cohort (with family number N = 150 and SNPs number M = 5000) and the right panel from a large cohort (with N = 5000 and M = 10⁶). The triangle points are the true top 10 significant SNPs. The horizontal dashed lines are the thresholds at 100(1–0.05/M)%-quantile of ${\mathit{\chi }}_1^2$ distribution, where M = 5000, 10⁶ in left and right panels respectively

We compare the performance of the DP mechanisms for TDT in terms of accuracy under a certain privacy budget $\epsilon$ and the number $K$ of releasing most significant SNPs. Our proposed DP mechanisms for TDT include: the Laplace and exponential mechanisms based on test statistics, the exponential mechanisms based on $p$-values and projected $p$-values, and the exponential mechanism based on the shortest Hamming distance (SHD). We set the privacy budget $\epsilon$ from 0.1 to 3 and the releasing number $K=\mathrm{1,3},\mathrm{5,10}$. We get the sensitivities for the mechanisms based on test statistics, $P$-values and projected $P$-values from Theorem 1-3, and the SHD score from Algorithm 3–4. To release top $K$ most significant SNPs, we apply the Laplace mechanism from Algorithm 1 and the exponential mechanism from Algorithm 2. In the small cohort, the exact algorithm takes about 4 hours and used up 38.5 GB memory on a 3.0 GHz 8-Core Intel Xeon E5 machine. (We are planning to develop a more efficient version for the exact algorithm.) Due to the computation complexity in the current version of the exact algorithm, we only apply the DP mechanism based on the SHD scores from the exact algorithm in the small cohort.

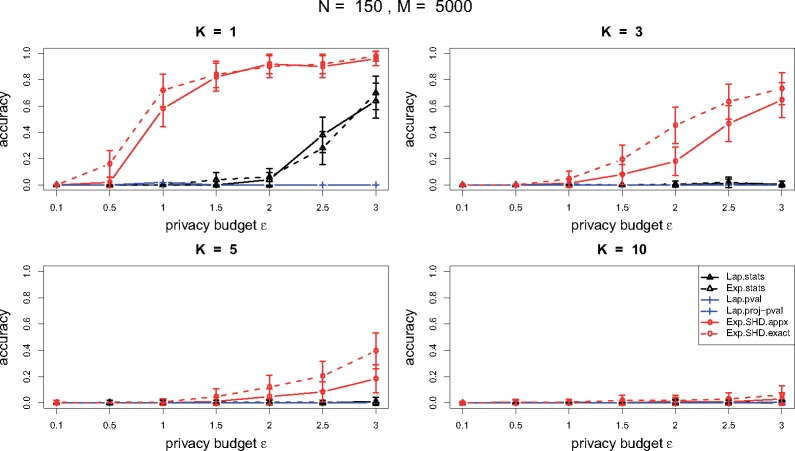
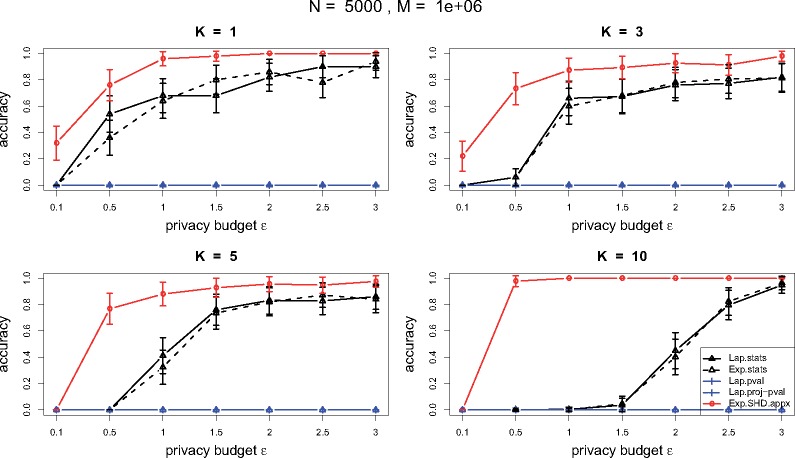
From the performance in the small cohort in Figure 5 and the large cohort in Figure 6, DP mechanisms based on $P$-values and projected $P$-values are almost useless due to their high sensitivities (see Theorem 2–3). The Laplace mechanism and the exponential mechanism based on the test statistics perform comparably. From both small and large cohort, the DP mechanism based on the SHD outperforms the others, and in the small cohort, the method from the exact algorithm performs slightly better than the one from the approximation algorithm. In the small cohort, since there is not a significant gap between the significant SNPs and non-significant ones from Figure 4, releasing top $K=3,\hspace{0.17em}5,\hspace{0.17em}10$ SNPs, even under a large privacy budget, the performance of a DP mechanism is hard to have a great accuracy. When $K=1$, the DP mechanism based on SHD achieves accuracy around 0.8 under $\epsilon =1.5$ while the DP mechanisms based on the test statistics requires $\epsilon >3$ for the same level of accuracy. In the large cohort, since there is a big gap between the significant SNPs and the others from Figure 4, we can ask for more top significant SNPs under a certain level of privacy protection and accuracy. The DP mechanism based on SHD achieves accuracy more than 0.8 under a small $\epsilon =0.5$ across all $K\le 10$.

Fig. 5.

Performance comparison of DP mechanisms for TDT in terms of accuracy under various privacy budgets and numbers of SNPs to release in a small cohort (with family size N = 150 and SNP number M = 5000). The solid and dashed curves with circle points are for the exponential mechanism based on SHD from the approximation algorithm and the exact algorithm. The solid and dashed curves with triangle points are for the Laplace and exponential mechanism based on the test statistics. The solid and dashed curves with square points are for the exponential mechanisms based P-value and projected P-value. The accuracy is reported in the average from repeatedly applying a DP mechanism 50 times. The small bars along the curves are the 95% confidence intervals

Fig. 6.

Performance comparison of DP mechanisms for TDT in terms of accuracy under various privacy budgets and numbers of NSP to release in a large cohort with family size N = 5000 and SNP number M = 10⁶. (The curve labels are the same as in Figure 5.)

3.2 Real data

We apply our proposed DP mechanisms for TDT in the study of a rare disease—Kawasaki Disease (KD) (Shimizu, 2011). In this datast, we have 187 KD families. After filteation, we get 906 SNPs of ponential interest. We would like to report top $K$ most significant SNPs under DP. From the comparison of applying the DP mechanisms to TDT to the small and large cohorts in the simulation studies, we can expect the small size of this real dataset makes the problem of protecting familiy-based information challenging. We just want to show a real world application here.

Since the DP mechanism on the Shortest Hamming Distance (SHD) outperforms the other proposed mechanisms from simulation studies, we only apply this method to the real dataset. To get SHD scores, we use both exact and approixmation algorithms (Algorithm 3–4). The exact algorithm took about 4.2 hours to compute the SHD for this real dataset. Due to the small size of the data, it could be hard to ensure both high coverage accurage and privacy protection as shown in the simulations. We relax the cirterion a little bit. Instead of concerning whether the top $K$ truly significant SNPs have been selected, we are interested in the average rank difference between the reported top $K$ significant SNPs and their true ranks. We measure the utility by rank error, defined by $\frac{1}{K}\sum _{k=1}^K|R_k-k|$ where $R_k$ is the rank of reported $k$-th significant SNP under DP. We set the privacy budget $\epsilon =\mathrm{3,5}$ and the number of significnat SNPs to release $K=\mathrm{3,5}$. We set the threshold as 95%-quantile of chi-squared distribution with one degree of freedom for the SHD score. We report the average utilitites in Table 3 from 200 repeated procedures. From Table 3, the utilities from these two methods in calculating the SHD scores are similar. Comparing the utilities under $K=3,\hspace{0.17em}5$, to maintain a certain of privacy protection and utility, our small datset is more suitable for releasing very few most significant SNPs, this pattern was also observed from the simulation studies. From the rank error in Table 3, when $K=1$ and $\epsilon =3$, the reported most significant SNP is among the truly top 10 most signifiant SNPs with high probability and when $K=1$ and $\epsilon =5$, the reported SNP is either the true top one SNP or the top two for most of the time.

Table 3.

Utility of the DP mechanism based on the SHD score calculated from exact and approximation algorithms for TDT in Kawasaki disease dataset

Method: Exp. Mech. SHD		Exact Alg.	Approximation Alg.
$\mathit{K}$	$\mathit{\epsilon }$	Rank error	Rank error
$\mathit{K}=1$	$\mathit{\epsilon }=3$	6.2	6.0
	$\mathit{\epsilon }=5$	0.8	0.8
$\mathit{K}=3$	$\mathit{\epsilon }=3$	190.8	187.5
	$\mathit{\epsilon }=5$	65.9	73.3

Imagine in practice, a researcher asks a query on this dataset and she would like to know a few most significant SNPs under DP TDT. She sets $K$, the number of most significant SNPs she would like to explore, and takes a privacy budget $\epsilon$ that bounds the error that she can tolerate. Since this is a small cohort, if she sets $K$ too large and $\epsilon$ too small, we will suggest her recruiting more patients into the study to guarantee both privacy and utility of our reported results under DP. Or we can suggest her reducing the number of $K$ in order to get a reasonable answer. Under a proper$\hspace{0.17em}K$ and $\epsilon$, for example, $K=1$ and $\epsilon =3$, the user will get the top most significant SNP ‘rs12569527’ under DP with a high probability. Athough outcomes of such a test-run may not be directly used for scientific discovery, our point is that the user will get a sense how the dataset is likely to be useful through her exploratory analysis, and can therefore decide on whether it is necessary to gain access to those data through the Institutional Review Board (IRB) application. This is the key idea of our proposed framework, which is illustrated in Figure 1.

4 Discussion and conclusion

In this paper, we make the assumption that an attacker intends to violate family information. We apply the Laplace and the exponential mechanisms, two major $\epsilon$-differentially private mechanisms, to achieve differentially private TDT in GWAS. However, there are still some limitations in the proposed method.

The proposed methods and the individual protected methods in Uhler (2013), Yu (2014) and Yu and Ji (2014) only focus on defining two neighbor datasets by exchanging one family/individual. Other ways of generating neighbor datasets can be used. To get the SHD score, we developed both exact and approximation algorithms. The approximation algorithm is efficient, but the sensitivity of the SHD score is not guaranteed to be 1 any more. We are planning to develop a more efficient version of the exact algorithm.

The choice of privacy budget $\mathrm{\epsilon }$, as we discussed in the section of ‘Results’, depends on the trade-offs among family size, privacy and utility. Since there is no explicit formula to quantify the relationship among those three quantities, the setting of ε depends on the context and on the application. How to pick a proper $\mathrm{\epsilon }$ is still an open question.

The proposed method protects privacy for trio-families. We can further develop privacy-preserving methods to the extended TDT on the families with more than one child and testing more alleles in a marker locus (Spielman, 1993) in the same manner. However, more discussion on the changes of two neighbor datasets should be considered. Furthermore, TDT is based on a ${\chi }^2$ test statistic and it has good asymptotic properties when the counts $b$ and $c$ are large. However, when the counts are small, TDT may lose some detection ability. In this case, other tests such as the Binomial exact test and continuity correction may be considered. Recently there are modified TDTs (Ewens and Spielman, 2004; Wittkowski and Liu, 2002) that can be more powerful under some circumstances. Hence, we can choose different TDT tests and then apply our privacy-preserving mechanisms to obtain higher utility. Additionally, in practice, real data always involve missing data and there are several imputation techniques to get more information. How to properly use imputation techniques in a privacy-preserving manner still needs further investigation.

Our analysis does not consider the correlation structure of SNPs but note that a DP mechanism does not depend on the correlation among SNPs to guarantee DP. However, to better use the dataset, if the dataset involves highly correlated SNPs, one can apply the DP TDT to the tag SNPs, the representatives in each correlated block (Gabriel et al., 2002); otherwise it might not be interesting that the reported top K most significant SNPs come from the same correlated block. Similar to (Johnson and Shmatikov, 2013), we can extend our DP mechanisms to TDT on the correlated SNPs.

Overall, from our simulation experiments and application in the Kawasaki Disease dataset, by applying TDT to trio-families in GWAS and defining the neighbor datasets by exchanging family genotypes, we found that the exponential mechanism based on the shortest Hamming distance score preserves both higher utility and privacy than the other proposed methods to protect family-based information.

Contribution statement

Analysis in the methods: M.W.; Algorithms: M.W., Z.J., S.W, X.J.; Data Processing and software: M.W., J.K., H.Y.; Editing and revising the manuscript: M.W., L.OM., X.J.