Protein–protein interaction specificity is captured by contact preferences and interface composition

Abstract

Motivation

Large-scale computational docking will be increasingly used in future years to discriminate protein–protein interactions at the residue resolution. Complete cross-docking experiments make in silico reconstruction of protein–protein interaction networks a feasible goal. They ask for efficient and accurate screening of the millions structural conformations issued by the calculations.

Results

We propose CIPS (Combined Interface Propensity for decoy Scoring), a new pair potential combining interface composition with residue–residue contact preference. CIPS outperforms several other methods on screening docking solutions obtained either with all-atom or with coarse-grain rigid docking. Further testing on 28 CAPRI targets corroborates CIPS predictive power over existing methods. By combining CIPS with atomic potentials, discrimination of correct conformations in all-atom structures reaches optimal accuracy. The drastic reduction of candidate solutions produced by thousands of proteins docked against each other makes large-scale docking accessible to analysis.

Availability and implementation

CIPS source code is freely available at http://www.lcqb.upmc.fr/CIPS.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

The large and constantly increasing number of protein structures highly encourages using protein docking to obtain protein complex structures from unbound conformations. In such experiments, a protein is fixed in the space and the interacting protein is rotated around it and around itself. The space of relative positions is explored through a large sampling of conformations, undergoing several energy minimizations for the computation of the associated free energy. Docking algorithms differ from one another basically upon the energy function used, the degree of flexibility allowed and the resolution chosen for protein representation (Gray, 2006). When a large-scale docking experiment is addressed, with hundreds or thousands of proteins docked against themselves, thousands of millions of poses have to be analysed, thus the computation of each of them should be as fast as possible. In this context, the bottleneck between structure accuracy and computational cost emerges: on the one hand, one seeks an accurate model of the complex structure, and on the other hand, wishes a fast screening of the docking decoys, realized with a scoring scheme that does not suffer from the level of accuracy of the structures. Once a reasonable set of candidate solutions is retrieved, more refined procedures, like flexible docking, can be applied (Andrusier et al., 2008).

The problem of properly defining a small subset of solutions from docking calculations has been widely studied in the literature (Moal et al., 2013). The idea is to rank all predicted conformations with ad hoc scores, drawn either from the free energy or from statistical potentials. Interface contact propensities, or pair potentials, capture the signal coming from the type of contacts at the interface. They provide a statistical model estimating how often a contact is expected to occur at the interface at random, given the residue (or contact) frequency observed on a set of experimental structures.

Previous studies showed the applicability of contact propensities to the prediction of near-native docking decoys (Moont et al., 1999; Lu et al., 2003; Huang and Zou, 2008; Liu and Vakser, 2011). The simplest docking score proposed in the literature is based on the sum of propensity values at the interface. Pioneering work is the one proposed by Moont et al. (1999), who rank the decoys of a small set of 9 complexes after extracting information from datasets of intramolecular (385 domains), homodimer (23 complexes) and heterodimer (11 complexes) interactions. Lu et al. (2003) define a residue-based propensity matrix on a dataset of true and false interactions and test the ability of their score to discriminate near-native decoys for a set of 21 complexes. Huang and Zou (2008) define a procedure iteratively improving the discrimination of near-native decoys by learning pair potentials on bound structures. Liu and Vakser (2011) propose five pair potentials, defined either on experimental structures or on decoy sets. More sophisticated approaches propose linear combinations of pair potentials and energy terms (Feliu et al., 2011; Fink et al., 2011; Pons et al., 2011), possibly weighted (Li et al., 2007). A common practice is to learn optimal coefficients for each term from docking decoys whose similarity to the native structure is known (Li et al., 2007). For example, SIPPER method (Pons et al., 2011) combines knowledge-based and desolvation energy terms to pre-screen docking poses for further refinement.

Here, we define a new contact propensity matrix, called CIPS for Combined Interface Propensity for decoy Scoring, in which interface propensity and local geometry are explicitly included; our pair potentials are computed from a diversified set of 230 bound structures (Vreven et al., 2015). We compare our method to three propensity matrices (Glaser et al., 2001; Pons et al., 2011; Mezei, 2015) and to two atomic potentials (Krissinel and Henrick, 2007; Pierce and Weng, 2007) on three datasets, very different from one another in composition, size and underlying docking algorithms. A simple combination of CIPS with atomic potentials, not requiring a learning step on the decoy sets, is also analysed. Finally, we study the impact in decoys ranking of four propensity-based descriptors, which provide different characterizations of the interaction either based on propensity values, contact counts or interface layers (Levy, 2010), either computed for the whole interface or between ‘propensity patches’. Supported by a series of computational experiments on both full-atom (Tovchigrechko and Vakser, 2005; Tovchigrechko and Vakser, 2006) and coarse-grain (Sacquin-Mora et al., 2008; Lopes et al., 2013) decoy sets, we demonstrate that CIPS can be proposed as a fast, accurate and robust method for decoys selection. It is expected to be very useful to discriminate millions of docking conformations quickly.

2 Materials and methods

2.1 Combined interface propensities

The bias of contact $\langle i,j\rangle$ abundance at the interface expresses the preference of amino acids i and j to be one in front of the other, provided that both i and j lie at the interface. Based on this idea, we model interface propensity as a combination of two terms: the one is contact-based, taking into account the preference of i and j to be in contact, the other one is residue-based, expressing the preference of i and j to be located at the interface (one belonging to a surface and the second to the other). We further include, in the definition of the contact-based term, a connectivity factor taking into account the number of per-residue contacts. The final formula expressing the bias of contact $\langle i,j\rangle$ abundance is given by

$$P_{i,j}=\overline{c_{i,j}}·r_{i,j},$$ (1)

where $\overline{c_{i,j}}$ is the contact-based term and r_i,j is the residue-based term (see also Fig. 1A). Detailed explanation formula (1) is provided below.

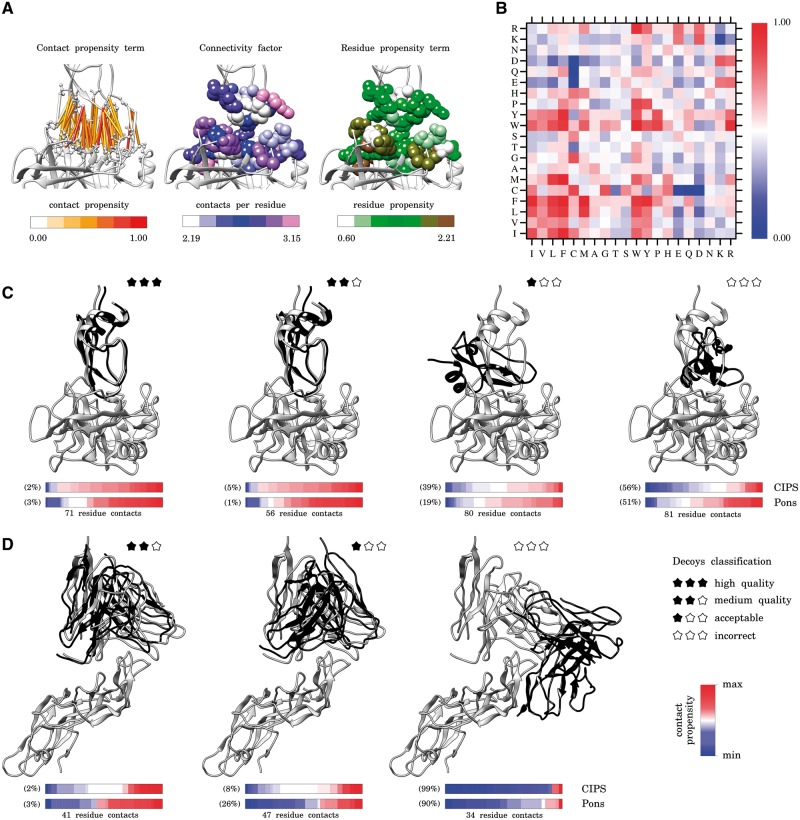
Fig. 1.

CIPS propensity matrix and scoring of docking decoys. (A) Representation of the three components of CIPS propensity: residue–residue contact propensity (left), connectivity level of interface residues (centre), and residue propensity at the interface (right). The contact propensity term is computed with Equation (2) and normalized in [0, 1]; the number of contacts for amino acid k is the value v_k in the expression of ${\alpha }_{i,j}$ in Equation (3); the residue propensity of amino acid k is the value from Negi and Braun (2007). (B) CIPS propensity matrix computed on PPDB v5.0 with Equation (1) by combining the three numerical components illustrated in (A). (C and D) For each complex, the receptor is fixed (grey, at the bottom) and the docking solution (black) and the native conformation (grey) of the ligand are shown on the top. The bar below each structure is coloured according to the propensity value (either from CIPS or Pons definition) of each contact at the interface; namely, for CIPS matrix, P_i,j values are represented and coloured according to the gradient reported in (B). All contacts are represented and ordered from lower to higher propensity values. The number of inter-protein residue contacts is reported below the bars; their number depends on the distance between receptor and ligand (compare structures of C and D). Note that CIPS and Pons values are not directly comparable. To account for this, we report the percentage ranking of the depicted structures within the set of decoys for the same complex. (C). Four docking decoys from Dockground decoy benchmark for trypsin (receptor) in complex with trypsin inhibitor (ligand) (PDB code: 2FI4). (D) Three docking decoys from CCD benchmark for antigen (receptor) in complex with antibody (ligand) (PDB code: 1QFW). Molecular graphics are performed with the UCSF Chimera package (Pettersen et al., 2004) (Color version of this figure is available at Bioinformatics online.)

The contact propensity term. The interface propensity of a contact $\langle i,j\rangle$ between amino acids i and j is a measure of how often the contact $\langle i,j\rangle$ occurs at protein interfaces compared to the expected frequency. It is usually defined as

$$\hspace{0.17em}{\text{log}}_2\frac{f_{i,j}^{\text{obs}}}{f_{i,j}^{\hspace{0.17em}\text{exp}\hspace{0.17em}}},$$ (2)

where $f_{i,j}^{\text{obs}}$ and $f_{i,j}^{\hspace{0.17em}\text{exp}\hspace{0.17em}}$ are the observed and the expected fraction of contacts of type $\langle i,j\rangle$, respectively. Note that the notation $\langle i,j\rangle$ does not impose any order between i and j. Given the number of contacts c_i,j of type $\langle i,j\rangle$ and the total number of inter-protein contacts $n=\sum _{\langle i,j\rangle }{c}_{i,j}$, the observed fraction of contacts of type $\langle i,j\rangle$ is given by $f_{i,j}^{\text{obs}}=c_{i,j}/n$. We compute the predicted fraction of contacts by means of the residue–residue contact frequency as follows. The amount of contacts involving amino acid i is given by $c_i=\sum _j{c}_{i,j}$ and the contact frequency of i is defined as $f_i=c_i/n$. The expected fraction of contacts between i and j is given by $f_{i,j}^{\hspace{0.17em}\text{exp}\hspace{0.17em}}=f_i{f}_j$.

The connectivity factor. We introduce a weight for $f_{i,j}^{\hspace{0.17em}\text{exp}\hspace{0.17em}}$ (see above). The connectivity factor ${\alpha }_{i,j}$ associated to $\langle i,j\rangle$ is a function of the average number of contacts for residue types i and j, respectively. It is defined as ${\alpha }_{i,j}=1-a·(v_i·v_j)$, where v_k is the average contact frequency of k, rescaled in [0, 1] (see Supplementary Table S1, third row), and a is a fixed parameter (see Supplementary Section S1.2). We obtain the following new expression for the interface contact propensity [compare to Equation (2)]

$$c_{i,j}={\text{log}}_2\frac{f_{i,j}^{\text{obs}}}{{\alpha }_{i,j}{f}_{i,j}^{\hspace{0.17em}\text{exp}\hspace{0.17em}}}.$$ (3)

The term $\overline{c_{i,j}}$ of (1) is the value c_i,j in Equation (3) rescaled in [0, 1].

The residue propensity term. The amino acid preference at the interface is modelled by the term r_i,j associated to the pair $\langle i,j\rangle$. It is defined as

$$r_{i,j}=1+b·(w_i+w_j),$$ (4)

where the w_k is the residue propensity of k from Negi and Braun (2007) rescaled in $[-1,1]$, and b is a fixed parameter (see Supplementary Section S1.2).

2.1.1 Interface residues and residue–residue contacts

The accessible surface area (ASA) is computed with NACCESS (Hubbard and Thornton, 1993) using a probe radius of $1.4\text{Å}$. The interface is identified by the residues that lose ASA upon binding (i.e. $\Delta \text{ASA}>0$) (Levy, 2010). Inter-protein contacts are computed between interface residues. Two residues are assumed to be in contact if the distance within any heavy atom pair is below $5\text{Å}$. We consider the support-core-rim model proposed in Levy (2010) defined according to the degree of exposure to the solvent; the surface is identified by the residues whose ASA is at least 25% of the total residue surface. A residue belongs to the support if it is buried both in the bound and in the unbound form, to the core if it is exposed in the unbound form and buried in the bound form, to the rim if it is exposed both in the unbound and in the bound form. Note that the $\Delta \text{ASA}$ cut-off of 25% was chosen so that the number of residues on each region is approximately the same (see Levy, 2010).

2.1.2 Experimental structures for propensity calculations

Properties of interface contacts are drawn from the analysis of the 230 bound structures of the Protein-Protein Docking Benchmark (PPDB) v5.0 (Vreven et al., 2015). The dataset consists of 39 antibody-antigen, 46 enzyme-inhibitor, 26 enzyme complexes with a regulatory or accessory chain, 17 enzyme-substrate, 23 G-protein containing, 24 receptor containing and 55 unclassified complexes (others). PDB structures are downloaded from https://zlab.umassmed.edu/benchmark/.

2.2 Benchmark sets of docking decoys

The Dockground decoy benchmark (Liu et al., 2008) and the Complete Cross Docking (CCD) benchmark (Lopes et al., 2013) are used for testing. Both contain decoys issued from docking unbound structures. The former is the result of rigid-docking experiments performed with GRAMM-X (Tovchigrechko and Vakser, 2006) on Dockground (Douguet et al., 2006). The decoy sets of the CCD were computed with the coarse-grain model MAXDo (Sacquin-Mora et al., 2008) on the PPDB v2.0 (Mintseris et al, 2005) (http://www.lcqb.upmc.fr/CCDMintseris/). For each complex, we considered two instances, where a protein is either a receptor or a ligand in the docking procedure. In this work, we use the 168 decoy sets for the 84 true protein complexes.

2.2.1 Comparison with other pair potentials

Comparison of the results is performed against the propensity matrices proposed in (Glaser et al., 2001), (Pons et al., 2011) and (Mezei, 2015). (Glaser et al., 2001) apply amino acid volume normalization to residue frequencies; Mezei (2015) normalizes interface propensity by surface propensity; Pons et al. (2011) compute residue frequencies bias either at the surface or at the interface (we use the latter for comparison). The matrix by Glaser et al. is computed on a set of 621 complexes, where a high fraction is constituted by homodimer interfaces. The matrix by Pons et al. is computed on the 70 complexes of the benchmark in (Chakrabarti and Janin, 2002). Mezei matrix is computed on 1172 high-resolution structures.

2.2.2 Preparation of training sets and testing sets

The docking decoy benchmarks described above are used to build two testing sets, as follows. To eliminate overfitting, all complexes used in either Glaser or Pons matrices (PDB codes for Mezei matrix are not available) are removed from both Dockground decoy benchmark and CCD benchmark. Note that we did not exclude the complexes used for computing CIPS matrix (i.e. the PPDB v5.0, see Section 2.1.2) from the testing sets, because they fully cover the structures used to build the CCD benchmark (i.e. the PPDB v2.0). The reduced testing set Dockground_ decoy_ filtered (DF) contains 51 of 61 decoy sets. Of note, 419 of 5523 decoys are classified as near-native. The reduced testing set CCDMintseris_ filtered (CF) contains 66 of 84 complexes, namely, 132 of 168 decoy sets (see above). It contains 611 (182) acceptable (medium quality) decoys of 247, 258; 105 (51) decoy sets contain an acceptable (medium quality) solution. See Supplementary Section S1.6 for decoys classification. The PDB codes of the testing sets are reported on Supplementary Tables S7 (DF) and S8 (CF).

Two training sets are defined, consisting of crystallographic structures from PPDB v5.0 (see Section 2.1.2). Redundancy between training sets and testing sets is removed as follows. Within PPDB v5.0, 19 complexes of 230 are shared with DF, thus they are removed from PPDB v5.0 and the remaining 211 are referred to as PPDB5\DF. Similarly, the 65 complexes of PPDB v5.0 already present in CF are removed and the remaining 165 are referred to as PPDB5\CF.

We further check the structural similarity between training and testing sets. For this purpose, we use PIFACE (Cukuroglu et al., 2014), a database of clusters of redundant protein–protein interfaces. The redundancy is very low: 20 of 211 complexes in PPDB5\DF are structurally redundant with some complexes of DF (see Supplementary Table S9); 8 of 165 complexes in PPDB5\CF are structurally redundant with some complexes of CF (see Supplementary Table S10). Training sets are filtered further: each complex of PPDB5\DF (of PPDB5\CF) belonging to the same structural cluster of DF (CF) is removed. The training sets obtained after this two-step filtering procedure are referred to as PPDB5\DF^(nr) (91 complexes) and PPDB5\CF^(nr) (157 complexes).

Summarizing, we built two testing sets: DF and CF, and four training sets: PPDB5\DF, PPDB5\CF, PPDB5\DF^(nr) and PPDB5\CF^(nr). Testing on DF is done with a model computed on either PPDB5\DF or PPDB5\DF^(nr), and testing on CF is done with a model computed on either PPDB5\CF or PPDB5\CF^(nr) (see also Section 3.3).

2.3 The CAPRI targets set

We select top predicted models for all protein–protein CAPRI targets from Round 7 on (http://www.ebi.ac.uk/msd-srv/capri). Targets with no acceptable models are discarded, resulting in 28 targets (see Supplementary Table S11) and 8213 models (1214 acceptable, 796 medium, and 225 high quality). Based on CAPRI evaluation (Lensink et al., 2007; Lensink and Wodak, 2010, 2013; Lensink et al., 2016), we could identify 10 easy (2857 models) and 9 difficult (2405 models) targets (we could not find enough information to classify the remaining 9 targets). The easy class contains 834 (598) acceptable (medium quality) models; the difficult class 88 (15) acceptable (medium quality) models.

2.4 Scoring structural models

We will refer to a decoy set for a complex C, denoted X_C, as the set of docking solutions for C. X denotes the union of X_C over all complexes C of a given dataset. Interface residues and contacts are defined in the same way for both experimental structures and docking decoys (see Section 2.1.1). A score S(x) for a decoy x is defined in two steps. First, each interface contact of type $\langle i,j\rangle$ is assigned the value P_i,j computed with Equation (1) (as illustrated on Fig. 1C and D). Second, the score for the whole interface is computed according to one of the following three scoring categories: (i) the sum of all P_i,js at the interface; (ii) the sum of P_i,js between specific interface regions (Levy, 2010): core/core (C–C), core/support + core (C–CS), core/core + rim (C–CR) and core/interface (C–SCR); (iii) the propensity-based descriptors (see Supplementary Table S2), which are computed either on the whole interface or on propensity patches, and expressed as either the sum of P_i,js or as contact counts (see Supplementary Section S1.3 for details). The final score assigned to x is averaged over the interface [scoring category (i)] or its regions [scoring categories (ii) and (iii)]. Unless specified otherwise, the score S(x) of x is computed according to (i), namely

$$S\left(x\right)=\frac{1}{n}\sum _{\langle i,j\rangle }{n}_{i,j}{P}_{i,j}, \text{with} n=\sum _{\langle i,j\rangle }{n}_{i,j},$$ (5)

where P_i,j is defined in Equation (1) and $n_{i,j}$ is the number of $\langle i,j\rangle$ contacts.

2.5 Availability and implementation

CIPS is available at http://www.lcqb.upmc.fr/CIPS. It is written in C++ and Perl and is supported on GNU/Linux and Mac OS X. Instructions to install and use the package are provided in Supplementary Section S1.11. In this work, the ASA is computed with NACCESS (Hubbard and Thornton, 1993), but this is not a requirement; the user can force CIPS to use the open-access library FreeSASA (Mitternacht, 2016). Experiments were run on an Intel Xeon CPU with 3.50 GHz speed. The computational bottleneck is interface calculation: it took 1 s (small complex < 500 residues) to 7 s (large complex > 2000 residues). The computation of the contacts and of CIPS scores [see Equation (5)] does not add significant overhead (< 0.1 s).

3 Results

The prediction of protein binding sites, successfully realized by several methods based on the observation that interface residues exhibit a compositional bias and undergo slower evolution (Lichtarge et al., 1996; Jones and Thornton, 1997; Zhou and Shan, 2001; Armon et al., 2001; Lichtarge and Sowa, 2002; Pupko et al., 2002; Caffrey et al., 2004; Neuvirth et al., 2004; Fernandez-Recio et al., 2005; Liang et al., 2006; Innis, 2007; Leis et al., 2010; Zhang et al., 2010; Segura et al., 2011; Jordan et al., 2012; Andreani et al., 2012; Laine and Carbone, 2015; Maheshwari and Brylinski, 2015; Aumentado-Armstrong et al., 2015), is not sufficient to correctly discriminate near-native conformations from a set of docking decoys (Lopes et al., 2013). This task requires joint information coming from both protein partners. A test on the Dockground decoy benchmark (Liu et al., 2008) shows that pair potentials pinpoint good quality models with higher precision with respect to residue propensities (see Supplementary Fig. S7). Docking scores realized with existing knowledge-based methods take into account the distribution of amino acid pairings, rather than residue distribution, at the interface. Nevertheless, both pieces of information might be used jointly to accurately select docking decoys. To corroborate this idea, we compare CIPS model with other pair potentials (Moont et al., 1999; Glaser et al., 2001; Pons et al., 2011; Mezei, 2015), on two decoy sets and on selected models from CAPRI competition. The importance of re-ranking structural models after docking calculations has been explicitly addressed in CAPRI competition (Lensink et al., 2016), where several groups specifically focused on models scoring could contribute to. Among the best performing ones, we mention HADDOCK, CLUSPRO and SWARMDOCK. Notice that energy-based terms are often coupled with scores derived from knowledge-based potentials. Combination of CIPS with atomic potentials (Krissinel and Henrick, 2007; Pierce and Weng, 2007) highlights the complementarity of the two approaches (statistical and energy-based) in capturing correct binding modes.

3.1 Local geometry of interface contacts and the propensity of residues to be at the interface

Contact propensities allow to capture the tendency of two amino acids to set up inter-protein contacts. They account for the variability in the number of contacts, which depends on the number of residues at the interface and, possibly, on their volume and degree of exposure to the solvent. The contact propensity we define on $\langle i,j\rangle$ is the contribution of two terms [see Equation (1)]. The first one is contact-based [$\overline{c_{i,j}}$, see Equation (3)] and expresses the tendency of i and j to make a contact (see Fig. 1A, left); this factor regards two proteins as paired upon complex formation. The second term is residue-based [r_i,j, see Equation (4)] and expresses the likelihood of i and j to be located at the interface rather than on the rest of the protein surface (see Fig. 1A, right); it is defined on single proteins, without knowing the partner. These two factors constitute the key ingredients modelling protein–protein interactions. Other important observations help us to refine the model. Namely, our definition of contact propensity takes into account the local connectivity of i and j at the interface (see Fig. 1A, centre). The number of per-residue contacts changes according to the amino acid (see Supplementary Fig. S1). Based on the observation that residues making a lot of contacts tend to have lower contact propensity, a connectivity factor is included [see Equation (3)] to correct for this bias (see Section 2.1 and Supplementary SectionS1.1). Notice that most interfaces contain at least one residue making at least five contacts (see Supplementary Fig. S2).

3.2 A matrix of combined interface propensities

Propensity values P_i,j computed with Equation (1) on PPDB v5.0 result in the propensity matrix reported on Figure 1B (see Supplementary Table S4). It will be referred to as CIPS: Combined Interface Propensity for decoy Scoring. The pattern shown by CIPS matrix essentially points out that: (i) there is a strong tendency of hydrophobic residues to be paired in the interaction; (ii) aromatic residues (i.e. W and Y) play a crucial role in binding, with both hydrophobic and positively charged residues, and (iii) oppositely charged residues tend to be in contact, whereas residues with the same charge are not. Detailed inspection of the matrix shows that R-R is more favourable than K-K: this is due to their different interface propensity and connectivity factor ${\alpha }_{i,j}$ (see also Negi and Braun, 2007 and Supplementary Table S1).

We study the distribution of the values associated to the amino acid pairs to test whether our statistical model for the interface contact frequencies well describes the data. We observe that contact propensities (i.e. the values c_i,j for the amino acid pairs $\langle i,j\rangle$) are roughly partitioned in two halves, representing contacts occurring at the interface respectively less often ($c_{i,j}<0$) or more often ($c_{i,j}>0$) than expected (see Supplementary Fig. S3). This observation supports the consistency of our definition. This is not the case for Glaser et al. (2001). The above test highlights that all-atom structures, implicitly considered in our computation of inter-protein contacts, are more accurate compared to methods approximating a residue with a single atom ($C_{\beta }$ or $C_{\alpha }$) (Moont et al., 1999), possibly weighted by the side chain volume (Glaser et al., 2001). To test the robustness of CIPS further, we replace residue–residue with atom–atom contact counts in Equation (1), by keeping the same distance threshold (see Section 2.1.1). The matrix obtained conserves the qualitative behaviour of CIPS, but the signal is less sharp (see Supplementary Fig. S4). Then, we test the effect of including hydrogen atoms on the structures [the Open Babel toolbox (O’Boyle et al., 2011) is used]. The change in the matrix pattern is negligible (see Supplementary Fig. S5).

We compare the performances among the matrix built with the contact-based term alone, the one where the expected contact frequency is weighted by the connectivity factor and the one where the residue term is included (i.e. CIPS). Note that the first case corresponds to a standard pair potential, defined on a given set of experimental complex structures, where the amino acid pairing at the interface is modelled according to the number of contacts per amino acid. The inclusion of ${\alpha }_{i,j}$ allows to better discriminate, with respect to the other matrices, near-native decoys on DF and medium quality decoys on CF. The inclusion of r_i,j boosts CIPS discriminative power, which turns out to outperform all existing methods (see Supplementary Fig. S8 and compare Supplementary Table S12 with Tables S15–17).

3.3 Scoring protein docking decoys at large scale

The ability of contact propensities to recognize docking structures close to the experimental one relies on capturing the relative orientation of protein partners. To discriminate such conformations, we make use of Equation (5) to score a docking structure, i.e. the average propensity value at the interface.

As described in Section 2.2.2, two distinct training sets are used, named PPDB5\DF and PPDB5\CF, for testing on Dockground_ decoy_ filtered (DF) and CCDMintseris_ filtered (CF), respectively. Note that they guarantee unbiased testing (see Section 2). Thus, two new matrices are computed: CIPS^DF on PPDB5\DF and CIPS^CF on PPDB5\CF. These matrices highlight the robustness of CIPS. Indeed, the correlation between CIPS and CIPS^DF and between CIPS and CIPS^CF is very high, with $\rho =0.99$ and $\rho =0.95$, respectively.

We observe that removing structural redundancy at the interface does not considerably affect the results (see below).

CIPS matrices and the pair potentials proposed by Glaser et al. (2001), Pons et al. (2011) and Mezei (2015) are used to score DF and CF. Correlations between the four propensity matrices are reported in Supplementary Table S5. We also consider an ‘ideal matrix’, describing pair potentials fitting the characteristics of the docking decoys we want to test (see Supplementary Section S1.8). We compute it [with Equation (S1)] in three scenarios (DF, CF with acceptable decoys and CF with medium quality decoys), the idea being to identify possible biases in near-native structures towards specific amino acid pairings. The discriminative power of this ideal matrix provides upper limits to the results obtainable with predictions. Note that a similar study was already proposed with DECK method (Liu and Vakser, 2011).

In the following, we measure the accuracy of the scoring schemes we tested with the criteria described in Supplementary Section S1.9.

3.3.1 Dissecting how different parts of the interface contribute to binding specificity

We ask whether either all interface contacts play a role in the specificity of the interaction, only the “propensity-favourable” part of them, or those connecting specific interface layers. We show that (i) the whole interface is important for the interaction specificity, (ii) all contacts, propensity-favourable or not, contribute to the recognition of true interfaces and (iii) propensity values provide more accurate discrimination compared to contact counts. To answer (i), we check whether focusing on specific interface layers allows to capture enough, possibly stronger, information for the discrimination of true interactions. We employ the support-core-rim model (Levy, 2010) (see Section 2). Contacts involving core residues are the most abundant at the interface (see Supplementary Fig. S9). Hence, we evaluate the effect of considering only core–core contacts, by progressively adding contacts involving support and rim. The analysis with CIPS shows that contacts involving core residues explain only part of the interaction, and that the best performance is obtained by including all interface contacts (see Supplementary Fig. S10). This effect remains consistent across different pair potentials (see Supplementary Table S14). To answer (ii) and (iii), we apply four propensity-based descriptors to the discrimination of true interactions (see Supplementary Section S1.3 and Supplementary Table S2). Two of them are computed on the whole interface; the other two are computed on patches connected to the protein partner by high propensity contacts (see Supplementary Section S1.4 for their definition). We consider either propensity values or the number of contacts with very high propensity value. We use normalized scores because they are invariant upon re-scaling, which is essential for our definition [see Equation (1)], and do not depend on interface size. Supplementary Figure S13 and Supplementary Tables S15–17 show the results obtained on DF and CF using the descriptors. “Total propensity” outperforms the other three. On DF, its predictive power reaches the ‘ideal’ result when patches are used (compare CIPS^DF and “decoy-based” on Supplementary Fig. S13A).

3.3.2 Scoring of all-atom docking decoys: Dockground_ decoy_ filtered

To evaluate CIPS^DF (see Section 2.2.2) on structures obtained with a full-atom model, we consider the Dockground decoy benchmark (Liu et al., 2008). Comparison of the discriminative power of the propensity matrices is reported in Figure 2A (top). CIPS^DF shows to be a well-designed pair potential, able to dissect native from non-native interfaces and to assign the highest scores to docking conformations that are close to the correct structure. CIPS^DF performs better than Glaser, Mezei and Pons matrices. Note that the correlation with the decoy-based propensity is higher for CIPS^DF matrix compared to the other three (see Supplementary Table S6). CIPS^DF performance (AUC 0.87) is very close to the ideal result (AUC 0.90) and the elimination of 19 complexes from the dataset of experimental structures does not affect much the outcome (compare CIPS and CIPS^DF curves in Fig. 2A). The discriminative power of Pons matrix is remarkable too (AUC 0.83). The results are coherent when ranking of near-native decoys is measured (compare Supplementary Tables S15 and S20). CIPS^DF assigns top 10% rank to 233 (56%) near-native decoys, Pons to 205 (49%), Mezei to 174 (42%) and Glaser 130 (31%), the ideal performance attaining 74% of near-native decoys ranked on top 10% (see Supplementary Table S15). By removing even structural redundancy at the interface, as described in Section 2.2.2, the training set PPDB5\DF^(nr) is used to compute a new matrix called CIPS^DF(nr). The correlation between CIPS^DF(nr) and CIPS^DF is high ($\rho =0.95$). We observe that the effect of structural redundancy is negligible (compare CIPS^DF and CIPS^DF(nr) performances in Supplementary Fig. S11A and Supplementary Table S18).

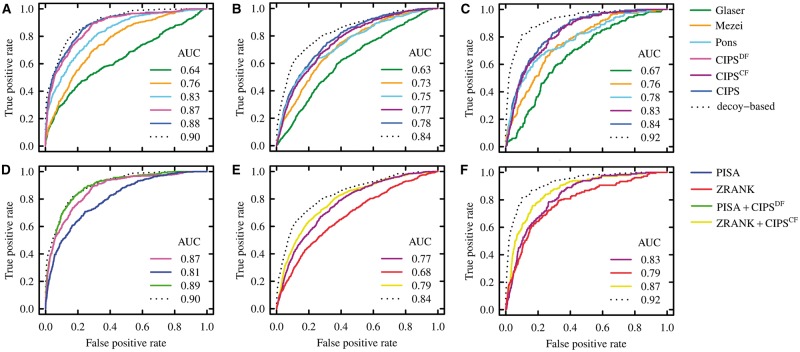
Fig. 2.

Discriminative power of pair potentials, of atomic potentials, and of the combination of the two on all-atom versus coarse-grain decoys datasets. ROC curves are computed on the union of the decoy sets and AUC values are reported for each method. (A–C) The score used is the average contact propensity at the interface [see Equation (5)]. Dotted lines refer to the performances of the decoy-based potential, a propensity defined as the log-ratio between the contact frequency on near-native and non–near-native decoys (see Supplementary Section S1.8). (D–F) The best performing pair potentials and atomic potentials on Dockground_ decoy_ filtered (DF) and CCDMintseris_ filtered (CF), and their combination. PISA + CIPS^DF and ZRANK + CIPS^CF are defined as in Equation (S1). (A and D) Analysis of DF. (B and E) Analysis of CF, with acceptable decoys labelled as near native. (C and F) Analysis of CF, with medium quality decoys labelled as near native. ROC curves and AUC values are computed with the R packages ROCR (Sing et al., 2005 and Tuszynski, 2014) (Color version of this figure is available at Bioinformatics online.)

3.3.3 Scoring of coarse-grain docking decoys: CCDMintseris_ filtered

Despite the optimal parameters for CIPS have been tuned on DF (see Supplementary Section S1.2 and Supplementary Table S3), its relative performance compared to other propensity matrices is robust. We show this with CIPS^CF (see Section 2.2.2) on CF; this control allows us to demonstrate that the propensity we define is actually able to dissect good signal from noise, even for coarse-grain conformations. We perform two separate evaluations by assuming in turn that a “near-native” decoy is either an acceptable or a medium quality solution according to CAPRI definition (Lensink et al., 2007) (see Supplementary Section S1.6). The results obtained by the four propensity matrices are reported in Figure 2B and C (top). As expected, compared to DF, all matrices exhibit worse performances on CF, due to a docking schema applied to a coarse-grain resolution of the structures. A general improvement is observed when going from acceptable to medium quality decoys. CIPS^CF is very precise in discriminating near-native structures from the whole set of decoys, especially for medium quality ones (AUC 0.83). CIPS^CF and Pons assign the highest number of near-native structures to the top 10% ranking; CIPS^CF outperforms all other methods on top 20% ranks and below (see Supplementary Tables S16 and S17). The results are in agreement with the fact that CIPS highly correlates with the decoy-based matrices (see Supplementary Table S6). The discriminative power of the decoy-based matrix is strikingly higher than statistical potentials, especially for medium quality structures (see Supplementary Fig. S13C and compare Supplementary Tables S16 and S17 with Supplementary Tables S21 and S22). Conversely, CIPS is robust with respect to the set of complexes used: inclusion of structures of CF in the computation of the propensity matrix lead to a very slight difference in performance (compare CIPS and CIPS^CF curves in Fig. 2B and C). Similar to DF, we test the elimination of structural redundancy at the interface (see Section 2.2.2) and use the training set PPDB5\CF^(nr) to compute a new matrix called CIPS^CF(nr). The correlation between CIPS^CF(nr) and CIPS^CF is very high ($\rho =0.98$). Structural redundancy does not have perceivable effects on the results (compare CIPS^CF and CIPS^CF(nr) on Supplementary Fig. S11 and Supplementary Table S18).

3.3.4 Comparison between CIPS and atomic potentials

Docking decoys are often ranked according to energy functions or atomic potentials. To corroborate the performances we obtained on DF and CF, we compare the above results with the predictive power of atomic potentials. We select two tools widely used in the scientific community for this purpose: PISA (Krissinel and Henrick, 2007), combining energetic and entropic terms weighted by the number of contacts; and ZRANK (Pierce and Weng, 2007), a sum of energy terms, where weights are learnt from decoy sets built on 15 complexes of PPDB v1.0 (Chen et al., 2003).

PISA outperforms ZRANK on DF, yielding 0.19 higher AUC (see Supplementary Fig. S12A) and ranking 25% more near-native decoys on top 10% (see Supplementary Table S19). On CF, atomic potentials show good performances (see Supplementary Fig. S12B). ZRANK is more precise in discriminating medium quality structures (see Supplementary Table S19); this improved behaviour might be due to the learning step performed on docking decoys. Note that the training set used in ZRANK does not contain complexes from PPDB v2.0. By comparing CIPS^DF with PISA and CIPS^CF with ZRANK, we observe that propensity matrix and atomic potential performances are close to each other. On DF, CIPS^DF outperforms atomic potentials both in global decoy classification (see Fig. 2A) and in the ranking within each decoy set (see Table 1). In contrast, CIPS^CF displays better decoys classification than ZRANK, but the latter better ranks near-native decoys on CF. This is particularly true on medium quality structure classification where for the top 20% ranks, ZRANK outperforms CIPS^CF.

Table 1.

Ranking of near-native decoys on all-atom versus coarse-grain decoys datasets

Top percentage rank	Dockground_ decoy_ filtered			CCDMintseris_ filtered (acceptable)			CCDMintseris_ filtered (medium quality)
	PISA	CIPSDF	PISA + CIPSDF	ZRANK	CIPSCF	ZRANK + CIPSCF	ZRANK	CIPSCF	ZRANK + CIPSCF
Top 1%	5	6	8 (63)	8	3	5 (18)	14	2	7 (22)
Top 10%	44	56	65 (90)	36	32	42 (66)	57	40	57 (78)
Top 20%	64	73	79 (94)	48	53	62 (90)	71	64	77 (90)
Top 30%	74	82	87 (98)	60	69	76 (96)	80	80	88 (94)
Top 40%	81	89	90 (98)	67	78	81 (96)	86	90	93 (98)
Top 50%	87	94	95 (100)	74	85	88 (98)	86	93	96 (98)

Entries represent the percentage of near-native decoys placed on each top percentage rank. The number reported in parentheses is the percentage of complexes having at least one near-native decoy placed on each top % rank. Bold values indicate best performance.

3.3.5 Combination of CIPS with atomic potentials reaches optimal discrimination of near-native decoys

We show how a combination of pair potentials and energy functions can improve both decoy classification and ranking. The ideal situation is the one where the two approaches capture distinct interface features. To check for this, we compute the correlation between the ranking assigned by pair potentials and atomic potentials, respectively, to all decoys of DF and CF (see Supplementary Table S23). Correlations are positive but low: 0.35 between PISA and CIPS^DF and 0.12 between ZRANK and CIPS^CF, hinting that the two approaches might use complementary information.

We combined pair potentials and atomic potentials (see Supplementary Section S1.5) and evaluate the discrimination of near-native decoys on DF and CF (see Fig. 2). PISA + CIPS^DF performs better on DF than either PISA or CIPS^DF alone; ZRANK + CIPS^CF performs better on CF than ZRANK and CIPS^CF alone. PISA is always the best choice on DF when combined to any pair potential (see Supplementary Figs S15A and S16A and Supplementary Table S24). Conversely, on CF, ZRANK outperforms PISA when coupled to any pair potential (see Supplementary Figs S15B and C and S16B and C and Supplementary Tables S25 and S26). The relative performance of pair potentials remains consistent on combined scores, showing that CIPS provides the best discrimination compared to the other matrices. Combined scores always perform better, compared to atomic potentials and pair potentials used alone, and almost reach the theoretical limit set by decoy-based propensities, especially on DF (see Fig. 2A). On CF, the difference in performance between the decoy-based matrix and pair potentials is more evident (see Fig. 2B and C). However, ZRANK + CIPS^CF discriminates medium quality decoys consistently better than ZRANK + Pons. By combining atomic potentials and CIPS as above, selection of near-native docking solutions is possible with high precision (see Table 1). On DF, picking the top 10% ranked decoys allows to retain 65% of near-native solutions and to have at least one near-native for 46 out of 51 complexes (90%). On CF, top 10% ranked decoys contain 42% and 57% of acceptable and medium quality structures, respectively. They represent 69 out of 105 decoy sets with at least one acceptable solution, 40 of them having also one medium quality solution.

3.4 Scoring high-quality structural models: CAPRI targets

CIPS performance is assessed on the top 10 models produced by CAPRI participants, for 28 targets (see Section 2.3). We use the near-native solution classification provided on CAPRI rounds. Evaluation on this testing set is reported on Figure 3 and Table 2 (see Supplementary Fig. S17 and Supplementary Table S27 for details). CIPS outperforms the other three propensity matrices, yielding at least 0.08 higher AUC (when acceptable or better decoys are considered as near native). We identify 10 easy and 9 difficult targets (see Supplementary Table S11). The performances of the four propensity matrices are reported on Supplementary Figure S18 and Supplementary Table S28. CIPS equals or outperforms existing pair potentials, irrespective of the quality of the solutions and on the conformational change upon binding.

Fig. 3.

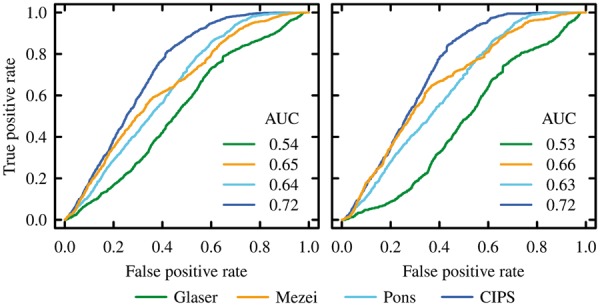
Discriminative power of pair potentials on 28 CAPRI targets. Scores are defined as for Figure 2. Acceptable (left) and medium quality (right) decoys are labelled as near native (Color version of this figure is available at Bioinformatics online.)

Table 2.

Ranking of near-native models of 28 CAPRI targets

	Acceptable				Medium quality
Top percentage rank	Glaser	Mezei	Pons	CIPS	Glaser	Mezei	Pons	CIPS
Top 1%	0	0	1	1	0	0	0	0
Top 10%	8	11	9	11	6	10	8	9
Top 20%	18	23	22	27	14	21	19	24
Top 30%	32	35	35	42	26	33	32	38
Top 40%	44	47	49	56	38	43	46	52
Top 50%	57	58	62	69	52	56	58	65

Entries represent the percentage of near-native decoys placed on each top percentage rank. Bold values indicate best performance.

3.5 Classes of complexes where CIPS fails

CIPS almost always assigns high score to near-native structures. When it fails, the best rank assigned by CIPS to a near-native is not far from the best rank assigned by other methods. In Supplementary Figures S21–25, we illustrated this observation on each decoy set of the CF dataset.

CIPS behaves better on DF rather than on CF. Namely, on DF, for 50 (for 44) out of 51 decoy sets, 75% of the near-native poses are ranked on top 50% (on top 20%). We recall that DF poses have been generated by full-atom docking while coarse-grain docking generated CF poses. This means that the quality of the poses might influence CIPS ranking.

In the attempt at characterising the decoy sets where CIPS does not perform well in CF, we defined three classes of decoy sets based on CIPS^CF ranking of near-native poses (see Supplementary Section S1.10). For each class, we computed the physico-chemical properties of the experimental interface and concluded that CIPS fails to rank near-native solutions on top when the interface is enriched in charged residues and in contacts between opposite charges (see Supplementary Fig. S26, top left). Note that the same observation holds true for the decoy set in DF that was not ranked properly by CIPS, also presenting a highly charged experimental interface.

Finally, we observed that the interface size does not affect CIPS^CF performance.

4 Discussion

It has been shown that protein–protein interfaces span a wide range of sizes, which are not related to binding strength, and that the apolar tendency is variable (Nooren and Thornton, 2003). We analyse in depth the characteristics of the interface by identifying groups of contacts that are susceptible to carry the strength of the interaction, we study which part of it is the most specific and we find that all contacts are important for recognition. Focusing only on sub-regions of the interface hinders the discriminative power of knowledge-based methods for decoy scoring. We demonstrate that capturing information coming from both amino acid specificity at the interface and their coupling in the interaction allows to discriminate high-quality structural models, among thousands of decoys, with high precision. Taking into account the level of connectivity of each residue type further refines the method. Previous studies (Pons et al., 2011) defined a performing propensity matrix based on the interface random model instead of the contact random model used in CIPS. Interface residues and contacts are detected with the same criterion for the two approaches and their difference in performance is mainly due to the introduction of the interface residue propensity in CIPS. We find out that CIPS is more powerful than three other propensity matrices available in the literature and two widely used atomic potentials: PISA (Krissinel and Henrick, 2007) and ZRANK (Pierce and Weng, 2007). On Dockground decoy benchmark, CIPS alone performs far better than a learning method previously proposed (Fink et al., 2011). A decoy-based potential, directly using experimental information on the complexes to be evaluated and representing the physico-chemical properties of the interaction contacts, allowed us to check how our method behaves with respect to a reference. We observe that a score defined as the combination of CIPS and atomic potentials almost reaches the “ideal” performance. This effect is more evident on the decoys obtained with a full-atom model. Note that no refinement is applied on coarse-grain structures, thus clashes might occur; moreover, on some structures of CF, the conformational change is not negligible (see Supplementary Section S1.7), but CIPS copes well with it (see Supplementary Fig. S14 and Supplementary Table S13). DF is an easier testing set compared to CF. On DF, decoys are selected by knowing the experimental structure; on CF, they are filtered according to a coarse-grain energy function. We observe that the total number of interface contacts well discriminates near-native solutions in DF (AUC 0.82), suggesting that normalized scores are needed to partially get rid of the bias associated to decoys pre-selection.

The construction of ‘ideal matrices’ for DF and CF (see Supplementary Fig. S6) leads us to observe that amino acid pairings involving aromatic residues and hydrophobic contacts are more abundant at near-native interfaces compared to non-near-native ones. Surprisingly, contacts between oppositely charged residues do not discriminate true interactions. This might be due to the inclusion of a Coulomb energy term in the docking procedure, which might drive the search towards wrong conformations with lots of positive/negative contacts. Instead, interaction specificity might be the result of a complex combination of signals at the interface, as suggested by our analysis performed with propensity-based descriptors. Note that the low specificity associated to positive/negative contacts in near-native conformations is in contrast with the pattern observed on most of the propensity matrices found in the literature, including CIPS (compare Fig. 1 and Supplementary Fig. S6B). Consistently, we observed that CIPS predictions are worse on highly charged interfaces (see Section 3.5), so alternative methods might be designed in this case.

5 Conclusion

Protein partner prediction is a fundamental problem in biology that needs to be tackled with robust computational pipelines, the first steps being docking calculations and filtering out incorrect conformations. CIPS is a valuable method for systematically screening the large amount of poses returned by large-scale cross-docking. It is fast, accurate and robust upon decrease of protein structure resolution; thus, it can be safely employed for scoring structural models obtained with coarse-grain docking methods. Further applications of the method might be CIPS direct inclusion in the docking procedure, similarly to Mintseris et al. (2007), to guide and speed up the search within the conformational space. From a broader point of view, CIPS can be seen as a method able to add constraints to the degrees of freedom of the quaternary structure. The usage of statistical methods have been successfully employed in the protein folding problem (Süel et al., 2003; Weigt et al., 2009; Marks et al., 2012). An emerging field of research focuses on the application of co-evolution methods to inter-protein contacts, but the problem has been shown to be much harder to solve (Wilkins et al., 2013; Hopf et al., 2014). Pair potentials could contribute in a completely novel manner to protein complex design.