Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2017 Sep 22;34(3):530–532. doi: 10.1093/bioinformatics/btx602

graphkernels: R and Python packages for graph comparison

Mahito Sugiyama 1,2,✉, M Elisabetta Ghisu 3,4,✉, Felipe Llinares-López 3,4, Karsten Borgwardt 3,4
Editor: Jonathan Wren
PMCID: PMC5860361  PMID: 29028902

Abstract

Summary

Measuring the similarity of graphs is a fundamental step in the analysis of graph-structured data, which is omnipresent in computational biology. Graph kernels have been proposed as a powerful and efficient approach to this problem of graph comparison. Here we provide graphkernels, the first R and Python graph kernel libraries including baseline kernels such as label histogram based kernels, classic graph kernels such as random walk based kernels, and the state-of-the-art Weisfeiler-Lehman graph kernel. The core of all graph kernels is implemented in C ++ for efficiency. Using the kernel matrices computed by the package, we can easily perform tasks such as classification, regression and clustering on graph-structured samples.

Availability and implementation

The R and Python packages including source code are available at https://CRAN.R-project.org/package=graphkernels and https://pypi.python.org/pypi/graphkernels.

Supplementary information

Supplementary data are available online at Bioinformatics.

1 Introduction

Graph-structured data are steadily growing and extensively being analyzed in computational biology. For example, chemical compounds are modeled as graphs in drug discovery (Takigawa and Mamitsuka, 2013), and proteins are represented as graphs in protein function prediction (Dhifli and Nguif, 2015). Finding efficient solutions for measuring the similarity between a pair of graphs, known as the graph comparison problem, is a fundamental step in graph analysis, in order to perform classification or regression on graph data. There are two approaches to graph comparison: alignment-based methods (Faisal et al., 2015) that compare graphs via finding node mappings and alignment-free methods (Yaveroğlu et al., 2015) that measure the similarity between graphs using features such as degree distributions or subgraph counts without identifying correspondences between nodes.

To date, among the alignment-free approaches, graph kernels have become a popular approach to quantify the similarity between graphs (Borgwardt and Kriegel, 2005; Costa and Grave, 2010; Gärtner et al., 2003; Kashima et al., 2003; Shervashidze et al., 2009, 2011; Sugiyama and Borgwardt, 2015; Vishwanathan et al., 2010), and are at the heart of many machine learning approaches in computational biology. A number of key applications of graph kernels exist such as biological function prediction from graph-based representations of chemical compounds. However, there is no convenient R or Python implementation that can simply and efficiently compute graph kernels, although R is a popular programming environment in Bioinformatics and Python in Machine Learning.

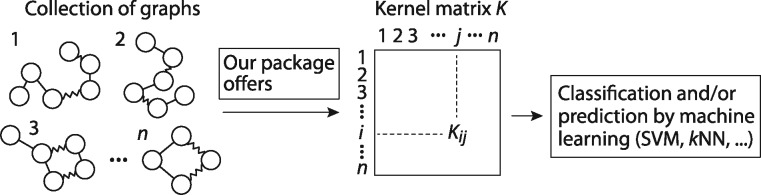
Here we present graphkernels, the first package in R and Python with efficient C ++ implementations of various graph kernels including the following prominent kernel families: (i) simple kernels between vertex and/or edge label histograms, (ii) graphlet kernels, (iii) random walk kernels (popular baselines) and (iv) the Weisfeiler-Lehman graph kernel (state-of-the-art kernels). The packages can be easily used to perform graph classification and regression by machine learning algorithms (Fig. 1), such as support vector machines (SVMs) or the k-nearest neighbors algorithm.

Fig. 1.

Fig. 1

Open in a new tab

Overview. The kernel value Kij represents the similarity between graphs i and j

2 Materials and methods

Each function implemented in the graphkernels packages receives a collection of graphs G1, G2, …, Gn and returns the kernel (Gram) matrix (Kij)∈ℝn×n with the respective graph kernel, where each kernel value Kij shows the similarity between graphs Gi and Gj. The packages support the following 14 graph kernels:

  • Linear kernels on label histograms: VertexHist, EdgeHist, VertexEdgeHist, VertexVertexEdgeHist.

  • Gaussian RBF kernels on label histograms: VertexHistGauss, EdgeHistGauss, VertexEdgeHistGauss.

  • Graphlet kernels: Graphlet, ConnectedGraphlet.

  • Random walk based kernels: KStepRandomWalk, Geometric RandomWalk, ExponentialRandomWalk, ShortestPath.

  • The Weisfeiler-Lehman subtree kernel: WL.

All kernels are implemented in C ++ and compiled through the packages Rcpp (Eddelbuettel, 2013) and RcppEigen (Bates and Eddelbuettel, 2013) in the R package. We use SWIG (Beazley, 1996) interfaces to wrap C ++ code in Python. See the Supplementary Material for detailed mathematical definitions of these graph kernels.

In our packages, each graph is treated as an igraph object (Csardi and Nepusz, 2006) and a collection of graphs is kept as a list of igraph graphs. An example usage in R is shown in the following, where we use the dataset MUTAG (Debnath et al., 1991), a typical benchmark dataset that is also provided in our package.

>library(graphkernels) # load the package

>data(mutag) # load a sample dataset,

 ## which is a list of (igraph) graphs

> mutag[[1]]

IGRAPH f2f3caf U— 23 27 –

+ attr: label (g/n), label (v/n), label (e/n)

+ edges:

 [1] 1– 2 1–14 2– 3…

 ## the first graph has 23 nodes and 27 labels

> K <- CalculateVertexHistKernel(mutag)

 ## compute the kernel matrix

> K[1, 2]

[1] 282 ## The kernel value b/w graphs 1 and 2

The entire kernel matrix can be easily computed by a single line of R code. Similar examples in Python can be found in the Supplementary Material.

3 Application

As a representative application, we demonstrate graph classification using the MUTAG dataset. In the dataset, there are 188 graphs, and the objective is to predict labels of graphs, indicating whether or not they are mutagenic. We used 10-fold cross validation for graph classification. We randomly divided the entire dataset into 10 folds. In each iteration 1 of the 10 folds was used for testing and the rest for training. We computed the kernel matrix of the training data using one of our functions implemented in graphkernels, and use these data to train an SVM using the kernlab package (Karatzoglou et al., 2004). We then predicted labels on the test data, and obtained the accuracy by comparison with the ground-truth labels. The detailed experimental methodology and the R code to reproduce these results are provided in the Supplementary Material.

Figure 2 shows the prediction accuracy for graph kernels in our package and the CPU running time needed to compute each kernel matrix. This example demonstrates that our package allows for an easy comparison of the effectiveness and the efficiency of various popular graph kernels and will serve as a baseline when designing new graph kernels for specialized applications in computational biology.

Fig. 2.

Fig. 2

Open in a new tab

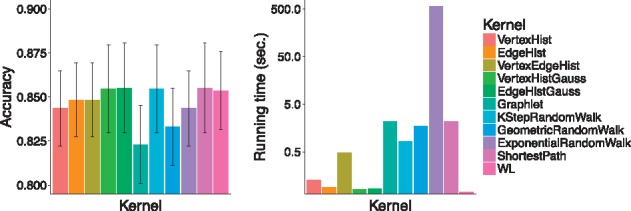
Accuracy (left) and running time (in seconds, right) on the MUTAG dataset

Funding

MS was funded by JSPS KAKENHI Grant Numbers JP16K16115 and JP16H02870. MEG was funded by Horizon 2020 project CDS-QUAMRI, Grant No. 634541.

Supplementary Material

Supplementary Data
Click here for additional data file. (79.1KB, zip)

References

  1. Bates D., Eddelbuettel D. (2013) Fast and elegant numerical linear algebra using the RcppEigen package. J. Stat. Softw., 52, 1–24.23761062 [Google Scholar]
  2. Beazley D.M. (1996). Swig: An easy to use tool for integrating scripting languages with c and c ++. In Proceedings of the 4th Conference on USENIX Tcl/Tk Workshop, Monterey, California, USA.
  3. Borgwardt K.M., Kriegel H.-P. (2005) Shortest-path kernels on graphs. In Proceedings of 5th IEEE International Conference on Data Mining, Houston, TX, USA, pp. 74–81. [Google Scholar]
  4. Costa F., Grave K.D. (2010) Fast neighborhood subgraph pairwise distance kernel. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, pp. 255–262. [Google Scholar]
  5. Csardi G., Nepusz T. (2006) The igraph software package for complex network research. InterJournal, Complex Systems, 1695. [Google Scholar]
  6. Debnath A.K. et al. (1991) Structure-activity relationship of mutagenic aromatic and heteroaromatic nitro compounds. correlation with molecular orbital energies and hydrophobicity. J. Med. Chem., 34, 786–797. [DOI] [PubMed] [Google Scholar]
  7. Dhifli W., Nguif E.M. (2015). Motif discovery in protein 3D-structures using graph mining techniques In: Elloumi M., Iliopoulos C., Wang J.T.L., Zomaya A.Y. (eds.), Pattern Recognition in Computational Molecular Biology: Techniques and Approaches. John Wiley & Sons, Inc., Hoboken, NJ. [Google Scholar]
  8. Eddelbuettel D. (2013). Seamless R and C ++ Integration with Rcpp. Springer-Verlag New York. [Google Scholar]
  9. Faisal F.E. et al. (2015) The post-genomic era of biological network alignment. EURASIP J. Bioinformatics Syst. Biol., 2015, 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Gärtner T. et al. (2003) On graph kernels: Hardness results and efficient alternatives. In Learning Theory and Kernel Machines, pp. 129–143. [Google Scholar]
  11. Karatzoglou A. et al. (2004) kernlab–an S4 package for kernel methods in R. J. Stat. Softw., 11, 1–20. [Google Scholar]
  12. Kashima H. et al. (2003). Marginalized kernels between labeled graphs. In Proceedings of the 20th International Conference on Machine Learning, pp. 321–328. Washington, DC, USA. [Google Scholar]
  13. Shervashidze N. et al. (2009). Efficient graphlet kernels for large graph comparison. In Proceedings of the 12th International Conference on Artificial Intelligence and Statistics, pp. 488–495. Clearwater Beach, FL, USA.
  14. Shervashidze N. et al. (2011) Weisfeiler-Lehman graph kernels. J. Mach. Learn. Res., 12, 2359–2561. [Google Scholar]
  15. Sugiyama M., Borgwardt K.M. (2015) Halting in random walk kernels. In: Cortes C.et al. (eds.), Advances in Neural Information Processing Systems 28, pp. 1639–1647. [Google Scholar]
  16. Takigawa I., Mamitsuka H. (2013) Graph mining: procedure, application to drug discovery and recent advances. Drug Discov. Today, 18, 50–57. [DOI] [PubMed] [Google Scholar]
  17. Vishwanathan S.V.N. et al. (2010) Graph kernels. J. Mach. Learn. Res., 11, 1201–1242. [Google Scholar]
  18. Yaveroğlu Ö.N. et al. (2015) Proper evaluation of alignment-free network comparison methods. Bioinformatics, 31, 2697–2704. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
Click here for additional data file. (79.1KB, zip)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES