scHiCNorm: a software package to eliminate systematic biases in single-cell Hi-C data

Abstract

Summary

We build a software package scHiCNorm that uses zero-inflated and hurdle models to remove biases from single-cell Hi-C data. Our evaluations prove that our models can effectively eliminate systematic biases for single-cell Hi-C data, which better reveal cell-to-cell variances in terms of chromosomal structures.

Availability and implementation

scHiCNorm is available at http://dna.cs.miami.edu/scHiCNorm/. Perl scripts are provided that can generate bias features. Pre-built bias features for human (hg19 and hg38) and mouse (mm9 and mm10) are available to download. R scripts can be downloaded to remove biases.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

The chromosome conformation capture (3C) techniques (Dekker et al., 2002) provide great opportunities to explore the genome architecture by capturing the spatial proximities between genomic regions. The recent Hi-C technique (Lieberman-Aiden et al., 2009) can capture genome-wide chromosomal contacts, which has been used for many researches, such as reconstructing the three-dimensional (3D) structures of chromosomes (Hu et al., 2013) and the study of topologically associated domains (TADs) (Dixon et al., 2012). However, the raw Hi-C contact maps are an ensemble based on millions of nuclei. In comparison, Ramani et al. (Ramani et al., 2017) conducted single-cell combinatorial indexed Hi-C (sciHi-C) experiment, which can simultaneously generate the single-cell Hi-C contact maps for thousands of cells. The sciHi-C experiment has generated 10 696 single-cell contact maps; and variance between these contact maps has been found that is believed to be caused by different cell-cycle stages (Ramani et al., 2017).

These sciHi-C profiles provide promising research opportunities to study cell-specific chromosomal structures. However, we will later demonstrate that similarly as Hi-C data single-cell Hi-C data also contains systematic biases in terms of effective length, GC content and mappability of fragment ends (Yaffe and Tanay, 2011). These biases need to be removed to further use the single-cell Hi-C data. However, the existent methods, Hicpipe (Yaffe and Tanay, 2011) and HiCNorm (Hu et al., 2012), for normalizing massive-cell Hi-C data (i.e. eliminating biases), are not specifically designed for zero-inflated single-cell Hi-C data.

2 Materials and methods

We download the raw single-cell Hi-C contact reads from GEO, GSE84920 (Ramani et al., 2017) and combine the data from four replicates (i.e. ML1, ML2, PL1 and PL2). We then discard the single cells with less than 50 000 uniquely mapped contacts, resulting in 74 human cells for the downstream analysis. In this work, we only consider intrachromosomal (cis) contacts, because interchromosomal (trans) contacts in single cells are too sparse to be normalized at a reasonable resolution (e.g. 1 Mb). For each chromosome, we generate a cis-contact matrix at the resolution of 1 Mb. For each 1 Mb bin in the matrix, we generate its local bias features including cutting site density (i.e. effective length), GC content and mappability (more details see Supplementary Material).

We assume that the entries in a contact matrix (i.e. raw Hi-C contact counts) follow six distributions individually: Poisson, Negative Binomial (NB), Zero-inflated Poisson (ZIP) (Lambert, 1992), Zero-inflated Negative Binomial (ZINB), Poisson Hurdle (PH) (Mullahy, 1986) and Negative Binomial Hurdle (NBH). The first two are previously used to eliminate biases for massive-cell Hi-C; and the last four are models specifically designed for zero-inflated Hi-C data. After fitting a regression model per chromosome per cell using the six distributions with bias features being variables, we normalize the raw contact counts by dividing it by the expected counts, which is the fitted values in the regression models (more details see Supplementary Material).

We compare the goodness of fit of these six models based on likelihood ratio test, Vuong test and Akaike information criterion (AIC). To test the effectiveness of eliminating the biases, we calculate the Pearson correlation coefficients between Hi-C data (raw and normalized) and the corresponding local features. A weaker correlation indicates less biases.

3 Results

We first confirm that the three systematic biases indeed exist in both the ensemble of the 74 cells (Supplementary Fig. S1) and one of individual cells (Supplementary Figs S2, S3a, b and c). After that, we go through the normalization process. For each of the six probability distributions, we fit about 1702 regression models (74 cells, each with 23 chromosomes).

The goodness of fit between six models are indicated by likelihood ratio test for nested models (Poisson versus NB, ZIP versus ZINB and PH versus NBH), Vuong test for non-nested models and Akaike information criterion (AIC) (see Supplementary Table S1). The results show that NB-related models (i.e. NB, ZINB and NBH) are fitted better than Poisson-related models (Poisson, ZIP and PH) respectively; and zero-inflated/hurdle models outperform standard Poisson and NB models in terms of Vuong test. However, the AIC criterion favors NB rather than ZINB.

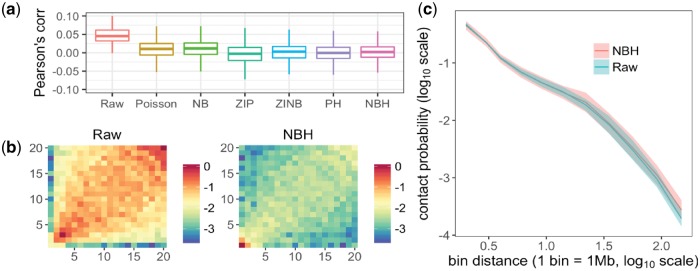
To test the effectiveness of eliminating biases, we calculate the Pearson’s correlation coefficients between Hi-C data (raw and normalized) and the corresponding local features. A weaker correlation indicates less biases. We benchmark four more Hi-C normalization methods, including three matrix-balancing methods: ICE (Imakaev et al., 2012), VC (Lieberman-Aiden et al., 2009), KR (Knight and Ruiz, 2013; Rao et al., 2014) and one more non-parametric regression. The results (see Fig. 1a and Supplementary Fig. S4) indicates that all the ten methods have eliminated biases with varying levels of success, with our methods (i.e. ZIP, ZINB, PH and NBH) most effectively, especially in terms of bias of mappability. In summary, NBH appears to be the best regression model in this work. An example of normalization result of a single-cell Hi-C matrix can be found in Figure 1b (Raw versus NBH), Supplementary Figures S2 and S3.

Fig. 1.

(a) Pearson’s correlation coefficients between Hi-C data (Raw and normalized) and the mappability feature. (b) An individual cell’s Hi-C heat map associated with mappability before and after normalization using NBH method (details see Supplementary Results). (c) The normalized Hi-C data via NBH method achieve larger standard deviations (variances) than raw Hi-C data

We next explore whether the normalization process remove noises and reveal the cell-to-cell variance by plotting the contact probability against the genomic distance (i.e. bin distance, bin width = 1 Mb). As shown in Figure 1c (Raw versus NBH), Supplementary Figures S7 and S8, our normalization methods successfully increase or reveal the cell-to-cell variances.

Funding

This work was supported by NIH R15GM120650 and UM start-up to ZW.

Conflict of Interest: none declared.