Multiple Imputation for Incomplete Data in Epidemiologic Studies

Abstract

Epidemiologic studies are frequently susceptible to missing information. Omitting observations with missing variables remains a common strategy in epidemiologic studies, yet this simple approach can often severely bias parameter estimates of interest if the values are not missing completely at random. Even when missingness is completely random, complete-case analysis can reduce the efficiency of estimated parameters, because large amounts of available data are simply tossed out with the incomplete observations. Alternative methods for mitigating the influence of missing information, such as multiple imputation, are becoming an increasing popular strategy in order to retain all available information, reduce potential bias, and improve efficiency in parameter estimation. In this paper, we describe the theoretical underpinnings of multiple imputation, and we illustrate application of this method as part of a collaborative challenge to assess the performance of various techniques for dealing with missing data (Am J Epidemiol. 2018;187(3):568–575). We detail the steps necessary to perform multiple imputation on a subset of data from the Collaborative Perinatal Project (1959–1974), where the goal is to estimate the odds of spontaneous abortion associated with smoking during pregnancy.

Epidemiologic studies are often susceptible to missing data. Common methods for analyzing data sets containing missing information for some variables, such as complete-case analysis (CCA), are often inefficient, and they can severely bias parameter estimates if the missingness is a function of the observed or unobserved data. Alternatively, techniques for mitigating potential bias from incomplete data are becoming more commonplace in the epidemiologic literature (1, 2). Multiple imputation (MI), an estimation approach introduced by Rubin (3), has become one of the more popular techniques, in part due to the improved accessibility of MI algorithms in existing software (4, 5). In this paper, we describe the assumptions, graphical tools, and methods necessary to apply MI to an incomplete data set. We focus on data from the Collaborative Perinatal Project (1959–1974) (6) as introduced in a companion paper by Perkins et al. (7), where the goal is to estimate the odds of spontaneous abortion associated with smoking during pregnancy.

To those unfamiliar with imputation techniques, imputing missing values can appear to be “making up data.” Indeed, simple imputation techniques, such as replacing missing values of a variable with the average of the observed values, can bias parameter estimates. However, ignoring missing data by removing all observations with missing values, as in complete-case or available-case analysis (the default strategy in software packages such as R (R Foundation for Statistical Computing, Vienna, Austria) and SAS (SAS Institute, Inc., Cary, North Carolina)), can induce similarly unwelcome biases. Detail about specific scenarios in which CCA may produce biased estimates versus unbiased estimates has been provided elsewhere by Bartlett et al. (8).

MI is a simulation-based procedure which replaces each missing value with a set of m > 1 plausible values, creating m complete data sets that can be individually analyzed using standard statistical procedures. The results from the m analyses are then combined into a final estimate that incorporates the variability of the data plus some additional variability acknowledging uncertainty about the missing values (9).

The most challenging step of MI is arguably the imputation stage, in which the relationship between the observed and missing parts of the data set is modeled. Often, a parametric model such as a multivariate normal model is chosen to represent these relationships. The joint normal model is a popular choice because it is robust to misspecification, performing well even when the data are not jointly normally distributed. More discussion about advantages and disadvantages of the joint normal model can be found elsewhere (10, 11).

An alternative to the joint normal parametric model, called multiple imputation by chained equations (MICE) (12–14), chooses a sequence of conditional regressions that reflect the distribution of the missing variable (e.g., logistic for binary data, Poisson for count data). This approach can be particularly useful when imputing data for binary, categorical, or count variables or when a joint normal assumption may impute values outside of the feasible range.

When these parametric imputation models are deemed inadequate to properly model the missing data, a nonparametric imputation procedure can be applied, such as hot-deck or predictive mean matching (15–17), which draws imputed values from the observed values in the data. Similar to MICE, these nonparametric strategies are popular for data subject to constraints, because they ensure that the imputed values will fall within a feasible range (18). In predictive mean-matching (15), for instance, observations with incomplete data are “matched” to those with complete data, and the missing values are drawn from the possible set of values observed among the matched complete cases. The matching is then done based on all observed covariates. These types of nonparametric approaches are popular options when a single imputation is needed, such as when producing complete data sets for public use. In these scenarios, ensuring that the imputed values are consistent with the observed data is imperative, to avoid discrepancies (e.g., imputing a sex of “male” for someone who is pregnant). In most epidemiologic studies, however, an MI approach is preferred over single imputation, because multiple imputations can better reflect the additional parameter variation due to uncertainty about the missing values.

Due to increasing availability of imputation techniques in common software packages such as SAS and R, implementation of these strategies is fairly straightforward, so long as the missing values depend only on the observed data. On the other hand, if the missing data depend on unobserved variables (or, more precisely, are not ignorable), then the underlying mechanism of the missingness must also be modeled together with the data (7). Models for imputations under nonignorable assumptions include selection models (19, 20), pattern-mixture models (21–23), and shared parameter models (24).

Our goal in this paper is to apply MI techniques to the data sets presented in the companion paper (7), to replicate the process an epidemiologic researcher might conduct when faced with incomplete data. In a methodological challenge, Perkins et al. (7) constructed 3 distinct data sets according to various missingness mechanisms, which were masked from us and the authors of another article (25). Our task involved applying available methods for missing data to test their ability to provide appropriate inference under the specified assumptions. Below, we briefly describe the data sets based on the information that was made available. We detail our process of applying MI to the incomplete data sets and present the results. Finally, we discuss the assumptions, limitations, and common concerns corresponding to application of MI and missing-data methods. While there are many steps needed to conduct a thorough analysis of incomplete data, we focus our analysis on the most relevant points, and we suggest additional references for more detail.

DATA

Data from the Collaborative Perinatal Project (6) served as the complete data set on which all subsequent analyses were based. The Collaborative Perinatal Project was a multisite US cohort study of pregnant women (1959–1974) who were followed throughout pregnancy and multiple times after delivery. Variables available for analysis included spontaneous abortion status (“Abort”), defined as a spontaneous abortion occurring at less than 20 weeks’ gestation; maternal smoking status at enrollment (“Smoke”); maternal race, categorized as white, black, or other (“Race”); maternal age at enrollment, in years (“Age”); and maternal prepregnancy body mass index (BMI; weight (kg)/height (m)²) (“BMI”). The goal of this analysis was to determine the odds of spontaneous abortion for women who smoked during pregnancy versus women who did not smoke, as assessed by the baseline questionnaire.

This task would be straightforward if all data were complete (and assuming no unmeasured confounding). However, when the collected data are incomplete, additional steps must be taken to reduce the potential for selection bias due to missing data. To illustrate this idea, Perkins et al. (7) generated 3 incomplete data sets based on the complete data from the Collaborative Perinatal Project. As they described in their paper, the missingness mechanism for each data set was chosen to be missing completely at random (MCAR), missing at random (MAR), or missing not at random (MNAR). More detailed information about the data and the missingness process is given in the companion paper (7).

The type of missingness in a data set has implications for the performance of missing-data methods. MI is effective at providing (asymptotically) unbiased estimates of the regression parameter of interest (e.g., log odds, log relative risk) when data are MCAR or MAR, but not when data are MNAR (without additional assumptions and modeling). In actual research settings, however, this information is rarely available. While tests for differentiating between MCAR and MAR data sets are available (26), it is not possible to detect MNAR with the observed data alone. To mimic this lack of knowledge, the data sets were blinded with respect to the missingness-generating process.

VISUALIZING MISSINGNESS PATTERNS

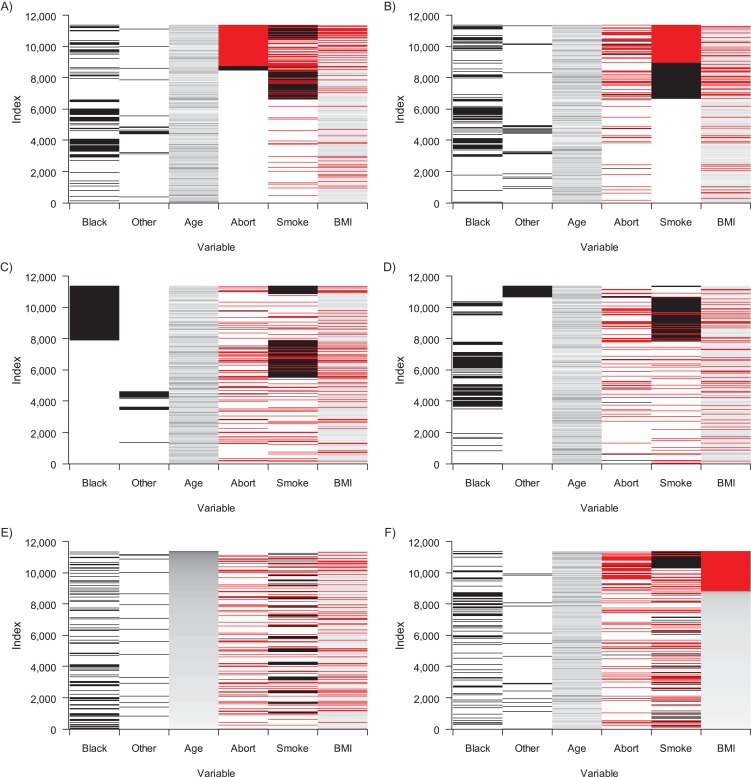
Before embarking on an MI procedure, it can be useful to visually inspect the data to better assess some of the assumptions necessary for MI, as well as the intended analysis—in this case, logistic regression. It is beneficial to look at the pattern of missingness, as well as histograms of the continuous variables, to ensure that the normality assumption is not grossly violated. While transformations are possible for skewed variables, in many cases they are not required, since MI is robust to the assumption of normality if the amount of missing information (defined below) is low (10). Figure 1 illustrates the missingness pattern for data set 1 in a matrix structure, where red represent missingness and gradations of white to black represent increasing values (shown here for data set 1). Each line represents an individual and each column a variable, and each subfigure is sorted by a different variable. Although it is not a formal test for determining the missingness mechanism, this type of visual analysis can help identify potential deviations from the MCAR assumption. For instance, based on this missingness matrix, data on spontaneous abortion and BMI tend to be missing together (lower right) and information on spontaneous abortion tends to be missing for higher values of smoking (upper left), suggesting that missingness may not be completely random. The remaining panels do not appear to provide any additional information concerning the missingness relationships.

Figure 1.

Matrix of missingness trends in data from the Collaborative Perinatal Project, 1959–1974. Each row represents an individual observation. The data are sorted according to different variables (black race, other race, age, spontaneous abortion status (“Abort”), smoking status (“Smoke”), and body mass index (BMI)) in order to assist with visual detection of correlation in missingness patterns, where red signifies a missing value and gradations of white to black represent increasing values of a variable. In parts A, C, and E, data are sorted by spontaneous abortion status, black race, and age. In parts B, D, and F, data are sorted by smoking status, other race, and BMI.

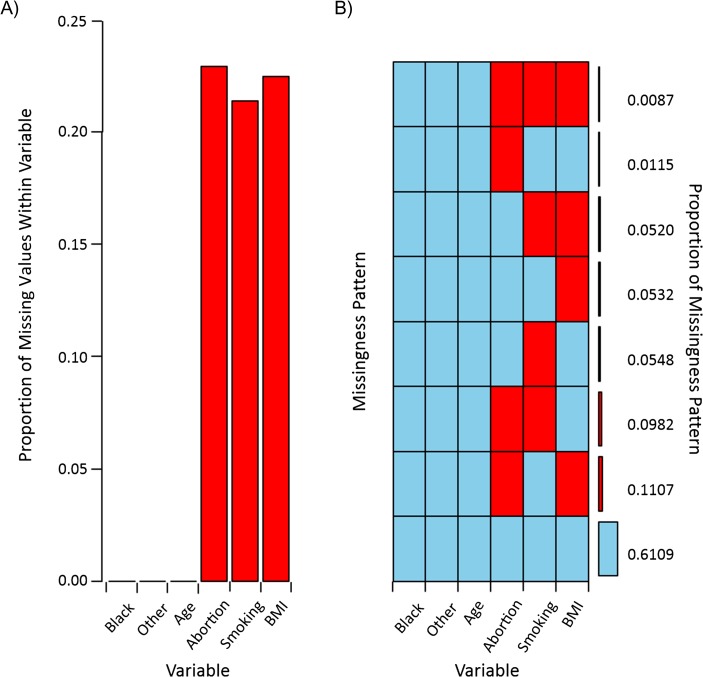
Another useful visualization is the aggregate missingness displayed in Figure 2 (a representation similar to that of Table 3 in Perkins et al. (7)). Figure 2A shows the proportion of missing values for each variable, while Figure 2B shows the missing-data patterns (red represents missing data and blue represents observed data), with the proportion of subjects within each pattern. This figure can identify the most common pattern of missingness, which may facilitate speculation on why missingness may be occurring for certain patterns more frequently. The cumulative missingness across variables illuminates the detriment of running a CCA. There may be a small proportion of missing values for each variable individually, but excluding an observation due to a single missing value may drastically reduce the number of observations available due to the missing-data pattern. In this scenario, only 61% of subjects had all variables observed (all blue). This type of plot can also help identify whether the missingness pattern is monotone (i.e., there may be ordering of the variables such that observing the jth variable ensures that all variables k > j in the ordering are observed for all j (9)). In this figure, for instance, it is not monotone because the bottom 3 patterns indicate a necessary structure of observed, missing, and observed, missing, which does not fit the definition of a monotone pattern. Alternatively, a monotone missingness pattern would display a triangular-shaped pattern. A monotone missingness pattern can accelerate the imputation process because under a monotone structure, the Markov chain Monte Carlo (MCMC) procedure (27) is not needed, since there are closed forms for the posterior distributions. In the general case of parametric MI, the MCMC procedure is necessary for the imputation stage.

Figure 2.

Missingness patterns in data from the Collaborative Perinatal Project, 1959–1974. A) Proportion of total missingness; B) proportion of each missingness pattern. Red, missing values; blue, observed values. BMI, body mass index.

Another useful exploration of the data is to examine the covariate distribution for complete and incomplete cases. In Table 1, we summarize the descriptive statistics for study participants with complete data compared with those with incomplete data. The sample sizes for the variables in the table differ for the incomplete cases but are the same for the CCA, since conducting a CCA will reduce the sample to the smallest size across variables. Additional details on comprehensive preprocessing of data can be found elsewhere (28, 29).

Table 1.

Characteristics of Complete and Incomplete Cases in Each of 3 Data Sets From the Collaborative Perinatal Project, 1959–1974^a

Variable	Incomplete Cases			Complete Cases
	No. of Persons	Mean (SD)	Median	No. of Persons	Mean (SD)	Median
Data set 1
Black raceb	4,425	0.31 (0.46)	0	6,948	0.30 (0.46)	0
Other raceb	4,425	0.06 (0.24)	0	6,948	0.06 (0.24)	0
Age, years	4,425	25.73 (6.00)	25.0	6,948	24.87 (5.75)	24.0
Abortion	1,819	0.04 (0.21)	0	6,948	0.02 (0.14)	0
Smoking	1,995	0.26 (0.44)	0	6,948	0.26 (0.44)	0
BMIc	1,871	22.88 (4.42)	21.9	6,948	22.45 (3.92)	22.0
Data set 2
Black raceb	4,285	0.31 (0.46)	0	7,088	0.30 (0.46)	0
Other raceb	4,285	0.06 (0.24)	0	7,088	0.06 (0.24)	0
Age, years	4,285	25.12 (5.85)	24.0	7,088	25.26 (5.87)	24.0
Abortion	1,748	0.04 (0.20)	0	7,088	0.03 (0.18)	0
Smoking	1,894	0.24 (0.43)	0	7,088	0.26 (0.44)	0
BMI	1,821	22.50 (3.97)	21.6	7,088	22.61 (4.14)	21.8
Data set 3
Black raceb	5,361	0.32 (0.47)	0	6,012	0.30 (0.46)	0
Other raceb	5,361	0.06 (0.24)	0	6,012	0.06 (0.24)	0
Age, years	5,361	25.21 (5.83)	24.0	6,012	25.2 (5.89)	24.0
Abortion	2,283	0.10 (0.30)	0	6,012	0.01 (0.11)	0
Smoking	2,017	0.26 (0.44)	0	6,012	0.28 (0.45)	0
BMI	2,515	22.68 (3.98)	21.7	6,012	22.51 (3.98)	21.7

Abbreviations: BMI, body mass index; SD, standard deviation.

^a Data were obtained from Perkins et al. (7). Values are proportions unless otherwise indicated.

^b Represents a complete variable.

^c Weight (kg)/height (m)².

STATISTICAL METHODS

Generally, MI consists of 3 steps. First, m imputed data sets are generated based on the chosen imputation strategy (e.g., normal model, MICE, predictive mean matching). Next, each imputed data set (now a complete data set) is analyzed based on the desired statistical model, such as logistic regression. Finally, the results from each of the m imputed data sets are combined to obtain a final estimate of the parameter of interest (e.g., log odds ratio) and its standard error.

Imputation step

The goal of MI is to estimate parameters of interest based on the full data set (Y), which might not be fully observed. Here Y is shorthand notation for the entire set of data including the outcome, the exposure of interest, confounders, and any other auxiliary variables. When data are incomplete, the imputation step leverages existing relationships between variables in the observed data (Y_obs), to impute the missing data (Y_mis), where Y = (Y_mis, Y_obs). Missing values are imputed from the conditional distribution of the missing data given the observed data. This first step is often the most difficult, because it requires specification of an imputation model, which includes specification of the conditional distribution for each variable. If the number of variables in the data set is not prohibitive, all of them could be used in the imputation model. Alternatively, we would prioritize all variables related to the primary and secondary analyses in addition to variables related to the missingness.

For this analysis, we focus on parametric MI based on a multivariate joint normal distribution. Under this assumption of joint normality, drawing from the conditional distribution of the missing data given the observed data is equivalent to drawing from a joint normal distribution. In this data set, it is clear that the assumption of joint normality does not hold (e.g., spontaneous abortion is a binary variable). However, MI is robust to this assumption when the data set is large and the rates of missing information are small (10). For these analyses, imputed binary variables were rounded to 0 or 1 (based on a cutoff of 0.5) after imputation.

When choosing which variables to include in each imputation model, it is important that the imputation models contain at least all the variables in the analysis model, and preferably more (30). Although not available for this exercise, additional auxiliary variables that are predictive of the missing data can inform the imputation procedure even when they are not considered as predictors in the analysis model. Since we do not know the true missingness mechanism, we use the same model across the 3 data sets, expecting (asymptotically) unbiased estimates for the MAR and MCAR data sets, and perhaps reduced bias (relative to the CCA) for the MNAR data set. Sensitivity analyses using different imputation models or procedures that consider the missingness process unknown can help assess the robustness of the chosen imputation procedure (31, 32).

The imputation process for our example is composed of 2 distinct steps. First, an expectation-maximization (EM) algorithm (33) is applied to calculate starting values for the mean of each variable, as well as a covariance matrix characterizing the correlations between the variables in the assumed joint normal distribution. Although this first step could be bypassed by choosing random starting values for the mean and variance matrix, the starting values calculated by the EM algorithm can improve convergence of the second component of the MI. In addition, the EM algorithm provides information about the convergence of the procedure, which can be used to estimate the convergence speed of the subsequent MCMC procedure. This step can be achieved by specifying the “EM” statement in PROC MI in SAS, or in R by using the “norm” package (34) (see the Web Appendix, available at https://academic.oup.com/aje, for example code).

The second step of the imputation procedure applies an MCMC process using a data augmentation method, prior to imputing the m values for each missing value. In the MCMC procedure, we simulate draws of Y_(mis), μ, and Σ from their joint posterior distribution given Y_(obs). Given the current random draws Y^(t)_(mis), μ^(t), and Σ^(t), we first draw, for instance, the “smoke” variable given all observed data and the parameters (μ and Σ) using the conditional normal distribution with mean

$$\begin{array}{c}E(\mathrm{Smoke})={\hat{\mathrm{\gamma }}}_0+{\hat{\mathrm{\gamma }}}_1\text{Race}:\text{black}+{\hat{\mathrm{\gamma }}}_3\text{Race}:\text{other}\hfill \\ +{\hat{\mathrm{\gamma }}}_4\mathrm{Age}+{\hat{\mathrm{\gamma }}}_5\mathrm{BMI}+{\hat{\mathrm{\gamma }}}_6\mathrm{Abort},\hfill \end{array}$$

where $\stackrel{\mathbf{ˆ}}{\mathbf{\gamma }}$ is initially estimated via the EM step and then iteratively estimated in the imputation step (I-step) of data augmentation. We then estimate the parameters of the normal distribution (μ and Σ) in the posterior step (P-step). Repeating the I-step and P-step many times generates a sequence of random draws from the data and its parameters. This data augmentation portion of the imputation step can be specified using the NITER option in the MCMC statement of PROC MI or using the “norm” package in R (34). In all analyses, we used the default normal-inverse Wishart prior distribution. Each run of the data augmentation algorithm produces a single imputed data set for use in the standard statistical analysis. This entire imputation procedure, including the EM step and the data augmentation step, is performed m times to produce the m imputed data sets. More details about the imputation process can be found elsewhere (4, 9, 10, 28, 29).

Analysis model

Once the m imputed data sets have been created, the analysis step is straightforward. The model is the same model we would use if we had complete data. In this case, the model of interest is a logistic regression model with spontaneous abortion as the binary outcome and smoking status as the exposure of interest, adjusting for race, age, and BMI:

$$\begin{array}{c}\mathrm{Logit}\left(P\left(\mathrm{Abort}=1\right)\right)={\mathrm{\beta }}_0+{\mathrm{\beta }}_1\mathrm{Smoke}+{\mathrm{\beta }}_2\text{Race}:\text{black}\hfill \\ +{\mathrm{\beta }}_3\text{Race}:\text{other}+{\mathrm{\beta }}_4\mathrm{Age}\hfill \\ +{\mathrm{\beta }}_5\mathrm{BMI}.\hfill \end{array}$$

Our main interest is the coefficient corresponding to the “smoke” variable (β₁). This model is applied to each of the m imputed (completed) data sets separately. Estimates and corresponding standard errors are stored to later be combined into a final result.

Combining results

Since we imputed the data m times (in our case, m = 100), we get 100 sets of estimates and their variances. We combine these results using Rubin’s rules (3) as follows: Let Q be the population quantity of interest and $\hat{Q}$ be its estimate, with estimated variance U. In the absence of $Y_{\mathrm{mis}}$, we have random versions or imputations, $Y_{\mathrm{mis}}^{(1)},\mathrm{\dots },Y_{\mathrm{mis}}^{(m)}$, from which we calculate the imputed-data estimates ${\hat{Q}}^{(j)}=\hat{Q}(Y_{\mathrm{obs}},Y_{\mathrm{mis}}^{(j)})$ and their estimated variances $U^{(j)}=U(Y_{\mathrm{obs}},Y_{\mathrm{mis}}^{(j)})$, $j=1,\mathrm{\dots },m$. The overall estimate of Q is $\overline{Q}=m^{-1}{\sum }^{}{\hat{Q}}^{(j)}$. To obtain a standard error for $\overline{Q}$, we calculate the between-imputation variance $B={(m-1)}^{-1}{\sum }^{}{({\hat{Q}}^{(j)}-\overline{Q})}^2$ and the within-imputation variance $\overline{U}=m^{-1}{\sum }^{}{U}^{(j)}$. B is essentially the variance of the 100 log odds ratio estimates, while U is the average of the 100 estimated variances. The estimated total variance is then $T=(1+m^{-1})B+\overline{U}$, and tests and confidence intervals are based on a Student’s t approximation $(\overline{Q}-Q)/\sqrt{T}~t_v$ with degrees of freedom

$$v^{-1}=\frac{1}{(m-1)}{\left[\frac{\left(1+m^{-1}\right)B}{T}\right]}^2.$$

Adjustments to the degrees of freedom are presented elsewhere (35–37) and are compared by Wagstaff and Harel (38). These combining equations and degrees of freedom are computed automatically in most statistical packages (39–41).

Another product of the MI combining rules is the estimate of the rate of missing information due to $Y_{\mathrm{mis}}$, $\hat{\mathrm{\lambda }}=B/(\overline{U}+B)$. This rate reflects the impact of the missingness on inference for a particular analytical model and does not tend to decrease as the number of imputations increases (3). A large value of this parameter indicates that the missing values contain a lot of information about the parameter of interest. Even if a variable has no missing values, its rate of missing information could still be nonzero, due to correlations with other predictors. Additional information about the rates of missing information and some extensions can be found elsewhere (42–44).

Assumptions

MI is a parametric procedure, since we make distributional assumptions about the data, similar to maximum likelihood (9) or Bayesian analysis (27). In our case, we assume that the data have a joint normal distribution and that the parameter of interest has a normal distribution, which holds in our case because we are interested in a regression coefficient, which is approximately normal in large samples (9).

Rubin (45) introduced concepts regarding how to find the minimum condition under which the missingness process does not need to be modeled (in likelihood or Bayes analyses)—in other words, when standard MI is valid. For that to occur, 2 assumptions must hold. First, the MAR or MCAR assumptions must be valid. Second, the parameter estimates used for imputation and those estimated in the analysis model must be independent (distinct). Together, these 2 assumptions imply ignorability, which means that the missingness model necessary under MNAR can be ignored and the observed data will be sufficient.

DATA ANALYSES: RESULTS

For each of the example data sets, the goal is to estimate the log odds ratio of the association between maternal smoking status and spontaneous abortion. In each analysis, we apply the same imputation procedures as outlined previously, where 100 imputed data sets were produced for each analysis.

Table 2 provides the summarized results from the 3 data sets, comparing CCA with MI after combining results from a separate logistic regression on each of the 100 imputed data sets into a single point estimate and confidence interval. Estimates of the log odds ratio, its standard deviation, its 95% confidence interval, and rates of missing information (λ) are reported.

Table 2.

Log Odds Ratio Estimates for Risk of Spontaneous Abortion According to Maternal Smoking During Pregnancy in Analyses Using Complete Cases and Multiple Imputation, Collaborative Perinatal Project, 1959–1974^a

Variable	Complete Case			Multiple Imputation
	Estimate	SE	95% CI	Estimate	SE	95% CI	λ
Data set 1
Intercept	−5.696	0.695	−7.06, −4.33	−5.201	0.390	−5.965, −4.437	0.157
Smoking	−0.853	0.401	−1.64, −0.07	0.262	0.158	−0.048, 0.571	0.348
Black race	0.565	0.233	0.11, 1.02	0.259	0.131	0.003, 0.515	0.059
Other race	−0.173	0.528	−1.21, 0.86	0.401	0.231	−0.052, 0.853	0.060
Age, years	0.052	0.018	0.02, 0.09	0.047	0.010	0.028, 0.066	0.083
BMIb	−0.007	0.028	−0.06, 0.05	0.011	0.016	−0.021, 0.043	0.287
Data set 2
Intercept	−4.954	0.403	−5.74, −4.16	−5.109	0.372	−5.838, −4.381	0.090
Smoking	0.331	0.140	0.06, 0.60	0.311	0.133	0.051, 0.571	0.144
Black race	0.319	0.140	0.04, 0.59	0.357	0.126	0.11, 0.604	0.050
Other race	0.338	0.258	−0.17, 0.84	0.346	0.232	−0.109, 0.801	0.044
Age	0.072	0.010	0.05, 0.09	0.064	0.009	0.046, 0.083	0.060
BMI	−0.018	0.016	−0.05, 0.01	−0.013	0.015	−0.043, 0.016	0.123
Data set 3
Intercept	−5.709	0.589	−6.86, −4.55	−5.208	0.430	−6.051, −4.364	0.187
Smoking	−0.069	0.265	−0.59, 0.45	0.133	0.172	−0.205, 0.471	0.350
Black race	0.390	0.210	−0.02, 0.80	0.233	0.141	−0.044, 0.509	0.053
Other race	0.649	0.325	0.01, 1.29	0.424	0.241	−0.048, 0.896	0.043
Age	0.057	0.015	0.03, 0.09	0.056	0.010	0.036, 0.077	0.072
BMI	0.004	0.023	−0.04, 0.05	−0.005	0.018	−0.041, 0.031	0.295

Abbreviations: BMI, body mass index; CI, confidence interval; SE, standard error.

^a Data were obtained from Perkins et al. (7).

^b Weight (kg)/height (m)².

Based on these results, the estimated odds of spontaneous abortion for women who smoke during pregnancy compared with those who do not are different depending on the analyzed data set. The log odds ratio estimates are 0.262 (95% confidence interval (CI): −0.05, 0.57) in data set 1, 0.311 (95% CI: 0.05, 0.57) in data set 2, and 0.133 (95% CI: −0.21, 0.47) in data set 3. Looking at the rates of missing information (Table 2), there is 35% missing information in data sets 1 and 3 but only 14% missing information in data set 2. It is important to remember that approximately 20% of observations on smoking are missing. This suggests that the model has more difficulty estimating the parameters in data sets 1 and 3 than in data set 2. These results emphasize the fact that inference based on multiply imputed data sets depends on the underlying missing-data mechanism.

Results from data set 2 indicate that women who smoke during pregnancy have 36% higher odds of spontaneous abortion (exp(0.311) = 1.36) than women who do not smoke during pregnancy. Results from data sets 1 and 3 showed similarly increased odds of spontaneous abortion among women who smoked during pregnancy, although this association was not statistically significant for these data sets. Note that under a CCA, the estimated coefficient can be almost entirely an artifact of the missing-data mechanism. For instance, in data set 1, the odds of spontaneous abortion actually appear to be lower for women who smoke during pregnancy. This result in particular highlights the importance of moving away from CCAs and towards principled methods for dealing with missing data, such as MI.

DISCUSSION

In this article, we treated all 3 data sets in the same manner. In practice, a researcher will have only 1 data set and may follow the steps above to analyze it using MI. While the variation of MI chosen to analyze a data set may not alter, it can be helpful to evaluate the missingness distribution and make the most reasonable assumption (MCAR, MAR, or MNAR). In particular, if data may be MNAR, we highly recommend sensitivity analyses to evaluate the impact of these assumptions (46).

Several common concerns remain when applying MI to missing data. For instance, one issue concerns how much missingness is too much, or at what point MI fails. Another related problem is the number of imputations needed (which increases as the amount of missing information increases). Unfortunately, there is no clear threshold that is generalizable across all settings, although some discussions on the topic are available (28, 42–44, 47, 48).

Another issue is whether to choose the MICE or multivariate normal approach. While robust to nonnormality, multivariate normal imputation is susceptible to imputing values that may not lie within the support of the variable being imputed (49). For instance, a binary variable may be imputed to have a value of 0.233 or −0.567. If this is the case for exposure variables, this discrepancy may not be a concern (50). However, for an outcome variable, it may be necessary to retain the original format (e.g., binary). In that case, MICE works well to retain missing variables on their original scale. However, since MICE imputations are not necessarily proper (28), rounding the imputed outcome and using the multivariate normal approach may be preferable when the data set is large and the rates of missing information are small (10). On the other hand, when imputing interaction terms, it is recommended to form the interaction term and then impute it directly, even if the resulting imputations do not match the multiple of the imputed individual terms (51).

When imputing longitudinal data or survival data, methods exist but can be more complicated. For longitudinal data, one strategy is to restructure the data into a wide format and run standard MI. Another approach is to use mixed-effect models using the PAN library in R, which was built for panel data.

In this article, we assumed that our imputation model was proper, meaning that the distribution from which the missing values were drawn was equivalent to a Bayesian posterior distribution (3). We also assumed that our model was congenial to the analysis model, such that the same variables in the analysis and imputation models were used (52). These assumptions are preferred but not required; in particular, one of the main advantages of MI over other missing-data procedures is the ability to use auxiliary variables in the imputation model that are related to the missingness process but are not needed for the analysis model. More discussion of the impact of proper imputations and congeniality can be found elsewhere (4, 53).

MI is a parametric approach to handling incomplete data which provides consistent estimates of parameters of interest under the ignorability assumptions. The evidence supporting the advantages of imputation procedures like MI is growing. Although CCA may appear to be the most straightforward, the possibility of bias due to informative missingness and possible remedies should be explored. With the increasing availability of imputation procedures in standard software packages, simple CCA should no longer be the norm for epidemiologic research.

Abbreviations

BMI

body mass index

CCA

complete-case analysis

CI

confidence interval

EM

expectation-maximization

MAR

missing at random

MCAR

missing completely at random

MCMC

Markov chain Monte Carlo

MI

multiple imputation

MICE

multiple imputation by chained equations

MNAR

missing not at random