Type- and Subtype-Specific Influenza Forecast

Abstract

Prediction of the growth and decline of infectious disease incidence has advanced considerably in recent years. As these forecasts improve, their public health utility should increase, particularly as interventions are developed that make explicit use of forecast information. It is the task of the research community to increase the content and improve the accuracy of these infectious disease predictions. Presently, operational real-time forecasts of total influenza incidence are produced at the municipal and state level in the United States. These forecasts are generated using ensemble simulations depicting local influenza transmission dynamics, which have been optimized prior to forecast with observations of influenza incidence and data assimilation methods. Here, we explore whether forecasts targeted to predict influenza by type and subtype during 2003–2015 in the United States were more or less accurate than forecasts targeted to predict total influenza incidence. We found that forecasts separated by type/subtype generally produced more accurate predictions and, when summed, produced more accurate predictions of total influenza incidence. These findings indicate that monitoring influenza by type and subtype not only provides more detailed observational content but supports more accurate forecasting. More accurate forecasting can help officials better respond to and plan for current and future influenza activity.

Local outbreaks of seasonal influenza are often associated with the elevated incidence of more than 1 cocirculating influenza type or subtype. Indeed, influenza vaccines are often trivalent or quadrivalent and may even be designed to confer protection against more than 1 strain of a single influenza type or subtype. For example, the quadrivalent version of the 2015–2016 seasonal influenza vaccine for the United States was designed to protect against A/California/7/2009(H1N1)pdm09-like virus, A/Switzerland/9715293/2013(H3N2)-like virus, B/Phuket/3073/2013-like virus, and B/Brisbane/60/2008-like virus (1). This strain composition includes 2 influenza A subtypes and 2 influenza type B strains.

While local influenza incidence often manifests from infections due to more than 1 type or subtype, it is most commonly estimated more crudely and in aggregate using influenza-like illness (ILI). ILI is a nonspecific diagnostic category defined by the Centers for Disease Control and Prevention as presentation with fever of ≥37.8°C, a cough or sore throat, and no determined causality other than influenza (2). In addition to ILI, many local and state health agencies and some hospitals carry out virological surveillance for influenza. Specimens from selected patients presenting with ILI are laboratory confirmed—commonly using a rapid influenza diagnostic test or reverse-transcription polymerase chain reaction (RT-PCR) molecular assay. These data provide a means for distinguishing influenza from infections due to other circulating respiratory viruses, such as coronaviruses and parainfluenza viruses.

A more specific estimate of influenza incidence can be developed by multiplying ILI by the concurrent fraction of specimens testing positive for influenza (3, 4). Our estimates extending this method are generated by multiplying municipal and state level ILI estimates by associated regional, weekly laboratory-confirmed influenza positive proportions as compiled through the National Respiratory and Enteric Virus Surveillance System and US-based World Health Organization Collaborating Laboratories (2); we term this metric ILI+. ILI+ provides a cleaner signal of influenza incidence and can be used to more precisely monitor influenza incidence and transmission. From a public health perspective, this greater resolution of infection allows better observation and more informed response. For example, by better defining influenza incidence in a local population, influenza antivirals and other influenza-targeted responses might be better supplied and more appropriately utilized.

Models of influenza also benefit from the use of a more influenza-specific metric such as ILI+. Infectious disease models are often designed to represent the propagation of a single pathogen through a population. Use of ILI or another nonspecific measure of influenza in conjunction with an influenza model provides a signal that is confounded by those other circulating respiratory viruses. Those additional signals potentially corrupt model behavior, undermine epidemiologic inference, and degrade generative forecasts. In our own work, we often use ILI+ rather than ILI to produce forecasts of influenza because it provides a cleaner signal of influenza incidence (4, 5).

Our group has been issuing real-time forecasts of influenza in the United States using ILI+ since the 2012–2013 season and posting these forecasts on a dedicated web portal (http://cpid.iri.columbia.edu/) since the 2013–2014 influenza season. Our forecasting approach uses a mathematical model-inference system in which a core compartmental model describing the propagation of influenza through a local population is optimized using data assimilation methods and real-time ILI+. The optimization is performed in order to constrain the model state variables and parameters to best represent the local outbreak as it has thus far manifested. The central idea is that if the model can represent the outbreak as thus far observed, model-simulated forecasts will be more likely to represent future epidemic trajectories (4, 6–9).

While ILI+ discriminates between influenza and other respiratory viruses, it still often represents an amalgamated signal of more than 1 cocirculating influenza virus type or subtype. In the present study, we explored whether further decomposition of the ILI+ metric into its constituent type and subtype signals improves forecast accuracy. We used the laboratory-confirmed influenza positive rates separated by type and subtype to create type- and subtype-specific estimates of influenza incidence. We then used these data to optimize type-specific and subtype-specific model simulations and generate retrospective type-specific and subtype-specific forecasts. We demonstrated that this further discrimination and representation of influenza activity generally improves model forecast accuracy.

METHODS

We generated retrospective weekly municipal forecasts for 95 cities and 50 states in the United States during the 2003–2004 through 2014–2015 influenza seasons. Due to the 2009 pandemic influenza outbreak, the 2008–2009 and 2009–2010 seasons were excluded from this analysis. Descriptions of the observations, models, data assimilation methods, and analysis conducted are provided below.

Influenza incidence data

Forecasts and analyses were generated at the state and municipal levels for the United States. State and municipal estimates of ILI were obtained from Google Flu Trends (10, 11). Previously, we have generated more specific estimates of influenza incidence by multiplying the weekly Google Flu Trends ILI estimates by regional weekly laboratory-confirmed influenza positive proportions from the Department of Health and Human Services as compiled through the National Respiratory and Enteric Virus Surveillance System and US-based World Health Organization Collaborating Laboratories (2). This combined metric, ILI+, provides a more specific measure of influenza incidence that removes much of the signal due to other cocirculating respiratory viruses (3, 4).

The influenza positive proportions are additionally discriminated by type and subtype: influenza A/H1N1, A/H3N2, and B. A weekly average of 651 samples were tested in each Health and Human Services region during the study period, yielding robust estimates of positive proportions. We used this information to generate type- and subtype-specific incidence estimates, termed hereafter H1N1+, H3N2+, and B+. As in the case of ILI+, we multiplied the weekly Health and Human Services regional positive proportion for each type or subtype by an associated state or municipal weekly ILI estimate to generate an influenza type- or subtype-specific incidence estimate.

For type A influenza, there were often many samples in the National Respiratory and Enteric Virus Surveillance System and US-based World Health Organization Collaborating Laboratories record for which subtyping was either not performed or not able to be performed. Rather than omit these data, we instead apportioned them among A subtypes in a ratio consistent with subtyped samples for that week. If, for instance, in a given Health and Human Service region and week, 180 samples were positive for H1N1, 20 samples were positive for H3N2, and 30 samples were not subtyped, those 30 samples would be distributed in a 9 to 1 ratio between H1N1 and H3N2, such that the adjusted estimates become 207 samples positive for H1N1 and 23 samples positive for H3N2. Those adjusted estimates would then be divided by the total number of specimens tested and multiplied by within-region state and municipal Google Flu Trends ILI estimates for that week to generate H1N1+ and H3N2+ estimates.

Epidemiologic models

Four different models were used to generate forecasts. All 4 forms are perfectly-mixed, absolute humidity–driven compartmental constructs with the following designations: 1) susceptible-infectious-recovered (SIR); 2) susceptible-infectious-recovered-susceptible (SIRS); 3) susceptible-exposed-infectious-recovered (SEIR); and 4) susceptible-exposed-infectious-recovered-susceptible (SEIRS). The differences among the model forms align with whether waning immunity (which allows recovered individuals to return to the susceptible class) or an explicit period of latent infection (the exposed period) is represented.

Because the SEIRS model is the most detailed, we present it here. All other forms are derived by reduction of these equations, which are as follows:

$$\frac{dS}{dt}=\frac{N-S-E-I}{L}-\frac{\mathrm{\beta }(t)IS}{N}-\alpha ,$$ 1

$$\frac{dE}{dt}=\frac{\mathrm{\beta }(t)IS}{N}-\frac{E}{Z}+\alpha ,$$ 2

$$\frac{dI}{dt}=\frac{E}{Z}-\frac{I}{D},$$ 3

where S is the number of susceptible people in the population, t is time, N is the population size, E is the number of exposed people, I is the number of infectious people, N-S-E-I is the number of recovered individuals, β(t) is the contact rate at time t, L is the average duration of immunity, Z is the mean latent period, D is the mean infectious period, and α is the rate of travel-related importation of influenza virus into the model domain.

The contact rate, β(t), is given by β(t) = R₀(t) ÷ D, where R₀(t), the basic reproductive number, is the number of secondary infections the average infectious person would produce in a fully susceptible population at time t. Specific humidity, a measure of absolute humidity, modulates transmission rates within this model by altering R₀(t) through an exponential relationship similar to how absolute humidity has been shown to affect both survival and transmission of the influenza virus in laboratory experiments (12), specifically:

$$R_0(t)=R_{0\min }+(R_{0\max }-R_{0\min })e^{-aq(t)},$$ 4

where R_0min is the minimum daily basic reproductive number, R_0max is the maximum daily basic reproductive number, a = 180, and q(t) is the time-varying specific humidity. The value of a is estimated from the laboratory regression of influenza virus survival upon absolute humidity (13). Simulations were performed with fixed travel-related seeding of 0.1 infections per day (1 infection every 10 days).

The models used in this study were all perfectly mixed, had no age structure, and did not account for differential mixing or multiple modes of transmission. While including such processes might make the models more realistic, for the purposes of generating accurate forecasts, as well as for the present comparison, model parsimony rather than complexity is necessary. A higher-dimensional model with more features, such as age classes, cannot be as effectively optimized unless there are more abundant observations available. Because we did not have age-discriminated observations of incidence with which to validate the performance or forecasts of more complicated models, we built off prior work and used simpler, more parsimonious models.

Specific humidity data

Specific humidity data were compiled from the Phase 2 data set of the North American Land Data Assimilation System. These gridded data are available in hourly time steps on a 0.125° regular grid from 1979 through the present (14). Local specific humidity data for each of the 95 cities and 50 states included in these forecasts were assembled for 1979–2002 and averaged to daily resolution. A 1979–2002 (24-year) daily climatology, a 24-year average of specific-humidity conditions for each day of the year, was then constructed for each city and used as the daily specific-humidity forcing input (in equation 4) for all retrospective forecasts.

Data assimilation

Three ensemble filter methods—the ensemble Kalman filter (15, 16), the ensemble adjustment Kalman filter (17), and the rank histogram filter (18)—were used in conjunction with influenza incidence data to optimize the compartmental models prior to forecast. All ensemble filter simulations were run with 300 ensemble members.

The ensemble filter algorithms were used iteratively to update ensemble model simulations of observed state variables (influenza incidence) to better align with observations (ILI+). These updates were calculated upon halting the ensemble integration at each new observation, per the specifics of each filter algorithm, as described below. Cross-ensemble covariability was used for all 3 filters to adjust both the unobserved state variables and model parameters (4, 6, 17). The posterior was then integrated to the next observation and the process was repeated. Through this iterative updating process, the ensemble of simulations provided an estimate of the observed state variable (i.e., influenza incidence), as well as the unobserved variables and parameters (e.g., susceptibility and mean infectious period).

Additional description of the filters is provided in the Web Appendix 1 (available at http://aje.oxfordjournals.org/). Further details on the application of the ensemble filters to infectious disease models are provided in Shaman and Karspeck (6) and Yang et al. (7). For information on scaling of observations to modeled incidence, see Web Appendix 1.

Forecasts

The recursive updating of model state variables and parameters, carried out by the filtering process, was meant to align these characteristics to better match the observed epidemic trajectory of influenza incidence. The premise is that if the model can be optimized to represent incidence as thus far observed, it stands a better chance of generating a forecast consistent with future conditions.

In practice for each city and season, we initiated our model simulations and data assimilation on week 40 of the calendar year. Each week, the ensemble of simulations was updated using a given filter. For weeks 45–64 of each flu season, following assimilation of the latest ILI+, H1N1+, H3N2+, or B+ observation, the posterior ensemble was integrated into the future to generate a forecast for the remainder of the season. All 12 combinations of the 4 models (SIR, SIRS, SEIR, SEIRS) and 3 filters were used to generate separate forecasts of ILI+, H1N1+, H3N2+, and B+.

Initial parameter values for all runs were chosen randomly from the following uniform ranges: R_0max ~ U[1.3, 4]; R_0min ~ U[0.8, 1.2]; Z ~ U[1,5] in days; D ~ U[1.5, 7] in days; L ~ U[1,10] in years. Initial state variable values—E(0), I(0) and S(0)—were chosen randomly from the week 40 state values generated through 10,000 multiyear free simulations of the compartmental models. For all runs the population size, N, was 100,000. To account for the stochastic effects of the randomly chosen initial conditions, each model-filter combination was run 5 separate times for each location, thus generating 60 separate ensemble forecasts for each week and location. The mean trajectory of each of these 60 forecasts was then averaged to provide a single average forecast. Findings were then further verified through analysis of forecasts segregated by model and/or filter.

Analysis of accuracy

Two types of analysis were conducted. The first assessed accuracy among different respective observed outcomes (specific type/subtype vs. ILI+). That is, forecasts generated for H1N1+, H3N2+, or B+ incidence were evaluated for accuracy against H1N1+, H3N2+, or B+ observations, respectively, for the period of forecast. Similarly, forecasts for ILI+ incidence were evaluated for accuracy against ILI+ observations for the period of forecast. The accuracy of forecasts of the dominant type/subtype was then compared with that of the ILI+ forecasts.

The second analysis compared forecast accuracy with the same ILI+ outcome. For this evaluation, the accuracy of ILI+ predictions made following optimization with ILI+ was compared with the summed predictions of H1N1+, H3N2+ and B+. Inclusion in the latter summation required that a type/subtype comprise at least 5% of total incidence for a given locality during each of the 3 weeks prior to the forecast. Consequently, for the second analysis, some comparisons were between predictions made with ILI+ and only the dominant type/subtype (when the other type/subtypes were each <5%), whereas others added the predictions for 2 or more types/subtypes.

For each of these analyses, we assessed the accuracy of predictions of peak timing and peak magnitude using absolute error—the absolute value of “predicted” minus “observed.” In addition we calculated the root mean square error (RMSE) of forecast trajectories 2, 4, and 8 weeks into the future. For the first analysis, the prediction of different targets (e.g., ILI+ vs. H3N2+) complicated the comparison of peak magnitude prediction error and forecast trajectory RMSE, because observed ILI+ incidence is generally larger than that of any single type/subtype. To account for this difference, we scaled ILI+ peak magnitude prediction error and RMSE values by the fraction made up by the observed dominant type/subtype. We also calculated the fraction of peak timing forecasts that were accurate within 1 week (before or after) and the fraction of peak-intensity forecasts that were accurate within 25% (above or below) of the observed magnitude.

For all analyses, lead time was defined as the week of forecast initiation minus the week of the simulated ensemble mean trajectory peak. Negative values correspond to forecast of a future peak—for example, −4 indicates outbreak peak incidence is forecast to occur 4 weeks in the future. We used the Wilcoxon signed-rank test to determine whether the forecasts generated using the dominant type/subtype and summing approach significantly improved accuracy over the ILI+ forecasts.

RESULTS

Optimization with and prediction of the dominant type/subtype

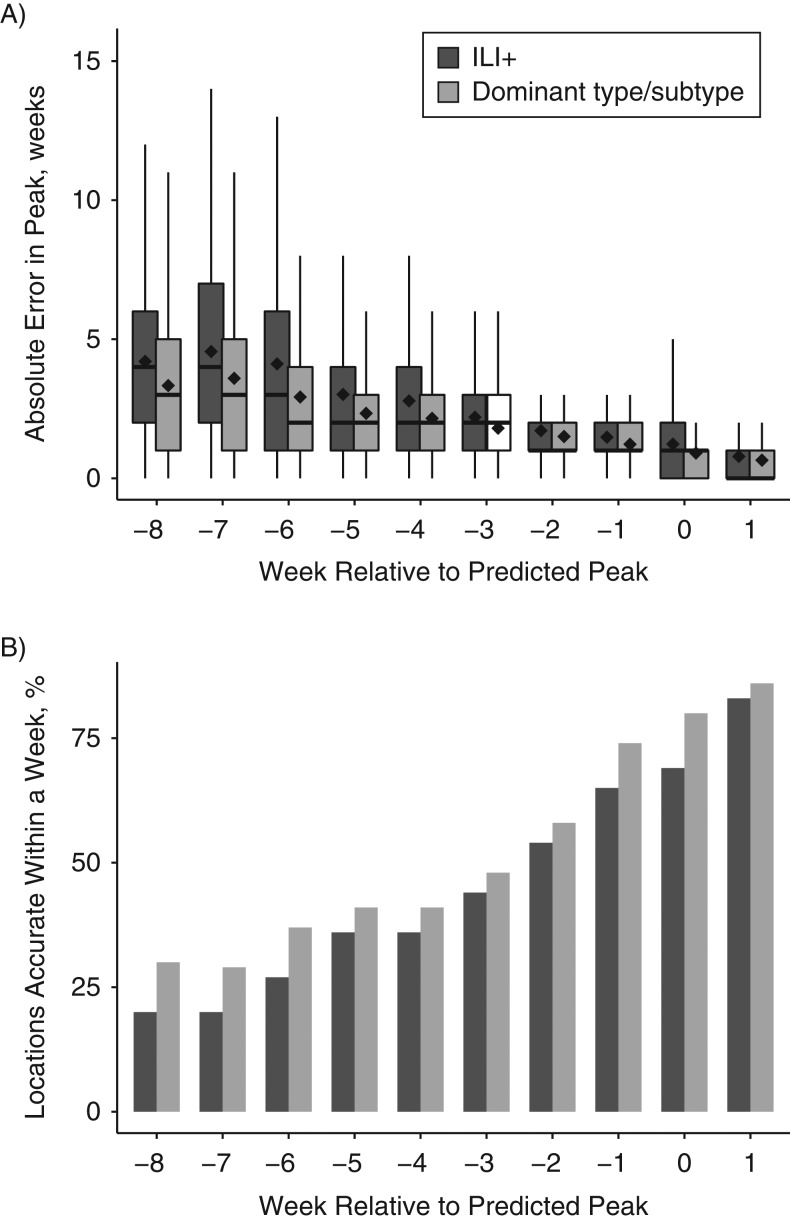
For peak-week timing, specific predictions of the dominant type or subtype in a given locality and week yielded lower error than those optimized and targeted to ILI+ (Figure 1A). That is, predictions of individual type/subtype (H1N1+, H3N2+, B+) peak timing were on average more accurate at all lead times than predictions of ILI+ peak timing. This advantage was most pronounced at longer leads. Across all seasons and leads, forecast error was reduced on average by 0.419 weeks (P < 0.001). This finding held when stratified by filter type (Web Figure 1) or model form (Web Figure 2). Indeed, all 3 filters and all 4 model forms demonstrated a statistically significant reduction of error when optimizing and targeting the dominant locally circulating type/subtype (P < 0.001).

Figure 1.

Accuracy of the prediction of peak-week timing for influenza, evaluated for all 95 cities and 50 states, all 10 seasons, and all 12 model-filter combinations, United States, 2003–2015. A) Box and whisker plots show the median (thick horizontal line), 25th and 75th percentiles (the bottom and top extent of the box), and extrema (the whiskers) of the absolute error of peak-week timing predictions. The black diamonds indicate the mean absolute error for each box and whisker. Error at all leads was significantly lower (P < 0.05) for optimization with and prediction of the dominant local type/subtype (i.e., H1N1, H3N2, or B). B) Fraction of forecast peaks accurate within 1 week of the observed peak. Accuracy at leads −8, −7, −6, −1, 0, and 1 was significantly higher (P < 0.05) for the optimization with and prediction of the dominant local type/subtype. The predictions are stratified by forecast lead. Negative values indicate mean trajectory forecast of a future peak; positive values indicate mean trajectory forecast that the peak has passed. ILI+, optimization with and prediction of influenza-like illness estimates multiplied by regional weekly laboratory-confirmed influenza positive proportions.

As an alternate metric, we often quantify the fraction of peak-week forecasts that are accurate within 1 week of the observed peak. Across all locations, years, and model filter combinations, optimization with and prediction of the dominant type/subtype provided a greater fraction of accurate peak-week predictions than forecasts generated and targeting ILI+ (Figure 1B).

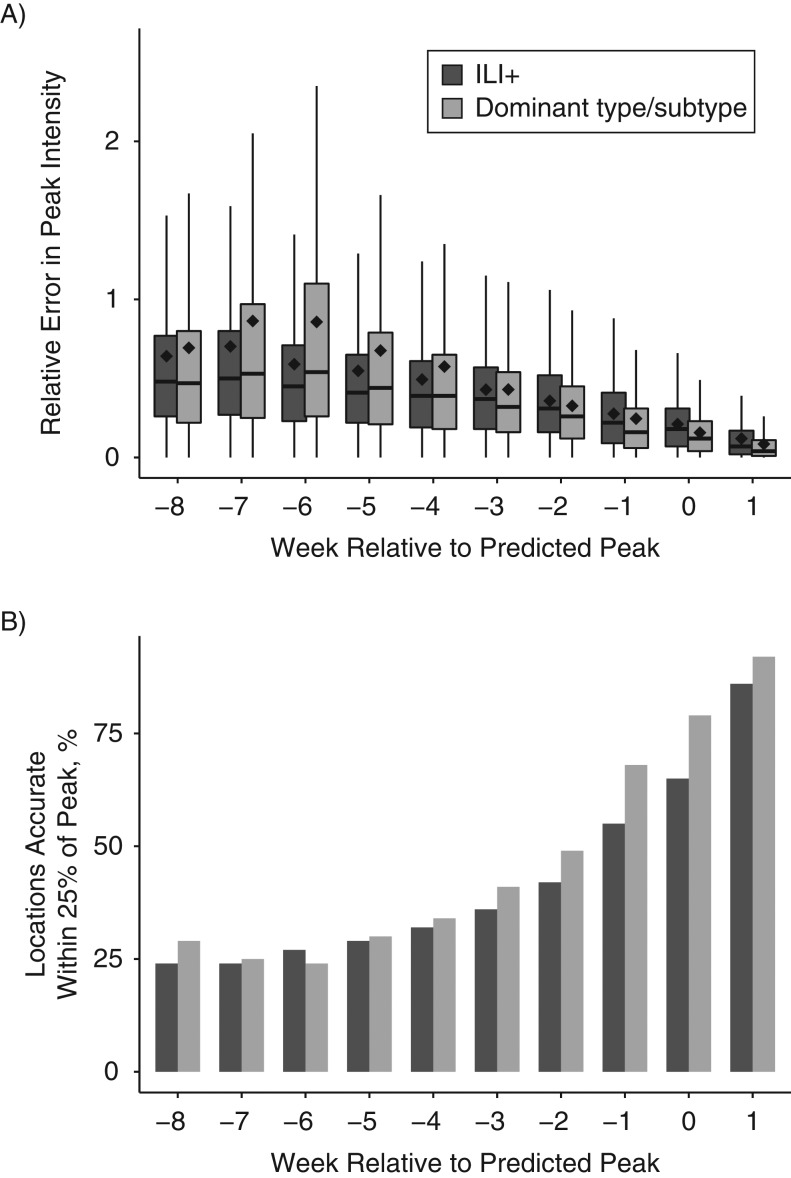
For peak intensity, specific predictions of the dominant type or subtype yielded lower error than those optimized and targeted to ILI+ for short leads (−3 to +1 weeks, Figure 2A); at leads of −5 to −7 weeks, forecasts targeted to ILI+ had significantly lower error. Similar to peak-week timing, we often quantify the accuracy of a peak-intensity forecast by using the fraction of forecasts accurate within 25% of the observed peak magnitude (Figure 2B). For this metric, the forecasts optimized to and predicting the dominant type/subtype produced a larger fraction accurate within 25% of the observed peak magnitude than the forecasts optimized to and predicting ILI+ for all leads but one (−6 weeks lead), and they were statistically significant for leads −2 to +1 weeks. Similar findings were evident when the forecasts were stratified by filter or model type (Web Figures 3 and 4).

Figure 2.

Accuracy of the prediction of peak intensity for influenza, evaluated for all 95 cities and 50 states, all 10 seasons, and all 12 model-filter combinations, United States, 2003–2015. A) Relative error of predictions stratified by forecast lead. Error at leads −3, −2, −1, 0, and 1 was significantly lower (P < 0.05) for the optimization with and prediction of the dominant local type/subtype (i.e., H1N1, H3N2, or B), whereas error at leads −7, −6, and −5 was significantly lower (P < 0.05) for the optimization with and prediction of influenza-like illness estimates multiplied by regional weekly laboratory-confirmed influenza positive proportions (ILI+). B) The fraction of forecasts accurate within 25% of the observed peak magnitude. Accuracy at leads −2, −1, 0, and 1 was significantly higher (P < 0.05) for the optimization with and prediction of the dominant local type/subtype.

Prediction of ILI+

We next examined forecast accuracy with respect to the same observed ILI+ target. Forecasts made using 1 or more types/subtypes (summed) had RMSE over the following 2, 4, and 8 weeks that was statistically equivalent to or lower than predictions made following optimization with ILI+ (Table 1). For example, when the peak was predicted to be 2–4 weeks in the future, RMSE over the next 4 weeks was lower for the summed forecasts (Web Figure 5).

Table 1.

Influenza Forecast Accuracy^a by Type and Subtype, United States, 2003–2015

	All Summed Forecastsb	Dominant Type/Subtype Onlyc	≥2 Types/Subtypesd
RMSE 2 weeks	18.86	NSe	18.03
RMSE 4 weeks	NSe	NSe	NSe
RMSE 8 weeks	NSe	NSe	NSe
Peak week correct	15.28	NSe	15.07
Peak week error	15.79	NSe	15.58
Peak intensity correct	16.61	13.02	16.24
Peak intensity error	18.89	NSe	17.98

Abbreviations: ILI, influenza-like illness; RMSE, root mean square error.

^a Wilcoxon signed-rank test (a measure of the distance of the median difference in errors from zero) comparing predictions of optimized influenza-like illness estimates (ILI+) made following model training with ILI+ to predictions of ILI+ made as the sum of optimized predictions specific to type/subtype (H1N1, H3N2, and/or B). All numbers indicate lower error for the summed forecasts. Predictions are compared for all 95 cities and 50 states in the United States, all 10 seasons (2003–2015, excluding pandemic outbreaks), and all 12 model-filter combinations.

^b Differences over all forecasts.

^c Differences for summed forecasts that used only the dominant type/subtype.

^d Differences for summed forecasts that used ≥2 types/subtypes.

^eP > 0.01.

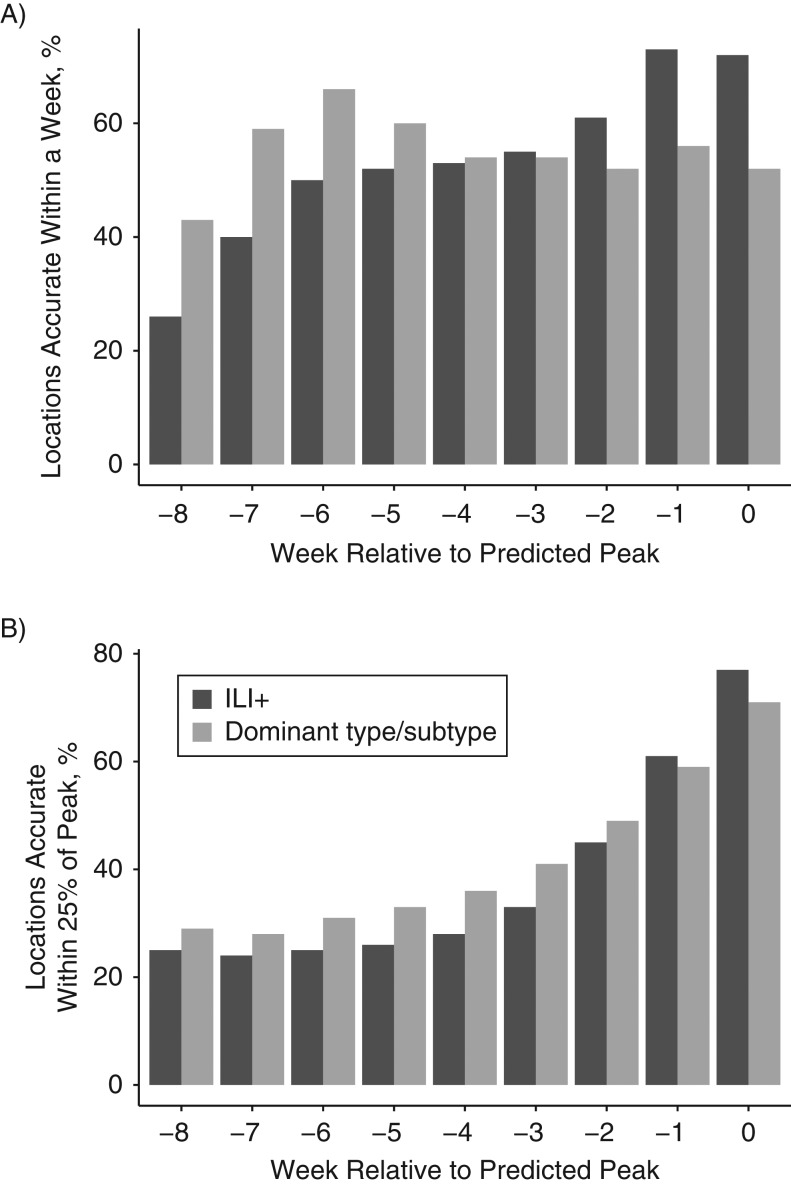
Longer-lead forecasts of both peak timing and peak intensity were improved when individual type/subtype forecasts were summed. Indeed, the fraction of peak-timing forecasts accurate within 1 week was significantly higher for −5- to −8-week lead summed predictions (Figure 3). Similarly, the fraction of peak-intensity forecasts accurate within 25% of the observed peak magnitude was higher for the −2- to −8-week lead summed predictions, and significantly higher for −3- to −5-week leads. However, for both metrics the ILI+ predictions were significantly more accurate at shorter lead times (−2 to 0 weeks for peak timing; 0 weeks for peak intensity).

Figure 3.

Accuracy of peak timing forecasts for influenza, comparing optimized influenza-like illness estimates (ILI+) with summed type/subtype-specific estimates, United States, 2003–2015. A) Fraction of peak timing forecasts accurate within 1 week of the observed ILI+ peak. Forecasts are stratified by lead. Negative values indicate mean trajectory forecast of a future peak; positive values indicate mean trajectory forecast that the peak has passed. Accuracy at leads −8, −7, −6, and −5 was significantly higher (P < 0.05) for the summed forecasts, whereas accuracy at leads −2, −1, and 0 was significantly higher (P < 0.05) for the ILI+ forecasts. B) Fraction of peak-intensity forecasts accurate within 25% of the observed ILI+ peak magnitude. Accuracy at leads −5, −4, and −3 was significantly higher (P < 0.05) for the summed forecasts, whereas accuracy at lead 0 was significantly higher (P < 0.05) for the ILI+ forecasts.

We also examined how the differences between ILI+ and summed prediction accuracy changed across seasons and among cities versus states. Significant improvement of forecast accuracy was evident in some seasons (2007−2008, 2010−2011, 2011−2012, and 2012−2013) but not in others (Web Table 1). In addition, at both the city and state level a similar pattern of improved accuracy was evident (Web Table 2).

Parameter estimates

We have previously used the SIRS model in conjunction with data assimilation methods and ILI+ estimates of incidence in the United States to infer critical epidemiologic parameters associated with influenza transmission dynamics (19). While not the principal focus of this study, we found similar estimates for the SIR, SEIR, and SEIRS models additionally used here (Web Figures 6–8). Indeed, the parameters are quite plausible. The mean infectious period, D, was estimated to be approximately 4.75 days for the SIR and SIRS models (lower during large H3N2 outbreaks), and slightly lower for the SEIR and SEIRS models, and overall matched well with published challenge-study estimates of viral-shedding duration (20). The effective reproductive number, R_e, maximizes between 1.3 and 1.8, depending on the season, dominant type/subtype, and model. It tends to be higher for H3N2 and the SEIR and SEIRS models (Web Figure 7). The basic reproductive number falls between 2.4 and 2.8 for all models (Web Figure 8).

DISCUSSION

The choice and use of a particular metric for monitoring and forecasting infectious disease incidence should be dictated by the informational content and public health relevance of that metric. As the cost of laboratory confirmation of influenza infection decreases and the ease and rapidity of these assays increases, these data will become more abundant and available at localized scales. We argue that this more plentiful identification of circulating influenza virus by type and subtype, and ultimately by strain, will provide an important, richer picture of influenza activity. Monitoring and forecasting this incidence will enable better targeting of type- or subtype-specific interventions, many of which likely have yet to be designed.

Our first analysis showed that prediction of peak week and intensity by influenza type and subtype was generally more accurate than optimization with and prediction of ILI+. Our second analysis showed that for longer lead times, the peak timing and intensity of ILI+ was more accurately predicted using the sum of separate type and subtype forecasts than with forecast using a single model following optimization with ILI+. Overall, these findings indicated that type- and subtype-specific forecasts can be used to predict both type- and subtype-specific incidence as well as the aggregate ILI+ signal. In the future, if testing resolution and ease improve so that strain-specific typing is provided abundantly, accurate strain-specific forecasts should be possible.

It is not surprising that the type- and subtype-specific forecasts generally outperformed those made using ILI+. Our compartmental models are designed to represent the transmission of a single pathogen in a local population. As data are pared to be more reflective of a single strain, removing the signal of other cocirculating influenza types and subtypes, the observations are more in line with model dynamics, and model simulation and forecast accuracy should improve. In the future, the forecasts might be improved further if the observations can also capture asymptomatic and mild infection incidence on a per capita basis.

Some specific features of the findings remain to be resolved. The summed forecasts significantly outperformed the ILI+ forecasts at longer lead times but not once the peak was predicted to be near (Figure 3). It may be that near the predicted peak, the aggregate ILI+ signal is pronounced enough to produce a better forecast and that the combined uncertainty of the individual type/subtype forecasts compounds when summed to generate a less accurate prediction. For peak intensity, the dominant type/subtype forecasts generally outperform ILI+ (Figure 2); however, there are some longer-lead exceptions (e.g., lead of −6 weeks). We do not know whether these exceptions reflect a real underlying process or are merely a statistical anomaly.

The use of type- and subtype-specific observations does not resolve certain issues associated with model misspecification. The compartmental models used here are highly idealized, perfectly mixed constructs representing a single pathogen. Cross-protection between cocirculating types, subtypes, or strains is not accounted for in these models and may be a source of simulation and forecast error. All seasons included in this study had at least 2 types/subtypes in circulation, and the years with significant improvement (Web Table 1) had either H3N2 and B or all 3 types/subtypes in circulation. Clearly, independent forecast of each of these types/subtypes can be summed to produce a more accurate forecast of future ILI+ at certain leads; however, there may be interactions among circulating types/subtypes, which, if represented, might improve forecast accuracy further. An alternate approach might use a single model construct depicting multiple cocirculating types/subtypes. The data assimilation and observations might then be used to estimate levels of cross-protection among the simulated types/subtypes. Such a forecast construct needs to be developed and tested.

The effects of other features, such as the school calendar and age-specific contact patterns, also need to be incorporated into the core dynamic models and tested for their impact on forecast accuracy. Inclusion of such effects is a logical next step for determining whether such increased model complexity improves prediction further; however, for some of these features, richer more detailed observations may be required. As more dynamical features are represented and the observations needed to constrain such simulations become available, forecast accuracy should continue to improve. An analogous continual improvement of forecast accuracy has been observed over many decades for numerical weather prediction (21).

Overall, the results indicated that our current methods are generally more accurate for generating type/subtype specific forecasts. Such information provides a richer palette of information for public health officials and will allow them to better track, respond to, and plan for current and future influenza activity by type and subtype as well as in aggregate.