Application of an Individual-Based Transmission Hazard Model for Estimation of Influenza Vaccine Effectiveness in a Household Cohort

Abstract

Household cohort studies are an important design for the study of respiratory virus transmission. Inferences from these studies can be improved through the use of mechanistic models to account for household structure and risk as an alternative to traditional regression models. We adapted a previously described individual-based transmission hazard (TH) model and assessed its utility for analyzing data from a household cohort maintained in part for study of influenza vaccine effectiveness (VE). Households with ≥4 individuals, including ≥2 children <18 years of age, were enrolled and followed during the 2010–2011 influenza season. VE was estimated in both TH and Cox proportional hazards (PH) models. For each individual, TH models estimated hazards of infection from the community and each infected household contact. Influenza A(H3N2) infection was laboratory-confirmed in 58 (4%) subjects. VE estimates from both models were similarly low overall (Cox PH: 20%, 95% confidence interval: −57, 59; TH: 27%, 95% credible interval: −23, 58) and highest for children <9 years of age (Cox PH: 40%, 95% confidence interval: −49, 76; TH: 52%, 95% credible interval: 7, 75). VE estimates were robust to model choice, although the ability of the TH model to accurately describe transmission of influenza presents continued opportunity for analyses.

Household studies were extensively used in the 1960s and 1970s to study acute respiratory illnesses (ARIs) such as influenza (1). Data from the classic household studies of ARI carried out in past decades have been used to inform models used to evaluate influenza pandemic mitigation strategies (2, 3). However, these studies were limited by their ability to determine illness etiology; typically, influenza infections were defined by rises in antibody titer observed between serum specimens bracketing the influenza season. The development of real-time, reverse-transcription polymerase chain reaction methods has allowed for more comprehensive identification of illness etiology again making household studies attractive for the study of ARI.

Modern household studies of influenza are generally based on one of two designs: cohort or case-ascertained (4). In the case-ascertained design, index cases are identified and enrolled when they seek medical care for ARI associated with laboratory-confirmed influenza. Household contacts of the index case are enrolled and followed for identification of any resulting secondary infections. Household cohort studies, by contrast, typically enroll households prior to the influenza season with subsequent prospective follow-up for identification of ARI. Case-ascertained studies are the more efficient design for studying transmission because influenza has been introduced in each household under study; however, bias may be introduced by selecting index cases with more severe illness requiring medical attention (4, 5). Although more resource intensive, household cohort studies are able to evaluate interventions affecting both primary introduction from the community and secondary household infection, and they are able to carry out evaluations requiring prospective follow-up, such as collection of serologic specimens to determine preseason susceptibility and vaccine response (6–8).

Since 2010, we have maintained a cohort of households with children with the objective of estimating annual influenza vaccine effectiveness (VE) (6–8) and examining the transmission of influenza (9) and other respiratory viruses (10). However, previous assessments of VE in preventing household-acquired influenza may have been limited by not accounting for increasing risk of infection as household contacts become infected. To address this potential limitation, it is necessary to explicitly model, for each individual, the risk of infection from the community and from each infected household contact.

Previous models accounting for household structure have estimated risks of influenza infection from the community and the household using the final number of serologically defined infections at the end of the epidemic (11, 12). However, these models ignore the potentially important information in timing of infections (e.g., a long duration between 2 infections within a household may indicate that the second infection was more likely to have been acquired from the community than within the household). Illnesses can now be reported more rapidly than in the past, and current laboratory methods allow rapid, accurate diagnosis. These data and modern computational resources now make it possible to build models considering not only the number but also the timing of infections. Cauchemez et al. (13, 14) have developed an individual-based transmission hazard (TH) model for the analysis of household data that includes timing of illness onset. This model, and similar extensions, have previously been applied only to data from case-ascertained household studies to estimate risks of community and household infection, measure the association between viral shedding and infectivity, and assess antibody titers as correlates of protection (13–16). However, this class of models has not been previously been applied to household cohort data, which require different assumptions in the model structure particularly with regards to community transmission.

We evaluated a new TH model for use in household cohort studies, based on those previously used in case-ascertained studies (13–16), and compared VE estimated in TH models to that estimated in Cox proportional hazards (PH) models using data collected during the 2010–2011 influenza season. We also demonstrated the predictive value of the model by simulating community- and household-acquired infections under varying levels of hypothetical VE.

METHODS

Study subjects and data

As previously described (6), households with ≥4 persons, with ≥2 children <18 years of age, receiving primary care from a University of Michigan Health System provider were invited to participate via direct mail prior to the 2010–2011 influenza season. Interested households attended an enrollment visit where adults provided informed consent for participation for themselves and their children (children aged 7–17 years also provided oral assent) and completed an enrollment interview. Influenza vaccination was documented in health system electronic medical records and the Michigan Care Improvement Registry. The presence of comorbid conditions that increase the risk of severe outcomes of influenza was also documented by electronic medical record (17). The study was approved by the institutional review board at the University of Michigan Medical School.

Respiratory illness surveillance and laboratory testing

Surveillance for detection of ARI was carried out from October 2010 through April 2011. Subjects were instructed at enrollment and via weekly email reminders to report all ARI with ≥2 of the following symptoms: cough, fever or feverishness, nasal congestion, chills, headache, body aches, or sore throat. Subjects with eligible illnesses were asked to attend an illness visit at the study site at the University of Michigan School of Public Health within 7 days from illness onset for collection of a throat swab, or a nasal swab for children <7 years of age, for identification of influenza virus.

Upper respiratory specimens collected from ill subjects were tested by reverse-transcription polymerase chain reaction in the investigators’ laboratory at the University of Michigan School of Public Health. Assays were performed using the testing protocol and primers and probes developed and provided by the Influenza Division of the Centers for Disease Control and Prevention. Primers and probes were designed for universal detection of influenza A and B viruses, and influenza A subtypes (pH1N1 and H3N2). Influenza A(H3N2) was the predominant circulating virus during the 2010–2011 season, though influenza A(pH1N1) and influenza B also circulated. Analyses here were limited to consideration of influenza A(H3N2) outcomes.

TH model

The TH model described in detail in Web Appendix 1 (available at https://academic.oup.com/aje) extends the work of Cauchemez et al. (13, 14) and Tsang et al. (15, 16) to examine VE in a prospectively followed cohort of households. The TH model computes the hazard for infection from the community for all individuals across the entire observed influenza season, and, separately, the hazard for infection from the each infected household contact for a 14-day period following the illness onset of the infected contact (Figure 1). The baseline community hazard varied with time and was defined by weekly counts of influenza cases reported to the Michigan Department of Health and Human Services Disease Surveillance System standardized to the peak week of activity (18). The baseline hazard of infection from the household was scaled using a probability distribution of the serial interval (time in days between symptom onset of prior and subsequent influenza cases in a chain of transmission) estimated as a Weibull function similar to previous models (14, 15). Model parameters were estimated in a Bayesian framework using Markov Chain Monte Carlo methods; convergence was visually assessed (Web Figure 1). Parameter identifiability was confirmed by examination of correlation plots (Web Figure 2).

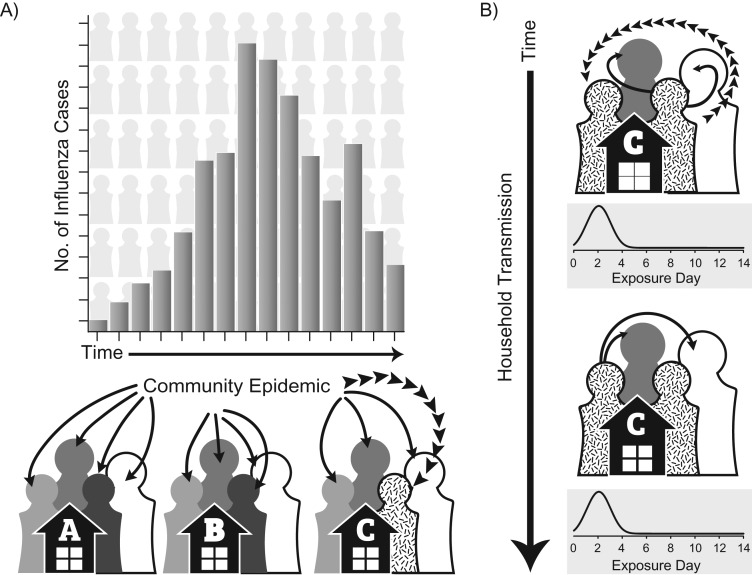
Figure 1.

Conceptual diagram of the individual-based transmission hazard model indicating hazard of infection from the community (A), and hazards of infection from infected household contacts (B). A) The hazard of influenza infection from the community is modeled for each individual household member for each day of the influenza season and is indicated by solid arrows. This hazard varies by time proportionally to weekly influenza cases reported to the Michigan Department of Health and Human Services Disease Surveillance System (18). Individual 3 from household C is infected from the community as indicated by broken arrows. B) The hazard of infection within the household is modeled for each individual in the household who is exposed to each infected household contact for a 14-day period beginning on the date of illness onset of the infected contact and is indicated by solid arrows. The hazard of infection within the household is proportional to a Weibull distribution representing the serial interval. Individual 1 from household C is infected by their infected household contact (individual 3) as indicated by broken arrows. The hazard of infection from individual 1 is then modeled for the remaining susceptible household contacts for an additional 14-day period. No additional infections are observed. All individuals, unless infected, remain at risk of infection from the community during these 14-day household exposure periods.

Statistical analyses

Associations between subject characteristics (e.g., age category, sex, race/ethnicity, high-risk health status) and vaccination status and influenza A(H3N2) infection status were assessed by χ² test.

The effectiveness of influenza vaccination in preventing laboratory-confirmed influenza A(H3N2) was estimated in TH models and in Cox PH models. Both Cox PH and TH models allowed vaccination status to vary by time, with subjects considered vaccinated 14 days following documented vaccine receipt, and were adjusted for age category and presence of ≥1 high-risk health condition documented in the electronic medical record. Robust variances were calculated for Cox PH model parameter estimates using sandwich estimators to account for correlation by household (19). VE was calculated as 100 × (1 − hazard ratio) for each model. VE specific to age group and infection source (community or household) was estimated in both Cox PH and TH models. Age group–specific VE was estimated by including terms for interaction (age group × vaccination) in each model.

For Cox PH analyses, community- and household-acquired infections were defined by their sequence of occurrence within the household (timing definition). Community-acquired influenza (household index cases) were defined as those subjects with the earliest date of symptom onset of laboratory-confirmed influenza in the household; subjects were considered co-index cases if more than 1 had illness onset on this first date of household introduction. Household-acquired influenza (secondary) cases were those with laboratory-confirmed influenza A(H3N2) with symptom onset ≤7 days following the onset of a household index case with influenza A(H3N2). Cox PH models estimating VE against community-acquired influenza A(H3N2) included all subjects; subjects with household-acquired influenza A(H3N2) were censored at the time of symptom onset. Cox PH models estimating VE against household-acquired influenza included only those household contacts of influenza A(H3N2) index cases with model time starting from the date of symptom onset of the index case.

For TH models, all subjects were considered at risk of infection from the community for the duration of the influenza season (even after influenza has been introduced to the household) or until the date of influenza A(H3N2) illness onset if they were infected. Subjects were also at risk of household-acquired infection from each influenza A(H3N2) infected household contact for a 14-day period following that contact’s date of illness onset. These two hazards were simultaneously estimated; specific VE estimates against community- and household-acquired influenza A(H3N2) were estimated by specifying separate parameters in each respective hazard function.

TH model simulations and comparisons

Based on the TH model parameter estimates, the community and household hazard functions were used to calculate daily risks of infection from the community and the household. Community- and household-acquired infections were then simulated stochastically based on these infection risks. Predictive simulations were also carried out to estimate the numbers of influenza infections expected if VE were 2 and 3 times higher than estimated. Simulations were run for 1,000 iterations, and median numbers of infections and 95% credible intervals were calculated from the distribution of simulation results.

Because VE estimation was the primary goal of this analysis, age and the presence of high-risk health conditions were included in the model as confounders. However, a secondary goal was to make predictions based on TH model simulations, and a model with fewer parameters might be more efficient while still making accurate predictions. For this reason, we compared the fit of the full model to alternative models with: 1) constant community hazard of transmission, 2) no effect of subject age on susceptibility, 3) no effect of high-risk health conditions on susceptibility, and 4) no effect of vaccination on susceptibility. Model fit was evaluated by the deviance information criterion (20) and a simulation-based χ² test comparing the number of community- and household-acquired influenza A(H3N2) infections observed in the data and predicted by each model (14, 15).

TH model analyses were carried out using R, version 3.1.0 (R Foundation for Statistical Computing, Vienna, Austria.). All other analyses were carried out using SAS, version 9.2 (SAS Institute, Inc., Cary, North Carolina). A P value <0.05, or 95% credible interval or 95% confidence interval not including the null, was considered to indicate statistical significance.

RESULTS

As previously reported, 1,441 individuals in 328 households were enrolled and followed for incident ARI (6). The average household size was 4.4 (range, 4–9) individuals. Among these participants, 58% were children <18 years of age, 11% had a high-risk condition documented in the electronic medical record, and 60% had a documented influenza vaccination for the 2010–2011 influenza season (Table 1). Children <9 years of age, those with high-risk conditions, and female participants were more likely to be vaccinated.

Table 1.

Participant Characteristics According to Documented Influenza Vaccination Status and Influenza A(H3N2) Case Status, Household Influenza Vaccine Effectiveness Study, Ann Arbor, Michigan, 2010–2011

Characteristic	All Subjectsa (n = 1,441)		Documented Influenza Vaccinationb,c (n = 864)		Influenza A(H3N2)-Positive Casesc (n = 58)
	No. of Individuals	%	No. of Individuals	%	No. of Individuals	%
Age category, years
<9	468	32.5	322	68.8d	32	6.8d
9–17	371	25.7	224	60.4	8	2.2
≥18	602	41.8	318	52.8	18	3.0
Race/ethnicity
White	1,097	76.1	660	60.2	46	4.2
Asian	120	8.3	81	67.5	4	3.3
Black	83	5.8	40	48.2	2	2.4
Other/unknown	141	9.8	83	58.9	6	4.3
Sex
Female	728	50.5	458	62.9e	25	3.4
Male	713	49.5	406	56.9	33	4.6
Documented high-risk health condition
Any	162	11.2	122	75.3d	6	3.7
None	1,279	88.8	742	58.0	52	4.1
Documented influenza vaccination
Yes	864	60.0			33	3.8
No	577	40.0			25	4.3

^a Denominator for percentages is all subjects (n = 1,441).

^b At least 1 dose of 2010–2011 influenza vaccine documented in the electronic medical record or state registry; vaccination must have occurred ≥14 days prior to illness onset for influenza A(H3N2) infected subjects.

^c Denominator for percentages is total subjects in the given characteristic row.

^d χ²P < 0.001.

^e χ²P < 0.05.

Overall, 130 influenza-associated ARIs were identified from January through April 2011, including 59 influenza A(H3N2), 44 influenza B, 26 influenza A(pH1N1), and 1 influenza B/A(pH1N1) coinfection. For simplicity, analyses were limited to influenza A(H3N2). One individual was laboratory-confirmed as positive for influenza A(H3N2) in 2 separate illnesses with reported onset of symptoms 32 days apart; only the first illness was considered here. Of the 58 influenza A(H3N2) infections, 41 were considered to be community-acquired by timing definition. Among these were 7 co-index cases (>1 case on first date of influenza introduction to a household); influenza A(H3N2) was introduced to 36 households, including 1 household with 2 separate introductions 39 days apart. Among 111 household contacts of those with community-acquired influenza A(H3N2), 17 household-acquired cases were identified by timing definition.

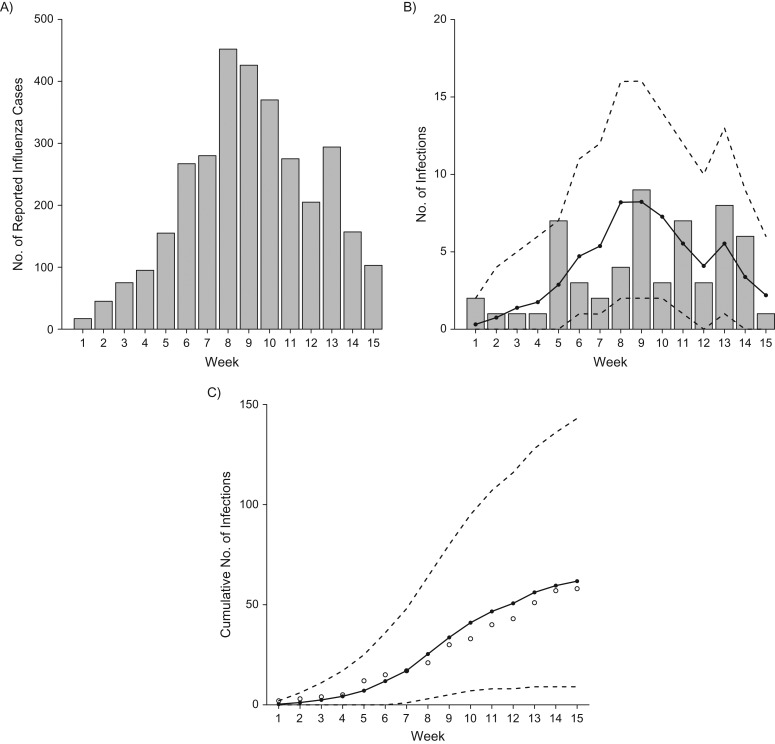
Overall, median numbers of influenza A(H3N2) cases predicted by the TH model were similar to those observed in the data, indicating good model fit (Table 2). The timing of influenza A(H3N2) cases during the influenza season as predicted by the TH model was also similar to the observed data (Figure 2). Numbers of predicted and observed cases were also similar by age group, high-risk status, and vaccination status. Infection risks were highest among children <9 years of age and similar by high-risk and vaccination status. Observed and predicted numbers of community- and household-acquired influenza cases were similar. Risk of infection from the household once influenza was introduced (15%) was approximately 5 times higher than risk of infection from the community (3%). Model simulations suggested that approximately one-sixth of household infections were the result of secondary cases infecting other susceptible household contacts (tertiary cases). Longer chains of transmission (i.e., quaternary cases) did not significantly contribute to the number of household-acquired infections predicted by the TH model.

Table 2.

Observed and Individual-Based Transmission Hazard Model–Predicted Influenza A(H3N2) Infections According to Infection Source, Age, Presence of High-Risk Health Condition, and Influenza Vaccination Status, Household Influenza Vaccine Effectiveness Study, Ann Arbor, Michigan, 2010–2011

Characteristic	Observed Data			TH Model Predictions
	No. of Cases(n = 58)	Total No. Exposed(n = 1,441)	% Positive	Median No. of Cases	95% CrI	% Positive	95% CrI	P Valuea
Community-acquired	41	1,441	2.8	43	31, 55	3.0	2.2, 3.8	0.70
Household-acquired	17	111	15.3	18	9, 30	13.2	6.6, 20.5
Secondary	N/O	N/O		15	7, 24
Tertiary	N/O	N/O		3	0, 9
Quaternary	N/O	N/O		0	0, 0
Age category, years								0.80
<9	32	468	6.8	36	22, 50	7.7	4.7, 10.7
9–17	8	371	2.2	8	3, 14	2.2	0.8, 3.8
≥18	18	602	3.0	18	9, 27	3.0	1.5, 4.5
Documented high-risk health condition								0.49
Any	6	162	3.7	5	1, 11	3.1	0.6, 6.8
None	52	1,279	4.1	56	38, 76	4.4	3.0, 5.9
Documented influenza vaccinationb								0.45
Yes	33	864	3.8	32	19, 48	3.7	2.2, 5.6
No	25	577	4.3	29	16, 44	5.0	2.8, 7.6
Overall model predictions				62	42, 82	4.3	2.9, 5.7

Abbreviations: CrI, credible interval; N/O, not observed; TH, transmission hazard.

^a Simulation-based χ² test.

^b At least 1 dose of 2010–2011 influenza vaccine documented in the electronic medical record or state registry; vaccination must have occurred ≥14 days prior to illness onset for influenza A(H3N2) infected subjects.

Figure 2.

Influenza infections during the 2010--2011 influenza season, Household Influenza Vaccine Effectiveness (HIVE) study, Ann Arbor, Michigan, 2010–2011. A) Total weekly influenza infections reported to the Michigan Department of Health and Human Services Disease Surveillance System; B) total weekly observed (gray bars) and predicted influenza A(H3N2) infections (solid line, with 95% credible interval indicated by dashed line) in the HIVE cohort; C) cumulative weekly observed (open circles) and predicted influenza A(H3N2) infections (solid line, with 95% credible interval indicated by dashed line) in the HIVE cohort.

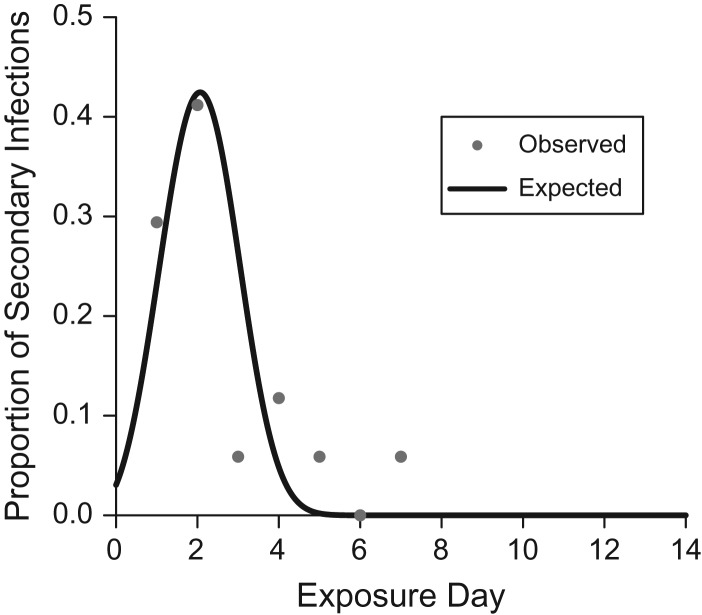
The serial-interval distribution estimated by the TH model is shown in Figure 3 with the observed distribution of serial intervals for household-acquired influenza A(H3N2) cases. The mean serial interval for influenza A(H3N2) estimated by the TH model (2.1, 95% credible interval (CrI): 1.5, 3.1) was similar to the mean serial interval calculated from the data (2.5, 95% confidence interval (CI): 1.8, 3.3).

Figure 3.

Observed and expected serial-interval distribution for household-acquired influenza A(H3N2), Household Influenza Vaccine Effectiveness study, Ann Arbor, Michigan, 2010–2011. The observed serial interval was defined as the days between illness onset in household index cases and subsequent illness onset in household contacts, not accounting for longer chains of transmission (e.g., tertiary cases).

Vaccine effectiveness

VE estimates derived from Cox PH models and TH models were generally similar overall, by age, and against community- and household-acquired influenza (Table 3). Overall VE against influenza A(H3N2) was not significant in either model (Cox PH: 20%, 95% CI: −57, 59; TH: 27%, 95% CrI: −23, 58). VE point estimates were highest for children <9 years of age in both models (Cox PH: 40%, 95% CI: −49, 76; TH: 52%, 95% CrI: 7, 75), and statistically significant in the TH model. VE point estimates for older children and adults were negative with very wide confidence intervals and credible intervals, indicating no evidence of VE. VE against household-acquired and community-acquired influenza did not significantly differ, although point estimates were higher against household-acquired influenza (Cox PH: 50%, 95% CI: −41, 82; TH: 45%, 95% CrI: −57, 80) than against community-acquired influenza (Cox PH: 16%, 95% CI: −65, 57; TH: 18%, 95% CrI: −53, 56).

Table 3.

Comparison of Vaccine Effectiveness Against Influenza A(H3N2) Estimated From Cox Proportional Hazards and Individual-Based Transmission Hazard Models, Household Influenza Vaccine Effectiveness Study, Ann Arbor, Michigan, 2010–2011

Risk Group	No. of Infected Individuals	Total No. of Individuals	%	Cox Proportional Hazards Model		Individual-Based TH Model
				VE, %a	95% CI	VE, %a	95% CrI
Overall A(H3N2)
All Ages	58	1,441	4.0	20.2	−56.6, 59.4	27.3	−23.0, 57.8
<9 years of age	32	468	6.8	39.9	−49.1, 75.8	51.5	7.2, 75.2
9–17 years of age	8	371	2.2	−10.5	−345.9, 72.6	−30.1	−617.7, 70.9
≥18 years of age	18	602	3.0	−13.2	−187.5, 55.4	−24.7	−247.5, 52.7
Community A(H3N2)	41	1,441	2.8	15.8	−65.4, 57.1	18.2	−52.5, 55.8
Household A(H3N2)	17	111	15.3	49.5	−41.3, 82.0	44.8	−56.5, 80.2

Abbreviations: CI, confidence interval; CrI, credible interval; TH, transmission hazard; VE, vaccine effectiveness.

^a VE was estimated via the hazard ratio in models that adjusted for age category (in years: <9, 9–17, ≥18) and presence of ≥1 high-risk health condition documented in the electronic medical record.

Model comparison

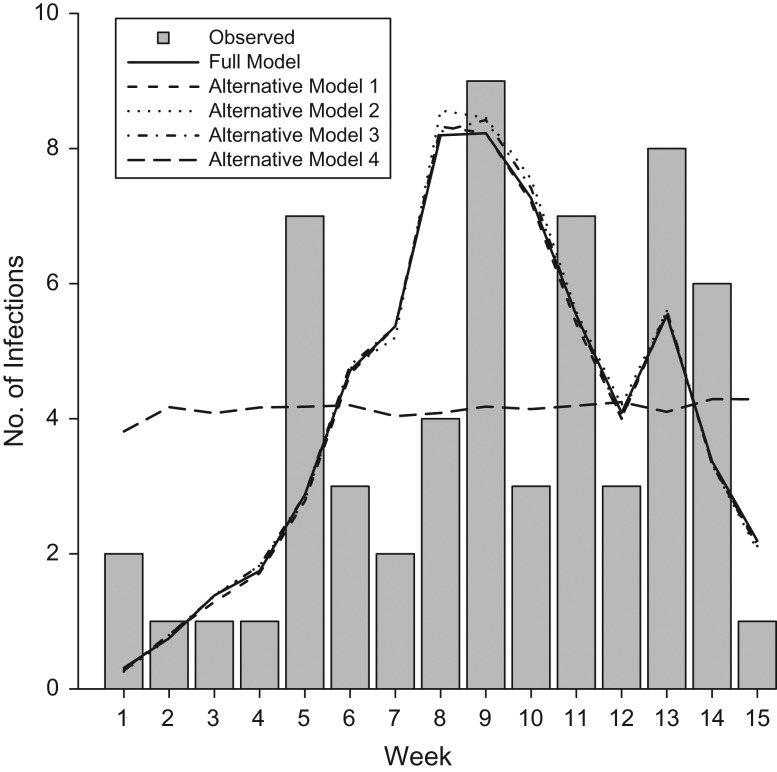
Parameter estimates from the full and alternative models (constant community hazard of transmission, no effect of subject age on susceptibility, no effect of high-risk health conditions on susceptibility, and no effect of vaccination on susceptibility) are presented in Web Table 1. All alternative models predicted similar final numbers of community- and household-acquired influenza A(H3N2) infections, which did not significantly differ from observed numbers of infections (Web Table 2). However, as expected, the alternative model with constant community hazard of transmission failed to accurately predict the timing of infections (Figure 4). The alternative models with constant community hazard of infection and without age terms resulted in the poorest model fit. Alternative models excluding high-risk health status and vaccination terms resulted in slightly better model fit.

Figure 4.

Weekly influenza A(H3N2) infection counts observed and expected under various model specifications, Household Influenza Vaccine Effectiveness study, Ann Arbor, Michigan, 2010–2011. The full model included covariate terms for age category (in years: <9, 9–17, ≥18), presence of ≥1 high-risk health condition documented in the electronic medical record, and time-varying vaccination status. Alternative model 1 is identical to the full model but with a constant hazard of infection from the community. Alternative model 2 is identical to the full model but excludes age-category covariates. Alternative model 3 is identical to the full model but excludes the high-risk health condition covariate. Alternative model 4 is identical to the full model but excludes the vaccination status covariate.

Model predictions

To demonstrate the value of the TH model for prediction, we ran simulations of the expected number of influenza A(H3N2) infections over time under varying VE. Epidemic curves generated by these simulations are plotted in Web Figure 3. As expected, the median number of predicted infections among the vaccinated decreased from 32 (95% CrI: 19, 47) to 18 (95% CrI: 10, 28) to 7 (95% CrI: 2, 13) when VE was increased by 2- and 3-fold (55% and 82%), respectively; predicted infections among the unvaccinated were similar in all models. Increasing VE by 2-fold reduced the number of community-acquired infections by 23% (95% CrI: 21, 26) and household-acquired infections by 28% (95% CrI: 23, 44). Similarly, increasing VE by 3-fold reduced community- and household-acquired infections by 42% (95% CrI: 39, 48) and 50% (95% CrI: 40, 67), respectively.

To validate the inferential framework, we also applied the Markov Chain Monte Carlo algorithm to simulated data to recover estimates of the model parameters. Nearly all recovered parameter estimates were similar to the parameters used to simulate the data, and credible intervals included the simulation parameters (Web Table 3). However, estimates of the α parameter, in particular, were systematically higher than those of the simulation parameter, and credible intervals were relatively wide. This could indicate some level of bias in the inferential framework; however, we would expect this bias to be limited to serial interval estimates given that estimates of the Weibull shape parameters defining the serial-interval probability distribution (α and γ) were not correlated with the estimates of other parameters (Web Figure 2). Further, the serial interval estimated by the TH model (2.1 days) was consistent with estimates using standard methods (2.5 days) and previously reported estimates (2.2 days) (21).

DISCUSSION

An individual’s risk of influenza infection increases as their close contacts become infected. This can result in violation of the assumption of independence for standard regression models and potentially bias results in unpredictable ways (22). Additionally, occurrences such as co-index cases and second introductions of influenza to a single household are difficult to handle with standard models and have traditionally been dealt with by exclusion (6–9). To examine the extent of these potential biases, we compared VE estimates from Cox PH models to those from a TH model that specifies household contact structures and transmission in a cohort of households with children.

VE estimates were similar for both Cox PH and TH models overall, and they followed similar patterns by age and against community- and household-acquired influenza. These findings indicate that previous published VE estimates were mainly robust to model choice (6). However, occurrences that would be expected to favor the TH model include co-index cases, second introductions of influenza, and a high proportion of household-acquired infections relative to community-acquired infections, and these factors were not observed in great numbers in the season studied here. In more severe influenza seasons, these situations may be expected to be more common, and differences in VE estimates could be larger.

Previously published estimates of VE in preventing community- and household-acquired influenza of any type from the 2010–2011 year in this study suggested that influenza vaccination was less effective in preventing household-acquired infections, although confidence intervals overlapped (6). Here, when analyses were limited to VE against influenza A(H3N2), differences were not statistically significant, but VE point estimates were higher for prevention of household-acquired infections. This apparent discrepancy is most likely due to chance given that there were relatively few household-acquired influenza outcomes. Differences in VE against community- and household-acquired influenza have not been observed in subsequent study years (7, 8).

The primary limitation of this analysis, and the household cohort design in general, is that costs associated with following a cohort often limit sample size and in turn statistical power. This is evident in the wide intervals around estimates reported here. This issue is exacerbated by recent low VE against influenza A(H3N2) (23–25), particularly in preventing influenza of any severity (6, 7). It should also be noted that influenza outcomes may have been missed even though households received weekly reminders to report ARI.

Although VE estimates from both models were similar, several advantages are associated with the TH model. One is the ability to estimate the serial-interval distribution accounting for continued community infection risk and chains of household transmission (26). Accurately determining the serial interval is important for informing the timing of interventions aimed at disrupting household transmission. Although estimates were similar (2.1 vs. 2.5 days), the slightly shorter serial interval estimated by the TH model is consistent with consideration of the small number of tertiary cases expected in the study population. The serial interval estimated for influenza A(H3N2) here is similar to previously reported estimates (21).

Another advantage of the TH model is its utility for prediction, which we illustrated as a proof of concept by simulating infections under varying VE. As expected, the number of predicted infections in the vaccinated group decreased as VE was increased. However, it is important to note that this simple demonstrative simulation did not account for any effects of increased VE on reducing the overall size of the outbreak in the community, which could have significant effects on the household model dynamics, reducing the number of cases among the unvaccinated as well. This could be achieved in future analyses by estimating the hazard of infection from the community with a compartmental model that considers vaccination in the broader community. Alternatively, the results of the simulation here could be thought of as evaluating an intervention applied only at the household level to reduce susceptibility, such as increased hand hygiene. So long as the household population considered was relatively small compared with the broader community (as is the case here), neglecting effects on the larger community dynamics may be a reasonable approximation.

The original TH model of Cauchemez et al. (13, 14) assumed constant hazard of influenza infection from the community, and sensitivity analyses indicated no change in parameter estimates using an exponentially growing community hazard. Tsang et al. (15, 16) extended the model to include a time-varying weekly proxy for the hazard of infection from the community; the degree to which this improved model fit was unclear. In this household cohort study—with follow-up over the entire influenza season and surveillance data for households where influenza was and was not introduced—a time-varying community hazard was essential. Models with constant community hazard resulted in worse fit and an inability to accurately predict the timing of influenza infections (Figure 4).

Although household cohorts lack the efficiency of case-ascertained studies, the design offers many advantages, including opportunities to follow and build similar TH models of households for multiple years to explore effects of previous vaccination and infection, to collect blood specimens for studies of antibody response to vaccination and infection, and to evaluate interventions affecting both primary introduction from the community and secondary household infection. Since 2010 we have been collecting these data prospectively as well as other information relevant to community and household exposures, such as providing care to ill household members and attendance at day care, school, and work attendance. The TH model is now another option in the toolbox for analysis of such data to further increase the value of the study.

Abbreviations

ARI

acute respiratory illness

CI

confidence interval

CrI

credible interval

PH

proportional hazards

TH

transmission hazard

VE

vaccine effectiveness