SNP interaction pattern identifier (SIPI): an intensive search for SNP–SNP interaction patterns

Abstract

Motivation: Testing SNP–SNP interactions is considered as a key for overcoming bottlenecks of genetic association studies. However, related statistical methods for testing SNP–SNP interactions are underdeveloped.

Results: We propose the SNP Interaction Pattern Identifier (SIPI), which tests 45 biologically meaningful interaction patterns for a binary outcome. SIPI takes non-hierarchical models, inheritance modes and mode coding direction into consideration. The simulation results show that SIPI has higher power than MDR (Multifactor Dimensionality Reduction), AA_Full, Geno_Full (full interaction model with additive or genotypic mode) and SNPassoc in detecting interactions. Applying SIPI to the prostate cancer PRACTICAL consortium data with approximately 21 000 patients, the four SNP pairs in EGFR-EGFR, EGFR-MMP16 and EGFR-CSF1 were found to be associated with prostate cancer aggressiveness with the exact or similar pattern in the discovery and validation sets. A similar match for external validation of SNP–SNP interaction studies is suggested. We demonstrated that SIPI not only searches for more meaningful interaction patterns but can also overcome the unstable nature of interaction patterns.

Availability and Implementation: The SIPI software is freely available at http://publichealth.lsuhsc.edu/LinSoftware/.

Contact: hlin1@lsuhsc.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

During the past decade, the genome-wide association studies (GWAS) have successfully identified many inherited genetic variants (or SNPs) associated with complex diseases, such as cancer or related phenotypes. However, the predictive power of cancer risk for the GWAS-identified SNPs is small by a median of 1.2 per-allele odds ratio (Ioannidis et al., 2010). The predictive power of these GWAS SNPs can be improved by combining multiple SNPs in a prediction model (Van den Broeck et al., 2014). We recently reported the polygenic genetic models to estimate their risk for prostate cancer (Al Olama et al., 2014; Amin Al Olama et al., 2015; Eeles et al., 2013). Despite these efforts, major proportion of familiar risk of prostate cancer remains unknown. The similar situation applies for using SNPs to predict prostate cancer prognosis (Van den Broeck et al., 2014). It is well known that biological associations among genes are complicated. The majority of GWAS focus on identification of individual SNP effects, which are not sufficient to explain the complexity of disease causality. It has been shown that gene–gene/SNP–SNP interactions play an important role in the etiology of complex diseases (Cordell, 2009; Moore, 2003; Moore and Williams, 2002; Onay et al., 2006). Although SNP–SNP or gene–gene interaction studies have been emerging, the statistical methods for evaluating SNP–SNP interactions are still underdeveloped.

The majority of genetic association studies focus on two-way interactions with two SNPs involved. In the past decade, various statistical methods have been proposed for evaluating two-way SNP–SNP interactions. These methods can be classified either model-based or pattern-based. The most common model-based approach tests an interaction based on a full interaction model (hierarchical model) with both main effects and their interaction and SNPs could be treated as different inheritance mode (such as additive, dominant, recessive and genotypic). Examples include the full interaction model in PLINK (Purcell et al., 2007), SNPassoc (Gonzalez et al., 2007) and the 2nd stage of the Boolean Operation-based Screening and Testing (BOOST) (Wan et al., 2010). For the model-based approaches, the impact of an interaction can be distinguished from the main effects, but the types of detectable interaction patterns are limited. In the pattern-based approach, interaction detection is based on risk patterns of the 3 × 3 genotype combination table of the two SNPs. The Hypothesis Free Clinical Cloning (HFCC) tests for 255 patterns for one SNP pair (Gayan et al., 2008), but some patterns may not be biologically meaningful or are rare. SNPmaxsel evaluates 16 interaction patterns and four main effects for a given SNP pair (Boulesteix et al., 2007). Multifactor dimensionality reduction (MDR) is also a pattern-based approach (Ritchie et al., 2001, 2003) to define based the best model based on classification accuracy. The strength of pattern-based approaches is that they are designed to detect wider range of interaction patterns. The limitation of the pattern-based approaches is that they search associations that allow for but are not limited to interactions. A significant result detected using the pattern-based approaches may be due to strong main effect without an interaction.

To overcome these weaknesses, we propose SNP Interaction Pattern Identifier (SIPI), which combines the advantages of the model-based and pattern-based approaches. Our approach can examine 45 interaction models that consider biologically meaningful factors. Each model has a straightforward corresponding pattern, and there is a formal statistical test for evaluating the interaction effect. This approach is powerful, and the identified patterns can be easily applied to assemble risk-prediction models. For evaluating the performance of SIPI, we conducted a simulation study to evaluate power and type I errors of SIPI with other four approaches: MDR, AA_Full, Geno_Full and SNPassoc. The details of these methods are listed in Section 2.2.

2 Methods

2.1 SNP interaction pattern identification (SIPI)

SIPI can intensively and effectively search pairwise SNP–SNP interactions. The conventional approach for identifying SNP–SNP interaction is to search a specific type of interaction using the full interaction model with the additive-additive mode based on the minor allele. The SIPI detects 45 interaction models, which take inheritance mode (both original and reverse coding), and risk category grouping (model structure) into consideration. The best interaction pattern is selected based on the Bayesian information criterion (BIC), which is used to deal with the trade-off between model fit and complexity of the model. BIC is also shown to be consistent in selecting the true model and tends to select a parsimonious model compared with the Akaike information criterion (AIC), especially in studies with a large sample size (Yang, 2005). The concept of SIPI can be applied to different types of outcomes, such as numeric, binary and time-to-event variables. In this study, we focused on the binary outcome using logistic regression models. The two primary components of SIPI are introduced separately below.

2.1.1 SNP inheritance modes

The SNP inheritance modes can impact on power to detect SNP interactions (Lin et al., 2008). We designate a lowercase letter ‘a’ to denote the minor (low frequency) allele, and an uppercase ‘A’ to denote the major (common) allele. Each SNP has three genotype categories: homozygous major type (‘AA’), heterozygous type (‘Aa’) and homozygous minor type (‘aa’). For a SNP, the inheritance mode for a disease risk refers to a specific relationship between genotype and phenotype. The inheritance modes include additive, dominant, recessive, genotypic and over-dominant modes. The dominant mode assumes that the impact of having one or two copies of a given allele on the outcome is the same, and the recessive mode implies that the subjects with the homozygous genotype of a given allele have a different risk to develop the outcome compared with the other two genotypes. Additive mode refers to the impact of each additional copy of a given allele on the outcome being equal. The genotypic mode, treats a SNP as a categorical variable with three groups, and assumes that each genotype has a distinct effect on risk. This genotypic mode needs four degrees of freedom for the interaction term itself, and interpretation of the result is not straightforward. The over-dominant mode, which assumes that heterozygote has a different risk than the other two homozygous genotypes (Aa versus AA/aa), is a rare case. Therefore, the SIPI takes three inheritance modes (dominant, recessive and additive) into consideration.

In the majority of genetic association studies, inheritance modes are defined based on the minor (or variant) allele. Under this scenario, the binary inheritance mode (dominant and recessive) is coded as ‘1’ for the group containing the homozygous minor type, and the other group as ‘0’ in modeling. For the AA, Aa and aa genotypes, the additive mode coding is 0, 1 and 2. The reverse coding (=1—original coding for dominant and recessive mode; and 2—original coding for additive mode) of inheritance mode is seldom to be considered in testing SNP–SNP interactions. The coding direction (original/reverse coding) of inheritance mode does not impact on statistical significance (P-values) for testing the main effect in a main-effect model and the interaction term in a full interaction model, but dramatically impacts testing the interaction term in a non-hierarchical interaction model. As shown in Table 1, there are six total possible coding methods for inheritance modes for each SNP. The three inheritance modes with the original coding based on the minor allele are additive (noted as aSNP1 for SNP1), dominant (dSNP1) and recessive (rSNP1). For the inheritance modes with the reverse coding, the three modes are reverse additive (raSNP1), reverse dominant (rdSNP1) and reverse recessive (rrSNP1).

Table 1.

SNP coding scheme of the inheritance modes

	Inheritance mode with original codingb			Reverse codingb
SNP1 Maj/Mina=A/a	Additive (aSNP1)	Dominant (dSNP1)	Recessive (rSNP1)	Reverse Additive (raSNP1)	Reverse Dominant (rdSNP1)	Reverse Recessive (rrSNP1)
AA	0	0	0	2	1	1
Aa	1	1	0	1	0	1
aa	2	1	1	0	0	0
Data type	Continuous	Binary	Binary	Continuous	Binary	Binary

^aMaj/Min= major/minor allele.

^bOriginal modes are based on a minor allele ‘a’; Reverse coding is (1—original coding) for the dominant and recessive mode and is (2—original coding) for the additive mode.

2.1.2 Risk category grouping/model structure

Both hierarchical and non-hierarchical interaction model were considered in this study. For evaluating 2-way interactions, the hierarchical or full interaction models are the models with two main effects and their interactions. This is the most common model type for testing pairwise SNP–SNP interactions, but this full model tests only one specific interaction pattern. Non-hierarchical models are defined as models with an interaction, and none or one main effects. In genetic association studies, non-hierarchical models, which combines genotypes with similar outcome risk are possible (Lin et al., 2008, 2013). Using non-hierarchical models, a parsimonious model based on risk profile can be generated; therefore power of detecting these specific interaction patterns increases (Piegorsch et al., 1994). As shown in Equations 1–4, four possible model structures for testing a two-way interaction include models with (i) two main effects plus an interaction (Full-int); (ii) the main effect of variable 1 plus an interaction (Main1 + int); (iii) the main effect of variable 2 plus an interaction (Main2 + int); and (iv) an interaction only (Int-only). It is worthy to note that the interaction only model for a SNP pair does not mean their main effects alone.

By considering a binary inheritance mode, there are four inheritance mode combinations (dominant–dominant, dominant–recessive, recessive–dominant and recessive–recessive). When treating SNPs as numeric variables, the additive-additive mode is taken into consideration. Thus, SIPI considers a total of five possible types of inheritance mode combinations. For each inheritance mode combination, there are nine unique interaction models/patterns when taking into consideration different model structures and inheritance modes (types and original/reverse coding direction). An example of coding direction impact on a recessive–dominant interaction model for a SNP pair in the prostate cancer study is listed in Table S1.Thus, a total of 45 interaction patterns are considered in SIPI for each SNP pair (Table 2).

Table 2.

List of 45 interaction models by considering the inheritance modes and model structures

SNP1 × SNP2 Inheritance modea	Model structureb	Model labelc	Model Details
Dom-Dom	Full-int	DD_Full	dSNP1 +	dSNP2 +	dSNP1 × dSNP2
	Main1+int	DD_M1_int_o1	dSNP1 +		dSNP1 × dSNP2
		DD_M1_int_r1	rdSNP1 +		rdSNP1 × dSNP2
	Main2+int	DD_M2_int_o2		dSNP2 +	dSNP1 × dSNP2
		DD_M2_int_r2		rdSNP2 +	dSNP1 × rdSNP2
	Int-only	DD_int_oo			dSNP1 × dSNP2
		DD_int_or			dSNP1 × rdSNP2
		DD_int_ro			rdSNP1 × dSNP2
		DD_int_rr			rdSNP1 × rdSNP2
Dom-Rec	Full-int	DR_Full	dSNP1 +	rSNP2 +	dSNP1 × rSNP2
	Main1+int	DR_M1_int_o1	dSNP1 +		dSNP1 × rSNP2
		DR_M1_int_r1	rdSNP1 +		rdSNP1 × rSNP2
	Main2+int	DR_M2_int_o2		rSNP2 +	dSNP1 × rSNP2
		DR_M2_int_r2		rrSNP2 +	dSNP1 × rrSNP2
	Int-only	DR_int_oo			dSNP1 × rSNP2
		DR_int_or			dSNP1 × rrSNP2
		DR_int_ro			rdSNP1 × rSNP2
		DR_int_rr			rdSNP1 × rrSNP2
Rec-Dom	Full-int	RD_Full	rSNP1 +	dSNP2 +	rSNP1 × dSNP2
	Main1+int	RD_M1_int_o1	rSNP1 +		rSNP1 × dSNP2
		RD_M1_int_r1	rrSNP1 +		rrSNP1 × dSNP2
	Main2+int	RD_M2_int_o2		dSNP2 +	rSNP1 × dSNP2
		RD_M2_int_r2		rdSNP2 +	rSNP1 × rdSNP2
	Int-only	RD_int_oo			rSNP1 × dSNP2
		RD_int_or			rSNP1 × rdSNP2
		RD_int_ro			rrSNP1 × dSNP2
		RD_int_rr			rrSNP1 × rdSNP2
Rec-Rec	Full-int	RR_Full	rSNP1 +	rSNP2 +	rSNP1 × rSNP2
	Main1+int	RR_M1_int_o1	rSNP1 +		rSNP1 × rSNP2
		RR_M1_int_r1	rrSNP1 +		rrSNP1 × rSNP2
	Main2+int	RR_M2_int_o2		rSNP2 +	rSNP1 × rSNP2
		RR_M2_int_r2		rrSNP2 +	rSNP1 × rrSNP2
	Int-only	RR_int_oo			rSNP1 × rSNP2
		RR_int_or			rSNP1 × rrSNP2
		RR_int_ro			rrSNP1 × rSNP2
		RR_int_rr			rrSNP1 × rrSNP2
Add_Add	Full-int	AA_Full	aSNP1 +	aSNP2 +	aSNP1 × aSNP2
	Main1+int	AA_M1_int_o1	aSNP1 +		aSNP1 × aSNP2
		AA_M1_int_r1	raSNP1 +		raSNP1 × aSNP2
	Main2+int	AA_M2_int_o2		aSNP2 +	aSNP1 × aSNP2
		AA_M2_int_r2		raSNP2 +	aSNP1 × raSNP2
	Int-only	AA_int_oo			aSNP1 × aSNP2
		AA_int_or			aSNP1 × raSNP2
		AA_int_ro			raSNP1 × aSNP2
		AA_int_rr			raSNP1 × raSNP2

^aDom: dominant, Rec: recessive, Add: additive.

^bFull-int: full interaction model with two main effects plus an interaction; Main1 + int: main effect of variable 1 plus an interaction; Main2 + int: main effect of variable 2 plus an interaction; and (4) Int-only: an interaction only.

^c_o₁, _r₁: minor allele (original coding), and reverse coding of SNP₁.

_o₂, _r₂: minor allele (original coding), and reverse coding of SNP₂.

_oo, _or, _ro, _rr: based on original-original, original-reverse, reverse-original and reverse-reverse coding for SNP1 and SNP2.

The best model among the 45 models is based on the lowest value of the Bayesian information criterion (BIC) (Schwarz, 1978). The significance of the interaction effect is tested using the Wald test of the interaction term (H0: β3 = 0). Although the likelihood ratio test (LRT) is usually recommended as the most powerful approach, it requires performing the two models one wishes to compare. The Wald test is similar to LRT in large scale studies and only one model needs to be estimated. In order to ease computation burden for high-dimensional data, the Wald test was primarily used in SIPI. In the SIPI R package, the users can choose to report P-values based on the Wald test or LRT. The Bonferroni method is applied to adjust for multiple comparisons.

Full interaction model (Full-int):

$$\text{logit}[\text{pr}(\mathrm{Y}=1)]={\beta }_0+{\beta }_1{\text{SNP}}_1+{\beta }_2{\text{SNP}}_2+{\beta }_3{\text{SNP}}_1\times {\text{SNP}}_2$$ (1)

Main 1+ interaction (Main1 + int):

$$\text{logit}[\text{pr}(\mathrm{Y}=1)]={ \beta }_0+{\beta }_1{\text{SNP}}_1+{\beta }_3{\text{SNP}}_1\times {\text{SNP}}_2$$ (2)

Main 2+ interaction (Main2 + int):

$$\text{logit}[\text{pr}(\mathrm{Y}=1)]={ \beta }_0+{\beta }_2{\text{SNP}}_2+{\beta }_3{\text{SNP}}_1\times {\text{SNP}}_2$$ (3)

Interaction only (Int-only):

$$\text{logit}[\text{pr}(\mathrm{Y}=1)]={ \beta }_0+{\beta }_3{\text{SNP}}_1\times {\text{SNP}}_2,$$ (4)

where Y is the binary outcome with a value of 0 or 1.

2.1.3 Translating interaction models to interaction patterns

By treating SNPs as binary variables (such as dominant or recessive), we can simplify genotype combinations from a three-by-three panel into a two-by-two panel, resulting in four possible sub-groupings. For the two-by-two panel, we can categorize the genotype combinations to 4-, 3- and 2-risk subgroups. As shown in Supplementary Figures S1 and S2, we can translate the interaction models to the corresponding genotype interaction patterns. The full-int model has 4 risk subgroups, the Main1 + int and Main2 + int models have 3 risk subgroups, and the Int-only model have 2 rsik subgroups. The non-hierarchical models have flexibility to combine genotype combinations with similar outcome risk. Our 45 model labels are based on a three-by-three table with an order of homozygous major, heterozygous and homozygous minor types (denote as AA, Aa and aa) and the homozygous major genotypes of the two SNPs as the top left corner.

2.2 Other approaches for SNP–SNP interactions

2.2.1 MDR

MDR (Ritchie et al., 2001, 2003) searches overall associations that allow for but are not limited to interactions. A promising MDR generates a binary risk variable (high/low risk) by comparing the case-to-control ratio in each genotype combination to a threshold and classifies each genotype to either a high risk set or low risk set. The best model is decided based on classification accuracy. The K-fold cross-validation is used to relieve over-fitting issue in MDR. The permutation testing (Motsinger-Reif, 2008) can be used to determine MDR overall significance (not just for an interaction). In this study, MDR with the 5-fold cross-validation and a permutation testing procedure (1000 randomized datasets) was performed. One major weakness of MDR is that its identified associations may be due to strong main effect without an interaction. Thus, another method for the MDR selected interaction is needed to distinguish the impact of main effects and interaction term.

2.2.2 AA_Full

The AA_Full [available in PLINK (Purcell et al., 2007)] approach uses a logistic regression model with both main effect and interaction. Each SNP is treated as an additive mode based on the minor allele. The significance test is evaluated using the Wald test of the interaction coefficient.

2.2.3 Geno_Full

The Geno_Full uses a full logistic regression model and each SNP is treated as a genotypic mode with two degrees of freedom. The significance test is evaluated using the likelihood ratio test of the interaction coefficient. This Geno_Full is equivalent to the 2^nd stage of BOOST (Wan et al., 2010), which uses the Kirkwood superposition approximation (KSA) is used to screen a subset of SNPs for the 2nd stage analyses.

2.2.4 SNPassoc

SNPassoc (Gonzalez et al., 2007) used the same full logistic regression and allows for five different inheritance modes [additive, dominant, recessive, genotypic and over-dominant (Aa versus AA/aa)] based on the minor allele. Two SNPs in the same pair are required to have the same inheritance mode.

2.3 Simulation

We conducted a simulation study to compare the power of SIPI with the conventional MDR, AA_Full, Geno_Full and SNPassoc approach for detecting two-way SNP–SNP interactions. For simulation settings, one SNP pair was considered. The two candidate SNPs were generated independently based on the Hardy-Weinberg equilibrium. Seven sets of a wide range of minor allele frequencies (MAF = 0.05–0.5) for SNP1 and SNP2 were investigated: (0.5, 0.3), (0.5, 0.2), (0.5, 0.05), (0.3, 0.3), (0.3, 0.1), (0.3, 0.05) and (0.1, 0.05). The sample sizes of 1000 and 5000 were chosen. All analyses were based on 1000 simulation runs.

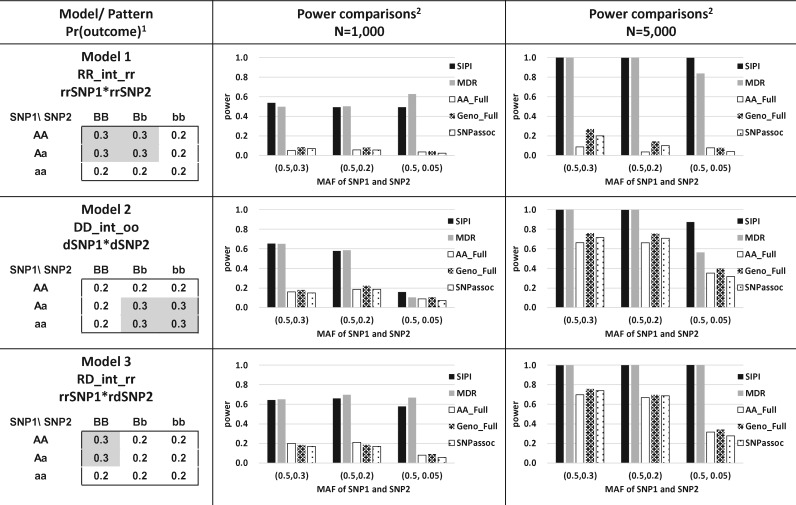
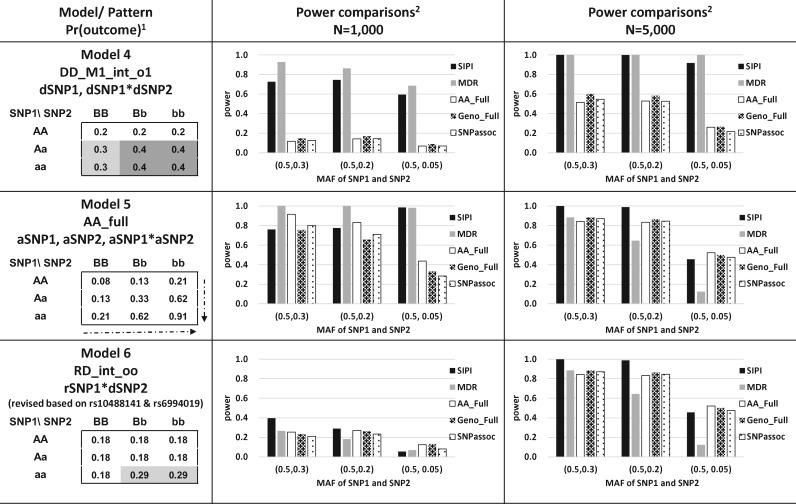
The binary outcome variable (such as case/control) was generated based on outcome prevalence (such as disease) in each genotype combination of the two given SNPs using multinomial distribution. We evaluated a total of six designed interaction patterns, including one real-data pattern (Figs 1 and 2). Most of these simulated models are based on the interaction patterns reported previously (Lin et al., 2012, 2013). One null model without a true interaction term was also tested. For the effect size of Models 1–4, the outcome prevalence was set to 0.3 or 0.4 in the high-risk subgroups and was 0.2 in the low-risk sub-groups. The corresponding odds ratio (OR) is 1.6 and 2.7, respectively. The settings of true interaction models are listed in Figures 1 and 2.

Fig. 1.

Power comparisons of the SNP Interaction Pattern Identifier (SIPI) and other four methods for Models 1–3. ¹Proportion of the outcome event in the genotype combination of the 3 × 3 table; a lowercase letter denotes the minor allele, and an uppercase letter denotes the major allele. ² MDR (Multifactor dimensionality reduction), AA_Full, Geno_Full (full interaction model and each SNP is treated as an additive or genotypic mode), and SNPassoc R package

Fig. 2.

Power comparisons of the SNP Interaction Pattern Identifier (SIPI) and other four methods for Models 4–6. ¹Proportion of the outcome event in the genotype combination of the 3 × 3 table; a lowercase letter denotes the minor allele, and an uppercase letter denotes the major allele. ² MDR (Multifactor dimensionality reduction), AA_Full, Geno_Full (full interaction model and each SNP is treated as an additive or genotypic mode) and SNPassoc R package

Models 1–3 were interaction-only models. For Model 1 (RR_int_rr pattern), both SNPs are considered as recessive with the reverse coding. The disease prevalence is 0.3 and 0.2 for the high- and low-risk groups, respectively. For Model 2 (DD_int_oo pattern), both SNPs are considered as dominant based on the minor alleles. In Model 3 (RD_int_rr), SNP1 is considered under a recessive mode, SNP2 is considered as dominant mode, and both SNPs have the reverse coding. Model 4 (DD_M1_int_o₁) includes the SNP1 main effect and an interaction, in which both SNPs are considered as dominant based on the minor allele of SNP1. The significance of the interaction term is the same regardless of the inheritance mode coding (original or reverse) for SNP2. Model 5 (AA_Full) is a full interaction model and both SNPs are treated as an additive mode based on the minor allele. This AA_Full model has the setting of ${\beta }_0=-2.5$ and ${\beta }_1={\beta }_2={\beta }_3=0.6$ in Eq. 1. Model 6 (RD_int_oo) was designed based on rs10488141 and rs6994019 from the PRACTICAL data (first SNP pair in Fig. 4) with an OR of 1.9. For the null model, the outcome prevalence of 0.2 was applied for all nine genotype combinations.

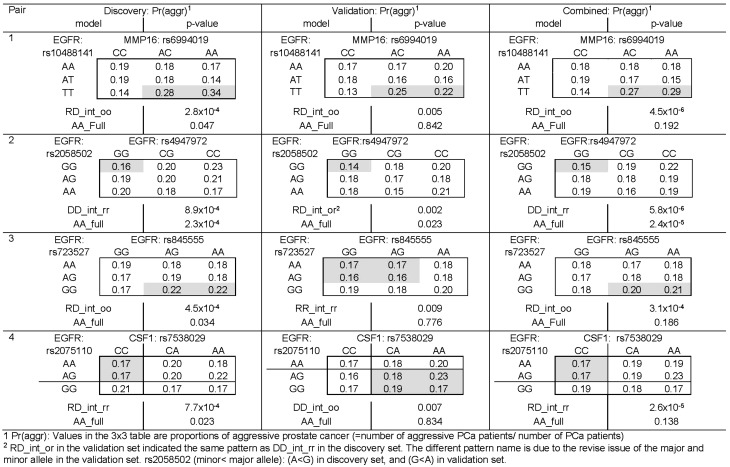
Fig. 4.

Proportions of prostate cancer aggressiveness by genotype combinations for the top four SNP–SNP interaction pairs associated with rostate cancer aggressiveness by datasets. ¹Pr(aggr): Values in the 3 × 3 table are proportions of aggressive prostate cancer (=number of aggressive PCa patients/ number of PCa patients). ²RD_int_or in the validation set indicated the same pattern as DDint rr in the discovery set. The different pattern name is due to the revise issue of the major and minor allele in the validation set. rs2058502 (minor< major allele): (A<G) in discovery set, and (G<A) in validation set

2.4 Performance evaluation

Both power and type I error were evaluated in the 1000 simulation runs. Power is defined as the percentage of detecting a significant interaction when there is a true interaction. Type I error is defined as percentage of detecting a significant interaction when there is no interaction. The significant tests of the interaction for all four approaches (SIPI, AA_Full, Geno_Full and SNPassoc) are based on testing the coefficient of the interaction term. Statistical significance for SIPI and SNPassoc is defined as a P < 0.001 (=0.05/45) and P < 0.01 (=0.05/5) based on the Bonferroni correction. For the AA_Full and Geno_Full approaches, the significance level is 0.05. The significance of MDR is based on the permutation P-values (1000 randomized datasets). In addition, we evaluated SIPI’s pattern identification rate, which is defined as the percentage of identified correct interaction pattern among the significant simulation runs.

2.5 Prostate cancer study application

SIPI was applied in evaluating SNP–SNP interactions in angiogenesis genes associated with prostate aggressiveness using Prostate Cancer Association Group to Investigate Cancer Associated Alterations in the Genome (PRACTICAL) consortium data. The study population includes 21 316 cases of European ancestry (3812 aggressive and 17 504 non-aggressive) from the 32 study sites. We randomly selected half of the cases as the discovery set and the other half as the validation set in each study site. The sample sizes in the discovery and validation sets are 10 664 and 10 652, respectively. Individuals were excluded from the study based on strict quality control criteria including: overall call rate <95% and extremely high or low heterozygosity (P < 1.0 × 10^-5). Aggressive prostate cancer was defined as a Gleason score > 8, PSA >100, disease stage of ‘distant’ (stage IV) or death from PCa. Ethnic groups were defined based on a subset of 37 000 uncorrelated markers that passed quality control (including ∼1000 selected as ancestry informative markers). Principal Component Analyses were carried out for the European subgroups. The details of this study population have been published previously (Eeles et al., 2013).

We evaluated the 148 SNPs in the six angiogenesis genes (EGFR, MMP16, ROBO1, CSF1, FBLN5,and HSPG2), which were reported in a genetic interaction network associated with prostate cancer aggressiveness(Lin et al., 2013). These result in 10 878 SNP pairs. The pairwise interactions among these SNPs associated with prostate cancer aggressiveness (yes/no) were investigated using the SIPI approach in the discovery set first. For the top SNP pairs identified in the discovery set, both SIPI and AA_Full were conducted in the validation set.

3 Results

3.1 Simulation

The power of comparing SIPI with other four methods (MDR, AA_Full, Geno_Full and SNPassoc) using the six simulated models for two SNPs with MAF of (0.5, 0.3), (0.5, 0.2) and (0.5, 0.05) is shown in Figures 1 and 2. As the sample size increased, power of all five approaches increased. In general, SIPI and MDR had similar power, and both of them are more powerful than the other three full-model approaches (AA_Full, Geno_Full and SNPassoc). SIPI and MDR suffer less negative impact of SNPs with a low MAF than the other three full-model approaches.

The four methods (SIPI, AA_Full, Geno_Full and SNPassoc) evaluate the impact of interactions, but MDR is used to test overall associations allow for an interaction. For fair comparisons, we discuss the MDR performance separately. In Models 1–4 for a SNP pair with a MAF ≥ 0.2 under a sample size of 1000, SIPI greater than 49% power while the other three approaches have low power (<25%). Under a sample size of 1000 with MAF of (0.5, 0.05), power decreases for all three full-model approaches but SIPI still has the highest power. As the sample size increased to 5000, SIPI has 100% power in most of the conditions for identifying an interaction with a SNP pair with MAF of (0.5, 0.3) and (0.5, 0.2). The order of power for detecting a SNP–SNP interaction is SIPI >Geno_Full > AA_Full (similar with SNPassoc) with a big sample size of 5000.

The three full-model approaches (AA_Full, Geno_Full and SNPassoc) have difficulty detecting Model 1, the ‘RR_int_rr’ pattern. With a recessive interaction-only pattern (RR_int_rr) in Model 1 for a sample size of 1000 (Fig. 1), SIPI has a power of 49–54% but the other three approaches only have a power <10%. When the sample size increases to 5000, the power of SIPI is approximately 100% while the other three approaches’ power remains low (<30%).

For Model 2 (DD_int_oo), SIPI have power 58–65%, but the other three approaches only have <25% power in a sample size of 1000 and MAF of (0.5, 0.3) and (0.5, 0.2). As the sample size increases to 5000, the power of all methods increase, and SIPI has the highest power compared with the other three approaches.

For Model 3 (RD_int_rr), SIPI have the highest power among all testing scenarios in Figure 1. For a sample size of 5000, SIPI has 100% power, while power of other three approaches is <80%. Similarly, the power of Model 4 (DD_M1_int_o₁) is 59–74% for SIPI and <20% for the other three approaches when the sample size is 1000. Power increases to close to close to 100% for SIPI and 22–60% for others when the sample size becomes 5000.

For Model 5 (AA_Full), the AA_Full method is the most powerful among all testing approaches in most of the conditions, except the condition of low MAF of (0.5, 0.05) in a sample size of 1000. Under this special condition, SIPI has the highest power and about 70% of the SIPI significant runs selected similar patterns (AA_M1_int and AA_M1_int_r). For Model 6 generated based on the real data, SIPI is still the most powerful approach in most of the conditions.

For comparing SIPI with MDR, both methods are more powerful than other three full model approaches (AA_Full, Geno_Full and SNPassoc).

SIPI has similar or higher power compared with MDR in majority of simulated conditions. For Model 6 with high risk groups in the minor genotypes, SIPI is more powerful than MDR under the sample size of 1000 and 5000.

For type I errors, SIPI using the Bonferroni correction is the most conservative method among all testing approaches. As shown in Figure 3, SIPI has the smallest type I errors (0.01–0.02) compared to the other three methods. Some of SNPassoc’s type I errors (0.021–0.057) are also less than 0.05. The type I errors for MDR, AA_Full and Geno_Full are close to 0.05. As shown in Supplementary Tables S2–S4, the power and type I error comparisons for additional MAF conditions show similar observations.

Fig. 3.

Comparisons of Type I errors of the SNP Interaction Pattern Identifier (SIPI) and other four methods. ¹Proportion of the outcome event in the genotype combination of the 3 × 3 table; a lowercase letter denotes the minor allele, and an uppercase letter denotes the major allele. ² MDR (Multifactor dimensionality reduction), AA_Full, Geno_Full (full interaction model and each SNP is treated as an additive or genotypic mode) and SNPassoc R package

3.2 Patten detection accuracy

The accuracy rate of pattern identification increases (Supplementary Figs S4 and S5) as the sample size increases. For Models 1, 2, 3 and 6 with 1000 samples, 56–84% of the significant simulation runs identify the correct pattern. For the sample size of 5000, all models have approximately 100% accuracy in identifying correct interaction patterns. For Models 4–5 and MAF = (0.3, 0.3) with a sample size of 1000, the pattern identification rates are low (10% and 2%, respectively). However, these rate becomes 100% for a sample size of 5000. Although pattern detection accuracy is low for the smaller sample, SIPI’s power can still be high due to detection of other similar patterns. Using Model 4 with MAF = (0.3, 0.3) as an example, only 10% of the significant runs detect the correct pattern (DD_M1_int_o₁) but other three similar patterns (39.9% DD_int_oo, 23% DR_int_rr and 12.6% DR_int_or) are identified (Supplementary Fig. S5). Thus, its power of detecting any interaction can reach 61.2%.

From the simulation results, we observed an interesting scenario for common variants with a MAF close to 0.5. Under this condition, the minor allele determination is unstable, which can affect SIPI’s model labels. The model label system are built upon the minor/major allele. As an example shown in Supplementary Figure S3, a low risk subgroup of a (GG+ GG) combination of SNP1 and SNP2 are classified as the ‘DD_int_rr’ pattern when SNP1 is with a major allele of ‘G’ and a minor allele of ‘A’ but is classified as ‘RD_int_or’ (called a ‘sister pattern’) when SNP1’s major allele is ‘A’. For an interaction with a SNP with a MAF close to 0.5, the pattern identification rate is the sum of the rates of the designed and sister patterns. We present the pattern identification rates for the significant simulation runs in Supplementary Figs S4 and S5. For Model 1 with a SNP pair with MAF = (0.5, 0.3), a total of 74% runs successfully identified the correct risk pattern (39% designed pattern and 5% sister pattern). A similar observations are presented for other models.

3.3 Example of prostate cancer aggressiveness

For the proposed SIPI approach, we considered SNP pairs with a P< 1 × 10^-7 to be statistically significant after the Bonferroni correction for 489 510 tests (=10 878 pairs × 45 models per pair). Although the SNP–SNP interaction results do not appear to be significant after adjusting for multiple comparisons, some of them show promising consistent results in both discovery and validation datasets. In the discovery set, 25 SNP pairs had a P < 0.001. Among these top 25 pairs, four pairs have a P-value < 0.01 in the validation set. Two pairs (rs10488141+ rs6994019 and rs2058502+  rs4947972) have the exact interaction pattern in both sets. The prevalence of prostate cancer aggressiveness by the nine genotype combinations are shown in Figure 4, and the prediction models are listed in Table 3. The prostate cancer patients with the TT + AC/AA genotype of the SNP pair of EGFR rs10488141 and MMP16 rs6994019 tend to suggest a higher risk of developing aggressive tumors (odds ratio (OR)=1.7, P = 4.5 × 10^-6). Those with GG+ GG of two SNPs in EGFR (rs2058502 and rs4947972) are less likely to have aggressive prostate cancer tumors (OR = 0.8, P = 5.8 × 10^-6). Those with GG+ AG/AA of two SNPs in EGFR (rs723527 and rs845555) are likely to have aggressive prostate cancer tumors (OR = 1.2, P = 3.1 × 10^-4). The patients with AA/AG and CC in EGFR rs2075110 and CSF1 rs7538029 have a lower chance of developing an aggressive prostate cancer (OR = 0.9, P = 2.6 × 10^-5).

Table 3.

Results of the PRACTICAL discovery and validation set for the top 25 SNP–SNP interaction pairs associated with prostate cancer aggressiveness with a P < 0.001 in the discovery set

			Discoverya	Validationa
SNP1	SNP2	Pattern	Pd	Pattern	Pv	Pattern Similarityb
rs10228436	rs723527	DR_int_oo	1.0 × 10−4	DR_int_rr	0.020
rs13222549	rs16880086	RR_int_oo	2.0 × 10−4	AA_int_ro	0.378
rs2017000	rs6981717	DR_int_ro	2.0 × 10−4	AA_int_oo	0.043
rs6956366	rs763317	RD_int_oo	2.7 × 10−4	DR_int_or	0.032
rs10488141	rs6994019	RD_int_oo	2.8 × 10−4	RD_int_oo	0.005	same
rs723527	rs845552	RD_int_oo	2.9 × 10−4	RR_int_oo	0.056
rs2058502	rs4947972	DD_int_rr	8.9 × 10−4	RD_int_or	0.002	Same (sister pattern)
rs6548616	rs7780270	DR_int_ro	3.2 × 10−4	RR_int_ro	0.181
rs12666347	rs7781264	DR_int_ro	3.6 × 10−4	DD_int_ro	0.082
rs2017000	rs723527	DR_int_oo	3.7 × 10−4	RR_int_rr	0.079
rs723527	rs845555	RD_int_oo	4.5 × 10−4	RR_int_rr	0.009	similar
rs16880086	rs6954351	AA_int_ro	4.6 × 10−4	RR_int_oo	0.123
rs10228436	rs7780270	DR_int_oo	4.7 × 10−4	DR_int_rr	0.070
rs13222549	rs16880099	RD_int_oo	4.9 × 10−4	AA_int_oo	0.424
rs10225877	rs16880086	AA_int_oo	5.6 × 10−4	RD_int_or	0.053
rs1519938	rs9842630	DD_int_ro	5.9 × 10−4	DR_int_or	0.040
rs13224708	rs17290392	DD_int_oo	6.1 × 10−4	DR_int_oo	0.943
rs10488141	rs1879202	RR_int_oo	6.4 × 10−4	RD_int_oo	0.021
rs10488141	rs2222294	RD_int_oo	7.3 × 10−4	DR_int_ro	0.063
rs2075110	rs7538029	RD_int_rr	7.7 × 10−4	DD_int_oo	0.007	similar
rs13222549	rs17666091	RD_int_oo	8.7 × 10−4	DR_int_oo	0.021
rs11986591	rs6954351	AA_int_ro	9.1 × 10−4	DR_int_oo	0.138
rs11977660	rs9842630	DD_int_ro	9.2 × 10−4	RD_int_ro	0.044
rs7780270	rs9832396	RD_int_or	9.6 × 10−4	RR_int_oo	0.191
rs759169	rs9842630	AA_int_rr	9.8 × 10−4	AA_int_rr	0.150

^aP_d: P-value in the discovery set, P_v: P-value in the validation set; P_d<0.001 and P_v<0.01 were in bold.

^bComparing patterns in the discovery and validation set for the SNP pairs with P_d<0.001 and P_v<0.01.

Three of the four SNP interaction pairs remain promising (rs10488141+ rs6994019, rs2058502+ rs4947972 and rs2075110+ rs7538029) after including these four SNP pairs and the first five principal components of European ancestry in the model (Table 4). For evaluating whether the SNPs in the top pairs in the discovery are comparable in the validation set, the MAF of these SNPs are calculated. As shown in Supplementary Table S5, the MAFs for these top SNPs are very similar in these two datasets. The individual effects of these SNPs in the combined dataset are also evaluated, and some SNPs did not have significant main effects. For example, the SNP pairs of rs10488141 and rs6994019 has an interaction with a P-value of 4.5 × 10^-6 but without significant main effects (P-value = 0.145 and 0.659, respectively). These show that some pure SNP–SNP interactions (without significant main effects) associated with prostate cancer aggressiveness. In summary, our results demonstrate SNP–SNP interactions in the two gene pairs (EGFR-MMP16 and EGFR-CSF1), and within EGFR. These findings support that EGFR may be the hub of this angiogenesis interaction network, which is consistent with the conclusion of the previous study (Lin et al., 2013).

Table 4.

SNP–SNP interaction models associated with prostate cancer aggressiveness

	Univariate model		Multivariable modelb
	Unadjusted OR (95% CI)a	P-value	adjusted OR (95% CI)a	P-value
rs10488141+ rs6994019, TT+ AC/AA versus others	1.7 (1.4–2.1)	4.5 × 10−6	1.8 (1.4–2.6)	6.3 × 10−7
rs2058502+ rs4947972, GG+ GG versus others	0.8 (0.7–0.9)	5.8 × 10−6	0.8 (0.7–0.9)	5.2 × 10−5
rs723527+ rs845555, GG+ AG/AA versus others	1.2 (1.1–1.3)	3.1 × 10−4	1.1 (1.0–1.3)	1.6 × 10−2
rs2075110+ rs7538029, AA/AG+ CC versus others	0.9 (0.8–0.9)	2.6 × 10−5	0.9 (0.8–0.9)	6.9 × 10−4

^aOdds ratio (95% confidence interval).

^bAll four SNP pairs and the first five principal components of European ancestry were included in the multivariable model.

4 Discussion

For evaluating two-way SNP–SNP interactions, SIPI is more powerful than the MDR, AA_Full, Geno_Full and SNPassoc approach, in general, even after applying stringent Bonferroni correction for multiple comparison justification. Although MDR and SIPI have similar power based on our simulation results, SIPI performs better than MDR is terms of testing significance of an interaction. MDR searches overall associations allowing interactions. For testing significance of an interaction, we need a two-stage MDR method, which has lower power than MDR alone. The primary strengths of SIPI are (i) taking non-hierarchical models, inheritance modes and mode coding direction into consideration and (ii) using BIC to search for a best interaction pattern. In practice, it is challenge to detect a true interaction pattern for studies with a limited sample size. These features equip SIPI for searching similar interaction patterns close to the truth, so it can overcome the unstable nature of detecting SNP–SNP interaction patterns.

Our study demonstrated that SIPI is a more comprehensive and flexible tool for detecting two-way SNP–SNP interactions compared with the three full model approaches: AA_Full in PLINK (Purcell et al., 2007), Geno_Full and SNPassoc (Gonzalez et al., 2007). All these methods are based on hierarchical models, and the difference is how they deal with inheritance modes. AA_Full treats SNPs as an additive mode and Geno_Full treats SNPs as categorical variables. SNPssoc considers five inheritance modes (additive, dominant, recessive, genotypic and over-dominant) but two SNPs in a pair need to have the same mode. Thus, these three approaches can only detect limited interaction patterns. For example, AA_Full, Geno_Full and SNPassoc experienced difficulty in detecting the RR_int_rr pattern (Model 1, power < 30%, Fig. 1), but SIPI had 100% power for a large sample size of 5000.

SIPI also provides advantages compared to other statistical approaches. BOOST (Wan et al., 2010) is a two-stage method using the log-linear model to test interactions and treats SNPs as the genotypic mode (same as Geno_Full in our study) as the 2^nd stage. SIPI is more powerful than Geno_Full (Figs 1 and 2 and Supplementary Tables S2 and S3), which is more powerful than the two-stage BOOST. SNPmaxsel (Boulesteix et al., 2007) evaluates 16 interaction patterns, which are parts of SIPI patterns. These 16 patterns are the interaction-only models for SNPs with a binary mode (dominant or recessive). HFCC (Gayan et al., 2008) is used to assess 255 patterns, but some are rare or biologically meaningless patterns. Compared with these approaches, SIPI tests the 45 biologically meaningful patterns, some of which have been reported previously (Lin et al., 2013).

For external validation of SNP–SNP interactions, we suggest loosening the validation criteria for evaluating SNP–SNP interactions to allow for similar matches. The optimal goal of a genetic association study is to build prediction models for clinical usage. External validation using an independent dataset is a key in identifying true prediction factors. The majority of previous studies use AA_Full in the two independent datasets or the exact interaction pattern identified in the discovery set to verify the same pattern in the validation set (Su et al., 2013). However, this exact match is too stringent for identifying SNP–SNP interactions. Our simulation findings (Supplementary Figs S4 and S5) indicate the unstable nature of interaction patterns due to unsteady risk profiles of the nine genotype subgroups. Thus, it should be more effective to allow for similar matches instead of exact matches in SNP–SNP interaction validation, especially in the studies with a small sample size. SIPI provides useful features that work to overcome this unstable pattern nature. SIPI uses the BIC to select the best pattern of 45 patterns so that the true pattern or the most similar pattern can be detected. This provides flexibility in terms of result validation. For a SNP pair with MAF of (0.3, 0.3) in Model 4 with a sample size of 1000, SIPI can still reach 61% power to detect an interaction with any type of SNP1 and SNP2, even though only 10% of the significant results point to the correct pattern.

The outcome prevalence table stratified using three-by-three genotypes (called the ‘3 × 3 outcome table’, available in SIPI software) is a useful way to boost result interpretation for interaction patterns. Using the 3 × 3 outcome table for real prostate cancer data application, it is easy to observe that two of the top SNP pairs had similar interaction patterns in the discovery set and validation set (Fig. 4). Combining the two testing sets with a larger sample size ensures that the interaction pattern is more reliable. In result validation, the sister pattern (one pattern with two different pattern labels) can be easily observed for an interaction with a SNP with a MAF close to 50%. In our prostate cancer application, three out of eight SNPs involved in the top SNP interactions have a MAF > 45%. In practice, the sister pattern issue can be identified by reviewing the 3 × 3 outcome table. Thus, we cannot purely rely on model labels to decide whether the two patterns are exactly matched. Due to the sister pattern and similar matching issues, it is suggested that the 3 × 3 outcome table should be consulted to further review interaction patterns.

For potential biological relevance of our identified SNP–SNP interactions (within EGFR, EGFR-MMP16 and EGFR-CSF1), the main key protein was epidermal growth factor receptor (EGFR), which interacted with the other two proteins that were also involved in cancers. The EGFR is a critical protein in proliferation of epithelial cells, differentiation and cell survival and is involved in oncogenesis. The EGFR has been known for a role in regulating prostate cellular growth and function (Bonaccorsi et al., 2007; Leotoing et al., 2007; Migliaccio et al., 2006). Results from a meta-analysis of prostate cancer expression datasets were consistent with our results. Wang et al. identified the EGFR pathway, which was associated with prostate cancer risk (Wang et al., 2011).

The interaction between matrix metalloproteinase16 (MMP16) and EGFR is interesting. These two proteins have also been implicated in several cancers including prostate cancer. MMPs are a family of proteolytic enzymes involved in tumor growth, invasion and metastasis (Rundhaug, 2005). Among 24 MMPs, the role of MMP16 in prostate cancer has not been well investigated. Jung et al. reported a down-regulation of MMP16 in malignant prostate tissues (Jung et al., 2003). MMP16 has been shown to be associated with pancreatic cancer cell migration and invasion (Lin et al., 2011) and lung development (Hadchouel et al., 2008). Several cancers in which EGFR signaling is involved were often observed abnormal high expression of MMPs (Davidson et al., 1999). Van Meter et al. reported MMP16 mRNA levels significantly increased after EGF stimulation in the glioma cell lines (Van Meter et al., 2004).

Colony stimulating factor-1 (CSF1) is a protein that promotes metastatic potential in breast cancer (Lin et al., 2001). Although there is no report on a role of CSF1 in prostate cancer, previous studies reported overexpression of serum CSF1 in several cancer sites, including pancreatic cancer (Pyonteck et al., 2012), breast, ovary and endometrial tissues (Espinosa et al., 2011; Kacinski, 1997). Recently, Pei et al (Pei et al., 2015) observed that CSF1 expression is positively correlated with progression and EGFR expression in lung cancer and concluded that co-expression of CSF1 and EGFR may be an independent prognostic biomarker for progression of lung cancer.

The SIPI software (SAS macro and SIPI R package) is freely available at http://publichealth.lsuhsc.edu/LinSoftware/. SIPI software can perform models adjusted for covariates. In SIPI R package, the original (‘SIPI’ function) and parallel computing functions (‘parSIPI’ function) are included. SIPI can finish the analyses of all pairwise analyses of 150 SNPs for a dataset with a sample size of 5000 within about 3 hours on a desktop computer (3.6 GHz CPU with 8 cores) using the ‘parSIPI’ R function. For large scale studies, it is recommended to apply some approaches (such as statistical screening or biological pathway selection) to decrease the number of candidate SNPs before applying the SIPI analyses.

In summary, SIPI is a powerful tool to search for 45 interaction patterns for pairwise SNP interactions. Although only binary outcome models were discussed in this study, it can be extended to various outcome data types, such as numeric and time-to-event data. The promising interaction pairs identified by SIPI can be included in a risk prediction model with other significant individual SNPs, other known clinical risk factors, and biomarkers in order to increase prediction accuracy.