A mass graph-based approach for the identification of modified proteoforms using top-down tandem mass spectra

Abstract

Motivation

Although proteomics has rapidly developed in the past decade, researchers are still in the early stage of exploring the world of complex proteoforms, which are protein products with various primary structure alterations resulting from gene mutations, alternative splicing, post-translational modifications, and other biological processes. Proteoform identification is essential to mapping proteoforms to their biological functions as well as discovering novel proteoforms and new protein functions. Top-down mass spectrometry is the method of choice for identifying complex proteoforms because it provides a ‘bird's eye view’ of intact proteoforms. The combinatorial explosion of various alterations on a protein may result in billions of possible proteoforms, making proteoform identification a challenging computational problem.

Results

We propose a new data structure, called the mass graph, for efficient representation of proteoforms and design mass graph alignment algorithms. We developed TopMG, a mass graph-based software tool for proteoform identification by top-down mass spectrometry. Experiments on top-down mass spectrometry datasets showed that TopMG outperformed existing methods in identifying complex proteoforms.

Availability and implementation

http://proteomics.informatics.iupui.edu/software/topmg/

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

A proteoform is a protein product of a gene that may contain various primary structure alterations (PSAs) including: genetic variations, alternative splicing, and post-translational modifications (PTMs) (Smith et al., 2013). The PSAs determine protein function in biological systems. For example, the combinatorial PTM patterns on histone proteins play a central role in epigenetic regulation (Cosgrove and Wolberger, 2005). Proteoform identification is essential to broadening our knowledge and deepening our understanding of proteoforms and their functions.

Despite the existence of various proteoforms, most protein sequence databases, such as Swiss-Prot (Boutet et al., 2016), contain only one reference protein sequence for each gene or each transcript isoform. A complex proteoform may contain multiple PSAs compared with its corresponding reference sequence in the database (Fig. 1). The differences between the target proteoform and its reference sequence make proteoform identification a challenging computational problem.

Fig. 1.

Comparison of a complex proteoform and its corresponding reference protein sequence in the database. The proteoform has an N-terminal truncation ‘MTTSE’, an amino acid mutation from ‘R’ to ‘K’, an insertion of ‘AA’, one phosphorylated serine residue, and two modified cysteine residues with carbamidomethylation.

In proteoform identification, PSAs are divided into several types: (a) sequence variations, such as mutations, insertions, and deletions; (b) fixed PTMs, which modify every instance of specific residues in the protein sequence; (c) variable PTMs, which may or may not modify specific residues in the protein sequence; (d) terminal truncations, which remove a prefix and/or a suffix of the protein sequence; and (e) unknown mass shifts of residues or subsequences, which are introduced by unknown PSAs. In Figure 1, carbamidomethylation is a fixed PTM that modifies every cysteine residue; phosphorylation is a variable PTM that may modify serine, threonine, and tyrosine residues (only one serine residue is modified in the proteoform).

Top-down mass spectrometry (MS) has unique advantages in identifying proteoforms with multiple PSAs because it analyzes intact proteoforms rather than short peptides (Catherman et al., 2014). Fragment ion series in top-down tandem mass (MS/MS) spectra provide essential information for identifying PSAs in proteoforms. Because top-down mass spectra are complex, they are often simplified by deconvolution algorithms (Kou et al., 2014; Liu et al., 2010) that convert fragment ion peaks into neutral fragment masses.

Let S be a spectrum of neutral fragment masses and F a proteoform with PSAs. Various scoring functions (Nesvizhskii, 2010) for peptide spectrum matches in bottom up MS can be applied to measure the similarity of the proteoform spectrum match (PrSM) (F, S). In this paper, we evaluate (F, S) using the shared mass counting score that counts the number of neutral masses in S explained by the theoretical neutral fragment masses of F.

The target protein of an MS/MS spectrum is generally unknown in proteome-wide studies, but we can assume that the target complex proteoform is a product of a known protein when purified proteins are analyzed. In this paper, we focus on the identification of proteoforms of known proteins with two types of PSAs: variable PTMs and terminal truncations. Fixed PTMs and amino acid mutations can be treated as special variable PTMs.

Let P be a reference sequence of the target proteoform and Ω a set of variable PTMs. We use $\text{DB}(P,\Omega )$ to represent the set of all proteoforms of P with variable PTMs in Ω and/or terminal truncations. Given a spectrum S, the proteoform identification problem is to find a proteoform $F\in \text{DB}(P,\Omega )$ that maximizes the shared mass counting score between F and S.

Extended proteoform databases and spectral alignment are the two main approaches for proteoform identification. ProSightPC (Zamdborg et al., 2007) and MascotTD (Karabacak et al., 2009) use the first approach, in which spectra are searched against a sequence database of commonly observed proteoforms. However, the number of candidate proteoforms increases exponentially due to the combinatorial explosion of PTMs and truncations. As a result, most uncommon proteoforms have to be excluded from the sequence database to keep its size manageable, limiting the ability to identify uncommon proteoforms.

Spectral alignment (Frank et al., 2008) is capable of identifying variable PTMs and unknown mass shifts by finding a best scoring alignment between the spectrum and the reference sequence. However, existing alignment algorithms have their limitations. MS-Align+ (Liu et al., 2012) can identify proteoforms with at most two unknown mass shifts because it treats all PSAs as unknown mass shifts except for fixed PTMs and protein N-terminal PTMs. MS-Align-E (Liu et al., 2013) and pTop (Sun et al., 2016) are capable of identifying proteoforms with variable PTMs, but not those with terminal truncations. MSPathFinder (http://omics.pnl.gov/software/mspathfinder) is also capable of identifying variable PTMs, but the identification of truncations depends on high quality sequence tags.

In this paper, we use mass graphs (Fig. 2) to efficiently represent proteoforms of a protein with variable PTMs and/or terminal truncations. We transform the proteoform identification problem to the mass graph alignment problem and propose dynamic programming algorithms for a restricted version of the problem.

Fig. 2.

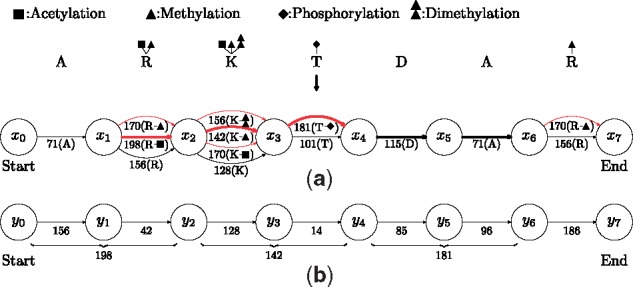
Construction of mass graphs. (a) An illustration of the construction of a proteoform mass graph from a protein ARKTDAR and four variable PTMs: acetylation on K and the first R; methylation on R and K, phosphorylation on T, and dimethylation on K. Each node corresponds to a peptide bond, or the N- or C-terminus of the protein; each edge corresponds to an amino acid residue (red edges correspond to modified amino acid residues). The weight of each edge is the mass of its corresponding unmodified or modified residue (a scaling factor 1 is used to convert weights to integers). (b) An illustration of the construction of a spectral mass graph from a prefix residue mass spectrum $0,156,198,326,340,425,521,707$. The spectrum is generated from a proteoform of RKTDA with an acetylation on the R, a methylation on the K, and a phosphorylation on the T. To simplify the mass graph, masses corresponding to proteoform suffixes (C-terminal fragment masses) are not shown. The full path from the start node y₀ to the end node y₇ is aligned with the bold path from node x₁ to node x₆. The path from y₀ to y₆ and the red bold path from x₁ to x₄ are consistent.

Many graph-based approaches have been proposed in bioinformatics studies. Splicing graphs were proposed by Heber et al. (2002) for solving the EST assembly problem and have been widely used in the identification of alternative splicing events (Xing et al., 2004). In proteogenomics studies, splicing graphs (Woo et al., 2014a) and variant graphs (Woo et al., 2014b) were employed for representing transcript variants. In the variant graph approach, both genetic variations and alternative splicing junctions of a gene are represented in a variant graph, in which each node represents a sequence of nucleotide bases and each path corresponds to a transcript variant of the gene. The transcript variants represented in a variant graph are translated into peptide or protein sequences for the identification of MS/MS spectra. Splicing graphs and variant graphs efficiently represent an exponential number of transcript variants and their corresponding proteoforms. Another example of graph-based methods is spectrum graphs that were proposed for de novo peptide sequencing and sequence tag generation in MS data analysis (Frank and Pevzner, 2005; Tanner et al., 2005). In a spectrum graph, each node represents a prefix residue mass in an MS/MS spectrum, and each path represents a peptide that may explain the spectrum. He et al. (2013) extended the spectrum graph approach to incorporate limited number of PTMs, and Bhatia et al. (2012) proposed to use a constraint graph to represent sequence constraints and combine a spectrum graph and a constraint graph in de novo sequencing.

The idea of mass graphs is inspired by splicing graphs, variant graphs, spectrum graphs and constraint graphs. Similar to variant graphs, a mass graph efficiently represents an exponential number of possible proteoforms of a gene. In addition, mass graphs are capable of representing site specific variable PTMs. Compared with variant graphs and spectrum graphs, the mass graph representation has its unique properties. While variant graphs store sequences of nucleotide bases (which can be translated into amino acids sequences) in nodes, mass graphs store amino acid residue masses in edges. Replacing nucleotides (or amino acids) with masses simplifies the representation of proteoforms with variable PTMs. (See Section Discussion.) While nodes in a spectrum graph represent prefix residue masses of an MS/MS spectrum, nodes in a mass graph represent prefix residue masses of many possible proteoforms.

The mass graph alignment problem is different from the spectral alignment problem (Bandeira et al., 2007; Frank et al., 2008) and the spliced alignment problem (Gelfand et al., 1996). While spectral alignment methods search for the best alignment between two lists of prefix residue masses, the mass graph alignment problem finds the best alignment between a prefix residue mass list and all possible paths in a mass graph, each of which corresponds a prefix residue mass list and a proteoform. In the spliced alignment problem, a variation of a nucleotide base does not significantly affect the whole sequence alignment. However, a mass shift in an amino acid and its corresponding edge in a mass graph dramatically affect the similarity score between a prefix residue mass list and a path containing the edge because the mass shift ‘propagates’ to the residue masses of all prefixes containing the amino acid. (See Section Discussion.)

We propose TopMG (TOP-down mass spectrometry-based proteoform identification using Mass Graphs), a software tool for identifying modified proteoforms using top-down tandem mass spectra, which is based on algorithms for the mass graph alignment problem. TopMG was tested on three top-down MS/MS datasets. Experimental results showed that TopMG was efficient in identifying proteoforms with variable PTMs and outperformed MS-Align-E (Liu et al., 2013) and ProSightPC (Zamdborg et al., 2007) in identifying complex proteoforms, especially those with terminal truncations.

2 Materials and methods

Mass graphs are used to represent candidate proteoforms and top-down MS/MS spectra. Mass graphs representing proteoforms are called proteoform mass graphs; those representing MS/MS spectra spectral mass graphs. With the representation, we formulate the proteoform identification problem as the mass graph alignment problem and design dynamic programming algorithms for a restricted version of the problem.

2.1 The mass graph alignment problem

2.1.1 Proteoform mass graphs

A proteoform mass graph is constructed from an unmodified protein sequence and its variable PTMs with three steps (Fig. 2a). (1) A node is added to the graph for each peptide bond of the protein. In addition, a start node and an end node are added for the N and C-termini of the protein, respectively. The left node of an amino acid is the one representing the peptide bond left of the amino acid. Specifically, the start node is the left node of the amino acid at the N-terminus. The right node of an amino acid is the one representing the peptide bond right of the amino acid. Specifically, the end node is the right node of the amino acid at the C-terminus. (2) For each amino acid in the protein, we add into the graph a directed black edge from its left node to its right node. The weight of the edge is the residue mass of the amino acid. (3) If an amino acid is a site of a variable PTM, we add into the graph a directed red edge from its left node to its right node. The weight of the edge is the residue mass of the amino acid with the PTM.

The locations of a PTM can be specified in a mass graph, thus reducing the number of candidate proteoforms. For example, the mass graph in Figure 2a specifies that acetylation occurs on only the first arginine residue, not the second, in the protein. As a result, mass graphs are capable of representing amino acid mutations because a mutation can be treated as a variable PTM that modifies only the amino acid at the mutation site. To represent an amino acid with a fixed PTM, the weight of the black edge corresponding to the amino acid is assigned as the mass of the residue with the fixed PTM.

Each path in a mass graph represents a proteoform of the protein. A path from the start node to the end node is called a full path of the graph, representing a proteoform without terminal truncations. In the graph, the number of nodes is proportional to n, and the number of edges is proportional to ln, where n is the length of the protein sequence and l is the largest number of edges between two nodes.

2.1.2 Spectral mass graphs

Mass graphs are also used to represent top-down MS/MS spectra. In the preprocessing of spectra, peaks are converted into neutral monoisotopic masses of fragment ions by deconvolution algorithms (Horn et al., 2000; Kou et al., 2014; Liu et al., 2010). Peak intensities are ignored to simplify the description of the methods. These monoisotopic masses are further converted to a list of candidate prefix residue masses, called a prefix residue mass spectrum (Liu et al., 2013).

A prefix residue mass spectrum with masses $a_0,a_1,\dots ,a_n$ in the increasing order is converted into a spectral mass graph as follows (Fig. 2b). A node is added into the graph for each mass in the spectrum. The nodes for $a_0=0$ and $a_n=PrecMass-WaterMass$ are labeled as the start and the end nodes, respectively. For each pair of neighboring masses a_i and $a_{i+1}$, for $0\le i\le n-1$, a directed edge is added from the node of a_i to that of $a_{i+1}$, and the weight of the edge is $a_{i+1}-a_i$. The spectral mass graph contains only one full path.

In the construction of mass graphs, the masses of all amino acids and PTMs are scaled and rounded to integers (a scaling constant 274.335215 was used in the experiments (Liu et al., 2013)). Precursor masses and candidate prefix residue masses in highly accurate top-down mass spectra are discretized using the same method. As a result, all edge weights are integers in mass graphs.

2.1.3 Formulation of the mass graph alignment problem

With the mass graph representation, the proteoform identification problem is transformed to an alignment problem between a proteoform mass graph and a spectral mass graph. The objective of the alignment problem is to find a path in the spectral mass graph and a path in the proteoform mass graph such that the similarity score between the two paths is maximized.

Let A be a path with k edges $e_1,e_2,\dots ,e_k$. The weight of the prefix $e_1,e_2,\dots ,$e_i, $1\le i\le k$, is called a prefix weight of A, denoted as w_i. Specifically, $w_0=0$ and w_k is the weight of the whole path. The path A is also represented as a list of prefix weights $w_0,w_1,\dots ,w_k$. For example, the prefix weight list of the red bold path in Figure 2a is $0,198,340,521$. Two paths are consistent if their weights are the same. For example, the red bold path in Figure 2a and the path from y₀ to y₆ in Figure 2b are consistent because they have the same weight 521.

We define the shared mass counting score of two consistent paths A and B as the number of shared prefix weights in their prefix weight lists, denoted as $\text{Score}(A,B)$. For example, the shared mass counting score of the red bold path in Figure 2a and the path from y₀ to y₆ in Figure 2b is 4 because they share 4 prefix masses 0, 198, 340 and 521. If A and B are inconsistent, $\text{Score}(A,B)=-\infty$.

Given a proteoform mass graph G and a spectral mass graph H, the mass graph alignment problem is to find a path A in G and a path B in H such that $\text{Score}(A,B)$ is maximized. There are several variants of the mass graph alignment problem. In the local alignment problem, the two paths in the mass graphs are not required to be full paths (from the start to the end node). It can identify a sequence tag of the target proteoform as well as its matched masses in the spectrum. For example, the alignment between the red bold path in Figure 2a and the path from y₀ to y₆ in Figure 2b is a local alignment. The proteoform identification problem is transformed into the semi-global mass graph alignment problem in which the path B in the spectral mass graph is required to be the full path. If the path A is a full path, a proteoform without terminal truncations is identified. Otherwise, a truncated proteoform is reported. For example, the bold path (not a full path) from x₁ to x₆ in Figure 2a is aligned with the full path in Figure 2b, corresponding to a truncated proteoform R[Acetylation]K[Methylation]T[Phosphorylation]DA. In the global alignment problem, both A and B are required to be full paths, that is, terminal truncations are forbidden.

In proteoform identification, we can reduce the search space by limiting the number of PTM sites in a proteoform. This limitation gives rise to a variant of the mass graph alignment problem in which the number of red edges corresponding to modified amino acids is limited. Given a proteoform mass graph G, a spectral mass graph H, and a number t, the restricted mass graph alignment (RMGA) problem is to find a path A in G and a path B in H such that A contains no more than t red edges and $\text{Score}(A,B)$ is maximized.

2.2 Consistent preceding node pairs

We use consistent preceding node pairs described below to solve the RMGA problem. In a mass graph, if there is a path from a node u₁ to another node u₂, we say u₁ precedes u₂. There may exist different paths from u₁ to u₂, each of which defines a distance that equals the weight of the path. Let $D(u_1,u_2)$ denote the set of all distinct distances defined by the paths from u₁ to u₂. The size of $D(u_1,u_2)$ is smaller than the number of paths from u₁ to u₂ when there are many duplicated distances introduced by consistent paths. For example, in Figure 2a, there are a total of 12 paths from x₁ to x₃, but $D(x_1,x_3)$ contains only 7 distances $\{284,298,312,326,340,354,368\}$. When u₁ is not a preceding node of u₂, $D(u_1,u_2)$ is an empty set.

Let u₁, u₂ be two nodes in G and let v₁, v₂ be two nodes in H. The node pair (u₁, v₁) is a consistent preceding node pair of the other node pair (u₂, v₂) if $D(u_1,u_2)\cap D(v_1,v_2)\ne \varnothing$, that is, there exist two consistent paths: one from u₁ to u₂, the other from v₁ to v₂. For example, the node pair (x₁, y₀) is a consistent preceding node pair of the node pair (x₃, y₄) in Figure 2, because $D(x_1,x_3)\cap D(y_0,y_4)=\left\{340\right\}$.

Given a proteoform mass graph G and a spectral mass graph H, the consistent preceding node pair problem is to find all consistent preceding node pairs for every node pair (u, v) where u is in G and v is in H. We study a variant of the problem in which the number of red edges in a path in G is restricted. Let $D(u_1,u_2,r)$ denote the set of distances defined by the paths from u₁ to u₂ that contain exactly r red edges, called an r-distance set. A node pair (u₁, v₁) is an r-consistent preceding node pair of the other node pair (u₂, v₂) if $D(u_1,u_2,r)\cap D(v_1,v_2)\ne \varnothing$.

2.2.1 Computing r-distance sets

Let $x_0,x_1,\dots ,x_n$ be the nodes in the proteoform mass graph G in the topological order. We propose a dynamic programming algorithm (Fig. 3) for computing $D(x_i,x_j,r)$ for $0\le i\le j\le n$ and $0\le r\le t$. In the initialization (Steps 1 and 2), we set for each node x_i in G

$$D(x_i,x_i,r)=\{\begin{array}{cc}\left\{0\right\}\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}r=0;\hfill \\ \varnothing \hfill & \hspace{0.17em}\text{otherwise}.\hspace{0.17em}\hfill \end{array}$$

Fig. 3.

The algorithm for computing all the r-distance sets of a proteoform mass graph.

For $0\le i<j\le n$ and $0\le r\le t$, the set $D(x_i,x_j,r)$ is computed based on the distances between x_i and $x_{j-1}$. Let $R(u_1,u_2)$ ($B(u_1,u_2)$) be the set of all red (black) directed edges from a node u₁ to another node u₂. The weight of an edge e is denoted by w(e). For each red edge $e_r\in R(x_{j-1},x_j)$ and each distance $d\in D(x_i,x_{j-1},r-1)$, we add $d+w(e_r)$ into $D(x_i,x_j,r)$ (Steps 7-10). For each black edge $e_b\in B(x_{j-1},x_j)$ and each distance $d\in D(x_i,x_{j-1},r)$, we add $d+w(e_b)$ into $D(x_i,x_j,r)$ (Steps 11-13). When the number of the types of variable PTMs in proteoform identification is c, the number of operations of the algorithm is proportional to $n^2{t}^{c+1}$, where n is the number of nodes in the mass graph and t is the largest number of variable PTMs in a proteoform. (See the Supplementary Material for details.)

2.2.2 Finding r-consistent preceding node pairs

A node pair (u₁, u₂) in G and its r-distance set $(u_1,u_2,r)=\{d_1,d_2,\dots ,d_k\}$ are represented by triplets $<u_1,u_2,d_1>,\dots ,<u_1,u_2,d_k>$. For a given r, the triplets of distance sets (u, v, r) for all node pairs (u, v) in G are merged and sorted based on the distance. Similarly, node pairs in H and their distances are also represented by a list of triplets sorted by the distance. The two sorted triplet lists are compared to find the r-consistent preceding node pairs for all node pairs (u, v) satisfying that u is in G and v is in H. The number of operations in this step is proportional to $n^{2}L\hspace{0.17em}\text{log}\hspace{0.17em}(nL)+m^2\hspace{0.17em}\text{log}\hspace{0.17em}m+Z$, where L is the size of the largest r-distance set in G, m is the number of nodes in H, and Z is the total number of reported r-consistent node pairs.

Prefix residue masses in deconvoluted top-down MS/MS spectra may contain small errors introduced in measuring the m/z values of fragment ions. To address this problem, an error tolerance ϵ is used in finding r-consistent preceding node pairs. With the error tolerance, two paths are consistent if the difference of their weights is no larger than ϵ, and a triplet $<u_1,u_2,d_u>$ from G matches a triplet $<v_1,v_2,d_v>$ from H if $|d_u-d_v|\le \mathrm{ϵ}$.

When the number of the types of variable PTMs in a proteoform is a constant, the algorithms for computing r-distance sets need polynomial time. In practice, we can further speed up the algorithms by removing some node pairs (u₁, u₂) from the computation. That is, we compute $D(u_1,u_2,r)$ only if the number of edges of the shortest path from u₁ to u₂ is no large than a user defined parameter L.

2.3 Algorithms for the RMGA problem

We present a dynamic programming algorithm (Supplementary Fig. S1) for the local RMGA problem. The algorithm can be modified to solve the semi-global and global RMGA problems. Let $x_0,x_1,\dots ,x_n$ be the nodes in the proteoform mass graph G in the topological order, and let $y_0,y_1,\dots ,y_m$ be the nodes in the spectral mass graph H in the topological order. We fill out a three dimensional table $T(i,j,k)$ for $0\le i\le n,\hspace{0.17em}0\le j\le m$, and $0\le k\le t$. The value $T(i,j,k)$ is the highest shared mass counting score among all consistent path pairs (A, B) such that A ends at x_i and contains k red edges, and B ends at y_j. Let $C(i,j,r)$ be the set of all r-consistent preceding node pairs of (x_i, y_j). The values of $T(i,j,k)$ are computed using the following function:

$$T(i,j,k)=\{\begin{array}{c}\underset{0\le r\le k}{\max }\hspace{0.17em}\hspace{0.17em}\underset{(x_{i\prime },y_{j\prime })\in C(i,j,r)}{\max }T(i\prime ,j\prime ,k-r)+1\hfill \\ \hspace{0.17em}\text{if}\hspace{0.17em}{\cup }_{r=0}^{k}C(i,j,r)\ne \varnothing ;\hfill \\ 1\hspace{0.17em}\text{if}\hspace{0.17em}{\cup }_{r=0}^{k}C(i,j,r)=\varnothing \hspace{0.17em}\text{and}\hspace{0.17em}k=0;\hfill \\ -\infty \hspace{0.17em}\text{otherwise}\hspace{0.17em}.\hfill \end{array}$$ (1)

When (x_i, y_j) has no consistent preceding node pairs and k = 0, the value $T(i,j,0)$ is set as 1 because two empty paths have a shared prefix weight 0. After all values in the table $T(i,j,k)$ are filled out, we find the largest one in the table and use backtracking to reconstruct a best scoring local alignment. The number of operations of the algorithm is proportional to $t^{2}nmM$, where M the size of the largest set $C(i,j,r)$.

The recurrence relation can be slightly modified to solve the semi-global and global RMGA problems. For the semi-global alignment problem, we change the second line in Equation (1) to $T(i,j,k)=1$ if ${\cup }_{r=0}^{k}C(i,j,r)=\varnothing$ and $j=k=0$, that is, y_j is required to be the start node. For the global alignment problem, we change the second line in Equation (1) to $T(i,j,k)=1$ if ${\cup }_{r=0}^{k}C(i,j,r)=\varnothing$ and $i=j=k=0$, that is, both x_i and y_j are required to be the start nodes.

3 Results

We developed TopMG (TOP-down mass spectrometry-based proteoform identification using Mass Graphs) based on the proposed algorithms using C ++. All the experiments were performed on a desktop with an Intel Core i7-3770 Quad-Core 3.4 GHz CPU and 16 GB memory.

3.1 Datasets

Three datasets were used in the evaluation of TopMG: one was generated from Escherichia coli (EC) K-12 MG1655 and the other two from histone proteins.

For the EC dataset, protein extract of Escherichia coli K-12 MG1655 was analyzed by a liquid chromatography system coupled with an LTQ Orbitrap Velos mass spectrometer (Thermo Scientific, Waltham, MA). MS and MS/MS spectra were collected at a 60 000 resolution. The top 4 ions in each MS spectrum were selected for LC-MS/MS analysis, in which the alternating fragmentation mode was used. In total, 2027 collision-induced dissociation (CID) and 2027 electron-transfer dissociation (ETD) top-down MS/MS spectra were collected.

The first histone dataset was generated from the histone H4 protein. Core histones were separated by a 2-dimensional reversed-phase and hydrophilic interaction liquid chromatography (RP-HILIC) system of which the histone H4 protein was isolated in the first dimension. The protein separation system was coupled with an LTQ Orbitrap Velos mass spectrometer to generate CID and ETD MS/MS spectra. A resolution of 60 000 was used for both MS and MS/MS spectra, and a total of 1 626 CID and 1 626 ETD spectra of the histone H4 protein were acquired. More details of the MS experiment can be found in Liu et al. (2013).

The second histone dataset was generated from the histone H2A, H2B, H3, and H4 proteins. Core histones were separated in the first dimension using a Jupiter C5 column and further separated in the second dimension by a weak cation exchange hydrophilic interaction LC (WCX-HILIC) using a PolyCAT A column. All acquisitions were performed by an LTQ Orbitrap Velos mass spectrometer with a 60 000 resolution. In total, 11 378 CID and 11 378 ETD top-down MS/MS spectra were collected. More details of the MS experiment can be found in Tian et al. (2012).

3.2 Evaluation on speed, memory usage and accuracy

A test dataset of PrSMs with mutations, which were treated variable PTMs, was generated from the EC dataset for evaluating the speed, memory usage, and accuracy of TopMG. The proteome database of Escherichia coli K-12 MG1655 was downloaded from the UniProt database (The UniProt Consortium, 2015) (Jun 18, 2015 version, 4 305 entries) and concatenated with a shuffled decoy database of the same size. All the 4 054 top-down MS/MS spectra from the EC dataset were deconvoluted by MS-Deconv (Liu et al., 2010) and then searched against the target-decoy concatenated EC proteome database using TopPIC (Kou et al., 2016). In the database search, the error tolerances for precursor and fragment masses were set as 15 ppm and no mass shifts were allowed. The settings of other parameters are given in Supplementary Table S1. A total of 861 PrSMs were identified with a 1% spectrum-level false discovery rate (FDR), which were further filtered by the number of matched fragment ions, resulting in 767 PrSMs with at least 15 matched fragment ions. The distribution of the matched fragment ions of these PrSMs is given in Supplementary Figure S2.

The 767 PrSMs without PTMs were used to generate test PrSMs with PTMs (mutations). Three mutations: lysine (K) to cysteine (C), threonine (T) to alanine (A), and valine (V) to glycine (G), were treated as variable PTMs. Let (P, S) be a PrSM between a spectrum S and a protein sequence $P=a_1{a}_2\dots a_n$ without PTMs and truncations, and Ω a set of variable PTMs (mutations). We change the protein sequence P to introduce variable PTMs (mutations) into the PrSM. We first randomly select a mutation from amino acid x to y in Ω and an amino acid a_i=y in P, then replace a_i with the amino acid x, resulting in a protein sequence P₁ with a mutation. In addition, a random amino acid sequence with a random length between 1 and 20 is appended to the N terminus of P₁, and another random sequence with a random length between 1 and 20 is appended to the C-terminus of P₁. The PrSM between the resulting sequence and S contains a variable PTM (mutation), an N-terminal truncation, and a C-terminal truncation. Using this method, a total of 11 505 test PrSMs (15 for each of the 767 PrSMs) were generated. In addition, PrSMs with $2,3,\dots ,10$ PTMs and N- and C- terminal truncations were generated using a similar method. A total of 11 5050 PrSMs were generated.

The semi-global mass graph alignment algorithm in TopMG was employed for identifying a top proteoform for each test PrSM. If the proteoform reported by TopMG has more than 15 matched fragment ions, we say TopMG identifies a PrSM. A reported proteoform may contain some mass shifts that are localized to several candidate PTM sites, not single ones. If one candidate site of a mass shift is correct, we say the mass shift is consistent with the correct site in the target proteoform. If a reported proteoform has the same N-terminal and C-terminal truncations as the target one and each mass shift in the reported proteoform is consistent with its corresponding PTM site in the target proteoform, the identification is treated as correct.

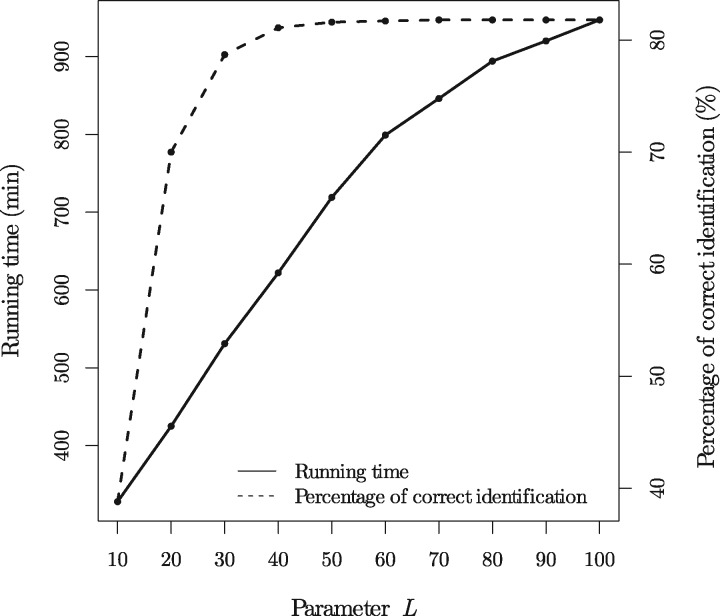
We tested the running time, memory usage, and accuracy of TopMG on the 11 505 test PrSMs with 5 variable PTMs each using various settings for L: $10,20,30,40,50,60,\hspace{0.17em}70,80,90,100$ (see Section ‘Finding r-consistent preceding node pairs’). The error tolerance ϵ was set as 0.1 Dalton (Da); the largest number of red edges (PTMs) t was set as 10; the three mutations were treated as variable PTMs. When the setting of L increases from 10 to 100, the running time increases from 328 minutes to 947 minutes, the memory usage increases from 1.2 GB to 2.2 GB, and the percentage of correctly identified proteoforms increases from 38.8% to 81.8% (Fig. 4). TopMG achieved a good balance between the speed and the accuracy rate when L = 40. Of the 11505 test PrSMs, TopMG (L = 100) reported 11308 (98.3%) PrSMs with at least 15 matched fragment ions, 11101 (96.5%) PrSMs with correct N- and C-terminal truncations, and 11019 (95.7%) PrSMs with both correct terminal truncations and correct numbers of variable PTMs. Most incorrectly identified proteoforms contained some PTMs that were not correctly localized because of the existence of random matches between experimental fragment masses and theoretical prefix residue masses.

Fig. 4.

The running time and percentages of correctly identified PrSMs for the 11505 test PrSMs with 5 variable PTMs each when the parameter L is set as $10,20,\dots ,100$.

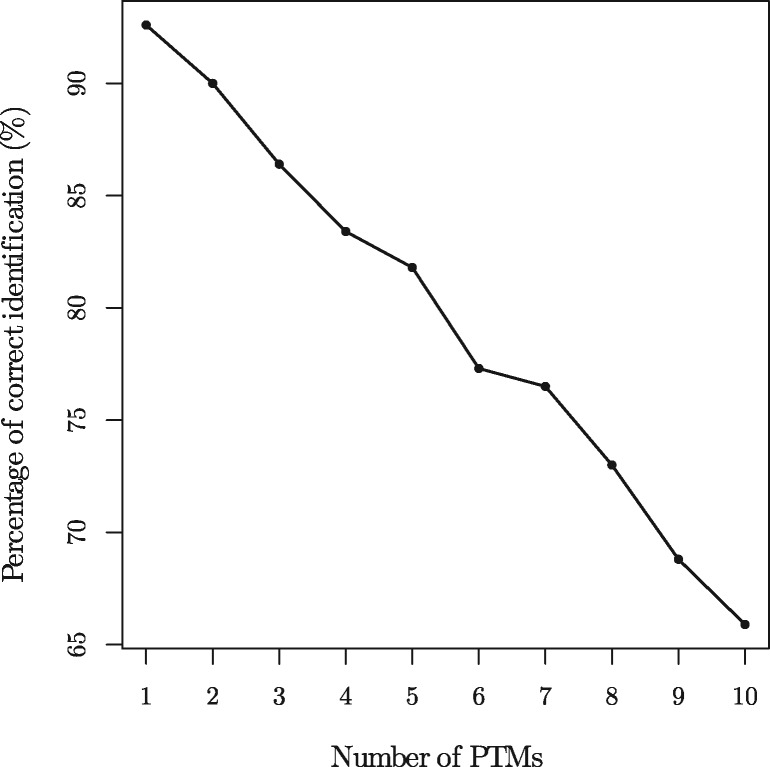
We tested the accuracy rates of TopMG on the test PrSMs with various numbers (1 to 10) of variable PTMs, in which the parameter L was set as 40 and all other parameters were set as the same as the previous experiment. When the number of variable PTMs increases from 1 to 10, the accuracy rate decreases from 92.6% to 65.9% (Fig. 5). Of the 11505 test PrSMs with 10 variable PTMs, TopMG reported 11019 (95.7%) PrSMs with at least 15 matched fragment ions, 10552 (91.7%) PrSMs with correct N- and C-terminal truncations, and 10056 (87.4%) PrSMs with both correct terminal truncations and correct numbers of variable PTMs, showing that most of the incorrectly identified proteoforms contained incorrectly localized PTMs.

Fig. 5.

The percentages of correctly identified PrSMs for the test PrSMs with various numbers of variable PTMs.

3.3 Proteoform identifications from the histone datasets

We deconvoluted all the MS/MS spectra in the histone datasets using MS-Deconv (Liu et al., 2010). Five common variable PTMs in the histone protein (Table 1) were included in the construction of proteoform mass graphs. For precursor masses, ±1 and ±2 Da errors were allowed, which may be introduced by the deconvolution algorithm. For a spectrum with a precursor mass m, we generated five candidate spectra with precursor masses m – 2, m – 1, m, m + 1, m + 2, respectively, and the spectrum with the best alignment result was reported. The error tolerance ϵ was set as 0.1 Da and the largest number of red edges t was set as 10; the parameter L was set as 40.

Table 1.

Five variable PTMs used in the identification of proteoforms of histone proteins

PTM	Monoisotopic mass shift (Da)	Amino acids
Acetylation	42.01056	R, K
Methylation	14.01565	R, K
Dimethylation	28.03130	R, K
Trimethylation	42.04695	R
Phosphorylation	79.96633	S, T, Y

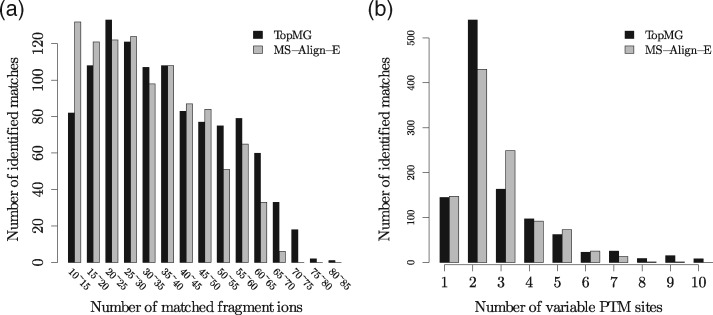
By aligning the spectra against the proteoform mass graph, TopMG (the algorithm for the semi-global RMGA problem) identified from the first histone dataset 1087 PrSMs with at least 10 matched fragment ions, including 918 matches with at least 20 matched fragment ions (Fig. 6a). Of the 1087 matches, 239 contain more than 3 PTM sites (Fig. 6b). Detailed results are provided in Supplementary Table S4.

Fig. 6.

Histograms for the PrSMs reported from the first histone dataset by TopMG with L = 40 and MS-Align-E. (a) the number of matched fragment ions; (b) the number of variable PTM sites.

The running time of TopMG was about 88 minutes. The running time depends on the sizes of the r-distance sets and the numbers of r-consistent preceding node pairs reported from the proteoform and spectral mass graphs. For the histone H4 protein with the five variable PTMs, the size of the largest r-distant set was 553. For each spectral mass graph, we count the total number N of the consistent preceding node pairs used in the mass graph alignment algorithm, that is, $N=\sum _i\sum _j{\sum }_{r=0}^{t}C(i,j,r)$. The average value of N for all the 3 252 spectra was $5.60\times {10}^6$, and the maximum value of N was $6.20\times {10}^7$.

We compared the performance of TopMG and MS-Align-E (Liu et al., 2013) on the first histone dataset. For MS-Align-E, the error tolerance for fragment masses was set as 15 ppm and all the other parameters were set as the same as TopMG. The running time of MS-Align-E was 505 minutes. MS-Align-E identified 1 031 PrSMs with at least 10 matched fragment ions (Supplementary Table S5). TopMG identified 991 of 1 031 matches reported by MS-Align-E as well as 96 PrSMs missed by MS-Align-E, all of which correspond to proteoforms with terminal truncations. The main reason why the 96 PrSMs were missed by MS-Align-E is that MS-Align-E is not able to identify truncated proteoforms. The comparison demonstrated that TopMG outperformed MS-Align-E in identifying truncated proteoforms. TopMG missed 40 PrSMs identified by MS-Align-E because it may fail to identify PrSMs with very low sequence coverage with the parameter setting L = 40. When L was set as 200, TopMG identified all the 40 PrSMs. Proteoforms reported by TopMG tend to have more matched fragment ions (Fig. 6a) and less PTM sites (Fig. 6b) compared with those reported MS-Align-E.

The second histone dataset contains 1 349 CID and 1 349 ETD spectra of the histone H4 protein. TopMG identified from these spectra 1 051 PrSMs of the histone H4 protein with at least 10 matched fragment ions, including 851 matches with at least 20 matched fragment ions (Supplementary Table S6). Of the 1 051 matches, 291 contain more than 3 PTM sites. Coupled with the Thrash algorithm (Horn et al., 2000), the absolute mass mode of ProSightPC reported 89 proteoforms as well as their corresponding PrSMs with at least 10 matched fragment ions from these spectra (In the supplementary material of Tian et al. (2012), 105 proteoform-spectrum matches are reported, of which 89 have at least 10 matched fragment ions.) (Supplementary Table S7). The parameter settings of ProSightPC are given in Supplementary Table S2. TopMG identified all the 89 spectra corresponding to the 89 matches reported by ProSightPC. In addition, TopMG identified 79 PrSMs whose precursor masses cannot match any proteoforms reported by ProSightPC, showing that the corresponding proteoforms were missed by ProSightPC (Supplementary Table S8). Manual inspection confirmed that a proteoform with an N-terminal truncation (18 amino acids are removed) was identified by TopMG, but missed by ProSightPC. TopMG also identified proteoforms missed by ProSightPC from the spectra of the histone H2A, H2B, and H3 proteins in the second histone dataset. (See the Supplementary Material for details.)

4 Discussion

Unlike splicing graphs (Heber et al., 2002) and variant graphs (Woo et al., 2014b), amino acid residue masses are stored as weights of edges, not of nodes, in mass graphs. Suppose residue masses are stored as weights of nodes. Let $u_1,u_2,u_3$ be the three nodes representing the first arginine (R) and its modified forms R[Acetylation] and R[Methylation] in the protein in Figure 2 and $v_1,v_2,v_3,v_4$ be the four nodes representing the first lysine (K) and its modified forms K[Aceyltation], K[Methylation] and K[Dimethylation]. We need 12 edges to connect all node pairs (u_i, v_j) for $1\le i\le 3$ and $1\le j\le 4$, making the graph more complex than the mass graph representation. The example shows that using edge weights in graphs is more efficient than node weights in representing proteoforms with variable PTMs.

The mass graph alignment problem is similar to the spliced alignment problem (Gelfand et al., 1996), but they are different. The spliced alignment problem studies sequence alignment, not mass alignment. In a sequence alignment problem, a substitution in a sequence does not significantly affect the alignment results. For example, changing ‘A’ to ‘T’ in x in the sequence alignment between x = ACGT and y = ACGT does not affect the matching pairs of CGT. However, this property does not hold for mass alignment. For example, the red bold path in Figure 2a and the path from y₀ to y₆ in Figure 2b has a shared mass counting score 4 because they share 4 prefix masses 0, 198, 340, and 521. If we change the mass on the red edge between x₁ and x₂ from 198 to 156, the two paths share only one prefix residue mass 0. The reason is that the mass shift ‘propagates’ to all non-zero prefix residue masses of the red bold path. The ‘propagation’ property makes mass alignment more challenging than sequence alignment.

Compared with MS-Align-E (Liu et al., 2013) and pTop (Sun et al., 2016), the main advantage of TopMG is that it is capable of identifying proteoforms with terminal truncations. Although using MS-Align-E or pTop to search spectra against a database containing all possible proteoforms with terminal truncations can also identify truncated proteoforms, the size of the database is extremely large, making the approach inefficient. For example, a protein sequence with 300 amino acids has 45150 different truncated forms.

The parameter L determines the sensitivity and speed of TopMG. The experiments showed setting L = 40 obtained a good balance between speed and sensitivity. In practice, users can adjust the setting of L to satisfy specific requirements in data analyses. When a long running time is acceptable, the setting of L can be increased to 100 or even the length of the target protein to increase the sensitivity of TopMG.

TopMG still have limitations. First, the speed of TopMG is slow for analyzing large top-down MS datasets. Analyzing one top-down MS dataset may take several hours, even several days. A pipeline that consists of the extended database approach and TopMG can speed up proteoform identification. The extended database approach is used to identify spectra that are matched to commonly observed proteoforms, and TopMG is used to analyze only spectra that are not identified by the extended database approach. Second, TopMG is designed for purified protein studies, not for proteome-level MS analyses. Efficient filtering algorithms are needed for proteome-level MS analyses. One possible filtering strategy is to keep a protein only if the difference between the precursor mass of the MS/MS spectrum and the molecular mass of the protein can be explained by a combination of variable PTMs and/or truncations. Another possible method is to filter proteins using sequence tags. Third, TopMG does not provide confidence scores for identified PTMs, which are important for proteoform characterization. Fourth, TopMG lacks a framework for the estimation of false discovery rates (FDRs) of identified proteoforms and modifications. The estimation of proteoform level FDRs is a challenging problem because an identified proteoform may have terminal truncations and multiple modifications compared with the database protein sequence. There is no existing method for solving this problem. As for FDRs of identified modifications, LuciPHOr (Fermin et al., 2013) and LuciPHOr2 (Fermin et al., 2015) provide a method based on the target-decoy framework for estimating false localization rates (FLRs) of identified phosphorylation sites in bottom-up MS. This method may be extended to estimate FLRs of modifications identified by top-down MS.

Funding

The research was supported by the National Institute of General Medical Sciences, National Institutes of Health (NIH) through Grant R01GM118470.

Conflict of Interest: none declared.