RNA-Enrich: a cut-off free functional enrichment testing method for RNA-seq with improved detection power

Abstract

Summary: Tests for differential gene expression with RNA-seq data have a tendency to identify certain types of transcripts as significant, e.g. longer and highly-expressed transcripts. This tendency has been shown to bias gene set enrichment (GSE) testing, which is used to find over- or under-represented biological functions in the data. Yet, there remains a surprising lack of tools for GSE testing specific for RNA-seq. We present a new GSE method for RNA-seq data, RNA-Enrich, that accounts for the above tendency empirically by adjusting for average read count per gene. RNA-Enrich is a quick, flexible method and web-based tool, with 16 available gene annotation databases. It does not require a P-value cut-off to define differential expression, and works well even with small sample-sized experiments. We show that adjusting for read counts per gene improves both the type I error rate and detection power of the test.

Availability and implementation: RNA-Enrich is available at http://lrpath.ncibi.org or from supplemental material as R code.

Contact: sartorma@umich.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Functional enrichment testing is one of the most common downstream analyses for transcriptomics experiments, facilitating a deeper interpretation of results. Examples of gene set databases used for testing are Gene Ontology (GO) which includes biological processes, cellular components and molecular functions, and the Kyoto Encyclopedia of Genes and Genomes which places genes in metabolic and other pathways. Most current gene set enrichment (GSE) methods, such as DAVID (Huang da et al., 2009), were developed for microarray data. These methods often only make use of differential expression (DE) P-values or ranks, or simply a list of significant genes. With RNA-seq, which uses whole transcriptome sequencing to quantify gene expression, tests for DE often exhibit a relationship between read count and likelihood of detecting DE. For example, when power is greater to detect longer and/or higher expressed genes, gene sets that have long genes or that are highly expressed are more likely to be detected as significant, violating common test assumptions. Thus, accounting for read count per gene may improve standard GSE methods, which may otherwise not be appropriate for RNA-seq data.

RNA-seq achieves a very high dynamic range, with gene read counts often varying across six or more orders of magnitude. Read-count-based methods such as those using a negative binomial model (e.g. edgeR and DEseq2) can be more likely to identify longer and highly expressed transcripts as significant. Methods that can account for this bias in GSE testing are GOseq (Young et al., 2010) which requires a P-value cut-off, and GSAASeqSP (Xiong et al., 2014) and SeqGSEA (Wang and Cairns, 2014), which require permutations and moderate to large sample sizes to obtain a sufficient number of unique permutations of phenotype labels. We have developed RNA-Enrich, a GSE method that empirically adjusts for average read count per gene, and does not require a cut-off to define differentially expressed genes (DEGs), time-consuming permutations or regression models. Similar cut-off free methods for microarray data have shown improved ability to detect gene sets enriched with either a few very strong DEGs or many only moderate DEGs (Kim et al., 2012; Sartor et al., 2009).

2 Methods

2.1 RNA-Enrich model

RNA-Enrich models the relationship between log₁₀(average read count) per gene and −log₁₀(significance score) using a binomial cubic smoothing spline. The significance scores, usually P-values, and read counts are input by the user. Per gene weights (w_g) are calculated from the spline fit as the ratio between mean −log₁₀(P-value) and fitted values, and then normalized to have a mean of 1. A modified version of the random sets method, as proposed by Newton et al. (2007), is used. We calculate the test statistic $\overline{x}$ for genes in a gene set:

$$\overline{x}=\text{mean}(w_{\text{g}}\times s_{\text{g}}),$$ (1)

where s_g is the −log₁₀(P-value) from a differential gene expression test such as edgeR or DESeq2. The distribution of the statistic to test whether $\overline{x}$ is significantly different from what is expected by chance is intractable. Instead, we use the first and second moments of the distribution to define approximate z-scores which are then used to calculate P-values of enrichment (Newton et al., 2007). Adjusted P-values (q-values) are calculated to correct for multiple testing.

The use of weights ensures that if a relationship exists between read count and DE P-values genes, it will be adjusted for properly. The original random sets method does not include the w_g terms, i.e. all genes are equally weighted; the method for calculating P-values using approximate z-scores was the same. Our website supports 16 different annotation databases plus custom gene sets, seven organisms and clustering of results.

2.2 Performance comparison

To assess the type I error rate for RNA-Enrich, we created permuted datasets from two experiments. The first, prostate cancer LNCaP cells treated with dihydrotestosterone (DHT), an androgen hormone (Li et al., 2008), showed increasing read counts with increasing significance (Fig. 1a). The second, A549 cells treated with dexamethasone (ENCODE dataset wgEncodeHaibRnaSeqA549Dex100nm) showed steady read counts with increasing significance (Fig. 1d).

Fig. 1.

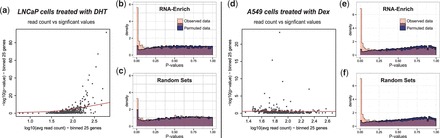
(a) RNA-seq data from LNCaP cells treated with DHT compared with a control showed a relationship between average gene read count and −log₁₀(P-values) from DE tests. (b–c) Histogram of P-values from the permuted data should be uniformly distributed for acceptable type I error rate. For RNA-Enrich, the type I error rate is approximately uniform (b), but for the random sets approach for which there is no correction, more P-values are significant than expected (c). With the original data, RNA-Enrich identifies more significant GO terms than the random sets method in the observed data. (d) RNA-seq data from A549 cells treated with Dex compared with ethanol showed no relationship between read count and −log₁₀(P-values). (e–f) With or without the read count bias correction, type I error rate is approximately uniform, indicating that no correction is needed and either test is valid. Histograms are transparent and overlaid. Additional permutations, enrichment testing methods and dataset are provided in the supplement

The original datasets were sorted by read counts, and then within each bin of 100 genes, GO term membership, DE P-value and average read count were permuted as a group. This scenario preserved the association between P-values and read count but removed functional enrichment significance from the data, allowing us to assess type I error under the null hypothesis and given the observed relationship with read count. We also tested the use of corrected fold changes instead of P-values; in this case the relationship with read count differed by dataset, but still existed (for additional details see Supplementary Methods). For both the LNCaP dataset and the A549 dataset, 100 permutations were performed. Each original dataset and permutation was tested using RNA-Enrich, the random sets method, GOseq and DAVID for all GO terms containing 10–500 genes. The median P-value of each GO term was calculated across all permutations for each dataset. In the supplement, we also provide results for a simpler type of permutations, where data were permuted over all genes; this does not preserve the association between DE P-values and read count, and is thus an estimate of what type I error would be if no relationship with read count existed (for additional details, see Supplementary Methods).

3 Results and Discussion

3.1 Method performance with permutated data

Using permuted datasets we compared the type I error of RNA-Enrich with the random sets method (does not account for any bias in the data), GOseq (can adjust for read counts, but using a cut-off based method) and DAVID (does not adjust for read counts, and uses a cut-off based method). We show that when there is a relationship between read count and −log₁₀(P-values), adjusting for read count improves the type I error rate compared with random sets (Fig. 1a–c and Supplementary Fig. S1). Without adjusting for read count, 37 GO terms were enriched in the permuted data for random sets but only three for RNA-Enrich (q-value ≤ 0.05). When the relationship does not exist, as is observed in the A549 dataset, RNA-Enrich and random sets have nearly identical type I error rates (Fig. 1d–f). DAVID had 0 GO terms enriched in the permuted data for the LNCap experiment, but its type I error was overly conservative in cases where no relationship exists (Supplementary Fig. S2). RNA-Enrich provides a diagnostic plot for the user to determine if a relationship between read count and −log₁₀(P-value) exists in their data (Fig. 1a and d). If a relationship does exist, we recommend using RNA-Enrich to provide more biologically relevant results. RNA-Enrich also has favorable type I error rate compared with GOseq and DAVID (Supplementary Figs. S2–S4). The performance of RNA-Enrich with P-values from DESeq2 instead of edgeR resulted in the same conclusions (Supplementary Fig. S5). Use of corrected fold change instead of P-values as input showed a different relationship exists, but similarly resulted in a benefit for RNA-Enrich compared with random sets (Supplementary Methods and Supplementary Fig. S6).

3.2 Method performance with experimental results

Using RNA-Enrich with the LNCaP cells treated with DHT we found 192 enriched GO terms (q-value ≤ 0.05) (Table 1 and Supplementary Table S1). In comparison, the random sets, GOseq and DAVID methods identified 35, 8 and 30 enriched GO terms, respectively. We tested a second dataset, mice embryonic fibroblasts treated with tunicamycin (see Supplementary Methods), that also revealed a relationship between read counts and significance levels, and resulted in conclusions similar to the LNCaP dataset (Supplementary Figs. S7–S9). Again, RNA-Enrich detected more GO terms than the alternatives (Supplementary Fig. S7).

Table 1.

Top ranked GO terms from RNA-Enrich for LNCaP cell line treated with DHT

Rank	GO term	P	FDR
1	Extracellular space	2.3 × 10−8	1.6 × 10−6
2	Vasculature development	4.6 × 10−9	3.4 × 10−6
7	Signaling receptor activity	3.9 × 10−7	1.3 × 10−4
9	Epithelial cell differentiation	2.3 × 10−6	5.0 × 10−4
10	Cellular biogenic amine metabolic process	2.4 × 10−6	5.0 × 10−4
12	Response to endoplasmic reticulum stress	8.9 × 10−6	1.3 × 10−3

Results shown are limited to the top unrelated GO terms.

In the A549 dataset, we did not expect an advantage to RNA-Enrich over random sets, since there was no observed relationship between read count and significance levels. RNA-Enrich found 367 enriched GO terms including negative regulation of transcription, vasculature development and fat cell differentiation—all top ranked enriched GO terms also found by random sets and GOseq. Random sets and GOseq identified 347 and 363 GO terms, respectively. Based on Figure 1e and f and our overall findings, RNA-Enrich has the desirable property of reducing to the random sets method when no relationship with read count exists.

Funding

National Institutes of Health Grants P30ES017885-01 and R01CA158286-01.

Conflict of Interest: none declared.