Robust Tests for Additive Gene-Environment Interaction in Case-Control Studies Using Gene-Environment Independence

Abstract

There have been recent proposals advocating the use of additive gene-environment interaction instead of the widely used multiplicative scale, as a more relevant public health measure. Using gene-environment independence enhances statistical power for testing multiplicative interaction in case-control studies. However, under departure from this assumption, substantial bias in the estimates and inflated type I error in the corresponding tests can occur. In this paper, we extend the empirical Bayes (EB) approach previously developed for multiplicative interaction, which trades off between bias and efficiency in a data-adaptive way, to the additive scale. An EB estimator of the relative excess risk due to interaction is derived, and the corresponding Wald test is proposed with a general regression setting under a retrospective likelihood framework. We study the impact of gene-environment association on the resultant test with case-control data. Our simulation studies suggest that the EB approach uses the gene-environment independence assumption in a data-adaptive way and provides a gain in power compared with the standard logistic regression analysis and better control of type I error when compared with the analysis assuming gene-environment independence. We illustrate the methods with data from the Ovarian Cancer Association Consortium.

There has been increasing interest in searching for gene × environment (G × E) interaction in the post–genome-wide association studies era, with limited success (1–5). A number of methods have been proposed for efficient searching for G × E effects that use the gene-environment independence assumption (2, 6–10). Almost all of these studies have focused on testing/estimation of multiplicative interaction, perhaps due to the fact that standard logistic regression is the most commonly used tool for analyzing case-control data (11–13). However, it has been suggested in the literature that additive interaction is a more relevant public health measure (3, 14, 15). If an environmental exposure, say E, can potentially be modified via an intervention, the additive G × E interaction measure can quantify the differences in the number of cases prevented if the intervention was offered in a prioritized way, across strata defined by genetic risk. This characterization helps with policy questions when there is limited access to an intervention. Moreover, the additive measure of interaction corresponds more closely to the notion of mechanistic or causal measures of interaction (16, 17).

Although this is not commonly recognized, it is possible to test for additive interaction in a logistic regression model using case-control data. While a direct estimate of additive interaction on a risk difference scale cannot be obtained from case-control data, an alternative parameter, the relative excess risk due to interaction (RERI), can be represented in terms of relative risks. Assuming that the disease is rare, relative risks can be approximated by corresponding odds ratios, and thus the RERI can be viewed as a function of both main effects and multiplicative interaction parameters in a logistic regression model. The standard delta theorem can be applied to provide asymptotic variance, and subsequently a Wald test for the null hypothesis RERI = 0 can be conducted (18–20). The fact that RERI = 0 if and only if the additive null hypothesis holds provides us with a way to test for interaction on the additive scale by testing H₀: RERI = 0. More recently, Han et al. (21) developed a likelihood ratio test (LRT) for H₀: RERI = 0, applying the retrospective likelihood framework proposed by Chatterjee and Carroll (22) that permits incorporation of the G-E independence assumption and leads to a more powerful test than the previously proposed Wald test, in modest sample sizes, for both the unconstrained and constrained maximum likelihood methods. However, it is not clear how to extend the LRT in an empirical Bayes-type adaptive framework, and thus we proceeded with combining estimates of RERI instead of deriving a combination LRT.

In this paper, we first consider the binary G, E scenario to illustrate our method for testing additive interaction in case-control studies. We provide closed-form expressions of the maximum likelihood estimates (MLEs) and the Wald test of the RERI parameter while assuming gene-environment independence (constrained MLE) and not assuming gene-environment independence (unconstrained MLE). We then extend the empirical Bayes-type shrinkage approach for multiplicative G × E interaction proposed by Mukherjee and Chatterjee (6) to estimate RERI and test for additive interaction. An adaptively weighted estimator of RERI that combines the constrained and unconstrained estimators is proposed to trade off between bias and efficiency. Finally, we extend the method to handle a completely general regression setting using the retrospective profile likelihood-based framework in Chatterjee and Carroll (22). We conduct a simulation study to compare the performance of various tests and illustrate our method by applying it to study of the interaction between use of oral contraceptive pills (OCPs) and previously identified genetic factors in a large consortium of case-control studies of ovarian cancer.

METHODS

We first consider a simple setup of an unmatched case-control study with a dichotomous genetic factor G and a dichotomous environmental exposure E. Let E = 1 (E = 0) denote an exposed (unexposed) individual and G = 1 (G = 0) denote whether an individual is a carrier (noncarrier) of the susceptible genetic marker. Let D denote disease status, where D = 1 (D = 0) stands for an affected (unaffected) individual. Let $N_0$ and $N_1$ be the numbers of selected controls and cases, respectively. The data can be represented in the form of a 2 × 4 table as displayed in Web Appendix 1 (available at https://academic.oup.com/aje).

Let ${\mathit{r}}_0=(r_{01},r_{02},r_{03},r_{04})$ and ${\mathit{r}}_1=(r_{11},r_{12},r_{13},r_{14})$ denote the vectors of observed cell frequencies in the controls and the cases, respectively. Let $r_G=r_{03}+r_{04}$ denote the frequency of G = 1 and $r_E=r_{02}+r_{04}$ denote the frequency of E = 1 among controls. Let ${\mathit{p}}_0=(p_{01},p_{02},p_{03},p_{04})$ and ${\mathit{p}}_1=(p_{11},p_{12},p_{13},p_{14})$ denote the true population parameters of the cell probabilities corresponding to a particular G-E configuration in the underlying control and case populations, respectively. Let $p_G=p_{03}+p_{04}$ denote the marginal prevalence of G = 1 among controls and $p_E=p_{02}+p_{04}$ denote the marginal prevalence of E = 1 among controls. The observed vectors of the cell counts can be viewed as random draws from 2 independent multinomial distributions in controls and cases, respectively, namely r₀ ~ multinomial (N₀, p₀) and r₁ ~ multinomial (N₁, p₁).

Let us introduce the following notation for the key parameters of interest. Let

$$\begin{array}{c}{\mathrm{OR}}_E=\frac{P(D=1|E=1,G=0)}{P(D=0|E=1,G=0)}/\frac{P(D=1|E=0,G=0)}{P(D=0|E=0,G=0)}\\ =p_{01}{p}_{12}/p_{02}{p}_{11}\end{array}$$

denote the odds ratio (OR) associated with E for nonsusceptible individuals (G = 0),

$$\begin{array}{c}{\mathrm{OR}}_G=\frac{P(D=1|G=1,E=0)}{P(D=0|G=1,E=0)}/\frac{P(D=1|G=0,E=0)}{P(D=0|G=0,E=0)}\\ =p_{01}{p}_{13}/p_{03}{p}_{11}\end{array}$$

denote the odds ratio associated with G for unexposed individuals (E = 0), and

$$\begin{array}{c}{\mathrm{OR}}_{GE}=\frac{P(D=1|E=1,G=1)}{P(D=0|E=1,G=1)}/\frac{P(D=1|E=0,G=0)}{P(D=0|E=0,G=0)}\\ =p_{01}{p}_{14}/p_{04}{p}_{11}\end{array}$$

denote the joint odds ratio associated with the subgroup G = 1 and E = 1 compared with the reference group of G = 0 and E = 0. The multiplicative interaction parameter $\mathrm{\psi }$ is defined as

$$\begin{array}{l}\mathrm{\psi }=\frac{{\mathrm{OR}}_{GE}}{{\mathrm{OR}}_G{\mathrm{OR}}_E}=\frac{p_{02}{p}_{03}{p}_{11}{p}_{14}}{p_{01}{p}_{04}{p}_{12}{p}_{13}}=\frac{(p_{11}{p}_{14}/p_{12}{p}_{13})}{\exp \left({\mathrm{\theta }}_{GE}\right)},\hfill \end{array}$$

where

$$\begin{array}{l}{\mathrm{\theta }}_{GE}=\log \frac{p_{01}{p}_{04}}{p_{02}{p}_{03}}.\end{array}$$

The parameter ${\mathrm{\theta }}_{GE}$ represents the log odds ratio between G and E among the controls, characterizing the gene-environment association. On the additive scale, the measure of interaction is defined as

$$\begin{array}{ll}{p}_{\mathrm{additive}}\hfill & =\left[P\right(D=1|E=1,G=1)\hfill \\ & -P\left(D=1|E=0,G=0\right)]\hfill \\ \hfill & -[P\left(D=1|E=1,G=0\right)\hfill \\ & -P\left(D=1|E=0,G=0\right)]\hfill \\ \hfill & -[P\left(D=1|E=0,G=1\right)\hfill \\ & -P\left(D=1|E=0,G=0\right)]\hfill \\ \hfill & =P(D=1|E=1,G=1)\hfill \\ & -P\left(D=1|E=1,G=0\right)\hfill \\ \hfill & -P\left(D=1|E=0,G=1\right)\hfill \\ & +P\left(D=1|E=0,G=0\right).\hfill \end{array}$$ (1)

Dividing equation 1 throughout by $P(D=1|E=0,G=0)$, we obtain a new measure, the RERI:

$${\mathrm{RERI}}_{\mathrm{RR}}={\mathrm{RR}}_{GE}-{\mathrm{RR}}_G-{\mathrm{RR}}_E+1.$$ (2)

When the disease is rare, the odds ratio approximates the relative risk (RR). Hence, we have

$${\mathrm{RERI}}_{\mathrm{OR}}\approx {\mathrm{OR}}_{GE}-{\mathrm{OR}}_G-{\mathrm{OR}}_E+1.$$ (3)

Note that by equations 1 and 3, testing ${\mathrm{H}}_0:p_{\mathrm{additive}}=0$ is equivalent to testing ${\mathrm{H}}_0:{\mathrm{RERI}}_{\mathrm{RR}}=0$, which is typically translated into ${\mathrm{H}}_0:{\mathrm{RERI}}_{\mathrm{OR}}=0$ in a case-control study, as described by VanderWeele (23). After defining the above relevant parameters of interest, we use the definition of RERI in equation 3 in terms of odds ratios to proceed with inference under case-control sampling, assuming that the disease is rare for all configurations of G and E.

Unconstrained maximum likelihood estimation

The unconstrained maximum likelihood (UML) estimate for all odds ratio parameters mentioned above is obtained by simply substituting $p_{dj}$ with its MLE, ${\hat{p}}_{dj}=r_{dj}/N_d$, implying

$${\hat{\mathrm{\psi }}}_{\mathrm{UML}}=\frac{{\widehat{\mathrm{OR}}}_{GE}}{{\widehat{\mathrm{OR}}}_G{\widehat{\mathrm{OR}}}_E}=\frac{r_{02}{r}_{03}{r}_{11}{r}_{14}}{r_{01}{r}_{04}{r}_{12}{r}_{13}}$$

and

$${\hat{\mathrm{\sigma }}}_{\mathrm{UML}}^2=\mathrm{Var}(\log ({\hat{\mathrm{\psi }}}_{\mathrm{UML}}))=\sum _{d=0}^1\sum _{j=1}^4\frac{1}{r_{dj}}.$$

The G-E association log odds ratio in controls can also be estimated as ${\hat{\mathrm{\theta }}}_{GE}=\log (r_{01}{r}_{04}/r_{02}{r}_{03})$.

The UML estimate of RERI can be easily obtained by plugging the corresponding estimated odds ratios in an unconstrained model into equation 3, and by the invariance property of MLE, it serves as a consistent and asymptotically unbiased estimate of RERI regardless of the gene-environment independence assumption.

$${\widehat{\mathrm{RERI}}}_{\mathrm{UML}}=\frac{r_{01}{r}_{14}}{r_{11}{r}_{04}}-\frac{r_{01}{r}_{13}}{r_{11}{r}_{03}}-\frac{r_{01}{r}_{12}}{r_{11}{r}_{02}}+1$$ (4)

Note that ${\mathit{r}}_0$ and ${\mathit{r}}_1$ are realizations from 2 independent multinomial distributions, and we can employ the delta method (Web Appendix 2) to obtain the asymptotic variance of ${\widehat{\mathrm{RERI}}}_{\mathrm{UML}}$, which is the same as noted in references 17–19. The Wald test for interaction is based on the standardized Z statistic

$$Z_{\mathrm{UML}}={\widehat{\mathrm{RERI}}}_{\mathrm{UML}}/\sqrt{\widehat{\mathrm{Var}}\left({\widehat{\mathrm{RERI}}}_{\mathrm{UML}}\right)},$$

which follows an N (0, 1) distribution under the null RERI = 0.

Constrained maximum likelihood estimation

Under G-E independence among controls (i.e., ${\mathrm{\theta }}_{GE}=0$) and the rare disease assumption, Zhang et al. (24) proposed the constrained maximum likelihood (CML) estimates for ${\mathit{p}}_0$ and ${\mathit{p}}_1$ as follows:

$$\begin{array}{c}{\hat{p}}_{01}=\frac{\left(r_{01}+r_{03}\right)\left(r_{01}+r_{02}\right)}{N_0^2},{\hat{p}}_{02}=\frac{\left(r_{01}+r_{02}\right)\left(r_{02}+r_{04}\right)}{N_0^2},\hfill \\ {\hat{p}}_{03}=\frac{\left(r_{01}+r_{03}\right)\left(r_{03}+r_{04}\right)}{N_0^2},{\hat{p}}_{04}=\frac{\left(r_{02}+r_{04}\right)\left(r_{03}+r_{04}\right)}{N_0^2},\hfill \end{array}$$

and

$$\begin{array}{c}{\hat{p}}_{1j}=\frac{r_{1j}}{N_1},j=1,2,3,4.\hfill \end{array}$$

We obtain the corresponding odds ratio estimates by substituting $p_{dj}$ with its constrained MLE under G-E independence:

$$\begin{array}{c}{\widehat{\mathrm{OR}}}_E=\frac{r_{12}\left(r_{01}+r_{03}\right)}{r_{11}(r_{02}+r_{04})},{\widehat{\mathrm{OR}}}_G=\frac{r_{13}\left(r_{01}+r_{02}\right)}{r_{11}(r_{03}+r_{04})},\\ \\ {\widehat{\mathrm{OR}}}_{\mathit{GE}}=\frac{r_{14}\left(r_{01}+r_{02}\right)\left(r_{01}+r_{03}\right)}{r_{11}(r_{02}+r_{04})\left(r_{03}+r_{04}\right)},\end{array}$$

and

$${\hat{\mathrm{\psi }}}_{\mathrm{CML}}=\frac{r_{11}{r}_{14}}{r_{12}{r}_{13}},{\hat{\mathrm{\sigma }}}_{\mathrm{CML}}^2=\mathrm{Var}(\log ({\hat{\mathrm{\psi }}}_{\mathrm{CML}}))=\sum _{j=1}^4\frac{1}{r_{1j}}.$$

Note that the estimated multiplicative interaction parameter $\hat{\mathrm{\psi }}$ is a function of only ${\mathit{r}}_1$ and is identical to the case-only estimator. The CML estimate of RERI can be computed by plugging the estimated odds ratios under the constraint into equation 3. Formally, the CML estimator for RERI is given by

$$\begin{array}{c}{\widehat{\mathrm{RERI}}}_{\mathrm{CML}}=\frac{\left(r_{01}+r_{03}\right)\left(r_{01}+r_{02}\right)r_{14}}{\left(r_{02}+r_{04}\right)\left(r_{03}+r_{04}\right)r_{11}}-\frac{(r_{01}+r_{02})r_{13}}{\left(r_{03}+r_{04}\right)r_{11}}\\ \\ -\frac{(r_{01}+r_{03})r_{12}}{\left(r_{02}+r_{04}\right)r_{11}}+1.\hfill \end{array}$$ (5)

Under the G-E independence assumption among controls, the CML estimator is consistent and asymptotically unbiased for the true RERI parameter. It is more precise than the UML estimator of RERI in equation 4 based on our simulations. The asymptotic variance of the CML estimator can also be approximated by means of the delta method, which is shown in Web Appendix 3. The Wald test for RERI in a constrained model again uses the standardized Z statistic

$$Z_{\mathrm{CML}}={\widehat{\mathrm{RERI}}}_{\mathrm{CML}}/\sqrt{\widehat{\mathrm{Var}}\left({\widehat{\mathrm{RERI}}}_{\mathrm{CML}}\right)},$$

and the power of the test is slightly lower than that of the LRT for additive interaction in Han et al. (21), as will be illustrated through our simulations. Under violation of the G-E independence assumption, ${\mathrm{\theta }}_{GE}\ne 0$, the CML estimate is asymptotically biased for the true RERI parameter and the tests are invalid.

Empirical Bayes estimation

Mukherjee and Chatterjee (6) proposed an empirical Bayes (EB) estimator of the multiplicative interaction which shrinks the UML and CML estimators in a data-adaptive way. It relaxes the G-E independence assumption and makes a tradeoff between bias and efficiency. Formally, the EB estimator of multiplicative interaction is given by

$$\begin{array}{c}\log ({\hat{\mathrm{\psi }}}_{\mathrm{EB}})=\frac{{\hat{\mathrm{\sigma }}}_{\mathrm{UML}}^2}{{\hat{\mathrm{\theta }}}_{GE}^2+{\hat{\mathrm{\sigma }}}_{\mathrm{UML}}^2}\log ({\hat{\mathrm{\psi }}}_{\mathrm{CML}})+\frac{{\hat{\mathrm{\theta }}}_{GE}^2}{{\hat{\mathrm{\theta }}}_{GE}^2+{\hat{\mathrm{\sigma }}}_{\mathrm{UML}}^2}\log ({\hat{\mathrm{\psi }}}_{\mathrm{UML}}),\hfill \end{array}$$ (6)

where ${\hat{\mathrm{\psi }}}_{\mathrm{CML}}=(r_{11}{r}_{14}/r_{12}{r}_{13})$, ${\hat{\mathrm{\psi }}}_{\mathrm{UML}}=(r_{02}{r}_{03}{r}_{11}{r}_{14}/r_{01}{r}_{04}{r}_{12}{r}_{13}),$${\hat{\mathrm{\sigma }}}_{\mathrm{UML}}^2={\sum }_{d=0}^1{\sum }_{j=1}^4(1/r_{dj}),$and ${\hat{\mathrm{\theta }}}_{GE}=\log (r_{01}{r}_{04}/r_{02}{r}_{03}).$

We employ the same idea of adaptive weighting and propose the EB estimator for RERI as

$$\begin{array}{c}{\widehat{\mathrm{RERI}}}_{\mathrm{EB}}=\frac{{\left({\widehat{\mathrm{RERI}}}_{\mathrm{UML}}-{\widehat{\mathrm{RERI}}}_{\mathrm{CML}}\right)}^2}{\widehat{\mathrm{Var}}\left({\widehat{\mathrm{RERI}}}_{\mathrm{UML}}\right)+{\left({\widehat{\mathrm{RERI}}}_{\mathrm{UML}}-{\widehat{\mathrm{RERI}}}_{\mathrm{CML}}\right)}^2}{\widehat{\mathrm{RERI}}}_{\mathrm{UML}}+\frac{\widehat{\mathrm{Var}}\left({\widehat{\mathrm{RERI}}}_{\mathrm{UML}}\right)}{\widehat{\mathrm{Var}}\left({\widehat{\mathrm{RERI}}}_{\mathrm{UML}}\right)+{\left({\widehat{\mathrm{RERI}}}_{\mathrm{UML}}-{\widehat{\mathrm{RERI}}}_{\mathrm{CML}}\right)}^2}{\widehat{\mathrm{RERI}}}_{\mathrm{CML}}\hfill \\ \\ ={\widehat{\mathrm{RERI}}}_{\mathrm{UML}}+K({\widehat{\mathrm{RERI}}}_{\mathrm{CML}}-{\widehat{\mathrm{RERI}}}_{\mathrm{UML}}),\hfill \end{array}$$ (7)

where $K=V{\left(V+{\hat{\mathrm{\kappa }}\hat{\mathrm{\kappa }}}^T\right)}^{-1}$ is a shrinkage factor of the same form as defined in Chen et al. (25) with $\hat{\mathrm{\kappa }}={\widehat{\mathrm{RERI}}}_{\mathrm{UML}}-{\widehat{\mathrm{RERI}}}_{\mathrm{CML}}$ and $V=\widehat{\mathrm{Var}}\left({\widehat{\mathrm{RERI}}}_{\mathrm{UML}}\right)$. To explain the intuitive rationale behind the estimator, observe that as $\widehat{{\mathrm{\theta }}_{GE}}\to 0$—that is, as the data provide the evidence in favor of G-E independence (${\widehat{\mathrm{RERI}}}_{\mathrm{UML}}-{\widehat{\mathrm{RERI}}}_{\mathrm{CML}}\to 0$)—the estimator puts more weight on the CML estimator to gain more efficiency; and as $\widehat{{\mathrm{\theta }}_{GE}}\to \infty$—that is, as the G-E dependence becomes stronger in the control population and ${\widehat{\mathrm{RERI}}}_{\mathrm{UML}}-{\widehat{\mathrm{RERI}}}_{\mathrm{CML}}$ becomes larger—then the EB estimator puts more weight on the UML estimator to reduce bias. In large samples, the EB estimator converges to the UML estimate and thus is asymptotically unbiased for the true RERI parameter (6). The asymptotic variance of ${\widehat{\mathrm{RERI}}}_{\mathrm{EB}}$ is derived via the delta method (see Web Appendix 4), assuming $\widehat{\mathrm{Var}}\left({\widehat{\mathrm{RERI}}}_{\mathrm{UML}}\right)$ as a constant relative to the order of magnitude of the point estimates (6). We use the Wald test for the EB estimator based on the standardized Z statistic

$$Z_{\mathrm{EB}}={\widehat{\mathrm{RERI}}}_{\mathrm{EB}}/\sqrt{\widehat{\mathrm{Var}}\left({\widehat{\mathrm{RERI}}}_{\mathrm{EB}}\right)}.$$

Remark 1

We also consider 2 other forms of adaptive weights. One is to modify the shrinkage factor K in equation 7 and let $\widehat{k^{⁎}}={\hat{\mathrm{\theta }}}_{GE}$ instead of ${\widehat{\mathrm{RERI}}}_{\mathrm{UML}}-{\widehat{\mathrm{RERI}}}_{\mathrm{CML}}$, namely,

$${\widehat{\text{RERI}}}_{\mathrm{EB}1}={\widehat{\mathrm{RERI}}}_{\mathrm{UML}}+K^{*}({\widehat{\mathrm{RERI}}}_{\mathrm{CML}}-{\widehat{\mathrm{RERI}}}_{\mathrm{UML}}),$$

where $K^{*}=V{\left(V+\widehat{{\mathrm{\kappa }}^{⁎}}{\widehat{{\mathrm{\kappa }}^{⁎}}}^T\right)}^{-1}$. The other is to plug in the EB estimates (${\widehat{\mathrm{OR}}}_{\mathrm{EB}}$) obtained from using the retrospective likelihood framework in Mukherjee and Chatterjee (6), as implemented in R package CGEN (R Foundation for Statistical Computing, Vienna, Austria) (6, 22, 25), directly into equation 3, namely,

$${\widehat{\mathrm{RERI}}}_{\mathrm{EB}2}={\widehat{\mathrm{OR}}}_{GE}-{\widehat{\mathrm{OR}}}_G-{\widehat{\mathrm{OR}}}_E+1,$$

where all estimated odds ratios are EB estimates proposed under the multiplicative model. The EB estimator we proposed in equation 7 demonstrates superior performance among the 3 choices, based on our simulation study.

Remark 2

As is shown in Chen et al. (25), the asymptotic theory for CML and consequently EB is nonregular under the independence assumption. The delta method does not technically apply for estimation of the asymptotic variance. Theoretically, the test statistic also fails to be asymptotically normal under G-E independence (25, 26). However, in practice, the estimated variance derived by the delta method approximates the empirical variance very well, as noted in the simulation studies (see Web Appendix 5, Web Tables 1 and 2, and Web Figures 1 and 2). Under G-E dependence, the EB estimate converges in large samples to the UML estimate and thus to the true RERI parameter, and standard likelihood asymptotics holds (6).

Profile likelihood framework for general regression setting

Consider the retrospective likelihood considered in the papers by Chatterjee and Carroll (22) and Mukherjee and Chatterjee (6) and as implemented in the R package CGEN:

$$\begin{array}{c}P\left(G,E,\mathit{Z}|D\right)\hfill \\ =\frac{P\left(D=1|G,E,\mathit{Z}\right)P(G|E,\mathit{Z})P(E,\mathit{Z})}{{\sum }_{G,E,\mathit{Z}}P\left(D=1|G,E,\mathit{Z}\right)P(G|E,\mathit{Z})P(E,\mathit{Z})}.\hfill \end{array}$$ (8)

The 3 ingredients of the above retrospective likelihood are as follows.

1. The logistic regression disease risk model of interest with multiplicative G × E interaction parameter $\text{logit}P(D=1|G,E,\mathit{Z})={\mathrm{\beta }}_0+{\mathrm{\beta }}_{G}G+{\mathrm{\beta }}_{E}E+{\mathrm{\beta }}_{GE}G\times E+{\mathbf{\beta }}_{\mathit{Z}}^{\mathit{T}}\mathit{Z},$ where $\mathit{Z}$ denotes other covariates.

2. $\text{Logit}P\left(G|E,\mathit{Z}\right)={\mathrm{\theta }}_0+{\theta }_{GE}E+{\mathbf{\theta }}_{\mathit{GZ}}^{\mathit{T}}\mathit{Z}$. While this is the gene model used for UML, allowing G-E dependence, in the CML method, $P(G|E,\mathit{Z})$ reduces to $P(G|\mathit{Z})$ under the assumption of G-E independence conditional on $\mathit{Z}$, implying ${\mathrm{\theta }}_{GE}\equiv 0$.

3. The distribution $P\left(E,\mathit{Z}\right)$ is allowed to be completely nonparametric. We then maximize the retrospective likelihood using existing routines in CGEN to obtain ${\widehat{\mathrm{\beta }}}_{\mathrm{UML}}$ and ${\widehat{\mathrm{\beta }}}_{\mathrm{CML}}$, the vector of all of the parameter estimates of the disease risk model in point 1 above, namely, $({\mathrm{\beta }}_0,{\mathrm{\beta }}_G,{\mathrm{\beta }}_E,{\mathrm{\beta }}_{GE},{\mathbf{\beta }}_{\mathit{Z}})$.

When it comes to defining RERI with a general G and E variable adjusting for covariates Z, particularly with case-control data, as described in VanderWeele (23), let us denote the RERI by ${\mathrm{RERI}}_{\mathrm{OR}}\left(E_0,E_1,G_0,G_1\right)$, by replacing risk ratios with corresponding odds ratios in the RERI expression in equation 3 as is typically done in a case-control study. With general continuous and ordinal exposures, one has to consider the magnitude of change in exposure for which one is examining the interaction. Let us consider the situation where the environmental risk factor changes from $E_0$ to $E_1$ and the genetic risk factor changes from $G_0$ to $G_1$ but other covariates $\mathit{z}$ are held constant. Formally, it is defined as

$$\begin{array}{c}{\mathrm{RERI}}_{\mathrm{OR}}\left(E_0,E_1,G_0,G_1\right)\hfill \\ =\mathrm{OR}\left(G_1,E_1\right)-\mathrm{OR}\left(G_1,E_0\right)-\mathrm{OR}\left(G_0,E_1\right)+1\hfill \\ =\exp \{{\mathrm{\beta }}_G(G_1-G_0)+{\mathrm{\beta }}_E(E_1-E_0)\hfill \\ +{\mathrm{\beta }}_{GE}(G_1\times E_1-G_0\times E_0)\}\hfill \\ -\exp \left\{{\mathrm{\beta }}_E\left(E_1-E_0\right)+{\mathrm{\beta }}_{GE}{G}_0\times \left(E_1-E_0\right)\right\}\hfill \\ -\exp \{{\mathrm{\beta }}_G(G_1-G_0)+{\mathrm{\beta }}_{GE}(G_1-G_0)\times E_0\}+1\hfill \\ =f\left({\mathrm{\beta }}_G,{\mathrm{\beta }}_E,{\mathrm{\beta }}_{GE}\right)\approx \mathrm{RERI}(E_0,E_1,G_0,G_1).\hfill \end{array}$$ (9)

This last approximation of risk ratios by odds ratios holds when the outcome is rare in each stratum defined by the 2 exposures or when controls are selected from the entire population, not just the noncases (27). More generally, if G and E are both categorical factors with I and J levels with coefficients corresponding to different levels of each factor, then ${\mathrm{\beta }}_G,{\mathrm{\beta }}_E,\mathrm{and}{\mathrm{\beta }}_{GE}$ in equation 9 become (I − 1)-, (J − 1)-, and [(I − 1)(J − 1)]-dimensional vectors instead of scalars. Note that ${\widehat{\mathrm{RERI}}}_{\mathrm{UML}}=f({\widehat{\mathbf{\beta }}}_{\mathrm{UML}})$ and ${\widehat{\mathrm{RERI}}}_{\mathrm{CML}}=f({\widehat{\mathbf{\beta }}}_{\mathrm{CML}})$ can be viewed as functions of UML and CML estimates of relative risk parameters, where f is the function in equation 9. The variance of ${\widehat{\mathrm{RERI}}}_{\mathrm{UML}}$ and ${\widehat{\mathrm{RERI}}}_{\mathrm{CML}}$ can be calculated by means of the delta method. The EB estimator of RERI is the same as in equation 7, and its estimated variance is calculated by the delta method using the joint distribution of $({\stackrel{\mathbf{ˆ}}{\mathbf{\beta }}}_{\mathrm{UML}},{\stackrel{\mathbf{ˆ}}{\mathbf{\beta }}}_{\mathrm{CML}})$ as proposed by Mukherjee and Chatterjee (6) (Web Appendix 6). The Wald tests for the 3 estimators are all based on the standardized Z statistic. We have provided general codes to test for RERI on GitHub (28).

Example: analysis of G × E interactions in case-control studies of ovarian cancer

Epithelial ovarian cancer is one of the most common malignancies of the female reproductive tract. Approximately 14,080 women in the United States died from ovarian cancer in 2017 (29), comprising more deaths than those from any other cancer of the female reproductive system. There are several well-established nongenetic risk factors for ovarian cancer (30–36), and recent genome-wide association studies have identified and replicated 18 genetic variants that influence disease risk (37). To this end, the Ovarian Cancer Association Consortium has undertaken an effort to study interactions focusing on the 18 confirmed single nucleotide polymorphisms (SNPs) and 7 well-established risk factors: race, history of endometriosis, first-degree family history of ovarian cancer, OCP use, parity, tubal ligation, and age. In our illustrative analysis, we focus on OCP × SNP interaction and use genetic data from 15 Ovarian Cancer Association Consortium studies (30, 38–55) that also have data on epidemiologic risk factors (see Web Table 3).

Each SNP is coded as the number of risk alleles a subject carries, and all subsequent analysis assumes this additive genetic susceptibility model. Published odds ratios for the 18 confirmed loci in Web Table 4 are from analyses presented in the Collaborative Oncological Gene-Environment Study (38, 39, 56–61). As a parsimonious and succinct way of summarizing the effects of genetic variants across all loci for each subject, we construct a “genetic risk score” (GRS) variable as the sum of the risk allele counts across all loci and a “weighted genetic risk score” (WGRS) as the weighted sum, where the weight for each individual SNP is determined by the published log odds ratio in large meta-analysis. Polygenic risk scores have been used for risk stratification in multiple G × E papers recently (3, 62). Analysis of the marginal effect for GRS and WGRS is shown in Web Table 5. Each environmental factor is coded as a categorical variable, as described in Web Table 6. The merged G × E data set has a sample size of 11,661 subjects of European ancestry, with 4,135 cases and 7,526 controls from 13 study sites (Web Table 3).

To illustrate our inference for interactions between OCP use (1 = ever and 0 = never) and genetic risk factors, we consider both single SNP × OCP interaction and W/GRS × OCP interaction (i.e., GRS or WGRS × OCP interaction). For single-SNP analysis, we consider the top 2 hits in the 18 confirmed loci—that is, rs62274042 (SNP 1) and rs10962691 (SNP 2) as reported in Web Table 4. We used additive coding for our SNP × OCP analysis. For GRS and WGRS, we use the quartiles in controls to define a categorical variable with 4 categories. The analysis model adjusts for study site and all other environmental risk factors except race.

Simulation design

In our simulation study, we first investigate the type I error, standard power at level $\mathrm{\alpha }$, and power at empirical $\mathrm{\alpha }$ (empirical type I error is used to report power in situations where type I error is not maintained) of Wald tests for ${\widehat{\mathrm{RERI}}}_{\mathrm{UML}}$, ${\widehat{\mathrm{RERI}}}_{\mathrm{CML}}$, and ${\widehat{\mathrm{RERI}}}_{\mathrm{EB}}$ under various alternative values of RERI across a spectrum of scenarios, varying the strength of the G-E association, the main effects of G and E, the minor allele frequency of G, the prevalence of exposure E, the test size, and sample sizes. We compare the power of the Wald test for ${\widehat{\mathrm{RERI}}}_{\mathrm{CML}}$ with the previously proposed LRT for additive interaction under G-E independence (21). We also explore estimation properties like the absolute relative bias and MSE of the 3 estimators, as well as those of 2 alternative proposals, ${\widehat{\mathrm{RERI}}}_{\mathrm{EB1}}$ and ${\widehat{\mathrm{RERI}}}_{\mathrm{EB2}}$. Note that both RERI and multiplicative interaction parameters are obtained from the underlying true logistic regression model

$$\mathrm{logit}P(D=1|G,E)={\mathrm{\beta }}_0+{\mathrm{\beta }}_{E}E+{\mathrm{\beta }}_{G}G+{\mathrm{\beta }}_{GE}GE,$$

where $\text{RERI}=\exp \left({\mathrm{\beta }}_G+{\mathrm{\beta }}_E+{\mathrm{\beta }}_{GE}\right)-\exp \left({\mathrm{\beta }}_G\right)-\exp \left({\mathrm{\beta }}_E\right)+1$ and $\mathrm{\psi }={\exp (\mathrm{\beta }}_{GE})$, so that the value of RERI is well-defined given $\mathrm{\psi }$ and vice versa, once the main effect parameters ${\mathrm{OR}}_G=\exp \left({\mathrm{\beta }}_G\right)$ and ${\mathrm{OR}}_E=\exp \left({\mathrm{\beta }}_E\right)$ have been specified.

We set the prevalences of G and E in controls, $p_G=(0.1,0.2,0.3)$and $p_E=(0.3,0.4,0.5)$; the main effects ${\mathrm{OR}}_G=(1.1,1.2,1.3)$ and ${\mathrm{OR}}_E=(1.3,1.5,1.7)$; the sample size $N_0=N_1=(4,000,20,000)$; the size of test $\mathrm{\alpha }=(0.05,5\times {10}^{-6});$a change in the strength of the G-E association, $\exp \left({\mathrm{\theta }}_{GE}\right)$, from 0.8 to 1.2 at a grid of 0.1; and a change in the RERI from 0 to 1.5 with a grid of 0.1. The number of simulated data sets is 1,000 when $\mathrm{\alpha }=0.05$, and it is 10⁶ when $\mathrm{\alpha }=5\times {10}^{-6}$. The population parameters of cell probability ${\mathit{p}}_0$ and ${\mathit{p}}_1$ are defined by solving the equations in Web Appendix 7 (9, 63).

We generate data independently from the 2 multinomial distributions corresponding to the case and control populations, according to the above probabilities, with numbers of cases and controls as$N_0$ and $N_1$, respectively. We also consider another simulation setting to mimic a large-scale genome-wide search of interactions where we use random distribution for the parameters corresponding to the set of null markers. We first compute the UML, CML, and EB estimators using equations 4, 5, and 7 and then compare their type I error, power, power at empirical $\mathrm{\alpha }$, absolute relative bias, MSE, and type I error over 1,000 replications. Power is estimated by the proportion of null hypothesis ${\mathrm{H}}_0:\mathrm{RERI}=0$ rejected at the given level of significance $\mathrm{\alpha }$—that is, the proportion of times $\left|Z\right|>Z_{1-\mathrm{\alpha }/2}$, where Z is the Wald test statistic. Power at empirical $\mathrm{\alpha }$ is a modified power which utilizes an empirical P value threshold as the rejection rule to control the type I error around the given significance level when the type I error at the desired nominal level is not maintained. The absolute relative bias is calculated by averaging $\left|\widehat{\mathrm{RERI}}-\mathrm{RERI}\right|/\mathrm{RERI}$, and MSE is calculated by averaging ${\left(\widehat{\mathrm{RERI}}-\mathrm{RERI}\right)}^2$.

RESULTS

Ovarian cancer data example

The distributions of GRS and WGRS in cases and controls are displayed in Web Figure 3. Relative to the control distributions, the upper tails of the case distributions are shifted slightly rightward. We calculate UML, CML, and EB estimators of interactions on both the multiplicative and additive scales. The estimates, corresponding confidence intervals, and Wald test P values are shown in Table 1. In SNP1 × OCP analysis, the strength of G-E association is modest: exp(θ_GE) = 1.07 (95% confidence interval (CI): 0.94, 1.21); the EB estimate of RERI is −0.16 (95% CI: −0.50, 0.18), where the weight on ${\widehat{\mathrm{RERI}}}_{\mathrm{UML}}$ is 43%. In SNP2 × OCP analysis, the G-E association seems weaker, with exp(θ_GE) = 0.96 (95% CI: 0.83, 1.11). The EB estimate of RERI is 0.04 (95% CI: −0.11, 0.18), with its weight on ${\widehat{\mathrm{RERI}}}_{\mathrm{UML}}$ decreasing to 11%. The confidence intervals corresponding to ${\widehat{\mathrm{RERI}}}_{\mathrm{EB}}$ are narrower than the corresponding intervals for ${\widehat{\mathrm{RERI}}}_{\mathrm{UML}}$. The point estimate ${\widehat{\mathrm{RERI}}}_{\mathrm{EB}}$ lies between ${\widehat{\mathrm{RERI}}}_{\mathrm{UML}}$ and ${\widehat{\mathrm{RERI}}}_{\mathrm{CML}}$, reflecting the combined efficiency-robustness feature of the EB estimator. In WGRS × OCP analysis, we evaluate interactions associated with a change in OCP use from 0 to 1 (ever users to never users) and a change in WGRS from the lowest quartile to the highest quartile (as defined through the distribution of WGRS in controls). The multiplicative measure of interaction ${\hat{\mathrm{\psi }}}_{\mathrm{EB}}$ is not significant at α = 0.05, but ${\widehat{\mathrm{RERI}}}_{\mathrm{EB}}$ departs from 0 significantly, with an estimate of −0.52 (95% CI: −0.91, −0.13) and a very small P value (P = 0.009).

Table 1.

Estimates of Ovarian Cancer Risk for Interactions Between Either Single Nucleotide Polymorphisms or Genetic Risk Scores and Use of Oral Contraceptive Pills on Both the Multiplicative and Additive Scales^a

Interaction	Multiplicative ($\mathrm{\psi }$)			Additive (RERI)
	Estimate	95% CI	P Valueb	Estimatec	95% CI	P Valueb
SNP1d × OCPe
UML	0.94	0.73, 1.22	0.645	−0.25	−0.60, 0.10	0.162
CML	1.06	0.88, 1.28	0.548	−0.09	−0.33, 0.14	0.432
EB	1.00	0.78, 1.29	0.970	−0.16	−0.50, 0.18	0.348
SNP2d × OCP
UML	0.93	0.82, 1.05	0.255	0.08	−0.18, 0.34	0.552
CML	0.94	0.85, 1.04	0.224	0.03	−0.18, 0.25	0.757
EB	0.94	0.85, 1.04	0.222	0.04	−0.11, 0.18	0.598
GRSc × OCP
UML	0.82	0.65, 1.02	0.073	−0.64	−1.01, −0.27	0.001
CML	0.92	0.77, 1.08	0.305	−0.43	−0.68, −0.18	0.001
EB	0.86	0.69, 1.07	0.197	−0.54	−0.93, −0.16	0.005
WGRSc × OCP
UML	0.90	0.76, 1.06	0.212	−0.61	−0.99, −0.23	0.002
CML	0.95	0.83, 1.08	0.417	−0.40	−0.67, −0.14	0.003
EB	0.93	0.81, 1.08	0.366	−0.52	−0.91, −0.13	0.009

Abbreviations: CI, confidence interval; CML, constrained maximum likelihood; EB, empirical Bayes; GRS, genetic risk score; RERI, relative excess risk due to interaction; SNP, single nucleotide polymorphism; UML, unconstrained maximum likelihood; WGRS, weighted genetic risk score.

^a The analysis was based on subjects with European ancestry, using data on 4,135 cases and 7,526 controls from 13 study sites in the Ovarian Cancer Association Consortium (30, 38–55). The model adjusted for history of endometriosis, first-degree family history of ovarian cancer, parity, tubal ligation, age, and study site.

^b Wald test P value.

^c W/GRS is a categorical variable defined by the quartiles of WGRS in controls—for example, W/GRS = 3 if it is at or above the 75th percentile in controls and 0 if it is below the 25th percentile in controls. The minimal, 25th, 50th, and 75th percentiles and the maximum are 3, 11, 12, 14, and 22 for GRS and 0.32, 1.33, 1.53, 1.75, and 2.86 for WGRS, respectively. In this table, we present only the coefficient for the interaction term corresponding to a change in OCP from 0 to 1 and a change in WGRS from 0 to 3.

^d SNP1 denotes rs62274042 and SNP2 denotes rs10962691. Marginal disease odds ratios corresponding to these SNPs are 1.45 (95% CI: 1.37, 1.54) and 1.25 (95% CI: 1.20, 1.30), respectively.

^e OCP = 1 if the individual had ever used OCPs and 0 if she had never used OCPs.

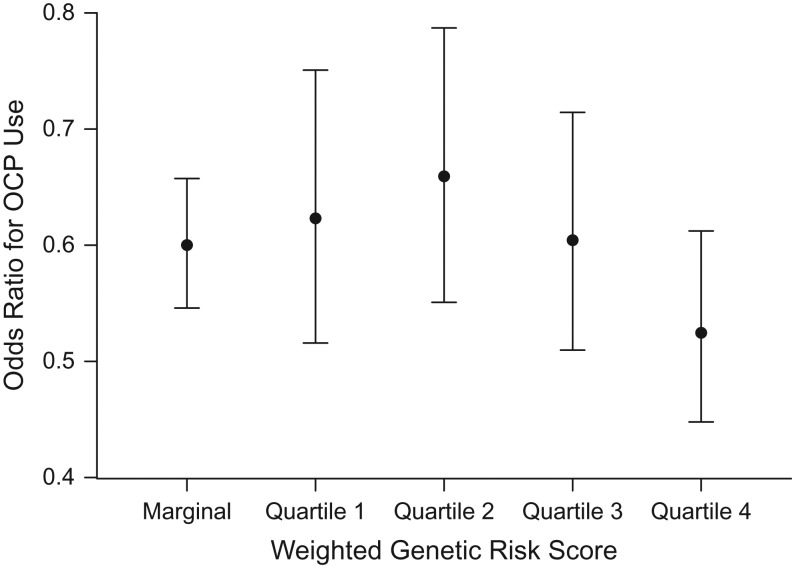
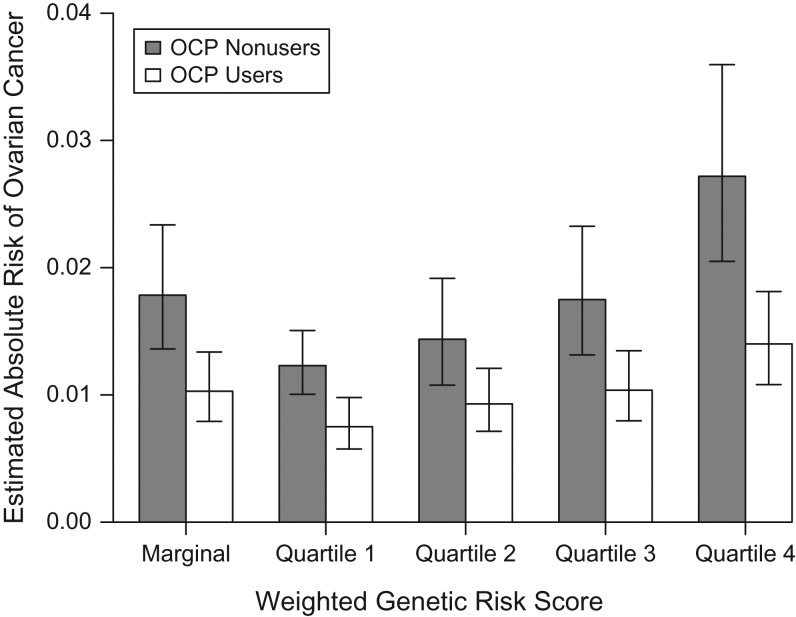
To visually present the results, we fit a standard logistic regression model including the main effects of OCP use and quartiles of WGRS as a categorical factor, and an interaction term for WGRS × OCP adjusting for study sites and other risk factors. Figure 1 shows the odds ratio for OCP and its corresponding 95% confidence interval according to WGRS. The odds ratio for OCP is 0.61 (95% CI: 0.50, 0.74) in the lowest WGRS quartile and 0.51 (95% CI: 0.43, 0.60) in the highest quartile. The overlapping confidence intervals indicate a nonsignificant multiplicative interaction. Additionally, if we assume that approximately 1.3% of women will be diagnosed with ovarian cancer at some point during their lifetime (29) and that 70% of women will use OCPs at some point in their life in this population (estimated from the Ovarian Cancer Association Consortium data), we can calculate the estimated lifetime risk of ovarian cancer and its corresponding 95% confidence interval within each WGRS stratum (Figure 2) for OCP users and nonusers. Estimates of lifetime absolute risk are 0.75% (95% CI: 0.57, 0.98) for OCP users and 1.23% (95% CI: 1.00, 1.51) for OCP nonusers in the lowest WGRS stratum, with a difference of 0.48% (95% CI: 0.02, 0.94); for subjects in the highest WGRS stratum, the corresponding numbers are 1.40% (95% CI: 1.08, 1.81) and 2.72% (95% CI: 2.05, 3.60), respectively, with a difference of 1.32% (95% CI: 0.24, 2.52), showing why the test for RERI is significant.

Figure 1.

Odds ratio for use of oral contraceptive pills (OCPs) by quartile of weighted genetic risk score in a simulated analysis of gene-environment interaction and ovarian cancer risk. Data were obtained from 15 studies in the Ovarian Cancer Association Consortium (30, 38–55). The odds ratios were estimated using standard logistic regression with adjustment for history of endometriosis, first-degree family history of ovarian cancer, parity, tubal ligation, age, and study site. Bars, 95% confidence intervals.

Figure 2.

Predicted probability of ovarian cancer among oral contraceptive pill (OCP) users and nonusers by quartile of weighted genetic risk score in a simulated analysis of gene-environment interaction and ovarian cancer risk. Data were obtained from 15 studies in the Ovarian Cancer Association Consortium (30, 38–55). The relative risk parameters were obtained from a standard logistic regression model adjusting for history of endometriosis, first-degree family history of ovarian cancer, parity, tubal ligation, age, and study site. We assumed that approximately 1.3% of women would be diagnosed with ovarian cancer at some point during their lifetime and that 70% of women would use OCPs at some point in their life. The predicted probabilities were estimated by fixing other covariates at their most frequent value. Bars, 95% confidence intervals.

Results from the simulation study

Type I error

Web Table 7 presents type I errors for different tests of RERI. One can observe that UML maintains a nominal level α across different choices of ${\mathrm{\theta }}_{GE}$. An inflated type I error associated with CML is observed when the G-E independence assumption is violated. The EB test is valid when exp(θ_GE) = 1 and modestly inflates type I error when G is associated with E. The maximal observed type I error of EB at α = 0.05 is 0.099 when the sample size is 40,000, the test size is 0.05, and exp(θ_GE) = 1.1. Web Figure 4 shows how type I error varies with exp(θ_GE) for the 3 estimators. The type I error of CML is very sensitive to the G-E association, but the performance of EB is relatively robust, with a marked reduction in type I error compared with CML. The findings remain similar for different choices of $p_G$, $p_E$, ${\mathrm{OR}}_G$, and ${\mathrm{OR}}_E$ (Web Tables 8 and 9).

Results from additional simulation mimicking a genome-wide association study

To justify the use of the EB estimator in genome-wide assessment of G-E interaction, we conduct another simulation study similar to that in Mukherjee et al. (8), which generates 2,000 cases and controls with 1 causal marker together with M − 1 null markers, where M is 10,000. The G-E independence parameter ${\mathrm{\theta }}_{GE}$ in controls has a random mixture distribution with a point mass around independence, and $p_{\mathrm{ind}}$ is the proportion of null loci that follow G-E independence. The detailed simulation setting is presented in Web Appendix 8. The expected nominal level for both the familywise error rate and the expected false-positive rate is 0.05 when G-E independence holds. However, if there is G-E dependence for a proportion of markers, Bonferroni correction cannot guarantee the nominal level for EB and CML. As shown in Table 2, when 99% of the markers are independent, EB maintains a familywise type I error rate of 0.06 and an expected number of false positives of 0.06. The performance of CML is significantly worse, with a familywise error rate of 99% and an expected number of false positives of 3.76.

Table 2.

Empirical Familywise Type I Error Rate at a 5% Overall Level of Significance and Expected Number of False-Positive Findings Corresponding to UML, CML, and the EB Wald Test

	Proportion of Markers Satisfying Gene-Environment Independence (pind)a
	0.95	0.99	0.995	0.9975	0.9995	1.00
Empirical familywise type I errorb
UML	0.084	0.072	0.062	0.071	0.041	0.058
CML	1.000	0.994	0.966	0.745	0.874	0.064
EB	0.138	0.056	0.045	0.038	0.042	0.035
Expected no. of false positivesc
UML	0.085	0.073	0.062	0.071	0.042	0.059
CML	23.451	3.761	2.814	1.050	0.937	0.067
EB	0.150	0.060	0.045	0.039	0.044	0.035

Abbreviations: CML, constrained maximum likelihood; EB, empirical Bayes; RERI, relative excess risk due to interaction; SD, standard deviation; UML, unconstrained maximum likelihood.

^a The population-level gene-environment (G-E) association structure among null loci is assumed to be of the form of a mixture distribution reflecting the fact that a large fraction (i.e., $p_{\mathrm{ind}}$) of the single nucleotide polymorphisms are indeed independent of E in the population, whereas the remaining $(1-p_{\mathrm{ind}})$ single nucleotide polymorphisms show some departures from the independence assumption following an N (0, SD = ln(1.5)/2) distribution.

^b The Wald test is for RERI = 0 under a large-scale genome-wide G × E scan simulation scenario with 10,000 markers and 2,000 cases and controls. Empirical familywise type I error is estimated as the empirical proportion of data sets declaring at least 1 null marker to be significant using the level of significance α/10,000. This estimates the probability of at least 1 false-positive discovery under the global null hypothesis.

^c The expected number of false positives is estimated as the average number of falsely rejected null hypotheses, averaged over 1,000 data sets.

Power

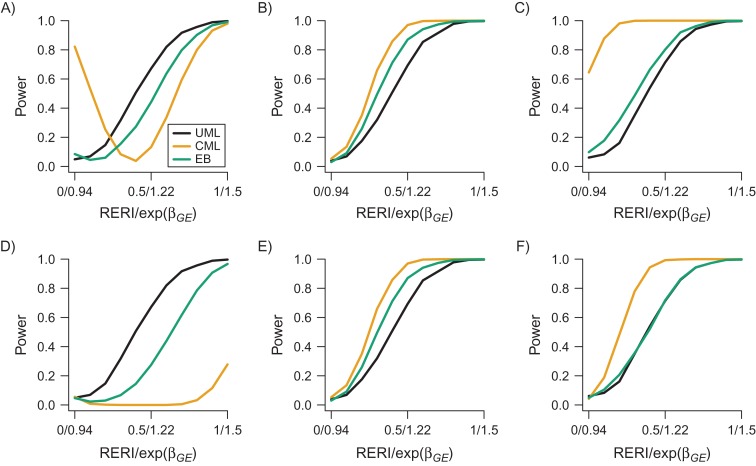
Figure 3 shows the power curves of the Wald test for 3 estimators with ${\mathrm{H}}_0:\mathrm{RERI}=0$ under different strengths of G-E association (Web Tables 10–15). It is hard to compare the estimated powers directly from the figure, as the inflated type I error of CML and EB leads to misleadingly high power values. Hence, we assess the power at empirical $\mathrm{\alpha }$ for CML and EB, which controls the corresponding type I error at 0.05. UML is most efficient when exp(θ_GE) = 0.8, CML is most efficient when exp(θ_GE) = 1 and 1.2, and EB power always lies in between. For a sample numerical comparison, let us compare the powers of the 3 approaches at RERI = 0.5 to represent one typical scenario. When exp(θ_GE) = 0.8, the empirical power of EB (0.275) is 41% lower than that of UML (0.672); meanwhile, CML has nearly 0 power. When exp(θ_GE) = 1, the empirical power of EB (0.870) is 25% higher than that of UML (0.693) but 10% lower than that of CML (0.970). When exp(θ_GE) = 1.2, the empirical power of EB (0.718) is slightly higher than that of UML (0.714) but 28% lower than that of CML (0.993). We then compare the power of the Wald test for ${\widehat{\mathrm{RERI}}}_{\mathrm{CML}}$ with that of the LRT for additive interaction (see Web Figure 5). The power of the LRT is uniformly slightly higher than that of the Wald test, with a true value of RERI varying from 0 to 0.5 with a grid of 0.1. Results for absolute relative bias and MSE are shown in Web Appendix 9, Web Tables 16–19, and Web Figure 6.

Figure 3.

Power curves of unconstrained maximum likelihood (UML), constrained maximum likelihood (CML), and the empirical Bayes (EB) Wald test for the relative excess risk due to interaction (RERI) under different strengths of gene-environment (G-E) association in a simulated analysis of gene-environment interaction and ovarian cancer risk. Data were obtained from 15 studies in the Ovarian Cancer Association Consortium (30, 38–55). Data were generated on 4,000 cases and 4,000 controls with the fixed parameters ${\mathit{p}}_{\mathit{G}}=0.2$, ${\mathit{p}}_{\mathit{E}}=0.3$, ${\mathrm{OR}}_{\mathit{G}}=1.2$, and ${\mathrm{OR}}_{\mathit{E}}=1.5$. RERI changes from 0 to 1.5 with a grid level of 0.1, and corresponding multiplicative interaction changes from 0.94 to 1.78. The top panels (A, B, and C) correspond to the raw power, whereas the bottom panels (D, E, and F) correspond to the power at empirical $\alpha$. The left, center, and right panels correspond to different values of the G-E association odds ratio (OR)—that is, exp(θ_GE) = 0.8, exp(θ_GE) = 1.0, and exp(θ_GE) = 1.2, respectively.

DISCUSSION

In this paper, we extend the EB estimator of G × E interaction proposed earlier on the multiplicative scale to the additive scale in case-control studies. The EB estimator exploits the G-E independence assumption to perform a tradeoff between bias and efficiency. The simulation study showed that the test based on the EB estimator can provide good control of type I error and that it is always intermediate between UML and CML with respect to power, relative bias, and mean squared error. In the ovarian cancer data example, we conducted a W/GRS × OCP analysis to illustrate the application of the proposed method. We found a significant additive W/GRS × OCP interaction but insignificant multiplicative interaction at α = 0.05.

As an inherent limitation of case-control studies, only the relative risk can be estimated (e.g., RERI) instead of the underlying direct measure (e.g., $p_{\mathrm{additive}}$ in equation 1), because $p_{11}$ can only be estimated from cohort data. However, general population incidence data from cohort studies can be combined with case-control risk-factor models to estimate absolute risks in population-based case-control studies (64), as we carried out in Figure 2. If the rare disease assumption for each configuration of G and E does not hold, approximating the relative risk by means of the odds ratio in case-control studies will not be accurate, and thus the proposed estimate of RERI may depart from the truth. By using the retrospective maximum likelihood estimates, prior guesses for disease prevalence, and adaptive combinations like the EB procedure, we can make our inference less biased under violation of the rare disease and G-E independence assumptions.

There is increasingly more interest in inference for additive interaction using case-control data. Tchetgen Tchetgen et al. (65) described a general approach to test for G × E additive interaction exploiting G-E independence which is robust to possible misspecification of main effects in the outcome regression. Han et al. (66) proposed a score test for UML and CML estimators of genetic associations under the additive null hypothesis. In the future, it will be of analytical interest to establish an EB version of the adaptive score test and the adaptive LRT, since most of the recent work has been in terms of combining estimators but not tests.

Abbreviations

CI

confidence interval

CML

constrained maximum likelihood

EB

empirical Bayes

GRS

genetic risk score

LRT

likelihood ratio test

MLE

maximum likelihood estimate

OCP

oral contraceptive pill

RERI

relative excess risk due to interaction

SNP

single nucleotide polymorphism

UML

unconstrained maximum likelihood

WGRS

weighted genetic risk score