Mammographic Density Reduction as a Prognostic Marker for Postmenopausal Breast Cancer: Results Using a Joint Longitudinal-Survival Modeling Approach

Abstract

Previous studies have linked reductions in mammographic density after a breast cancer diagnosis to an improved prognosis. These studies focused on short-term change, using a 2-stage process, treating estimated change as a fixed covariate in a survival model. We propose the use of a joint longitudinal-survival model. This enables us to model long-term trends in density while accounting for dropout as well as for measurement error. We studied the change in mammographic density after a breast cancer diagnosis and its association with prognosis (measured by cause-specific mortality), overall and with respect to hormone replacement therapy and tamoxifen treatment. We included 1,740 women aged 50–74 years, diagnosed with breast cancer in Sweden during 1993–1995, with follow-up until 2008. They had a total of 6,317 mammographic density measures available from the first 5 years of follow-up, including baseline measures. We found that the impact of the withdrawal of hormone replacement therapy on density reduction was larger than that of tamoxifen treatment. Unlike previous studies, we found that there was an association between density reduction and survival, both for tamoxifen-treated women and women who were not treated with tamoxifen.

Reductions in mammographic density after a diagnosis of breast cancer have been linked to an improved prognosis among women treated with adjuvant tamoxifen therapy (1–3). The studies that have made this link have focused on short-term change. For example, Li et al. (1) measured this change as the difference between the density at a baseline measurement (taken close to diagnosis and prior to treatment) and a follow-up measurement, at most 3 years after the baseline measurement. Moreover, the analyses have been carried out as a 2-stage process, first quantifying change and then using the calculated change as a fixed covariate in a regression model for event times (prognosis). Nyante et al. (2) recently reported a “pilot study” that sampled 40 patients from their prior study of patients taking tamoxifen (3) who were alive 5 years after diagnosis, for whom they obtained 5 (approximately yearly) postdiagnosis mammograms. They used these mammograms to investigate patterns of change in mammographic density after diagnosis using linear regression models. They concluded that most of the mammographic density reduction occurred within 12 months of the start of tamoxifen treatment and that a single time point could identify patients with substantial density decline.

In Li et al. (1), analysis was based on 2 mammograms per woman (a large number of images were discarded). In the present study, we revisit their study database and carry out an analysis based on all available images, approximately 6 times the number that were used in Li et al. (1). By including all images, we hope to learn more about change in mammographic density after breast cancer diagnosis. The original study focused on studying survival from breast cancer and considered mammographic density only as a covariate. Here, we analyze the data using a joint longitudinal-survival modeling approach (4–6), an approach that can be used to analyze a repeatedly measured biomarker or exposure (in this case, mammographic density) within a time-to-event setting (here, breast cancer–specific death). For studying the longitudinal process, the joint model correctly accounts for loss to follow-up (i.e., correctly handles the potential association between the longitudinal measurements and drop-out) while taking random variation into account (breast density is known to be measured with considerable measurement error). For studying survival, the joint model efficiently accounts for measurement error in the longitudinal exposure. Although descriptions of the concept of joint modeling, and tutorials on the method, have appeared in clinical and epidemiologic journals (7–9), the approach is not used as widely as it could be.

In addition to demonstrating the use of the joint-modeling statistical approach, we contribute to the literature aimed at understanding mammographic density change after diagnosis and treatment and its association with prognosis. Using joint modeling allows us to include all available images, thus enabling improved estimation of changes in mammographic density after diagnosis and treatment, and to quantify change for different groups of women. In our context, it is the density change shortly after diagnosis that is of main interest. Our study included women who were not treated with tamoxifen, as well as women who were, and we had information on hormone replacement therapy (HRT) prior to diagnosis. We were therefore able to use modeling to compare treatment groups (HRT prior to diagnosis and tamoxifen use after diagnosis) in terms of density change and its association with survival, and we could additionally explore interaction effects between density change and treatment.

METHODS

We used data from an observational, population-based case-control study on breast cancer in Sweden (10). All Swedish-born women who were diagnosed with a breast cancer in Sweden during 1993–1995, at ages 50–74 years, were invited to participate in the study; 84% participated by answering a questionnaire. Mammograms for these women were collected at a later stage from radiology departments. For the present study, we included postmenopausal women with a baseline image, defined as an image taken at most 1 year prior to diagnosis and before 1 month after diagnosis. Individuals with missing covariate information were not included, unless the missing information was only with respect to estrogen receptor (ER) status and grade (for which a “missing” category was included when fitting the models); this is the same approach as used by Li et al. (1) (This removed 90 individuals.) For the eligible women, images during the first 5 years after diagnosis were included in the analysis. Only mediolateral oblique (MLO) images from the contralateral breast were considered. For details on the collection of mammograms and measurement of mammographic density, see Li et al. (11). In brief, film mammograms were digitized by using an Array 2905HD Laser Film Digitizer (Array Corp., Tokyo, Japan). As in the original study, density measurements were obtained using the automated thresholding method described in Li et al. (11). This machine-learning method incorporates the knowledge of a trained reader by using segmentations obtained by Cumulus (Byng et al. (12)) as training data.

The time scale was time since diagnosis, and death due to breast cancer was the event of interest. Individuals were censored at emigration, death due to other causes, or, if alive, at end of follow-up (December 31, 2008). Individuals who started tamoxifen treatment later than 122 days after diagnosis were also censored at that date (77 individuals). The maximum duration of follow-up was just over 15 years.

For analysis, a joint model was used to model mammographic density over time since diagnosis as well as breast cancer–specific survival. A joint model consists of 2 parts: a model for the trajectory of the longitudinal measurements and a model for the time-to-event data. The most common form of joint model combines a linear mixed effects model with a survival model (time-to-event model), in which the submodels are linked through shared random (and common fixed) effects.

The longitudinal submodel can be expressed as:

$${\mathit{y}}_{\mathit{i}}({\mathit{t}}_{\mathit{ij}})={\mathit{m}}_{\mathit{i}}({\mathit{t}}_{\mathit{ij}})+{\mathrm{\epsilon }}_{\mathit{ij},}{\mathrm{\epsilon }}_{\mathit{ij}}~\mathit{N}(0,{\mathrm{\sigma }}^2),$$ (1)

where $y_i(t_{ij})$ is the jth observed value of the repeatedly measured exposure (mammographic density) for individual $i$, measured at time point $t_{ij}$, and $m_i(t_{ij})$ includes fixed effects and random effects. Measurement error is incorporated through ${\mathrm{\epsilon }}_{ij}$, under the assumption that $cov\left({\mathrm{\epsilon }}_{ij,}{\mathrm{\epsilon }}_{ik}\right)=0;j\ne k$, and that ${\mathrm{\epsilon }}_{ij}$ is independent of the random effects included in $m_i(t_{ij})$. In our longitudinal model for mammographic density, time since diagnosis (measured in years) was modeled with a polynomial of degree 3 for the fixed effects and linearly for the random effect. As the measure of mammographic density, we used dense area in cm², which was square-root transformed when entering the model. We allowed the trend over time to differ according to tamoxifen treatment (yes/no) and HRT use (yes/no). For mammographic density at baseline, we included an effect of HRT use, age at diagnosis (as a continuous variable), and body mass index (BMI). BMI was calculated as weight (kg)/height (m)² and divided into quartiles, with lowest quartile as the referent. The longitudinal submodel used in our analyses can be expressed as:

$$\begin{array}{ll}{m}_i\left({\mathit{t}}_{\mathit{ij}}\right)\hfill & ={\mathrm{\beta }}_0+b_{0_i}+({\mathrm{\beta }}_1+b_{1_i}){\mathit{t}}_{\mathit{ij}}+{\mathrm{\beta }}_2{{\mathit{t}}_{\mathit{ij}}}^2+{\mathrm{\beta }}_3{{\mathit{t}}_{\mathit{ij}}}^3\hfill \\ \hfill & +({\mathrm{\beta }}_4{\mathit{t}}_{\mathit{ij}}+{\mathrm{\beta }}_5{{\mathit{t}}_{\mathit{ij}}}^2+{\mathrm{\beta }}_6{{\mathit{t}}_{\mathit{ij}}}^3)\mathrm{T}\mathrm{A}{\mathrm{M}}_i\hfill \\ \hfill & +({\mathrm{\beta }}_7{\mathit{t}}_{\mathit{ij}}+{\mathrm{\beta }}_8{{\mathit{t}}_{\mathit{ij}}}^2+{\mathrm{\beta }}_9{{\mathit{t}}_{\mathit{ij}}}^3)\mathrm{H}\mathrm{R}{\mathrm{T}}_i+{\mathrm{\delta }}_1\mathrm{H}\mathrm{R}{\mathrm{T}}_i\hfill \\ \hfill & +{\mathrm{\delta }}_2\mathrm{A}\mathrm{G}{\mathrm{E}}_i+{\mathrm{\delta }}_3\mathrm{B}\mathrm{M}{\mathrm{I}}_{1i}+{\mathrm{\delta }}_4\mathrm{B}\mathrm{M}{\mathrm{I}}_{2i}+{\mathrm{\delta }}_5\mathrm{B}\mathrm{M}{\mathrm{I}}_{3i},\hfill \end{array}$$ (2)

where β terms and δ terms represent fixed effects, b terms are normally distributed random effects, TAM is an indicator for tamoxifen treatment, HRT is an indicator for HRT use, AGE is the variable for age at diagnosis, and BMI₁, BMI₂, and BMI₃ denote BMI quartiles 2, 3, and 4. In the literature, such models are often written in shorthand matrix form, as in:

$${\mathit{m}}_{\mathit{i}}({\mathit{t}}_{\mathit{ij}})={\mathit{X}}_{\mathit{i}}^{\mathit{T}}({\mathit{t}}_{\mathit{ij}})\mathbf{\beta }+{\mathit{Z}}_{\mathit{i}}^{\mathit{T}}({\mathit{t}}_{\mathit{ij}}){\mathit{b}}_{\mathit{i}}+{\mathit{u}}_{\mathit{i}}^{\mathit{T}}\mathbf{\delta },{\mathit{b}}_{\mathit{i}}~\mathit{N}(0,{\mathbf{\Sigma }}_{\mathit{b}}),$$ (3)

where fixed effects β, with design matrix ${\mathit{X}}_i$, are shared across individuals, and patient-specific random effects ${\mathit{b}}_i$, with design matrix ${\mathit{Z}}_i$, serve to capture the correlation between measurements of the same patient. It is possible to model nonlinear trajectories by including (fractional) polynomials of time in both ${\mathit{X}}_i$ and ${\mathit{Z}}_i$, and the effect of covariates on the trajectory can be modeled by including interactions with time in ${\mathit{X}}_i$ and possibly ${\mathit{Z}}_i$, as seen in equation (2). Baseline covariates can be included, represented by ${\mathit{u}}_i$, with a vector of corresponding regression coefficients, δ.

The survival submodel is generally chosen to be a proportional hazards model. We chose to model the baseline hazard in the survival submodel with a flexible parametric model (13, 14), which uses restricted cubic splines for the underlying cumulative hazard, with proportional hazards for covariate effects. The model included the covariates age at diagnosis (as a continuous variable; AGE), BMI (in quartiles with lowest as referent; BMI₁, BMI₂, BMI₃), size of tumor (in mm categories: <10 as referent, 10–19, 20–29, 30–39, 40–49, ≥50; indicator variables SIZE₁ to SIZE₅ for nonreference categories), number of affected lymph nodes (in categories: 0 as referent, 1–3, 4–9, ≥10; NODES₁, NODES₂, NODES₃), ER status (positive as referent, negative, missing; ER₁, ER₂), grade (well differentiated as referent, moderately differentiated, poorly differentiated, missing; GRADE₁, GRADE₂, GRADE₃), an indicator for chemotherapy treatment (CHEM), an indicator for radiotherapy treatment (RAD), an indicator for low mammographic density at baseline (LOWBASE), and an indicator for tamoxifen treatment (TAM), as well as the estimated random effect ${\hat{b}}_{1_i}$ from the longitudinal submodel. Our model, for the cumulative hazard $H_i(t)$, can be written as:

$$\begin{array}{ll}{H}_i(t)\hfill & =exp\left({\mathrm{\lambda }}_0{+\mathrm{\lambda }}_1{s}_1(t){+\mathrm{\lambda }}_2{s}_2(t){+\mathrm{\lambda }}_3{s}_3(t)\right)\hfill \\ \hfill & \times exp{(\mathrm{\phi }}_1\mathrm{A}\mathrm{G}{\mathrm{E}}_i{+\mathrm{\phi }}_2\mathrm{B}\mathrm{M}{\mathrm{I}}_{1i}{+\mathrm{\phi }}_3\mathrm{B}\mathrm{M}{\mathrm{I}}_{2i}{+\mathrm{\phi }}_4\mathrm{B}\mathrm{M}{\mathrm{I}}_{3i}\hfill \\ \hfill & {+\mathrm{\phi }}_5\mathrm{S}\mathrm{I}\mathrm{Z}{\mathrm{E}}_{1i}{+\mathrm{\phi }}_6\mathrm{S}\mathrm{I}\mathrm{Z}{\mathrm{E}}_{2i}{+\mathrm{\phi }}_7\mathrm{S}\mathrm{I}\mathrm{Z}{\mathrm{E}}_{3i}{+\mathrm{\phi }}_8\mathrm{S}\mathrm{I}\mathrm{Z}{\mathrm{E}}_{4i}\hfill \\ \hfill & {+\mathrm{\phi }}_9\mathrm{S}\mathrm{I}\mathrm{Z}{\mathrm{E}}_{5i}{+\mathrm{\phi }}_{10}\mathrm{N}\mathrm{O}\mathrm{D}\mathrm{E}{\mathrm{S}}_{1i}{+\mathrm{\phi }}_{11}\mathrm{N}\mathrm{O}\mathrm{D}\mathrm{E}{\mathrm{S}}_{2i}\hfill \\ \hfill & {+\mathrm{\phi }}_{12}\mathrm{N}\mathrm{O}\mathrm{D}\mathrm{E}{\mathrm{S}}_{3i}{+\mathrm{\phi }}_{13}\mathrm{E}{\mathrm{R}}_{1i}{+\mathrm{\phi }}_{14}\mathrm{E}{\mathrm{R}}_{2i}\hfill \\ \hfill & {+\mathrm{\phi }}_{15}\mathrm{G}\mathrm{R}\mathrm{A}\mathrm{D}{\mathrm{E}}_{1i}{+\mathrm{\phi }}_{16}\mathrm{G}\mathrm{R}\mathrm{A}\mathrm{D}{\mathrm{E}}_{2i}{+\mathrm{\phi }}_{17}\mathrm{G}\mathrm{R}\mathrm{A}\mathrm{D}{\mathrm{E}}_{3i}\hfill \\ \hfill & {+\mathrm{\phi }}_{18}\mathrm{C}\mathrm{H}\mathrm{E}{\mathrm{M}}_i{+\mathrm{\phi }}_{19}\mathrm{R}\mathrm{A}{\mathrm{D}}_i{+\mathrm{\phi }}_{20}\mathrm{D}\mathrm{E}\mathrm{N}{\mathrm{S}}_i{+\mathrm{\phi }}_{21}\mathrm{T}\mathrm{A}{\mathrm{M}}_i\hfill \\ \hfill & {+(\mathrm{\alpha }}_0{+\mathrm{\alpha }}_1\mathrm{T}\mathrm{A}{\mathrm{M}}_i{+\mathrm{\alpha }}_2\mathrm{L}\mathrm{O}\mathrm{W}\mathrm{B}\mathrm{A}\mathrm{S}{\mathrm{E}}_i{+\mathrm{\alpha }}_3\mathrm{T}\mathrm{A}{\mathrm{M}}_i\hfill \\ \hfill & \times \mathrm{L}\mathrm{O}\mathrm{W}\mathrm{B}\mathrm{A}\mathrm{S}{\mathrm{E}}_i){\hat{b}}_{1_i}),\hfill \end{array}$$ (4)

where the first term is the baseline cumulative hazard including restricted cubic splines for time (s(t)), and the second includes the log hazard ratios for covariate effects (φ) and terms linking the longitudinal and the survival submodel (α).

More generally, the survival submodel can be expressed on the hazard scale as:

$$h_i(t)=h_0(t)exp({\mathbf{\phi }}^T{\mathit{v}}_i+f(m_i(t))\mathrm{\alpha }),$$ (5)

where $h_0(t)$ is the baseline hazard, and ${\mathit{v}}_i$ is a set of baseline covariates with log hazard ratios φ. The association parameter, $\mathrm{\alpha }$, links the longitudinal trajectory and the hazard through some functional form $f(m_i(t))$. In the present study, focused on the reduction of mammographic density after a breast cancer diagnosis, we are most interested in the estimated rate of change shortly after diagnosis, because the majority of density reduction is expected to occur then, and how it affects prognosis for women using tamoxifen and/or stopping HRT. We have used the estimated rate of change at baseline (t = 0) in the hazard equation (5), which can be expressed as:

$$\mathit{f}({\mathit{m}}_{\mathit{i}}(\mathit{t}))=\frac{d{m}_i(t)}{dt}{|}_{\mathit{t}=0}={\hat{\beta }}_1+{\stackrel{\mathit{ˆ}}{\mathit{b}}}_{1_{\mathit{i}}}+\mathit{X}{\mathit{S}}_{\mathit{i}}^{\mathit{T}}\stackrel{\mathbf{ˆ}}{\mathbf{\beta }}\mathit{S},$$ (6)

where $\mathit{X}{\mathit{S}}_i^T\stackrel{\mathbf{ˆ}}{\mathbf{\beta }}\mathit{S}$ represents the effect of covariates that are modeled with an interaction with time. The notation S is used to indicate that this is a subset of β and ${\mathit{X}}_i$. Because both ${\hat{\mathrm{\beta }}}_1$ and $\mathit{X}{\mathit{S}}_i^T\stackrel{\mathbf{ˆ}}{\mathbf{\beta }}\mathit{S}$ are constant across individuals with the same covariate pattern, we simplified equation (6) to:

$$f(m_i(t))={\hat{b}}_{1_i},$$ (7)

which represents the individual deviation in rate of change at baseline from the mean rate of change of their subgroup defined by $\mathit{XS},$ and is the link between the submodels that we have used in our model. Therefore, $\mathrm{\alpha }$ is the log hazard ratio for a 1-unit increase in deviation in rate of change at baseline from the expected rate of change at baseline given the covariate pattern $\mathit{XS}$, where we assume that this deviation has the same effect across all subgroups defined by $\mathit{XS}$. Even though this does not have an intuitive interpretation, it gives valid P values for the association of interest between the longitudinal and survival processes, and this parameterization is easily implemented in existing software (15) and an established association structure (16).

To formally compare the effect of early density reduction on prognosis between women treated and not treated with tamoxifen, we included a term for interaction between the random effect and tamoxifen treatment (${\mathrm{\alpha }}_1$). Li et al. (1) excluded women in the lowest density quantile at baseline because women with a low density at diagnosis cannot experience a large reduction in absolute density. Because we explicitly modeled density (jointly with survival), we included all women in our analysis, even those with low density at baseline. We allowed, however, for a different association between baseline slope (as measured by the random effect) and prognosis for the quartile with lowest density by including additional interactions (${\mathrm{\alpha }}_2$ and ${\mathrm{\alpha }}_3$).

We note that our approach to linking the longitudinal trajectory and the hazard is not common—more usually the 2 submodels are linked through the current value of the repeatedly measured exposure, expressed as:

$$f(m_i(t))=m_i(t)={\mathit{X}}_i^T(t)\stackrel{\mathbf{ˆ}}{\mathbf{\beta }}+Z_i^T(t){\stackrel{\mathit{ˆ}}{\mathit{b}}}_i+{\mathit{u}}_i^T\stackrel{\mathbf{ˆ}}{\mathbf{\delta }},$$ (8)

and $\mathrm{\alpha }$ is interpreted as the log hazard ratio for a 1-unit increase in the longitudinal outcome at time $t$. Another common approach is to link the 2 parts by the estimated current rate of change of the estimated exposure trajectory, where:

$$f(m_i(t))=\frac{d{m}_i(t)}{dt}=\frac{d{\mathit{X}}_i^T(t_{ij})\stackrel{\mathbf{ˆ}}{\mathbf{\beta }}+{\mathit{Z}}_i^T(t_{ij}){\stackrel{\mathbf{ˆ}}{\mathbf{b}}}_i+{\mathit{u}}_i^T\stackrel{\mathbf{ˆ}}{\mathbf{\delta }}}{dt},$$ (9)

and $\mathrm{\alpha }$ is interpreted as the log hazard ratio for a 1-unit increase in the rate of change of the longitudinal outcome at time $t$.

All models were fitted using Stata, version 13 (StataCorp LP, College Station, Texas), using the stjm command developed by Crowther et al. (15). Assumptions regarding normality of the residuals and random effects of the longitudinal model were checked using QQ-plots. The study was approved by the institutional review board at Karolinska Institutet.

RESULTS

The final study population consisted of 1,740 individuals, of whom 269 died due to breast cancer during follow-up (Table 1). Among the study participants, 796 individuals (45.7%) were treated with tamoxifen, and 866 (49.8%) had been treated with HRT prior to diagnosis (Table 2). The participants had a total of 6,317 mammograms available and measured from the first 5 years of follow-up, including the baseline image. There were 329 individuals with only 1 image, and 1 woman had as many as 8 images during follow-up (Table 3).

Table 1.

Number of Individuals, Person-Years, and Number of Deaths Due to Breast Cancer, According to Tumor Characteristics, Body Mass Index, and Treatment, Among Women Aged 50–74 Years, Diagnosed With Postmenopausal Breast Cancer in Sweden During 1993–1995

Characteristic	No. of Individuals	Person-Years	No. of Deaths
Estrogen-receptor status
Negative	242	2,727.6	60
Positive	1,003	12,532.8	159
Missing	495	6,405.5	50
Grade
Well differentiated	186	2,494.1	8
Moderately differentiated	509	6,441.4	74
Poorly differentiated	497	5,940.2	114
Missing	548	6,790.1	73
Body mass indexa
First quartile (14.53–22.89)	435	5,489.7	61
Second quartile (22.94–25.28)	434	5,500.2	60
Third quartile (25.31–28.08)	431	5,396.8	64
Fourth quartile (28.13–52.34)	440	5,279.1	84
Size of tumor, mm
1–9	366	4,741.1	21
10–19	817	10,617.7	92
20–29	359	4,229.3	90
30–39	116	1,273.7	29
40–49	43	448.0	17
≥50	39	356.1	20
No. of affected lymph nodes
0	1,253	16,323.2	110
1–3	335	3,954.7	78
4–9	106	1,069.9	47
≥10	46	318.0	34
Chemotherapy
No	1,613	20,383.6	216
Yes	127	1,282.3	53
Radiotherapy
No	973	11,580.4	196
Yes	767	10,085.5	73

^a Weight (kg)/height (m)².

Table 2.

Number of Individuals and Number of Deaths Due to Breast Cancer, According to Hormone Replacement Therapy and Tamoxifen Treatment Groups, Among Women Aged 50–74 Years, Diagnosed With Postmenopausal Breast Cancer in Sweden During 1993–1995

Treated With Tamoxifen	Hormone Replacement Therapy Use
	No			Yes			Overall
	No. of Individuals	No. of Deaths	%	No. of Individuals	No. of Deaths	%	No. of Individuals	No. of Deaths	%
No	466	66	26.8	478	52	27.5	944	118	54.3
Yes	400	88	23.0	396	63	22.8	796	151	45.7
Total	866	154	49.8	874	115	50.2	1,740	269	100.0

Table 3.

Number of Mammograms During Follow-up (5 Years After Diagnosis), Including Baseline Image, Among Women Aged 50–74 Years, Diagnosed With Postmenopausal Breast Cancer in Sweden During 1993–1995

No. of Images	No. of Individuals	%
1	329	18.9
2	148	8.5
3	255	14.7
4	321	18.5
5	504	29.0
6	159	9.1
7	23	1.3
8	1	0.1

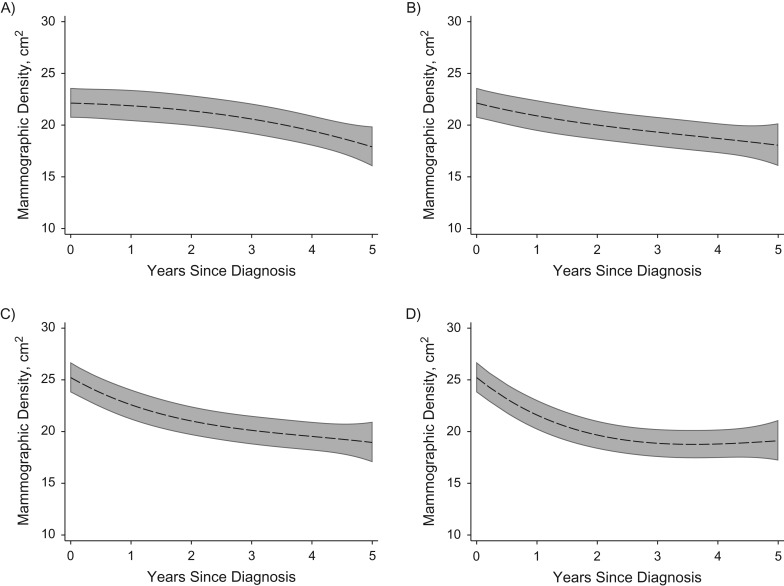
Figure 1 shows the estimated average longitudinal trajectories of mammographic density after diagnosis, by HRT treatment and tamoxifen treatment, for women of age 60 at diagnosis, within the lowest category of BMI. For women not using HRT and not treated with tamoxifen (Figure 1A), the estimates were obtained from equation (2) as:

$${\hat{\mathrm{\beta }}}_0+{\hat{b}}_{0_i}+({\hat{\mathrm{\beta }}}_1+{\hat{b}}_{1_i}){\mathit{t}}_{\mathit{ij}}+{\hat{\mathrm{\beta }}}_2{{\mathit{t}}_{\mathit{ij}}}^2+{\hat{\mathrm{\beta }}}_3{{\mathit{t}}_{\mathit{ij}}}^3+{\hat{\mathrm{\delta }}}_2\times 60.$$

Figure 1.

Estimated mean trend of mammographic density (in cm²) after diagnosis, according to treatment group and hormone replacement therapy (HRT) use, with 95% confidence intervals, for a woman aged 60 years at diagnosis and within the lowest body mass index (BMI) quartile. A) HRT nonusers, tamoxifen nontreated; B) HRT nonusers, tamoxifen-treated; C) HRT users, tamoxifen-nontreated; D) HRT users and tamoxifen-treated.

Similarly, for women who were HRT nonusers and tamoxifen-treated (Figure 1B) estimates were obtained as:

$$\begin{array}{c}{\hat{\mathrm{\beta }}}_0+{\hat{b}}_{0_i}+({\hat{\mathrm{\beta }}}_1+{\hat{b}}_{1_i}){\mathit{t}}_{\mathit{ij}}+{\hat{\mathrm{\beta }}}_2{{\mathit{t}}_{\mathit{ij}}}^2+{\hat{\mathrm{\beta }}}_3{{\mathit{t}}_{\mathit{ij}}}^3+{\hat{\mathrm{\beta }}}_4{\mathit{t}}_{\mathit{ij}}\hfill \\ +{\hat{\mathrm{\beta }}}_5{{\mathit{t}}_{\mathit{ij}}}^2+{\hat{\mathrm{\beta }}}_6{{\mathit{t}}_{\mathit{ij}}}^3+{\hat{\mathrm{\delta }}}_2\times 60,\hfill \end{array}$$

while for women who were HRT users and not treated with tamoxifen (Figure 1C), estimates were obtained as:

$$\begin{array}{c}{\hat{\mathrm{\beta }}}_0+{\hat{b}}_{0_i}+({\hat{\mathrm{\beta }}}_1+{\hat{b}}_{1_i}){\mathit{t}}_{\mathit{ij}}+{\hat{\mathrm{\beta }}}_2{{\mathit{t}}_{\mathit{ij}}}^2+{\hat{\mathrm{\beta }}}_3{{\mathit{t}}_{\mathit{ij}}}^3+{\hat{\mathrm{\beta }}}_7{\mathit{t}}_{\mathit{ij}}\hfill \\ +{\hat{\mathrm{\beta }}}_8{{\mathit{t}}_{\mathit{ij}}}^2+{\hat{\mathrm{\beta }}}_9{{\mathit{t}}_{\mathit{ij}}}^3+{\hat{\mathrm{\delta }}}_1+{\hat{\mathrm{\delta }}}_2\times 60,\hfill \end{array}$$

and last, for women who were HRT users and tamoxifen-treated (Figure 1D), estimates were obtained as:

$$\begin{array}{c}{\hat{\mathrm{\beta }}}_0+{\hat{b}}_{0_i}+({\hat{\mathrm{\beta }}}_1+{\hat{b}}_{1_i}){\mathit{t}}_{\mathit{ij}}+{\hat{\mathrm{\beta }}}_2{{\mathit{t}}_{\mathit{ij}}}^2+{\hat{\mathrm{\beta }}}_3{{\mathit{t}}_{\mathit{ij}}}^3\hfill \\ +{\hat{\mathrm{\beta }}}_4{\mathit{t}}_{\mathit{ij}}+{\hat{\mathrm{\beta }}}_5{{\mathit{t}}_{\mathit{ij}}}^2+{\hat{\mathrm{\beta }}}_6{{\mathit{t}}_{\mathit{ij}}}^3+{\hat{\mathrm{\beta }}}_7{\mathit{t}}_{\mathit{ij}}+{\hat{\mathrm{\beta }}}_8{{\mathit{t}}_{\mathit{ij}}}^2\hfill \\ +{\hat{\mathrm{\beta }}}_9{{\mathit{t}}_{\mathit{ij}}}^3+{\hat{\mathrm{\delta }}}_1+{\hat{\mathrm{\delta }}}_2\times 60.\hfill \end{array}$$

Women on HRT prior to breast cancer diagnosis had, in general, higher mammographic density at diagnosis than did women who never used HRT, but their density was also reduced more after diagnosis (when patients are encouraged to stop taking HRT). The difference in average densities at baseline, according to HRT use, was statistically significant (P < 0.001 for ${\mathrm{\delta }}_1$ in equation 2), and the difference in trajectories was also statistically significant (P < 0.001 for the combined effect of β₇, β₈, and β₉). Women who were treated with tamoxifen had a greater reduction in mammographic density than did women not treated with tamoxifen, and the effect was statistically significant (P = 0.011 for the combined effect of β₄, β₅, and β₆).

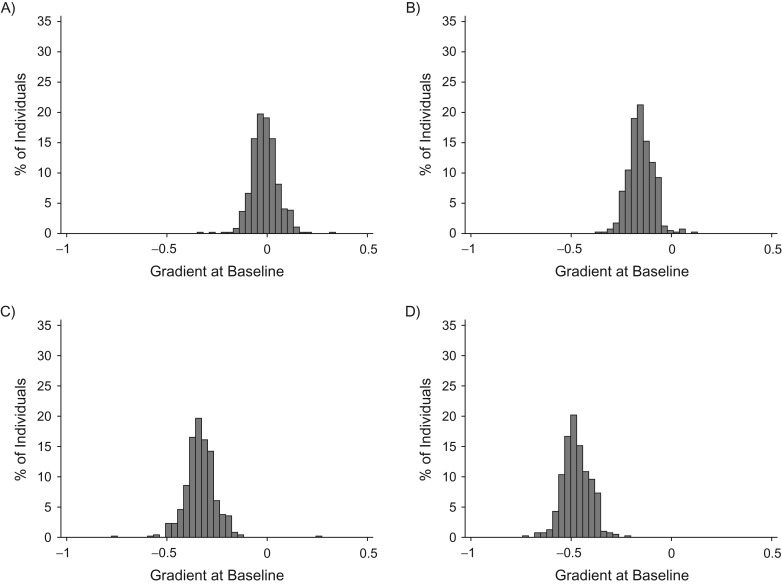
To aid comparison of density changes across treatment groups, we estimated the rate of change at baseline (equation 6) for each individual, and we plotted these estimates according to prior HRT use and tamoxifen use after diagnosis (Figure 2). Because the model is using square root of density, this shows the rate of change in the square root of density at baseline. There was a clear decline in mammographic density among almost all individuals that used HRT prior to diagnosis (Figure 2C and 2D), and the decline was greater among women who used HRT and were subsequently treated with tamoxifen (Figure 2D) than for women who used HRT but were not treated with tamoxifen (Figure 2C). For nonusers of HRT and tamoxifen (Figure 2A), the estimated rate of change at baseline was centered just below 0, and for nonusers of HRT who were treated with tamoxifen (Figure 2B), only a few had an estimated increase at baseline. Overall, the impact on early density reduction was greater from HRT withdrawal than from tamoxifen treatment (Figure 2).

Figure 2.

Histogram of estimated baseline rate of change (in square root of mammographic density) for each individual, according to treatment group and hormone replacement therapy (HRT) use. A) HRT nonusers, tamoxifen nontreated; B) HRT nonusers, tamoxifen-treated; C) HRT users, tamoxifen-nontreated; D) HRT users and tamoxifen-treated.

The estimated deviation in rate of change at baseline (${\hat{b}}_{1_i}$) was used as the main exposure of interest for prognosis, and this effect was allowed to be different for women treated and not treated with tamoxifen as well as those with the lowest quartile of baseline density and those in the 3 higher quartiles. For women in the 3 highest quartiles of baseline density, the deviation in rate of change at baseline was significantly associated with prognosis, with a greater reduction giving a better prognosis, and this effect was significant among both tamoxifen-treated and tamoxifen-nontreated women (P = 0.014 for tamoxifen-treated; P = 0.002 for tamoxifen-nontreated). The effect was not significantly different for tamoxifen-treated versus tamoxifen-nontreated women (P = 0.318). The standard deviation for ${\hat{b}}_{1_i}$ was 0.069, and the hazard ratio for a 1-standard-deviation difference in ${\hat{b}}_{1_i}$ was 1.8 (95% confidence interval: 1.2, 2.7) for tamoxifen-nontreated patients and 1.5 (95% confidence interval: 1.1, 2.1) for tamoxifen-treated patients. The effect of rate of change at baseline (${\hat{b}}_{1_i}$) was not significant for the quartile with the lowest baseline density. We also looked only at women with no previous use of HRT, and within this group the hazard ratio for a 1-standard-deviation difference in ${\hat{b}}_{1_i}$ (standard deviation, 0.048) was 3.2 (95% confidence interval: 1.8, 5.5) for tamoxifen-nontreated women and 2.2 (95% confidence interval: 1.2, 3.8) for tamoxifen-treated women, and again this difference was not statistically significant.

All parameter values, together with 95% confidence intervals, for the model fitted to the full data, are presented in Table 4. As expected, mean baseline mammographic density decreased with increasing age and increasing BMI. Size of the tumor (P value < 0.001), number of affected lymph nodes (P value < 0.001), ER status (P value = 0.037), and grade (P value = 0.036) were significantly associated with prognosis. However, age (P value = 0.781), BMI (P value = 0.232), chemotherapy treatment (P value = 0.840), radiotherapy treatment (P value = 0.403), tamoxifen treatment (P value = 0.915), and baseline density (P value = 0.648) were not significantly associated with prognosis.

Table 4.

Parameter Estimates From the Main Model, Among Women Aged 50–74 Years, Diagnosed With Postmenopausal Breast Cancer in Sweden During 1993–1995

Parameter	Coefficient	95% CI
Longitudinal submodela
t (β1)	−0.02	−0.16, 0.12
t2 (β2)	−0.01	−0.09, 0.07
t3 (β3)	−0.00	−0.01, 0.01
TAM × t (β4)	−0.14	−0.30, 0.03
TAM × t2 (β5)	0.03	−0.06, 0.13
TAM × t3 (β6)	−0.00	−0.02, 0.01
HRT × t (β7)	−0.31	−0.48, −0.14
HRT × t2 (β8)	0.08	−0.02, 0.17
HRT × t3 (β9)	−0.00	−0.02, 0.01
HRT (δ1)	0.32	0.18, 0.45
Age at diagnosis (δ2)	−0.05	−0.06, −0.04
BMI quartile 2 (δ3)	−0.38	−0.56, −0.21
BMI quartile 3 (δ4)	−0.63	−0.81, −0.46
BMI quartile 4 (δ5)	−0.81	−0.98, −0.63
Constant (β0)	7.73	7.11, 8.35
Random effects
SD(b0)	1.25	1.20, 1.31
SD(b1)	0.13	0.11, 0.16
Correlation(b0, b1)	−0.24	−0.35, −0.13
Survival submodelb
Slope association for tamoxifen-nontreated within the 3 highest quartiles of baseline density (α0)	8.63	3.08, 14.17
Slope association for tamoxifen-treated within the 3 highest quartiles of baseline density (α0 + α1)	5.93	1.22, 10.63
Slope association for tamoxifen-nontreated within the lowest quartile of baseline density (α0 + α2)	−6.82	−15.8, 2.15
Slope association for tamoxifen-treated within the lowest quartile of baseline density (α0 + α3)	0.61	−6.65, 7.86
Age at diagnosis (φ1)	0.00	−0.02, 0.03
BMI quartile 2 (φ2)	−0.13	−0.54, 0.27
BMI quartile 3 (φ3)	0.10	−0.30, 0.50
BMI quartile 4 (φ4)	0.26	−0.14, 0.65
Size of tumor, 10–19 mm (φ5)	0.41	−0.11, 0.93
Size of tumor, 20–29 mm (φ6)	1.01	0.46, 1.56
Size of tumor, 30–39 mm (φ7)	0.99	0.34, 1.65
Size of tumor, 40–49 mm (φ8)	1.56	0.78, 2.34
Size of tumor, ≥50 mm (φ9)	1.26	0.52, 2.01
Number of affected lymph nodes, 1–3 (φ10)	0.92	0.52, 1.32
Number of affected lymph nodes, 4–9 (φ11)	1.61	1.12, 2.12
Number of affected lymph nodes, ≥10 (φ12)	2.69	2.02, 3.37
ER status, negative (φ13)	0.49	0.10, 0.88
ER status, missing (φ14)	−0.02	−0.39, −0.35
Grade, moderately differentiated (φ15)	0.87	0.10, 1.65
Grade, poorly differentiated (φ16)	1.08	0.30, 1.86
Grade, missing (φ17)	0.78	−0.00, 1.56
Chemotherapy (φ18)	0.05	−0.44, 0.55
Radiotherapy (φ19)	−0.14	−0.47, 0.19
Baseline mammographic density (φ20)	0.00	−0.01, 0.01
Tamoxifen treatment (φ21)	0.03	−0.47, 0.52
Constant (λ0)	−6.23	−8.13, −4.33
Time spline 1 (λ1)	1.46	1.23, 1.70
Time spline 2 (λ2)	0.36	0.20, 0.52
Time spline 3 (λ3)	−0.02	−0.05, 0.01

Abbreviations: BMI, body mass index; CI, confidence interval; ER, estrogen receptor; HRT, hormone replacement therapy; SD, standard deviation; TAM, tamoxifen treatment.

^a On square root scale.

^b On log cumulative hazard scale. For the time-constant covariates φ_1–φ₂₁, the coefficients are log hazard ratios; hazard ratios can be obtained by exponentiating the coefficient and the CI.

DISCUSSION

To our knowledge, this is the first study to model change in mammographic density after breast cancer diagnosis in a nonselected sample of women (Nyante et al. (2) included only patients treated with tamoxifen). We quantified the decrease in mammographic density after a breast cancer diagnosis in a large sample of women, including both previous HRT users and nonusers, as well as in tamoxifen-treated women and women not treated with tamoxifen. We found that the reduction was greater among HRT users and among women treated with tamoxifen, and that the impact of HRT withdrawal on density change was larger than the impact of tamoxifen. The reduction in density close to diagnosis was associated with prognosis, with a better prognosis with greater reduction. Interestingly, this association was not restricted to women treated with tamoxifen; the association also persisted when we restricted the analysis to women who had not previously used HRT.

We found that the decline in mammographic density was most pronounced shortly after diagnosis, but that this pattern differed between treatment groups. For women who had not used HRT, the decline was stable across time, whereas for HRT-treated women, a steep decline was observed during the first 1.5–2 years following diagnosis. Nyante et al. (2) restricted their study to women who had survived at least 5 years post diagnosis and that had been treated with tamoxifen, and they did not estimate the decline by HRT status. In our study, even though the density reduction was greater among women treated with tamoxifen, we observed a statistically significant effect of density reduction on prognosis among both the treated and the nontreated women. Although we found that the effect of HRT withdrawal on density was considerable, the fact that the association between density reduction and prognosis persisted in women who were not using HRT prior to diagnosis points to withdrawal from HRT not being responsible for the observed association between density change and prognosis observed in earlier studies (1–3).

There are clear advantages to using the joint model rather than separate analyses; perhaps the most important is modeling of the density allowing for measurement error. Mammographic density is influenced by the positioning of the breast on the x-ray plate, and 2 mammograms of the same breast can give substantially different density measures even when taken close in time. Another advantage is that the joint model allows the inclusion of many images; we were able to use all available measures for our study, which improved estimation of density change at all points, including at baseline, which we used as the exposure of interest when studying survival. Additionally, unlike Li et al. (1), we did not have to use a delayed-entry approach.

One limitation of our joint model is that it assumes that there is a smooth change in mammographic density over time. The methodology could, in principle, be adapted to handle a sudden change (e.g., around menopause). However, in our study, only women with postmenopausal breast cancer were included, so this limitation is not likely to be too severe here.

There may be further limitations of our analysis, connected to the variables used to define treatment groups. For tamoxifen, we know only which women were assigned to treatment following diagnosis. We have no information on compliance, which is unfortunate because it is not unusual for women treated with tamoxifen to stop the treatment due to side effects (17). However, if anything, this would likely have resulted in an underestimated effect of tamoxifen on density decline. Another limitation is that we were not able to include tamoxifen treatment as a time-varying effect. We instead censored individuals who started tamoxifen treatment later than 122 days after diagnosis. The binary variable for HRT use was the same as that used in Li et al. (1), which included any HRT use between menopause and diagnosis. This means that we have potentially underestimated the effect of HRT withdrawal on density because some women may have stopped using HRT prior to the baseline mammogram. For a subset of women (n = 1,436), we obtained sufficient information to define HRT use according to date of baseline mammogram. When we repeated our analysis on data from this subset of women, using this variable, we obtained very similar results, in all parts of the model. For example, we obtained estimates of median density change of 0.05, 0.19, 0.40, and 0.54 (instead of 0.01, 0.15, 0.34, and 0,48, in our main analysis) for the 4 groups defined by HRT use and tamoxifen treatment (no/no, no/yes, yes/no, yes/yes).

In summary, we have confirmed earlier findings that reduction in mammographic density after breast cancer diagnosis is associated with prognosis. We have also quantified the reduction by prior HRT use and tamoxifen treatment following diagnosis, using sophisticated methods for jointly modeling longitudinal measurements and time-to-event data.