Epigenomics in 3D: importance of long-range spreading and specific interactions in epigenomic maintenance

Abstract

Recent progresses of genome-wide chromatin conformation capture techniques have shown that the genome is segmented into hierarchically organized spatial compartments. However, whether this non-random 3D organization only reflects or indeed contributes—and how—to the regulation of genome function remain to be elucidated. The observation in many species that 3D domains correlate strongly with the 1D epigenomic information along the genome suggests a dynamic coupling between chromatin organization and epigenetic regulation. Here, we posit that chromosome folding may contribute to the maintenance of a robust epigenomic identity via the formation of spatial compartments like topologically-associating domains. Using a novel theoretical framework, the living chromatin model, we show that 3D compartmentalization leads to the spatial colocalization of epigenome regulators, thus increasing their local concentration and enhancing their ability to spread an epigenomic signal at long-range. Interestingly, we find that the presence of 1D insulator elements, like CTCF, may contribute greatly to the stable maintenance of adjacent antagonistic epigenomic domains. We discuss the generic implications of our findings in the light of various biological contexts from yeast to human. Our approach provides a modular framework to improve our understanding and to investigate in details the coupling between the structure and function of chromatin.

INTRODUCTION

The ability of organisms to precisely regulate gene expression is central to their development. Proper temporal and spatial expressions of genes in higher eukaryotes require activation of transcription during the appropriate developmental stages. In response to environmental and developmental cues, cells can adopt different gene expression patterns to differentiate into a variety of cell types. Once established, this pattern is frequently maintained over several cell divisions despite the fact that the initiating signal is no longer present. This capacity of translating transient external stimuli into diverse and stable phenotypes without alteration of the genomic sequence is at the heart of ‘epigenetic’ regulation of gene expression (1). Epigenetic processes are involved in the control of somatic inheritance and maintenance of cellular identity after cell fate decisions during development as well as in the transgenerational inheritance of some expression patterns by transmission via the germline (2).

In eukaryotes, at the molecular level, information on the gene activity is partly encoded by the local chromatin state, characterized by various properties like the nucleosome density and positioning, biochemical modifications of histone tails or of DNA itself (3). The pattern of chromatin states along the genome, the so-called ‘epigenome’, is itself regulated by the combined action of different specialized chromatin regulators like chromatin remodelers, modifying enzymes or histone chaperones. Recent statistical analysis of hundreds of epigenomic features across entire genomes revealed that eukaryotic chromatin is linearly organized into epigenomic domains characterized by a specific chromatin types (4–6): euchromatic states that account for most active or regulatory genomic regions, and heterochromatic states covering facultative (Polycomb-like), constitutive (HP1-like) or null inactive regions.

The mechanisms of assembly of these chromatin states, their maintenance and how they achieve their function, either active or repressive, remain to be elucidated. Recent studies provide compelling evidence that the establishment and maintenance of both euchromatin and heterochromatin are governed by similar general rules involving the combined and self-reinforcing action of specific chromatin proteins and enzymes (7,8). Chromatin state assembly first proceeds by a nucleation stage via the targeting of regulators at specific sequences by either DNA binding proteins or the RNAi pathway (7,9–13). Once initiated, the state is able to propagate to the neighboring sequences and to form extended epigenomic domains. In particular, molecular cooperativity, such as the ubiquitous ability for modifying enzymatic complexes to ‘read’ an epigenomic mark at a given locus and to ‘write’ the same mark at other loci, is believed to be a key ingredient of such processes (12,14).

In addition, there is a large body of experimental results that now suggest that the spatial folding of chromatin is an important factor contributing to the regulation of the epigenome (15). Recently, high-throughput chromosome conformation capture (HiC) experiments have shown that chromatin is folded into subnuclear domains, the so-called topologically-associating domains (TADs), marked by enhanced intra- and reduced inter-domain contacts. These spatial domains correlate strongly with linear epigenomic domains (6,16–18), suggesting a dynamic coupling between the 3D chromatin organization and the 1D epigenomic information. For example, during development, cell differentiation proceeds by global and concomitant rearrangements of epigenomic profile, chromatin organization and transcriptional activity (19–22). Similarly, epigenetic deregulation in cancer is associated with a strong reorganization of chromatin positioning inside the nucleus (23). All this suggests a functional role for higher-order chromosome organization in epigenomic regulation (24,25). However, experimental sets up for direct demonstration of such effects are still lacking, and the involved processes and mechanisms are mostly unknown or poorly characterized.

Previous mathematical models of epigenomic regulation (13,26–33) have suggested that molecular cooperativity coupled to effective long-range interactions between epigenomic features is essential to the maintenance of a stable epigenomic state. Motivation behind this effective long-range cross-talk is the inherent polymeric nature of chromatin that can bring in spatial proximity two loci that are far apart along the genomic sequence. However, such approaches did not integrate explicitly the 3D organization of chromatin and therefore failed to describe the effects of the chromatin dynamics and heterogeneities. Recently, using (hetero)polymer physics, we suggested that epigenomic-driven attractions mediated by architectural proteins associated to epigenomic states may be main drivers of 3D chromatin organization, controlling TAD formation, interaction and dynamics (34–36). However, in this previous approach the epigenome was assumed to be fixed in time, and therefore it failed to account for local epigenomic dynamics and variability. Recently, annealed copolymer-like models allowing the epigenome to fluctuate have suggested that the formation of compact 3D structure may favor the epigenomic maintenance (36,37).

In this article, we develop a novel quantitative framework allowing to investigate and dissect precisely the coupling between chromatin folding and epigenetic regulation, based on realistic biological processes, and thus to make predictions leading to experimental validations. We introduce the ‘living chromatin’ (LC) model that helps to rationalize this dynamic coupling by allowing the combined simulation of the epigenome and chromatin organization dynamics. Using this new formalism, we show that 3D compartmentalization helps epigenome maintenance by a spatial colocalization effect that would increase the local concentration of the epigenome effectors. After introducing the LC model, we first explore the generic properties of the system by studying the effects of the 1D–3D coupling in the establishment of a single epigenomic domain. In a second part, we show that boundaries between different epigenomic domains might be even maintained in the absence of initial external forcing as a consequence of spatial clustering. Finally, we discuss the implications of these results in the light of various biological epigenetic processes ranging from telomere clustering in yeast, Hox genes clustering in Drosophila to X inactivation in metazoans.

MATERIALS AND METHODS

Chromatin is modeled as an isolated self-interacting polymer on a face-centered cubic lattice. The chain is composed by N beads, one bead representing n bp. Nodes are the possible occupation sites for monomers and each site possesses 12 neighbors at equal distance b, the monomer–monomer bond size. For example, if one monomer represents one nucleosome b ≈ 10 nm. The local dynamics of the chain proceeds by random hopping of monomers to nearest-neighbor lattice sites following the local move scheme developed by Hugouvieux et al. (35,38). Basic restrictions on the moves are imposed in order to maintain connectivity, ensure excluded volume interaction and non-crossing of the polymer strands (35,38). Bending rigidity is accounted by introducing a local energy cost E_bend = k_int(1 − cos θ) where θ is the angle between two successive bonds and k_int is a measure of the bending stiffness. Controversy still exists about the value of this stiffness for in vivo chromatin. Measurements of the corresponding Kuhn length N_K go from about one nucleosome (200 bp) (39) to more than 5  kbp (40). For simplicity, we use k_int = 0 (N_K = 1 monomer) and k_int = 1 (N_K ≈ 2 monomers). Epigenomic-driven specific interactions between monomers of the same chromatin state are introduced via a binding rate approach: two neighboring (in space) monomers can be either in a bound or an unbound state with an interaction stochastic dynamics that is controlled by the binding k_b and unbinding k_u rates. At equilibrium, general compaction of the chain would only depend on the ratio k_b/k_u while dynamics is controlled by the absolute values of k_b and k_u.

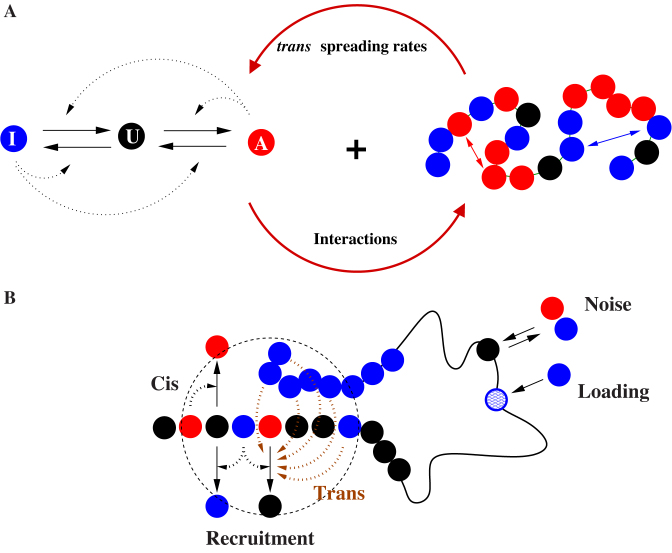
As in (26,28,29), we consider for monomer three different possible chromatin microstates, A for active, I for inactive and U for unmarked. The chromatin state of each monomer can fluctuate from one state to another according to four biochemical reactions as illustrated in Figure 1. This reaction scheme formalizes the ‘reader–writer’ (14) mechanism where, due to molecular cooperativity, the chromatin state of a given monomer can stimulate the conversion of adjacent monomers toward its own state. The conversion cannot be direct, i.e from A to I or I to A, but occur in a two-step way via an intermediate unmarked state U. In this work, we further test the hypothesis that such conversion by recruitment can be performed either in cis (from adjacent monomers along the chain) or in trans (from any spatially close monomer). For a monomer i, we note n_cX(i) the number of nearest-neighbors along the chain with state X (X ∈ {A, U, I}, n_cX(i) ∈ {0, 1, 2}) and n_tX(i) the corresponding number of spatial nearest-neighbors (n_tX(i) ∈ {0, 1, ..., 10}).

Figure 1.

The Living Chromatin model. (A) The LC model is a combination of the copolymer model (34,35) (right) and of the epigenome regulation model (26,28) (left). Each monomer can be in one of the three states: A, U and I; the inter-conversion dynamics between these states results from random or recruited (in cis or in trans) conversions. The chain is modeled by a semi-flexible self-avoiding bead-spring model with specific short-range attractions between monomers of the same epigenomic states (A or I). (B) Recruited conversions are achieved either by recruitment in cis (nearest-neighbor along the chain) or by recruitment in trans (3D neighborhood); there is also noisy conversion (I↔U, A↔U) and the possibility of external loading at some specific recruitment sites.

The transition rates are given by:

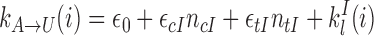(1)

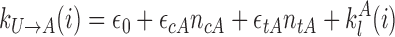(2)

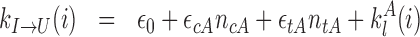(3)

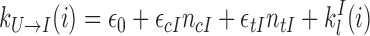(4)

with ϵ₀ the contribution of leaky enzymatic activity or of nucleosome turnover, ϵ_cX the spreading rate in cis (c) and in trans (t) of A or I states. For simplicity, in the rest of the paper, we will assume equal rates for both states, i.e. ϵ_cA = ϵ_cI ≡ ϵ_c (similarly ϵ_tX ≡ ϵ_t). The model also offers the possibility for locus-specific nucleation via the 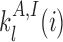rates (= 0 in all sections except at the end of the “Results” section). Let us notice that, in terms of polymer physics ‘nomenclature’, this LC model belongs to the ‘annealed copolymer’ family where, as opposed to the quenched copolymer framework, the states of the monomers are allowed to fluctuate.

Numerical simulations were performed using a home-made program coding for a Markov Chain Monte-Carlo algorithm. One Monte-Carlo step (MCS) consists in (i) N trial monomer moves; (ii) N/2 trial binding/unbinding transitions; and (iii) N trial monomer state conversions. In each trial move:

1. A monomer is randomly picked and an attempt to move it to one of its nearest neighbors on the lattice is performed. The move is accepted according to a standard Metropolis scheme (41) and only if the connexions along the chain and with the bound monomers are maintained.

2. In each binding/unbinding trial transition, a monomer is randomly picked and if its state is either A or I, a binding (resp. unbinding) event is attempted with probability k_b (resp. k_u) with every unbound (resp. bound) neighboring monomer of the same state.

3. In each state trial conversion, a monomer is randomly picked and a state transition is attempted according to the rules defined in Equations (1-4).

Let us note that such local dynamics, both for the chain and for the epigenome, satisfies the principle of detailed balance and does not require energy feeding. For a given set of parameters, we simulate  2x10⁸ MCS-long trajectories and record data every  2x10³ MCS in order to ensure conformational and epigenomic equilibration and independence between data points. For each stored snapshot of the system, we compute the global epigenomic state s = (n_A − n_I)/N and the pair-wise squared distances R²(i, j). Radius of gyration R_g is defined as R_g = [(1/2N²)∑_{i, j}〈R²(i, j)〉]^1/2. Shown results for R²(i, j) and R_g are expressed in b unit.

Elementary motion of the chain takes place on small time scales. Depending on the coarse-graining n, it may vary from 10⁻⁴-10⁻² s (Ghosh S. and Jost D., BioRxiv:https://doi.org/10.1101/200584). That would correspond to the typical time-scale of one Monte-Carlo time step in our simulation (1 MCS). Binding/unbinding transitions between monomers are likely to occur at the second scale, as we showed recently in a study in yeast combining experimental measurement and modeling (Socol et al., BioRxiv: https://doi.org/10.1101/192765). Hence, we fix k_u = 0.001 that would correspond to an unbinding rate of 0.1−10 s⁻¹. Regarding the epigenomic transitions, to the best of our knowledge, there is no direct measurement of the corresponding rates. Previous experimental and modeling studies on epigenetic stability suggest that they may take place on different time scales from seconds to hours (26,42). Most of the results shown in the paper are for ϵ₀ = 0.001. However, we verify that our conclusions are qualitatively robust over changes in ϵ₀ (Figure 5B).

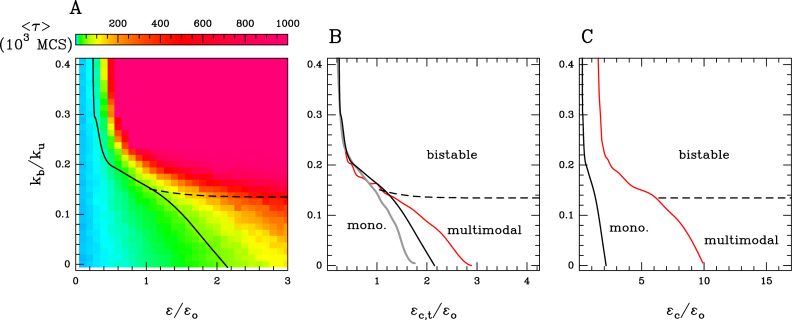
Figure 5.

(A) Stability of the global epigenomic state for the ‘cis &trans’ spreading model with epigenomic-driven self-attraction (ϵ_c = ϵ_t ≡ ϵ, ϵ_o = 0.001, k_u = 0.001). Heatmap of the MFPT 〈τ〉 to switch from the I macro-state s = −1 to a A state (s > 0) (see ‘Materials and Methods’ section) as a function of the attraction k_b/k_u and recruitment strength ϵ/ϵ_o. The monostable and multimodal/bistable regions are demarcated by the transition black curve. (B and C) Epigenomic phase diagrams for different dynamical regimes (B) Transition curves for an epigenomic dynamics ten times slower (ϵ_o = 0.0001) (gray) and ten times faster (ϵ_o = 0.01) (red) than the reference case considered in Figure 4A) (ϵ_c = ϵ_t, ϵ_o = 0.001) (black). (C) Transition curve for a cis spreading ten times greater than the trans spreading (ϵ_c = 10ϵ_t, ϵ_o = 0.001) (red) and for the reference case (ϵ_c = ϵ_t, ϵ_o = 0.001) (black). In (A–C) the limit between multimodality and bistability is represented by the black dashed line.

Monostable/multimodal transition curves in the phase diagrams are computed by searching for parameters where the probability distribution for s passes from monomodal to multimodal. The transition between multimodal and bistable dynamics has been computed as the start of the collapse transition (see Supplementary Figure S3A).

The stability of the epigenomic domains is measured by computing the mean first passage time (MFPT) 〈τ〉 to switch from the inactive macro-state s = −1 to an active state (s > 0): starting from the initial inactive domain (s = −1) we record the time τ (in MC steps) needed to reach s = 0 for the first time.

Similarly, the stability of the boundary is measured by computing the MFPT for each compartment to switch from its initial I (s(i) = −1, i < 49) and A (s(i) = 1, i > 51) macro-state to the s = 0 state. Starting from the initial compartmentalization, we record, in each A and I compartment, the time τ_{A, I} (in MC steps) needed to reach s = 0 for the first-time and take the minimum value τ = min (τ_A, τ_I). In Figure 6 and Supplementary Figure S4 (resp. in Figure 7) we report the mean value 〈τ〉 computed from a set of 100 (resp. 1000) independent realizations.

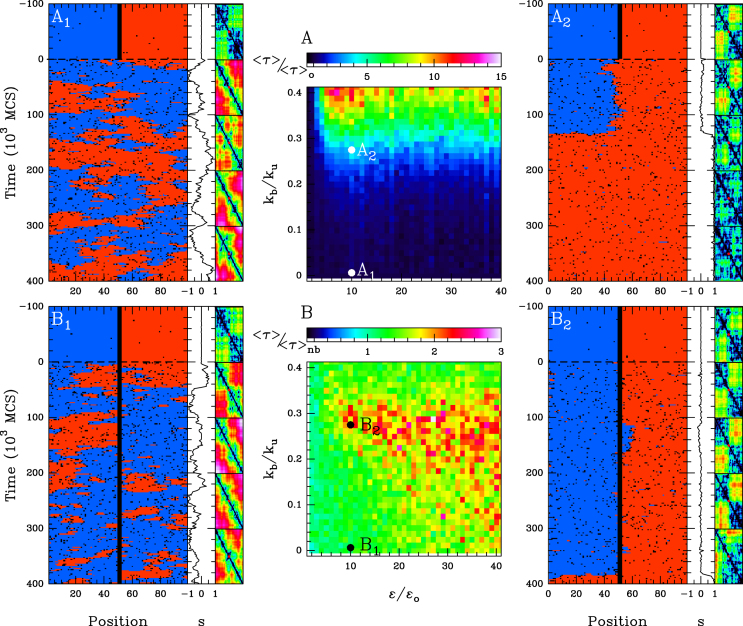
Figure 6.

Maintenance of two neighbouring epigenomic domains. Stability time (see ‘Materials and Methods’ section) of the I-A compartmentalization as a function of the attraction k_b/k_u and recruitment strength ϵ/ϵ_o for the cis& trans model with k_u = 0.001, ϵ_o = 0.001, ϵ_c = 10ϵ_t, k_int = 1, without 1D boundary (A) and with a remaining 1D boundary (B). In (A) is reported the heatmap of the stability time fold-change 〈τ〉/〈τ〉₀ relatively to the ‘non interacting’ case k_b/k_u = 0 and in (B) the stability time fold-change 〈τ〉/〈τ〉_nb relatively to the ‘no boundary’ case considered in (A). Typical time-evolution of the epigenome (left panel), of the corresponding global epigenomic state s (middle panel) and of the distance map R²(i, j), i, j = 1, .., 101 (right panel, at every 100. 10³ MCS steps, the first one on the top corresponding to t = 0 ), when considering no interaction k_b = 0, t > 0 and k_b/k_u = 0.28 .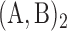

Figure 7.

Stability of the two-domains compartmentalization (A) Mean ‘stability time’ 〈τ〉 versus boundary size (number of monomers forming the boundary) for the cis & trans model with interaction (ϵ_c = 0.01, ϵ_t = 0.001, ϵ_o = 0.001, k_b = 0.00028, k_u = 0.001) (B) Mean ‘stability time’ 〈τ〉 versus loading rate k_l for the cis & trans model with interaction (ϵ_c = 0.01, ϵ_t = 0.001, ϵ_o = 0.001, k_b = 0.00028, k_u = 0.001) (•), with a smaller interaction k_b = 0.00018 (), k_b = 0.0001 (), with no interaction (k_b = 0) ().

The initial compartmentalization (t = 0) is obtained by ‘forcing’ the epigenetic states at the four following positions: s(i) = −1, i = 10, 35 for the inactive domain and s(i) = 1, i = 77, 92 for the active domain; we impose a strong recruitment in cis ϵ_c = 0.15 (ϵ_t = 0.0001, ϵ_o = 0.001) and a strong interaction strength k_b/k_u = 0.28 except in Supplementary Figure S5C where we impose k_b/k_u = 0; the 1D insulation between the two domains is performed by imposing an unmarked state for the central monomers (s(i) = 0, i = 49, 50, 51), except for Supplementary Figure S5B where no boundary has been imposed. After this ‘establishment phase’ of duration 5.10⁵ MCS, the forcings are switched off and the system is free to relax toward the equilibrium state. In Figure 6B, B₁, B₂, Supplementary Figure S4B and Figure 7A, the boundary is maintained during the relaxation phase. In Figure 7B, in every compartment, we impose a residual forcing toward the desired states for different values of the loading rate k_l < 1, meaning that at every MCS, a forcing of the state s(i) = −1 at positions i = 10, 35 or of s(i) =  1 at i = 77, 92 is attempted with a probability k_l.

The home-made program (written in Fortran) that simulates the epigenome and chain dynamics using this Monte-Carlo algorithm can be downloaded at http://perso.ens-lyon.fr/cedric.vaillant/doku.php/software/.

RESULTS

The living chromatin model: a modular framework to investigate the coupling between function and organization of chromatin

In the LC model, chromatin is modeled as an interacting semi-flexible self-avoiding polymer. Each monomer represents a DNA genomic region and is characterized by its epigenomic state. We assume three possible states: an unmarked U state and two epigenetically marked states A and I (representing for example, H4ac and H3K4me or H3K9me and H3K27me histone modifications). The state of a monomer can dynamically fluctuate between these three flavors according to biochemical reaction rules: (i) random transitions (with rate ϵ_o) due to leaky enzymatic activities, nucleosome turnover or dilution at replication; (ii) specific transitions associated to the spreading of a mark by the recruitment of corresponding modifying enzymes. The latter transitions are based upon the biochemical ability of modifying enzymes to preferentially associate with components of the chromatin state they catalyze or promote (8,12,14,43). This is the so-called ‘reader-writer-eraser’ mechanism that introduces a positive feedback in the reactions scheme (Figure 1A, left): every A or I monomer promotes the spreading of its state or the erasure of the antagonistic mark to the spatially neighbor monomers (Figure 1B). To dissect the impact of such mechanism, we formally consider two different contributions: (i) spreading in cis, i.e. to its two nearest neighbors along the chain (with a rate ϵ_c); (ii) and spreading in trans, i.e. to every monomer that colocalizes in space due to the folding of the fiber (with a rate ϵ_t) (Figure 1B). The number of recruiting monomers that participate to the conversion in trans depends on the current 3D configuration of the chain and on the spatial range of action of the modifier.

We introduce such conversion in trans to account for the 1D–3D coupling that has been evidenced by several experiments, where disruption of clustering is followed by the loosening of the local chromatin state. At the nucleosome level, there is no direct evidence that spatial colocalization is sufficient for an enzyme to promote conversion in trans. The mechanism that controls cis-spreading is even not well understood. When recruited at a given locus, the activity of enzyme on the adjacent nucleosomes may be stimulated. Experimental studies on the Suv39/clr4 system have shown that this was not due to allosteric changes of the involved enzymes but more likely to the favorable, stable spatial and orientational arrangement of the enzyme relatively to the H3 tails of adjacent nucleosomes, hence leading to an enhanced enzymatic activity (44). The local chromatin structure induced by the architectural proteins such as HP1, PRC1, Sir3 that are known to produce compact or ordered arrays of nucleosomes, might thus reinforce such cis activity. However, whether or not such process is restricted to nucleosome in cis or can also apply to any spatially proximal nucleosome in trans, is still an open question. Propagation of silencing in trans at the nucleosomal array scale have been evidenced in the Polycomb system (45) but the precise molecular mechanism underlying such spreading remains to be elucidated. In vitro experiments similar to (44–46) but with more extended engineered arrays of nucleosomes will be required for a better understanding of the cis versus trans spreading mechanisms. We emphasize that our current LC model, if not realistic at the nucleosome scale, may be relevant for more coarse-grained descriptions of the chromatin with effective cis and trans conversion rate.

Motivated by recent biochemical evidence showing that proteins associated to some epigenomic states (like HP1-like or Polycomb-like chromatin) may oligomerize (45,47–50), we introduce also the possibility for two monomers of the same epigenomic state (A or I, but not U) and neighbors in space to interact with each other with the formation of a chemical bond (Figure 1A, right). Stochastic transitions between the bound and unbound states are controlled by the binding k_b and unbinding k_u rates. For further details on the LC model, on the used parameters and on the simulation method, we refer the reader to the ‘Materials and Methods’ section.

The LC model can be viewed as a combination of the block copolymer model of chromatin developed in (34,35) and of the epigenome regulation model (28,29), adapted from the seminal work of Dodd et al. (26). It represents a powerful theoretical and numerical formalism to study the dynamical coupling between the 1D epigenomic information along the chain and the 3D chromatin organization: 3D acts on 1D via the trans spreading mechanism while the 1D feedbacks the 3D via epigenomically driven contact interactions (Figure 1). Physically speaking, the LC model is analogous to a three-state Ising spin system on a polymer chain with local ferromagnetic coupling: random conversion stands for the temperature (k_BT) and recruited conversion for the ferromagnetic coupling (J); the mean epigenomic state can be associated to the magnetization. A well known results in statistical physics is that such ‘1D’-Ising model exhibits a second order phase transition only if there is strong enough effective long-range interactions between spins (here due to the underlying polymer dynamics of the chain) (52). Moreover, our LC framework is modular and can be easily generalized to any number of epigenomic states and any biochemical reactions or interaction scheme. Recently, Michieletto et al. have also developed a physical model of such 1D–3D coupling of chromatin (37). In their approach, the dynamics of the epigenome and of the polymer are governed by the same Hamiltonian, i.e. the spreading of a mark is tightly related to the (pre)existence of chemical bonds with the nearest monomers. This is a fundamental difference with the LC model where spreading in trans is not directly coupled to the copolymer dynamics but rather depends only on the presence of monomers in spatial neighborhood.

Stability of a single epigenomic domain

To probe the power of the LC model in describing the complex interplay between the 1D epigenomic information and the 3D chromatin organization, we first aim to understand how an epigenomic domain—composed by a majority of A or I states—may be stably formed and maintained, and in particular, how the folding properties of the polymer chain influence such processes. In this section, we consider a genomic region composed by N = 100 monomers. If one monomer represents a nucleosome, this typically corresponds to a small domain—a gene for example—of 20 kbp. To simplify, we assume in this section that this region is isolated from the rest of the chromatin by the presence of insulators at its boundaries.

Cis-spreading alone cannot maintain a stable epigenomic domain

We first study the simple case where there is no long-range—trans—spreading (ϵ_t = 0): the dynamics of the epigenome does not depend on the folding of the chain and thus reduces to a simple 1D problem. To quantify, the epigenomic composition of the domain we define the global epigenomic state s as s = (n_A − n_I)/100 with n_A (resp. n_I) the number of nucleosomes of type A (resp. I). If s ∼ 1 (resp. ∼−1), the domain is globally in a A (resp. I) state. For an undefined or unmarked global state s ∼ 0.

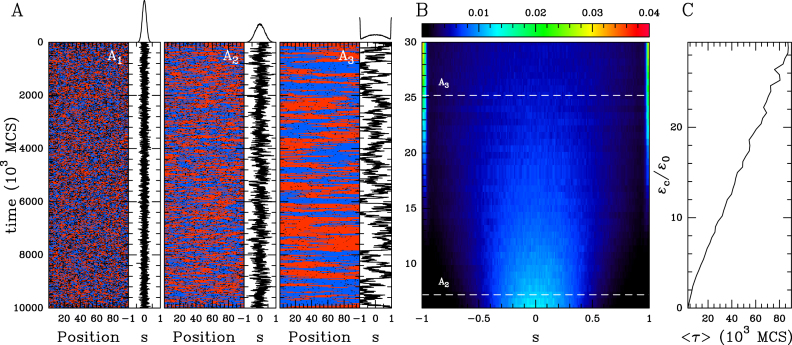
At equilibrium, the global epigenomic state fluctuates around zero whatever be the recruitment strength (Figure 2 and Supplementary Figure S1A). At weak recruitment strength, random interconversion dominates and the epigenome is made of short-lived small A, I and U subdomains (Figure 2A₁). When increasing the recruitment, epigenomic fluctuations are enhanced but the system remains monostable around the s = 0 (Figure 2A₂ and Supplementary S1A). For very strong recruitment (ϵ_c > 13), the typical sizes of the fluctuations are greater than the domain size, and large, but, unstable, A or I macro-states start to emerge leading to a trimodal distribution for s (Figure 2 A₃ and B; Supplementary Figure S1A). The emergence of these s ± 1 peaks results from finite size effects, since no multimodality or phase transition can arise in the infinite size system with the distribution being always monomodal around s = 0 for any value of ϵ_c. The illustration of such finite-size effects is reported in Supplementary Figure S2A where the s = ±1 peaks decrease when extending the size of the chain. This monostability is illustrated by the evolution of the MFPT 〈τ〉 to switch from a pure I macro-state (s = −1) to a A state (s > 0) as a function of the cis recruitment strength ϵ_c (Figure 2C). 〈τ〉 remains very low and is a weak linear function of ϵ_c. This is the characteristic of the absence of any phase transition in 1D systems with only short-range interactions, and was already mentioned in previous studies of epigenetic switches (26,28). Let us note that very similar results were obtained by recent theoretical studies of cis-spreading models in the HP1/H3K9me3 system (11,31,51).

Figure 2.

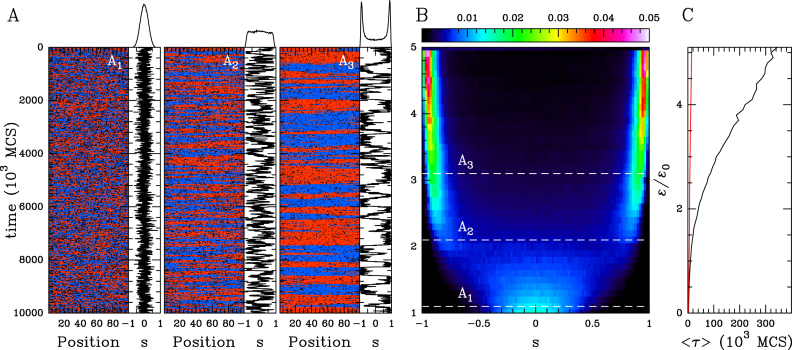
The ‘cis’ spreading model (ϵ_t = 0, ϵ_o = 0.001). (A) Examples of time evolution of the local epigenomic state (A in blue, I in red and U in black) and of the global epigenomic state s = (n_A − n_I)/100 for different values of the cis spreading recruitment strength ϵ_c/ϵ_o = 1 (A₁), 6 (A₂) and 25 (A₃). The corresponding equilibrium probability distribution functions (pdf) ρ(s) are reported on the top of each time series. (B) Heatmap of ρ(s) as a function of ϵ_c/ϵ_o. (C) MFPT 〈τ〉 to switch from s = −1 to s > 0 as a function of ϵ_c/ϵ_o. Time in (A) and (C) is defined in simulation time unit (MCS for Monte-Carlo time Step, see ‘Materials and Methods’ section).

Stronger stability arises from trans-spreading activity

Then we introduce the impact of 3D organization on the 1D information by authorizing trans-spreading (ϵ_t = ϵ_c ≡ ϵ) but we still neglect the 1D to 3D feedback (k_b/k_u = 0). Recruited conversions for a given monomer are now influenced by the potential spatial proximity with distal monomers along the domain (Figure 1), but the polymer chain remains in a swollen configuration that does not depend on the epigenome (Figure 4A_{1, 4}).

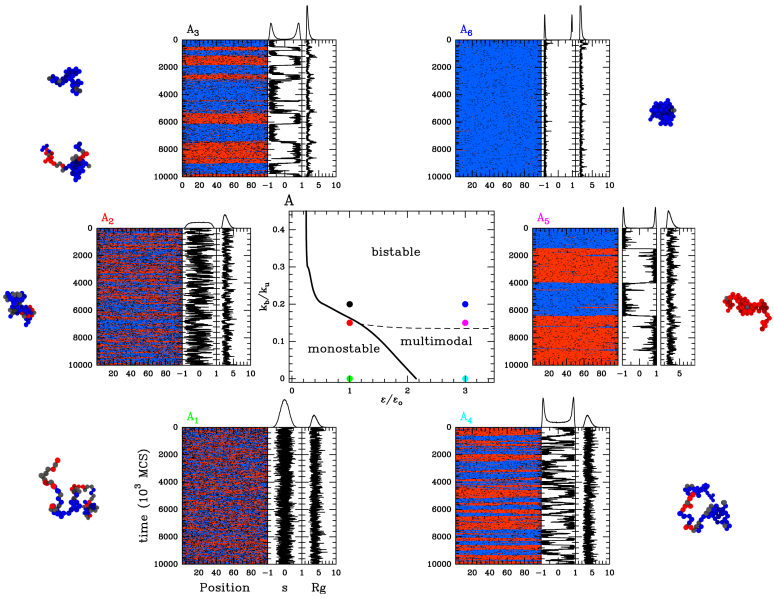
Figure 4.

The ‘cis& trans’ spreading model with epigenomic-driven self-attraction (ϵ_c = ϵ_t ≡ ϵ, ϵ_o = 0.001, k_u = 0.001). Epigenomic phase diagram in the (ϵ/ϵ_o, k_b/k_u) plane. The monostable and multimodal/bistable regions are demarcated by the transition black curve. Due to finite-size effects, the observed multimodality might not reflect a true bistable dynamics (see text). The limit between multimodality and bistability is represented by the black dashed line. (A_{1, .., 6}). Examples of time evolution of the local epigenomic state, of the global epigenomic state and of the radius of gyration R_g for ϵ/ϵ_o = 1, k_b/k_u = 0 (A₁), ϵ/ϵ_o = 1, k_b/k_u = 0.15 (A₂), ϵ/ϵ_o = 1, k_b/k_u = 0.2 (A₃), ϵ/ϵ_o = 3, k_b/k_u = 0 (A₄), ϵ/ϵ_o = 3, k_b/k_u = 0.15 (A₅) and ϵ/ϵ_o = 3, k_b/k_u = 0.2 (A₆).

At weak recruitment strength, the epigenome is monostable with fluctuations around s ∼ 0 (Figure 3A₁ and Supplementary Figure S1B). The variability around 0 is larger than previously observed for the ‘cis’ spreading model at the same conversion rate ϵ_c due to the additional contribution from long-range conversion. The strength of recruited conversion where fluctuations become larger than the domain size is therefore strongly reduced (ϵ/ϵ_o ∼ 2.1, Figure 3A₂ and Supplementary Figure S1B), and the distribution of s becomes essentially bimodal after this transition (Figure 3A₃ and Supplementary S1B), the system fluctuating between two coherent A or I macro-states. However, such observed bimodality reflects also finite-size effects. This again is illustrated in Supplementary Figure S2B, where the peaks decrease when extending the size of the chain. As illustrated by the evolution of the MFPT, the stability of these states still increases linearly with ϵ (Figure 3C), but the introduction of effective long-range interaction dramatically stabilizes these large-scale states by more than 30-fold compared to the ‘cis’ spreading model. This means that above a given efficiency of the ‘reader/writer’ mechanism, the 3D—trans—spreading of a mark leads to the spontaneous formation of more stable and coherent epigenomic domains (26,28,31).

Figure 3.

The ‘cis & trans’ spreading model in the coil phase (ϵ_t = ϵ_c ≡ ϵ, ϵ_o = 0.001 and k_b/k_u = 0). (A) Examples of time evolution of the local epigenomic state and of s for ϵ_c/ϵ_o = 1 (A₁), 2 (A₂) and 3 (A₃). Corresponding ρ(s) are reported on the top of each time series. (B) Heatmap of ρ(s) as a function of ϵ/ϵ_o. (C) MFPT 〈τ〉 as a function of ϵ/ϵ_o (black). For comparison purpose, the corresponding curve for the ‘cis’ spreading model is shown (red).

Epigenomically driven interactions leads to more enhanced domain stability

We now ask how the impact of epigenomics on the 3D chain folding via specific interactions modifies quantitatively the behavior of the system. In this situation, contact interactions between monomers of the same epigenomic state may lead to local compaction of the chain, and thus to a more efficient spreading activity.

In Figure 4, we plot the phase diagram when varying the strength of specific interactions (via the ratio k_b/k_u). In presence of interactions, we still observe the transition between a monostable—epigenetically undefined region at weak spreading intensity and a multimodal—epigenetically coherent- area for larger ϵ. The value where the transition occurs decreases with the attraction strength. Indeed contact interactions between monomers of the same epigenomic state promote the compaction of the polymer chain (Supplementary Figure S3A), leading to spatial colocalization of epigenetic factors and thus to an enhanced trans spreading activity. This implies that even at low values of the transition rate ϵ, a coherent A or I macro-state might emerge solely by increasing the strength of attraction between monomers. Interestingly, below a given recruitment strength (ϵ/ϵ_o ∼ 0.25), the system remains monostable whatever the value of k_b/k_u (Figure 4A): random transitions always dominate the system dynamics even if the polymer chain is fully collapsed (28). This limit nicely corresponds to the position of the second-order phase transition for a epigenomic system where every monomer is ‘seeing’ each other (28). In this system, the transition to bistability occurs for 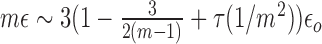where m is the number of monomers that participate to the recruited conversion in this infinite-range model. By analogy, this gives for our lattice model, ϵ/ϵ_o ∼ 0.22 (m = 12), a value very close from what we obtained numerically. The correlated evolution of the global epigenomic state s and of the radius of gyration R_g of the chain (Figure 4A₂ and A₃; Supplementary Figure S3B and Movie S1) illustrates nicely how the local 1D–3D feedback mechanisms induce a large scale coupling between the epigenome and the spatial chain folding: incoherent epigenomic states (s ∼ 0) tend to be associated with larger values of R_g (relative decondensation) whereas coherent states (s ∼ ±1) to lower values of R_g (relative condensation).

A dramatic impact of introducing contact-specific interactions is to greatly enhance the stability of A or I domain in the multimodal region (Figure 5A). By favoring the trans activity induced by the spatial colocalization of monomers of the same epigenomic state, augmenting the strength of interactions may lead to stabilization up to 20-fold for strong interactions. Strikingly, even at weak attraction strengths (k_b/k_u ∼ 0.1) that lead to minor variations in the typical size of the domain (10−30%), stabilization of the domain is already significant (∼2- to 3-fold).

Compared to the ‘cis’ spreading model or the ‘cis & trans’ spreading model in the coil phase, we also remark that above a given strength of attractions (k_b/k_u ∼ 0.14), transitions from monostability to multimodality occur via a phase transition (Figure 4A₂ and A₃), strong values of ϵ being associated with bistability. In this phase, cooperative effects are dominant and lead to the emergence of super-stable A or I macro-states, associated to a MPFT that now evolves exponentially as a function of the recruited conversion rate (Figure 5A). This limit (k_b/k_u ∼ 0.14) arises when the chain starts to compact (Supplementary Figure S3A) passing from a swollen coil to a globule. This is characteristic of the presence of phase transitions in 1D systems with effective long-range interactions only if the strength of interactions between two monomers i and j decreases more slowly than 1/|j − i|² (52), i.e. in our case, only if epigenomic-driven interactions are strong enough to partially collapse the polymer so that the contact probability between two monomers scales slower than 1/|j − i|².

In that bistability region, the ‘infinite range’ model also predicts that stability (MFPT) increases exponentially with m (28). In our case, in the fully collapsed state, m = 12 whatever the size of the chain. At lower attraction strength, when the chain is not fully collapsed, we expect that the relevant values for m would rather correspond to the mean number of monomer that can participate to conversion in trans, i.e. the mean value of occupied sites among the 12 neighboring sites. This number increases obviously with the attraction strength and, at a fixed attraction, it should also augment with the size of the chain, since the compaction level increases with the size of the chain above the collapse transition (35,53). We thus expect, from this theoretical argument derived from the infinite range model (28), that stability should increase with the size of the chain, which is indeed illustrated by highest s ± 1 peaks in the ρ(s) distribution above the collapse transition when increasing the chain size (Supplementary Figure S2C and D). Note that the nature of the transition is different from the related work of Michieletto et al. (37) where they found a first-order transition. This difference originates from the model they used where epigenetic and polymer dynamics evolve under the same Hamiltonian, while in our case, they are driven by different—yet coupled—mechanisms.

So far we have assumed similar time-scales for the epigenome dynamics and epigenomic-driven interactions (k_u = 0.001, ϵ_o = 0.001), as well as the same rates for cis and trans conversion (ϵ_c = ϵ_t). Here, we wonder if asymmetries in the dynamical regimes lead to enriched behaviors. Molecularly, i.e. at the nucleosomal scale, there is no evidence that the ‘reader/writer’ mode of action should have the same efficiency in cis and in trans. Figure 5C shows the phase diagram of the system when the cis activity is stronger than the trans spreading (ϵ_o = 0.001, ϵ_t = ϵ_c/10, k_u = 0.001). We observe that the transition to bistability (high k_b/k_u region) and multimodality (low k_b/k_u region) is delayed compared to the case where ϵ_t = ϵ_c by about a factor 5. This underlines the importance of efficient trans spreading mechanisms in the maintenance of stable epigenomic domain. This also suggests that biological or physical mechanisms that directly or effectively favor the cis spreading in disfavor of the trans activity would result in similar delays. For example, when accounting for a more rigid chromatin fiber by increasing the local bending stiffness, chain configurations are more extended leading to lower long-distance contact probability and thus lower trans activity (Supplementary Figure S1D). As we increase the relative epigenomics dynamics (Figure 5B and Supplementary Figure S1C), the environment of one monomer—which most of the time consists of its nearest-neighbors along the chain for a swollen configuration—remains almost constant during an increased number of epigenomic transitions, hence reducing also effectively the trans spreading. Consistently, when now decreasing the relative epigenome dynamics, the transition to multimodality is now advanced (Figure 5B). We note that changing relative epigenomic and interactions dynamics only affects the transition to multimodality in the low k_b/k_u region, the phase transition to bistability being unchanged.

Stability of a boundary between two antagonistic epigenomic domains

In the previous part, we showed that trans activity coupled to epigenomic-driven interactions may dramatically enhance stability of an isolated epigenomic domain. However, the question of the stability of a boundary between two antagonistic chromatin states (A and I) remains unclear. In this section, as a proof of concept, we address this question by following the dynamics of a genomic region initially prepared with one I domain directly adjacent to a A domain of the same size.

1D–3D coupling is essential for stability

First, we aim to understand how spreading in trans and epigenomic self-attraction may help to maintain a 1D compartmentalization in the absence of any local forcing. We build an initial configuration with two spatially insulated adjacent I (blue) and A (red) domains and for t > 0, we let the system relax toward the equilibrium state (Figure 6A_1,2 and ; Supplementary Figure S5, see ‘Materials and Methods’ section.). Such compartmentalization is always unstable, but depending on the model parameters, the system may keep the memory of this initial segmentation for a reasonably long period τ before eventually being destabilized. To address the effect of the 1D–3D coupling, we compute the mean stability time 〈τ〉 (see ‘Materials and Methods’ section) as a function of the self-attraction k_b/k_u and recruitment ϵ_c/ϵ_o (Supplementary Figure S4A and B). In Figure 6A, we report the fold-change in stability relatively to the non-interacting case (i.e. 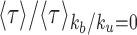) for an asymmetrical recruitment (ϵ_c = 10ϵ_t, ϵ_o = 0.001) and a semi-flexible chain (k_int = 1). The results for the symmetrical recruitment (ϵ_c = ϵ_t, ϵ_o = 0.001) and for a flexible chain (k_int = 0) (Supplementary Figure S5D) are qualitatively similar albeit stability is overall lower. As for single isolated domains, the stability in presence of trans spreading is order-of-magnitude higher than with only cis spreading (Supplementary Figure S5A) and increases with the strength of recruitment and of self-attraction (Figure 6A and Supplementary Figure S4A). Below, the multimodal/bistable limit, the boundary is only slightly more stable compared to the non-interacting case, while above the limit, stronger stabilities are observed (2- to 15-fold). The stability of such a compartmentalization has an upper-limit which simply corresponds to the stability of a single isolated domain. In that case, as already discussed previously, only internal perturbations can lead to the destabilization of the macro-state. In our situation, there is an additional contribution coming from the antagonistic domain that fastens destabilization as compared to isolated domains. Such external perturbations mostly occur at the initial boundary between the two domains: one domain can indeed extend toward the other by cis spreading activity (which is in our case much more efficient than trans) but also by facilitated trans spreading due to the spatial proximity of flanking boundary monomers. For sufficiently large self-attraction (Figure 6A₂), however, the strong 1D–3D coupling still maintain each domain in a collapsed configuration that limits the ‘contamination’ in trans between the two domains. Indeed, in addition to the strong 1D–3D coupling that stabilizes the epigenomic state against any small perturbations, the compact globular chain configurations limit inter-domain contacts and thus limit long-range spreading from the antagonistic compartment. The importance of such 3D insulation is illustrated in Supplementary Figure S5C where the initial spatial insulation of the antagonistic domains is not present: inter-domain contamination is dramatically enhanced and stability drops down.

Presence of 1D boundary and weak external forcing further enhances stability

A way to improve insulation between domains and thus to limit the effect of external perturbations from the antagonistic domain is to introduce a 1D barrier. Such imposed boundary hinders propagation in cis from one to the other domains and external contamination can only arise from the trans spreading activity across the frontier. We know that such barriers are biologically relevant and can be achieved, for example, by the binding of insulators at specific sites. As expected, doing so enhances stability, as illustrated by the stability heatmap reported in Supplementary Figure S4B. For a 3-monomer wide boundary, the enhancement of stability (relatively to the no-boundary case) occurs mainly in the multimodal/bistable region and is in the range of ∼2- to 3-fold (Figure 6B). Increasing the size of the 1D barrier limits even more 3D spreading and thus enhances the stability, with a 3-fold enhancement for a 11 monomer wide boundary (Figure 7A). Interestingly, we observe that for very large self-attraction, keeping 1D boundary mildly increases stability (fold-change ≳ 1): in that case, as discussed before, the 1D–3D coupling within each domain prevents efficiently the 1D spreading of the antagonistic domain leading to an effective ‘1D’ barrier.

Previously, the two adjacent antagonistic domains were forced to be one in state I and one in state A and at t > 0, we let the system evolves in absence of forcing. Here, we asked whether maintaining a weak permanent forcing of the initial state inside each compartment could impact on their stability. Concretely, for the system with a 1D barrier (size 3), at different positions along each domain, the local transition rates controlling the epigenomic state dynamics are now biased toward I or A (k_l ≠ 0, see ‘Materials and Methods’ section). We observe a strong increase of the mean stability time even at low loading rates in (Figure 7B) whatever the value of the 1D–3D coupling, while for large k_l values, the stability remains almost constant. Interestingly, the enhancement of stability is weaker when the system is in the bistable part of the phase diagram (black dots in Figure 7B) since the 1D–3D coupling is optimal and thus forcing locally the epigenomic state would be less efficient.

DISCUSSION

In this article we have specifically addressed the question of the coupling between the spatial folding of chromatin and the assembly of a stable epigenomic state. We have introduced a new theoretical framework, the so-called ‘Living Chromatin’ model that allows to simulate the simultaneous stochastic dynamics of the global chromatin 3D organization and of the local biochemical state. Our main motivation was to provide a concrete formalization of the emerging idea that spatial folding may not be only a by-product of genome activity but also could contribute to its regulation. We confirmed that the ability for a chromatin locus to promote the conversion of other chromatin fragments located at distant loci along the genome is a key factor for the maintenance of a stable and coherent epigenomic state over a large domain (26,54,55). In our model, this trans spreading activity is inherent to the polymeric nature of chromatin, and therefore depends on the global folding state of the chain, the spreading efficiency of an epigenomic state being an increasing function of its local spatial density. Therefore, mechanisms directly involved in the 3D organization of the domain might influence greatly epigenomic regulation. In our model, the 3D compaction is self-controlled by a positive feedback mediated by contact interactions between loci of the same epigenomic state: within a domain, stochastic fluctuations in compaction would enhance the spreading of a chromatin mark which in return would enhance global compaction, accelerating the spreading and thus facilitating the maintenance of a coherent and stable state over the entire domain. In particular, we showed how reducing the local self-conversion rate of a state can be compensated by increasing the self-association strength between monomers.

A main prediction of the LC model is that the stability of epigenome domain as well as the robustness of compartmentalization are achieved when the chain is at least partially collapsed. This means that the self-attraction strength is sufficiently high to induce the contact probability between two loci separated by a genomic distance d to decrease slower than 1/d², the prerequisite for (bi)stability (52). This is fully consistent with experimental data on chromatin folding that report for all investigated species a contact probability with scaling exponent ranging from −1.5 to −0.5 at the TADs typical size, with an average value of ∼−1. We showed in our previous works (34,35) how a block copolymer framework accounting for a fixed epigenomic landscape can account for experimental data in Drosophila for attraction parameter that drives the chain around the collapse transition.

Compared to the recent work of Michieletto et al. (37) on ‘epigenetic recoloring’ using also an explicit polymer model, our approach allows more precisely to dissect the role and impact of the different mechanistic contributions to the 1D-3D coupling: cis and trans spreading, and epigenomic-driven self-interactions. Qualitatively, we retrieve that stable epigenomic domains arise from the concomitant action of trans spreading and chain compaction, even if the nature of the transition is different (second-order in our work versus first-order in (37)) due to differences in the employed models. Note that there is no experimental evidence for one or the other type of transition. In addition, we used our framework to investigate different—complementary—properties like the role of 1D barriers and of weak site-specific recruitment into the 3D insulation of nearest, epigenetically antagonistic compartments.

Our work suggests that the basic biochemical concept behind the structure/function coupling of chromatin—formalized here within the LC model—is the increase of local concentration of regulatory proteins due to spatial co-localization. Molecular crowding and spatial confinement increase the binding affinities of regulators (activators and repressors) to their chromatin/DNA targeted regulatory sequences. The nuclear compartments would correspond to bio-chemical nano-reactors where a few number of reacting biomolecules are co-localized in space favoring their (co-)activity on chromatin and in fine on DNA. This paradigm has been evidenced for many years in the context of the well known lac operon system in bacteria (56,57). In the lac system, the presence of few additional dispersed recruitment sequences (operators) and the ability of oligomerization of the lac-repressor enhance the association of a repressor to the effective ‘repressing’ site (57). In eukaryotes, similar strategies are acting at the level of promoter–enhancer genomic modules: the long-range action of enhancer sequences on promoter is conditioned to their physical contact (Chen et al., BioRxiv:https://doi.org/10.1101/099523). As for the lac system, distal enhancer sequences might actually act as secondary recruitment sequences for transcription factors that, by associating with mediators or other architectural proteins, can promote recruitment and stabilization of the transcriptional machinery at promoters via long-range looping (58). Along the same line, in Drosophila, PcG-mediated repression involves the spatial colocalization of several silencer sequences (the so-called PREs). This spatial proximity is mediated by the polycomb protein complex that may promote multi-loops structures, the PC bodies (59,60). For example, the level of PcG-mediated repression of the ANT-C and BX-C domains has been directly correlated to the level of clustering between these two domains Mbp-distant domains (61). Therefore, 3D clustering not only impacts the genome regulation in cis, i.e. within an epigenomic domain, but may also act in trans between distant domains. Of note, colocalization of PcG repressed genes are also observed in mammals (25). Similarly, in the yeast SIR-mediated heterochromatinization system, gene silencing has been correlated to the level of SIR-mediated clustering of telomeres, which are the main nucleation centers for the loading of the silenced state (62). All this is fully consistent with our prediction that clustering enhances stability of epigenomic states. Along the same line, several studies have reported that the local condensation of the nucleosomal array into a more compact chromatin fiber (mediated by architectural proteins and nucleosome–nucleosome stacking interactions) is associated to an enhanced level of repression (44,46). On one hand, compaction may stimulate enzyme activity in cis, on the other hand, consistently with our results, the strong nucleosome density and—even weak—trans spreading ability may lead to a stable propagation of the epigenomic state at the chromatin fiber scale. This suggests that even in the case where only cis spreading occurs at the nucleosome level, clustering may act as a ‘sink’ of modifier enzyme leading to an enhanced cis spreading by a trans stimulation effect.

In the second part of our work, we showed how self-association can help stably maintaining two compartments carrying antagonistic epigenomic signals. Formation of two separated TADs by epigenomic-driven interactions limits the ability of spreading in trans due to long-range contacts that may lead to the ‘invasion’ of one epigenomic domain by the state of its neighboring domains. TADs may provide a ‘basal’ level of large-scale confinement and of selectivity that are then finer-tuned at lower scale within sub-TADs modules (63). Implication of TADs in regulating transcription has been also recently proposed in the process of mammalian X inactivation, where Giorgetti et al. (64) showed that, consistently with the nano-reactor hypothesis (15), the expression of the Tsix transcript was positively correlated with the compaction level of its embedding TAD.

When avoiding cis spreading at the boundary between the two domains, the LC model suggests that 1D insulation may significantly participate in the stabilization of such compartmentalization and of a well-defined boundary. Indeed, insulator proteins such as CTCF, by physically preventing the action in cis of epigenomic enzymes, may contribute to the selective insulation of the active/repressive structural domains (65). Recent studies have shown that disrupting boundaries might lead to concomitant deregulation of 3D chromatin organization, epigenome and genome activity (66). It would be interesting to experimentally further decipher the role of the spatial folding in that deregulation, for which other mechanisms than self-association, such as the loop-extrusion (67,68) may participate in the regulation of the local compaction.

We report in this article a theoretical work that aims, within a minimal framework, to rationalize the generic effect of 1D-3D coupling in the formation and maintenance of one stable epigenomic domain and in the maintenance of a local stable compartmentalization between antagonistic domains. The modularity of the LC model will allow in the future to theoretically investigate the impact of biologically relevant conditions such as titration effects (27,69), replication and cell cycle duration (29), conversion asymmetries (28), multicolor epigenome (70) or of more complex epigenome organization. Building such framework that could reproduce quantitatively both linear and spatial epigenome organization in real system and make testable predictions would certainly be a valuable tool for the epigenomics community. However, this will require to design experiments that can record the large-scale dynamics of both the 1D and 3D organization, during the establishment and the maintenance stages, both in wild-type and mutant backgrounds. The perturbations of the enzymatic activity and of the cross-linking abilities of architectural proteins, as well as the modifications of the recruiting sites (genomic locations and activities) and of the boundaries, will allow to quantify the relative contribution of the different cis and trans spreading mechanisms to the long term epigenomic maintenance. Recent studies have shown that this relies on self-propagation and on sequence-specific cis-recruitment mechanisms (71–73). Our results suggest that spatial compaction by promoting self-propagation in trans might cooperate with cis-recruitment to achieve strong stability. This means that a weakening of the recruitment might be compensated by an increase of the compaction. Whether this compensatory mechanisms indeed occur in real system at both developmental and evolutionary time scales has to be further investigated.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Agence National de la Recherche [ANR-15-CE12-00006-EpiDevoMath]; Fondation pour la Recherche Médicale [DEI20151234396]. Funding for open access charge: Agence National de la Recherche [ANR-15-CE12-00006-EpiDevoMath].

Conflict of interest statement. None declared.