Skip to main content
PMC home page
Nucleic Acids Research logoLink to Nucleic Acids Research
. 2017 Dec 19;46(5):e27. doi: 10.1093/nar/gkx1246

TAD-free analysis of architectural proteins and insulators

Raphaël Mourad 1,✉, Olivier Cuvier 1
PMCID: PMC5861416  PMID: 29272504

Abstract

The three-dimensional (3D) organization of the genome is intimately related to numerous key biological functions including gene expression and DNA replication regulations. The mechanisms by which molecular drivers functionally organize the 3D genome, such as topologically associating domains (TADs), remain to be explored. Current approaches consist in assessing the enrichments or influences of proteins at TAD borders. Here, we propose a TAD-free model to directly estimate the blocking effects of architectural proteins, insulators and DNA motifs on long-range contacts, making the model intuitive and biologically meaningful. In addition, the model allows analyzing the whole Hi-C information content (2D information) instead of only focusing on TAD borders (1D information). The model outperforms multiple logistic regression at TAD borders in terms of parameter estimation accuracy and is validated by enhancer-blocking assays. In Drosophila, the results support the insulating role of simple sequence repeats and suggest that the blocking effects depend on the number of repeats. Motif analysis uncovered the roles of the transcriptional factors pannier and tramtrack in blocking long-range contacts. In human, the results suggest that the blocking effects of the well-known architectural proteins CTCF, cohesin and ZNF143 depend on the distance between loci, where each protein may participate at different scales of the 3D chromatin organization.

INTRODUCTION

In higher eukaryotes, chromosomes are packed in three dimensions and form complex structures (1). Such three-dimensional (3D) structure has recently been investigated by chromosome conformation capture combined with high-throughput sequencing technique (Hi-C) at an unprecedented resolution (2–4). Hi-C experiments reveal multiple levels of genome organization including compartments A/B (5) and topologically associating domains (TADs) (2,3). Most notably, TADs are relatively constant between different cell types and are highly conserved across species. These TADs play important roles in key cell processes such as long-range regulation of genes by enhancers (4) or replication-timing regulation (6).

The identification of architectural proteins and functional elements involved in shaping the genome in 3D represents an intensive field of research (7). Seminal works using enhancer-blocking assays (EBAs) revealed that functional elements called insulators (or boundary elements) can suppress the activation of a promoter by a distant enhancer when interposed (8,9). Multiple evidence actually supports the role of insulator binding proteins (IBPs) such as CTCF, and co-factors like cohesin, as mediators of long-range chromatin contacts (3,10–13), which may in turn result in blocking enhancers from contacting promoters by forming alternative DNA loops. In mammals, high-resolution mapping of long-range contacts has recently revealed that loops occur at domain boundaries and bind CTCF in a convergent orientation where cohesin is recruited (12,14). Depletion of CTCF and cohesin decreased chromatin contacts (13). However, the impact of those depletions was limited suggesting that other proteins might be involved in shaping the chromosome in 3D. Accordingly, other IBPs, co-factors and functional elements were also shown to colocalize at TAD borders (11,15).

A classical approach to identify proteins involved in shaping the 3D genome structure consists in assessing their enrichments at TAD borders (2,3,12). Among a set of enriched proteins, multiple logistic regression (MLR) can be further used to characterize which proteins are more likely to influence the presence of borders (15). However, an important drawback of the enrichment test and MLR is that they rely on accurate TAD mapping, which is problematic for multiple reasons: (i) TAD mapping strongly depends on the algorithm used (16), (ii) TADs only capture a fraction of the information from Hi-C data, and other important 3D domains including A/B compartments (5), loop domains (12) and subTADs (4) were discovered and (iii) TAD borders are blurry (11).

Here, we propose a model named ‘blocking model’, to systematically analyze the roles of architectural proteins and functional elements in blocking long-range contacts between loci. The proposed model does not rely on TAD mapping from Hi-C data. Thus, the model’s outcome is not affected by the blurriness of borders. Instead of testing the enrichment/influence of protein binding at TAD borders, the model directly estimates the blocking effect of proteins on long-range contacts between flanking loci, making the model intuitive and biologically meaningful. The model only depends on a simple biological parameter: the distance between insulated loci. The model directly analyzes the Hi-C contact matrix, thus taking advantage of the whole Hi-C information content (2D information) instead of only focusing on TAD borders (1D information). Moreover, the model successfully predicts in silico the outcomes from low-throughput enhancer blocking assays, thus enabling genome-wide analyses. Using recent Drosophila and human Hi-C data at high resolution, combined with a large number of ChIP-seq and DNA motif data, we revealed numerous combinations of proteins, functional elements and DNA motifs that block long-range contacts depending on scale and synergistic/antagonistic effects.

MATERIALS AND METHODS

Hi-C data

For Drosophila data analysis, we used publicly available high-throughput chromatin conformation capture (Hi-C) data of embryonic Kc167 cells from Gene Expression Omnibus (GEO) accession GSE62904 (17). We also used Kc167 Hi-C data from GEO accession GSE89112 (18). Hi-C data were binned at 1, 2 and 5 kb resolutions.

For human data analysis, we used publicly available Hi-C data of lymphoblastoid GM12878 cells from GEO accession GSE63525 (12). We used Hi-C data binned at 10, 40 and 100 kb resolution.

ChIP-seq data

For Drosophila data analysis, we used publicly available protein-binding profiles of Kc167 cells (except for Pnr whose data were from 6–8 h embryos). ChIP-seq data for CP190, Su(Hw), dCTCF and BEAF-32 were obtained from GEO accession GSE30740 (19). ChIP-seq data for Barren (condensin I), Cap-H2 (condensin II), Chromator, Rad21 (cohesin), GAF and dTFIIIC were obtained from GEO accession GSE54529 (11). ChIP-seq data for Fs(1)h-L were obtained from GEO accession GSE42086 (20). ChIP-seq data for Ttk69k were obtained from GEO accession GSE34698 (21). ChIP-seq peak calling was done using MACS 2.1.0 with default parameters for all proteins (https://github.com/taoliu/MACS). ChIP-chip peaks for Pnr were directly downloaded from (22).

For human data analysis, we used publicly available binding peaks of 73 chromatin proteins (Rad21, CTCF, YY1, ZBTB33, MAZ, JUND, ZNF143, EZH2, ATF2, ATF3, BATF, BCL11A, BCL3, BCLAF1, BHLHE40, BRCA1, CEBPB, CFOS, CHD1, CHD2, CMYC, COREST, E2F4, EBF1, EGR1, ELF1, ELK1, FOXM1, GABP, IKZF1, IRF4, MAX, MEF2C, MTA3, MXI1, NFATC1, NFE2, NFIC, NFKB, NFYA, NFYB, NRF1, NRSF, P300, PAX5, PBX3, PML, POL2, POL3, POU2F2, RFX5, RUNX3, RXRA, SIN3A, SIX5, SMC3, SP1, SPI1, SRF, STAT1, STAT3, STAT5, TBLR1, TBP, TCF12, TCF3, TR4, USF1, USF2, WHIP, ZEB1, ZNF274 and ZZZ3) of GM12878 cells from ENCODE (23). We downloaded peaks that were uniformly processed (Uniform Peaks).

DNA motifs

To scan the genome for motif occurrences, we used Find Individual Motif Occurrences (FIMO) with default parameters and with position-specific priors (PSPs) to improve the identification of true motif occurrences (24). GM12878 DNase data from ENCODE were used as PSPs (23). The motif information was taken either from the litterature (using consensus motif) or from JASPAR database (http://jaspar.genereg.net/).

For Drosophila data analysis, we used transcription factor-binding site (TFBS) motifs from the JASPAR database. For some proteins, we used instead motif consensuses from the litterature: BEAF-32 (CGATA) (25), dCTCF (AGGTGGCG) (26), Su(Hw) (TGCATATTT) (27), GAF (GAGAGA) (28), ZW5 (GCTGMG) (29), DREF (TATCGATA) (30), M1BP (GGTCACACT) (31), Ttk69k (GGTCCTGC) (32), dTFIIIC A box (TGGNNNAGNNG), Pita (GGTTNNNNNNNNNGCT) (29), ZIPIC (AGGGNTG) (29), Ibf (ATGTANAA) (33), Elba (CCAATAAG) (34) and Zelda (CAGGTAG) (35).

For human data analysis, we also used TFBS motifs from the JASPAR database. In human, motifs with <2000 occurrences were removed from the analysis to reduce uncertainty in the β estimation.

The blocking model

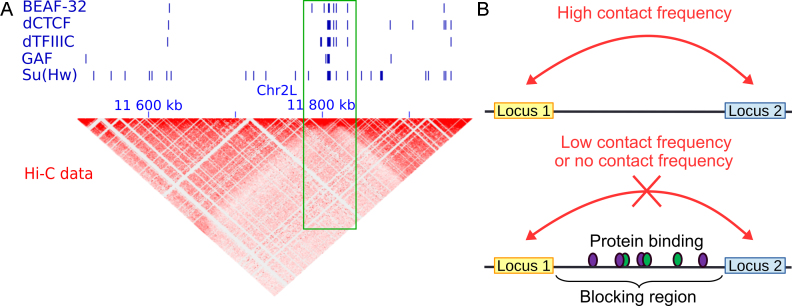
To illustrate the blocking model, we first plotted the example of a Drosophila genomic region with embryonic Kc167 cell Hi-C heatmap and ChIP-seq peaks of well-known architectural proteins (Figure 1A). We observed that all architectural proteins BEAF-32, dCTCF, dTFIIIC, GAF and Su(Hw) accumulated on a specific locus (green frame) that acted as an insulator of long-range contacts between flanking regions. This observation suggested that the binding of those proteins blocked long-range contacts (Figure 1B), thereby contributing to the formation of 3D domains.

Figure 1.

Figure 1.

Open in a new tab

Illustration of the blocking model. (A) Example showing that the accumulation of insulator-binding proteins (IBPs) is associated with a blocking effect of long-range contacts between flanking loci in Drosophila (see green frame). (B) Schema representing the blocking effect of protein binding on long-range contacts between two loci, such as between an enhancer and a promoter.

By integrating Hi-C data with ChIP-seq data or DNA motif data, we propose to model the blocking effects of protein bindings with a generalized linear model:

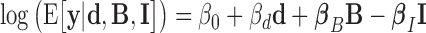graphic file with name M3.gif (1)

where, variable y denotes Hi-C count for any pair of bins on the same chromosome. The log-distance variable d accounts for the background polymer effect (power law decay relation between distance and Hi-C count modeled by a log–log linear relation) (36). Bias variables B = {len, GC, map} are known Hi-C biases including fragment length (len), GC-content (GC) and mappability (map) that are computed as in (37). Including those bias variables into the model allows correcting for biases in Hi-C data. Note that bias variables do not need to be included in the model if Hi-C counts were previously normalized by matrix balancing (38). Variable set I = {i1, ..., ip} represents the p blocking variables of interest. A blocking variable stores a value corresponding to a ‘blocking region’ (Figure 1B), which is the region in-between two bins whose Hi-C contacts are measured. For ChIP-seq data, a blocking variable is defined as the average of the base coverage computed from the log2 fold-enrichments of peaks found into the blocking region divided by the length of the blocking region. A base within a peak has a coverage value equal to the log2 fold-enrichment of the peak and a base outside a peak has a coverage value equal to zero. For DNA motif data, a blocking variable is defined as the number of motif occurrences found into the blocking region divided by the length of the blocking region. The corresponding βi parameter value reflects the blocking effect of the protein on Hi-C counts. A positive value (βi > 0) reveals a blocking effect on long-range contacts. Conversely, a negative value (βi < 0) shows a facilitating effect on contacts. A null value (βi = 0) means that the protein does not have any effect in blocking or facilitating contacts.

Using the model, one can also assess the co-blocking effects of two or more proteins using statistical interaction terms:

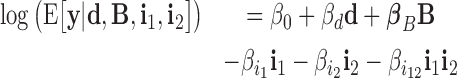graphic file with name M4.gif (2)

where, variables i1 and i2 are two blocking variables. The product i1i2 is a second-order statistical interaction. The corresponding parameter 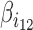Inline graphic reflects the co-blocking effect of the two proteins on contacts. A positive value (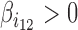Inline graphic) reveals a synergistic effect of the two proteins in blocking contacts. Conversely, a negative value (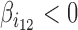Inline graphic) shows an antagonistic effect of the two proteins in blocking contacts. In equation (2), a second-order interaction was included, but higher-order interactions (products of more than two variables) can be included to model co-blocking effects of more than two proteins.

The model only depends on a single parameter: the distance range between insulated loci. This parameter has a strong biological meaning since it reflects the analysis scale of hierarchical 3D genome organization. For instance, in Drosophila, we will focus on Hi-C data for 20–50 kb distances which are below the median size of TADs (median size of 60 kb (3)), therefore allowing TAD-scale analyses. But we will also vary the scale of analysis in human (see below).

In some situations, we standardize the blocking variables before computing the model. Standardization allows to reduce the effect of very large differences in the blocking variables between different proteins when estimating the βs and makes the latter more comparable in magnitude. In fact, these blocking variable differences might be due to very large differences in the ChIP-seq signal and the number of peaks that might not be linked to the real blocking activity of proteins. For instance, when analyzing human ChIP-seq data, we found that the highest βs were often associated to proteins with few binding sites when no standardization was used, and that these βs were strongly reduced after standardization (see below).

Because of Hi-C count overdispersion, we use negative binomial regression as the most appropriate specification of the generalized linear model. However, Poisson regression with lasso shrinkage can also be used. We believe that the choice between both depends mainly on the number of variables to analyze. On the one hand, if there are a few candidate variables (<10), it is interesting to estimate β parameters together with corresponding P-values to assess significance using negative binomial regression. On the other hand, if there are a large number of variables (10 or more), it is more convenient to use Poisson lasso regression in order to select the key variables and to account for correlations among the variables (frequent in ChIP-seq and motif occurrence data).

The model is available in the R package ‘HiCblock’ which can be downloaded from the Comprehensive R Archive Network (https://cran.r-project.org/web/packages/HiCblock/index.html). For the negative binomial regression, model βs are learned by iterative weighted least squares (glm.nb function from MASS R package with default parameters). For the Poisson lasso regression, model βs are learned by cyclical coordinate descent and lambda parameter is estimated with 10-fold cross-validation (cv.glmnet function from glmnet R package with default parameters).

Simulation of random protein-binding sites and motif occurrences

For Poisson lasso regression in human, we simulated protein binding sites by randomly drawing genomic regions from the genome whose numbers and fold-enrichments were similar to those observed from real proteins. We then used these random proteins to compute associated β coefficients with the Poisson lasso regression. We expected these βs to be close to zero but with a certain standard deviation 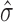Inline graphic. We then used this standard deviation to compute a confidence interval as 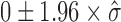Inline graphic under the null hypothesis that a random protein did not have any blocking or facilitating effect on long-range contacts. For DNA motifs, we used a slightly different approach. We randomly draw 14 base DNA sequences (random motifs) whose number of occurrences over the genome were similar to those of real DNA motifs. We scanned the genome for random motif occurrences. Then, we used these random motif occurrences to compute associated β coefficients with the Poisson lasso regression. As for random proteins, we used these βs to compute a confidence interval under the null hypothesis.

RESULTS

Model validation with enhancer-blocking assays

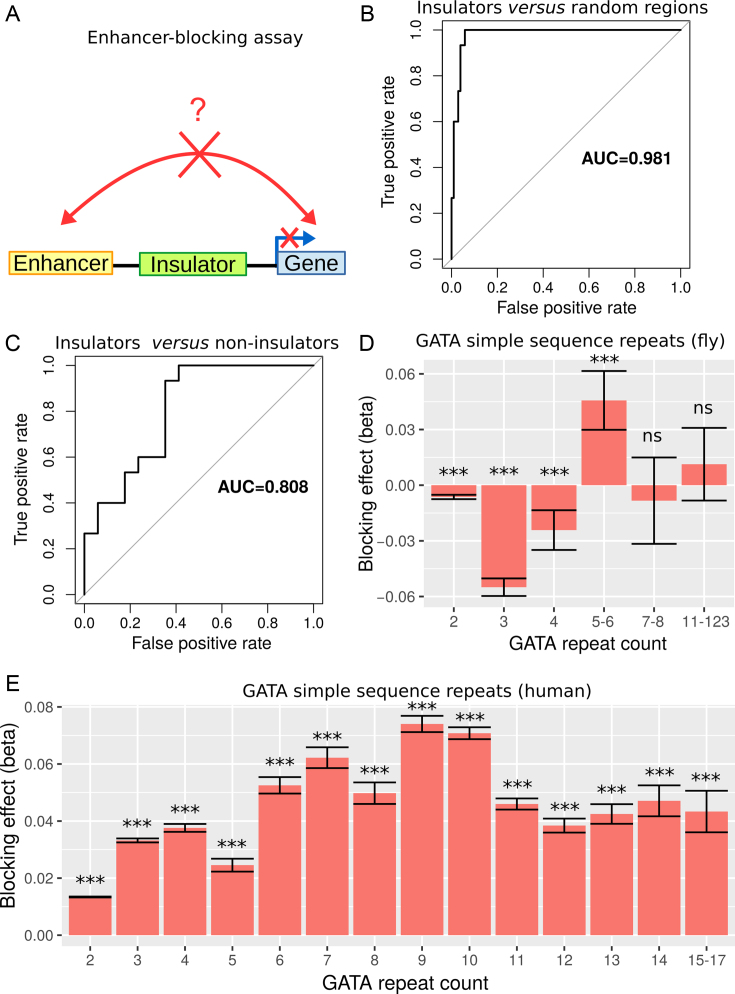
We first sought to validate our model using EBAs from Drosophila. EBA is a classical low-throughput method that can be used to show the ability of an insulator sequence to block the activation of a promoter by a distant enhancer when interposed between them (39) (Figure 2A). We used the model to predict the blocking effect of an insulator region depending on protein binding. For this purpose, we used a compilation of EBA results from (11). It consisted of 32 regions with varying reported insulating activity (15 regions with insulating activity and 17 regions with no insulating activity). In the first benchmark, we selected the 15 regions with insulating activity (positive class). In order to have a large set of regions with no insulating activity, we generated >100 control regions (negative class) by randomly drawing from the Drosophila genome with sizes, GC and repeat contents similar to those of the abovementioned 15 regions (40). For each region, we computed blocking variables I = {i1, ..., ip} using p ChIP-seq data from Kc167 cells. We also used 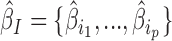Inline graphic model parameters independently learned from Kc167 Hi-C data from Li et al. (17) at 2 kb resolution and for 20–50 kb distances, for which Hi-C coverage was high. Model parameters were not learned from EBA assays to prevent overestimation of predictive performance. We predicted insulating activities of the regions by the matrix product 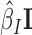Inline graphic. We then assessed the accuracy of our model’s predictions using receiver operating characteristic (ROC) curve and the area under the ROC curve (AUC). We found that predicted insulating activity was very close to the observed insulator activity from EBA (AUC = 0.981; Figure 2b). In the second benchmark, we did not use generated controls but instead the 17 regions reported to have no insulating activity as negative class. We again predicted insulating activity, and found that predictions were still good (AUC = 0.808; Figure 2C). We found that changing Hi-C data resolution to 1 or 5 kb only slightly affected predictions for the two benchmarks (Supplementary Figure S1). In the third benchmark, we assessed the blocking effect of simple sequence repeats (SSRs) of GATA that were shown to have an insulating activity by EBAs in both drosophila and human (41). In drosophila, we estimated a blocking effect for SSRs that comprised >4 repeats (Figure 2D and Supplementary Table S1). In particular, we found a significant blocking effect for SSRs with five to six repeats (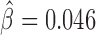Inline graphic, P = 2 × 10−8). SSRs with >6 repeats were too few to detect any significant blocking effect (only 8 SSRs with 7 to 8 repeats and 9 SSRs with >11 repeats). In human, we detected significant blocking effects for all GATA repeat counts (P < 10−20) at short distances (100–250 kb at 10 kb resolution; Figure 2E and Supplementary Table S2). Most notably, we found the highest blocking effects for SSRs with 9 to 10 repeats (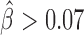Inline graphic, P < 10−20), revealing that the blocking effect depends on the number of repeats. For larger distances (950–1000 kb), we could only detect a slight blocking effect for eight repeats, suggesting that SSR blocking effect acted at short distance (Supplementary Figure S2 and Table 3). Using EBAs, we thus concluded that the model was successfully validated.

Figure 2.

Figure 2.

Open in a new tab

Validation of the model with enhancer-blocking assays (EBAs) from Drosophila and human. (A) Illustration of the EBAs. (B) ROC curves of the prediction of insulating regions (positives) as compared to randomly drawn regions (negatives) in Drosophila. Area under the ROC curve (AUC) is plotted. (C) ROC curves of the prediction of insulating regions (positives) as compared to non-insulating regions (negatives) in Drosophila. (D) Blocking effects of GATA SSRs depending on the repeat count in Drosophila. (E) Blocking effects of GATA SSRs depending on the repeat count in human.

Analysis of insulator proteins and comparison with current approaches

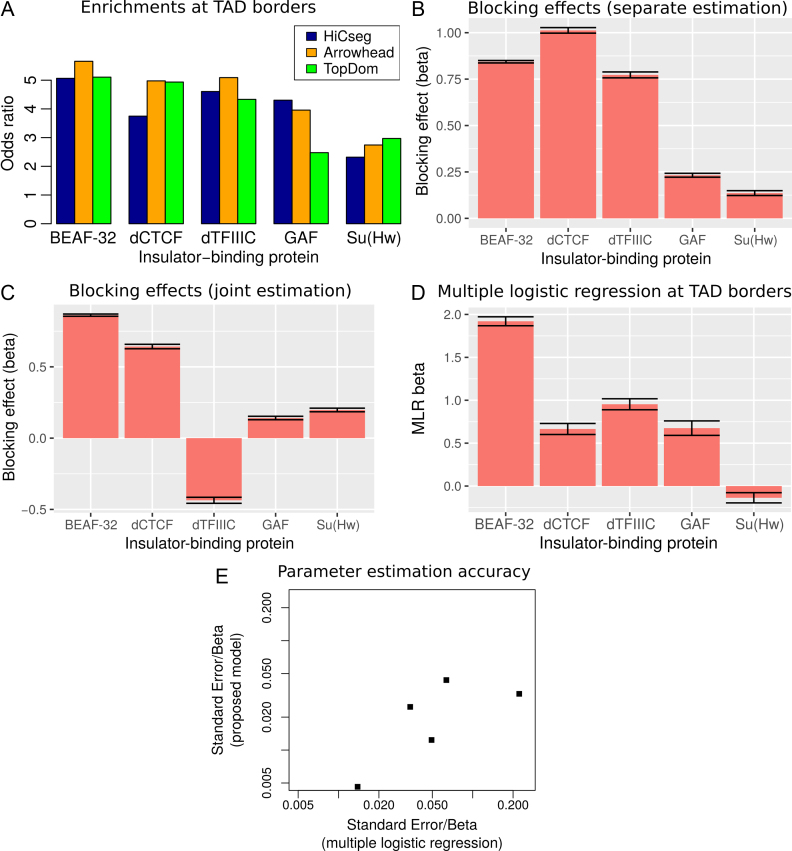
A major problem of testing protein enrichment at TAD borders is that different algorithms have been developed for TAD mapping which can yield large differences of enrichments for the same protein (42). Accordingly, we observed that the enrichments of BEAF-32, dCTCF, dTFIIIC, GAF and Su(Hw) could greatly vary depending on the TAD algorithm used in Drosophila (Figure 3A). For instance, GAF presented an odds ratio (OR) of 4.3 with HiCseg (43), an OR of 4 with Arrowhead (12), whereas it only showed an OR of 2.5 with TopDom TADs (16). Conversely, dCTCF presented an OR of 3.7 with HiCseg, and ORs around 5 with Arrowhead and TopDom.

Figure 3.

Figure 3.

Open in a new tab

Analysis of IBPs in Drosophila. (A) Enrichment of IBPs at TAD borders, depending on the TAD mapping algorithm used. (B) Blocking effect (β) estimated separately. (C) Blocking effect (β) estimated jointly. (D) MLR βs estimated from TAD borders (15). (E) Parameter estimation accuracy of the proposed model compared to MLR.

Instead of testing protein enrichments at TAD borders, we used our model to directly assess the blocking effect of protein binding on long-range contacts. We first estimated separately the blocking effects of IBPs, by including only one IBP in the model at a time. This allowed to compare with previous enrichments. We used Kc167 Hi-C data from Li et al. (17) at 2 kb resolution and focused on 20–50 kb distances. Using our model, we found that BEAF-32, dCTCF and dTFIIIC showed the strongest blocking effects (Figure 3B), which was similar to the enrichments observed at TAD borders (Figure 3A) and previously observed by Sexton et al. (3). Because the blocking effect might be influenced by the number of protein-binding sites, we sampled different numbers of peaks from BEAF-32 and estimated the corresponding βs. As expected, we found that β accuracy was lower for smaller number of peaks (Supplementary Figure S3). We also observed that the blocking effect was inflated, but such inflation remained reasonable (+63%), even for 1000 sampled peaks which represented only 15% of all BEAF-32 peaks.

Because IBPs often colocalize linearly (e.g. correlate) on the chromosome, one might estimate a blocking effect for a protein, although the protein does not directly impede long-range contacts (15). Hence, we re-estimated blocking effects of IBPs jointly (e.g. by including all IBPs within the same model). BEAF-32 presented the highest blocking effect (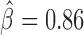Inline graphic, P < 10−20) compared to the other proteins (Figure 3C), similarly to previously published MLR analysis at TAD borders (15) (Figure 3D). Our model also estimated a negative β for dTFIIIC, suggesting that the protein could in fact facilitate long-range contacts between flanking regions, contrary to what is found by the separate estimation (previous paragraph). This meant that dTFIIIC blocking effect estimated by separate estimation was in fact due to the colocalization (correlation) of dTFIIIC with other IBPs such as BEAF-32 (correlation between dTFIIIC and BEAF-32 blocking variables equals 0.59, P < 10−20). Our model outperformed MLR in terms of parameter estimation accuracy. Standard errors of beta parameters were dramatically lower than the ones from MLR, revealing the higher performance of our model in assessing blocking effects of proteins (Figure 3E). To further compare our new model with MLR, we assessed the ability to discriminate between known architectural proteins (11 true positives including IBPs and co-factors) and random protein peaks (200 false positives) using ROC curves (Supplementary Figure S4). Based on the absolute values of βs, we found that our blocking model was highly accurate (AUC = 0.991) and performed better than MLR (AUC = 0.827). Moreover, we performed the joint analysis of IBPs for different binning resolutions (1 and 5 kb) and found similar results with 2 kb, revealing that the resolution did not have a big impact on the estimation of blocking effects (Supplementary Figure S5). In addition, we analyzed recent Hi-C data with higher coverage from Eagen et al. (18) at 1 kb resolution and obtained results that were close to those obtained from Li et al. data (Supplementary Figure S6). Thus, by processing the whole Hi-C matrix information, instead of focusing only on TAD borders, the proposed model was more accurate than MLR.

Numerous protein-binding DNA motifs act as blockers

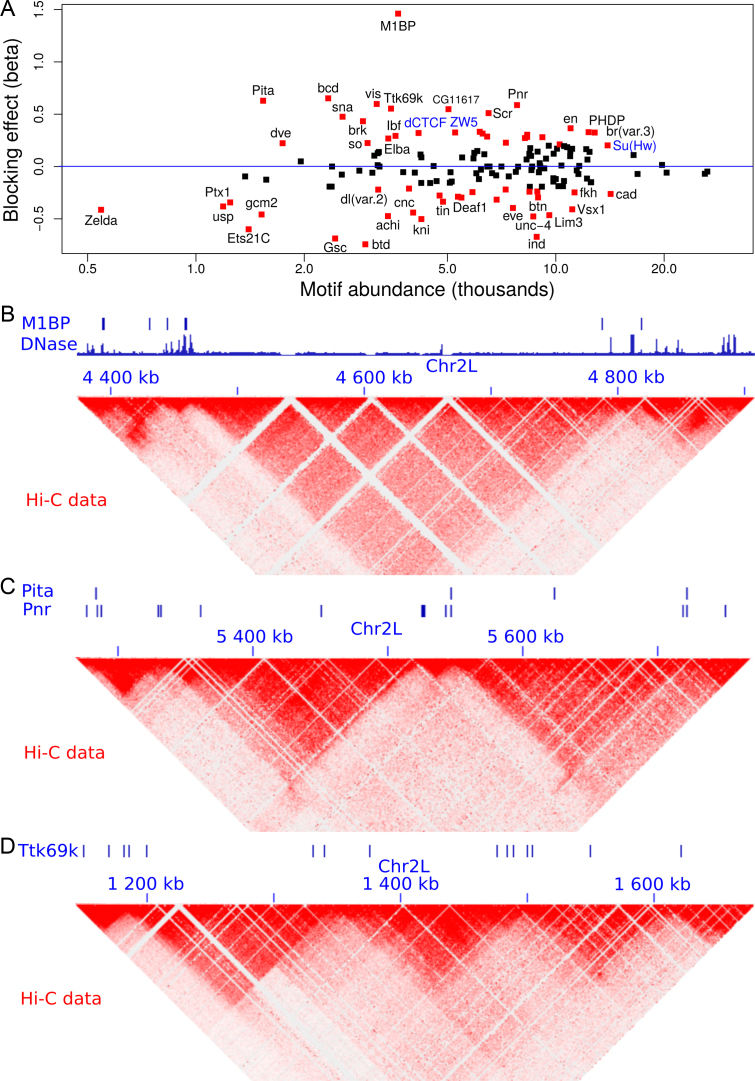
We next sought to analyze the blocking effects of protein-binding DNA-motifs (Figure 4A and Supplementary Table S4). Interestingly, our model found motif 1-binding protein (M1BP) as the motif with the strongest blocking effect (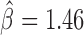Inline graphic), which was recently found to be enriched at TAD borders during development (35) and was implicated in transcriptional pausing of genes (31). Such transcriptional pausing was recently shown to be involved in long-range contacts (44). When we looked at Hi-C heatmaps, we observed that M1BP motifs accumulated at the borders of 3D domains (Figure 4B; DNase I hypersensitivity is shown to represent the potential activity of the motifs). We also identified other motifs with strong blocking effects including bcd (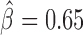Inline graphic), Pita (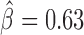Inline graphic), vis (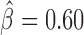Inline graphic), Pnr (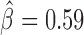Inline graphic) and Ttk69k (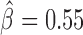Inline graphic). Among those proteins, Pita was a recently discovered insulator protein able to target CP190 to chromatin (45) and was found at 3D domain borders (Figure 4C). When we used Ttk69k ChIP-seq and Pnr ChIP-chip data, we found that both Ttk69k and Pnr colocalized at or near architectural protein peaks (Supplementary Figure S7a). For instance, Pnr was enriched at condensin I (Barren), CP190, BEAF-32 and Chromator peaks (Supplementary Figure S7b). Interestingly, Ttk69k was mostly enriched near architectural proteins but did not overlap them, except for condensin I, suggesting that Ttk69k might participate to the formation of 3D domains in a very specific way (Supplementary Figure S7c). Accordingly, we found numerous Pnr and Ttk69k motifs located between 3D domains (Figure 4C and D). We also identified architectural proteins ZW5 (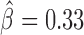Inline graphic), dCTCF (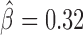Inline graphic) and Ibf (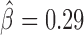Inline graphic). Of note, Ibf was shown to be a novel CP190 interacting protein with insulating activity (33). When we compared with MLR, we also found that M1BP presented a very high positive influence on TAD borders (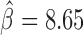Inline graphic; Supplementary Table S5). However another motif, Zelda, presented the highest positive influence (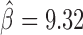Inline graphic), whereas the same motif was identified as a long-range contact facilitator with the blocking model (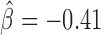Inline graphic; Supplementary Table S4). This suggests that the blocking model can capture effects on long-range contacts that could not be assessed by the analysis at the TAD border level. Using the blocking model, we could conclude that many proteins including pannier, a transcriptional regulator involved in several developmental processes (46) and tramtrack 69k, a widely expressed transcriptional factor (TF) related to cell fate specification, cell proliferation and cell-cycle regulation (47), might represent novel candidate architectural proteins in Drosophila.

Figure 4.

Figure 4.

Open in a new tab

Analysis of protein binding DNA motifs in Drosophila. (A) Blocking effect (β) in function of motif abundance (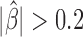Inline graphic are shown in red; known architectural proteins are written in blue). (B) Example showing the accumulation of M1BP motifs and DNase I hypersensitive sites between 3D domains. (C) Example showing the accumulation of Pita and Pnr motifs between 3D domains. (D) Example showing the accumulation of Ttk69k motifs between 3D domains.

Co-blocking effects of insulator-binding proteins and co-factors

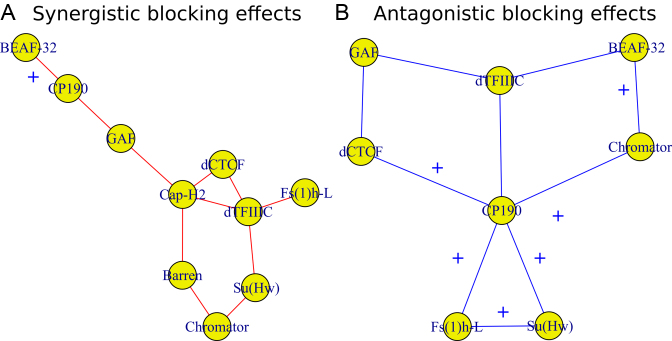
Long-range contacts not only involve IBPs but also co-factors that regulate or stabilize them (11,12,48). Hence, we sought to analyze potential effects of IBPs and co-factors in co-blocking long-range contacts. We first modeled the co-blocking effects of protein pairs using second-order statistical interactions (for every protein pair, we estimated a co-blocking effect). We detected 38/55 significant interactions after Bonferroni correction. Among the significant interactions, the model identified 19 positive co-blocking effects (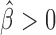Inline graphic), reflecting protein pairs that synergistically blocked long-range contacts (Supplementary Table S6). We represented these synergistic blocking effects by a network of proteins (Figure 5A). In agreement with (49), CP190 co-blocked contacts with BEAF-32 (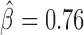Inline graphic, P < 10−20) and with GAF (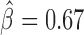Inline graphic, P < 10−20). Interestingly, we found that Condensin II (Cap-H2) played a central role in helping other proteins to block contacts, including dCTCF (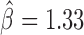Inline graphic, P = 4 × 10−13), Barren (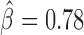Inline graphic, P < 10−20), dTFIIIC (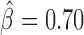Inline graphic, P = 10−6) and GAF (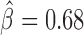Inline graphic, P = 2 × 10−10). dTFIIIC also represented an important protein for co-blocking effects. Conversely, Fs(1)h-L had only one co-blocking partner, dTFIIIC. The model also estimated 19 negative co-blocking effects (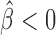Inline graphic), reflecting protein pairs that had antagonistic effects in blocking long-range contacts (Figure 5B and Supplementary Table S6). Most notably, we found numerous antagonistic effects of CP190 in blocking contacts with other proteins, such as dTFIIIC (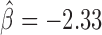Inline graphic, P < 10−20), Su(Hw) (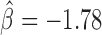Inline graphic, P < 10−20), Chromator (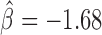Inline graphic, P < 10−20), dCTCF (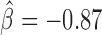Inline graphic, P < 10−20) and Fs(1)h-L (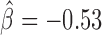Inline graphic, P = 4 × 10−6). Interestingly, Su(Hw) had a slight blocking effect on long-range contacts (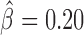Inline graphic, P < 10−20; Figure 3C), but when combined with CP190, they presented a strong antagonistic effect which reduced its blocking effect (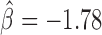Inline graphic, P < 10−20; Figure 5B). Among the synergistic and antagonistic effects, we found that many corresponded to physical interactions reported in Flybase and previous studies (49), supporting the idea that physical interactions may account for some of them. Analysis of second-order interactions thus revealed the complexity behind the establishment of 3D domains. This may notably depend on numerous synergistic and antagonistic effects of IBPs with key architectural co-factors such as structural maintenance complex (SMC) family of proteins including cohesin and condensin (50,51).

Figure 5.

Figure 5.

Open in a new tab

Effects of IBPs and co-factors in co-blocking long-range contacts. (A) Synergistic blocking effects estimated by positive second-order interaction βs. An edge between two protein nodes i and j means 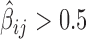Inline graphic. (B) Antagonistic blocking effects estimated by negative second-order interaction βs. An edge between two protein i and j nodes means 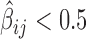Inline graphic. Blue cross: physical interaction reported in Flybase.

Analysis in human

We then analyzed blocking effects of proteins and DNA motifs in human, depending on the scale of 3D genome organization. For this purpose, we used GM12878 Hi-C data for varying distance ranges: [200–400 kb], [400–600 kb], [600–800 kb], [800–1000 kb], [1000–1300 kb], [1700–2000 kb], [2700–3000 kb], [2700–3000 kb], [3700–4000 kb] and [4700–5000 kb]. We performed analyses at 40 kb resolution to have sufficient coverage at long distance (even though for short distance higher resolution could be used). By varying the distance range, we could assess blocking effects at different scales, thus allowing the analysis of the well-known hierarchical nature of 3D domains (52). Because of the large number of variables (>50), we used Poisson lasso regression. Moreover, for ChIP-seq data analysis, we scaled the blocking variables because the ChIP-seq peak numbers and fold-enrichments greatly varied between proteins and that prevented further comparison of βs. For each analysis, we also computed confidence intervals under the null hypothesis that a protein or DNA motif did not have any blocking or facilitating effect on long-range contacts (see ‘Materials and Methods’ section, simulation of random protein-binding sites and motif occurrences).

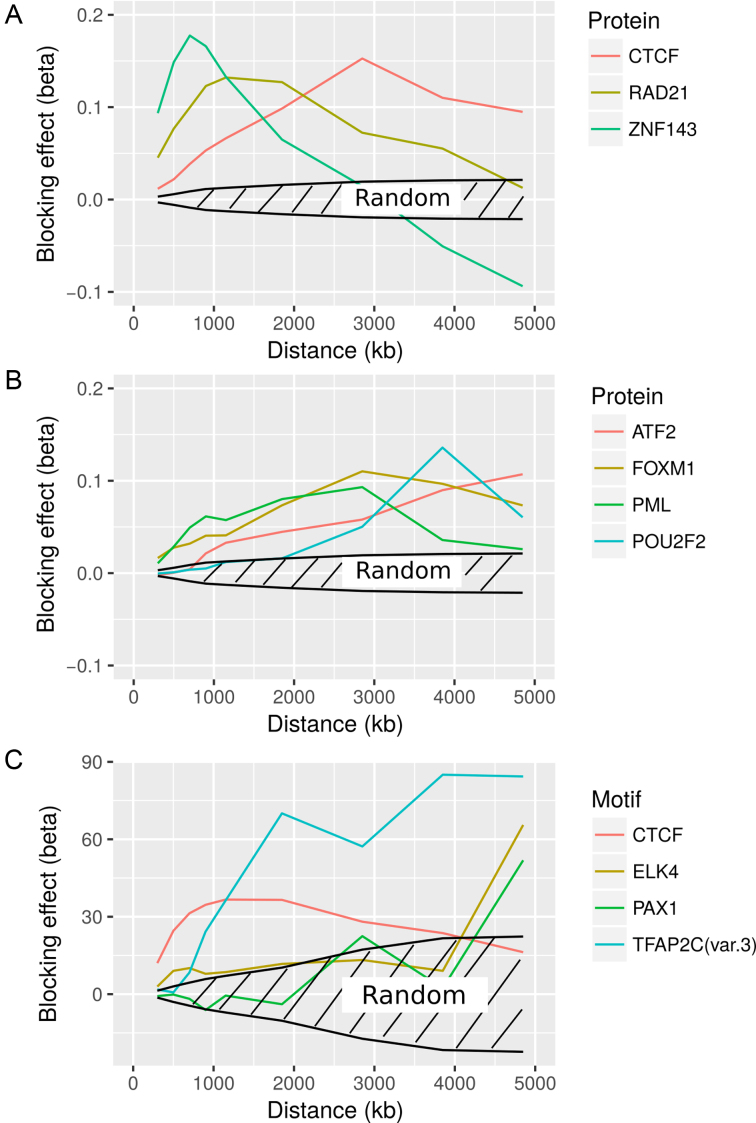
We first focused on known architectural proteins CTCF, Rad21 (cohesin subunit) and ZNF143. Remarkably, we observed that the blocking effects of architectural proteins strongly depended on the distance between loci (Figure 6A and Supplementary Table S7), a question that could not be addressed by previous enrichment or MLR analyses at TAD borders. For instance, CTCF blocking effects peaked around 3 Mb. Interestingly, the main looping partner of CTCF, cohesin, had a blocking effect that peaked at a lower distance, from 1000 to 2000 kb. Another partner of CTCF, ZNF143, also showed a different blocking effect that strikingly peaked at 800–900 kb. This means that although CTCF, cohesin and ZNF143 were known to act together in establishing chromatin loops (7), they might participate at different scales. We next studied the blocking effects of TFs (Figure 6B and Supplementary Table S7). Compared to architectural proteins, TFs were less abundant over the genome (around few thousands peaks, compared to tens of thousands of peaks for architectural proteins). Among the strongest blockers, we found ATF2, FOXM1, PML and POU2F2, whose effects also depended on distance. POU2F2 effect peaked at 3800 kb, and FOXM1 and PML both peaked at 3 Mb. Interestingly, some TFs, such as ATF2, presented high blocking effects for very large distance (>5 Mb). Thus, although TFs were less frequent over the genome than architectural proteins, they might collectively contribute significantly to the establishment or maintenance of 3D organization. Lastly, we analyzed protein-binding DNA motifs (Figure 6C and Supplementary Table S8). CTCF motif showed a strong blocking effect that peaked from 1000 to 2000 kb, at a shorter distance than found using ChIP-seq data. However, another motif, TFAP2C, presented the strongest blocking effect, especially at long distance. TFAP2C has been implicated in breast cancer oncogenesis, and was previously shown to be a collaborative factor in estrogen-mediated long-range interaction and transcription (53). We also identified ELK4 and PAX1 as strong blockers at long distance. ELK4 is a member of the Ets family of transcription factors, and PAX1, is essential during fetal development. We thus concluded that architectural proteins, but also transcription factors, shaped the 3D human genome at different genomic scales.

Figure 6.

Figure 6.

Open in a new tab

Analysis of protein binding and DNA motif in human. (A) Blocking effects of architectural proteins depending on the distance between loci. (B) Blocking effects of TFs depending on the distance between loci. (C) Blocking effects of protein binding motifs depending on the distance between loci. For all three subfigures, we also plotted confidence intervals under the null hypothesis that a random protein or DNA motif did not have any effect on long-range contacts.

DISCUSSION

In this paper, we propose a model to comprehensively study the roles of architectural proteins, insulators and DNA motifs in blocking long-range contacts between flanking loci at different scales, thereby demarcating the genome into functional 3D domains. The proposed approach is TAD-free: it does not rely on any TAD mapping algorithm, it does not focus on TADs but instead on all possible 3D domains at all scales, and it is not affected by the blurriness of TAD borders. The model is validated by numerous EBAs. It outperformed previous MLR of TAD borders (15) in terms of blocking effect estimation accuracy. The model is flexible and can identify both synergistic and antagonistic effects of architectural proteins depending on the presence of specific IBPs and co-factors.

The proposed model also uncovers a number of results. In Drosophila, we find that the blocking effect for the GATA SSRs depends of the number of repeats, and in particular, we estimate a significant blocking effect for 5–6 repeats. In human, we find that GATA repeat effect peaks for 9–10 repeats. Moreover, analysis of motifs identifies pannier and tram track as two novel candidate architectural proteins. Interestingly, the protein pannier is a member of the GATA family known to bind to GATA motifs (46), which may explain the insulating activity of GATA repeats by recruiting multiple pannier proteins contiguously to DNA. Moreover, tram track has a homomeric dimerization BTB/POZ domain that could help bridging two distant proteins through long-range contacts (54) and that is known to interact with GAF (55). Analysis of co-blocking effects between architectural proteins further suggests a role for co-factor condensin II in helping other proteins to block contacts. Conversely, CP190 presents numerous antagonistic effects with other proteins, meaning that it reduces their blocking activities. Such co-blocking analyses thus reveal the modulating effects of specific proteins in blocking contacts with other proteins. In human, analyses for varying distance ranges uncover strong distance-dependent blocking effects depending on the protein or DNA motif, that could not be addressed by enrichment test or MLR at TAD borders. For instance, we find that CTCF, cohesin and ZNF143 blocking effects peak at different distances, although the three proteins are known to act together in establishing chromatin loops (7). This suggests that they may participate at different 3D chromatin scales, or alternatively that their mechanisms of action is not always associated with their binding. Supporting this idea, recent results showed that cohesin is recruited at transcription start sites and positioned to CTCF sites by transcription-mediated translocation (56). In addition, we observed changes of the β sign depending on the distance. For instance, ZNF143 presented a blocking effect at short distance (<2500 kb) and a facilitating effect at longer distance. This can be due to ZNF143-mediated loops at short distance that have allosteric effects on long distance interactions (57).

There are different reasons why we restricted our analysis within a limited distance range, e.g. 20–50 kb in Drosophila (and not 20–1000 kb, for instance). First, at the high resolution of 2 kb, most of the Hi-C signal is observed within short distance (20–50 kb). Second, our model assumes a power law decay between Hi-C count and distance (equivalent to a log–log linear relation between Hi-C count and distance) which only holds for a limited distance range. Third, not restricting the analysis to a limited distance range can lead to heavy computational burden. One simple way to analyze Hi-C data within a wider distance range would be to analyze data at 10–20 kb resolutions.

There are several limitations of the proposed approach. First, model learning can be computationally demanding in time and memory depending on the distance range or Hi-C data resolution. New big data learning algorithms could be used to process the data at a higher resolution that would allow in-depth analysis of 3D chromatin drivers (58). Second, the model makes the assumption that the accumulation of protein binding blocks long-range contacts, but other scenarios could explain the formation of borders. For instance, attraction/repulsion forces between histone marks can predict the folding of chromatin (59). Third, in human, we observed large changes of βs over distance, for instance for protein ZNF143 and DNA motif TFAP2C(var.3). Because lasso regression is not designed to estimate beta standard deviations, the significance of the difference between two βs obtained for two different distances cannot be tested. Instead, one could use a standard regression with selected variables to assess the significance.

AVAILABILITY

The model is available in the R package ‘HiCblock’ which can be downloaded from the Comprehensive R Archive Network (https://cran.r-project.org/web/packages/HiCblock/index.html).

Supplementary Material

Supplementary Data
Click here for additional data file. (506.4KB, pdf)

ACKNOWLEDGEMENTS

The authors are grateful to Corces lab (Emory University, USA) for data.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

University of Toulouse; CNRS. Funding for open access charge: Fondation pour la Recherche Médicale (DEQ20160334940) to our team (R.M. and O.C.).

Conflict of interest statement. None declared.

REFERENCES

  • 1. Halverson J.D., Smrek J., Kremer K., Grosberg A.Y.. From a melt of rings to chromosome territories: the role of topological constraints in genome folding. Rep. Prog. Phys. 2014; 77:022601. [DOI] [PubMed] [Google Scholar]
  • 2. Dixon J.R., Selvaraj S., Yue F., Kim A., Li Y., Shen Y., Hu M., Liu J.S., Ren B.. Topological domains in mammalian genomes identified by analysis of chromatin interactions. Nature. 2012; 485:376–380. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3. Sexton T., Yaffe E., Kenigsberg E., Bantignies F., Leblanc B., Hoichman M., Parrinello H., Tanay A., Cavalli G.. Three-dimensional folding and functional organization principles of the Drosophila genome. Cell. 2012; 148:458–472. [DOI] [PubMed] [Google Scholar]
  • 4. Jin F., Li Y., Dixon J.R., Selvaraj S., Ye Z., Lee A.Y., Yen C.A., Schmitt A.D., Espinoza C.A., Ren B.. A high-resolution map of the three-dimensional chromatin interactome in human cells. Nature. 2013; 503:290–294. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5. Lieberman-Aiden E., van Berkum N.L., Williams L., Imakaev M., Ragoczy T., Telling A., Amit I., Lajoie B.R., Sabo P.J., Dorschner M.O. et al. . Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science. 2009; 326:289–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6. Pope B.D., Ryba T., Dileep V., Yue F., Wu W., Denas O., Vera D.L., Wang Y., Hansen R.S., Canfield T.K. et al. . Topologically associating domains are stable units of replication-timing regulation. Nature. 2014; 515:402–405. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7. Cubenas-Potts C., Corces V.G.. Architectural proteins, transcription, and the three-dimensional organization of the genome. FEBS Lett. 2015; 589:2923–2930. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8. Kellum R., Schedl P.. A position-effect assay for boundaries of higher order chromosomal domains. Cell. 1991; 64:941–950. [DOI] [PubMed] [Google Scholar]
  • 9. Kellum R., Schedl P.. A group of scs elements function as domain boundaries in an enhancer-blocking assay. Mol. Cell. Biol. 1992; 12:2424–2431. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10. Phillips-Cremins J.E., Sauria M. E.G., Sanyal A., Gerasimova T.I., Lajoie B.R., Bell J.S., Ong C.T., Hookway T.A., Guo C., Sun Y. et al. . Architectural protein subclasses shape 3D organization of genomes during lineage commitment. Cell. 2013; 153:1281–1295. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11. Van Bortle K., Nichols M.H., Li L., Ong C.-T., Takenaka N., Qin Z.S., Corces V.G.. Insulator function and topological domain border strength scale with architectural protein occupancy. Genome Biol. 2014; 15:R82. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12. Rao S.S.P., Huntley M.H., Durand N.C., Stamenova E.K., Bochkov I.D., Robinson J.T., Sanborn A.L., Machol I., Omer A.D., Lander E.S. et al. . A 3D map of the human genome at kilobase resolution reveals principles of chromatin looping. Cell. 2015; 159:1665–1680. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13. Zuin J., Dixon J.R., van der Reijden M.I.J.A., Ye Z., Kolovos P., Brouwer R.W., van de Corput M.P., van de Werken H.J., Knoch T.A., van IJcken W.F. et al. . Cohesin and CTCF differentially affect chromatin architecture and gene expression in human cells. Proc. Natl. Acad. Sci. U.S.A. 2014; 111:996–1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14. Vietri-Rudan M., Barrington C., Henderson S., Ernst C., Odom D., Tanay A., Hadjur S.. Comparative Hi-C reveals that CTCF underlies evolution of chromosomal domain architecture. Cell Rep. 2015; 10:1297–1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15. Mourad R., Cuvier O.. Computational identification of genomic features that influence 3D chromatin domain formation. PLoS Comput. Biol. 2016; 12:e1004908. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16. Shin H., Shi Y., Dai C., Tjong H., Gong K., Alber F., Zhou X.J.. TopDom: an efficient and deterministic method for identifying topological domains in genomes. Nucleic Acids Res. 2016; 44:e70. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17. Li L., Lyu X., Hou C., Takenaka N., Nguyen H.Q., Ong C.T., Cubeñas-Potts C., Hu M., Lei E.P., Bosco G. et al. . Widespread rearrangement of 3D chromatin organization underlies Polycomb-mediated stress-induced silencing. Mol. Cell. 2015; 58:216–231. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18. Eagen K.P., Lieberman Aiden E., Kornberg R.D.. Polycomb-mediated chromatin loops revealed by a sub-kilobase resolution chromatin interaction map. Proc. Natl. Acad. Sci. U.S.A. 2017; 114:8764–8769. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19. Wood A.M., Van Bortle K., Ramos E., Takenaka N., Rohrbaugh M., Jones B.C., Jones K.C., Corces V.G.. Regulation of chromatin organization and inducible gene expression by a Drosophila insulator. Mol. Cell. 2011; 44:29–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20. Kellner W.A., Van Bortle K., Li L., Ramos E., Takenaka N., Corces V.G.. Distinct isoforms of the Drosophila Brd4 homologue are present at enhancers, promoters and insulator sites. Nucleic Acids Res. 2013; 41:9274–9283. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21. Negre N., Brown C.D., Ma L., Bristow C.A.A., Miller S.W., Wagner U., Kheradpour P., Eaton M.L., Loriaux P., Sealfon R. et al. . A cis-regulatory map of the Drosophila genome. Nature. 2011; 471:527–531. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22. Junion G., Spivakov M., Girardot C., Braun M., Gustafson E.H., Birney E., Furlong E.E.. A transcription factor collective defines cardiac cell fate and reflects lineage history. Cell. 2012; 148:473–486. [DOI] [PubMed] [Google Scholar]
  • 23. The ENCODE Consortium An integrated encyclopedia of DNA elements in the human genome. Nature. 2012; 489:57–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24. Cuellar-Partida G., Buske F.A., McLeay R.C., Whitington T., Noble W.S., Bailey T.L.. Epigenetic priors for identifying active transcription factor binding sites. Bioinformatics. 2012; 28:56–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25. Zhao K., Hart C.M., Laemmli U.K.. Visualization of chromosomal domains with boundary element-associated factor BEAF-32. Cell. 1995; 81:879–889. [DOI] [PubMed] [Google Scholar]
  • 26. Holohan E.E., Kwong C., Adryan B., Bartkuhn M., Herold M., Renkawitz R., Russell S., White R.. CTCF genomic binding sites in Drosophila and the organisation of the Bithorax complex. PLoS Genet. 2007; 3:e112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27. Adryan B., Woerfel G., Birch-Machin I., Gao S., Quick M., Meadows L., Russell S., White R.. Genomic mapping of suppressor of hairy-wing binding sites in Drosophila. Genome Biol. 2007; 8:R167. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28. Negre N., Brown C.D., Shah P.K., Kheradpour P., Morrison C.A., Henikoff J.G., Feng X., Ahmad K., Russell S., White R.A. et al. . A comprehensive map of insulator elements for the Drosophila genome. PLoS Genet. 2010; 6:e1000814. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29. Zolotarev N., Fedotova A., Kyrchanova O., Bonchuk A., Penin A.A., Lando A.S., Eliseeva I.A., Kulakovskiy I.V., Maksimenko O., Georgiev P.. Architectural proteins Pita, Zw5 and ZIPIC contain homodimerization domain and support specific long-range interactions in Drosophila. Nucleic Acids Res. 2016; 44:7228–7241. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30. Hart C.M., Cuvier O., Laemmli U.K.. Evidence for an antagonistic relationship between the boundary element-associated factor BEAF and the transcription factor DREF. Chromosoma. 1999; 108:375–383. [DOI] [PubMed] [Google Scholar]
  • 31. Li J., Gilmour D.S.. Distinct mechanisms of transcriptional pausing orchestrated by GAGA factor and M1BP, a novel transcription factor. EMBO J. 2013; 32:1829–1841. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32. Read D., Manley J.L.. Alternatively spliced transcripts of the Drosophila tramtrack gene encode zinc finger proteins with distinct DNA binding specificities. EMBO J. 1992; 11:1035–1044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33. Cuartero S., Fresan U., Reina O., Planet E., Espinas M.L.. Ibf1 and Ibf2 are novel CP190-interacting proteins required for insulator function. EMBO J. 2014; 33:637–647. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34. Dai Q., Ren A., Westholm J.O., Duan H., Patel D.J., Lai E.C.. Common and distinct DNA-binding and regulatory activities of the BEN-solo transcription factor family. Genes Dev. 2015; 29:48–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35. Hug C.B., Grimaldi A.G., Kruse K., Vaquerizas J.M.. Chromatin architecture emerges during zygotic genome activation independent of transcription. Cell. 2017; 169:216–228. [DOI] [PubMed] [Google Scholar]
  • 36. Dekker J., Marti-Renom M.A., Mirny L.A.. Exploring the three-dimensional organization of genomes: interpreting chromatin interaction data. Nat. Rev. Genet. 2013; 14:390–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37. Hu M., Deng K., Selvaraj S., Qin Z., Ren B., Liu J.S.. HiCNorm: removing biases in Hi-C data via Poisson regression. Bioinformatics. 2012; 28:3131–3133. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38. Imakaev M., Fudenberg G., McCord R.P., Naumova N., Goloborodko A., Lajoie B.R., Dekker J., Mirny L.A.. Iterative correction of Hi-C data reveals hallmarks of chromosome organization. Nat. Methods. 2012; 9:999–1003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39. Gaszner M., Felsenfeld G.. Insulators: exploiting transcriptional and epigenetic mechanisms. Nat. Rev. Genet. 2006; 7:703–713. [DOI] [PubMed] [Google Scholar]
  • 40. Ghandi M., Mohammad-Noori M., Ghareghani N., Lee D., Garraway L., Beer M.A.. gkmSVM: an R package for gapped-kmer SVM. Bioinformatics. 2016; 32:2205–2207. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41. Kumar R.P., Krishnan J., Singh N.P., Singh L., Mishra R.K.. GATA simple sequence repeats function as enhancer blocker boundaries. Nat. Commun. 2013; 4:1844. [DOI] [PubMed] [Google Scholar]
  • 42. Dali R., Blanchette M.. A critical assessment of topologically associating domain prediction tools. Nucleic Acids Res. 2017; 45:2994–3005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43. Levy-Leduc C., Delattre M., Mary-Huard T., Robin S.. Two-dimensional segmentation for analyzing Hi-C data. Bioinformatics. 2014; 30:i386–i392. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44. Ghavi-Helm Y., Klein F.A., Pakozdi T., Ciglar L., Noordermeer D., Huber W., Furlong E.E.. Enhancer loops appear stable during development and are associated with paused polymerase. Nature. 2014; 512:96–100. [DOI] [PubMed] [Google Scholar]
  • 45. Maksimenko O., Bartkuhn M., Stakhov V., Herold M., Zolotarev N., Jox T., Buxa M.K., Kirsch R., Bonchuk A., Fedotova A. et al. . Two new insulator proteins, Pita and ZIPIC, target CP190 to chromatin. Genome Res. 2015; 25:89–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46. Herranz H., Morata G.. The functions of pannier during Drosophila embryogenesis. Development. 2001; 128:4837–4846. [DOI] [PubMed] [Google Scholar]
  • 47. Wang C., Xi R.. Keeping intestinal stem cell differentiation on the Tramtrack. Fly. 2015; 9:110–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 48. Djekidel M.N., Liang Z., Wang Q., Hu Z., Li G., Chen Y., Zhang M.Q.. 3CPET: finding co-factor complexes from ChIA-PET data using a hierarchical Dirichlet process. Genome Biol. 2015; 16:288. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 49. Liang J., Lacroix L., Gamot A., Cuddapah S., Queille S., Lhoumaud P., Lepetit P., Martin P.G.P., Vogelmann J., Court F. et al. . Chromatin immunoprecipitation indirect peaks highlight functional long-range interactions among insulator proteins and RNAII pausing. Mol. Cell. 2014; 53:672–681. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 50. Hirano T. Condensins: organizing and segregating the genome. Curr. Biol. 2005; 15:R265–R275. [DOI] [PubMed] [Google Scholar]
  • 51. Hirano T. At the heart of the chromosome: SMC proteins in action. Nat. Rev. Mol. Cell Biol. 2006; 7:311–322. [DOI] [PubMed] [Google Scholar]
  • 52. Gibcus J., Dekker J.. The hierarchy of the 3D genome. Mol. Cell. 2013; 49:773–782. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 53. Tan S.K., Lin Z.H., Chang C.W., Varang V., Chng K.R., Pan Y.F., Yong E.L., Sung W.K., Cheung E.. AP-2γ regulates oestrogen receptor-mediated long-range chromatin interaction and gene transcription. EMBO J. 2011; 30:2569–2581. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 54. Vogelmann J., Le Gall A., Dejardin S., Allemand F., Gamot A., Labesse G., Cuvier O., Nègre N., Cohen-Gonsaud M., Margeat E. et al. . Chromatin insulator factors involved in long-range DNA interactions and their role in the folding of the Drosophila genome. PLoS Genet. 2014; 10:e1004544. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 55. Pagans S., Ortiz-Lombardia M., Espinas M.L., Bernues J., Azorin F.. The Drosophila transcription factor tramtrack (TTK) interacts with Trithorax-like (GAGA) and represses GAGA-mediated activation. Nucleic Acids Res. 2002; 30:4406–4413. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 56. Busslinger G.A., Stocsits R.R., van der Lelij P., Axelsson E., Tedeschi A., Galjart N., Peters J.-M.. Cohesin is positioned in mammalian genomes by transcription, CTCF and Wapl. Nature. 2017; 544:503–507. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 57. Doyle B., Fudenberg G., Imakaev M., Mirny L.A.. Chromatin loops as allosteric modulators of enhancer-promoter interactions. PLoS Comput. Biol. 2014; 10:e1003867. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 58. Facchinei F., Scutari G., Sagratella S.. Parallel selective algorithms for nonconvex big data optimization. IEEE Trans. Sig. Process. 2015; 63:1874–1889. [Google Scholar]
  • 59. Jost D., Carrivain P., Cavalli G., Vaillant C.. Modeling epigenome folding: formation and dynamics of topologically associated chromatin domains. Nucleic Acids Res. 2014; 42:9553–9561. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
Click here for additional data file. (506.4KB, pdf)

Articles from Nucleic Acids Research are provided here courtesy of Oxford University Press

RESOURCES