Structure, Function, and Applications of the Georgetown-Einstein (GE) Breast Cancer Simulation Model

Abstract

The Georgetown University-Albert Einstein College of Medicine breast cancer simulation model (Model GE) has evolved over time in structure and function to reflect advances in knowledge about breast cancer, improvements in early detection and treatment technology, and progress in computing resources. This article describes the model and provides examples of model applications. The model is a discrete events micro-simulation of single life histories of women from multiple birth cohorts. Events are simulated in the absence of screening and treatment, and interventions are then applied to assess their impact on population breast cancer trends. The model accommodates differences in natural history associated with ER and HER2 biomarkers, as well as conventional breast cancer risk factors. The approach to simulation of breast cancer natural history is phenomenological, relying on dates, stage, and age of clinical and screen detection for a tumor molecular subtype without explicitly modeling tumor growth. The inputs to the model are regularly updated to reflect current practice. A number of technical modifications, including use of object-oriented programming (C++), and more efficient algorithms, along with hardware advances, have increased program efficiency permitting simulations of large samples. The model results consistently match key temporal trends in US breast cancer incidence and mortality. The model has been used in collaboration with other CISNET models to assess cancer control policies and will be applied to evaluate clinical trial design, recurrence risk, and polygenic risk-based screening.

INTRODUCTION

Empiric evidence is used to support a wide range of healthcare decisions, including individual decision-making in clinical encounters, guidelines for clinical practice standards, and public health choices to improve population health. (1–4) The success of the evidence-based paradigm depends on having high-quality data about multiple interventions collected in a standard manner for the population of interest to facilitate comparisons among the relevant choices. Unfortunately, this is not always the case. More often, there is limited information on long-term outcomes or direct comparisons among relevant alternative strategies or comparisons incorporating individual or population preferences. Simulation modeling can be a useful research method to synthesize existing data and compare a broader range of alternatives than can be feasibly included in clinical trials or other studies. (5, 6, 7) The Cancer Intervention and Surveillance Network (CISNET) was launched by the National Cancer Institute in 2000 to promote open collaboration to advance modeling science to provide a range of decision-makers with tools for synthesizing evidence to determine the impact of alternative cancer control strategies on US population incidence and mortality.

The goal of this article is to provide decision-makers and future consumers of CISNET breast cancer simulation models with an in-depth overview of the Georgetown University-Albert Einstein College of Medicine breast cancer simulation model (Model GE). Model GE was one of seven original breast cancer simulation models. The model has evolved over time in structure and function to reflect advances in knowledge about breast cancer, improvements in early detection and treatment technology, and progress in computing resources. This article describes the history of Model GE, the current structure and functioning of the model, and provides examples of model applications. This summary is intended to provide CISNET model users with sufficiently detailed methods to understand the approach, compare model GE to other CISNET models, evaluate the results, and appreciate how the model could be applied to inform assessments of future cancer control interventions and policies.

HISTORY OF MODEL GE

The pre-CISNET versions of Model GE (GE pre-C) focused on sub-groups in the US population. GE pre-C was similar to the version developed for CISNET in terms of how natural history was captured, having screening benefits based on age- and stage-shift, and calculating stage at screen detection backwards from the stage the cancer would have been in the absence of screening and lead time. GE pre-C, however, modeled only a single birth cohort, did not model any secular trend in age-specific breast cancer incidence, and could simulate only simple, strictly periodic screening programs. Two examples of the use of GE pre-C related to evaluating strategies to improve breast cancer outcomes in African-American women (8) and to determine upper age limits for mammography screening. (9) The results indicated that the burden of breast cancer in African-American women could be reduced more by focusing on access and adherence to optimal treatment strategies rather than by efforts to increase screening, given high rates of screening use. (8) Among older women, the model demonstrated the value of considering life expectancy and underlying health in making recommendations about upper age limits. (9) This history informed Model GE’s participation in subsequent CISNET projects to examine age- and race-related disparities. (10–12)

MODEL OVERVIEW

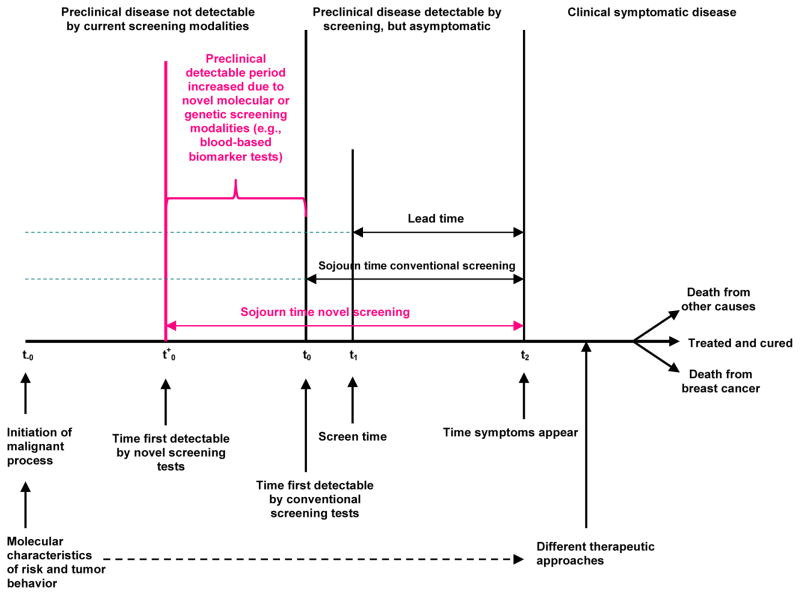
The initial goal of CISNET was to have investigators with existing breast cancer simulation models adapt them to examine the relative contributions of dissemination of mammography screening and utilization of adjuvant treatment to the decline in breast cancer mortality observed from 1975–2000 in the US. (13) To this end, the Model GE team modified its earlier model to address US population trends. Since then, Model GE has continued to evolve to reflect the growing understanding of breast cancer. The focus of this paper is to describe the model as implemented in 2016; Table 1 summarizes key model changes over time; Table 2 provides a detailed chronology of the model’s development. Briefly, Model GE is programmed in C++ following the ISO standard. (16) The model is a continuous-time event-driven micro-simulation utilizing a parallel universes approach. The parallel universes approach starts with the generation of a basic life history for each simulated woman in the absence of any screening or adjuvant treatment. The effects of each screening and adjuvant treatment strategy under study are then simulated starting using the same basic life history. In this manner, the outputs for the different screening and adjuvant treatment strategies are matched pairs (tuples). Breast cancer incidence depends on age, time period, and birth cohort, and can be modified based on risk. The incidence includes a subset of DCIS tumors that never surface clinically and eventually regress. Breast cancers include four molecular sub-types based on estrogen receptor (ER) and human epidermal growth factor receptor 2 (HER2) status. The approach to simulation of breast cancer natural history is phenomenological, relying on dates, stage, and age of clinical and screen detection for a tumor molecular subtype without explicitly modeling tumor growth. In general, Model GE uses the common CISNET input parameters either directly or as calibration targets to conduct this modeling; (17) other parameters are model-specific and exemplar values are summarized on Table 3. An overview of the model approach is included on Figure 1. The detailed description of the model is included below.

Table 1.

Key Changes in Model GE Structure, Function, and Inputs over Time

Attribute	2000 Version	2016 Version
Computer Programming
Programming Language	C (ANSI standard)	C++ (ISO standard)
Programming Approach	Modular	Object-Oriented
Compiler	Microsoft Visual Studio v. 6	Microsoft Visual Studio 2013
Simulation of Different Scenarios	In Series (Independent Outcomes)	In Parallel (Matched Outcomes)
Sequencing of Events	Event Queue	State vector updated in loop over screening and treatment events
Sampling of Empirical Distributions	Linear Search	Binary Search
Execution Time on Mid-Range Desktop Computers	4 Strategies, N = 50,000,000 36 hours per strategy	4 Strategies, N = 200,000,000 2 hours per strategy.
Cancer Epidemiology
Non-Progressive Disease	None	Some DCIS have a clinically detectable period, but never surface clinically
Incidence without Screening	APC Model 1975–1999 (14)	APC Model 1972–2010 (15)
Risk factors for Incident Breast Cancer	None	Generic risk levels (e.g., two-fold increase associated with family history); age-specific increases in risk for obesity or breast density
Biomarkers	Estrogen receptors	Estrogen, HER2 receptors
Sojourn Time Distributions	Conditional on age	Conditional on age and biomarkers
Screening Test Operating Characteristics	Conditional on age, first vs. subsequent screen	Conditional on age, first vs. subsequent screen, and breast density
Breast Density	Not modeled	Modeled at age 40, with possible changes at ages 50 and 65
Clinical Stages	SEER Historical	AJCC version 6
Lead-Time Survival Guarantee	Survival time reckoned from date of CLINICAL diagnosis even if tumor was screen detected	Survival time sampled from right tail of distribution beyond lead-time, and counted from date of actual detection.
Competing Non-cancer Mortality	Age and cohort-specific through 1999	Age and cohort-specific through 2010; modifications available for obesity levels; race; or comorbidity level
Interventions
Adjuvant Treatment	CMF, Tamoxifen	CMF, Taxanes, Anthracyclines, Trastuzumab, Tamoxifen, Aromatase Inhibitors
Screening Modalities	Plain Film Mammography	Plain Film Mammography, Digital Mammography, Hand-held Breast Ultrasound
Output
	Counts of mammograms, incident cases by stage, breast cancer deaths, and surviving population for each age and calendar year combination.	Additional outputs added for counts of non-progressive cases diagnosed, over-diagnosed cases, and life-years and QALYs (overall and in specific stages of breast cancer treatment)

Table 2.

Detailed Chronology of the Evolution of Model GE.

Year	Innovation(s)	Publications
1998 (Pre-CISNET)	TOSS Model	8, 9
2000	Model GE 2000	13
2006	Programmed in C++; Parallel scenario simulation; improved search algorithms; State vector; Modeling non-progressive disease; AJCC staging; Improved lead-time guarantee; Estimation of overdiagnosis	22, 25
2008	Inputs specific for obesity, race.	10, 11, 28, 31
2010	Variation in non-breast cancer mortality due to comorbidity; expanded adjuvant treatment options	12
2013	Variation in breast cancer risk based on density and conventional risk factors; updated age-period-cohort model of breast cancer incidence	23, 26, 27, 29
	Modeling effects of adjunctive sonography	29
	Modeling digital and plain-film mammography	23, 26, 27
2014	Separate natural histories for ER and HER2 biomarkers	Work in progress

Table 3.

Model-Specific Input Parameters for Model GE

Description	Conditional On	Source(s)	Exemplar Values
Stage at clinical diagnosis without screening	Age	SEER 1975 Incidence and BCSC clinically detected cases	----*
Sojourn time duration (pre-clinical detectable period)	Age, ER, HER2	Calibrated parameters; gamma distributions by ER/HER2	Average mean sojourn time: Age 40–49: 2 years Age 50+: 4 years with biomarker-dependent multipliers ranging between 0.85 and 1.05
Mammogram sensitivity and specificity	Technology, age, density, 1st vs. subsequent	Calibrated to BCSC data	----*
Marginal Distribution of Stage at Screen Detection	Age	BCSC	----*
Proportion of DCIS that is non-progressive	Age	Calibrated	One-third of the incidence of progressive DCIS at each age are assume to be non-progressive
Mean AJCC stage dwell times	Unconditional exponential distributions	Calibrated	DCIS -5.00 years Stage I - 2.6 years Stage IIA -1.26 years (to IIB) Stage IIB -1.27 years Stage III - 4.0 years

^*Many parameters have very large underlying data tables. Data are available from CISNET under data sharing agreements.

Figure 1. Overview of Model Schema.

The figure provides a schematic representation of the events in the breast cancer control process included in Model GE.

Model Top-Level Iteration Cycle

The top-level logic of the simulation is shown in pseudocode in Figure 2. Several life history event counts are provided as model output, including in each age (single years) and calendar year, the number of women alive at the start of the year, incident breast cancers (disaggregated by stage, ER, and HER2), mammograms (disaggregated into true positive, false positive, true negative and false negative), deaths from breast cancer, and deaths from other causes. Additional events may be tallied for specific applications.

Figure 2.

Top-level Logic of CISNET Model GE in Pseudocode

Basic Life History in the Absence of Screening and Treatment

The generation of simulated individual life histories is done by random sampling from specified probability distributions. The time of occurrence of any event is sampled from a time-to-event distribution (survival function). The levels of categorical attributes are sampled from tables of the corresponding random variables. Sampling is accomplished with pseudo-random numbers generated using the Mersenne twister algorithm. (18) In order to maximize the “matched tuple” nature of the results for parallel universes under different strategies, all simulated life histories start from a common basic life history.

The Basic Life History object contains a date of birth, breast density at ages 40, 50, and 65, a date of onset of clinically diagnosed breast cancer (which may be never), a date of death from breast cancer in the absence of adjuvant treatments (which may be never, even if breast cancer is diagnosed in the simulated woman’s lifetime). If the date of onset of clinical breast cancer is finite (i.e., it is not “never”), then the basic life history also specifies a stage at clinical diagnosis (DCIS, I, IIA, IIB, III, or IV) and ER and HER2 biomarker status. A sojourn time duration for the breast cancer is also sampled, conditional on age at clinical diagnosis, ER, and HER2. The start date of the sojourn period is calculated by subtracting the sojourn duration from the date of clinical incidence. Life history objects can also store information on the number and timing of any mammograms and types of adjuvant therapy administered, but in the basic life history these are set to null values to depict outcomes in the absence of screening and treatment.

In population applications, the date of birth is randomly sampled from a distribution of birth cohorts in the US population (a common input). (17) In single cohort applications, the birth date is stipulated to be January 1 of the birth year for the cohort being modeled. Breast densities at ages 40, 50, and 65 are then sampled (a common input). The age at onset of clinical breast cancer is randomly sampled from a time-to-event distribution, conditional on birth cohort and year based on an age-period-cohort (APC) model. (10) Incidence can also be conditional on breast density at ages 40, 50, and 65 by applying density-specific hazard ratios to the marginal distribution. Each birth cohort and density-trajectory has its own input file, so the application of density hazard ratios is part of the generation of program inputs, not part of the simulation itself. Prevention interventions could be considered based on effects on the underlying onset of clinical disease in the absence of screening.

The age at clinical onset of breast cancer (i.e., cancer in the absence of screening) is added to the date of birth to arrive at a date of cancer onset. Conditional on age, the stage at clinical diagnosis is sampled. Next, conditional on age and stage, ER and HER2 status are sampled. To arrive at a date of death, a survival time for that stage and ER/HER2 is sampled, and that interval is added after the date of diagnosis. To complete the basic life history object, an age at death from causes other than breast cancer is sampled conditional on birth cohort. In creating output for the basic life history, the actual death event is tallied in the age and year corresponding to the earlier of the breast cancer mortality date or the other cause mortality date.

Women who do not develop breast cancer in their basic life history may still have non-progressive DCIS and these cases are treated as a distinct disease in the model. The non-progressive cases were required to calibrate the model to match observed US trends in incidence and mortality using reasonable assumptions about unobservable events. Without including non-progressive DCIS, matching observed incidence and mortality would have required some combination of extreme assumptions about the underlying secular trends in breast cancer incidence between 1975 and 2000 in the absence of screening, extremely long breast cancer pre-clinical sojourn times, and very long dwell times in DCIS. Since there are, by definition, no observable data to inform the values for these parameters, we chose to assume that the simultaneous increase in breast cancer incidence, especially incidence of DCIS, and the dissemination of screening in the population were related phenomena. (19) Therefore, we used sojourn time distributions similar to those estimated from clinical trials, and ascribe part of the excess incidence of breast cancer to non-progressive DCIS. A date of initial mammographic detectability and a later date at which the non-progressive lesion regresses are sampled from simulation inputs. These inputs are calibrated so that the one-fifth of all DCIS is non-progressive. The duration of these non-progressive lesions is sampled from a distribution calibrated to observed incidence of DCIS reported to SEER in the mammography era. These non-progressive lesions never surface clinically. If these non-progressive DCIS lesions are detected during screening, they are staged as DCIS. Because clinicians cannot distinguish progressive from non-progressive DCIS, if screen-detected, these lesions both receive the same clinical therapies (see below for treatment). Non-progressive DCIS, however, never leads to breast cancer death, whereas progressive DCIS can result in death from breast cancer.

Modeling Effects of Screening

There are two separate aspects to modeling the effects of screening: a simulated screening schedule, and screen-detection.

Simulated Screening Schedules

Screening schedules are simulated through calling two functions. The first function uses the simulated woman’s birth year to sample a date of first mammogram. This function also initializes the mammogram routines with information used to schedule later mammograms based on the patterns of mammography use that are being modeled. Subsequent mammogram dates are sampled by calling another function that samples the next mammogram date and updates the running information about the woman’s screening history.

When depicting screening as actually disseminated in the US population, these model functions generate random screening schedules following the model developed by Cronin & Krapcho,(20, 21) and updated recently to capture trends from 2000–2010. (17) When modeling hypothetical periodic screening strategies (e.g. biennially from age 50 through 74), the same approach is used to set the date of the initial mammogram; each subsequent date is then modeled based on the strategy-prescribed screening interval. These intervals may be conditional on age, breast density, or other attributes of the simulated woman, depending on the research question. All screening strategies have a fixed or random stopping date, after which the function call for the next mammogram returns “never.” The logic of screening, in pseudo-code is shown in Figure 3.

Figure 3.

Logic of Screen-Detection in CISNET Model GE in Pseudocode

The sensitivity and specificity of early detection depends on which screening technology is in use (plain film, digital, tomography, sonography, etc.), age at screening, and breast density. These parameters are inputs to the program, derived by calibrating from unpublished Breast Cancer Surveillance Consortium (BCSC) detection data. Note that this implementation of screening makes detection probability a step function in time: 0 prior to the onset of the sojourn period, and a constant equal to sensitivity thereafter. Sensitivity is higher for the initial than the subsequent screens.

When any mammogram (or other screening test) has taken place, its date is added to a running list of mammogram dates, along with its result. When a true positive mammogram is recorded, early detection is applied to the breast cancer. Early detection entails revision of the date of diagnosis to the date of the detecting mammogram, and also entails modification of stage at diagnosis, treatment modalities, and breast cancer death date, and hence, screening benefits. The procedures for modification of stage is presented in the following narrative; details related to treatment and survival are included later.

Stage Shift Due to Screen Detection

Model GE works backwards in time from the date at which the lesion would have been diagnosed clinically, and its stage at that time, to the time at which a true positive mammogram is obtained. At this point the simulation has available to it the date at which the tumor would have been clinically diagnosed, as well as the parameters of the exponential distributions of dwell times in each stage, and calculates the lead time gained by screening by subtracting the date of screen detection from the date of clinical detection. To determine the stage at the time of the positive mammogram, we use a marginal distribution of screen detected stage distributions and apply Bayes’ theorem to calculate a distribution for the stage at screen detection conditional on the known (in the simulation) lead-time and stage at clinical detection. The simulated stage is then sampled from that posterior distribution. We make the simplifying assumption that ER and HER2 status do not change with early detection, although there is some data to suggest that screening may differentially detect ER positive vs. negative tumors. Non-progressive DCIS are staged as DCIS regardless of when they are detected.

Simulated Treatment

When simulating a strategy that includes adjuvant treatment, the simulation must identify a treatment to apply, and a possible modification of underlying survival according to the treatment. We have simulated three treatment approaches: no adjuvant treatment, dissemination of adjuvant treatment (intended to reflect adjuvant therapy as actually used in the US since its introduction in the 1980’s), and “optimal” treatment (intended to represent the most effective therapy available for the woman at the time she is diagnosed). The dissemination and optimal treatment strategies may result in the application of no adjuvant therapy to some women. The probability of each adjuvant treatment’s being applied to a woman is conditional on calendar year, age, stage, ER and HER2 based on CISNET common inputs. (17) The optimal treatment strategy is also a common input, calculated by selecting the age, stage, ER-, and HER2-specific treatment associated with the greatest prolongation of survival among therapies available in the year of diagnosis.

The effect of treatment on breast cancer survival can be modeled by applying a probability that treatment will result in cure of the patient’s breast cancer, and/or by applying a hazard reduction for those women not cured. Based on the evidence available, we assume the cure probabilities are zero, and use only hazard reduction. The hazard ratio associated with the selected treatment, conditional on age, stage, ER, and HER2 is based on the common inputs (17) and a new time to breast cancer death is calculated by applying a proportional hazard ratio to the function originally used in the no-adjuvant-treatment condition. Each combination of age, stage, and biomarkers has its own input file for treatment effectiveness, so the application of hazard ratios is part of the generation of program inputs, not part of the simulation itself. This structure would permit use of non-proportional hazards if there were sufficient evidence about this assumption for the different molecular subtypes. Finally, to assure that screen-detected women survive their lead-time (unless other-cause mortality intervenes), the breast cancer survival time is sampled only from the right tail of this distribution beyond the date at which she would have been diagnosed clinically.

VALIDATION

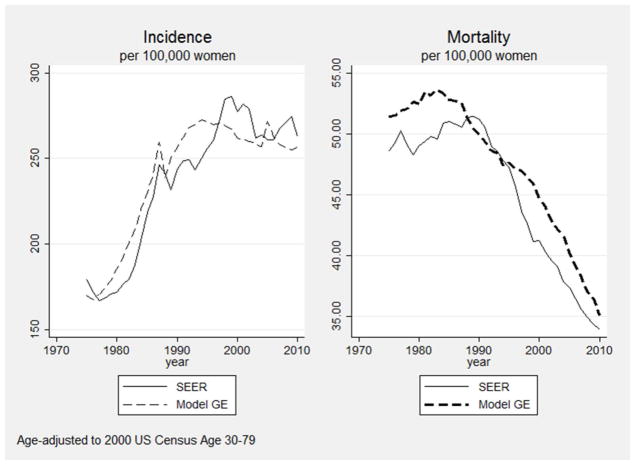
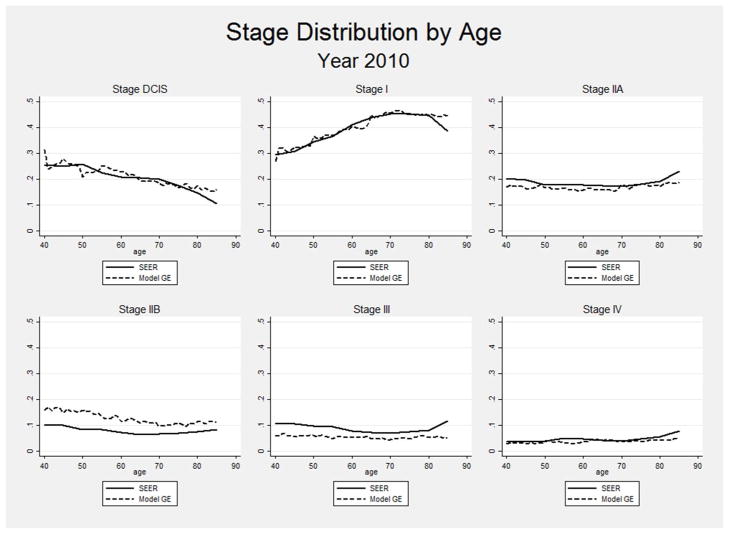
Validation of breast cancer simulation models raises conceptual and practical difficulties. Many aspects of breast cancer natural history are unobservable, intervention penetrance has varied over time, and some key aspects of the cancer control process are context dependent. For example, the criteria for considering a mammogram to be abnormal have differed over time. These differences would be reflected in the model by different mammogram sensitivity and specificity estimates. In this situation, the use of a model calibrated to one context (e.g., a set of mammography performance characteristics) would not result in good fit to the outcomes in another. In particular, attempting to model the results of older clinical trials without recalibrating some input parameters to that specific context might result only in grossly approximate fit to observation. Many applications of Model GE have involved estimation of the outcomes that would arise with counterfactual schedules of mammography screening. Therefore, perhaps the most relevant aspect of model validity would be a demonstration that its outputs change in the appropriate way when mammography utilization patterns change over time. Using common input parameters on mammography and treatment dissemination from 1975 to 2010, Figure 4 shows Model GE’s ability to generate the pattern of rising and falling breast cancer incidence and mortality rates paralleling those observed in SEER in the same period. Additionally, Figure 5 shows the close match between modeled and SEER-observed stage distributions by age in 2010. These types of evaluations provide users with information about the ability of Model GE to use independent data (i.e., not used as model inputs) to accurately replicate external data.

Figure 4.

Fit of Model GE to SEER Incidence and Mortality During an Era of Rapid Change in Mammography Utilization and Treatment (1975–2010)

Figure 5.

Comparison of Modeled and SEER-observed Age-specific Stage Distributions in 2010

LIMITATIONS

As do all simulations, Model GE has limitations. Some assumptions are inaccurate in minor ways. For example, women with screen-detected breast cancer are assumed not to experience breast-cancer related death during their lead time, whereas in reality a small fraction, lethal complications of breast cancer treatment may occur. The modeling of treatment effects by proportional hazard reduction may be inaccurate. Model GE does not incorporate estimates of quality of life, although these can be estimated subsequently by applying quality of life adjustments to the various states whose durations are part of model output, as was done in some recent applications (27, 29).

Perhaps the greatest limitation is the necessity of specifying parameters for inherently unobservable processes, specifically, incidence of breast cancer in the absence of screening since 1975, sojourn time distributions, mammogram sensitivity, proportions of non-progressive cancers, and their durations. While only certain combinations of assumed values for these parameters are consistent with the observed trends in incidence and stage distribution, it must be stressed that the data do not identify a unique best-fit estimate of these parameters. In using a grid search to select these values, we necessarily imposed constraints that rely on our intuitions and beliefs. We did not allow calibration to deviate far from the sojourn time estimates estimated from early mammography clinical trials by Walter and Day (30), believing that more recent developments in mammographic technology, though resulting in somewhat higher sensitivity, have not drastically changed the sojourn time distribution. We also relied on an age-period-cohort model of breast cancer incidence in the absence of screening that reflects our belief that the rising incidence of breast cancer seen in the 1940–1975 era did not abruptly abate thereafter. These assumptions determine a narrower range of combinations of incidence rates and durations for non-progressive lesions to fill the gap between incidence of breast cancer with and without screening. As a consequence, of these assumptions our estimated rates of overdiagnosis are relatively low. Of course, none of these assumptions can be confirmed. So, while we are confident of Model GE’s ability to reflect differences in incidence and mortality that would be observed under a variety of screening strategies, we have limited confidence in our estimates of overdiagnosis rates.

APPLICATIONS OF MODEL GE

Since its inception in 2000, Model GE has been used to make several important contributions to public health and has directly impacted practice guidelines. For example, Model GE has been used to evaluate ages of screening initiation and intervals for the US Preventive Services Task Force.(22, 23) In the initial analysis done for the 2009 recommendations, all six CISNET breast cancer models concluded that biennial screening from 50–74 was more efficient than earlier starting ages or annual intervals. This finding was influential in the Task Forces’ choice to recommend biennial plain-film mammography from ages 50 to 74. (24) This work was extended in collaboration with the BCSC to determine that women with a 2-fold or higher than average risk could start screening at age 40 and have a similar harm-benefit ratio as seen with biennial screening for average risk women 50 to 74. (25) The Model GE team also recently led new analyses for the Task Force extending the prior work to include digital mammography, breast density and risk sub-groups, impact of quality-adjustment, and over-diagnosis. (23, 26)

In other key research, Model GE was used to examine the impact of screening and adjuvant treatment on reducing race disparities (10) in breast cancer mortality and to ask how much of the observed disparity was attributable to differences in obesity prevalence by race.(11) The model was also applied to evaluate the economic and health impacts of substituting digital for plain film mammography in the CDC’s National Breast and Cervical Cancer Early Detection Program, (27) test how comorbidities affect ages of cessation of screening, (12) and determine the relative impact of prevention of obesity, screening, and treatment for reaching American Cancer Society goals for breast cancer mortality reduction. (28) Model GE was also one of three models to examine the impact of supplemental screening ultrasound for women with dense breasts. (29) Model GE also was one of two breast cancer models used to assess how level of comorbidity affects decisions about upper ages of screening cessation. (12) Lastly, Model GE has been applied to assist in local cancer control planning by projecting the past and future impact of changes in use of screening and adjuvant treatment on outcomes for African-American women in Washington, DC. (31)

Model GE is being extended for future work to address emerging cancer control questions. Previously, Model GE has only considered overall survival and has not explicitly modeled survival based on local therapy or local-regional or distant recurrences. In current work, the model is being reformulated to explicitly consider the effects of local therapy on recurrences and partition survival into time to local-regional and distant recurrence and from these events to breast cancer death. This adaption will be used in a novel analysis with another CISNET model to simulate a clinical trial concept comparing radiation vs. no radiation for women with early stage, favorable prognosis cancers. This research is intended to demonstrate the feasibility and utility of modeling to inform clinical trial design. Model GE (and several other CISNET models) are also being extended to link polygenic risk data to the probability of developing breast cancer by ER status and stage. These data will be used to evaluate the added value of using polygenic risk data to tailor screening schedules.

SUMMARY

Model GE has a flexible structure to evaluate a broad array of screening and treatment strategies in the US population and sub-groups of the population based on age, health status, race, or other characteristics. The model could be readily adapted to consider primary prevention. The model will be also be able to assess the value of different approaches to reducing metastatic breast cancer and metastatic cancer deaths and could be adapted to evaluate the impact of matching treatment with tumor molecular profile results.