Abstract
The MISCAN-Fadia microsimulation model uses continuous tumor growth to simulate the natural history of breast cancer and has been used extensively to estimate the impact of screening and adjuvant treatment on breast cancer incidence and mortality trends. The model simulates individual life histories from birth to death, with and without breast cancer, in the presence and in the absence of screening and treatment. Life histories are simulated according to discrete events such as birth, tumor inception, the tumor’s clinical diagnosis diameter in the absence of screening, and death from breast cancer or death from other causes. MISCAN-Fadia consists of four main components: demography, natural history of breast cancer, screening, and treatment. Screening impact on the natural history of breast cancer is assessed by simulating continuous tumor growth and the “fatal diameter” concept. This concept implies that tumors diagnosed at a size that is between the screen detection threshold and the fatal diameter are cured, while tumors diagnosed at a diameter larger than the fatal tumor diameter metastasize and lead to breast cancer death. MISCAN-Fadia has been extended by including a different natural history for molecular subtypes based on a tumor’s estrogen receptor (ER) status and human epidermal growth factor receptor 2 (HER-2) status. In addition, personalized screening strategies that target women based on their risk such as breast density have been incorporated into the model. This personalized approach to screening will continue to develop in light of potential polygenic risk stratification possibilities and new screening modalities.
Introduction
Randomized trials are considered the gold standard to assess the efficacy of cancer screening interventions. However, ethical concerns, participants lost to follow-up, feasibility issues regarding the number of evaluated screening strategies, and limited quantification abilities of the harms of screening such as overdiagnosis, emphasize the need for ways to complement randomized trials. The breast cancer models of the Cancer Intervention and Surveillance Modeling Network (CISNET) simulate the effects of screening and treatment for lifetime follow up, with varying compliance rates, for an unlimited number of screening strategies, and thereby extrapolate the findings from randomized trials.
MISCAN-Fadia, acronym for Micro Simulation Screening Analysis – Fatal Diameter, has been part of CISNET since its start in 2000, usually referred to as Model E (i.e., Erasmus Medical Center). Before the development of MISCAN-Fadia, a microsimulation model with discrete tumor progression was developed at Erasmus already in the 1980’s to evaluate the effects of breast cancer screening in the Netherlands [1]. However, compared to observed stage distribution data, the model over-estimated the number of early-stage cancers diagnosed at subsequent screens. Sensitivity analysis of screening sensitivity did not lead to better estimates [2]. Moreover, it was difficult to explore different natural history assumptions because tumor progression was directly linked to discrete stages. MISCAN-Fadia, with continuous tumor growth, was initiated to overcome this rigid property. This model was developed with the intent of creating a more biologically oriented breast cancer model to evaluate the impact of screening and treatment on breast cancer incidence and mortality. Since tumor size is measurable and tumor growth is continuous, these properties form the biological approach to modeling the natural history of breast cancer. In the model, a distinction is made between tumor biology (growth function) and other model variables that are more likely to vary by calendar year and possibly differ between geographical areas such as access to screening facilities, screening equipment and consequently screening test sensitivity, clinical diagnosis in the absence of screening due to fewer breast self-examinations and less public awareness of breast cancer risk. Sensitivity of a screening test is translated into a diameter size at which tumors become screen detectable. In MISCAN-Fadia, ductal carcinoma in situ (DCIS) as well as invasive tumors are simulated. Tumor properties like exponential growth rate, clinical diagnosis diameter, minimal diameter for screen detection and fatal diameter are drawn from probability distributions to account for variability between tumors. The fatal diameter concept implies that available treatment only cures tumors that are diagnosed at a smaller diameter than the tumor’s fatal diameter. Available treatment options are not sufficient for tumors diagnosed past their fatal diameter and these tumors will cause breast cancer death.
Disease processes such as the moment of onset of breast cancer and progression or regression of DCIS and breast cancer are unobservable in reality. These are nonetheless important determinants that influence the balance of harms and benefits of screening and treatment. Modeling allows us to explore the effect of changing one of these unobservable factors on modelled outcomes such as breast cancer incidence and mortality. Likewise, it is possible to study the effect of changing tumor onset and tumor growth while keeping all other parameters unchanged to gain insight into the natural history of breast cancer and its interaction with cancer control interventions. To quantify the harms and benefits of different screening and treatment strategies, the model simulates the same female population twice. First, a population is simulated in the absence of screening, and second, in the presence of screening. Key outcomes such as the number of breast cancers, the number breast cancer deaths and over diagnosed breast cancers can be calculated for lifetime follow-up for any possible screening strategy.
Population demography, natural history of breast cancer, screening and treatment are the four main parts of the model. All model inputs and model parameters belong to one of these components and are either calibrated to data from trials or are based on empirical research [3–5]. This paper presents the current model status and in particular the progress and extensions with respect to the first model paper [6], as well as the latest model applications that explore the possibilities of risk-based breast cancer screening.
Methods
Discrete event-driven microsimulation
Discrete event simulation implies that the model moves from the time of one event (e.g., birth) to the next event (e.g., tumor onset). The events in a woman’s lifetime are discrete and mutually exclusive. Microsimulation modeling entails simulation of independent life histories that can be aggregated to estimate the effects of screening and treatment at the population level. Life histories are simulated according to discrete events such as birth, a possible tumor inception, the diameter of the tumor when it would be clinically diagnosed in the absence of screening, a date of death from other causes, or, for woman with breast cancer, a date of breast cancer death. Events that affect the natural history of breast cancer, such as screening and treatment, are tied to the tumor’s continually growing diameter (i.e., screen detection of the tumor may take place from a certain tumor size and treatment may treat tumors successfully up to a certain tumor size). Each woman is simulated from birth and followed until death and time plays an essential role in the order of events in a woman’s life.
Parallel universe approach
In randomized controlled trials, randomization of participants is a key step to reduce the chance of systematic differences between study participants in the intervention and control group. In MISCAN-Fadia, this is imitated by simulating the same female population twice. First, the population is simulated in a no screening world, then, the identical population is simulated again and subjected to screening to evaluate the effects of screening and treatment on incidence and mortality. In microsimulation modeling this approach is often referred to as a parallel universe structure. Usually, populations of tens of millions of women are simulated with a model runtime of approximately fifteen minutes.
Breast cancer onset
The risk of developing breast cancer increases as women get older, while at the same time breast cancer risk may differ by birth cohort [7, 8]. Therefore, breast cancer onset in Model E is mainly driven by an age risk factor combined with a birth cohort risk factor to account for variations in the prevalence of risk factors that are related to birth cohort. The model uses as input breast cancer incidence (invasive and DCIS) in the absence of screening to derive breast cancer onset probabilities that vary by age and cohort. Considering breast cancer incidence in the absence of screening has not been available at the population level in the U.S. since routine mammography screening started in the 1980’s, most CISNET breast models used the breast cancer incidence in the absence of screening derived by Holford et al. [9]. Currently in Model E, the breast cancer onset parameters are calibrated to the U.S. incidence in the absence of screening that was derived and estimated by Gangnon et al. who extended the work by Holford by disentangling breast cancer incidence by cohort- and age-related factors, and the impact of mammography screening dissemination in the U.S.. [10].
The continuous tumor growth natural history model
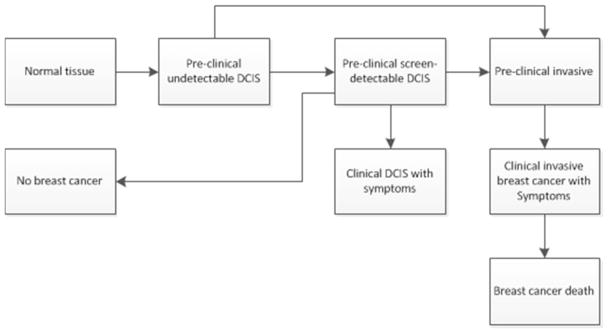
Among women who develop breast cancer, the natural history of the disease is simulated as a continuously growing tumor. At tumor inception, the tumor’s diameter is 0.1 millimeter and based on the time it takes for the tumor to double in size, (i.e., the tumor volume doubling time) it grows exponentially. The DCIS model was originally based on the DCIS model of the Erasmus MISCAN breast model [11]. Once a breast lesion emerges from normal breast tissue, a woman is in the pre-clinical undetectable DCIS phase (Figure 1). The two possible transitions from there are either: pre-clinical screen-detectable DCIS, the state that all CISNET breast models that include DCIS have in common [12], or pre-clinical invasive breast cancer. From the pre-clinical screen-detectable state three different transitions are possible; regression to a breast cancer-free life, progression to pre-clinical invasive breast cancer, or progression to the clinical DCIS state. The duration (years) in each DCIS state is assumed to be exponentially distributed and transitions between DCIS states happen at exponential rates. These transition rates were estimated using SEER American Joint Committee on Cancer (AJCC) data on stage distributions and age-specific DCIS and invasive incidence rates between 1975 and 1999 [3].
Figure 1.
Ductal carcinoma in situ model in MISCAN-Fadia. Once a breast lesion emerges from normal breast tissue, a woman is in the preclinical undetectable DCIS phase. The two possible transitions from there are either: preclinical screen detectable DCIS or preclinical invasive breast cancer. From the preclinical screen detectable DCIS phase the tumor may regress and the woman will end up in the ‘No Breast Cancer’ pool. However, from the preclinical screen detectable DCIS phase the tumor may also progress to preclinical invasive breast cancer or the tumor may cause clinical symptoms and a DCIS case will be diagnosed as a result of clinical symptoms. If a tumor is in the preclinical invasive breast cancer state, the cancer may be screen detected or cause clinical symptoms that lead to a clinical breast cancer diagnosis. Depending on the moment of diagnosis and the type of treatment a women may cure or die from breast cancer.
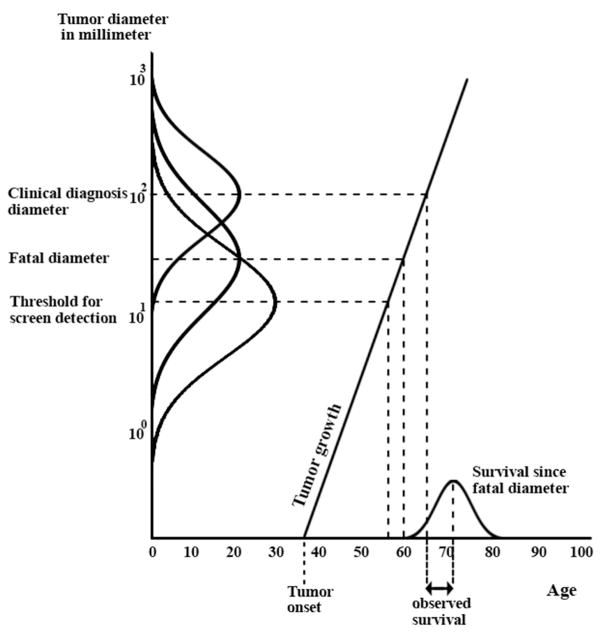
The tumor diameter at which available treatment options no longer result in cure is the fatal disease diameter and reflects the spread of breast cancer, i.e., distant metastasis. If the disease is fatal at the moment of diagnosis (i.e., the tumor diameter at diagnosis is larger than the tumor’s fatal diameter), the time until death from breast cancer is determined by a draw from the survival distribution at the moment the disease became fatal (Figure 2). Tumors that are diagnosed at a smaller diameter than their fatal diameter are surgically removed, possibly radiated and adjuvant treatment ensures the woman will not die of breast cancer. Each tumor is unique and has different diameter sizes for: clinical diagnosis, screen detectability and metastasis (fatal diameter). As listed under ‘the life course of a tumor’, these tumor properties are governed by probability distributions to bring about variation between tumors.
Figure 2.
The MISCAN-Fadia breast cancer natural history model. After tumor onset, the values of six tumor characteristics are generated: growth rate of the tumor, the tumor’s fatal diameter that represents distant metastasis, survival time after reaching the fatal diameter, screen detectability diameter (threshold), and the clinical diagnosis diameter. The distribution curves on the y-axis demonstrate the probabilistic nature of the simulations and the variation between the screen-detection, fatal and clinical diagnosis diameter of tumors. The growth rate of the tumor determines the times since its initiation at which the tumor reaches the screen detectability diameter, the clinical diagnosis diameter, and the fatal diameter. If in the absence of screening the clinical diagnosis diameter is larger than the fatal diameter, the woman will die of breast cancer and the observed survival time is given as depicted in Figure 2. A woman will be cured if the breast cancer is detected, either clinically or through screening, before the fatal diameter is reached. Treatment (not shown in Figure 2) is modeled as a shift in fatal diameter and may affect survival and in the best scenario cause of death.
Our natural history approach makes a distinction between tumor biology (i.e., growth rate of the tumor) and variables that are more likely to change over time, by age, or differ by geographical region. The advantage of this approach is that it readily lends itself to define separate distributions for different parameters based on risk groups and molecular tumor subtypes for example [13, 14]. As such, adapting the model to simulate subgroups of more aggressive and faster growing tumors (e.g., ER/HER2 molecular subtypes of breast cancer) was done by changing the growth rate of tumors while keeping other tumor aspects such as the clinical diagnosis diameter and tumor diameter threshold for screen detectability unchanged.
The life course of a tumor is described by
Tumor growth rate ~ Log Normal (μ1,σ1)
Fatal diameter of the tumor ~ Weibull (λ1,K1)
Survival time after reaching fatal diameter ~ Log Normal (μ2,σ2)
Screen detectable (threshold) tumor diameter ~ Weibull (λ2,K2)
Clinical diagnosis diameter of the tumor ~ Log Normal (μ3,σ3)
Clinical diagnosis of the tumor caused by distant metastasis. This is modeled as a constant fraction of the survival after reaching the tumor’s fatal diameter.
Correlation between tumor growth rate and the tumor’s clinical diagnosis diameter: ρ1 e.g., fast growing tumors are diagnosed at larger diameters.
Correlation between tumor growth rate and survival time after reaching the tumor’s fatal diameter: ρ2 e.g., fast growing tumors have a shorter survival.
Correlation between tumor diameter at clinical diagnoses and survival time after reaching the tumor’s fatal diameter: ρ3 e.g., tumors with a large size at clinical diagnosis have a shorter survival.
The tumor diameter at which N1 lymph node disease becomes detectable ~ Weibull (λ3,K3)
Difference in tumor size at which N1 and N2 lymph node disease become detectable.
When a breast tumor is initiated in a simulated woman, values of the six (1–6) tumor variables are generated. For each simulated tumor, the clinical diagnosis diameter is determined by the smallest tumor diameter of either the diameter at clinical diagnosis or the diameter at clinical diagnosis because of fatal metastases. After tumor initiation, the growth rate of the tumor determines the times at which the tumor reaches the threshold diameter for detectability by screening, the clinical diagnosis diameter, and the fatal diameter. If the tumor diameter at diagnosis is larger than the fatal diameter, then the survival time after reaching the fatal diameter will give the time at which a woman will die of breast cancer. On the other hand, if a tumor is detected, either clinically or through screening, before the fatal diameter is reached, the woman will be cured of cancer and die of other causes. A graphical representation of how the natural history of breast cancer is modeled in MISCAN-Fadia is provided in Figure 2. In MISCAN-Fadia, initially, Weibull distributions were assumed for all variables. However, when it became apparent that correlations had to be assumed, the more convenient multivariate lognormal distribution was used for three correlated variables. The main reason was to get a better fit on the data of the base-case analysis.
For the CISNET breast “Base Case” analysis [15, 16], the maximum likelihood estimates of MISCAN-Fadia for the natural history parameters were initially based on detailed data from the Swedish Two County Study [4, 5]. These included estimates for tumor growth, tumor fatal diameter, survival duration since fatal diameter, clinical diagnosis diameter, and screen detectability diameter. The tumor size distribution and number of screen detected cancers and interval cancers per screening round were simulated and compared to the findings of the trial. A detailed description and estimation of these natural history parameters can be found elsewhere [6]. Since the base case analysis, the natural history parameters such as tumor growth rate, tumor fatal diameter, survival duration after reaching the fatal diameter, and the threshold for screen detection have been re-estimated for the simulation of various breast cancer molecular subtype combinations of ER and HER2. [13, 14]
Population Demographics
MISCAN-Fadia can simulate one specific birth cohort, or, to account for varying demographic characteristics, a dynamic population consisting of multiple birth cohorts can be simulated. Certain birth cohorts may be assigned a different relative risk of developing breast cancer when cohort effects are present in the population. Nevertheless, each birth cohort is assigned an all-cause mortality table from which breast cancer as cause of death is removed. These mortality tables determine the date of non-breast cancer related death. A woman dies either from breast cancer or from other causes, whichever comes first. MISCAN-Fadia uses population parameters such as the number of birth cohorts and the proportion of each birth cohort in the overall U.S. population. These model inputs, as well as the other cause mortality tables are common CISNET model inputs [3].
Screening and screen detection
Characteristics of organized screening programs, such as screening ages, intervals, screening modality, and attendance by first and subsequent screens can be inserted directly into the model. The mammography screening dissemination that reflects the historic opportunistic screening patterns observed in the U.S. can also be simulated [17, 18]. Parameters to simulate screen detection, such as the sensitivity of the screening test, are translated into a diameter size at which tumors become screen detectable. By means of model calibration of tumor size distributions to observed tumor size distributions, the model estimates the screen detection (threshold) parameter. By varying of only the screen detection parameters, the model finds the parameter values that resemble the best match between the simulated data and observed data.
If a woman is screened after a tumor onset, but before the threshold tumor diameter of screen-detectability, the result of the screening test is false negative. If that woman would be screened when the tumor diameter is larger than the tumor’s screen-detectability diameter, the result of the screening test is true positive. This structure for screen detection implies that no false positives are registered as direct output from the model. The number of false positive mammograms is calculated based on the total number of mammograms performed in the model and the observed false positive rates. Screening sensitivity differences between screening modalities, as well as improvements in screening performance are modeled as a shift in the threshold diameter for screen-detectability. The advent of digital mammography between 2000 and 2010 has been incorporated into the model by calibrating the threshold to digital mammography data [19].
Overdiagnosis is defined as screen-detected DCIS or invasive breast cancer that would not have been diagnosed in a woman’s life in the absence of screening. The parallel universe approach; simulating the same population of women twice, implies that the women in the screened population are exactly the same women as in the unscreened population. This allows for exact quantification of overdiagnosis due to screening because of the lifetime follow-up of all women.
Breast cancer staging
In MISCAN-Fadia, the severity of breast cancer is described by the diameter of the primary tumor and the extent to which the cancer has spread to lymph nodes or distant organs. This corresponds to the Tumor Node Metastasis (TNM) staging system that was developed and is maintained by the AJCC union that classifies tumors based on the size of the primary tumor (T), the nearby lymph nodes that are involved (N), and the spread of cancer as distant metastasis (M). To get to a stage at diagnosis, MISCAN-Fadia links tumor diameter to staging by including 3 parameters. First, continuous growth of the tumor diameter; the main concept of the natural history model, covers the T part of the staging system by the unique size of the tumor at diagnosis. Second, the lymph node status of tumors is covered by the inclusion of two parameters; N1: the size of the tumor that reflects the spread to 1–3 nearby lymph nodes, N2: the size of the tumor that corresponds to the diameter at which breast cancer has spread to 4 to 9 lymph nodes. This is modeled as a fixed diameter size larger than N1. Third, metastasis of the primary tumor is modeled and covered by the unique fatal diameter of each tumor. The values of N1 and N2 were calibrated to SEER data on stage at diagnosis of cancers diagnosed between 1975 and 2000 as part of the base-case analysis[6]. The definition of the AJCC staging system determines how cancers are staged at diagnosis; all DCIS diagnoses are staged as 0. Tumors smaller than 2 cm that have not spread to any nearby lymph nodes are staged as 1, tumors that are between 2 and 5 cm at diagnosis that have not spread to nearby lymph nodes are staged as 2a, and so on.
Adjuvant treatment
The benefit of adjuvant treatment is modeled as a shift in the fatal diameter. For each adjuvant treatment an age-specific cure proportion is estimated using the common CISNET model inputs [3] based on treatment effectiveness data from the meta-analyses by the Early Breast Cancer Trialists’ Collaborative Group (EBCTCG) [20, 21]. The cure proportions are translated into tumor diameters so that more effective treatment can cure a larger tumor. Women diagnosed at a tumor diameter greater than the tumor’s fatal diameter, benefit from adjuvant treatment by a shift to a larger fatal disease diameter. If the new fatal diameter is larger than the diameter at diagnosis, the treatment results in cure and ultimately death from other causes. However, if the new fatal diameter is still smaller than the diameter at diagnosis, surgery and radiation combined with adjuvant treatment will not results in cure and the tumor will eventually cause breast cancer death. The dissemination of adjuvant treatment is modeled as the probability of being treated with a certain type of treatment (e.g. chemotherapy, tamoxifen) given stage at diagnosis, calendar year, age at diagnosis, ER and HER2 status.
Parameter estimation
Parameter estimates are obtained by optimizing the goodness of fit between simulated data and observed data. The stochastic nature of the model output and duration of the model runs make the process of finding solid parameter estimates time-consuming. For selected starting values of the parameters, one microsimulation run will produce, for instance, age-specific breast cancer incidence trends over time, and compare it to the observed breast cancer incidence levels. Maximum likelihood estimates of the model parameters are obtained by repeated evaluation of the simulated breast cancer incidence for different sets of parameter values. Parameters are estimated by minimizing the sum of squared differences between observed and simulated data. This weighted sum measures the goodness of fit of the simulation results and is defined as a chi-squared distributed statistic. [22]. Minimization of the goodness of fit statistic leads to the optimal parameters, but requires frequent, and time-consuming evaluations of the objective function. We used the Nelder and Mead Simplex (NMSM) algorithm [23], which has the advantage that it only uses the value of the objective function, i.e., the goodness of fit of the model, to find the minimum. In the NMSM approach, each step in the optimization algorithms is based on output from previous simulation runs in which large numbers of life histories have been simulated, and it performs quite well in locating the optimum.
Extensive model calibration for the CISNET base case analysis provided parameter estimates that resulted in a close match between the simulated U.S. incidence and mortality over time and the observed trends in incidence and mortality from 1975 to 2000 [16]. These parameter estimates from the base case analysis were only re-calibrated for a limited number of parameters at a time and within logical parameter bounds (e.g., new screening modalities with higher sensitivity of screening correspond to, and resulted in, a smaller threshold diameter for screen-detectability).
Validation
Establishing the degree to which MISCAN-Fadia is an accurate representation of the real world, is validation. Five types of validation [24] are addressed: face validity, internal validity, cross validity, external validity, and predictive validity. Face validity means the model makes sense at face value. MISCAN-Fadia’s structure with a biological entry of continuous tumor growth makes sense at face value. The model structure and data sources used as input lead to credible results that show no logical contradictions such as screening resulting in the diagnosis of more late stage tumors, or decreasing risk of developing breast cancer as women get older. Internal consistency, or verification, examines the mathematical calculations performed and its consistency with what could be expected based on the model’s specification. MISCAN-Fadia, programmed in Delphi, is a microsimulation model in which disease processes are mainly driven by clearly specified probability distributions that are widely used in modern programming software packages. Results of mathematical calculations for published parameter values can easily be verified when using these probability distributions.
Cross-validity covers the aspect of comparing model results to the results of other modeling groups. As MISCAN-Fadia has been part of CISNET since the start of its collaboration, this form of validation of the model has been done extensively [15, 25, 26]. External validity is the comparison of model outcomes to observed data that was not used for calibration and development of the model. MISCAN-Fadia is currently part of an independent external validation exercise wherefore we validated the results of five CISNET breast cancer models against the UK Age trial [27]. In the past, we conducted a dependent model validation against the UK Breast Screening Frequency trial [28]. UK specific breast cancer incidence and life tables were used, and the threshold diameter as well as the diameter of clinical diagnosis were re-estimated based on the trial’s data. The model accurately reproduced the cumulative incidence in the intervention and control groups. Also, the percentage of screen detected and clinically diagnosed breast cancers were similar to the observed percentages in both groups, as were the number of breast cancer deaths [29]. Predictive validation is done by making model predictions for future outcomes of, for example, patterns in incidence and mortality. MISCAN-Fadia has made predictions about future trends in incidence and mortality [30], but it still remains to be seen how these predictions unfold.
Model input and output of MISCAN-Fadia
Differences in patterns of breast cancer incidence and mortality can often be traced back to different screening and treatment regimens, adherence patterns, and different underlying risks. To simulate the harms and benefits of screening and treatment at the population level, the model requires data for the four major model components: population demographics, natural history of breast cancer, screening and treatment. A list of inputs of MISCAN-Fadia is provided and described as common CISNET model inputs [3].
The outcomes listed in Table 1 can be produced for any screening scenario with different start and stop ages of screening, screening frequency and screening modality. In addition to different screening strategies, the model output can also be broken down by: calendar year, age group, and by tumor size or breast cancer stage such as AJCC. By assigning health utilities to specific health states and unit costs to specific events, total costs and Quality Adjusted Life Years (QALYs) can be calculated. Consequently cost-effectiveness analyses can be performed [31]. In addition, radiation-induced breast cancers and breast cancer deaths can be calculated using model output together with radiation dose [32].
Table 1.
Model output MISCAN-Fadia model
| Output description | |
|---|---|
| 1 | Invasive Breast cancer cases diagnosed clinically |
| 2 | Invasive Breast cancer cases diagnosed by screening |
| 3 | DCIS cases diagnosed clinically |
| 4 | DCIS cases diagnosed by screening |
| 5 | Life years in the absence of screening |
| 6 | Life years in the presence of screening |
| 7 | DCIS over diagnosed cases (in the presence of screening) |
| 8 | Invasive over diagnosed cases (in the presence of screening) |
| 9 | Breast cancer deaths in the absence of screening |
| 10 | Breast cancer deaths in the presence of screening |
| 11 | Deaths from other causes in the absence of screening |
| 12 | Deaths from other causes in the presence of screening |
| 13 | Number of mammograms |
| 14 | Number of cancers diagnosed in AJCC stage I, II, III, IV |
| 15 | Number of cancers diagnosed in SEER stage local, regional, distant |
| 16 | Number of cancers diagnosed by tumor size 0–20mm, 20–50mm, 50+ mm |
| 17 | Number of cancers treated with adjuvant treatment |
| 18 | Intervals between events, e.g., lead time (time between screen detection and diagnosis in the absence of screening), survival (time between diagnosis and death) |
Extensions and applications of the model
Targeting screening to women with the highest potential benefit and lowest potential harm can improve the overall balance between benefits and harms in the population. In recent years, we explored the effects of obesity and race on U.S. breast cancer mortality [30, 33] as well as the cost effectiveness of ultrasonography screening [31]. In the past years, we also examined the contributions of screening and treatment to reduction in molecular subtype specific breast cancer mortality by evaluating different screening scenarios, including risk-based screening strategies. We present some examples of the model adaptations that formed the basis of these collaborative modeling studies.
Personalizing screening
To evaluate screening outcomes while taking into account advances in mammography and treatment of breast cancer, several screening strategies were modeled differing by age at which screening starts and screening interval. Biennial screening from age 50 to 74 years avoided a median of 7 breast cancer deaths per 1,000 women screened compared to no screening and is generally considered to have a favorable balance between benefits and harms. More intensive screening leads to more benefits (breast cancer deaths averted), but also to more harms (false-positives and over diagnosis). For example, annual screening from age 40 to 74 years avoided an additional 3 deaths, but yielded 1988 more false-positive results and 11 more over diagnosed cases per 1000 women screened [26]. Women aged 40 with a two-fold risk (compared to average risk) can expect the same balance of benefits and harms as average-risk women who receive biennial screening starting from age 50 [25].
Breast density and breast cancer
Breast density has been proposed to personalize mammography screening. Dense breast tissue is prevalent and associated with a higher risk of developing breast cancer [34]. Moreover, since breast density is relatively easy to measure on a mammogram, it can be used for risk stratification. Some studies have found that tumors in dense breasts (categorized as BI-RADS 3 and 4) may progress more rapidly than those in fatty breasts, categorized as BI-RADS 1 and 2 [35]. Based on this, breast density could be taken into account when personalizing a woman’s screening frequency. Breast density does not only affect risk of developing breast cancer, it also affects screening test sensitivity as dense breast tissue is comprised of less fat and more connective breast tissue which appears white on a mammogram. Moreover, cancer appears white on a mammogram and is therefore easier overlooked by radiologists, resulting in a lower screening test sensitivity.
Breast density in MISCAN-Fadia
Breast density has been incorporated into MISCAN-Fadia to assess the effects of personalized screening; breast density was assumed to influence the sensitivity of the screening test (threshold diameter) as well as the onset of breast cancer. We also incorporated the decrease in breast density as women age because mammographic density decreases after the menopause when ovarian function declines. When modeling both risk and density, we found that average-risk women (low breast density) undergoing triennial screening and higher-risk women (high breast density) receiving annual screening will maintain a similar or better balance of benefits and harms compared to biennially screening average-risk women [36].
Simulating molecular subtypes of breast cancer
It has been widely acknowledged that breast cancer is a heterogeneous disease and more knowledge is emerging on distinct molecular subtypes. Combinations of Estrogen Receptor (ER) and Human Epidermal Growth Factor Receptor 2 (HER-2) status have different tumor growth and are associated with different treatment responses that have been found to be important in targeting the treatment of breast cancer. To understand the relative contributions of screening and treatment to U.S. breast cancer mortality, first the major subtype combinations of ER positive and ER negative have been included in MISCAN-Fadia. Across CISNET models we found greater absolute breast cancer mortality declines in ER-positive cancers than among ER-negative cancers. The relative contribution of adjuvant treatment vs screening to breast cancer mortality reductions was higher for ER-positive cases; for ER-negative cases, the relative contributions were similar [13]. We have recently also included HER-2 in the model [14], as well as the treatment Trastuzumab (Herceptin) that is an antibody that interferes with the HER2 receptor.
Future directions of MISCAN-Fadia
Risk based screening based on genetic risk profile
Genomic discoveries of genes associated with breast cancer risk may have the potential to personalize screening based on a woman’s genetic risk profile. It is one of our primary goals in the upcoming years to continue our research on estimating the population impact of using polygenic risk to tailor screening strategies. A growing group of single nucleotide polymorphisms (SNPs) are discovered that are associated with an elevated risk for breast cancer [37]. Individual SNPs identify a small increase in risk, however, multiple SNPs combined together can be translated into a polygenic risk score to stratify women based on their polygenic risk. We divide the population into risk groups based on observed polygenic risk score distributions. For each risk group, the models simulate routine digital mammography screening strategies by varying starting and stopping ages of screening and screening frequency. To warrant a more intense screening scenario for high risk groups and a less intense screening strategy for low risk groups, we compare the benefits and harms of the different screening strategies. The polygenic risk distribution in the U.S. female population determines how many women are eligible for each selected screening strategy and what the overall harms and benefits of polygenic risk-based screening will be.
A simplified analysis of using polygenic risk to inform screening strategies, can be performed by dividing the population into three (low, median, high) risk groups with varying prevalence (Figure 3). Targeted screening based on polygenic risk leads to a redistribution of benefits and harms. A more in-depth analysis will be performed in the near future within CISNET. MISCAN-Fadia will be used to quantify the benefits such as the breast cancer deaths averted, quality-adjusted life years saved, breast cancer mortality reduction, costs, and harms such as the false positive mammograms, over diagnosed cases, unnecessary biopsies, false negatives.
Figure 3.
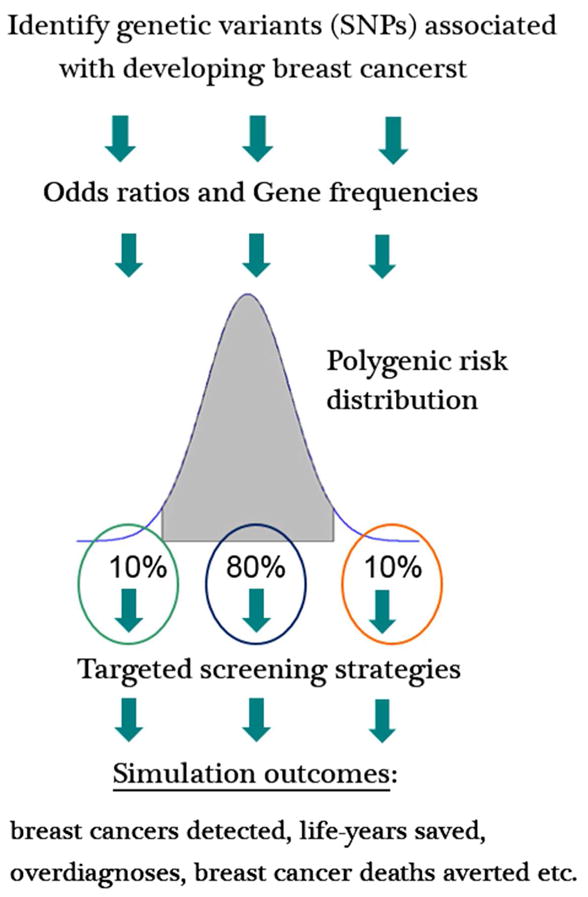
Simulating a personalized approach to breast cancer screening based on genetic risk profile. Genetic variants for breast cancer have different risk alleles. Multiple single nucleotide polymorphisms (SNPs) combined together can be translated into a polygenic risk score to stratify women based on their polygenic risk. In Figure 3, a simplified analysis of the potential population impact of using polygenic risk to inform screening strategies is demonstrated by dividing the population into three (low, median, high) risk groups with varying prevalence. In this simplified example 10% of the population has a low risk of developing breast cancer, 80% an average risk, and 10% a high risk. More frequent screening could be offered to the high risk group and less frequent screening (compared to average risk group) could be offered to the low risk group. With more risk groups, or even a continuous risk distribution we could potentially optimize the tailoring of screening strategies based on polygenic risk which would lead to a redistribution of benefits and harms compared to current practice. A more in depth analysis will be performed in the near future within CISNET.
Strategies to reduce overtreatment of DCIS
While early detection of breast cancer and consequently less invasive treatment are often mentioned as benefits of screening, overtreatment of DCIS lesions that otherwise would not have clinically surfaced without screening is an increasing harm of screening since DCIS rates have increased dramatically over the last 30 years. Studies have shown that an increase in breast cancer mortality reduction due to screening comes with a substantial increased number of over diagnosed DCIS cases [11, 38]. MISCAN-Fadia will be extended to investigate if, how, and to what extent the harms of screening and treatment of DCIS can be reduced. By simulating ‘watchful waiting’ strategies and exploring risk factors for progression to invasive breast cancer such as cytological grade, ER status, age at diagnosis and ethnicity, MISCAN-Fadia will be used to assess how different screening strategies and treatment routines may affect incidence and mortality for varying progression and regression rates of DCIS.
Conclusion
Trends in breast cancer incidence and mortality depend on many factors related to the biology and natural history of breast cancer. As tumor size is observable at diagnosis and tumors are considered to grow in continuous time rather than discrete time, these two aspects form MISCAN-Fadia’s biological entry to modeling the effects of screening and treatment on breast cancer incidence and mortality. The advantage of this biologically oriented approach is that it allows for simple hypothesis testing because the core biological mechanisms are separated from cancer control interventions. Changes or improvements in screening and treatment that may vary by age, or over time, can be implemented directly and be dealt with without changing breast cancer onset or tumor growth parameters. On the other hand, simulating less or even more aggressive tumor subtypes with a different growth function is also possible. Moreover, correlations that were added to the base case model in order to get a good overall fit with observed data, were plausible, and with a biological reasoning, intuitive to understand. In particular, one may expect faster growing tumors to be diagnosed at larger tumor diameters, and faster growing tumors to have a shorter survival as well as a larger clinical diagnosis diameter.
However, MISCAN-Fadia also has limitations and makes use of simplifying assumptions. We model only one tumor per woman while it may be possible that breast cancer develops in both breasts independently or at the same time, although such cancer development is not prevalent. Also, recurrence of breast cancer is not simulated in our model. We do not model specific factors associated with an elevated risk for breast cancer such as reproductive history, alcohol use, hormone therapy use or familial risk. These different risk groups are assumed to be captured by the distribution we simulate tumors from. The spread between slower and faster growing tumors with unique tumor characteristics is assumed to capture the entire population risk profile.
Future development of the model will focus on evaluating the impact of using polygenic risk to inform screening strategies, evaluating the clinical management of screen-detected DCIS, and incorporating alternative and emerging screening modalities such as breast MRI and tomosynthesis.
Acknowledgments
Support: This work was supported by the National Institutes of Health under National Cancer Institute Grants U01CA152958 and U01CA199218
References
- 1.Habbema JD, van Oortmarssen GJ, Lubbe JT, van der Maas PJ. The MISCAN simulation program for the evaluation of screening for disease. Comput Methods Programs Biomed. 1985;20(1):79–93. doi: 10.1016/0169-2607(85)90048-3. [DOI] [PubMed] [Google Scholar]
- 2.Boer R, de Koning H, van Oortmarssen G, Warmerdam P, van der Maas P. Stage distribution at first and repeat examinations in breast cancer screening. J Med Screen. 1999;6(3):132–8. doi: 10.1136/jms.6.3.132. [DOI] [PubMed] [Google Scholar]
- 3.Mandelblatt JS, Near AM, Miglioretti DL, Munoz D, Sprague BL, Trentham-Dietz A, et al. Common Model Inputs used in CISNET Collaborative Breast Cancer Modeling Medical Decision Making. 2016 doi: 10.1177/0272989X17700624. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tabar L, Fagerberg G, Duffy SW, Day NE, Gad A, Grontoft O. Update of the Swedish two-county program of mammographic screening for breast cancer. Radiol Clin North Am. 1992;30(1):187–210. [PubMed] [Google Scholar]
- 5.Tabar L, Fagerberg G, Day NE, Duffy SW. The Swedish two-county trial of mammographic screening for breast cancer: recent results on mortality and tumor characteristics. Pathol Biol (Paris) 1992;39(9):846. [PubMed] [Google Scholar]
- 6.Tan SY, van Oortmarssen GJ, de Koning HJ, Boer R, Habbema JD. The MISCAN-Fadia continuous tumor growth model for breast cancer. J Natl Cancer Inst Monogr. 2006;(36):56–65. doi: 10.1093/jncimonographs/lgj009. [DOI] [PubMed] [Google Scholar]
- 7.Clemmesen J. Carcinoma of the breast; results from statistical research. Br J Radiol. 1948;21(252):583–90. doi: 10.1259/0007-1285-21-252-583. [DOI] [PubMed] [Google Scholar]
- 8.Weedon-Fekjaer H, Bakken K, Vatten LJ, Tretli S. Understanding recent trends in incidence of invasive breast cancer in Norway: age-period-cohort analysis based on registry data on mammography screening and hormone treatment use. BMJ. 2012;344:e299. doi: 10.1136/bmj.e299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Holford TR, Cronin KA, Mariotto AB, Feuer EJ. Changing patterns in breast cancer incidence trends. J Natl Cancer Inst Monogr. 2006;(36):19–25. doi: 10.1093/jncimonographs/lgj016. [DOI] [PubMed] [Google Scholar]
- 10.Gangnon RE, Sprague BL, Stout NK, Alagoz O, Weedon-Fekjaer H, Holford TR, et al. The contribution of mammography screening to breast cancer incidence trends in the United States: an updated age-period-cohort model. Cancer Epidemiol Biomarkers Prev. 2015;24(6):905–12. doi: 10.1158/1055-9965.EPI-14-1286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.de Gelder R, Fracheboud J, Heijnsdijk EA, den Heeten G, Verbeek AL, Broeders MJ, et al. Digital mammography screening: weighing reduced mortality against increased overdiagnosis. Prev Med. 2011;53(3):134–40. doi: 10.1016/j.ypmed.2011.06.009. [DOI] [PubMed] [Google Scholar]
- 12.van Ravesteyn NT, van den Broek JJ, Li X, Weedon-Fekjar H, Schechter CB, Alagoz O, et al. Modeling ductal carcinoma in situ (DCIS) – an overview of CISNET model approaches Medical Decision Making. 2016 doi: 10.1177/0272989X17729358. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Munoz D, Near AM, van Ravesteyn NT, Lee SJ, Schechter CB, Alagoz O, et al. Effects of screening and systemic adjuvant therapy on ER-specific US breast cancer mortality. J Natl Cancer Inst. 2014;106(11) doi: 10.1093/jnci/dju289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Plevritis S, Munoz D, Kurian A, Alagoz O, Near AM, Stout NK, et al. Contributions of screening and systemic therapy to molecular subtype specific U.S. breast cancer mortality from 2000 to 2010. 2016 submitted. [Google Scholar]
- 15.Berry DA, Cronin KA, Plevritis SK, Fryback DG, Clarke L, Zelen M, et al. Effect of screening and adjuvant therapy on mortality from breast cancer. N Engl J Med. 2005;353(17):1784–92. doi: 10.1056/NEJMoa050518. [DOI] [PubMed] [Google Scholar]
- 16.Feuer EJ. Modeling the impact of adjuvant therapy and screening mammography on U.S. breast cancer mortality between 1975 and 2000: introduction to the problem. J Natl Cancer Inst Monogr. 2006;(36):2–6. doi: 10.1093/jncimonographs/lgj002. [DOI] [PubMed] [Google Scholar]
- 17.Cronin KA, Mariotto AB, Clarke LD, Feuer EJ. Additional common inputs for analyzing impact of adjuvant therapy and mammography on U.S. mortality. J Natl Cancer Inst Monogr. 2006;(36):26–9. doi: 10.1093/jncimonographs/lgj005. [DOI] [PubMed] [Google Scholar]
- 18.Cronin KA, Yu B, Krapcho M, Miglioretti DL, Fay MP, Izmirlian G, et al. Modeling the dissemination of mammography in the United States. Cancer Causes Control. 2005;16(6):701–12. doi: 10.1007/s10552-005-0693-8. [DOI] [PubMed] [Google Scholar]
- 19.Stout NK, Lee SJ, Schechter CB, Kerlikowske K, Alagoz O, Berry D, et al. Benefits, harms, and costs for breast cancer screening after US implementation of digital mammography. J Natl Cancer Inst. 2014;106(6):dju092. doi: 10.1093/jnci/dju092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Early Breast Cancer Trialists’ Collaborative G. Peto R, Davies C, Godwin J, Gray R, Pan HC, et al. Comparisons between different polychemotherapy regimens for early breast cancer: meta-analyses of long-term outcome among 100,000 women in 123 randomised trials. Lancet. 2012;379(9814):432–44. doi: 10.1016/S0140-6736(11)61625-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yin W, Jiang Y, Shen Z, Shao Z, Lu J. Trastuzumab in the adjuvant treatment of HER2-positive early breast cancer patients: a meta-analysis of published randomized controlled trials. PLoS One. 2011;6(6):e21030. doi: 10.1371/journal.pone.0021030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Barton RR, Ivey JS. Nelder-Mead simplex modifications for simulation optimization. Management Science. 1996;42:954–73. [Google Scholar]
- 23.Tan SYGL, Van Oortmarssen GJ, Piersma N. Estimating Parameters of a Microsimulation Model for Breast Cancer Screening Using the Score Function Method. Annals of Operations Research. 2003;119(1):43–61. [Google Scholar]
- 24.Eddy DM, Hollingworth W, Caro JJ, Tsevat J, McDonald KM, Wong JB, et al. Model transparency and validation: a report of the ISPOR-SMDM Modeling Good Research Practices Task Force-7. Med Decis Making. 2012;32(5):733–43. doi: 10.1177/0272989X12454579. [DOI] [PubMed] [Google Scholar]
- 25.van Ravesteyn NT, Miglioretti DL, Stout NK, Lee SJ, Schechter CB, Buist DS, et al. Tipping the balance of benefits and harms to favor screening mammography starting at age 40 years: a comparative modeling study of risk. Ann Intern Med. 2012;156(9):609–17. doi: 10.1059/0003-4819-156-9-201205010-00002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mandelblatt JS, Stout NK, Schechter CB, van den Broek JJ, Miglioretti DL, Krapcho M, et al. Collaborative Modeling of the Benefits and Harms Associated With Different U.S. Breast Cancer Screening Strategies. Ann Intern Med. 2016;164(4):215–25. doi: 10.7326/M15-1536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Moss SM, Wale C, Smith R, Evans A, Cuckle H, Duffy SW. Effect of mammographic screening from age 40 years on breast cancer mortality in the UK Age trial at 17 years’ follow-up: a randomised controlled trial. Lancet Oncol. 2015;16(9):1123–32. doi: 10.1016/S1470-2045(15)00128-X. [DOI] [PubMed] [Google Scholar]
- 28.Breast Screening Frequency Trial G. The frequency of breast cancer screening: results from the UKCCCR Randomised Trial. United Kingdom Co-ordinating Committee on Cancer Research. Eur J Cancer. 2002;38(11):1458–64. doi: 10.1016/s0959-8049(01)00397-5. [DOI] [PubMed] [Google Scholar]
- 29.van Ravesteyn NT, Heijnsdijk EA, Draisma G, de Koning HJ. Prediction of higher mortality reduction for the UK Breast Screening Frequency Trial: a model-based approach on screening intervals. Br J Cancer. 2011;105(7):1082–8. doi: 10.1038/bjc.2011.300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Mandelblatt J, van Ravesteyn N, Schechter C, Chang Y, Huang AT, Near AM, et al. Which strategies reduce breast cancer mortality most? Collaborative modeling of optimal screening, treatment, and obesity prevention. Cancer. 2013;119(14):2541–8. doi: 10.1002/cncr.28087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sprague BL, Stout NK, Schechter C, van Ravesteyn NT, Cevik M, Alagoz O, et al. Benefits, harms, and cost-effectiveness of supplemental ultrasonography screening for women with dense breasts. Ann Intern Med. 2015;162(3):157–66. doi: 10.7326/M14-0692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Miglioretti DL, Lange J, van den Broek JJ, Lee CI, van Ravesteyn NT, Ritley D, et al. Radiation-Induced Breast Cancer Incidence and Mortality From Digital Mammography Screening: A Modeling Study. Ann Intern Med. 2016;164(4):205–14. doi: 10.7326/M15-1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.van Ravesteyn NT, Schechter CB, Near AM, Heijnsdijk EA, Stoto MA, Draisma G, et al. Race-specific impact of natural history, mammography screening, and adjuvant treatment on breast cancer mortality rates in the United States. Cancer Epidemiol Biomarkers Prev. 2011;20(1):112–22. doi: 10.1158/1055-9965.EPI-10-0944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.McCormack VA, dos Santos Silva I. Breast density and parenchymal patterns as markers of breast cancer risk: a meta-analysis. Cancer Epidemiol Biomarkers Prev. 2006;15(6):1159–69. doi: 10.1158/1055-9965.EPI-06-0034. [DOI] [PubMed] [Google Scholar]
- 35.Aiello EJ, Buist DS, White E, Porter PL. Association between mammographic breast density and breast cancer tumor characteristics. Cancer Epidemiol Biomarkers Prev. 2005;14(3):662–8. doi: 10.1158/1055-9965.EPI-04-0327. [DOI] [PubMed] [Google Scholar]
- 36.Trentham-Dietz A, Kerlikowske K, Stout NK, Miglioretti DL, Schechter CB, Ergun MA, et al. Tailoring breast cancer screening intervals by breast density and risk for women 50 and older: Collaborative modeling of screening outcomes. 2016 doi: 10.7326/M16-0476. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mavaddat N, Pharoah PD, Michailidou K, Tyrer J, Brook MN, Bolla MK, et al. Prediction of breast cancer risk based on profiling with common genetic variants. J Natl Cancer Inst. 2015;107(5) doi: 10.1093/jnci/djv036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.van Luijt PA, Heijnsdijk EA, Fracheboud J, Overbeek LI, Broeders MJ, Wesseling J, et al. The distribution of ductal carcinoma in situ (DCIS) grade in 4232 women and its impact on overdiagnosis in breast cancer screening. Breast Cancer Res. 2016;18(1):47. doi: 10.1186/s13058-016-0705-5. [DOI] [PMC free article] [PubMed] [Google Scholar]