Comparing CISNET Breast Cancer Models Using the Maximum Clinical Incidence Reduction Methodology

Abstract

Background

Collaborative modeling has been used to estimate the impact of potential cancer screening strategies worldwide. A necessary step in the interpretation of collaborative cancer screening model results is to understand how model structure and model assumptions influence cancer incidence and mortality predictions. In this study we examined the relative contributions of the pre-clinical duration of breast cancer, the sensitivity of screening, and the improvement in prognosis associated with treatment of screen-detected cases to the breast cancer incidence and mortality predictions of five Cancer Intervention and Surveillance Modeling Network (CISNET) models.

Methods

To tease out the impact of model structure and assumptions on model predictions, the Maximum Clinical Incidence Reduction (MCLIR) method compares changes in the number of breast cancers diagnosed due to clinical symptoms and cancer mortality between 4 simplified scenarios: 1) no-screening; 2) one-time perfect screening exam that detects all existing cancers and perfect treatment (i.e., cure) of all screen-detected cancers; 3) one-time digital mammogram and perfect treatment of all screen-detected cancers; and 4) one-time digital mammogram and current guideline-concordant treatment of all screen-detected cancers.

Results

The five models predicted a large range in maximum clinical incidence (19%–71%) and in breast cancer mortality reduction (33%–67%) from a one-time perfect screening test and perfect treatment. In this perfect scenario, the models with assumptions of tumor inception prior to when it is first detectable by mammography predicted substantially higher incidence and mortality reductions than models with assumptions of tumor onset at the start of a cancer’s screen-detectable phase. The range across models in breast cancer clinical incidence (11%–24%) and mortality reduction (8%–18%) from a one-time digital mammogram at age 62 with observed sensitivity and current guideline-concordant treatment was considerably smaller than achievable under perfect conditions.

Conclusions

The timing of tumor inception and its effect on the length of the pre-clinical phase of breast cancer had substantial impact on the grouping of the models based on their predictions for clinical incidence and breast cancer mortality reduction. This key finding about the timing of tumor inception will be included in future CISNET breast analyses to enhance model transparency. The MCLIR approach should aid in the interpretation of variations in model results and could be adopted in other disease screening settings to enhance model transparency.

Introduction

Collaborative modeling can enhance the rigor of modeling research through the use of multiple independent models to answer the same research question. The National Cancer Institute-funded Cancer Intervention and Surveillance Modeling Network (CISNET) was established in 2000 to use collaborative modeling to improve our understanding of the impact of cancer prevention, screening, and treatment dissemination on population trends in cancer incidence and mortality. The CISNET Breast Cancer Working Group includes six modeling teams: Dana-Farber (Model D) [1], Erasmus (Model E) [2], Georgetown-Einstein (Model GE) [3], MD Anderson (Model M) [4], Stanford (Model S) [5], and Wisconsin-Harvard (Model W) [6]. The modeling groups have collaborated to estimate the effects of breast cancer prevention [7], mammography screening [8–11], and systemic adjuvant treatment on trends in breast cancer incidence and mortality [12, 13]. Prior research has also investigated the impact of different screening scenarios on the balance of population-level benefits and harms, and the results have been used by policymakers to inform breast cancer screening guidelines [9, 14, 15].

Each of the models is unique in its structure, assumptions, and methods of synthesizing data. Consequently, they are unique in how they project the impact of screening and treatment on breast cancer incidence and mortality. Results that are similar across multiple models despite differences in assumptions and modeling approach, enhance the credibility of the findings and are more likely to be robust than conclusions obtained from a single model. For instance, in prior analyses, the models all closely estimated observed trends in US breast cancer incidence and mortality and consistently agreed on the ranking of screening scenarios based on several metrics, including mortality reductions. [9, 15]

Despite the consistency of prior conclusions about the effects of screening across the models, there are variations in the magnitude of the effects. [9, 15] For the interpretation of collaborative modeling results, it is important to understand how different model structures and combinations of assumptions contribute to this variation. Detailed model descriptions (Table 1) are informative and contribute to model transparency. However, conveying between-model differences is not always straightforward for reasons related to the nature of modeling disease processes and their interaction with cancer control interventions. In particular, breast cancer modeling involves the representation of unobservable aspects of natural history such as tumor onset and tumor progression upon which interventions (e.g., screening and treatment) are overlaid. To do so, models make assumptions about the timing of tumor inception, tumor progression (e.g., discrete or continuous tumor growth), and progression variability among tumors. These assumptions in conjunction with model structure impact the three key determinants of screening effectiveness: 1) pre-clinical duration of breast cancer, i.e., the time period during which prevalent undiagnosed cancers could be detected by screening; 2) sensitivity of the screening test, i.e., the likelihood that cancers are detected at screening; and 3) improvement in prognosis from treatment, e.g., whether (earlier) treatment reduces (more) breast cancer mortality.

Table 1.

Overview of Key Differences and Similarities Between The CISNET Breast Models Structures and Key Model Components

Model	D	E	GE	S	W
Model type	Analytic, Parallel universe	Simulation, Parallel universe	Simulation, Parallel universe	Simulation, Parallel universe	Simulation, Parallel universe
Tumor progression modeled as	State-transition	Continuous tumor growth	Stage-transition	Continuous tumor growth	Continuous tumor growth
Incidence in the absence of screening	Age Period Cohort model	Age Period Cohort model	Age Period Cohort model	Age Period Cohort model*	Age Period Cohort model
DCIS included	Yes	Yes	Yes	No	Yes
ER/HER2 Included	Yes	Yes	Yes	Yes	Yes
Individual risk factors for breast cancer	Breast density	Breast density, obesity	Breast density	Hormone replacement	Breast density
Screen detection conditioned on	Modality, age, density, frequency	Tumor size, modality, age, density, frequency	Modality, age, density, frequency	Tumor size, ER status, age, hormone repl., frequency	Tumor size, modality, age, density, frequency
Implementation of screen benefit	Stage shift	Detection at smaller tumor size	Younger age, earlier stage	Stage shift, detect at smaller tumor size	Younger age, detect at smaller tumor size
Estimation of over diagnosis	Difference screen & no-screen	Difference screen & no-screen	Difference screen & no-screen	Difference screen & no-screen	Difference screen & no-screen
Implementation treatment benefit	Hazard reduction	Cure fraction, larger fatal diameter	Hazard reduction, cure fraction	Hazard reduction, non-proportional	Cure fraction
Death from breast cancer determined by	Survival from BC < survival other cause mortality	Fatal diameter, survival from BC < survival OC mortality	Survival from BC < survival other cause mortality	Survival from BC < survival other cause mortality	Survival from BC < survival other cause mortality
SEER data used for calibration	No	Incidence, mortality, stage distribution	Incidence, stage distribution	Incidence, stage distribution	Incidence, mortality
Addition based on MCLIR analyses
Tumor inception point	At the start of pre-clinical screen-detectable phase	Prior to start of pre-clinical screen-detectable phase	At the start of the pre-clinical screen-detectable phase	Prior to start of the pre-clinical screen-detectable	At the start of the pre-clinical screen-detectable phase

^*Model S uses background breast cancer incidence derived from the APC framework that explicitly considers the effects of screening and menopausal hormone replacement therapy. [5] Among the other modeling groups breast cancer incidence in the absence of screening is estimated starting from a common APC model. [19, 24]

Given the complexity of interpreting outcomes from multiple models in a collaborative setting, it can be useful to isolate portions of the models to gain greater insight into how model structure and natural history assumptions systematically affect model results. The maximum clinical incidence reduction (MCLIR) method can be used to isolate the effects of tumor onset, tumor progression, screening test sensitivity, and treatment by comparing model results before and after imposing a one-time screening intervention under varying assumptions about screening performance and treatment effectiveness.

In the absence of screening, breast cancers will only be diagnosed as a result of clinical symptoms, i.e., clinical incidence, which is defined as breast cancers diagnosed due to symptoms. Screening is assumed to detect some of these cancers prior to symptomatic diagnosis, thereby reducing clinical incidence, and possibly cancer mortality. The MCLIR method measures this reduction in breast cancer clinical incidence and mortality. While all models use the same data on screening sensitivity and breast cancer treatment, the implementation of screening and treatment in the models varies as model structures are different. Therefore, differences in clinical incidence reduction should reflect model-specific choices in their portrayal of the pre-clinical detectable phase of breast cancer (tumor onset and progression) and mechanisms of screen detection (e.g., how they incorporate sensitivity). Differences in breast cancer mortality are expected to capture model-specific assumptions about tumor onset and progression and how the implementation of treatment affects the natural history.

To date, the MCLIR method has been applied to three CISNET colorectal cancer models to clarify the effect of natural history assumptions and model structure on colorectal cancer incidence predictions. [16] In this study, we extended the MCLIR method to understand how differences among the CISNET breast cancer models affect predictions for screening effectiveness by projecting the clinical incidence and mortality reductions after a one-time screening exam at age 62 among women without prior screening or a past breast cancer diagnosis. The results are intended to provide a greater understanding of how the CISNET breast models depict unobservable processes, and how those representations may systematically affect conclusions about screening effects on incidence and mortality.

Methods

This research was approved as exempt by the Georgetown Institutional Review Board based on use of de-identified, publically available data. Five of the six CISNET breast models (those with natural history components) participated in this analysis.

Model Overview

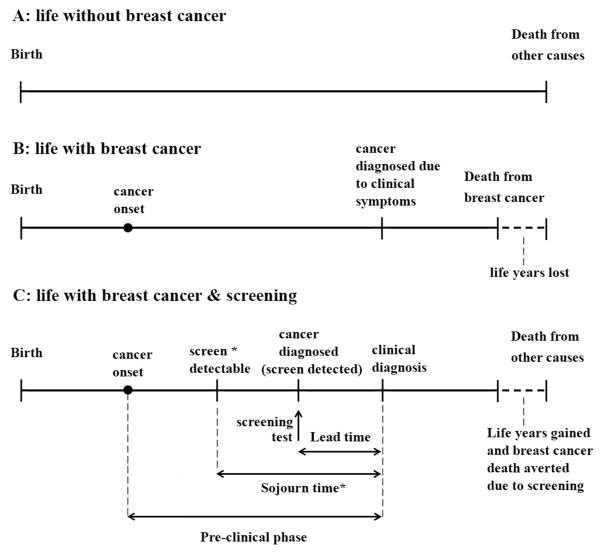
The general model structure of the five models involves the simulation of women who may develop breast cancer in the absence or presence of screening. In all models, the majority of women live a breast cancer-free life and eventually die of causes other than breast cancer (Figure 1, panel A). For women who develop breast cancer, tumor inception is simulated either prior to (models E and S) or at the start of (models D, GE, and W) the tumor’s sojourn time. We define the sojourn time as the portion of time in the pre-clinical phase between when a cancer can be first screen-detectable (e.g., by mammography) and when clinical cancer diagnosis would occur due to symptoms in the absence of screening.[17] Tumor sojourn time is also termed ‘pre-clinical screen-detectable phase‘ (Figure 1).

Figure 1.

Three versions of a woman’s life history: A, without breast cancer; B, with breast cancer and without screening; C, with breast cancer and mammography screening. In scenario C, the preclinical phase is the period of time between tumor inception and clinical diagnosis in the absence of screening. The sojourn time for a screening test, e.g., mammography is the period of time within the preclinical phase that a cancer can be screen detectable; this period can also be termed the preclinical screen-detectable phase. The point when the cancer is detected by screening depends on when the screening test is performed and the sensitivity of the screening test. The period before the sojourn time represents a period in which the tumor is present but undetectable by mammography. Should the sensitivity of mammography improve, or new types of screening tests evolve, the point of screen-detectability would shift to the left and tumors could be detected closer to tumor inception.

The point when a tumor becomes screen-detectable may depend on the sensitivity of the screening test, such that more sensitive tests can detect tumors closer to inception, and hence in earlier stages or at smaller tumor sizes. Tumor growth is simulated either continuously (models E, S, and W) or as movement through discrete stages (models D and GE). All models except model S include ductal carcinoma in situ (DCIS). Nonetheless, model S simulates the progression of breast cancers prior to clinical symptoms based on continuous tumor growth of invasive cancer (Table 1). [5]

In the absence of screening, the models assume that some cancers will eventually cause symptoms and be clinically diagnosed (Figure 1, panel B). If a woman participates in screening during the cancer’s sojourn time, the cancer may be screen-detected in an earlier stage or at a smaller size than would have occurred with clinical diagnosis in the absence of screening.

The time period between when a cancer is screen-detected and when it would have been clinically diagnosed in the absence of screening is referred to as the lead-time (Figure 1, panel C). The lead time is part of the sojourn time, and the duration of the sojourn time is an important unobservable determinant of screening effectiveness because a longer sojourn time implies a longer period during which a screening test can potentially detect cancer. The sojourn time is based on assumptions about tumor inception and tumor growth, and the start of the sojourn time is determined by the sensitivity of the screening test (Figure 1, panel C).

Mortality reductions from screening may occur via improvements in survival related to the earlier stage or smaller tumor size at diagnosis of screened vs. unscreened women, given receipt of breast cancer treatment.

MCLIR Analysis

To illustrate the effects of model structure and assumptions about tumor inception, tumor progression, screening test ability to detect tumors, and treatment on breast cancer incidence and mortality predictions, the MCLIR analysis consists of comparisons between four scenarios. Three scenarios involve a one-time screening test at age 62 and the remaining no-screening scenario serves as a comparator (Table 2). The study population for each scenario is a cohort of average risk women born in 1965, that have never been screened or diagnosed with breast cancer prior to age 62. Age 62 was chosen to illustrate model differences because it is in the middle of the start and stop ages of the generally recommended mammography screening guidelines [14, 18] and there is sufficiently high prevalence of breast cancer at this age to illustrate model differences. While all models have the capacity to include risk factors, to isolate model differences these analyses focused on the average risk population. Women were followed for 15 years (i.e., up to age 77) to capture the immediate and long-term effects of the intervention. Model outcomes were breast cancer clinical incidence and breast cancer mortality by age.

Table 2.

Description of Maximum Clinical Incidence Reduction (MCLIR) Method

Scenarios	Scenario Description	Implication	Analyses
No Screening (Scenario 1)	No screening: no screening during a woman’s lifetime. Diagnosed breast cancers will be treated with current treatment*	All cancers diagnosed in this scenario are diagnosed due to clinical symptoms and will be treated with guideline-concordant treatment.	Comparator to calculate the screening effect in scenarios 2, 3, and 4.
Perfect screening Perfect treatment (Scenario 2)	A one-time perfect screen with 100% sensitivityΦ at age 62, all screen-detected cancers are treated with perfect treatment≈	All existing cancers at age 62 will be screen-detected and cured by perfect treatment and will not lead to breast cancer death.	Comparison of Scenario 2 to 1 isolates the effect of the pre-clinical detectable duration of breast cancer and provides the tumor progression distribution.
Current sensitivity Perfect treatment (Scenario 3)	One-time digital mammogram with current sensitivity^ at age 62, all screen-detected cancers are treated with perfect treatment	Some of the existing cancers at age 62 are screen-detected. All screen-detected cancers are cured and will not lead to breast cancer death.	The comparison of scenario 3 to 2 isolates the effect of digital mammography (non-perfect) sensitivity on reductions in clinical incidence and breast cancer mortality.
Current sensitivity Current Treatment (Scenario 4)	One-time digital mammogram with current sensitivity at age 62, all screen-detected cancers are treated with current treatment	Some of the existing cancers at age 62 are screen-detected. All screen-detected cancers are treated with guideline-concordant treatment and some will not lead to breast cancer death.	Comparison of scenario 4 to 3 isolates the effect of guideline-concordant (imperfect) treatment effectiveness on breast cancer mortality reduction.

^*Current treatment: All diagnosed breast cancers receive guideline-concordant breast cancer treatment with observed treatment effectiveness. [19]

^ΦPerfect sensitivity: All existing breast cancers are screen-detected at screening (e.g., Sensitivity is 100%).

^≈Perfect treatment: All diagnosed breast cancers are “cured” and women will not die of breast cancer.

^{^}Current sensitivity: Screening is performed with the observed sensitivity of digital mammography. [19]

MCLIR Scenarios

Scenario 1 is the baseline scenario without screening where all breast cancers will be diagnosed due to clinical symptoms. Upon diagnosis, cancers are treated according to current guideline recommended treatment. [19] Guideline concordant treatment roughly implies that, after surgical removal of the tumor, estrogen receptor (ER)-positive breast cancers are primarily treated with hormone therapy and advanced stage ER positive tumors may also receive chemotherapy. ER-negative breast cancers are treated with chemotherapy only. Tumors that are Human epidermal growth factor Receptor 2 (HER2) positive are also treated with Trastuzumab (Herceptin). The effectiveness of breast cancer treatment was based on the most recent meta-analyses of randomized clinical trials reported by the Early Breast Cancer Trialists’ Collaborative Group (EBCTCG). [20] Scenario 1 provides baseline information about the number of cancers that will lead to symptoms and be clinically diagnosed as well as the number of breast cancer deaths occurring in the 15-year follow-up period.

Scenario 2 involves a one-time perfect screening test at age 62 and perfect treatment. The hypothetical perfect screening test assumes that all tumors in existence are screen-detected, including those that may not be detectable by digital mammography. Perfect treatment means treatment is curative and that all women will be cured and will die from other causes than breast cancer. Comparing results from this scenario with the baseline (no-screening) scenario provides the maximum achievable clinical incidence and mortality reduction. It is a measure of the pool of cancers that technically could be screen-detected at age 62 and thus avoid clinical diagnoses of these cancers at a later age when they would cause symptoms. The change in the maximum achievable clinical incidence reduction over time as women age provides insight into the distribution of sojourn times of the existing tumors at age 62, i.e., key determinant 1 of screening effectiveness. The mortality results from this scenario provide information on how many of the breast cancer deaths between ages 62 and 77 stem from cancers that were present at age 62. Relative to the no-screening scenario, it is the maximum achievable mortality reduction from screening and treatment, and the converse (1 minus the maximum mortality reduction) is the portion of unavoidable breast cancer deaths because these cancers had tumor onset after age 62 when the screening test was done (Figure 3). The age-specific maximum achievable mortality reduction after the screen test at age 62 also provides insight into the survival time of pre-clinical cancers in existence at age 62.

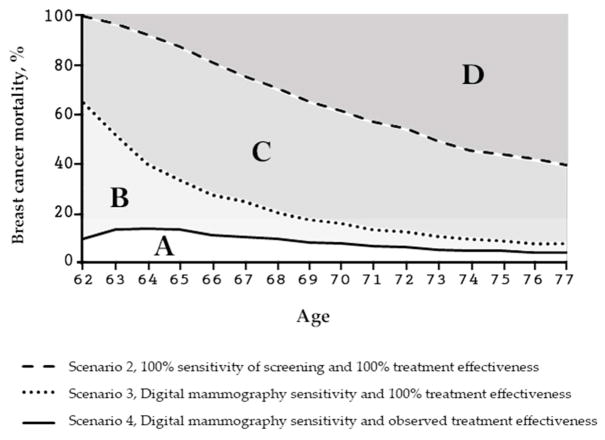
Figure 3.

The MCLIR metrics explained for breast cancer mortality.

Overall reductions in breast cancer mortality at 15-year follow-up: The light gray area denoted by A is the overall breast cancer mortality reduction over the 15 years after one digital mammogram at age 62 and guideline recommended treatment with observed treatment effectiveness. The area B alone represents the proportion of breast cancer mortality that could not be reduced because of the non-perfect treatment effectiveness of current guideline recommended treatment. Since guideline recommended treatment does not cure all screen-detected cancers, B provides a measure of the room to further reduce breast cancer mortality if better (more effective) treatment would become available.

The area C alone represents the proportion of breast cancer mortality that could not be reduced because of the non-perfect sensitivity of currently available digital mammography. As a digital mammogram does not detect all tumors in existence, B provides a measure of the room to further reduce breast cancer mortality if better (more sensitive) screening would become available. The 3 areas combined (A, B and C) are the maximum mortality reduction from perfect screening and perfect treatment where B + C represent the maximum room to further reduce breast cancer mortality if screening sensitivity and treatment effectiveness would become improve. The dark gray area, denoted by D, is the proportion of breast cancer deaths that is not reducible by a perfect screen at age 62 and perfect treatment because these breast cancer deaths had tumor onset after age 62.

Age-specific reductions in breast cancer mortality: Scenario 1, the no-screening scenario, serves as comparator from which the reductions, as measured on the y-axis, are calculated. Scenario 2 (dashed line) is the age-specific percent breast cancer mortality reduction from one perfect screening test with perfect sensitivity and perfect treatment relative to the breast cancer mortality in the no-screening scenario. Scenario 3 (dotted line) is the age-specific percent breast cancer mortality reduction from one digital mammogram at age 62 and perfect treatment relative to the no-screening scenario. Scenario 4 (solid line) is the age-specific percent mortality reduction from one digital mammogram at age 62 and guideline-concordant treatment with observed treatment effectiveness in screen-detected cases relative to the no-screening scenario.

Scenario 3 involves a one-time digital mammogram at age 62 with sensitivity based on observed mammography performance in the Breast Cancer Screening Consortium [9, 19] and perfect treatment (i.e., cure) of screen-detected cancers. In this scenario, some of the cancers in existence at age 62 will be missed by screening and this will affect clinical incidence and mortality at later ages. Because scenarios 2 and 3 vary screening performance while holding the treatment effects constant, the comparison of these two scenarios isolates the impact of perfect vs. observed sensitivity of screening on reductions in clinical incidence and breast cancer mortality, i.e., key determinant 2 of screening effectiveness. This comparison also illustrates the room for improvement in terms of fewer clinically diagnosed cases and cancer deaths should the sensitivity of screening would improve (e.g., new radiology technology or circulating tumor DNA detection).

Scenario 4, the realistic scenario, involves a one-time digital mammogram at age 62 and treatment according to current guidelines [19]. Because scenarios 3 and 4 vary treatment effectiveness while holding the sensitivity of screening constant, the comparison of these scenarios isolates the impact of perfect vs. actual treatment effectiveness on breast cancer mortality, i.e., key determinant 3 of screening effectiveness. This comparison isolates the portion of cancers that, despite earlier detection by screening, will not be cured with current guideline recommended treatment. Also, this provides insight into the room for improvement should breast cancer treatment improve in the future, given current performance of digital mammography.

For ease of comparison and interpretation of outcomes across the four scenarios for five different models, results are reported as percent reductions in clinical incidence and breast cancer mortality relative to each model’s clinically diagnosed breast cancers and breast cancer deaths in the absence of screening (Figure 2 & 3).

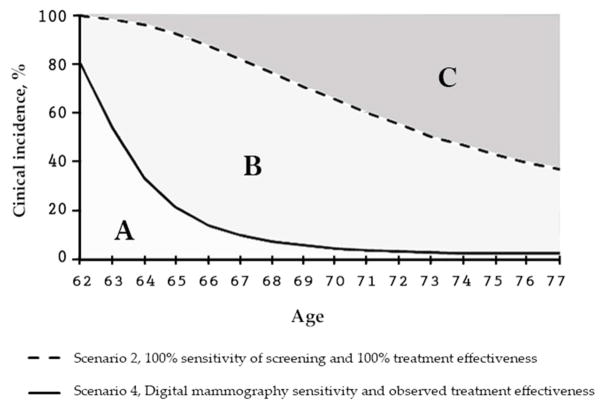
Figure 2.

The MCLIR metrics explained for breast cancer incidence.

Overall reductions in breast cancer incidence at 15-year follow-up: The light gray area denoted by A is the overall clinical incidence reduction over the 15 years after the digital mammogram at age 62. The area B alone represents the proportion of clinical incidence that could not be reduced because of the non-perfect sensitivity of the digital mammogram. As a digital mammogram does not detect all tumors in existence, the area B provides a measure of the room to further reduce breast cancer clinical incidence if better (more sensitive) screening would become available. The 2 light gray areas combined (A and B) are the maximum clinical incidence reduction from perfect screening. The dark gray area denoted by C, is the proportion of clinical incidence that is not reducible by a perfect screen at age 62 because these clinical cancers had a tumor onset after age 62.

Age-specific reductions in breast cancer incidence: Scenario 1, the no-screening scenario, serves as comparator from which the reductions, as measured on the y-axis, are calculated. Scenario 2 (dashed line) is the age-specific percent reduction in clinical incidence from one perfect screening test at age 62 with perfect sensitivity relative to the clinical incidence in the no-screening scenario. Scenario 4 (solid line) is the age-specific percent clinical incidence reduction from one digital mammogram at age 62 relative to the no-screening scenario. Scenario 3 (also solid line) uses sensitivity of current digital mammography and in contrast to scenario 4 has perfect treatment effectiveness which only affects breast cancer mortality, and thus, scenario 3 has the same impact on breast cancer incidence as scenario 4.

Results

The results for each scenario for the impact of a one-time screen at age 62 among women with no prior screening or past diagnosis of breast cancer are presented separately for incidence and mortality.

Breast Cancer Incidence

Tumor Onset and Progression

The maximum achievable clinical incidence reduction from a perfect screening test at age 62 (scenario 2) relative to the no-screening scenario (scenario 1) illustrates the impact of natural history assumptions such as tumor onset and tumor progression on screening effectiveness. The maximum clinical incidence reduction ranged from 19% to 71% across the five models with models D, GE, and W grouping towards the lower end of the range and models E and S towards the top of the range (Table 3). This wide variation was the result of differences in the modeling of the timing of tumor inception relative to the start of the sojourn time. For example, Model E’s assumption of tumor onset long before the start of the sojourn time led to a large screening effect when the perfect screening test was applied that detects all tumors from their inception even before the pre-clinical screen-detectable phase begins. The majority (71%) of the cancers in this model had an onset prior to age 62 and were therefore screen-detected by a perfect screening test at age 62, avoiding clinical diagnoses at a later age. The remaining (29%) of cancers had an onset after age 62. Model S makes similar assumptions about tumor onset and growth as Model E, and has fairly similar patterns in their results as Model E. In contrast, in Models D, GE, and W, which simulate tumor inception at the start of the pre-clinical screen-detectable phase, only 19% to 27% of cancers were in existence at age 62, leading to a lower maximum clinical incidence reduction from a perfect screening test than Models E and S.

Table 3.

Percent Reductions in Breast Cancer Incidence after One Mammography Screen at Age 62 over a 15-Year Follow-Up, %

Scenario	Intervention	D	E	GE	S	W
2	100% screening sensitivity and 100% treatment effectiveness (vs. no screening)	23	71	27	43	19
4	Current screening sensitivity and current treatment effectiveness (vs. no screening)	21	15	24	16	11
4 vs. 2	Breast cancer clinical incidence not reduced because of imperfect (current) screening sensitivity	2	56	3	27	8

Scenario 3 is not shown because this scenario has the same screening sensitivity (digital mammography) as scenario 4 and hence has the same clinical incidence reduction as scenario 4.

The shape of the maximum clinical incidence reduction curve provides insight into the variability of tumor growth and disease progression of tumors in existence at age 62 (Figure 4). In models D, GE and W, the age-specific clinical reductions from the perfect screen declined more rapidly in the first five years than in the other two models, indicating the presence of more quickly progressing tumors relative to the other models. The non-steep and slower linear decline of the age-specific maximum clinical incidence reduction in Models E and S is the consequence of greater variability in tumor progression and overall slower tumor growth among the tumors in existence at age 62 than seen in the other models.

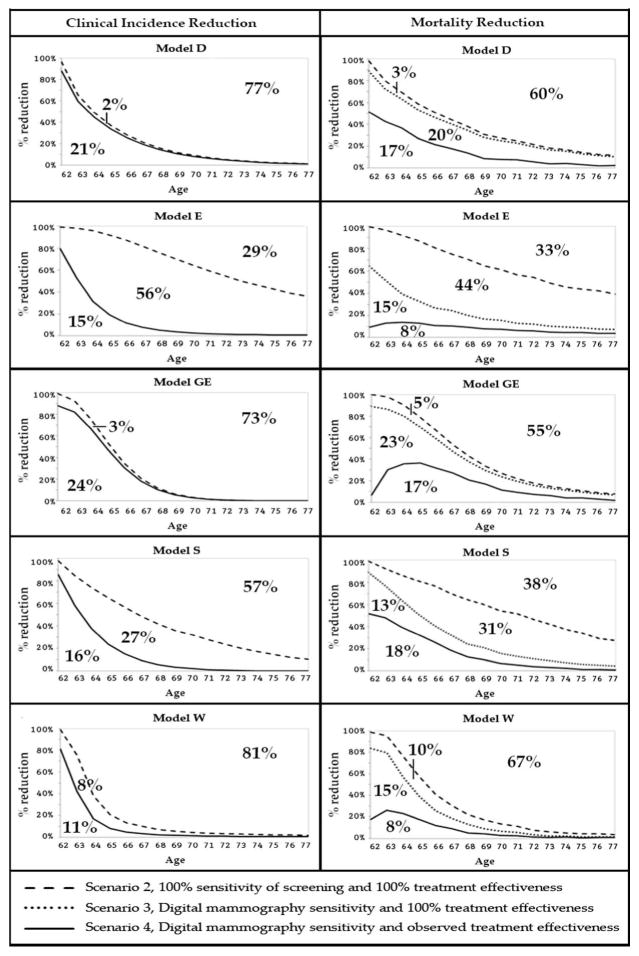
Figure 4.

Age-specific reductions in breast cancer clinical incidence and mortality over 15 years after a one-time screening test at age 62 by model. The percent marks in the panels of Figure 4 represent the cumulative outcomes for the 15-year follow-up period from age 62 to age 77.

The line at the top in the breast cancer incidence panels on the left of Figure 4 is the maximum clinical incidence reduction from a screening test at age 62 with 100% sensitivity and perfect treatment of screen-detected cancers (Scenario 2). Just after the screening test, the reduction in clinical incidence (panels on the left) is highest and decreases by age as it becomes less likely that clinical cancers at later ages were already in existence at age 62 and could have been prevented by a screening test at that age.

The percentages in the left-panel figures represent, for example for Model S: 57% of the cancers that are clinically diagnosed in the absence of screening between ages 62 and 77 have an onset after age 62, this implies that 100-57=43% (Scenario 2, Table 3) of the cancers diagnosed in the absence of screening could be prevented from becoming clinical diagnosis at later ages by a perfect screening test at age 62. The solid line below the dashed line is the clinical incidence reduction from a digital mammography screening test: 16% of clinical diagnoses could be prevented by a one-time digital mammogram at age 62 (Scenario 3, Table 3). This implies that 27% of clinical incidence between ages 62 and 77 was not reduced by the one-time digital mammogram at age 62 (Scenario 3 vs 2).

The dashed line at the top in the breast cancer mortality panels on the right of Figure 4 is the maximum achievable mortality reduction from a screening test with 100% sensitivity combined with perfect treatment in screen-detected cases (Scenario 2). The dotted line below the top line represents the breast cancer mortality reduction over the 15-years after a current digital mammogram at age 62 and perfect treatment in the screen-detected cases (Scenario 3). The solid line at the bottom is the reduction in breast cancer mortality from a current screening test combined with current treatment (Scenario 4).

The percentages in these figures are, for example for Model S: 38% of breast cancer deaths observed in the scenario without screening stem from cancers with onset after age 62 and could therefore not be screen-detected and prevented from breast cancer death by screening at age 62. This implies that 100-38=42% of breast cancer deaths could be reduced by perfect screening and perfect treatment of screen-detected cases (Scenario 2, Table 4). However, 31% of breast cancer deaths are not prevented due to lack of screen-detection if screening is performed with a digital mammogram (Scenario 3 vs 2, Table 4), and 13% of breast cancer deaths is not prevented because current guideline-concordant treatment lacks the effectiveness to cure those screen-detected breast cancers (Scenario 4 vs 3). The 18% mortality reduction follows from current screening and current treatment (Scenario 4).

The models have structural differences in the timing of tumor inception relative to the sojourn time and they had the same calibration targets (observed trends in U.S. breast cancer incidence and mortality) in their development phase. This explains why Models E and S with tumor inception long before the start of the sojourn time have slower overall tumor progression and Models D, GE, and W with tumor inception at the start of the sojourn time have faster progressing tumors.

Screening Sensitivity

Reductions in clinical incidence based on the observed sensitivity of digital mammography varied less across models than when assuming perfect sensitivity, with ranges of 11% to 24%. Since assumptions about tumor onset and progression differ, how the models arrive at this result differs and is illustrated by comparison to their predictions for maximum reductions achievable (Scenario 3 vs 2). In models D, GE, and W, the differences in clinical incidence reduction were 2%, 3%, and 8%, respectively, and in models E and S these were 56% and 27%. While models E and S have more tumors in existence at age 62, the majority of tumors were in their pre-sojourn period and not yet screen-detectable with a digital mammogram having actual observed sensitivity. On the other hand, in models D, GE, and W, the majority of tumors in existence at age 62 were in their sojourn period and could be detected by the digital mammogram. Thus, the variations between model clusters E and S vs. D, GE, and W indicate that modeling assumptions about the timing of tumor inception in relation to the implementation of digital mammography can have substantial impact on screen detection and reductions in clinical breast cancer incidence.

Breast Cancer Mortality

Tumor Onset and Progression

Based on one perfect screening test at age 62 and perfect treatment for screen-detected cancers, the maximum reductions in breast cancer mortality relative to the no-screening scenario ranged from 33% to 67% over 15 years of follow-up (Table 4). Similar to the impact of tumor onset on clinical incidence reductions, Models D, GE and W had a higher percent (55% to 67%) of breast cancer deaths stemming from cancers with onset after age 62 than Models E and S (33% to 38%). These variations reflect interactions between assumptions about tumor onset and survival times.

Table 4.

Percent Reduction in Breast Cancer Mortality after One Digital Mammography Screen at Age 62 with 15-Year Follow-Up, %

Scenario	Intervention	D	E	GE	S	W
2	100% screening sensitivity and 100% treatment effectiveness (vs. no screening)	40	67	45	62	33
	% Breast cancer deaths with onset after age 62.*	60	33	55	38	67
3	Current screening sensitivity and 100% treatment effectiveness (vs. no screening)	37	23	40	31	23
3 vs. 2	Breast cancer mortality not reduced because of imperfect (current) screening sensitivity	3	44	5	31	10
4	Current screening sensitivity and current treatment effectiveness (vs. no screening)	17	8	17	18	8
4 vs. 3	Breast cancer mortality not reduced because of imperfect (current) treatment effectiveness	20	15	23	13	15
4 vs. 2	Breast cancer mortality not reduced because of imperfect screening sensitivity and imperfect treatment effectiveness	23	59	28	44	25

^*The percent breast cancer deaths that stem from cancers with onset after age 62 is given by 100% minus the cancer deaths from cancers with onset before age 62 (Scenario 2).

Scenarios 3 vs. 2, 4 vs. 3, and 4 vs. 2, show the percentage point breast cancer mortality that is not reduced due to imperfect screening sensitivity and/or imperfect treatment effectiveness.

The steep declines of the maximum mortality reduction curves (Figure 4, right panels) of models D, GE and W reveal that, on average breast cancers in these models have shorter survival times and less variability in survival times relative to models E and S. These results for average survival times correspond to the findings about tumor progression in the models: the relatively slow tumor progression, based on earlier inception of tumors, in models E and S relate to longer survival times, and the faster tumor progression in Models D, GE and W arising from tumor inception at the beginning of the sojourn period ultimately lead to shorter survival times on average.

Screening sensitivity

Compared to the maximum achievable mortality reduction, a one-time digital mammogram having actual observed sensitivity missed between 3% (Model D) to 44% (Model E) of the avoidable cancer deaths. Overall, the mortality reduction from a one-time digital mammogram at age 62 and perfect treatment relative to no-screening (scenario 3 vs. 1) was 23% to 40% across models (Table 4, Figure 4). The ability to detect lethal tumors by mammography screening was higher among the models (D, GE, and W) with assumptions of tumor onset at the start of the sojourn time than the models (E and S) with tumor onset prior to the start of the sojourn time.

Treatment effectiveness

Assuming observed guideline-concordant treatment effectiveness in screen-detected cancers (scenario 4), the percent breast cancer mortality that was not reduced compared to Scenario 3 with perfect treatment was 13% to 23% (Table 4, Figure 4). The difference between scenario 3 and 4 show that Models E and GE, have a relatively high percentage of cancer deaths that were not averted in the first 3 years after the screen at age 62. This illustrates the substantial portion of cancers screen-detected at a relatively advanced stage that was not curable with current treatment effectiveness. These findings showed that the lethality of the cancers found at screening impacts breast cancer mortality differently over time and in magnitude by model.

Sensitivity and Treatment

The combination of screening with a digital mammogram at age 62 and guideline-concordant treatment with current treatment effectiveness (Scenario 4 vs. Scenario 1) provides insight into how assumptions about currently available screening and treatment interact with breast cancer natural history to affect breast cancer mortality. Models E, W and S grouped towards the lower end and models D and GE towards the higher end of the clinical incidence reductions (Table 3). But for breast cancer mortality slightly different groupings of models were seen: Models D, GE and S predicted 17 to 18% breast cancer mortality reduction relative to the no-screening scenario, whereas models E and W predicted 8% breast cancer mortality reduction (Table 4).

The lower breast cancer mortality reductions predicted by models E and W were primarily the result of a low screen-detection rate of lethal cancers and the lack of improving prognosis with treatment of screen-detected cases: in both models 23% of the cancers destined to cause breast cancer death were screen-detected (Scenario 3), and of those detected only one-third (8 out of 23; Scenario 4 vs. Scenario 3, Table 4) were cured.

Models D and S predicted a similar 17 and 18% mortality reduction as model GE, also due to a combination of relatively high screen-detection and high improvement of prognosis from treatment. However, the shape of the mortality reduction curve of Model GE, relative to other models, was distinct. The inverted shape of model GE can be explained by the presence of more advanced-stage cancers at screen detection, where breast cancer death could not be avoided.

Discussion

This study is the first to apply the maximum clinical incidence reduction (MCLIR) method to illustrate how model structure and assumptions impact both clinical incidence and cancer mortality predictions. To understand variations in model estimates of screening effects, the analysis decomposed the relative contributions of model-specific structures and assumptions regarding the pre-clinical duration of breast cancer, the ability of a screening test to detect cancers, and breast cancer treatment to breast cancer incidence and mortality predictions. The results illustrated that models with similar predictions for screening effectiveness may use differing assumptions about screening, treatment, tumor onset, and tumor progression. Altogether, the key finding was that assumptions about the timing of tumor inception and its effect on the pre-clinical duration of breast cancer had the greatest impact on the model groupings on predicted clinical breast cancer incidence and mortality reductions. As a result of this finding, we now include this model-specific tumor attribute in our CISNET model comparison table (Table 1).

The MCLIR scenarios showed that models E and S simulate the longest pre-clinical duration of breast cancer. While this implies a longer period to detect cancers by screening and possibly avert cancer deaths, these models showed the greatest difference in breast cancer mortality reduction between the scenarios with perfect detection to those with (realistic) digital mammography. Again, this was related to those models’ assumptions about early tumor onset prior to the start of a cancer’s sojourn time. The loss in breast cancer mortality reduction due to digital mammography (imperfect) screening provides information about the further reductions in breast cancer mortality should screening sensitivity improve in the future, given the current state of the models. On the other hand, models D, GE and W had similar and relatively short pre-clinical durations due to their assumptions of tumor inception at the start of the sojourn time and therefore ultimately predicted smaller losses in breast cancer mortality reduction due to digital mammography screening. The effect of guideline-concordant treatment with actual observed treatment effectiveness on breast cancer mortality reduction differed by model structure. In general, greater breast cancer mortality reductions were predicted by models that use a hazard-reduction treatment structure than the models with cure fractions to implement breast cancer treatment. These types of insights from the MCLIR results provide further clarity on the differences and similarities across models and can be used to interpret variations in model outcomes.

The MCLIR analyses also illustrated model variation in the distributions for tumor progression assumed in the models, with models D, GE, and W tending to have faster progressing tumors than models E and S. This knowledge about the models can help interpret model differences in predictions of screening effectiveness by screening frequency. For example, one would expect more cancers to be diagnosed with more frequent screening in models that have relatively faster tumor progression on average and vice versa. This was confirmed in a recent analysis of the impact of screening intervals on breast cancer mortality, with Models D, GE, and W showing greater benefits (breast cancer deaths averted preceded by more cancer diagnoses) from more frequent screening than models E and S. [9]

The MCLIR methodology was first used to evaluate differences in the CISNET colorectal cancer screening models. [16] The colorectal cancer findings indicated that assumptions about the duration between adenoma onset and clinical diagnosis were an important factor in explaining colorectal cancer model differences. The results of this study were similar in demonstrating that models with long pre-clinical durations of breast cancer and relatively low screen detection rates project similar screening effects as models with a shorter pre-clinical durations and higher screen detection rates.

Usually, models are characterized by describing modeling approach, model inputs and assumptions. [19,21,22] In this research, we examined model outcomes to drill down to the mechanics of incidence and mortality predictions. There are several caveats that should be considered in evaluating this method. First, the effect of a single screen on breast cancer incidence and mortality is not the same as the effect of routine screening from age 50 to 74. The results in this study are therefore not directly translatable to projections of the effects of a periodic screening program on overall breast cancer incidence and mortality. Second, it was beyond the scope of this paper to perform and evaluate the MCLIR scenarios at different ages or at multiple ages across five different models. Evaluating the MCLIR scenarios at different ages would provide insight into age-specific and between-model differences in tumor inception, progression, and test-characteristics and the impact of these on breast cancer incidence and mortality. Third, the MCLIR methodology employed did not explicitly allow for formal assessments of the factors that account for differences in rates of over-diagnosis. This will be an interesting area for future research and extended use of the MCLIR method.

CISNET collaborative modeling predictions are increasingly used by policy makers to inform screening guidelines [9, 14], evaluate screening and treatment programs [12, 13], and can be used by clinicians to assist in decision-making about breast cancer screening. [23] How different models arrive at their predictions of harms and benefits of screening and treatment may be perceived as opaque due to the complexity of the models. This study complements model descriptions [1–6] by using MCLIR analyses to illustrate and compare which structural differences and natural history assumptions may be important to consider by policy makers when using collaborative modeling outcomes. The MCLIR approach could be adopted in other comparative modeling research to improve model transparency.

Explanation of Terms Used in Table 1

Model type

Analytic

Analytical approach to estimate the impact of mammography screening and breast cancer treatment on incidence and mortality of breast cancer

Simulation

Stochastic simulation is based on the Monte Carlo method and use of random numbers to evaluate the impact of screening on life histories, cancer incidence and mortality

Parallel universe

Screening and treatment is modeled in a parallel universe, implying that the same population is simulated twice: once to determine the impact of breast cancer without screening, and once to determine the impact of breast cancer with screening

Natural history and factors affecting breast cancer onset

APC model

Breast cancer onset and breast cancer in the absence of screening was derived by Gangnon et al. [23] and is driven by an age-period-cohort model:

• Age: As women age, their risk of developing breast cancer increases
• Period: Onset of breast cancer is different in certain calendar time periods
• Cohort: Year of birth influences the risk of developing breast cancer

Breast density

Breast density is associated with different levels of risk for developing breast cancer and modifies the operating characteristics of breast cancer screening

ER/HER2

Onset of breast cancer is different for molecular subtypes ER and HER2

Tumor stage transition

Tumor progression is modeled as transitions between discrete stages

Continuous tumor growth

Tumors grow continuously after tumor inception

Screening mechanism

Sensitivity

Sensitivity can be used directly or indirectly (e.g., when translated to tumor size)

Overdiagnosis

The detection and diagnosis of a condition that would not go on to cause symptoms or breast cancer death in a woman’s lifetime in the absence of screening

Duration of preclinical detectable phase

The period between tumor onset and the start of a cancer’s screen-detectable phase

Treatment effect

Hazard reduction

Reduction in breast cancer mortality hazard, derived from the hazard ratio reported for the different treatment regimens [19]

Cure fraction

If hazard rate reduction is not a direct model input, it can be translated into a cure fraction to implement breast cancer treatment

Death from breast cancer

Once diagnosed with breast cancer, a survival until breast cancer death is competing with the other cause mortality survival. That is, breast cancer death occurs only if the patient does not die from other causes