Abstract
Background
The U.K. Age trial compared annual mammography screening of women ages 40 to 49 to no screening and found a statistically significant breast cancer mortality reduction at 10-year follow-up, but not at 17-year follow-up. The objective of this study was to compare the observed Age trial results to the Cancer Intervention and Surveillance Modeling Network (CISNET) breast cancer model predicted results.
Methods
Five established CISNET breast cancer models used data on population demographics, screening attendance, and mammography performance from the Age trial together with extant natural history parameters to project breast cancer incidence and mortality in the control and intervention arm of the trial.
Results
The models closely reproduced the effect of annual screening from ages 40 to 49 on breast cancer incidence. Restricted to breast cancer deaths originating from cancers diagnosed during the intervention phase, the models estimated an average 15% (range across models 13% to 17%) breast cancer mortality reduction at 10-year follow-up compared to 25% (95% CI 3% to 42%) observed in the trial. At 17-year follow-up, the models predicted 13% (range 10% to 17%) reduction in breast cancer mortality compared to the non-significant 12% (95% CI -4% to 26%) in the trial.
Conclusions
Overall, the models captured the observed effect of screening from age 40 to 49 on breast cancer incidence and mortality in the U.K. Age trial, suggesting that the model structures, input parameters, and assumptions about breast cancer natural history are reasonable for estimating the impact of screening on mortality in this age group.
Introduction
The breast cancer models of the Cancer Intervention and Surveillance Modeling Network (CISNET) synthesize data on breast cancer epidemiology, population demographics, screening accuracy, and treatment to simulate the impact of screening and treatment interventions on breast cancer incidence and mortality. Prior comparative modeling studies, i.e., cross-validations [1], by the CISNET models have illustrated the ability of the models to reproduce the trends in breast cancer incidence and mortality in the United States. [2–4] The models generated similar rankings of the effects of different screening scenarios and the relative impact of screening and treatment on breast cancer mortality. Moreover, the simulation results provided quantitative information about the harms and benefits of various screening strategies not examined in randomized clinical trials, and have been used by policy makers to inform decisions about breast cancer screening guidelines. [3, 5]
The consistency of previous collaborative modeling research provides a level of evidence for cross-validation. However, none of the prior collaborative CISNET research by the Breast Working Group has included external model validation. The International Society for Pharmacoeconomics and Outcomes Research in collaboration with the Society for Medical Decision Making (ISPOR-SMDM) recommends external model validation as part of good modeling practices, where external model validation is defined as, “the comparison of model predictions to observed event data not used in model development”[1]. The purpose of this paper is to conduct an external validation and compare CISNET breast cancer incidence and mortality predictions to observed clinical trial results of mammography screening from ages 40 to 49.
To date, the model parameters were primarily developed based on U.S. data on breast cancer epidemiology, screening, treatment, and population demographics.[6] Outcomes of our simulations indicated that offering screening to women in their fifties results in a more favorable ratio of benefits and harms than offering screening to women in their forties. [3, 7] This difference between the benefits and harms between these age groups, corresponds to the available evidence of screening women aged 50 and older [8] and the uncertainty about screening women in their forties, considering the inconclusive evidence from fewer studies, and the different guidelines for this age group [5, 9, 10]. Given the high prevalence of dense breast tissue, faster growing tumors, and inferior sensitivity of mammography in these younger women [11–13], it is important to validate the models for the effectiveness of screening in the forties. The U.K. ‘Age’ trial is a well-documented [14–20] trial, investigating the effect of annually screening women from ages 40 to 49 compared to no screening, and provided a unique opportunity to externally validate the CISNET breast cancer models for screening in the forties.
In this study, we present the first external validation performed by the CISNET breast cancer models that use different structures and assumptions about breast cancer natural history to project the impact of screening. We compare breast cancer incidence and mortality predictions to the observed results from the U.K. Age trial. The findings from this study are intended to inform CISNET model users as they can account for this information when considering and interpreting future model outcomes.
Methods
The U.K. Age trial was the only randomized controlled trial designed specifically to investigate the effect of annual mammography screening from ages 40 to 49. Between October 1990 and September 1997, 160,836 women aged 40–41 were randomly assigned in a ratio of 1 : 2 to either the intervention group or the control group. The 53,883 women in the intervention arm were offered annual screening by mammography, and the 106,953 women in the control arm received usual care (no screening). We collaborated with the Age trial investigators to obtain the observed de-identified data from the trial.
Simulation models
Five CISNET breast cancer models were included in this analysis: Model D (Dana-Farber), Model E (Erasmus), Model M (MD Anderson), Model S (Stanford), and Model W (Wisconsin-Harvard). These models have been developed independently within CISNET over the past 15 years and are described in detail elsewhere [21–25]. Briefly, women are born in a breast cancer-free stage, some women develop a tumor that may progress to a pre-clinical stage where it could be screen-detected in its pre-clinical sojourn time, or be diagnosed with breast cancer due to clinical symptoms. Once diagnosed with breast cancer, women receive age-, stage-, and biomarker-specific treatment. Breast cancer incidence and mortality projections depend on age, start and stopping ages of screening, screening frequency, mammography screening performance, stage at diagnosis, estrogen receptor (ER) and Human Epidermal growth factor Receptor 2 (HER2) status of the tumor, breast cancer treatment, and factors related to the natural history of breast cancer (Tables 1 & 2). However, since the Age trial did not collect HER2 status, the models did not simulate HER2 specific molecular subtypes of breast cancer. The models adopt a ‘parallel universe’ approach; the same population of women is simulated twice: in one scenario women were invited to annual screening in the forties (intervention group), and in the second scenario women did not receive any screening in the forties (control group).
Table 1.
Key differences and similarities between the CISNET breast models.
| Model | D | E | M | S | W |
|---|---|---|---|---|---|
| Model type | Analytic, Parallel universe | Simulation, Parallel universe | Bayesian, Parallel universe | Simulation, Parallel universe | Simulation, Parallel universe |
| Natural history modeled as | State-transition | Continuous tumor growth | Bayesian model | Continuous tumor growth | Continuous tumor growth |
| Tumor inception | Start of the sojourn time | Prior to start of sojourn time | N/A | Prior to start of sojourn time | Start of the sojourn time |
| DCIS included | Since 2014 | Yes | Yes | No | Yes |
| Tumor ER status | Yes | Yes | Yes | Yes | Yes |
| Screen detection depends on | Modality, age, density, frequency | Tumor size, modality, age, density, frequency | Modality, age, frequency | Tumor size, ER status, age, hormone repl., frequency | Tumor size, modality, age, density, frequency |
| Screening benefit | Stage shift | Detection at smaller tumor size | Stage shift, beyond stage shift | Stage shift, smaller tumor size | Younger age, smaller tumor size |
| Estimation of over diagnosis | Difference screen & no-screen | Difference screen & no-screen | Difference screen & no-screen | Difference screen & no-screen | Difference screen & no-screen |
| Treatment benefit | Hazard reduction | Cure fraction, larger fatal diameter | Cure fraction, hazard reduction, | Hazard reduction, non- proportional | Cure fraction |
| Death from breast cancer determined by | Survival from BC < survival other cause mortality | Fatal diameter, survival from BC < survival other cause mortality | Survival from BC < survival other cause mortality | Survival from BC < survival other cause mortality | Survival from BC < survival other cause mortality |
Model type
Analytic: Analytical approach to estimate the impact of mammography screening and treatment on incidence and mortality of breast cancer.
Simulation: Stochastic simulation is based on the Monte Carlo method and use of random numbers.
Bayesian: The model does not include a natural history and estimates prior probability distributions for all unknown parameters.
Parallel universe: Screening and treatment is modeled in a parallel universe, implying that the same population is simulated twice: once to determine the impact of breast cancer without screening, and once to determine the impact of breast cancer with screening.
Breast cancer natural history and breast cancer death
ER: Onset and progression of breast cancer is different for Estrogen Receptor positive and negative tumors.
Tumor stage transition: Tumor progression is modeled as transitions between different stages of breast cancer.
Continuous tumor growth: Tumors grow continuously after tumor onset.
Death from breast cancer: Once diagnosed with breast cancer, a survival until breast cancer death is competing with the other cause mortality survival. That is, breast cancer death occurs only if the patient does not die from other causes.
Screening & Treatment
Sensitivity: Sensitivity can be used directly or indirectly (e.g., when translated to tumor size).
Over diagnosis: The detection and diagnosis of a condition that would not go on to cause symptoms or breast cancer death in a woman’s lifetime.
Hazard reduction: Reduction in breast cancer mortality hazard, calculated by 1 minus the hazard ratio for the different treatment regimes.
Cure fraction: If hazard rate reduction is not a model input, it is translated into a cure fraction.
Table 2.
Model inputs used for the Age trial simulation:
| Model Input | Description | Source |
|---|---|---|
| Population demographics | ||
| Birth cohort | Birth years of women participating in the Age trial | Age trial |
| Life years | Number of life years by trial arm by age | Age trial |
| Natural history of breast cancer | ||
| Incidence | Control arm incidence (incidence in the absence of screening) | Age trial |
| Tumor onset | The moment tumors start to grow (tumor inception) | CISNET1 |
| Sojourn time | Time between when a cancer is first screen-detectable and cancer diagnosis in the absence of screening. | CISNET2 |
| Tumor progression | Tumor growth, tumor progression and regression affect tumor sojourn times and breast cancer survival. | CISNET3 |
| Estrogen receptor distribution | Age-specific ER positive and ER negative distributions | U.K.4 |
| Breast cancer screening | ||
| Attendance | Adherence to annual screening in the intervention arm | Age trial |
| Sensitivity | Probability that the screen will be positive among women with breast cancer by age, screening round (first vs. subsequent) | Age trial |
| Mammography | Two-view mammography for first screens, for all subsequent screens one-view mammography | Age trial |
| Breast cancer treatment | ||
| Treatment dissemination | Breast cancer treatment by age, stage and ER-status | BASO5 |
| Effectiveness | Hazard reduction breast cancer mortality by age and ER-status | EBCTCG6 |
| Breast cancer survival | ||
| Survival | Breast cancer survival by age, stage and ER-status | CISNET7 |
| Other-cause mortality | Probability of dying from causes other than breast cancer | U.K.8 |
Tumor onset, sojourn time and tumor progression are model-specific parameters. These, and other model-specific assumptions about breast cancer natural history are described elsewhere [6, 21–25].
Estrogen receptor status comes from observed U.K. data [26].
The treatment dissemination was derived from BASO reports [26] published by the NHSBSP.
Treatment effectiveness / hazard reduction for breast cancer death was published by the Early Breast Cancer Trialists Collaborative Group (EBCTCG) that included the U.K. trials [27]
Breast cancer survival by age and ER status from the UK is not available for the time period of the trial, the existing survival in the models which is based on U.S. data was used.
Other cause mortality was taken from the Human Mortality Database [30] with breast cancer deaths removed.
As summarized in Table 1, the models differ in the ways they approximate unobservable events in the natural history of breast cancer. In model D, tumors progress via discrete state transitions [23], models E, S and W have continuous tumor growth [21, 22, 25], and model M uses Bayesian simulation [24] and does not have a natural history component. In models D and W, tumors are technically screen-detectable from the moment at tumor inception. Models E and S start simulating tumors at small tumor sizes, prior to the start of the sojourn time, when tumors are not yet screen-detectable by film or digital mammography. Screening benefit in models D and M is modeled as a stage shift to earlier stage breast cancer, with the latter model including an additional benefit of screening beyond stage shift. The benefits of screening in models E, S and W are simulated by the detection of tumors at smaller sizes than at clinical diagnosis in the absence of screening. (Table 1)
Model inputs
The Age trial data that the CISNET models obtained included control arm incidence in the absence of screening, mammography screening performance, screening attendance patterns, and demographic data such as life years and the distribution of birth years of women participating in the trial (Table 2). In the Age trial, data were not collected for breast cancer treatment. To fill this gap we modeled the breast cancer treatment dissemination between 1991 and 2006, the intervention period of the trial, based on reports from the British Association of Surgical Oncology [26]. The effectiveness of breast cancer treatment was taken from analyses by the Early Breast Cancer Trialists’ Collaborative Group (EBCTCG) that included trials conducted in the U.K. [27]. Model parameters related to the natural history of breast cancer such as tumor onset and tumor growth were based on the original CISNET parameters and no calibration was performed to the results from the Age trial.
Simulation of the Age trial
The women who participated in the Age trial were born between 1950 and 1957, therefore, we simulated the 1950–1957 birth cohort. In the trial, two thirds of women aged 40 to 41 were randomized to the control group and were not invited to any screening in their forties. The models simulated 2 to 10 million women in each arm of the trial as they were not limited by practical issues concerning invitations and the number of women who can be included in the simulation of the trial. (Table 3) Any unscheduled screening in the control group was primarily a consequence of clinical symptoms and not because of routine screening [17], so we did not model screening contamination in the control group explicitly.
Table 3.
Number of women included in the control and intervention group
| Nr. of women in the control arm | Nr. of women in the intervention arm | |
|---|---|---|
| Age trial | 106,953 | 53,883 |
| Model D | N/A* | N/A |
| Model E | 10,000,000 | 10,000,000 |
| Model M | 4,000,000 | 4,000,000 |
| Model S | 5,000,000 | 5,000,000 |
| Model W | 2,000,000 | 2,000,000 |
All models simulated at least about 20 times as many women in the control group and 40 times as many women as in the intervention group. The number of women simulated was selected by each model to balance feasibility of simulation time with model output that yields relatively smooth incidence and mortality curves.
Model D uses entirely analytical formulations to evaluate the impact of screening and treatment on breast cancer incidence and mortality, i.e., the number of women simulated does not apply to Model D.
We used the control arm incidence as model input for a baseline projection of breast cancer incidence in the absence of screening. The models then overlaid the screening parameters according to the observed screening attendance patterns of the 53,883 women in the intervention group of the Age trial [18]. The percent uptake of invitations increased by screening round while the absolute number of invitations sent to the women in the trial decreased by almost 50% near the end of the intervention period and consequently the absolute number of women who were screened decreased as well. [18] The models accounted for this by simulating the decrease in the number of women who were screened by age. The first analog mammogram in the trial included two views, and all subsequent mammograms were single-view, similar to the standard practice in the U.K. at the time of the trial. Screen detection of pre-clinical breast cancer was modeled on the basis of observed sensitivity data published by the trial investigators [16].
The U.K. treatment dissemination developed for this project indicated whether a breast cancer is treated with hormone therapy and/or chemotherapy after surgical removal of the tumor. Overall, ER-positive breast cancers were primarily treated with hormone therapy and ER-negative breast cancers with chemotherapy. Since, the trial did not collect HER2 status, and Trastuzumab (Herceptin) was not yet disseminated in the U.K. at the time of the trial, it was not included in the treatment regimens.
Analysis
Model predictions were compared to breast cancer incidence and mortality observations from the Age trial by arm without calibrating the natural history parameters of the models to the trial. In addition, we compared the number of mammograms in the intervention group to that of the Age trial to investigate whether any differences in model predictions were related to variations in the number of mammograms.
We compared model outcomes to those from the trial at 10-year and 17-year follow-up, corresponding to the most recent analysis by the Age trial investigators [15]. The trial used ‘incidence based mortality’ to measure the effect of screening and treatment on breast cancer mortality. This implies, only counting cancer deaths that originated from cancers diagnosed during the intervention phase of the trial (ages 40 to 49). This is necessary because all women from both the intervention and control group ‘rolled’ into the national U.K. breast cancer screening program at age 50 and were invited to screening once every three years. For example, if at age 54 there would be fewer breast cancer deaths among women randomized to the intervention group than among the women in the control group, one could conclude that the intervention of annual screening in the forties effectively reduced breast cancer mortality at age 54. However, because all women ‘rolled’ into the national screening program at age 50, it may be the case that the breast cancer deaths prevented at age 54 were actually from breast cancers diagnosed by screening at age 50 as part of the national program and not by the trial’s annual screening intervention in the forties. Therefore, the trial and the models only used breast cancer deaths from cancers diagnosed during the intervention phase to measure the effect of annual screening in the forties on breast cancer mortality.
The confidence intervals associated with the mortality reduction observed in the Age trial at 10-and 17-year follow-up are useful as these are mainly influenced by the finite number of women included in the trial. The CISNET models have not included confidence intervals on their results given the millions of women simulated per trial arm. The model estimates will have a negligible range, given that the model outcomes are based on simulations of millions of women, each with varying combinations of variables constituting the life history, and sampled across the distribution of each variable. However, the model results do have uncertainty due to assumptions about unobservable parameters and structural uncertainties that are addressed. The use of multiple models provides a range of results that captures this structural uncertainty and could be considered to provide information comparable conceptually to a confidence interval.
Results
Breast cancer incidence
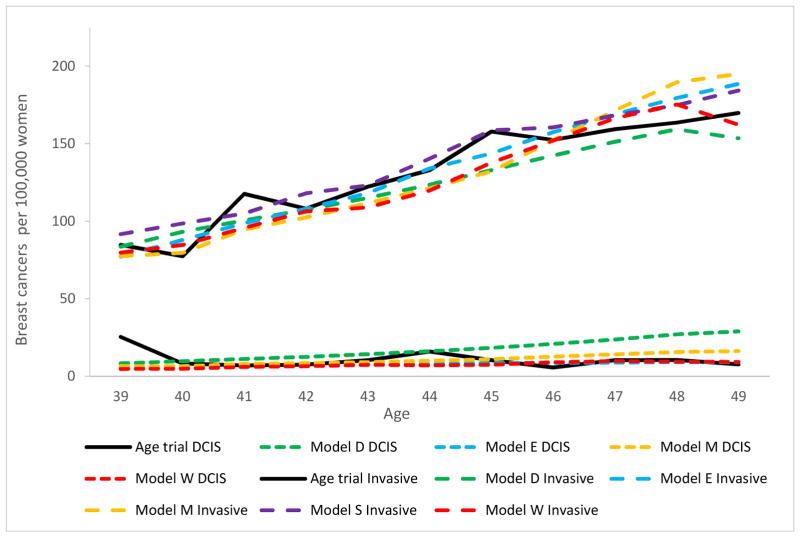
The average simulated invasive breast cancer incidence among women aged 40 to 49 in the control arm was 131 per 100,000 women (range across models 124 – 138) compared to 132 observed in the Age trial (Figure 1). The modeled ductal carcinoma in situ (DCIS) incidence was 11 per 100,000 women on average (range across models 7 – 17), and equivalent to the 11 per 100,000 observed in the Age trial.
Figure 1.
Control group breast cancer incidence (DCIS and invasive separately) per 100,000 women, compared to the Age trial.
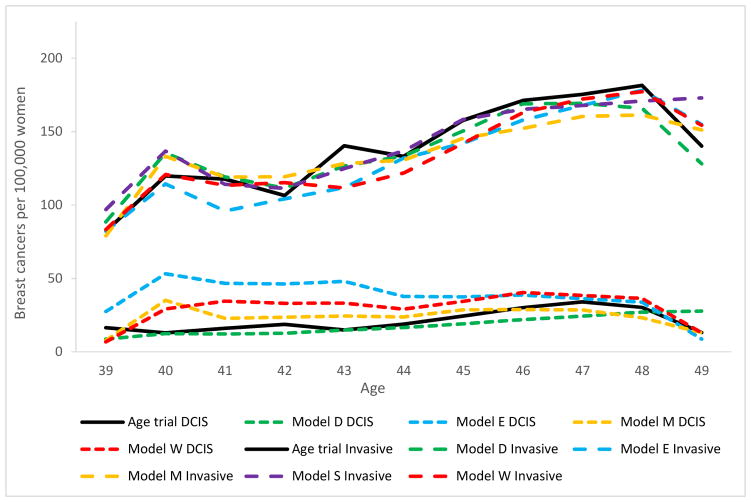
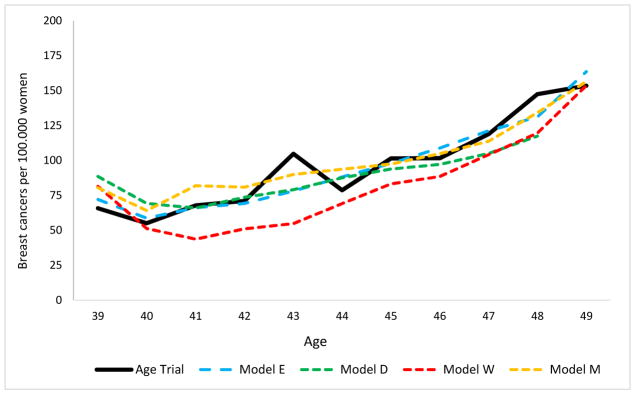
The average number of mammograms per woman in the intervention arm of the simulated trial was 5.2 (range across models 4.9 – 5.4) compared to 4.84 in the Age trial. Modeled invasive breast cancer incidence in the intervention arm increased by age and was an average of 135 per 100,000 among women aged 40 to 49 (range across models 131 – 141). This is consistent with the pattern for the 139 invasive breast cancers diagnosed per 100,000 women in the trial (Figure 2). DCIS intervention arm incidence varied more across the models (range 18 – 38) and with 27 diagnoses on average, higher than the 21 DCIS diagnoses per 100,000 women in the trial. Models with continuous tumor growth (Models E and W) and models with tumor inception prior to the start of the tumor’s sojourn time (Model E) tend to have the highest incidence of screen-detected DCIS.
Figure 2.
Intervention group breast cancer incidence (DCIS and invasive separate) per 100,000 women, compared to the Age trial.
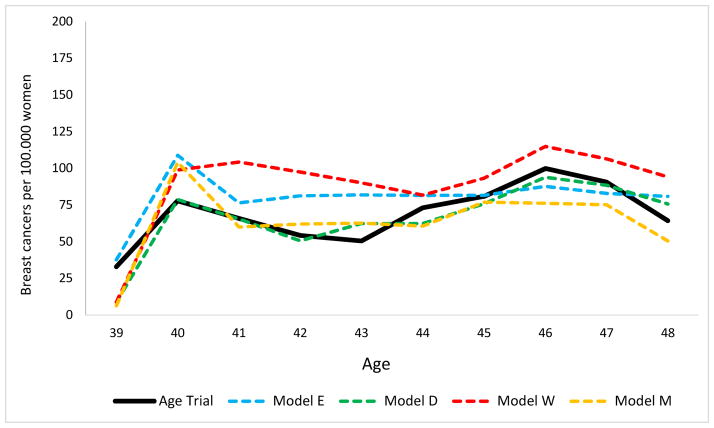
Both the model results and the observed Age trial data included a small peak (Figure 3) at age 40 in screen-detected breast cancers due to the detection of (prevalent) cases on the first mammogram, the only two-view mammogram in the trial with better sensitivity than subsequent screens (Table 4). This was the only age during the trial at which the rate of screen detected cancers was higher than the rate of clinically diagnosed cancers in the intervention group. The average rate of screen-detected DCIS and invasive breast cancers in the intervention arm in the age range 40 – 49 was 69 per 100,000 women in the Age trial, compared to the models’ average of 75 (range 63 – 89). The rate of clinically diagnosed cases (DCIS and invasive breast cancers) in the intervention arm was 97 in the trial and 93 in the models (range 82 – 99). Regardless of mode of detection, the rate of breast cancers diagnosed in the intervention arm between ages 40 – 49 was 161 per 100,000 women on average (range across models 154 – 169) and similar to 162 in the Age trial.
Figure 3.
Intervention group (screen detected) breast cancer incidence per 100,000 women. Screening ceased at age 48 in the Age trial.
Table 4.
Sensitivity of screening in the Age trial and in the models.
| First screen (two view mammography) | Subsequent screens (single view mammography) | |
|---|---|---|
| Age trial | 73.6 | 55.2 |
| Model D | 73.6 | 55.3 |
| Model E | 72.5 | 55.7 |
| Model M* | - | - |
| Model S | 75.5 | 59.0 |
| Model W | 67.7 | 59.6 |
Model M is a Bayesian without a natural history part and a woman’s disease status is unknown. As a result sensitivity is not applicable. Model M simulates screen- and clinically-detected incidences without knowing the true disease status.
Sensitivity of screening and screen detection is modeled differently in various models. In the continuous tumor growth models E, S, and W screen detection of tumors is simulated by transforming sensitivity to a threshold tumor size at which tumors can be screen detected. On the other hand, model D uses sensitivity of screening by simulating a shift to a less-advanced stage of breast cancer.
Breast cancer mortality
Among breast cancers diagnosed between ages 40 to 49, the Age trial found a total of 83 breast cancer deaths in the first 10 years of follow-up in the intervention arm (16 breast cancer deaths per 100,000 women) and 219 breast cancer deaths in the control arm (21 per 100,000 women). At 10-year follow-up, the rate of breast cancer deaths per 100,000 women predicted by the models was 20 on average (range across models 17 to 22) in the intervention arm, and 23 (range across models 20 to 25) in the control arm (Table 5). The number of breast cancer deaths predicted by the different models consistently somewhat higher in both arms than in the trial.
Table 5.
Breast cancer mortality outcomes at 10-years follow-up.
| Mammograms per woman | Breast cancer deaths per 100,000 women | Rate ratio BC deaths | Breast cancer ** mortality reduction | ||
|---|---|---|---|---|---|
| intervention group | control group | ||||
| Age trial | 4.84 | 16 | 21 | 0.75 | 25% (3 to 42%) * |
| Model average | 5.23 | 19 | 23 | 0.85 | 15.3% [range 13–17%] |
| Model D | 5.30 | 17 | 20 | 0.83 | 17.0% |
| Model E | 4.90 | 20 | 25 | 0.83 | 16.9% |
| Model M | 5.43 | 20 | 23 | 0.86 | 13.6% |
| Model S | 5.29 | 22 | 25 | 0.87 | 13.2% |
| Model W | 5.23 | 19 | 22 | 0.84 | 16.0% |
95% confidence interval in parentheses
The Age trial measured the effect of annual screening of women aged 40 to 49 on breast cancer mortality. Therefore, the trial and the simulation models excluded breast cancer deaths that occurred in women diagnosed with breast cancer before age 40 and after age 49.
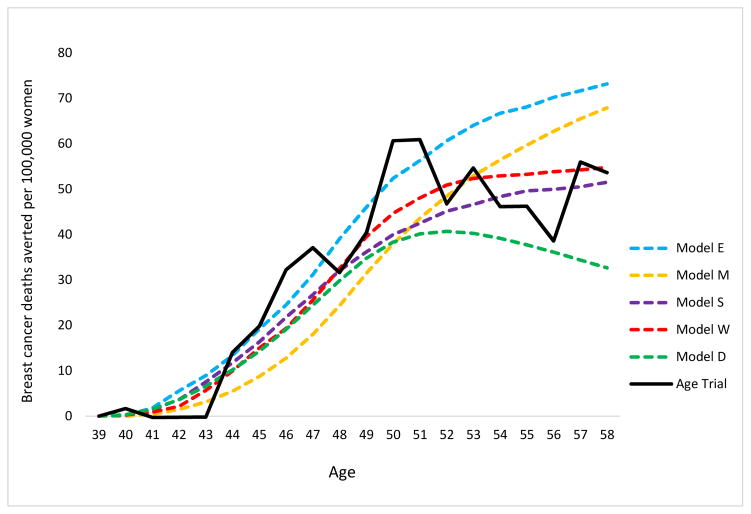
On average, the modeled breast cancer mortality reduction due to screening was 15% (range across models 13% to 17%) at 10-year follow-up vs. 25% (95% CI 3% to 42%) observed in the Age trial. At 17-year follow-up, the models predicted 13% (range across models 10 – 17%) breast cancer mortality reduction when restricted to breast cancer deaths that originated from breast cancers diagnosed during the intervention phase (incidence-based mortality) vs. 12% (95% CI -4% to 26%) observed in the trial (Table 6). The models with either tumor onset at tiny tumor sizes prior to the start of the sojourn time and on average slow tumor progression (Model E), or with tumor cure fractions for treatment benefit (Models E, M and W) maintained their 10-year follow-up breast cancer mortality reduction prediction at 17-year follow-up, whereas mortality reduction in the trial decreased. Similar to the Age trial, the models showed a turning point around age 50 where the increase in the cumulative number of breast cancer deaths averted started to diminish (Figure 5).
Table 6.
Breast cancer mortality outcomes at 17-years follow-up, restricted to breast cancer deaths that stem from cancers diagnosed during the intervention phase.
| Mammograms per woman | Breast cancer deaths per 100,000 women | Rate ratio BC deaths | Breast cancer ** mortality reduction | ||
|---|---|---|---|---|---|
| intervention group | control group | ||||
| Age trial | 4.84 | 19 | 22 | 0.88 | 12% (−4 to 26%) * |
| Model average | 5.23 | 20 | 23 | 0.87 | 13.2% [range 10 −17%] |
| Model D | 5.30 | 20 | 22 | 0.90 | 9.7% |
| Model E | 4.90 | 18 | 22 | 0.83 | 17.1% |
| Model M | 5.43 | 20 | 24 | 0.85 | 15.2% |
| Model S | 5.29 | 21 | 24 | 0.89 | 11.0% |
| Model W | 5.23 | 18 | 21 | 0.86 | 13.7% |
95% confidence interval in parentheses
Figure 5.
Cumulative breast cancer deaths averted per 100,000 women*.
*Cumulative breast cancer deaths averted only using breast cancer deaths from cancers diagnosed in the intervention period per 100.000 women. Calculated by the rate of breast cancer deaths in the control group minus the rate of breast cancer deaths in the intervention group.
Discussion
This is the first collaborative CISNET breast cancer study comparing model predictions to observed clinical trial results not used in the development of any model parameters. The results indicate that all five models estimate the long-term effect of annual screening between the ages of 40 to 49 well within the observed confidence intervals of the U.K. Age trial. The impact of screening on breast cancer mortality was also internally consistent with individual model structures regarding the natural history of breast cancer.
The ISPOR-SMDM Modeling Good Research Practices TaskForce-7 [1] states that predictive and external validation are the strongest forms of model validation as decision-makers can account for this information when considering model outcomes. In the past, the breast CISNET models have illustrated accurate predictions of molecular-subtype-specific and overall U.S. breast cancer incidence and mortality trends. [3, 4, 28] This study extends these prior cross-validations by independently estimating the observed results from a U.K. randomized controlled trial.
All models reproduced the trend in control group breast cancer incidence from ages 40 to 49, implying that the extant model structures and assumptions about the natural history of breast cancer in the absence of screening are reliable. Despite the intensive (annual) screening intervention, the models predicted more clinically diagnosed than screen-detected breast cancers in the intervention group. This was likely to be explained by the relatively low sensitivity of all subsequent single-view mammograms that followed after the more sensitive prevalent two-view mammogram, and the decrease in the number of women screened by screening round in the trial [18]. Although the models utilized different mechanisms such as a threshold tumor size (Models E, S, and W) or stage shift (Models D and M) to simulate screen detection of pre-clinical breast cancer, they were all able to accurately estimate the impact of screening from ages 40 to 49 on invasive breast cancer incidence.
The effect of screening and treatment on breast cancer mortality was underestimated by all models at 10-year follow-up compared to the reduction observed in the Age trial. Since all models accurately predicted breast cancer incidence, and the fact that the underestimation of the mortality reduction was present across all models, it might be explained by a common model input not related to screening. Specifically, the derived U.K. treatment dissemination may not represent the actual treatment received by women diagnosed with breast cancer in the trial. This is in line with the higher rate of breast cancer deaths predicted by the models in the control arm in the absence of screening.
After 10 years of follow-up, breast cancer mortality reduction observed in the trial decreased and lost significance, whereas most models predicted a fairly constant mortality reduction between 10- and 17-year follow-ups. Previous analysis of the CISNET models [29] illustrated that Model D, with tumor inception at the start of the sojourn time, has fast tumor progression on average, and Model E, with tumor inception prior to the start of the sojourn time, has the slowest tumor progression on average. These individual model structures affect the pattern in breast cancer deaths averted after age 49 when screening ceased, because cancers diagnosed in the control arm caused breast cancer death at a younger age in Model D and at a later age in Model E. Consequently, mortality reduction due to screening was greater at later ages (between 10- and 17-year follow-up) in Model E than in Model D. While the model structure of Model S is similar to that of Model E, Model S does not include DCIS, which implies no possible benefit in terms of mortality reduction from screen-detected DCIS. However, these otherwise screen-detected DCIS cases will likely be diagnosed as local stage small invasive tumors (size <1 cm.) in Model S with relatively high, and similar survival as DCIS cases. Model W is unique in that it simulates tumors with a limited malignant potential [25]. This may have resulted in a substantial amount of screen-detected tumors that did not cause breast cancer death during the 17-year follow-up. Consequently, Model W’s mortality reduction decreased slightly after age 49 despite their high rate of screen-detected cancers in the forties.
In summary, at 10- and 17-year follow-up, the models reproduced the effects of annual screening in the forties on breast cancer mortality well within the trial’s confidence intervals [15]. In terms of model validation, it can be questioned what these model outcomes imply, as it is quite common to have relatively wide confidence intervals in randomized trials on cancer screening. The wide confidence intervals in the trial are partly due to the limited number of women included and breast cancer deaths observed in the trial. The models’ outcomes may be less sensitive to the number of women that are simulated because they simulated at least 2 million women in each arm of the trial, notwithstanding the fact that the models are ultimately based on observed data as well.
The CISNET breast models used Age trial-specific model inputs and data sources applicable to the U.K., but we can still draw a comparison between the outcomes of this study and published results from a recent collaborative modeling study on screening in the United States [3]. In the U.S. study, we simulated annual screening from age 40 to 74 and compared it to annual screening from age 50 to 74. This implies that the difference in breast cancer deaths averted between these two scenarios over the women’s lifetime, is due to the effect of annual screening in the forties. Similar to the results of this analysis, the outcomes indicated that Model M and E avert the most breast cancer deaths from annual screening in the forties followed by Models W, S and D. In other words, the ranking of the models is fairly consistent when applied in another country with different model inputs.
This study presented the first external comparison performed by multiple breast cancer simulation models applied in a different country and setting. A strength of this analysis is that we used detailed observed de-identified trial data as model inputs. Another important strength is that we performed an independent external validation [1] in which no model calibration was performed to ensure credibility of the model outcomes.
Although the CISNET breast models used Age trial-specific model inputs and data sources applicable to the U.K., there were several limitations in this analysis. The trial did not collect data on breast cancer molecular sub-type and treatment, these were estimated based on U.K. data. It is possible that these data underestimated the actual treatment patterns of trial participants. That this is the case is suggested by the fact that all models had estimates for mortality reduction that were consistently lower than the point estimate from the trial. Moreover, when the models simulated the Age trial assuming all women received the most effective therapy available, the average model estimate was very close to trial result. [3] The lack of precision in being able to model the treatment of women in the Age trial is likely to have contributed more to the differences between model and trial results than the screening and natural history components of the models. Other limits include the fact that the models did not explicitly simulate screening in the control arm because the reported amount of unscheduled screening was low, and primarily due to symptomatic reasons. [17] While this may not affect conclusions of the simulations, it is a limitation.
The quantitative information in this study demonstrated how well the models reproduced the effects of annual screening from ages 40 to 49 on breast cancer incidence and mortality. In the future, the CISNET models could simulate the impact of what would have happened if two-view digital mammography had been used for all screening examinations in the Age trial, simulate the impact of different patterns of screening attendance, provide estimates on overdiagnosis, and estimate the lifetime effects of different screening programs offered to women in their forties. The demonstration that the models can reproduce observed external trial results should increase confidence in models results to inform policy decisions about breast cancer screening.
Figure 4.
Intervention group (clinically diagnosed) breast cancer incidence per 100,000 women.
Acknowledgments
The authors thank the Age trial investigators for providing de-identified Age trial data. The authors also acknowledge the contributions of Stephan W. Duffy to this project.
Support: This work was supported by the National Institutes of Health under National Cancer Institute Grants U01CA152958 and U01CA199218
Contributor Information
Jeroen J. van den Broek, Department of Public Health, Erasmus Medical Center, Rotterdam, the Netherlands
Nicolien T. van Ravesteyn, Department of Public Health, Erasmus Medical Center, Rotterdam, the Netherlands
Jeanne S. Mandelblatt, Department of Oncology, Georgetown-Lombardi Comprehensive Cancer Center, Georgetown University School of Medicine, Washington DC, USA
Hui Huang, Department of Biostatistics and Computational Biology, Dana-Farber Cancer Institute and Harvard Medical School Boston, Massachusetts, USA.
Mehmet Ali Ergun, Department of Industrial and Systems Engineering, University of Wisconsin-Madison, Wisconsin, USA.
Elizabeth S. Burnside, Department of Radiology, University of Wisconsin School of Medicine and Public Health, Madison, Wisconsin, USA
Cong Xu, Department of Radiology, School of Medicine, Stanford University, California, USA.
Yisheng Li, Department of Biostatistics, University of Texas M.D. Anderson Cancer Center, Houston, Texas, USA.
Oguzhan Alagoz, Department of Industrial and Systems Engineering, University of Wisconsin-Madison, Wisconsin, USA.
Sandra J. Lee, Department of Biostatistics and Computational Biology, Dana-Farber Cancer Institute and Harvard Medical School Boston, Massachusetts, USA
Natasha K. Stout, Department of Population Medicine, Harvard Medical School and Harvard Pilgrim Health Care Institute, Boston, Massachusetts, USA
Juhee Song, Department of Biostatistics, University of Texas M.D. Anderson Cancer Center, Houston, Texas, USA.
Amy Trentham-Dietz, Department of Industrial and Systems Engineering, University of Wisconsin-Madison, Wisconsin, USA.
Sylvia K. Plevritis, Department of Radiology, School of Medicine, Stanford University, California, USA
Sue M. Moss, Department of cancer prevention, Wolfson Institute, Queen Mary University of London, London, United Kingdom
Harry J. de Koning, Department of Public Health, Erasmus Medical Center, Rotterdam, the Netherlands
References
- 1.Eddy DM, Hollingworth W, Caro JJ, Tsevat J, McDonald KM, Wong JB, et al. Model transparency and validation: a report of the ISPOR-SMDM Modeling Good Research Practices Task Force-7. Med Decis Making. 2012;32(5):733–43. doi: 10.1177/0272989X12454579. [DOI] [PubMed] [Google Scholar]
- 2.Plevritis S, Munoz D, Kurian A, Alagoz O, Near AM, Stout NK, et al. Contributions of screening and systemic therapy to molecular subtype specific U.S. breast cancer mortality from 2000 to 2010. 2016 submitted. [Google Scholar]
- 3.Mandelblatt JS, Stout NK, Schechter CB, van den Broek JJ, Miglioretti DL, Krapcho M, et al. Collaborative Modeling of the Benefits and Harms Associated With Different U.S. Breast Cancer Screening Strategies. Ann Intern Med. 2016;164(4):215–25. doi: 10.7326/M15-1536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Berry DA, Cronin KA, Plevritis SK, Fryback DG, Clarke L, Zelen M, et al. Effect of screening and adjuvant therapy on mortality from breast cancer. N Engl J Med. 2005;353(17):1784–92. doi: 10.1056/NEJMoa050518. [DOI] [PubMed] [Google Scholar]
- 5.Siu AL On behalf of the U S. Preventive Services Task Force. Screening for Breast Cancer: U.S. Preventive Services Task Force Recommendation Statement. Ann Intern Med. 2016;164(4):279–96. doi: 10.7326/M15-2886. [DOI] [PubMed] [Google Scholar]
- 6.Mandelblatt JS, Near AM, Miglioretti DL, Munoz D, Sprague BL, Trentham-Dietz A, et al. Common Model Inputs used in CISNET Collaborative Breast Cancer Modeling Medical Decision Making. 2016 doi: 10.1177/0272989X17700624. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.van Ravesteyn NT, Miglioretti DL, Stout NK, Lee SJ, Schechter CB, Buist DS, et al. Tipping the balance of benefits and harms to favor screening mammography starting at age 40 years: a comparative modeling study of risk. Ann Intern Med. 2012;156(9):609–17. doi: 10.1059/0003-4819-156-9-201205010-00002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Independent U K. Panel on Breast Cancer Screening. The benefits and harms of breast cancer screening: an independent review. Lancet. 2012;380(9855):1778–86. doi: 10.1016/S0140-6736(12)61611-0. [DOI] [PubMed] [Google Scholar]
- 9.American College of O-G. Practice bulletin no. 122: Breast cancer screening. Obstet Gynecol. 2011;118(2 Pt 1):372–82. doi: 10.1097/AOG.0b013e31822c98e5. [DOI] [PubMed] [Google Scholar]
- 10.Oeffinger KC, Fontham ET, Etzioni R, Herzig A, Michaelson JS, Shih YC, et al. Breast Cancer Screening for Women at Average Risk: 2015 Guideline Update From the American Cancer Society. JAMA. 2015;314(15):1599–614. doi: 10.1001/jama.2015.12783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sprague BL, Gangnon RE, Burt V, Trentham-Dietz A, Hampton JM, Wellman RD, et al. Prevalence of mammographically dense breasts in the United States. J Natl Cancer Inst. 2014;106(10) doi: 10.1093/jnci/dju255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Anders CK, Fan C, Parker JS, Carey LA, Blackwell KL, Klauber-DeMore N, et al. Breast carcinomas arising at a young age: unique biology or a surrogate for aggressive intrinsic subtypes? J Clin Oncol. 2011;29(1):e18–20. doi: 10.1200/JCO.2010.28.9199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Boyd NF, Guo H, Martin LJ, Sun L, Stone J, Fishell E, et al. Mammographic density and the risk and detection of breast cancer. N Engl J Med. 2007;356(3):227–36. doi: 10.1056/NEJMoa062790. [DOI] [PubMed] [Google Scholar]
- 14.Moss SM, Cuckle H, Evans A, Johns L, Waller M, Bobrow L, et al. Effect of mammographic screening from age 40 years on breast cancer mortality at 10 years' follow-up: a randomised controlled trial. Lancet. 2006;368(9552):2053–60. doi: 10.1016/S0140-6736(06)69834-6. [DOI] [PubMed] [Google Scholar]
- 15.Moss SM, Wale C, Smith R, Evans A, Cuckle H, Duffy SW. Effect of mammographic screening from age 40 years on breast cancer mortality in the UK Age trial at 17 years' follow-up: a randomised controlled trial. Lancet Oncol. 2015;16(9):1123–32. doi: 10.1016/S1470-2045(15)00128-X. [DOI] [PubMed] [Google Scholar]
- 16.Moss S, Thomas I, Evans A, Thomas B, Johns L Trial Management G. Randomised controlled trial of mammographic screening in women from age 40: results of screening in the first 10 years. Br J Cancer. 2005;92(5):949–54. doi: 10.1038/sj.bjc.6602396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kingston N, Thomas I, Johns L, Moss S Trial Management G. Assessing the amount of unscheduled screening ("contamination") in the control arm of the UK "Age" Trial. Cancer Epidemiol Biomarkers Prev. 2010;19(4):1132–6. doi: 10.1158/1055-9965.EPI-09-0996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Johns LE, Moss SM Trial Management G. Randomized controlled trial of mammographic screening from age 40 ('Age' trial): patterns of screening attendance. J Med Screen. 2010;17(1):37–43. doi: 10.1258/jms.2010.009091. [DOI] [PubMed] [Google Scholar]
- 19.Johns LE, Moss SM Age Trial Management G. False-positive results in the randomized controlled trial of mammographic screening from age 40 ("Age" trial) Cancer Epidemiol Biomarkers Prev. 2010;19(11):2758–64. doi: 10.1158/1055-9965.EPI-10-0623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Moss S. A trial to study the effect on breast cancer mortality of annual mammographic screening in women starting at age 40. Trial Steering Group. J Med Screen. 1999;6(3):144–8. doi: 10.1136/jms.6.3.144. [DOI] [PubMed] [Google Scholar]
- 21.van den Broek JJ, van Ravesteyn NT, Heijnsdijk EA, de Koning HJ. Estimating the effects of risk-based screening and adjuvant treatment using the MISCAN-Fadia continuous tumor growth model for breast cancer. Medical Decision Making. 2016 submitted. [Google Scholar]
- 22.Munoz D, Xu C, Plevritis S. A Molecular Subtype-Specific Stochastic Simulation Model of US Breast Cancer Incidence and Mortality Trends from 1975 to 2010 Medical Decision Making. 2016 doi: 10.1177/0272989X17737508. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lee SJ, Li X, Huang H. Assessment of Screening Strategies for Breast Cancer: Model-Based Approaches Medical Decision Making. 2016 submitted. [Google Scholar]
- 24.Huang X, Li Y, Song J, Berry DA. The MD Anderson CISNET Model for Estimating Benefits of Adjuvant Therapy and Screening Mammography for Breast Cancer: An Update. Medical Decision Making. 2016 submitted. [Google Scholar]
- 25.Alagoz O, Ergun MA, Cevik M, Sprague BL, Fryback DG, Gangnon R, et al. The University Of Wisconsin Breast Cancer Epidemiology Simulation Model: An Update (Medical Decision Making. 2016 doi: 10.1177/0272989X17711927. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.National Health Service. Breast Screening Programme & British Association of Surgical Oncology. Audit of screen detected breast cancers. 2000–2007 doi: 10.1002/bjs.4013. [DOI] [PubMed] [Google Scholar]
- 27.Early Breast Cancer Trialists' Collaborative G. Peto R, Davies C, Godwin J, Gray R, Pan HC, et al. Comparisons between different polychemotherapy regimens for early breast cancer: meta-analyses of long-term outcome among 100,000 women in 123 randomised trials. Lancet. 2012;379(9814):432–44. doi: 10.1016/S0140-6736(11)61625-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mandelblatt JS, Cronin KA, Bailey S, Berry DA, de Koning HJ, Draisma G, et al. Effects of mammography screening under different screening schedules: model estimates of potential benefits and harms. Ann Int Med. 2009;151:738–47. doi: 10.1059/0003-4819-151-10-200911170-00010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.van den Broek JJ, van Ravesteyn NT, Cevik M, Schechter CB, Lee SJ, Munoz D, et al. Comparing CISNET breast cancer models using Maximum Clinical Incidence Reduction methodology. Medical Decision Making. 2016 doi: 10.1177/0272989X17743244. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Barbieri, Magali, et al. Data Resource Profile: The Human Mortality Database (HMD) International Journal of Epidemiology. 2015;44(5):1549–1556. doi: 10.1093/ije/dyv105. [DOI] [PMC free article] [PubMed] [Google Scholar]