COMMON MODEL INPUTS USED IN CISNET COLLABORATIVE BREAST CANCER MODELING

Abstract

Since their inception in 2000, the Cancer Intervention and Surveillance Network (CISNET) breast cancer models have collaborated to use a nationally representative core of common input parameters to represent key components of breast cancer control in each model. Employment of common inputs permits greater ability to compare model output than when each model begins with different input parameters. Use of common inputs also enhances inferences about the results, and provides a range of reasonable results based on variations model structure, assumptions, and methods of use of the input values. The common input data are updated for each analysis to ensure that they reflect the most current practice and knowledge about breast cancer. The common core of parameters includes population rates of births and deaths; age- and cohort-specific temporal rates of breast cancer incidence in the absence of screening and treatment; effects of risk factors on incidence trends; dissemination of plain film and digital mammography; screening test performance characteristics; stage or size distribution of screen-, interval-, and clinically- detected tumors by age; the joint distribution of ER/HER2 by age and stage; survival in the absence of screening and treatment by stage and molecular sub-type; age-, stage-, and molecular subtype-specific therapy; dissemination and effectiveness of therapies over time; and competing non-breast cancer mortality. In this paper we summarize the methods and results for the common input values presently used in the CISNET breast cancer models, note assumptions made because of unobservable phenomena and/or unavailable data, and highlight plans for development of future parameters. These data are intended to enhance the transparency of the breast CISNET models.

INTRODUCTION

A key feature of the Cancer Intervention and Surveillance Network (CISNET) collaborative modeling approach is the shared use of a common set of input values. Employment of common model inputs permits greater ability to compare model output than when each model begins with different parameters. Use of common inputs also enhances the ability to more directly compare trends in results across models, strengthens inferences about the results, and provides a range of reasonable results based on variations in model structure, assumptions, and methods of use of the input values. Further, sharing a common core of inputs is efficient and facilitates examination of intermediate outputs to trouble-shoot and identify model program or processing errors that can otherwise be difficult to detect. Experience from weather and climate predictions has shown that a combination of several different models often gives better prediction than any single model.(1) Hence, the median and range of results for several models based on the same input data should provide greater confidence in results than those from any single individual model.

In this chapter we summarize the methods and results for the common input values presently used in the CISNET breast cancer models to estimate trends in US breast cancer incidence and mortality, note how the data is organized, and highlight future parameters being developed to expand the library of data to address evolving topics, such as genomics in cancer care.

COMMON PARAMETERS

This section summarizes the approach and data used for common data parameters used in the most current breast CISNET models. There are presently six models: Model D (Dana-Farber); Model E (Erasmus), Model GE (Georgetown-Einstein), Model M (MD Anderson), Model S (Stanford), and Model W (Wisconsin-Harvard). (2–8)

Common parameters were developed for the majority of model inputs, including: US population rates of births and deaths; age- and cohort-specific temporal data for breast cancer incidence in the absence of screening and treatment; effects of risk factors on incidence trends; dissemination of plain film and digital mammography; screening test performance characteristics; stage or size distribution of screening-, interval-, and clinically- detected tumors by age; the joint distribution of breast cancer molecular subtype based on estrogen receptor (ER) and human epidermal growth factor 2 (HER2) biomarkers by age and stage; survival in the absence of screening and treatment by stage and molecular sub-type; age-, stage-, and molecular subtype-specific therapy; dissemination and effectiveness of treatment modalities over time; and competing non-breast cancer mortality. Based on the goals of any given analysis, there are also common inputs available for age- and gender-specific utilities and costs for model health states. The models either used the common input parameters directly, or as a calibration target depending on individual model structures (Table 1).

Table 1.

Summary of Use of Common Input Parameters by Model

Common Parameter	Description	Use of Parameter by Model
		Model D	Model E	Model GE	Model M	Model S	Model W
Birth cohorts	Life tables of US births and deaths
Incidence in the absence of screening	Age-period-cohort model(s)	Used directly	Calibration target	Used as starting point of calibration to incidence	Does not use an APC model; samples from a a prior distribution of rates, where rates are based on observed incidince and mammography use. This yields a 0.3–0.6% linear increase per year over 1975 incidence	Modified APC model explicitly considering hormone replacement	Calibration target
Mammography rates	Age at first screen based on National Health Interview Survey data and intervals between screens from BCSC	Used directly	Used directly	Used directly	Used directly	Used directly	Used directly
Mammography performance	Sensitivity of initial and subsequent digital mammography by age group and screening interval (BCSC)	Used directly	Used to derive tumor size threshold for screen detection	Calibration target; probability of detection within preclinical detectable period when cancer present; probability of negative screen when no cancer present	Uses cancer detection rates as prior probability of detection	Calibration target for detection based on tumor size	Calibration target
Stage distribution	Stage distribution (and tumor size) by mode of detection, age group (<50, 50–64, ≥65 years), screening round (first, subsequent), and interval between screens (BCSC)	AJCC 6 stage data used directly	Tumor size data used directly	AJCC 6 stage data used directly	Used to construct prior probability	SEER stage (local, regional, distant) used directly	SEER stage (DCIS, local, regional, distant) used directly
ER/HER2 joint distribution	The probability of ER/HER2 conditional on age and stage/tumor size at diagnosis (BCSC)	Used directly	Used directly	Used directly	Used to construct prior probability	Used directly	Used directly
Treatment patterns	Treatments and rates of use by time period. ER/HER2, stage, and age	Used directly	Used directly	Used directly	Used to construct prior probability	Used directly	Used directly
Survival in the absence of screening and treatment	26-year breast cancer survival before adjuvant treatment by joint ER/HER2 status, age group, AJCC/SEER stage or tumor size	Used directly	Used directly	Used directly	Used to construct prior probability	Used directly	Used directly
Treatment effects	Meta-analyses of clinical trial results by ER/HER2	Used directly to reduce the hazards of death from breast cancer	Cured vs. not based on being below or above a fatal diameter at detection	Used directly to reduce the hazards of death from breast cancer	Used to construct prior probability for hazards of death and cure disease	Used directly to reduce the hazards of death from breast cancer	Used directly to reduce hazards of death and cure disease
Other-cause mortality	Age- and cohort-specific allcause mortality rates by year	Used directly as a competing risk	Used directly as a competing risk	Used directly as a competing risk	Used directly as a competing risk	Used directly as a competing risk	Used directly as a competing risk

Model D (Dana-Farber); Model E (Erasmus), Model GE (Georgetown-Einstein), Model M (MD Anderson), Model S (Stanford), and Model W (Wisconsin-Harvard) BCSC is the Breast Cancer Screening Consortium; de-identified data provided via personal communication under BCSC data use agreements.

The common inputs are used with model-specific parameters related to unobservable aspects of breast cancer history (e.g., tumor growth, proportions and types of tumors that are non-progressive, sojourn time, lead-time, and how systemic therapy affects survival); these are described elsewhere. (2–8)

To ensure that the models reflect current knowledge, common parameters were estimated from the highest quality and most current nationally representative data from published studies, studies in progress, and current disease registries such as the Surveillance, Epidemiology, and End Results (SEER) program. (9) Older studies and registries are used as pertinent to informing inputs, especially trends pre-dating widespread mammography use or discovery of systemic adjuvant treatments. In this context, when considering data sources for common parameters, CISNET uses the hierarchy of evidence promoted by the U.S. Preventive Services Task Force to select the highest quality available data for a given parameter and research question,(10) including randomized-controlled trials, meta-analyses, observational studies, and registries (11) and surveys. Data were selected to derive inputs that were independent of the model outputs. For example, since the models were designed in part to estimate the impact of screening on breast cancer mortality, data from randomized trials on screening effects were not used as direct parameter inputs.

US Population Births and Deaths

To represent the current female population in the United States, the models incorporate population counts by single year of age from 1975 to 2011. Census data is abstracted from two sources based on time period: 1975–1989 (12) and 1990–2011.(13) Population counts are provided by single year of age (up to age 85) and calendar year.

Incidence in the Absence of Screening and Treatment

In the absence of a non-screened reference population, US breast cancer incidence without screening is estimated from the observed time trends before and after screening introduction. Breast cancer risk increases with age, and varies by birth cohort (e.g., based on differences in life style factors).(14–16) Age–period–cohort (APC) modeling is a statistical approach to determine the underlying incidence of disease by age, year of diagnosis (period), and year of birth (cohort), considering the effects of use of interventions such as mammography screening, and trends in risk factors across time and cohorts. (17–20)

The majority of the CISNET breast models originally used an APC model of breast cancer incidence from 1975 to 2000 developed by Holford and colleagues.(21) While observed incidence reported to SEER increased over that period, after 2000 there was a substantial decline that has been attributed, in part, to changes in patterns of post-menopausal hormone use.(22) Thus, the models could not simply continue to use linear extrapolations forward in time from the original APC model, so new APC models were developed.

For one of these APC models, the original Holford APC model was revised and extended through 2010. A detailed review of the methods has been summarized by Gangnon et al. (23) Briefly, beyond temporal extension, the Gangnon APC model accounts for differential incidence of invasive and ductal carcinoma in situ (DCIS), the explicit effect of postmenopausal hormone use by menopausal status, and varying assumptions about the effect of screening by cohort and time period.(23) For practical reasons, variations in incidence due to hormone use were included in the time period effect. Since a linear increase in incidence over time could be explained by either period or cohort effects, Gangnon et al attributed these changes to cohort effects. Mammography screening became widespread in the US around 1982 and began to impact the observed breast cancer incidence trends shortly thereafter. Therefore, the model added a second period function for women of the various birth cohorts who were ages 40 and older in 1982, and would have been exposed to screening.

Age, period, and cohort effects are likely to vary gradually by time, and smoothing the year-to-year variations limits the number of parameters that need to be estimated. Smoothed age, period and cohort effects were estimated using natural cubic splines. The degree of smoothing was chosen by best fitting values according to the Bayesian Information Criterion. With cohort effects estimated separately pre- and post-menopause, a weighted average of the pre- and postmenopause cohort effects was used in the 46 to 54 years age span.

The overall (invasive and DCIS) breast cancer incidence in the absence of mammography screening for nine SEER registries combined and as estimated by this revised APC model is presented in Figure 1. The green line represents observed SEER breast cancer incidence. The blue line represents the estimated incidence in the absence of mammography screening from the APC model, and the orange line represents the estimated incidence with mammography screening from the APC model. The two estimates are identical until 1982, the date of introduction of mammography screening in the APC model. The estimated incidence in the absence of mammography screening only increased slightly after 1982, from 243.1 cases per 100,000 women in 1985 to 259.5 in 2010, while the estimated incidence with mammography screening increased dramatically from 274.8 in 1985 to 337.4 in 2010, with a large proportion of the additional cases (82%) being DCIS. One implication of this result is that mammography screening is accompanied by a sizable over-diagnosis rate. Another important implication of this result is that the method used by each breast model to portray age-period-cohort incidence in the absence of screening affects model differences in over-diagnosis rates. (24)

Figure 1.

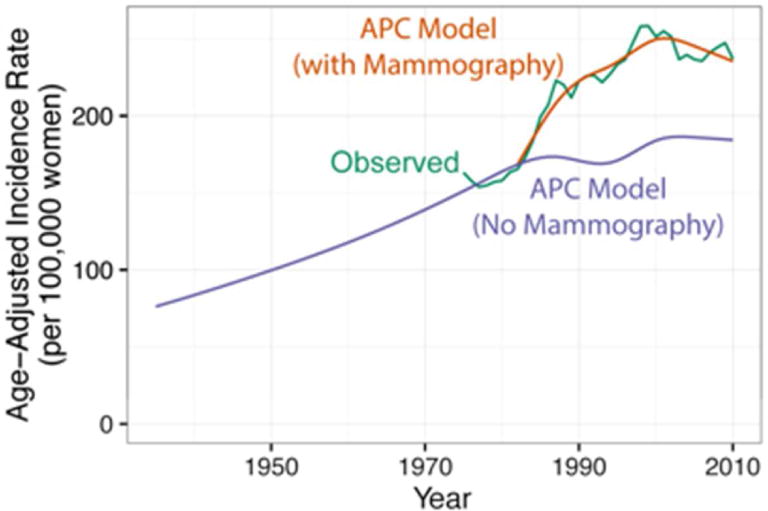
Age-adjusted overall breast cancer incidence rates per 100,000 women for ages 25 to 84 years. Incidence rates from the age-period-cohort (APC) model estimated with (orange line) and without (blue line) the mammography screening period effect. The green line is observed SEER incidence based on data from nine SEER Registries, 1935–2010. Adapted from Gangnon et al. (23)

Four of the six models used the Gangnon APC model as an input or calibration target to estimate the counterfactual underlying breast cancer incidence rates in the absence of screening from 1975 to 2010. Model S developed a similar, but more integrated approach combining CISNET model fitting, hormone therapy effects estimation, and APC estimation. Model M extended 1975–79 SEER rates forward in time with comparatively lower temporal increases.

All six models closely replicate observed US incidence rates regardless of their individual method of implementation of this common input parameter. (25, 26) However, differences in assumptions about the underlying incidence and the impact of screening on incidence rates contribute to variability in model results for the absolute rates of mortality reduction attributable to screening and estimates of over-diagnosis.(25, 26) Prediction of future incidence trends are accompanied by large uncertainties, but APC models have been shown to provide better predictions than assuming a constant incidence rate over time.(27)

Risk Factors Affecting Incidence

The models focus primarily on average US populations. However, in selected analyses two to three models have collaborated to examine the impact of breast cancer risk factors and changes in their prevalence on incidence rates, mortality outcomes, and/or ranking of screening schedules.(24, 25, 28–36) The risk factors that have been considered to date include postmenopausal hormone therapy, obesity, family history of a first-degree relative with breast cancer, and breast density.

These factors were chosen since they are common exposures (two with secular changes in prevalence), are clearly related to breast cancer risk (e.g., obesity increases post-menopausal breast cancer rates), and/or related to screening performance (e.g., breast density, hormone therapy) and treatment effectiveness (e.g., obesity can reduce effectiveness based on dose reductions). Prevalence estimates of these key breast cancer risk factors over time were developed using National Health Interview Survey (NHIS), the Breast Cancer Surveillance Consortium (BCSC), and other sources. (28–32) Prevalence estimates were generally provided for all four factors by single year of age (25–100) for the calendar years 1970–2020. Prevalence of body mass index (BMI) according to calendar year and age was provided in three categories (<25, 25–29.9, and 30+ kg/m²) from NHANES. (33) Relative risks of breast cancer according to these three BMI categories, menopausal status, hormone use, and breast cancer subtype were derived from a meta–analysis.(28)

Prevalence of breast density was calculated in four Breast Imaging Reporting and Data System (BI–RADS) categories by age and BMI based on data provided by the BCSC (unpublished data). Calendar year estimates were not provided since the distribution of breast density appears to have remained relatively constant over time within age and BMI groups. Relative risk of breast cancer according to breast density and age were based on BCSC data (Table 2). (24)

Table 2.

Relative Risk of Invasive Breast Cancer by Breast Density and Age and Prevalence of Density by Age Group

Age Group	BI-RADS Density	Breast Density–Related Risk*	Prevalence of Density Level within Age Group
40–49	A	0.37	0.05
	B	0.72	0.35
	C	1.16	0.46
	D	1.46	0.13
50–64	A	0.50	0.09
	B	0.84	0.46
	C	1.25	0.38
	D	1.53	0.07
65–74	A	0.61	0.13
	B	0.94	0.53
	C	1.28	0.31
	D	1.45	0.03

Note: the base models include average population density. When density is explicitly included for specific analyses, these data are used to modify incidence. In density-specific analyses, density also modifies mammography performance.

^*Referent group is average population density

Density a refers to entirely fatty; b to scattered density; c to heterogeneously dense, and d to extremely dense

Source: Breast Cancer Surveillance Consortium. (24)

Screening Test Performance

The Breast Cancer Surveillance Consortium (BCSC) provided screening performance data. (11) While only covering certain geographic regions, and over-representing women who present for screening, the BCSC is the oldest, and largest network of breast imaging registries in the US, with data on more than 10.3 million mammography examinations from six breast active imaging registries with linked data on demographics, risk factors, mammography reports, diagnostic evaluations, tumor and/or pathology registries, and vital statistics. As such, the BCSC provides an unprecedented source of data not available from any other data source.

Observed film-screen and digital screening mammography performance data from the BCSC were used to develop age-specific parameters for the detection of DCIS and invasive cancer (Model S uses only data for invasive cancers). Film-screen screening mammography performance measures were used up through 2002, and digital screening mammography performance measures were used for 2003 and later.

BCSC provided sensitivity, specificity, screen detected cancer, rate and interval invasive cancer rate based on BI-RADS^® (37) assessment categories for mammography results (1=negative, 2=benign, 3=probably benign, 0=needs additional evaluation, 4=suspicious, 5=highly suggestive of malignancy). A positive screen was considered as a BI-RADS assessment of 0, 4, or 5; a negative screen included initial assessments of 1, 2, or 3. Starting with the BIRADS 5^th edition (38) in late 2013 an assessment of 3, which typically resulted in a recommendation for short-interval follow-up, was also considered positive; this change will be reflected in future analyses.

A positive screen was defined as a false positive if no breast cancer was diagnosed within 12 months and as a true positive if cancer was diagnosed within 12 months. A negative exam was considered a true negative if no breast cancer was diagnosed within 12 months and a false negative if cancer was diagnosed within 12 months. The screen-detected cancer rate was the rate of cancers detected within 12 months of a positive exam. An interval invasive cancer was an invasive cancer diagnosed within 1 year of a negative screen. The follow-up period was truncated at the next screen if it occurred within 9–11 months; thus, a cancer diagnosis was only associated with the most recent screen for calculating performance measures.

Using these definitions, point estimates and 95% confidence intervals for sensitivity, specificity, and cancer rates were estimated using logistic regression models including age group and screening interval. Separate regression models were used for initial and subsequent mammography and for invasive cancer vs. DCIS. Sensitivity and specificity have also been calculated by breast density in prior analyses. (25)

The models incorporate these performance data in different manners based on how they depict natural history and cancer detection (Table 1). (2–8) Briefly, one model (D) used these data directly as input variables. (6) In three models (Models GE, S, and W) these data were used as calibration targets to estimate the probability of detection when there is a pre-clinical detectable cancer present in the sojourn time at the time of screening and the probability of a negative screen when there is no pre-clinical detectable cancer present within the sojourn time period when screening occurs. (2, 3, 5) Model M used the cancer detection rates (4) as a calibration target and the last model, model E, (7) fit estimates of tumor size detection thresholds from this and other sources.

Screening Dissemination

When the breast models are evaluating the efficacy of specific screening scenarios, such as annual or biennial screening, they assume 100% of women obtain all screening tests as prescribed in the scenario. However, in analyses to estimate the impact of screening on population incidence and mortality rate, the models use a common input to quantify actual US screening practices over time. In previous CISNET analyses, Cronin et al. modeled US mammography screening dissemination from 1975 to 2000. (39, 40) Recently, the dissemination parameter was extended to 2010. The methods to develop (and extend) the estimation of screening dissemination are summarized here; detailed descriptions have been published elsewhere. (39, 40) Briefly, the dissemination estimation process was based on two distinct statistical models: one to estimate the time of a woman’s first mammography exam based on her age and birth cohort and calendar year and another to reflect the patterns of use of exams following the initial mammography. The two statistical models were then combined to generate screening exam histories for individual women. The CISNET models used this screening history until a woman stopped screening, developed breast cancer, or died of other causes.

Data from the National Health Information Survey (NHIS) were used to first estimate the cumulative distribution for the time to first mammogram for each birth cohort using crosssectional estimates of the percentage of the population that reported ever having a mammogram from the 1987, 1990, 1992, 1993, 1994, 1998, and 2000 surveys. (41) For women born prior to 1948, estimates of the proportion of women in a particular birth cohort having their first mammogram between two NHIS surveys was computed by subtracting the proportion reporting ever having a mammogram in the earlier survey from the proportion reported in the later survey. Since the observed data could be used to construct only a portion of the life history from 1987 to 2000, a dissemination of innovations model was fitted to extrapolate the curve for the entire life history of age at first mammography for each birth cohort.

NHIS data from 2003, 2005, 2008, and 2010 were recently added to reflect mammography dissemination and patterns among birth cohorts born after 1948. These women would have turned age 40 in 1988 or later when mammography was commonly used for screening. For these cohorts, NHIS data indicated that age rather than birth cohort or calendar year was the primary factor that determined when a woman received a first mammogram. Therefore, NHIS data from after 2000 was combined to estimate a distribution curve for the age of first mammogram.

The statistical models used to develop the mammography dissemination parameter assumed that some women never received a mammogram and that no screening occurred before 1980 or before age 30. It also assumed that women did not obtain a first mammogram after age 63. Analyses were adjusted for the significant amount of diagnostic mammography prior to age 40 since the NHIS data does not distinguish between screening and diagnostic mammography. (42) Thus, 48% of women ages 30–34 that reported a first screening exam were assumed to have a screening exam (and 52% diagnostic), and 84% of those 35–39 who reported a first screening exam were assumed to have a screening exam. No further adjustment for screening vs. diagnostic mammography was made for ages 40 and older, since at this point a woman was likely to have had multiple screening mammograms and it was not possible to estimate an adjustment factor to distinguish screening vs. diagnostic examinations. A linear trend was fit to the data for age at first screening examination for ages 30–35 and 35–40 and a logistic survival curve for ages 40+. The distribution curve included a jump at age 36 and age 40, since the data indicated a large percent of women began screening at those specific ages. Distribution curves were estimated for all races combined and for white and black women separately.

To model time between screening exams, we used individual-level longitudinal data from the BCSC. (39, 40) Three general groups of screeners were defined a priori to represent regular annual screeners (women with a mean time between screening exams of ≤ 1.5 years), biennial screeners (women with a mean time of 1.5 – 2.5 years), and irregular screeners (women with a mean time of >2.5 years) (Figure 2a). These groups represented targets to which the dissemination model was fitted, rather than direct inputs.

Figure 2. Mammography Use of Time.

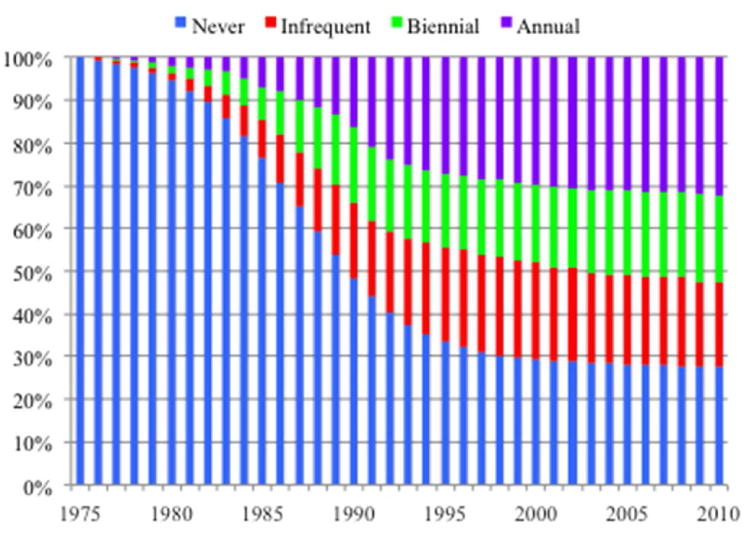
Panel A. The use of screening (annual, every two years, irregular, and never) among women ages 30–79 by calendar year. These observed data were used a targets in modeling dissemination of screening and intervals between screens. Note that the rate of never screened includes women ages 30–39.

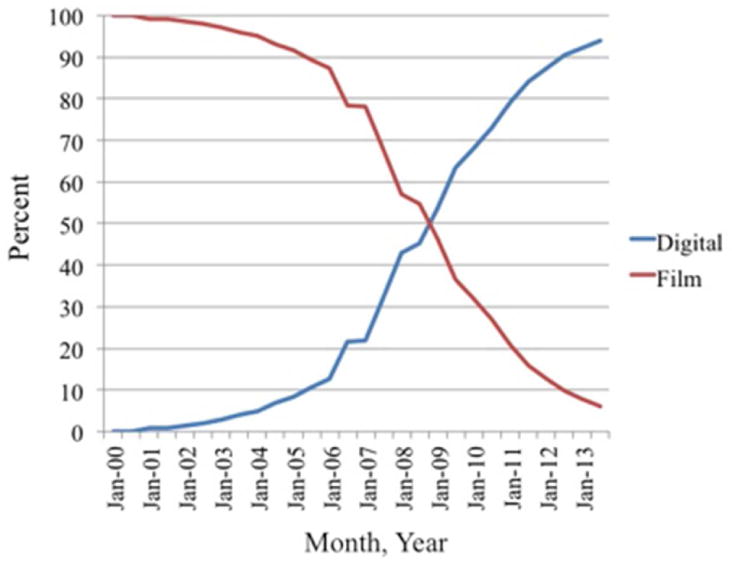
Panel B. The percent of total mammograms performed in the US that were digital vs. plain film by calendar year. Source: Breast Cancer Surveillance Consortium (BCSC, unpublished data) and the FDA’s Mammography Quality Standards Act and Program. (43)

Next, stratified survival analyses with event times defined as the time between subsequent screening mammograms were then performed using gamma frailty models for each group to account for correlations between multiple intervals for one woman. Women could maintain a schedule or change schedule depending on their age. For example, a woman could be an annual screener from ages 40–49, and then a biennial screener after age 50, and become an irregular screener at age 75.

Based on observed patterns of care from the FDA Mammography Quality Standards Act and Program (43) and the BCSC (unpublished data) for the rapid diffusion of digital mammography, mammograms were assumed to be plain-film until 2002 and digital thereafter (Figure 2b).

Characteristics of Cancers by Mode of Detection

To estimate the breast cancer stage of screened and unscreened women, the models incorporate data from the BCSC (unpublished data). The stage (American Joint Committee on Cancer [AJCC v. 6] (44) and SEER) and tumor size (<2, 2–5, 5+ cm) distribution of clinically-, interval- and screen-detected cancers by age group (<50, 50–64, 65+) uses data from 1994–2013 for film-screen mammography and 2003–2013 for digital mammography. The first year of the transition to digital mammography (2002) was excluded to ensure data completeness at reporting facilities. Among screen-detected women, the data are also stratified by first vs. subsequent screen and screening interval (e.g., annual, biennial, irregular). The definitions of screen, interval, and clinical mode of detection for these parameters are summarized on Table 4.

Table 4.

Definitions of Breast Cancer Mode of Detection

Mode of Detection	Definition
Screen-detected	Cancer diagnosed within 12 months after a positive screen and prior to the next screening mammogram (with and without self-reported symptoms)
Interval-detected*	Cancer diagnosed within 6 months after or 30 days before a diagnostic mammogram, with a screening mammogram within 42 months prior to that mammogram
Clinical-detected	A diagnostic mammogram between 6 months prior to and 30 days after the cancer diagnosis and no prior mammogram within 3.5 years (42 months) of the diagnostic mammogram

^*Note that the definition of interval cancer varies from that used to determine screening performance.

To model the four molecular subtypes of breast cancer characterized by ER and HER2 status, joint prevalence estimates of ER and HER2 status by age and stage at clinical detection were derived from BCSC data. We make the simplifying assumption that screen- and interval-detected lesions have the same joint distribution of ER and HER2 as clinically detected cases, because HER2 has not been collected in registries until recently, leading to insufficient data to determine joint distribution by mode of detection. As more HER2 data become available, this parameter will be updated for future analyses.

Treatment Dissemination

The survival data used in the models assume all women receive local treatment by stage (surgery and/or radiation) but to date these initial therapies have not been modeled explicitly. The models use two common parameters to incorporate the effects of adjuvant chemotherapy and/or hormonal therapy. The first depicts temporal changes in availability and use of different regimens over time and the second provides the modelers with the effectiveness of each potential systemic therapy combination.

Treatment dissemination for the period from 1975–1996 was derived from US adjuvant treatment patterns by age, calendar year, ER (and HER2 in 2006) based on SEER special patterns of care studies. (45, 46) For analyses that included the period after 1996, the models used National Comprehensive Cancer Network (NCCN) data for 1997–2010. (47) These data span the first year of aromatase inhibitor (AI) (1997) and the first year of taxane use (1998) through guidelines for use of Trastuzamab (2006). The NCCN data was based on patterns reported from US academic cancer centers and may represent earlier adoption and higher use than general community practice of certain regimens.

Treatment dissemination was based on initiation of therapy; the effectiveness of therapy (see below) assumes completion of the regimen. For instance, women who had ER-positive invasive tumors who initiated hormonal therapy were modeled to have received 5 years of treatment (tamoxifen if age at diagnosis is <50 years and aromatase inhibitors if ≥50 years from 1997 to 2010; tamoxifen and other selective estrogen receptor modulating (SERM) agents were the only therapies available prior to 1997). In the future, the models can consider longer durations (e.g., 10 years of hormonal therapy) (48) and treatment adherence. The input parameter included a zero rate of hormonal therapy for women with ER-negative invasive tumors.

Chemotherapy included CMF and anthracycline-based regimens based on calendar year, age, ER, and stage. Taxanes and Herceptin could be added to these regimens starting in 1997 and and 2006, respectively. Trastuzumab was disseminated independently of the other treatments and, based on its immediate rapid uptake, all HER2+ patients were assumed to receive trastuzumab with 100% probability beginning in year 2006. It was assumed that patients diagnosed in Stage IV received the same treatments as those with Stage III breast cancer. Additionally, since there were no national data on treatment patterns for DCIS, expert opinion was used to make the simplifying assumption that half of ER-positive DCIS tumors were treated with hormonal therapy, and that ER-negative DCIS did not receive any adjuvant systemic treatment. A summary of major classes of systemic therapies used over time for an exemplar age and stage group is included on Figure 3.

Figure 3.

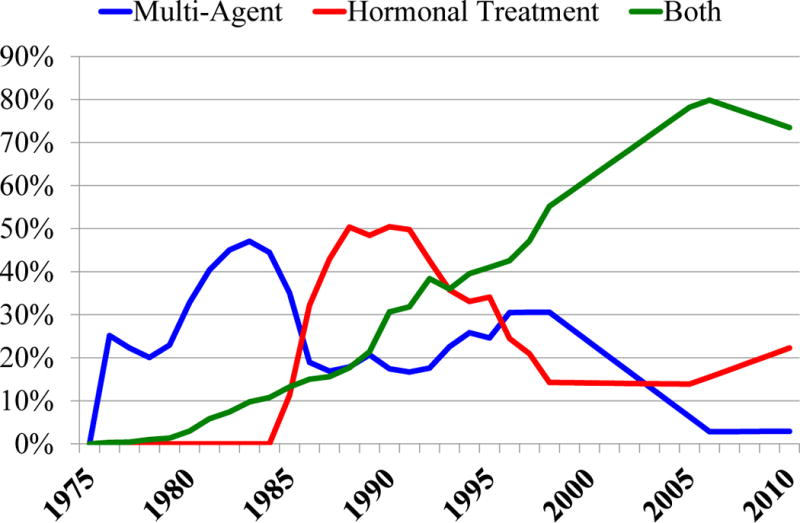
Treatment dissemination. The figure depicts use of adjuvant systemic treatment dissemination from 1975–2010 for an exemplar stage and set of molecular markers (node positive stage IIb, ER+/HER2−) among women 50 to 69 years of age at diagnosis. In the 1980’s and early 1990’s multi-agent chemotherapy (blue line) included primarily CMF regimens; starting in the mid-1990’s antracycline-based regimens were included and increased in use, and in 1998 taxanes could be added to those regimens. Hormonal therapy (red line) began with tamoxifen in the 1980’s and starting in 1997 also included aromatase inhibitors. Hormonal therapy could be used alone or in combination with multi-agent chemotherapy (“both”, green line). Over time, there was an increasing use of both multi-agent chemotherapy and hormonal therapy.

In lieu of this treatment dissemination input, models have also used analysis-specific assumptions for adjuvant systemic treatment (e.g., every woman receives the most effective treatment available at the time for her age and ER/HER2 subtype combination). (25)

Treatment Effectiveness

Systemic treatment effectiveness is based on synthesis of recent clinical trials.(49) The input parameter is provided to the modeling groups as a rate of reduction in hazards of breast cancer death based on age, stage, and ER/HER2, assuming proportionate hazards. Depending on the specific model structure, these data are used directly or as calibration targets for depicting cure rates.

DCIS is assumed to have the same treatment benefit as Stage I disease, although, based on the dissemination data, this was applied only to ER-positive DCIS that is treated with hormonal therapy. Based on expert opinion, because Stage IV is fatal and treatment is not thought to affect the hazard of death, we have assumed no treatment benefit for Stage IV, HER2-negative disease. This is consistent with our prior assumptions of no treatment benefit for Stage IV disease before the year 2000. Trastuzumab does increase the survival of women with HER2-positive, Stage IV disease, and accordingly, the hazard ratio for Stage IV, HER2-positive tumors that receive trastuzumab was adjusted to reflect this based on the literature. (50) With the advent of matching tumor molecular profiles with treatments, and discovery of new approaches to Stage 4 therapy, future iterations of this parameter will be updated as practice changes. Incorporation of improvements in survival associated with treatment of distant metastases will also require new model programming, since, as described in the next section, the current version of the models only include overall survival from the date of diagnosis, and do not consider distant recurrence. Treatment effectiveness for current exemplar regimens is presented in Table 5.

Table 5.

Estimates of Hazards of Death from Breast Cancer by Treatment Modality and Stage - Example for ER+/HER2+

	CMF	CMF + H	A+Tax+ H	CMF+Tras	A+Tras	CMF+H+Tras	A+Tax+H+Tras
Stage 0–III	0.847	0.593	0.469	0.661	0.599	0.462	0.366
Stage IV	1.0	1.0	1.0	1.0	0.8	0.8	0.8

CMF= Cyclophosphamide, Methotrexate, Fluorouracil; A= Anthracycline based; Tax=Taxane; H=Tamoxifen and/or Aromatase Inhibitor (AI) (the efficacy is assumed to be equal); Tras=Trastuzumab

Survival in the Absence of Screening and Treatment

To evaluate the relative contributions of ER and HER2 molecularly targeted treatments such as tamoxifen, aromatase inhibitors, and Trastuzumab on breast cancer mortality reduction in the presence of screening, it was necessary to first generate ER/HER2-specific survival and other inputs for the CISNET breast cancer models in the absence of screening and adjuvant treatment. These inputs are not readily accessible in existing databases. In particular, ER/HER2-specific survival in the absence of screening and adjuvant therapy is not accessible in SEER because registry-based collection of ER and HER2 status only began when screening and adjuvant treatment were already widespread. This posed a major challenge when updating the CISNET models to estimate the relative effects of screening and adjuvant treatment by ER and HER2.

To address this problem and incorporate the natural history differences in ER and HER2 tumor subtypes into the models, the Model S team developed a novel method to “back-calculate” breast cancer- specific survival by joint ER and HER2-status, age group, and AJCC/SEER stage or tumor size in the absence of screening and treatment. This algorithm leveraged data on tumor features, age at detection, and screening histories by ER/HER2 subtypes from the BCSC. The approach incorporated data from two distinct sources: 1) SEER survival from 1975–1979 in the absence of screening and treatment (which represents a period when screening and adjuvant treatment were not widespread) and; 2) data from 23,000 women diagnosed with breast cancer between 1996 and 2009 provided by the BCSC (unpublished data), which included ER, HER2-status and screening histories.

Full details describing the methods for calculation of this parameter are presented elsewhere in this issue. (51) Briefly, BCSC data were used to construct an ER/HER2-specific decision tree classifier to infer (“back-calculate”) these molecular markers based on a patient’s screening history and age, tumor size, stage and grade at detection. The “back-calculation” algorithm consists of leveraging one model (Model S) to simulate a large cohort of women and then utilizing the ER/HER2-status classifier to infer their molecular markers. In essence, this procedure generated a “virtual database” of women that allowed calculating population-level parameters by ER and HER2 subtypes as if these were measured directly from the general population. Contrary to an actual registry, however, the virtual registry permitted assignment of the clinical and screen-detected age, tumor size, stage, grade and ER, HER2-status of each individual woman. Consideration of the breast tumor’s features at clinical detection allowed the estimation of survival in the absence of screening and treatment by sampling from the 1975–1981 SEER survival curves. The new parameter includes survival by age, tumor size, stage, and ER/HER2 in the absence of screening and treatment. The ER-specific portion of the input was published in a CISNET analysis of the contributions of screening and treatment to ER-specific mortality trends from 1975–2000 (Figure 4).(26)

Figure 4.

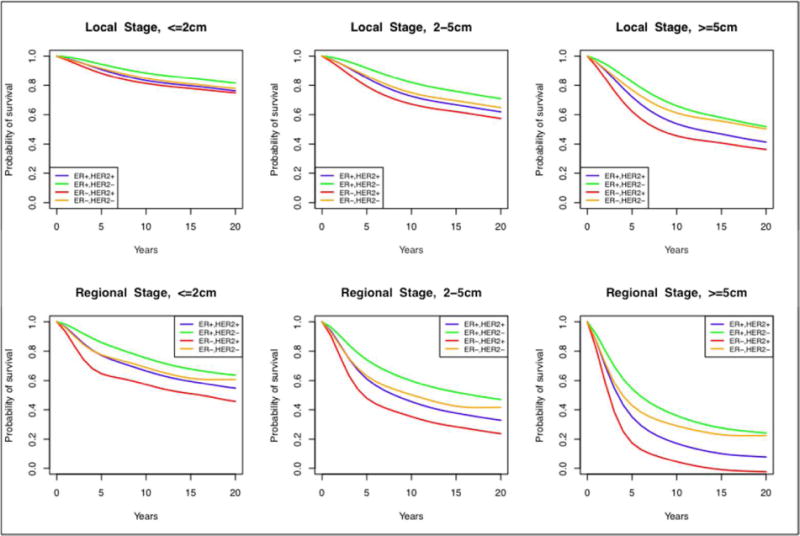
Breast cancer survival curves in the absence of screening and treatment effects stratified by ER and HER2-status, stage and tumor size. These survival curves were shared across all modeling groups.

OTHER PARAMETERS

There are other common model input parameters, such as non-breast cancer mortality. (52) Model inputs for non-breast cancer mortality have been updated since prior publication (53) to include the period 2000–2010 and mortality by body mass index (BMI), since BMI affects risk of postmenopausal breast cancer as well as mortality from other causes, and the prevalence of BMI has increased dramatically since 1980. For certain analyses, survival is modified using common parameters to reflect quality-adjusted life years using published estimates and/costs. (24) Finally, the models have begun using data on other cause mortality among breast cancer patients for analyses that focus on the patient (vs. the general) population.

In addition to these common parameters, based on structure and assumptions, each model included model-specific parameters such as estimated pre-clinical sojourn times, proportion of DCIS or invasive cancer that will not progress, lead times, and dwell times within tumor stage. These types of parameters could be estimated for all cancers or separately based on ER and HER2 status.

DATA DOCUMENTATION AND MANAGEMENT

A Coordinating Center at Georgetown University has organized input parameter development, documentation, dissemination, and archiving. The common input data were updated for each analysis to ensure that they reflected the most current practice and knowledge about breast cancer. The Coordinating Center worked closely with the modeling teams to identify parameters needed, format required to read the parameters into the model programs, and discuss the best sources of data for these parameters. Data are generally analyzed at the Coordinating Center to provide the modeling groups with the results in a flexible format, but some parameters were developed by the modeling teams and results were forwarded to the Coordinating Center for distribution and archiving. The Coordinating Center developed the associated documentation using standard reporting formats. For every analysis, all parameters and supporting documentation were posted on a project webpage located on the private CISNET member website. Documentation of all data sources and analytic methods was posted to maintain transparency.

Table 3.

Mammography Performance for Detection of Breast Cancer -All Density Groups ^†

Mammogram Type	Age	Screen Interval*	Sensitivity - Invasive	Sensitivity-DCIS	Specificity
Film-screen	30–39	First	0.68	0.88	0.87
		Annual	0.42	0.81	0.92
		Biennial	0.55	0.87	0.91
		Triennial	0.60	0.87	0.90
	40–49	First	0.80	0.93	0.85
		Annual	0.58	0.90	0.91
		Biennial	0.70	0.93	0.90
		Triennial	0.74	0.93	0.89
	50–64	First	0.89	0.94	0.87
		Annual	0.74	0.91	0.92
		Biennial	0.82	0.94	0.92
		Triennial	0.85	0.94	0.91
	65+	First	0.92	0.94	0.89
		Annual	0.80	0.90	0.94
		Biennial	0.87	0.93	0.93
		Triennial	0.89	0.93	0.92
Digital	25–39	First	0.74	0.91	0.84
		Annual	0.49	0.86	0.90
		Biennial	0.61	0.90	0.90
		Triennial	0.66	0.90	0.89
	40–49	First	0.84	0.95	0.83
		Ann	0.64	0.92	0.89
		Biennial	0.75	0.95	0.88
		Triennial	0.78	0.95	0.87
	50–64	First	0.91	0.96	0.85
		Annual	0.78	0.93	0.91
		Biennial	0.86	0.95	0.90
		Triennial	0.88	0.95	0.89
	65+	First	0.94	0.95	0.88
		Annual	0.84	0.92	0.92
		Biennial	0.90	0.95	0.92
		Triennial	0.91	0.95	0.91

^†Data from the BCSC; 1994–2013 for film-screen and 2003–2013 for digital mammogram.

^*First screen-detected cancers are cancers detected on the first screen or those found after a gap of more than 4 years