Variance component score test for time-course gene set analysis of longitudinal RNA-seq data

SUMMARY

As gene expression measurement technology is shifting from microarrays to sequencing, the statistical tools available for their analysis must be adapted since RNA-seq data are measured as counts. It has been proposed to model RNA-seq counts as continuous variables using nonparametric regression to account for their inherent heteroscedasticity. In this vein, we propose tcgsaseq, a principled, model-free, and efficient method for detecting longitudinal changes in RNA-seq gene sets defined a priori. The method identifies those gene sets whose expression varies over time, based on an original variance component score test accounting for both covariates and heteroscedasticity without assuming any specific parametric distribution for the (transformed) counts. We demonstrate that despite the presence of a nonparametric component, our test statistic has a simple form and limiting distribution, and both may be computed quickly. A permutation version of the test is additionally proposed for very small sample sizes. Applied to both simulated data and two real datasets, tcgsaseq is shown to exhibit very good statistical properties, with an increase in stability and power when compared to state-of-the-art methods ROAST (rotation gene set testing), edgeR, and DESeq2, which can fail to control the type I error under certain realistic settings. We have made the method available for the community in the R package tcgsaseq.

1. Introduction

Gene expression is a dynamic biological process of living organisms, whose dysfunction and variation can be related to numerous diseases. During the past two decades, gene expression measurements have developed rapidly, thanks to wide dissemination of microarray technology. In recent years, gene expression measurement technology has been shifting from microarrays to sequencing (RNA-seq) technology. The higher resolution of RNA-seq technology provides a number of advantages over microarrays, among which are the ability to make de novo discoveries and an increased sensitivity to low-abundance variants (Marioni and others, 2008). Indeed, RNA-seq is not restricted to a predefined set of probes like microarrays but can instead measure the genome in its entirety.

A large body of statistical methods have been developed to analyze microarray data. But as technology for measuring gene expression is transitioning to RNA-seq, new methodological challenges arise. RNA-seq produces count data, while microarray analysis techniques generally assume continuity. Due to their underlying count nature, RNA-seq data are intrinsically heteroscedastic. Various approaches have been proposed to deal with these issues, mostly relying on modeling the underlying count nature of the data through the use of Poisson or negative binomial distributions (Marioni and others, 2008; Anders and Huber, 2010; Robinson and others, 2010). Recently, Law and others (2014). have instead proposed to use normal-based methods to analyze RNA-seq data by explicitly modeling the heteroscedasticity and accounting for it by weighting. All of these methods currently make potentially restrictive assumptions about the distribution of the data.

While most methods for gene expression data focus on univariate differential gene expression analysis, it has been shown that gene set analysis (GSA) can be a more powerful and interpretable alternative (Subramanian and others, 2005; Hejblum and others, 2015). GSA uses a priori defined gene sets annotated with biological functions and investigates their potential association with biological conditions of interest. There are many different approaches to GSA, and a GSA method is typically defined by the type of hypothesis tested as well as how information across genes is aggregated. Rahmatallah and others (2016) recently showed that self-contained GSA tests tend to be more powerful and more robust than competitive ones (Goeman and Bühlmann, 2007). Furthermore, some GSA tests rely on univariate gene-level statistics as a first step, aggregating them afterwards in a bottom-up enrichment approach. But when signal strength is weak, single-step, top-down GSA methods relying on direct multivariate modeling are better than those enrichment based ones at leveraging the additional power of GSA (Hejblum and others, 2015).

As costs keep decreasing for RNA-seq experiments, more complex study designs, such as time-course experiments, have become more common (Dorr and others, 2015; Baduel and others, 2016). However, very few GSA approaches can properly accommodate and test hypotheses more complex than simple differential expression, such as change over time. The ROAST method (Wu and others, 2010) is a linear-model-based gene set testing procedure. Law and others (2014) have proposed to use it in conjunction with their heteroscedasticity weighting method voom on RNA-seq data, and this combination of voom and ROAST has been identified in the recent review by Rahmatallah and others (2016) as one of the top-performing GSA methods for RNA-seq data. Additionally, DESeq2 (Love and others, 2014) and edgeR (Robinson and others, 2010; McCarthy and others, 2012), are currently the most prominent approaches used for gene-level differential analysis of RNA-seq data. They both rely on the assumption that gene counts from RNA-seq measurements follow a negative binomial distribution. edgeR can use the ROAST method to propose a built-in framework for self-contained gene set testing, while DESeq2 can only perform gene-wise tests. Nueda and others (2014) have also developed a gene-wise method for dealing with time-course course RNA-seq data, considering Poisson and negative binomial distributions through generalized linear models.

Another concern, particularly in the longitudinal setting, is adequately accounting for heterogeneity of effects (Cui and others, 2016). GSA approaches often overlook the potential longitudinal heterogeneity within a gene set while such heterogeneity is not infrequent (Ackermann and Strimmer, 2009) and can be of biological interest (Hu and others, 2013), especially if considered gene sets correspond to biological pathways or networks. Hejblum and others (2015) showed the potential statistical power gain when accounting for this heterogeneity in longitudinal microarray studies.

In this article, we propose tcgsaseq, a method to analyze RNA-seq data at the gene-set level, with a particular focus on longitudinal studies. We derive a variance component score test, similar to those that have been proposed in other testing situations (Wu and others, 2011; Huang and Lin, 2013), that facilitates testing both homogeneous and heterogeneous gene sets simultaneously. Variance component tests offer the speed and simplicity of standard score tests, but potentially gain statistical power by using many fewer degrees of freedom, and have been shown to have locally optimal power in some situations (Goeman and others, 2006). Inspired by the voom approach from Law and others (2014), we propose to estimate the mean-variance relationship in a more principled way using local linear regression, to account for the inherent heteroscedasticity of the data. Despite this nonparametric step, we demonstrate that the test statistic has a simple limiting distribution that is valid regardless of any model specification. We also propose a permutation version of the test to deal with small sample sizes. Our method is implemented in the R package tcgsaseq, available on the Comprehensive R Archive Network at % https://cran.r-project.org/web/packages/tcgsaseq.

Our general approach to GSA in longitudinal RNA-seq studies has three primary advantages over existing approaches. First, unlike ROAST, our variance component approach remains valid under model misspecification and does not rely on ad hoc aggregation of information across genes. Second, unlike previous approaches to variance component testing in microarray data (Huang and Lin, 2013), our approach can accommodate the intrinsic mean-variance relationship in RNA-seq data, while remaining fast to compute. Third, our test remains powerful even when patients display heterogeneous trajectories over time.

The remainder of the article is organized as follows: Section 2 describes our variance component score test, while its asymptotic properties are derived in Section 3, and an estimation strategy and practical recommendations are detailed in Section 4. In Section 5, we present numerical studies assessing the potential impact of ignoring the mean-variance relationship in RNA-seq data, and comparing our approach to state-of-the-art methods of GSA. In Section 6, we apply tcgsaseq to the analysis of real data. Final remarks and comments are discussed in Section 7.

2. Variance component score test for longitudinal GSA

2.1 Problem setup

Consider 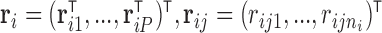a vector of sequence read counts for subject 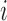, that have been mapped to each of 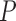genes measured at times 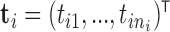. Meanwhile, 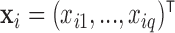is a vector of baseline covariates describing experiment design conditions, all measured on individual 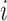. So the full data considered for analysis are 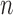independent realizations from random vectors 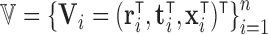. Typically, the counts 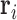are normalized in some way in a preprocessing step (Hansen and others, 2012). We take 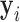to be a normalized version of 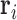. For example, one standard normalization procedure accounts for the library size 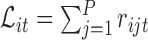by computing the log-counts per million as

$$\begin{array}{c}{y}_{ijt}={\log }_2\left({10}^{\mathrm{6}}\times \frac{0.5+r_{ijt}}{1+{\mathcal{L}}_{it}}\right).\hfill \end{array}$$ (2.1)

Based on these data, our interest is in identifying gene sets that have longitudinally changing expression patterns. The rest of this section will develop the proposed test statistic and its limiting distribution.

2.2 The test statistic

We are interested in testing for longitudinal changes in a pre-specified gene set, which for the purposes of illustration we take to be the first 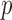genes, 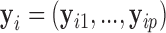. To develop a variance component score test statistic, we start from the following working model, which is a linear mixed effect model (Laird and Ware, 1982; Fitzmaurice and others, 2012)

$$\begin{array}{cc}& y_{ijt}={\alpha }_{0j}+a_{0ij}+{\mathbf{x}}_i^{\mathsf{T}}{\mathit{\alpha }}_j+{\mathit{\varphi }}_{it}^{\mathsf{T}}{\mathit{\beta }}_j+{\mathit{\varphi }}_{it}^{\mathsf{T}}{\mathit{\xi }}_{ij}+{ϵ}_{ijt}\end{array}$$ (2.2)

and which can be rewritten as

$$\begin{array}{cc}& {\mathbf{y}}_i={\mathit{\alpha }}_0+{\mathit{a}}_{0i}+X_i\mathit{\alpha }+{\mathrm{\Phi }}_i\mathit{\beta }+{\mathrm{\Phi }}_i{\mathit{\xi }}_i+{\mathit{\epsilon }}_i,\end{array}$$ (2.3)

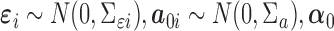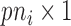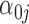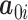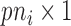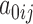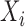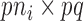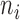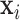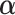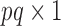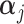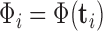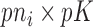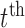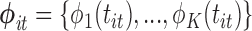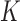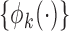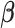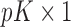where is a vector of gene-specific intercepts , is a vector of random intercepts , is a block diagonal matrix with each block consisting of rows equal to the fixed effect baseline covariates , is a vector of gene-specific fixed effects , is a block-diagonal matrix encoding the effect of time with each block having row for some set of basis functions , is a vector of gene-specific fixed effects of time 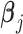, 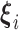is a 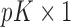vector of gene-specific individual-level effects of time, and 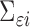is a 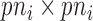covariance matrix of measurement errors. Note that 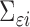is indexed by 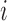and may depend on the mean of 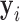. We assume that 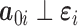. It is important to note that, in practice, the above model is unlikely to hold. Fortunately, the testing procedure we propose is entirely robust to its misspecification.

We are interested in testing the null hypothesis of no longitudinal change in the normalized gene expression for any genes in the gene set

$$\begin{array}{c}{H}_0:\text{The mean of }{\mathbf{y}}_i\text{ does not depend on }{\mathbf{t}}_i\hfill \end{array}$$ (2.4)

or, that is, 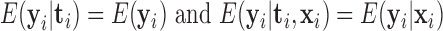. Under the model (2.3), the null hypothesis (2.4) corresponds to the following null: 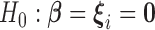, which tests for both homogeneous and heterogeneous dynamics within the gene sets. In section 3, we demonstrate that the corresponding variance component score test can be written as

$$\begin{array}{c}Q={\mathbf{q}}^{\mathsf{T}}\mathbf{q},{\mathbf{q}}^{\mathsf{T}}=n^{-\frac{1}{\mathrm{2}}}\sum _{i=1}^n{\mathbf{y}}_{\mu i}^{\mathsf{T}}{\mathrm{\Sigma }}_i^{-1}{\mathrm{\Phi }}_i{\mathrm{\Sigma }}_{\nu }^{1/2},\hfill \end{array}$$ (2.5)

where 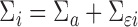, , 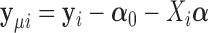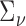is a working covariance matrix defined in (3.2), and 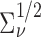is the symmetric half matrix such that 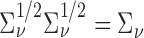. We also show in the supplementary material available at Biostatistics online that given the dimension of 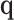(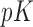) is small relative to the number of individuals (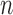), the asymptotic distribution of the test statistic is a mixture of 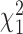random variables, 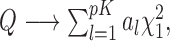where the mixing coefficients 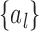depend on the covariance of 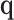. This asymptotic distribution holds regardless of the distribution of .

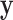In the end, p-values may be computed by comparing the observed test statistic 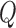to the distribution of 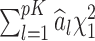where 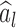is an estimate of 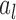. Details are developed further in Section 3 and the supplementary material available at Biostatistics online. When the entries of 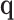are correlated—that is, there is correlation between genes in the gene set—then the degrees of freedom for the test based on 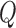may be much lower than the degrees of freedom for a similar Wald or score test, yielding more power to detect departures from the null hypothesis.

In practice, the parameters 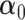, , 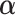, 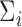and 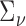are unknown and must be estimated. In particular, accounting for the mean-variance relationship encoded in 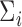is vital in RNA-seq data. Hence we estimate the test statistic as

$$\begin{array}{c}\hat{Q}={\hat{\mathbf{q}}}^{\mathsf{T}}\hat{\mathbf{q}},{\hat{\mathbf{q}}}^{\mathsf{T}}=n^{-\frac{1}{\mathrm{2}}}\sum _{i=1}^n({\mathbf{y}}_i-{\hat{\mathit{\alpha }}}_0-X_i\hat{\mathit{\alpha }}{)}^{\mathsf{T}}{\hat{\mathrm{\Sigma }}}_i^{-1}{\mathrm{\Phi }}_i{\hat{\mathrm{\Sigma }}}_{\nu }^{1/2}\hfill \end{array}$$ (2.6)

and we further demonstrate in section 3 that plugging in standard estimates of 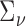, , 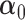and 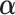and a nonparametric estimator of 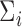for the estimated test statistic still yields a similar asymptotic distribution:

$$\begin{array}{c}\hat{Q}⟶\sum _{l=1}^{pK}{\tilde{a}}_l{\chi }_1^{\mathrm{2}}\hfill \end{array}$$ (2.7)

for mixing coefficients 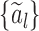given in the supplementary material available at Biostatistics online.

The strength of our approach is that this simple limiting distribution holds even when the model (2.3) may be misspecified and despite the presence of the nonparametric estimator of 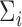in (2.6). In this way, we may account very flexibly for the mean-variance relationship in 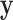while maintaining a simple, powerful test statistic that does not require any particular model to hold.

The convergence in (2.7) relies on the central limit theorem. There may of course be situations where the central limit theorem fails to kick in, either when the number of genes in the gene set 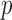is quite large, or else when the number of individuals 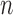is small. We now discuss two modifications for these scenarios.

2.2.1 Testing for homogeneous gene sets.

When the number of genes 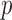is large relative to 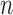, the convergence of 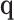to a limiting normal distribution may be in doubt. In these cases, it might be better to begin from a working model that assumes that all genes share a common trajectory over time as a useful approximation. 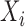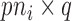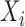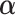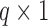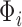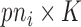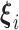To wit, we may reduce the number of parameters in the model by taking in model (2.3) to be a counterpart of , and similarly to be , to be , and to be 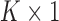counterparts, respectively, of the original quantities. The derivation of the test statistic follows precisely the same lines with updated dimensions.

2.2.2 Using permutation.

When 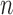is very small (or alternatively when 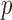is relatively large but the homogeneous strategy described above seems unwise), relying on the limiting distribution (2.7) may not be accurate. In these cases, permutation may be used to estimate the empirical distribution of 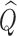under the null (2.4). To perform the permutations, we simply shuffle the time labels within each individual to get permuted observations for the 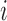th individual 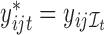, where 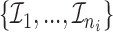is a permutation of 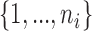. Indeed, under the null, observations of a given gene 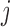for a given individual 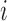are exchangeable, regardless of sampling time. A large number 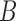of permutation-based test statistics 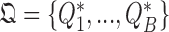can thus be generated where each 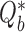is computed using the 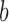th set of permuted data. p-values may then be computed as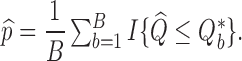

3. Properties of the test statistic

In this section, we derive the test statistic and demonstrate its asymptotic distribution assuming all parameters known. We then take up the distribution of the test statistic when estimating all relevant parameters.

3.1 Test statistic derivation

Under the working model (2.3), 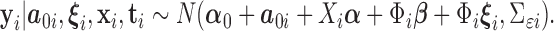Integrating over the random intercepts 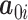, we can rewrite the model as

$${\mathbf{y}}_i|{\mathit{\xi }}_i,{\mathbf{x}}_i,{\mathbf{t}}_i\stackrel{~}{}N({\mathit{\mu }}_i+{\mathrm{\Phi }}_i{\mathit{\theta }}_i,{\mathrm{\Sigma }}_i),$$ (3.1)

where 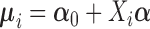denotes time-independent fixed effects, 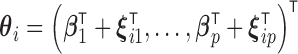denotes combined effects of time.

The test for no longitudinal changes in expression corresponds to the model-based hypothesis 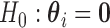. We write 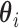as 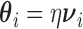and we consider the working assumption that the 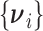are independently distributed such that 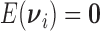(under the null) and

$$\begin{array}{c}\text{Var}({\mathit{\nu }}_i)={\mathrm{\Sigma }}_{\nu }.\end{array}$$ (3.2)

Under this working assumption, 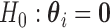is equivalent to 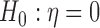. To obtain the variance component test statistic, rewrite the model as: 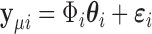for centered outcome 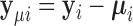. Then 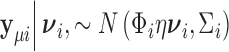and the log-likelihood for 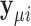can be written as

$$\begin{array}{c}\log \mathcal{L}(\eta )=-\frac{1}{\mathrm{2}}\sum _{i=1}^n\left\{\log \left|{\mathrm{\Sigma }}_i\right|+{\left({\mathbf{y}}_{\mu i}-\eta {\mathrm{\Phi }}_i{\mathit{\nu }}_i\right)}^{\mathsf{T}}{\mathrm{\Sigma }}_i^{-1}\left({\mathbf{y}}_{\mu i}-\eta {\mathrm{\Phi }}_i{\mathit{\nu }}_i\right)\right\}.\end{array}$$ (3.3)

Because the target of inference is 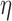, we marginalize over the nuisance parameter 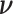conditional on the observed data to obtain 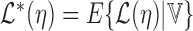where the expectation is taken over the distribution of 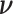. We follow the argument in Commenges and Andersen (1995) and note that the score at the null value is 0: 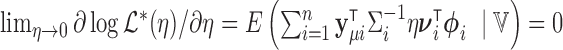. So we instead consider the score with respect to 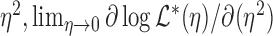, which is equal to

$$\begin{array}{cc}& E{\left\{{\hspace{0.17em}\frac{\mathrm{\partial }\log \mathcal{L}(\eta )}{\mathrm{\partial }\eta }|}_{\eta =0}\mid \mathbb{V}\right\}}^2+\text{constant}+o_p(1)\end{array}$$ (3.4)

$$\begin{array}{cc}& \hspace{0.17em}=\left(\sum _{i=1}^n{\mathbf{y}}_{\mu i}^{\mathsf{T}}{\mathrm{\Sigma }}_i^{-1}{\mathrm{\Phi }}_i\right){\mathrm{\Sigma }}_{\nu }{\left(\sum _{i=1}^n{\mathbf{y}}_{\mu i}^{\mathsf{T}}{\mathrm{\Sigma }}_i^{-1}{\mathrm{\Phi }}_i\right)}^{\mathsf{T}}+\text{constant}+o_p(1)\end{array}$$ (3.5)

Thus, after normalizing by 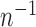, the variance component score test statistic can be written 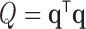, as described in (2.5). If the dimension of 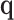is small relative to the sample size, 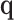is asymptotically normal by the central limit theorem, which means that the limiting distribution of 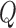is a mixture of 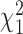s (see supplementary material available at Biostatistics online for more details).

3.2 Estimated test statistic limiting distribution

In practice, estimates need to be supplied for many of the quantities in the test statistic to be estimated in (2.6). Following the argument for the limiting distribution of 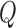, 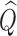has a limiting distribution of a mixture of 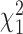s so long as 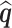has a limiting normal distribution. To establish this, we define 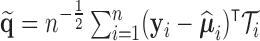to be a version of 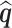where 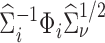is replaced with its limit, 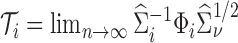. The quantities 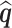and 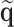are asymptotically equivalent, and the central limit theorem ensures that 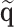has a limiting normal distribution. Therefore, the asymptotic distribution of 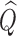is a mixture of 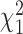s (see supplementary material available at Biostatistics online for details), and the corresponding testing procedure is valid under any data-generating function and robust to misspecification of the working model 2.3.

4. Estimation

The test statistic (2.6) contains the estimated quantities 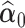, , 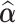, 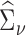and 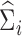. In this section, we take up practical issues involved in the estimation of these quantities.

4.1. Estimating model parameters

In this section, we will discuss estimation of 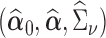, assuming that we have a consistent estimator of 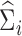in hand (we leave discussion of estimating 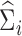to the following section). A natural way to estimate 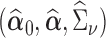, taking into account the heteroscedasticity in 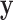, is to fit a weighted mixed effects model corresponding to

$$\begin{array}{c}{y}_{ijt}={\alpha }_{0j}+{\mathbf{x}}_i^{\mathsf{T}}{\mathit{\alpha }}_j+{\mathit{\varphi }}_{it}^{\mathsf{T}}{\mathbf{\theta }}_{ij}+{\widetilde{ϵ}}_{ijt},\end{array}$$ (4.1)

where the random intercepts 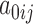have been integrated out and 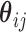is taken to be 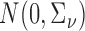. The weights are taken to be 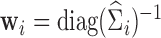. This model corresponds to the model (3.1).

In practice, fitting the full mixed effects model for each of many gene sets may be computationally demanding. In these cases, the simpler fixed effects model

$$\begin{array}{c}{y}_{ijt}={\alpha }_{0j}+{\mathbf{x}}_i^{\mathsf{T}}{\mathit{\alpha }}_j+{\mathit{\varphi }}_{it}^{\mathsf{T}}{\mathit{\beta }}_j+{\widetilde{ϵ}}_{ijt}\end{array}$$ (4.2)

may be fit to estimate 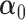and 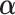. 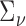may not be estimated directly from (4.2). In this case, it may be specified using a working estimate or taken to be the identity matrix.

4.2. Estimating the mean-variance relationship

One key feature of our approach is to estimate 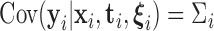in such a way as to account for the heteroscedasticity in 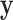. It is important to note that accurate estimation of 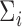will likely increase power but will not affect the validity or type I error of the testing procedure.

To approximate the mean-variance relationship in 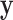, we use information from all 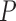genes. We assume that the diagonal elements of 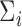, which we will denote 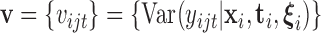, may be modelled as a function of their means 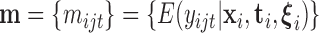. Specifically, 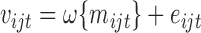for some unknown function 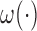and errors which follow the moment conditions .

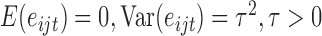We follow Law and others (2014) in using local linear regression in estimating 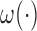. We will first write out the form of the estimator if all parameters were known: 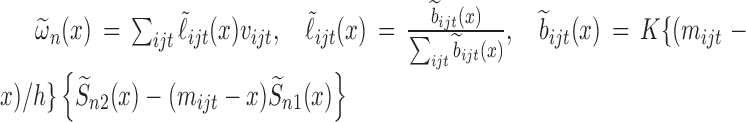, where 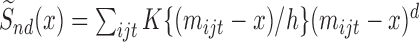for some kernel function 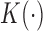and bandwidth .

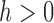The means 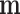and variances 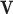could in principle be estimated using some parametric model like (4.1) for all 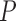genes. Let 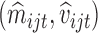denote the estimated mean and variance for 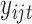. Then the mean-variance relationship may be estimated as

$$\begin{array}{c}{\hat{\omega }}_n(x)={\hspace{0.17em}{\tilde{\omega }}_n(x)|}_{m_{ijt}={\hat{m}}_{ijt},v_{ijt}={\hat{v}}_{ijt}}\end{array}$$ (4.3)

As with any smoothing procedure, choice of the bandwidth 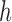is paramount in producing a reliable estimator. Standard cross-validation techniques may be used to select in practice. Then the diagonal entries of 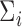can be estimated as .

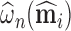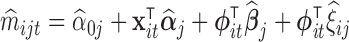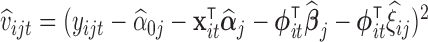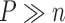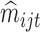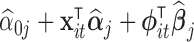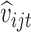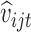Practical considerations. Under the model (4.1), we could take and . However, because , fitting (4.1) for such a large number of genes is not practical. Instead, the simpler model (4.2) could be used. Then could be taken to be and to be to be 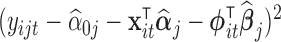. A similar approach was used to model heteroscedasticity in the context of linear regression in Carroll (1982).

On the other hand, fitting a local linear regression on all of 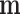and 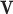– a total of 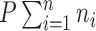observations – may be computationally difficult. In order to reduce the number of points used in the nonparametric fit (4.3), one could follow Law and others (2014) and model the mean-variance relationship at the gene level

$$\begin{array}{c}{v}_j=\omega (m_j)+e_j.\end{array}$$ (4.4)

The gene-level mean may be estimated as 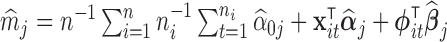and the gene-level variance as .

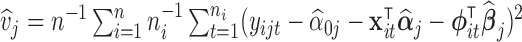5. Numerical study

In this numerical study section, we illustrate both the importance of accounting for RNA-seq data’s heteroscedasticity and the superiority of tcgsaseq in terms of statistical power and robustness. We have performed simulations under two different settings. The first one demonstrates the good behavior of the asymptotic test under various scenarios in synthetic data. The second one focuses on a very realistic situation where sample size is small and gene counts are generated from a distribution of real observed RNA-seq data. Throughout, for the purposes of testing, we take 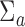and 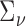to be the identity for simplicity. In practice, more precise estimation of 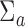and 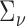would serve to increase power. Finally, throughout we use Davies’s approximation method (Davies, 1980) to compute p-values for the mixture of 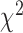s, implemented in the CompQuadForm R package (Duchesne and Lafaye De Micheaux, 2010).

5.1. Synthetic data

In this subsection, we use synthetic data to illustrate the behavior of our estimator when the distribution of the data is known. We first look at the importance of accounting for the mean-variance relationship in 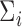in tcgsaseq, and then we compare tcgsaseq to other competing methods, including ROAST, edgeR-ROAST, and DESeq2. In order to adapt DESeq2 to self-contained gene set testing, we use the minimum P-value test to adequately combine univariate p-values for testing a whole gene set while taking into account gene correlation (Lin and others, 2011) and we refer to it as DESeq2-min test. We demonstrate that the tcgsaseq testing procedure is robust to even heavy misspecification of the mean model and the mean-variance relationship, while ROAST, edgeR-ROAST and DESeq2-min test may suffer from extreme lack of power compared to tcgsaseq or inflate type I errors under misspecification.

5.1.1. Mean-variance relationship

To illustrate the importance of estimating the mean-variance relationship, we generated data under the model 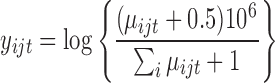where

$$\begin{array}{c}{\mu }_{ijt}={\eta }_{ijt}\sum _{i,t}{\eta }_{ijt}/P+b_{ij}{t}_{it}+\beta t_{it},{\eta }_{ijt}=a_{ij}+{\alpha }_j+\sum _{k=1}^3{x}_{itk}+{ϵ}_{ijt},\end{array}$$ (5.1)

with 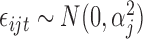, , 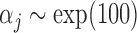, , 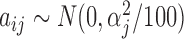, 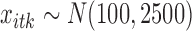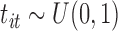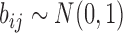. We set 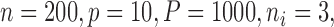and 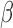was allowed to be set to 6 different values within a range from 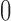to 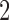: 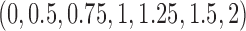. We considered three methods of accounting for the mean-variance relationship: (i) gene-level estimates using equation (4.4); (ii) voom-type estimation Law and others (2014); (iii) specifying 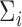to be the identity. Throughout this section, we test at the 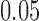level. The model (4.2) was used to generate the test statistic and adjust for covariates, and the gene-level equation (4.4) was used to estimate the mean-variance relationship. Note that the mean model (4.2) is misspecified.

When applying our variance component test, type I error was at the nominal level using either strategy (i) or (iii), but was deflated to 0.035 when using strategy (ii). On the other hand, ROAST, which similarly relies on estimating the mean-variance relationship, inflated type I error to 0.56 when using (ii), and had adequate type I errors using the other weighting strategies. Such results indicate that ROAST may drastically inflate type I error rates in some cases, and that using (ii), the voom-type estimator, to account for heteroscedasticity led to worse performance in general.

Figure 1 demonstrates the effect of accounting for heteroscedasticity under the alternative hypothesis. The more accurate modeling of the mean-variance relationship with method (i) yields large power gains over method (ii). Conversely, by drastically mis-modelling the mean-variance relationship, the naive method (iii) yields almost no power for detecting longitudinal changes.

Fig. 1.

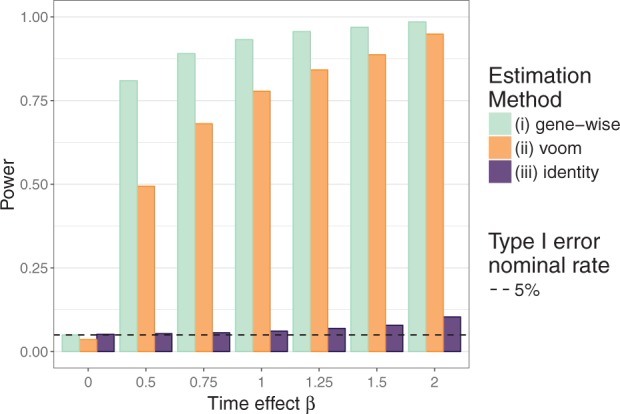
Power evaluation in synthetic data according to how heteroscedasticity is accounted for, based on 1000 simulations.

5.2. Comparison to competing methods

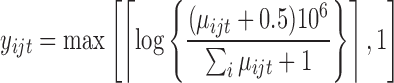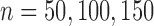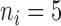In this subsection, we compare tcgsaseq to ROAST, edgeR-ROAST, and DESeq2-min test using a highly misspecified model and using a negative binomial model. For the misspecified model, we again generate data under model (5.1) with one modification to ensure that the data are positive integers . We set and , and 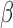took values between 2 and 2. Because DESeq2 is computationally intractable at higher sample sizes with large 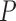, we set the total number of genes 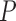to be 100. We used model (4.4) to compute the mean-variance relationship for both tcgsaseq and ROAST. Gene-based estimates were used for dispersions in DESeq2, and likelihood ratio tests were used to produce test statistics for both edgeR and DESeq2.

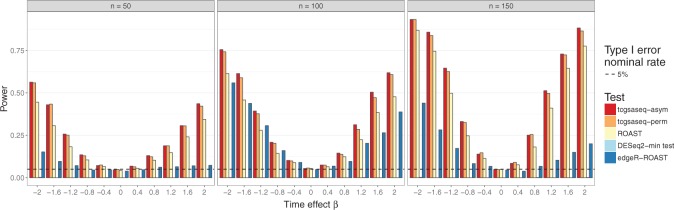
The results are depicted in Figure 2. We see that tcgsaseq has the highest power at all sample sizes and at all values of 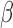. Though the model is highly misspecified for all methods, the negative-binomial-based methods edgeR-ROAST and DESeq2-min test suffer greatly in terms of power, in particular DESeq2-min test. In Figure 2, we show ROAST using the mean-variance relationship estimated from model (4.4), but it’s important to note that if the voom-type strategy were used, the type I error for ROAST rises to more than 0.1 at all sample sizes. Asymmetrical power curves around the null are expected for both edgeR and DESeq2 as they both assume the data have a negative binomial distribution (which is asymmetric with a heavier right tail).

Fig. 2.

Power evaluation in synthetic data comparing tcgsaseq, ROAST, edgeR-ROAST, and DESeq2-min test, based on 1000 simulations.

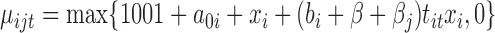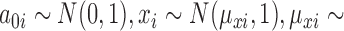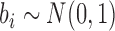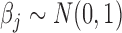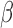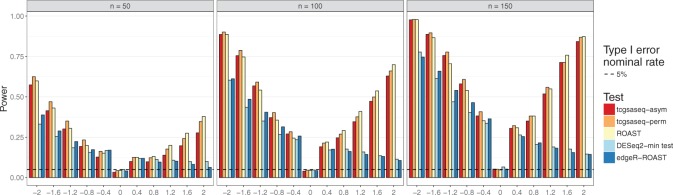
Secondly, we generated data under the negative binomial model, a distributional assumption that edgeR and DESeq2 make. The mean of the negative binomial was specified as where exponential(1/10), , , and the negative binomial dispersion parameter was set to 1. We again let vary between 2 and 2 and considered sample sizes of 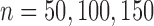. In this setting, the default procedure to estimate dispersions was used for DESeq2. The results depicted in Figure 3 show that tcgsaseq and ROAST outperform edgeR-ROAST and DESeq2-min test despite the fact that the distributional assumptions of edgeR and DESeq2 are true. The performance of tcgsaseq and ROAST is in general comparable. Furthermore, it is important to highlight that DESeq2-min test does not control the type I error, and the type I error gets worse as sample size increases.

Fig. 3.

Power evaluation in negative binomial data comparing tcgsaseq, ROAST, edgeR-ROAST, and DESeq2-min test, based on 1000 simulations.

5.3. Realistic small samples simulations

In this subsection, we simulated another dataset to illustrate the good behavior of the tcgsaseq permutation test in the realistic setting of a small sample size. We generated data for 6 individuals each measured at 3 time points according to the scenario described in Law and others (2014), using the script provided in their supplementary material: 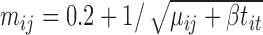and 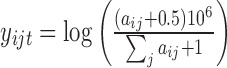where 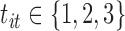, , 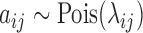, , 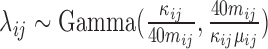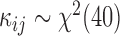and 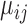follows an empirical baseline distribution derived from real RNA-seq counts data, provided in supplementary material of Law and others (2014). This simulation scheme allows us to generate data that realistically resemble real RNA-seq count data. We set 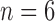with 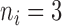, and gene sets were constructed such that 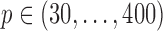and for every gene pair 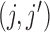in the set 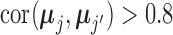. 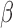was allowed to be set to 8 different values within a range from 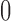to : .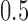

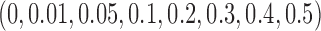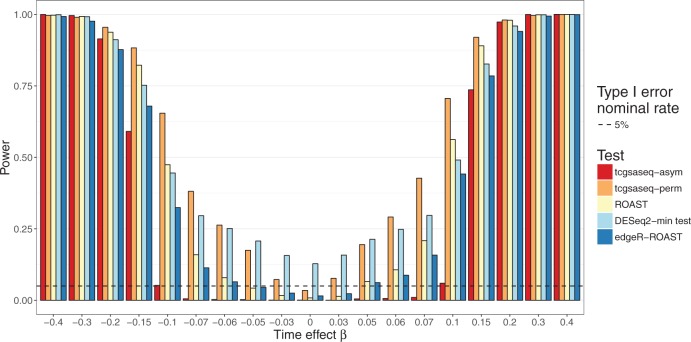
As shown in Figure 4, under this setting, edgeR-ROAST, ROAST, and the proposed permutation test all control the type I error at nominal rate. However, DESeq2-min test fails to control the type I error, while it is highly deflated for the asymptotic version of tcgsaseq (0.001) which is not surprising given that with such a small sample size it is unlikely the central limit theorem would have come into effect yet. Nonetheless, we observe a steady and consistent increase of power for our method using the permutation test over the compared state-of-the-art approaches. The deviation from the negative binomial distribution hypothesis (which both edgeR and DESeq2 rely upon), as well as the univariate gene-wise step first needed, explain those poor performances compared to tcgsaseq. Similar results are obtained when adding a random effect of time simulating heterogeneous gene sets (see supplementary material available at Biostatistics online). In addition, as gene sets were constructed with correlated genes, these results also indicates that tcgsaseq is robust to and can take advantage of inter-gene correlation.

Fig. 4.

Power evaluation in realistically simulated data with a small sample size, based on 500 simulations.

6. Application to two real datasets

In this section, we present analyses of two real datasets. In both analyses, 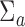and 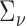were again taken as the identity while 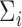was estimated at the gene level using equation (4.4) for tcgsaseq. The ROAST method was applied in combination with precision weights estimated through the voom approach. Given the sample sizes available in both studies, we used the tcgsaseq permutation test. In both cases, only transformed data were available and not original counts data, preventing us from applying either edgeR-ROAST or DESeq2-min test.

6.1. Longitudinal RNA-seq measurements in successful kidney transplant patients

We analyzed a RNA-seq dataset from Dorr and others (2015), in which gene expression was measured in the peripheral blood mononuclear cells of 32 kidney transplant patients. Gene expression was measured at 4 time points: before transplantation, 1 week after transplantation, 3 months after transplantation and 6 months after transplantation. The patients had no graft rejection at the time of each sample.

We investigated custom gene sets targeted specifically towards kidney transplant. Those kidney-oriented gene sets were derived by the Alberta Transplant Applied Genomics Center from specific pathogenesis-based transcripts (Halloran and others, 2010), and their definition is available at http://atagc.med.ualberta.ca/Research/GeneLists. We tested for a linear change in gene expression over time while adjusting for patient’s age and gender.

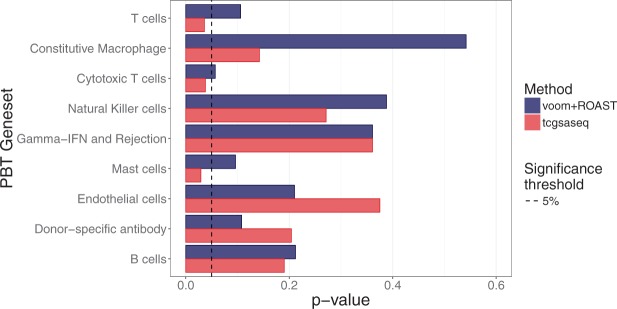
Figure 5 shows the p-values for those 9 gene sets for both tcgsaseq and ROAST. At a 5% threshold, our approach tcgsaseq identifies three significant gene sets while the combination of voom and ROAST identifies none. Among those significant gene sets, two relate to T-cell gene expression, corroborating the original results from Dorr and others (2015). The gene set annotated as “T-cells” notably includes the gene CD3D, previously highlighted in Dorr and others (2015). On the other hand, gene sets related to transplant rejection such as “Donor-specific antibody” or “Gamma-IFN and Rejection” have much higher p-values here, which is what one would expect as these data include only successful transplant patients. Besides, tcgsaseq also detects a significant change in expression for the gene set related to Mast cells, which have recently been highlighted as playing an ambiguous role in kidney transplant (Papadimitriou and others, 2013). Mast cells have been linked both to peripheral tolerance (de Vries and others, 2009), as well as to late graft loss (Jevnikar and Mannon, 2008). These results both reinforce and broaden the original findings from Dorr and others (2015).

Fig. 5.

p-values from testing the 9 kidney oriented gene sets investigated.

6.2. Time-course RNA-seq comparative study of Arabidopsis arenosa physiology

In a recent experiment, Baduel and others (2016) measured time-course gene expression of the plant Arabidopsis arenosa through RNA-seq. They sampled 48 plants across 13 weeks at four different time points. Baduel and others (2016) were especially interested in the difference between two populations of Arabidopsis arenosa, respectively denoted KA and TBG, that have adopted different flowering strategies. In addition, half of the plants were exposed to cold and short day photoperiods (vernalization) between week 4 and week 10 in order to study the corresponding effect on flowering in both populations. Different plant siblings were sampled at each time point in order to avoid the important stress effect of leaf removal on the plants.

Dealing with this complex experiment design, we used tcgsaseq to address two separate biological questions: (i) which gene sets have a different activation between the two populations, adjusted for the plant age and the cold exposure, (ii) which gene sets have a different activation due to cold exposure, adjusted for population differences and plant age. Using two different modeling strategies, we found that one data-driven gene set constructed by Baduel and others (2016) from the top 1% differentially expressed genes between the two populations was significant at a 5% threshold for (i) and for (ii). On the contrary two other data-driven gene sets, again constructed by Baduel and others (2016) and identified as the respective population-specific responses to cold exposure, were both significant at this 5% threshold for (ii) but not for (i). In addition, two gene sets from Gene Ontology associated with salt and cold response pathways, respectively, were also investigated and found significant at the 5% level for (ii) but not for (i). In comparison, ROAST gave similar results for (i), but lacked power for (ii) identifying only 1 out of 4 significant gene sets. This analysis corroborates the results obtained by Baduel and others (2016), and it further illustrates the good behavior of tcgsaseq in complex time-course RNA-seq studies.

7. Discussion

The proposed method detailed in this article constitutes an innovative and flexible approach for performing GSA of longitudinal RNA-seq gene expression measurements. The approach relies on a principled variance component score test that accounts for the intrinsic heteroscedasticity of RNA-seq data, and for which we derive a simple limiting distribution without requiring any particular model to hold. As illustrated in the previous sections, the good performance of the method when applied to various datasets constitutes a major strength of the method.

Our numerical study shows the importance of accurately accounting for heteroscedasticity when analyzing RNA-seq data. We also demonstrate the robustness of our testing procedure to model misspecification. When comparing our proposed approach to ROAST, edgeR, and DESeq2, state-of-the-art methods, we illustrate the competing methods’ sensitivity to model misspecification, failure to control Type I error, and reduced statistical power compared to tcgsaseq.

Of particular biological interest in longitudinal studies, the proposed approach can test for both homogeneous and heterogeneous gene sets simultaneously. This is especially relevant for gene sets constructed from biological pathways encompassing both regulators and targets, where different expression dynamics are expected across genes. In addition, the proposed solution for accounting for heteroscedasticity can also deal with non-count data and could in principle be applied widely.

As demonstrated by the simulation studies, the proposed approach is also robust to inter-gene correlation within tested gene sets. While in our simulations we do not estimate inter-gene correlations, one could account for them more formally by following Wang and others (2009) and estimating a working correlation matrix with the residuals from an initial gene-wise modelling of 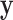. The resulting estimates could be incorporated into the structure of 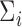to increase power.

This work features 4 important novelties: (i) we propose a statistically sound nonparametric estimation of the inherent mean-variance relationship in RNA-seq data; (ii) we present an original variance component score test statistic for which we derive an asymptotic distribution, and we show that it possesses the conventional root-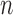 convergence rate despite the presence of a nonparametric estimator and is robust to model misspecification; (iii) we conduct a numerical study comparing the proposed method and illustrating its good statistical performances under various settings; (iv) we provide an implementation of the proposed method as an R package available to the community.

These innovations contrast with previous works from either Law and others (2014) or Hejblum and others (2015). While the nonparametric estimation of heteroscedasticity from Law and others (2014) is more of a heuristic procedure, our statistically rigorous approach does not include unmotivated transformations or extrapolation outside the range of the estimating function. Furthermore, we show that our test statistic has the conventional root-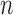 rate despite the presence of the nonparametric estimator. As for Hejblum and others (2015), they focus exclusively on microarray data and therefore completely ignore the heteroscedasticity issue. In addition, while the modeling proposed in this article is similar to theirs, our test statistic is completely different. While they rely on a likelihood ratio test, we propose an original variance component score test that remains valid even if the model was misspecified and is very fast to compute.

Finally, in this article, we focus primarily on longitudinal measurements of RNA-seq. However, our approach directly applies to virtually all RNA-seq study designs, including traditional case-control and more complex studies. Our approach allows researchers to incorporate the natural heteroscedasticity in the data into a powerful test statistic that makes no modeling assumptions. Of note, the inclusion of time-varying covariates would require further assumptions concerning the model to be made to ensure the limiting distribution of the test statistic. Evaluating tcgsaseq’s performance in a broader array of studies is an area for future research.

Software

Software is available on the Comprehensive R Archive Network as an R package tcgsaseq.

Supplementary material

Supplementary material is available at http://biostatistics.oxfordjournals.org.

Funding

This work was supported by the National Institutes of Health (NIH) [U54 HG007963 to B.P.H.].