Linear-In-Flux-Expressions Methodology: Toward a Robust Mathematical Framework for Quantitative Systems Pharmacology Simulators

Abstract

Quantitative Systems Pharmacology (QSP) modeling is increasingly used as a quantitative tool for advancing mechanistic hypotheses on the mechanism of action of a drug, and its pharmacological effect in relevant disease phenotypes, to enable linking the right drug to the right patient. Application of QSP models relies on creation of virtual populations for simulating scenarios of interest. Creation of virtual populations requires 2 important steps, namely, identification of a subset of model parameters that can be associated with a phenotype of disease and development of a sampling strategy from identified distributions of these parameters. We improve on existing sampling methodologies by providing a means of representing the structural relationship across model parameters and describing propagation of variability in the model. This gives a robust, systematic method for creating a virtual population. We have developed the Linear-In-Flux-Expressions (LIFE) method to simulate variability in patient pharmacokinetics and pharmacodynamics using relationships between parameters at baseline to create a virtual population. We demonstrate the importance of this methodology on a model of cholesterol metabolism. The LIFE methodology brings us a step closer toward improved QSP simulators through enhanced capture of the observed variability in drug and disease clinical data.

Introduction

In recent years, there has been increasing recognition of the need to develop drugs within the context of the specific patient biology and disease, in order for therapies to be better regarded as safe and effective.^1–3 One field that has arisen to address this need is Quantitative Systems Pharmacology (QSP), which has been increasingly used in the industry and has been gaining support from governmental agencies and academic programs.^1–4 Quantitative Systems Pharmacology involves the creation of mathematical models to represent the biological processes and mechanisms of a disease and its treatment and to connect molecular and cellular level processes to measurable clinical outcomes. Parameters of the model are informed by a combination of different data sources. Understanding the underlying structure across model parameters brings us a step closer to more rigorous parameter estimation and calibration of QSP models, as the number of parameters relative to available data presents obstacles to more traditional model fitting paradigms useful for smaller models.^2,5 By including detail in the model about the behavior and kinetics of the proteins or pathways that will be directly targeted by the treatment, and relating these mechanisms to clinical outcomes, QSP models are an important tool for identifying components of the biological background that will alter the efficacy and safety of a drug. In this way, QSP models can be used to investigate new targets for treatment and suggest potential combination therapies that would improve drug response.

Quantitative Systems Pharmacology models have been developed in many different disease areas,⁵ such as dysregulation of cholesterol,^6–8 human immunodeficiency virus,⁹ and rheumatoid arthritis.^10,11 They have been successfully used to inform selection of drug candidates by connecting predictions of safety and efficacy or by comparing predicted efficacy of a new therapy to the standard of care.³ To fully use this type of model, we not only need to understand the biology and response to therapy of an “average” patient but also be able to represent and explore the spectrum of disease phenotypes present in the larger population so that we can predict how these populations will differ in their response to therapies of interest.^1,5 However, the best methodology for generating representative and useful virtual subpopulations for a disease is still up for debate.

Variability in patient response to drug can be caused by many diverse aspects of a patients’ background biology, which are not always well understood; thus it is not straightforward to qualify and represent this variability in a QSP model.^1,5 Virtual patient (VP) constructs in QSP models consist of different parameterizations of the model which produce a range of possible responses to therapy reflecting the range of clinical responses.¹² The approach to creating virtual populations generally includes the following: selection of parameters which have the most impact on model output to individually vary across VPs, optimization of these parameters to fit the biological range measured in clinical data, and qualification of this parameter choice, often by testing the model on a new clinical data set.^7,9,10,12 The rationale for the initial choice of parameters is somewhat arbitrary and is not often discussed in detail. Correlation between parameters can be estimated and included in the model¹⁰ but is often expected to be 0 or very low,^9,10,12 and the process of including parameter covariance is not systematically handled for all parameters.

Existing VP methods have led to insights about patient populations. For example, by analyzing the VPs that best responded to rituximab, Schmidt et al¹⁰ identified patients with low IFN-β production rates as the best responders, which was in agreement with clinical reports. The effectiveness of anti-PCSK9 therapy in patients on statin background or with impaired low-density lipoprotein receptor (LDLR) function has been analyzed using VP methodology previously,⁷ predicting that patients on statins will be better treated than patients with no statin exposure, and patients with low functional LDLR will be low responders to therapy. Our goal in this work is to build on these existing methods of VP creation using parameters identified as having a large effect on the model, but to use concepts from control theory¹³ to suggest an avenue for describing structural relationship among parameters and systematically propagating variability in identified parameters throughout the system to create VP profiles representative of the full range of variability in response that we can anticipate from measurably similar patients. This will help us not only to predict patient response but also to understand the key mechanisms controlling the effectiveness of therapy in patient populations.

We demonstrate the use of the Linear-In-Flux-Expressions (LIFE) by applying it to a model of cholesterol metabolism, described in detail in this issue.¹⁴ Many different types of patients have high cholesterol levels; patients have different comorbidities and respond differently to available therapies. Our current work discusses the development of virtual populations of patients whose cholesterol is effectively lowered by statin therapy (“statin responders”) or patients who are not treated effectively by statin therapy (“statin nonresponders”). We show that our approach will create 2 virtual populations with distinct responses to anti-PCSK9 therapy, and that within each population, patients may have the same baseline values, but response to therapy will vary around the mean population value. The methodology described in this article was developed with the recognition that patients with the same baseline clinical levels at the start of a trial may respond in different ways to treatment. We aim not only to optimize the parameters that control typical response of a patient to drug but also to understand the myriad different ways in which a patient can come to have the same clinical levels before treatment. Through this understanding, we can predict how these different biological characteristics will alter the effect of treatment, and how we can better differentiate and treat patient subpopulations.

Methods

The LIFE method gives us a systematic way to define structural relationships between model parameters

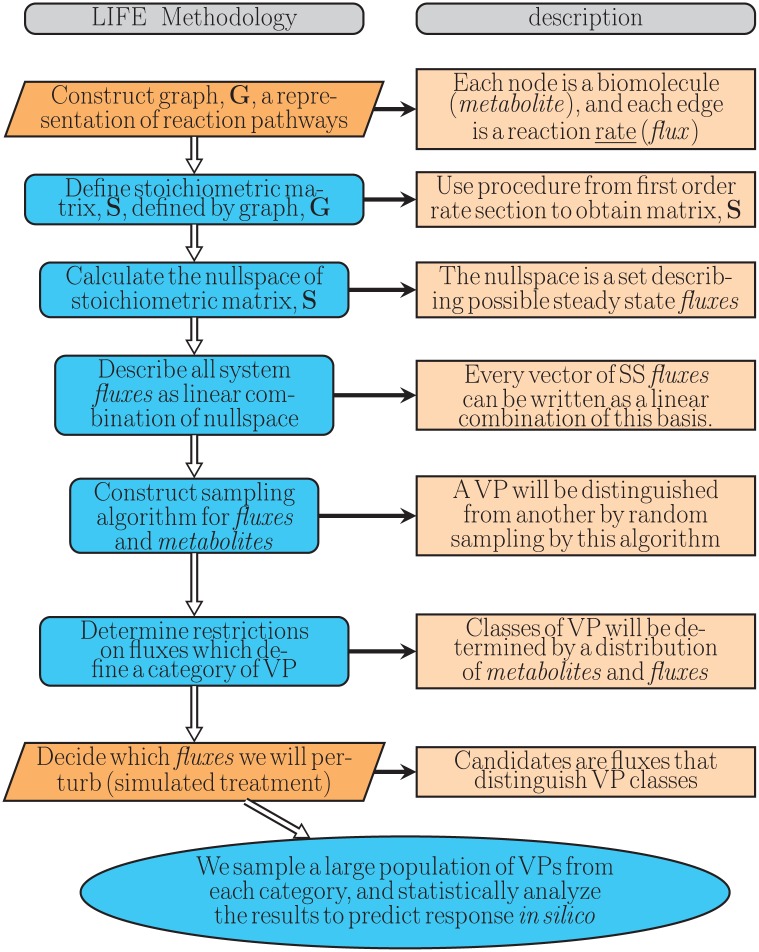
We refer to this technique as the “LIFE” method (Figure 1). The LIFE method begins by precisely defining a network of biochemical reactions (metabolism) as a graph, where the nodes are reactants/products of metabolic reactions; the edge labels represent reaction rate constants. We describe a system of ordinary differential equations (ODEs) which governs the quantities of biochemical molecules over time.

Figure 1.

Outline of the LIFE algorithm used to model human lipid metabolism and generate VPs. The orange steps indicate steps of the algorithm requiring supervision, whereas blue steps can be automated. LIFE indicates Linear-In-Flux-Expressions; VP, virtual patient.

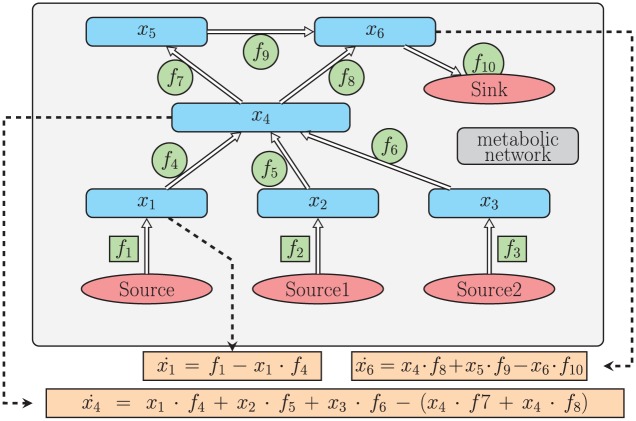
In Figure 2, a simple graph of a metabolic network is shown. In this network, there are 6 metabolites $X=x_i\left|\right\{i=1,2,\dots ,6\}$. ${\stackrel{·}{x}}_i$ indicates the time derivative of metabolite, $x_i$. Although the system itself can be generally nonlinear, it is linear with respect to the flux, and we represent the system as a matrix multiplied by a vector of fluxes:

Figure 2.

Example metabolic network. Each node represents a biomolecule, or metabolite and each edge represent a rate constant, or flux. From this graph, we obtain a system of ordinary differential equations that govern metabolite levels over time.

$$\stackrel{·}{X}=\left(\begin{array}{cccccccccc}1& 0& 0& -x_1& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& -x_2& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& -x_3& 0& 0& 0& 0\\ 0& 0& 0& x_1& x_2& x_3& -x_4& -x_4& 0& 0\\ 0& 0& 0& 0& 0& 0& x_4& 0& -x_5& 0\\ 0& 0& 0& 0& 0& 0& 0& x_4& x_5& -x_6\end{array}\right)\cdot \left(\begin{array}{c}{f}_1\\ f_2\\ f_3\\ f_4\\ f_5\\ f_6\\ f_7\\ f_8\\ f_9\\ f_{10}\end{array}\right)$$ (1)

In Figure 2, the fluxes inside squares $(f_1,f_2,f_3)$ represent constant source terms, whereas those in circles are the rates of first-order reactions. Specifically, the amount of $x_1$ (in units of nmol) molecules increases at a rate of $f_1$ (in units of nmol/h). This gives us the first term on the right-hand side of ${\stackrel{·}{x}}_1$. The other term in ${\stackrel{·}{x}}_1$ is “$x_1\cdot f_4$” This term represents the conversion of metabolite $x_1$ into $x_4$ at the rate $f_4$. All 6 equations ${\stackrel{·}{x}}_1,\mathrm{\dots },{\stackrel{·}{x}}_6$ govern the dynamics of our example system. We write this system as follows:

$$\stackrel{·}{X}=S(X)\cdot f$$

$S(X)$ is a matrix dependent on metabolite values, $X$. $S(X)$ is referred to as the “stoichiometric matrix.” Traditionally, this type of system is modeled differently, whereby the system is written $\stackrel{·}{X}=S(f)\cdot X$, as in Mirzaev and Gunawardena.¹⁵

For this example, $S(X)$ is a $6\times 10$ matrix. The entries of this matrix are either real numbers or algebraic expressions of variables (representing metabolite values), and $f$ is a vector composed of all 10 rate constants, called fluxes: $(f_1,\dots ,f_{10})$ (Figure 2). A similar method for modeling biochemical networks is explained in the study by Palsson.¹⁶

We may write this system of 6 ODEs from our example matrix in equation (1). One advantage of writing our system this way is we can calculate the null-space for large systems, as in the study by Palsson.¹⁶ The null-space of $S$ is a set of flux vectors which describe the steady states of a system. We call an element of this set $\widehat{f}$. These vectors are special in the sense that the following equation holds for all $\widehat{f}$:

$$S(X)\cdot \widehat{f}=0$$ (2)

$\widehat{f}$ in equation (2) leads to steady-state dynamics because the metabolite levels do not change over time. For each $\widehat{f}$, there are many configurations of metabolites which will remain in steady state. This steady state represents the disease state maintained for a patient on standard of care therapy or not on treatment. Regimens such as PCSK9 inhibitor therapy perturb the system dynamics and can lead to a new steady state reflecting the treatment effect. We calculate the null-space of $S(X)$ for Figure 2 as follows:

$$\hat{f}=a_1\left[\begin{array}{c}{x}_6\\ 0\\ 0\\ \frac{x_6}{x_1}\\ 0\\ 0\\ 0\\ \frac{x_6}{x_4}\\ 0\\ 1\end{array}\right]+a_2\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \frac{x_5}{x_4}\\ \frac{-x_5}{x_4}\\ 1\\ 0\end{array}\right]+a_3\left[\begin{array}{c}-x_3\\ 0\\ x_3\\ \frac{-x_3}{x_1}\\ 0\\ 1\\ 0\\ 0\\ 0\\ 0\end{array}\right]+a_4\left[\begin{array}{c}-x_2\\ x_2\\ 0\\ \frac{-x_2}{x_1}\\ 1\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right]=\left[\begin{array}{c}{a}_1{x}_6-a_3{x}_3-a_4{x}_2\\ a_4\cdot x_2\\ a_3\cdot x_3\\ \frac{a_1{x}_6}{x_1}-\frac{a_3{x}_3}{x_1}-\frac{a_4{x}_2}{x_1}\\ a_4\\ a_3\\ \frac{a_2{x}_5}{x_4}\\ \frac{a_1{x}_6}{x_4}-\frac{a_2{x}_5}{x_4}\\ a_2\\ a_1\end{array}\right]$$ (3)

In equation (3), we can see the null-space for our matrix from the system shown in Figure 2. Note that there are 4 free variables, $a_1\mathrm{,}{a}_2\mathrm{,}{a}_3\mathrm{,}{a}_4$, in this null-space for any fixed set of metabolite levels, X $X$. We call these free variables as “core parameters”:

$$\begin{array}{l}\mathrm{Let}{\widehat{f}}_i\mathrm{be\; the}i\mathrm{th\; element\; of}\widehat{f}\\ {\widehat{f}}_5=a_4\\ {\widehat{f}}_6=a_3\\ {\widehat{f}}_9=a_2\\ {\widehat{f}}_{10}=a_1\end{array}$$ (4)

The advantage of this representation is that we are able to identify fluxes in the model that are independent, as well as fluxes that are dependent, or calculated from other fluxes. The independent subset of fluxes facilitates the identification process for parameters, so that fewer parameters must be given values based on the literature or available data. Thus, by bounding the core parameters of the null-space, we generate bounds for the remaining fluxes. To randomly sample a set of fluxes $f$, we randomly choose a’s that represent the flux $f$, as shown in Figure 2. Choosing all coefficients this way permits us to randomly sample fluxes in the steady state of the system.

Remark

The basis (4 vectors) shown in equation (3) is not unique; however, we view the null-space of the system with respect to these fluxes.

VP generation

Traditional approach for VP generation

To demonstrate the advantages of the LIFE method, we contrast our approach for generating VPs to a standard approach used in the literature. In both approaches, we begin with a parameterization of the model that has been calibrated to the average patient response. In the traditional approach, key fluxes that have been identified to prominently contribute to variability in the model are sampled to create a patient population. Typically, bounds are placed on the parameters of interest based on experiments or guidelines in the literature, and some type of optimization or weighting is used to narrow down which parameter values within these bounds are feasible based on how simulated trajectories compare with clinical data.^7,9,12 In this work, we aim to evaluate the performance of the LIFE method, rather than to validate the QSP model to which this method is applied, so we use a simpler traditional VP method for comparison. The traditional approach we implement does not use clinical data to tailor results but generates all results proscribed by the model based on the parameter values given and constrained by physiological knowledge of plausible output ranges. We sample key flux values from lognormal distributions, using the optimized parameter values as the mean and the same sigma value (set to 0.25 in these simulations). Once the key flux values are chosen, the simulation is run to generate VP response.

LIFE method approach

We again start with the objective of introducing variability into the identified key fluxes of the model, but do this by directly varying the core fluxes in the null-space which control the variability of the key fluxes (equation (4)). If multiple fluxes in the null-space control variability for a key flux, we choose to vary the null-space flux with the largest effect. In inducing variability in the null-space flux parameters, our goal is to sample randomly from a lognormal distribution. To sample from a distribution that reflects variability in the clinical data, our approach needs to envelope the observed variability while remaining within known physiological bounds and maintaining positivity for all fluxes.

A sample flux $s$ is called “suitable” if it satisfies the inequality:

$$0.5\times \overline{f}\le s\le 1.5\times \overline{f}$$ (5)

where $\overline{f}$ is the average value of the flux we are sampling.

For a parameter, our goal is to find a standard deviation for our sampling distribution such that it will generate a “suitable” $s$ with a 95% confidence interval. A standard deviation for a parameter is found when all fluxes dependent on the parameter generate “suitable” sample at least 95% of the time.

To evaluate the standard deviation of a parameter $(a_1)$ we use a simplified “importance sampling.”¹⁷ We choose equally spaced values from the 2.5th percentile of the lognormal distribution to the 97.5th percentile. From these chosen values, we observe which fluxes, which are dependent on $a_1$, are “suitable” fluxes. This is depicted in Figure 3. If the total number of “suitable” fluxes dependent on $a_1$ is below 95%, we decrease our standard deviation, $\sigma$, effectively narrowing the sampling distribution; if the number of “suitable” fluxes is above 95%, we increase $\sigma$.

Figure 3.

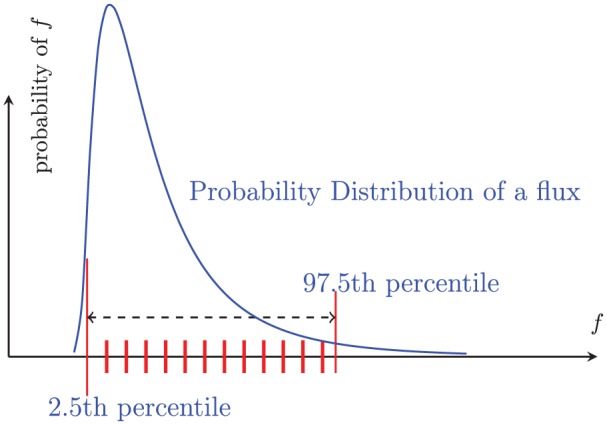
An example of “importance sampling.” The blue curve is a sampling distribution of a flux f. To estimate the range of fluxes resulting from a sample, we calculate fluxes dependent on f using the red tick marks, which are equally spaced from 2.5th percentile to the 97.5th percentile.

For example, in equation (3), the fluxes dependent on $a_1$ are ${\widehat{f}}_1\mathrm{,}{\widehat{f}}_4\mathrm{,}{\widehat{f}}_8\mathrm{,}$ and ${\widehat{f}}_{10}$.

For each VP, extra bounds may be needed to ensure that all fluxes are positive. The 9 fluxes we sample determine other flux values to guarantee that our system has a steady state.

The standard deviations in Table 1 do provide more than 90% confidence that all fluxes are between $0.5\overline{f}$ and $1.5\overline{f}$; however, for simple cases, we add several strict bounds to be sure that a flux is not sampled in a way that will cause another flux to be negative (Supplementary Table 1).

Table 1.

Standard error ($\sigma /\mu$; σ = standard deviation, µ = mean) of flux sampling distributions for each VP class.

	f 1	f 2	f 3	f 4	f 5	f 6	f 7	f 8	f 9
VP0	1.2545	0.7855	0.2020	0.0466	152.1765	17.5696	0.7536	3.4829 10−6	2.9733
VP1	1.3230	0.8745	0.2910	0.0365	97.6538	12.2185	0.7536	4.4700 10−7	0.6412
VP2	1.2310	0.6585	0.2900	0.0365	97.6538	12.2185	0.7536	7.4850 10−6	0.5211
VP3	1.3170	0.5575	1.0420	0.0361	97.6538	12.2185	0.7389	4.3671 10−6	0.6154
VP4	1.4870	1.1310	0.0117	0.0370	97.6538	12.2185	0.7608	6.4475 10−6	3.7740

Abbreviation: VP, virtual patient.

f₁ = rate constant for the trafficking of newly synthesized low-density lipoprotein receptor (LDLR) to the surface of peripheral cells.

f₂ = rate constant for the trafficking of newly synthesized LDLR to the surface of hepatocytes.

f₃ = rate constant for the clearance of PCSK9 from the plasma.

f₄ = PCSK9 LDLR internalization rate in peripheral cells.

f₅ = rate constant for the exchange of cholesterol from high-density lipoprotein (HDL) to low-density lipoprotein.

f₆ = rate constant for the exchange of cholesterol from HDL to very-low-density lipoprotein.

f₇ = PCSK9 LDLR association rate in plasma.

f₈ = rate of cholesterol production by hepatocytes.

f₉ = rate constant for secretion of biliary cholesterol into the gastrointestinal tract plus bile acid cholesterol secretion rate k.

f₁₀ = PCSK9 intracellular to plasma release rate in hepatocytes. f₁₀ is dependent on the sample flux f₃.

We use this algorithm separately for each of 9 fluxes that we intend to sample. This method generated the following standard errors shown as $\sigma /\mu$ in Table 1. Once we have determined the distributions of each of the core null-space fluxes to use for our VP population, we use the following steps to run simulations of the VP population:

1. Sample each core null-space flux value from its distribution to generate values for these fluxes for each VP.

2. Calculate values for all fluxes in the model, using the VP-specific core flux values, and the constant values for the remaining fluxes in the null-space and the steady-state species values.

3. Run the simulation for each VP.

Results

LIFE methodology has 3 main benefits compared with the traditional way of defining populations of VPs

We have developed the LIFE method to create VP populations which are informed by the biological structure represented in the QSP model. Our approach has 3 main methodological advantages over the traditional approach (see “Methods” section for details on both LIFE and traditional methods for VP generation). Linear-In-Flux-Expressions first allows us to identify a subset of parameters which represent variability along the pathways controlling mechanistic phenotypes of disease, rather than leaving the choice of parameters to be more empirically evaluated. Once parameters are identified, LIFE allows us to represent the relationships between parameters so that their interdependence is systematically taken into account, and we do not need to assume that parameters are independent. Finally, when a perturbation is introduced into the system (such as a drug), the LIFE method gives us a mechanistic way of understanding the impact of this perturbation on the network.

To compare the performance of our method with the traditional method used to simulate VP response to therapy, we apply both approaches to a QSP model of cholesterol metabolism, which encompasses the processes of lipoprotein creation and transfer of cholesterol, the role of PCSK9 in regulating LDLR levels, and the action of statin or PCSK9 inhibitor therapy in this system.¹⁴ In the original development of the model, we identified 12 parameters which could be used to define 2 typical patient profiles (Table 2)—the first represents a patient treated effectively by statin therapy (“statin responder”) and the second of which represents a patient who is poorly treated by statins (“statin nonresponder”). Although the creation of these 2 patients allowed us to gain insight into the most important individual mechanisms for statin response, these patient profiles represented extreme examples of response or nonresponse and do not give us an understanding of how a representative population of patients with different underlying biological characteristics would fall between these extremes. It further did not allow us to predict which of these patient populations would be best treated by a different therapeutic intervention, such as PCSK9 inhibitors, which could be beneficial for patients on statin with elevated levels of PCSK9.¹⁸ We demonstrate here how the performance of the traditional vs the LIFE virtual population methods compare in generating populations of statin responders and nonresponders in terms of the 3 key areas described above: identification of key model parameters, representation of relationships between parameters, and prediction of the systemic effect of a perturbation to the model.

Table 2.

Identified and core parameters defining variability in virtual patients.

Name of flux identified to define variability in virtual patients	Control flux used to set variability in identified flux
Biliary cholesterol secretion rate	Biliary cholesterol secretion rate
Hepatic cholesterol production rate	Hepatic cholesterol production rate
HDL to VLDL exchange rate	HDL to VLDL exchange rate
HDL to LDL exchange rate	HDL to LDL exchange rate
PCSK9 plasma clearance rate	PCSK9 plasma clearance rate
Hepatic intracellular production rate of PCSK9	Rate of hepatic secretion of intracellular PCSK9 into plasma
Hepatic intracellular production rate of LDLR	Rate of peripheral cell intracellular LDLR trafficking to cell surface
Peripheral cell intracellular production rate of LDLR	Rate of hepatic intracellular LDLR trafficking to cell surface
Isolated LDLR degradation rate in hepatic endosomes	Rate of hepatic intracellular LDLR trafficking to cell surface
PCSK9-LDLR dissociation rate in endosomes	PCSK9-LDLR association rate in plasma and PCSK9-LDLR peripheral cell internalization rate
PCSK9-LDLR dissociation rate in plasma	PCSK9-LDLR association rate in plasma and PCSK9-LDLR peripheral cell internalization rate
Isolated LDLR degradation rate in peripheral cell endosomes	Rate of peripheral cell intracellular LDLR trafficking to cell surface

Abbreviations: HDL, high-density lipoprotein; LDL, low-density lipoprotein; LDLR, low-density lipoprotein receptor; VLDL, very low-density lipoprotein.

LIFE methodology can be used to identify parameters controlling variability along key mechanistic pathways

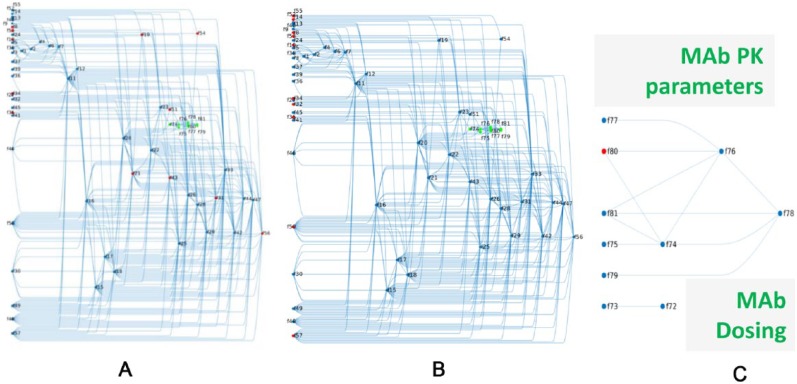
We represent the model at steady state as a network of “fluxes,” representing the rates at which different biological processes are conducted. This representation allows us to see the interconnections between these processes and to calculate how a change in one rate can be compensated by changes in the kinetics of other processes to maintain the same steady-state biology. The placement of the identified typical patient parameters within the network representation of the cholesterol model is shown in Figure 4A. Within this network, all independent fluxes defining the null-space are on the left side of the graph; fluxes past this left side of the graph are defined as a linear combination of the independent fluxes. Some subnetworks can be identified in this depiction, such as the cluster of fluxes controlling absorption of dietary cholesterol in the top-left corner (f₁-f₉) and the cluster of fluxes related to the antibody (in green). Overall, one can see that there are many interconnections between different processes in the model and that fluxes chosen to define pharmacodynamics (PD) variability in VPs are located in different places throughout the network (colored in red, Figure 4A).

Figure 4.

From the original set of identified virtual patient–defining parameters, LIFE method determines a core set of parameters which control this variability in the model. The Quantitative Systems Pharmacology model of cholesterol synthesis can be represented as a network of fluxes (f’s). The null-space defines a connectivity matrix between all reaction rates (f’s) of the model and the core f’s controlling the variability in the model. (A) highlights (in red) the 12 reaction rates originally identified to define virtual patients within this network context. (B) shows core fluxes (in red) used to control variability in network approach. The target-mediated drug disposition model of anti-PCSK9 inhibitor is incorporated into the model (green nodes) and is shown in isolation in (C). One flux was used to create variability in the PK portion of the model (shown in red). LIFE indicates Linear-In-Flux-Expressions; PK, pharmacokinetics.

Using LIFE, we found the 10 core independent parameters included in the null-space of the system, controlling variability in the 12 identified typical patient fluxes (Table 2 and Figure 4B). Some of the fluxes identified to define VPs were confirmed to be core parameters, such as those fluxes controlling reverse cholesterol transport (f₃₄ and f₃₅). In other instances, core parameters differed from the identified parameters and may appear to be less evenly distributed across different parts of the network. This is because in subsections of the model without any core parameters, variability could be induced through interconnections to other parts of the model (Figure 4B).

We also represent the pharmacokinetic (PK) parameters in the model as fluxes in part of the larger network (in green, Figure 4A). The drug dose is included as a flux and is connected only to the rate of drug absorption (Figure 4C, f₇₂ and f₇₃, respectively). The other parameters defining the PK model for the anti-PCSK9 antibody (MAb) are dependent on the steady-state level of PCSK9 but form an interconnected network that is independent of the fluxes involved in the PD part of the model. We choose to vary the rate of MAb-PCSK9 elimination to simulate variability in patient processing of drug (indicated in the network as f₈₀ in Figure 4C) which will be propagated through to the 2 direct connections of this flux, f₇₄ and f₇₆.

LIFE approach results in less variability in simulated outputs because the interdependencies among parameters are taken into account. This allows for better differentiation of statin responder and nonresponder virtual populations

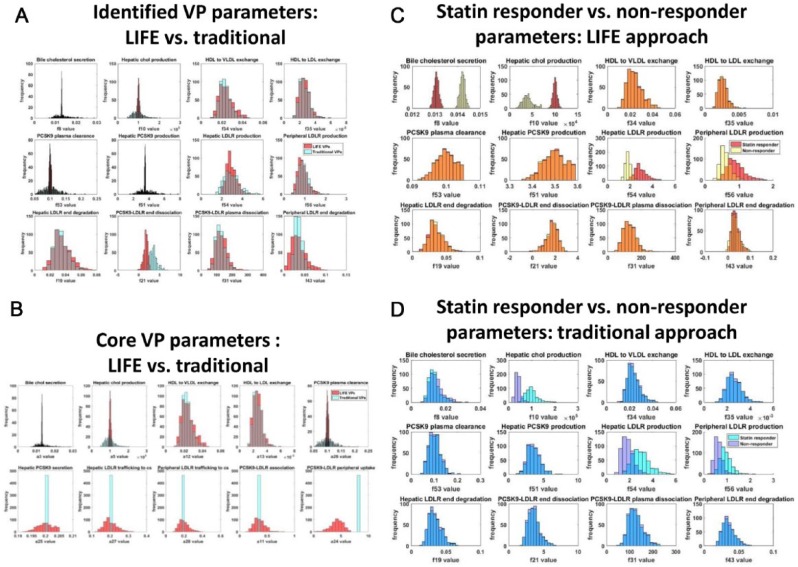
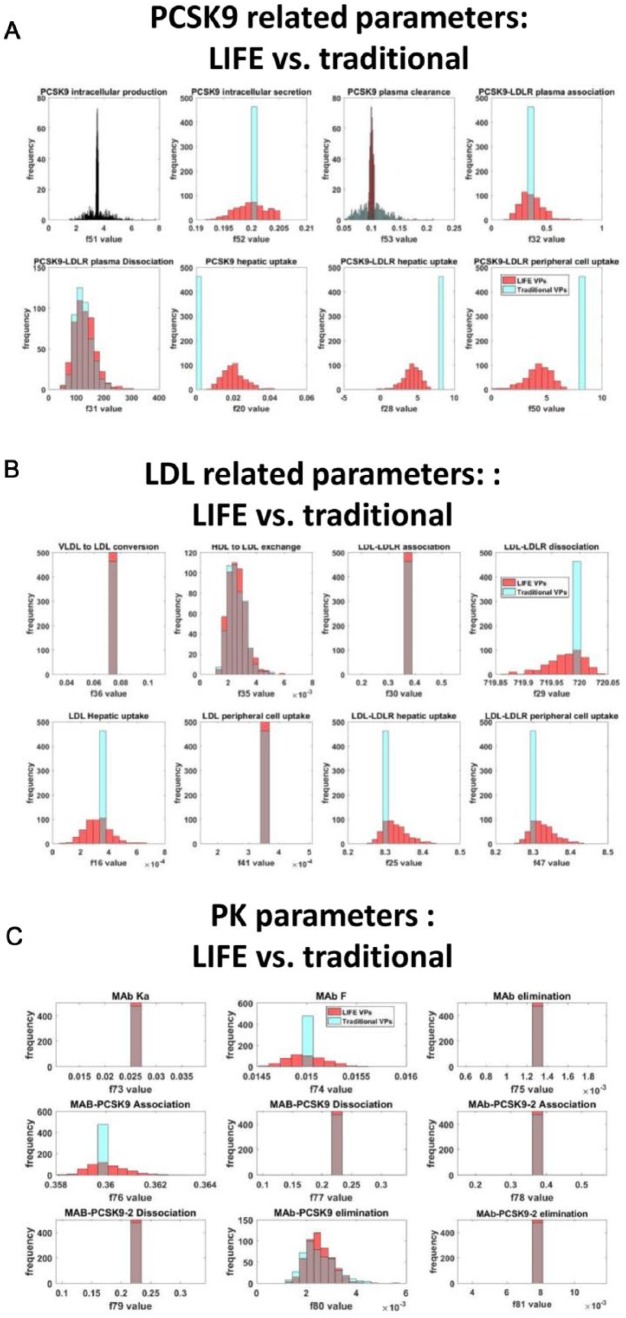
We induced variability in the key model parameters using the LIFE method or the traditional VP approach. Lognormal distributions were created for each of the identified parameters through both methods, but the distributions were noticeably different for some parameters (Figure 5A). The LIFE method generates variability in the values of core parameters that govern the variability in the original 12 VP fluxes rather than the original parameters themselves (Table 2, Figure 5B), which contributes to the different distributions seen in 7 of the identified VP parameters which are not directly varied in LIFE (Figure 5A, bottom row and last 3 plots of middle row). For the other 5 identified VP parameters, particularly for the bile cholesterol secretion, hepatic cholesterol production, and PCSK9 plasma clearance rates (Figure 5B), distributions generated by LIFE are significantly narrower (10-fold lower in range) due to restrictions on what parameter values are physiologically relevant when parameter relationships are considered (distribution parameters given in Table 1 and further constraints imposed to ensure positivity of all fluxes given in Supplementary Table 1). This is of key importance in creating virtual populations which distinguish the statin responder and nonresponder virtual populations. Because of the very limited range for the bile cholesterol secretion rate and hepatic cholesterol production rate generated by the LIFE method, we can clearly distinguish that the distinct values for these parameters define the main difference between statin responders and nonresponders across the identified fluxes (Figure 5C, top left plots). This distinction is strongly reduced in the traditional VP method because of the uniformly wide distributions generated for all parameters (Figure 5D). Using the traditional approach, the distribution of bile cholesterol secretion rates is nearly identical between statin responders and nonresponders, and the intersection between distributions generated for hepatic cholesterol production, and hepatic and peripheral LDLR production rates is noticeably larger in the traditional method. Comparing the virtual population parameterizations generated by these 2 methods (Figure 5C and D), we can predict that the distinct responses of statin responder and nonresponder subpopulations will not be well preserved using the traditional approach.

Figure 5.

Both LIFE and traditional VP methods generate variability around parameters originally identified to define VPs. However, the LIFE method also creates variability in other key model parameters, and it generates different parameter distributions for identified parameters. Parameter distributions were generated either by individually varying identified VP-defining fluxes (blue, cyan) or using LIFE method (red, yellow) to vary core fluxes controlling variability in the network and to calculate values for parameters dependent on these fluxes. Plots show overlaid histograms of the parameter value distributions generated with both approaches for (A) identified VP-defining parameters, defining the statin responder population and (B) core parameters controlling variability in the model for the statin responder population. In (C and D), identified VP-defining parameter distributions are shown for (C) the LIFE method, using parameter values for a typical statin responder (red) vs nonresponder (yellow) patient and for (D) the traditional method, using parameter values for a typical statin responder (cyan) vs nonresponder (blue) patient. Unstable or unphysiological simulations (with final LDL > 300 mg/dL) were excluded from plots. HDL indicates high-density lipoprotein; LDL, low-density lipoprotein; LDLR, low-density lipoprotein receptor; LIFE, Linear-In-Flux-Expressions; VLDL, very low-density lipoprotein.

To gain insight from these parameterizations of the model into how each patient will react to a PCSK9 inhibitor therapy, we can look at parameters altered in the production and clearance pathways that are most important in controlling response to the new therapy (Figure 6). Using the traditional individual fluxes approach, we see that some of the identified parameters lie in the PCSK9 and low-density lipoprotein (LDL) pathways, including PCSK9 plasma clearance, PCSK9 intracellular production, PCSK9-LDLR dissociation, and high-density lipoprotein (HDL) to LDL exchange rate, and will likely generate some variability in response to this new therapy. In the LIFE method, many of the core parameters used to control variability in the identified parameters are in the PCSK9/LDL pathways themselves, such as PCSK9-LDLR peripheral uptake (Figure 6A, bottom-right plot). In addition to these parameters, we see that variability has been propagated to all other parameters involved in PCSK9 production and clearance in the model using the LIFE method (Figure 6A), suggesting that PCSK9 biology is highly involved in statin response and that there is likely to be a variability in response to PCSK9 inhibitor therapy as well. Using LIFE, there is variability generated for 5 out of 8 parameters controlling LDL flux, whereas only HDL to LDL exchange rate is varied in the traditional approach (Figure 6B).

Figure 6.

The different VP approaches generate different levels of variability in key pathways of interest. Virtual populations based on the statin responder profile were created using the LIFE (red) and traditional (cyan) VP methods. Variability generated in (A) parameters controlling synthesis and clearance of PCSK9, (B) parameters controlling synthesis and clearance of LDL, and (C) pharmacokinetics-related parameters is shown. Unstable or unphysiological simulations (final LDL > 300 mg/dL) were excluded from plots. LDL indicates low-density lipoprotein; LDLR, low-density lipoprotein receptor; LIFE, Linear-In-Flux-Expressions, VP, virtual patient.

In the PK portion of the model, the same flux was used in both the traditional and LIFE VP approaches, the MAb-PCSK9 elimination rate (Figure 6C). However, in the LIFE method, variability was generated in 2 additional fluxes of the PK model due to connections across the network, representing relationships between parameters (Figure 6C). The implementation of the target-mediated drug disposition (TMDD) model in the LIFE framework and propagation of variability through parameters that will affect both the model PK (through MAb) and PD (through PCSK9) shows that the LIFE method can be used not only to represent relationships within the PD vs PK compartment but also to represent covariance of parameters across these categories.

LIFE prediction of the effect of PCSK9 inhibitor treatment on the biological network allows us to differentiate variability in patient response from variability in baseline values and to produce VPs who have reduced variability in key outputs of the model

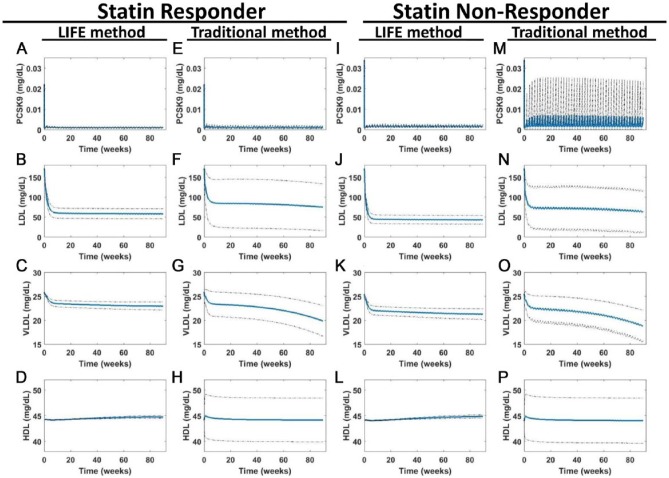
Although the traditional approach generates patient profiles with different baseline levels of lipoproteins and PCSK9 which can then be weighted or optimized based on the baseline distribution of patients in clinical trials, the LIFE method allows us to create a population of patients with the same baseline levels of lipoproteins and PCSK9, but with fundamentally different biology, based on the structure of the network represented in the model itself. We used both the traditional and LIFE approaches, for both statin responder and statin nonresponder patients to simulate population response to PCSK9 inhibitor treatment (Figure 7). Subcutaneous administration of a 150-mg dose of the PCSK9 inhibitor was simulated every 2 weeks from baseline to 90 weeks. At this point, outputs of the LIFE method appeared to be in a steady state (on drug), but there were some continuing downward trends in the very-low-density lipoprotein (VLDL) levels of VPs created by the traditional approach. Overall trends predicted by both approaches were similar; MAb therapy had an effect on all VPs, but of varying degrees. However, there were some key differences in the simulated outputs from virtual populations created under the 2 approaches.

Figure 7.

LIFE methodology minimizes variability by taking covariance between parameters into account and creates populations with the same baseline values but different drug responses. Simulations were run to simulate 90 weeks of once every two weeks dosing with 150-mg anti-PCSK9 antibody. Predicted outputs are shown for (A-H) statin responder and (I-P) nonresponder populations, created by fluxes using the traditional or using the LIFE network approach. Plots show the mean (in blue) ± SD (dotted line) of the virtual patient responses generated from each simulation of (A, E, I, and M) PCSK9, (B, F, J, and N) LDL, (C, G, K, and O) VLDL, and (D, H, L, and P) HDL. Unstable or unphysiological simulations (with final LDL > 300 mg/dL) were excluded from plots. HDL indicates high-density lipoprotein; LDL, low-density lipoprotein; LDLR, low-density lipoprotein receptor; LIFE, Linear-In-Flux-Expressions; VLDL, very low-density lipoprotein.

The traditional approach consistently inflated variability predicted for lipoprotein outputs over the LIFE methodology. This is readily apparent by comparing predictions of HDL using the LIFE approach (Figure 7D and L) and the traditional approach (Figure 7H and P). The LIFE approach predicts a very small level of variability in HDL throughout treatment, whereas the traditional approach creates a virtual population where the standard deviation of the distribution is 10% of the mean value. This is likely due to the variability added to parameters controlling transfer of cholesterol from HDL to LDL and VLDL through the reverse cholesterol transport (RCT) pathway (Figures 5A and B and 6B). In the traditional approach, this variability is not compensated for by changes to any other parameters in the model and has a disproportionate effect on HDL at baseline, which contributes to the wide HDL variability throughout the simulation. In contrast, the LIFE approach imposes variability across RCT-related parameters to balance out the HDL level (Figure 6B). Larger variability can also be seen in the populations predicted for LDL and VLDL using the traditional approach (Figure 7F, G, N, and O). The final standard deviation across VP simulations of LDL is 4.6 times larger (58.56 vs 12.62) using the traditional approach compared with the LIFE approach, for the statin responder population, and the standard deviation of VLDL is 3.9 times larger (3.17 vs 0.82). Again, this is a combination of variability at baseline and in response to drug. More VPs created this way develop unrealistic levels of LDL over time compared with the LIFE approach: 0 statin responder and 2 statin nonresponder VPs had final LDL levels > 300 mg/dL using the LIFE approach compared with 38 and 13 VPs using the first approach.

Overall, the LIFE approach allows us to better distinguish between the statin responder and nonresponder populations once a drug is given. The populations created by the traditional approach have a lot of variability in their response to drug, to the point where these 2 populations cannot be clearly distinguished. The HDL and VLDL responses seem to be nearly the same in both VP populations, and the range of LDL levels predicted for the statin nonresponder population by the traditional approach seems to correspond to the LDL in a subset of the statin responder population (Figure 7N to P vs F to H). Using the LIFE methodology, the population responses can be more clearly distinguished for statin responder and nonresponder populations. The LDL and VLDL mean responses are observably higher for statin responders after MAb treatment, and there is little overlap in the ranges of responses for both VPs (Figure 7B and C vs J and K). As we noted, the overlap between parameter distributions in statin responders and nonresponders generated by the traditional approach makes the parameterizations of these virtual populations less distinguishable and thus generates patient responses that are not distinct (Figure 5D vs C).

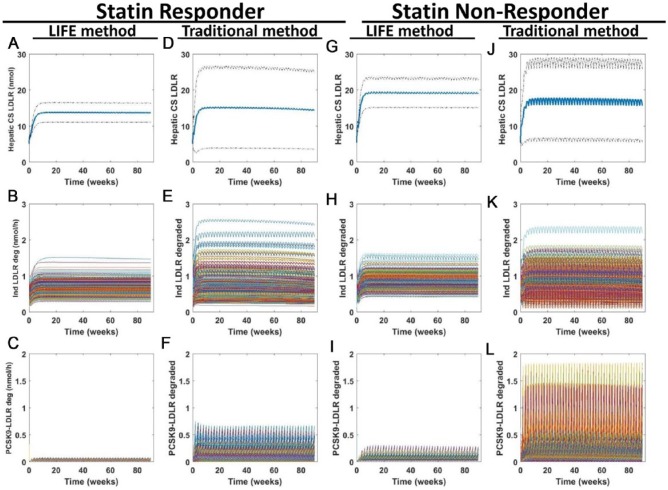
Low-density lipoprotein receptor expression level is key to the efficacy of PCSK9 inhibitor therapy. By examining LDLR levels at the cell surface and degradation of LDLR in both approaches, we can get insight into the mechanism of action of the therapy. We find that the statin nonresponder population gains a higher level of LDLR at the cell surface with treatment than the statin responder population (Figure 8A, D, G, and J) in accordance with the better response of this population to PCSK9 inhibitor therapy. In examining the degradation of LDLR in endosomes when it is alone or in complex with PCSK9 (Figure 8B, C, E, F, H, I, K, and L), we find that there is a similar range of LDLR degraded independently of PCSK9 for both VP populations, but that there is more variability in the amount of LDLR degraded in complex with PCSK9 over time for statin nonresponders using both approaches. For both populations, again, more variability is present in simulations using the traditional approach than in simulations from LIFE.

Figure 8.

Model predictions about LDLR again show increased variability predicted from simulations of a virtual population created using the traditional approach compared with the LIFE method. Simulations were run to simulate 90 weeks of once every two weeks dosing with 150-mg anti-PCSK9 antibody. Predicted outputs are shown for (A-F) statin responder and (G-L) nonresponder populations, created with (A-C, G-I) the LIFE approach or (D-F, J-L) the traditional approach. Plots of hepatic LDLR at the cell surface (A, D, G, and J) show the mean (in blue) ± SD of the VP responses generated from each simulation. Plots of the amount of LDLR degraded in the endosome per hour when isolated (B, E, H, and K) or in complex with PCSK9 (C, F, I, and L) show time courses for each VP. Unstable or unphysiological simulations (with final LDL > 300 mg/dL) were excluded from plots. LDL indicates low-density lipoprotein; LDLR, low-density lipoprotein receptor; LIFE, Linear-In-Flux-Expressions; VP, virtual patient.

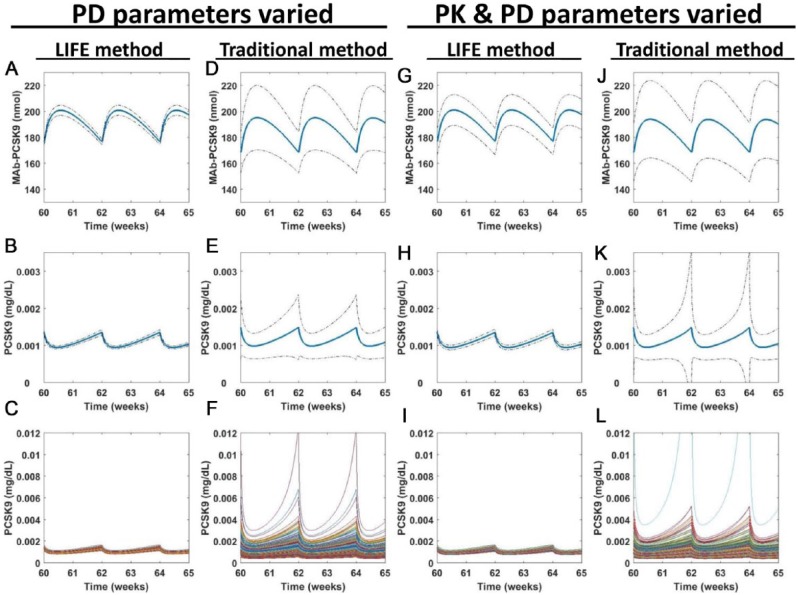
Finally, we can see the contribution of PK vs PD variability throughout the system using the LIFE method. We ran simulations of the model for 90 weeks of biweekly treatment with a 150-mg dose of the antibody. We compared outputs from simulations which included only PD variability with outputs where both PK and PD variability was used (Figure 9) and found that the additional influence of PK variability was evident in some but not all outputs. Because the PK of the antibody are represented as a TMDD model and are dependent on the levels of PCSK9 in plasma, there is some variability in the MAb-PCSK9 compound in the simulation where only PD variability is used (Figure 9A and D). This variability is noticeably enhanced when the PK variability is added (Figure 9G and J). Other MAb outputs from the model, such as free MAb in the plasma, did not noticeably change when PK variability was added (data not shown). Similarly, for lipoproteins, the effect of the included PK was not always noticeable, but in PCSK9, we noted an increase in the variability of predicted levels when PK was added (Figure 9H, K, I, and L compared with 9B, E, C, and F). Moreover, as we have consistently showed, the simulations of the traditional VP approach have much larger variability compared with the LIFE approach in both PK and PD simulations, inflating the contribution of PD variability on PK outputs such as MAb-PCSK9 concentration (Figure 9D) and making it more difficult to distinguish variability in response to treatment from variability in the original population.

Figure 9.

Key model outputs are influenced by both PK and PD variability. Simulations were run after using either the traditional or the LIFE approach to generate parameter distributions for use in the model. Simulations were based on the typical statin responder profile. Parameters varied included (A-F) PD parameters only or (G-L) PD and PK parameters. The simulation was run over a period of 90 weeks. 2.5 stable cycles once every two weeks MAb dosing are shown, for simulated levels of (A, D, G, and J) MAb-PCSK9 in plasma and (B-C, E-F, H-I, and K-L) PCSK9 in plasma. The mean (blue) ± SD (dotted black lines) values are shown in plots (A-B, D-E, G-H, and J-K), whereas individual virtual patient predictions are overlaid on the same plot in (C, F, I, and L). Unstable or unphysiological simulations (with final LDL > 300 mg/dL) were excluded from plots. LDL indicates low-density lipoprotein; LIFE, Linear-In-Flux-Expressions; PD, pharmacodynamics; PK, pharmacokinetics.

Discussion

We present a VP methodology which leverages the QSP model structure to derive relationships among parameters and uses these relationships to create VP populations, thus systematically taking into account the interdependence of parameters in the model. We show a method for sampling parameter values, which creates distributions for each parameter of interest that maximizes variability in the parameter space while constraining fluxes in the null-space to produce biologically reasonable values for all fluxes in the model. This will ensure that most of the simulations will produce results within the physiological range. The LIFE method propagates variability in key model parameters to other fluxes in the model, generating more variability in pathways of interest. These pathways can be analyzed with a view to a new therapeutic intervention, to predict the range of responses expected to a different type of treatment. Our methodology generates VPs with tighter ranges of variability around model outputs than the traditional method of VP creation, which uniformly predicts large variance in all model outputs. In this way, our method better maintains separation between distinct patient populations and allows us to see clearly what outputs will differ across VPs in response to treatment and which should not. We show that variability in both PK and PD parameters can be incorporated using this methodology so that interdependence of PK and PD parameters can be taken into account as well. This representation will allow us to systematically analyze whether patient response is due to properties of the drug that can be altered to make treatment more effective or whether there is an underlying biological cause of nonresponsiveness. Finally, it is important to note that VPs generated by the LIFE methodology can have the same baseline values, but different responses to drug, because drug response is dictated by the underlying processes which give rise to this state. By enabling us to systematically identify and analyze the factors controlling the different responses of patients with similar baseline clinical measurements to treatment, the LIFE method enables us to better understand what clinical data are needed to accurately identify drug responders.

A VP consists of a set of specific parameter values which represent different kinetic rates in a patient’s biology. To determine how the parameter values should vary across VPs, different approaches are used. Generally, a typical value or an upper and lower bound is set for each parameter based on what is known in the literature, and each parameter is sampled from a normal or uniform distribution within these bounds.^7,9,12 From this initial set of VPs, a subset is selected by comparing model predictions for these VPs with clinical baseline or time course data of key outputs and using a weighting scheme such as prevalence weighting¹⁹ to select patients who replicate the distribution of this data.^7,9,10,12 Thus, the distributions of parameters can be examined after the virtual population is defined, but there is no fundamental understanding of what the distribution and covariance of parameters should be. Using the LIFE methodology, we sample parameters in a directed way from a lognormal distribution and calculate the feasibility of the resulting parameter set by considering the values of other parameters generated from the core fluxes. We use a cost function which considers feasibility of the parameter set generated rather than the feasibility of the baseline patient values because we know that the baseline values will be equal to the steady-state values that we put into the LIFE method. Using this procedure, we demonstrated how the LIFE method can be useful for discerning the differential impact of key parameter values and treatment responses in distinct VP populations.

The LIFE method allows us to systematically include the structural relationship of parameters in the model by representing the relationships between the parameters at steady state. This representation tells us which parameters can be independently varied, and how these independent fluxes will propagate variability to other parts of the model through these relationships. This way of representing interdependence in the model is an advantage over current VP methodologies where this interdependence must be empirically explored for sets of parameters^9,12 or potentially estimated from the data set.¹⁰ The LIFE method allows the interdependence to be an intrinsic part of the parameter calculation. As shown in Figures 7 to 9, this results in outputs which have more realistic variability. This also helps to reduce the number of parameters in the model which can be used to generate variability in a VP response, better informing the initial choice of parameters to define a VP. Finally, it gives us mechanistic insight into how clinical steady-state levels will change based on different parameter values or on treatment with a new drug before we run the model.

Extensive work has been done in the field of population PK to model interindividual variability of parameters in the model by fitting the variance and covariance of PK and simple PD parameters to clinical data.²⁰ Many VP cohorts developed from QSP models are created by varying PD parameters affecting intrinsic patient biology, without considering PK variability.^9,10 The work by Gadkar et al⁷ simulates variability in both PD and PK parameters using the prevalence weighting method, but covariance between these parameters is not mentioned. The LIFE methodology is a novel approach to enable modeling of variability in PK and mechanistically specific PD parameters, where interdependence among these parameters is handled in the same coherent way as interdependence among PD parameters. This approach more accurately represents the different factors that can alter patient response. It is especially important for TMDD models, such as the one used for the anti-PCSK9 antibody in this work, because the clearance and transport of the drug are inextricably linked to the target.

Virtual patient methods in the literature focus on generating patients with a range of initial output values that are similar to the clinical range and distribution for each output.^7,12 This approach seeks to replicate the range of patients who enter into a trial, with different baseline levels across patients for key parameters. The LIFE method can be used to create population of subjects with a distribution of baseline measurements. However, the LIFE method was developed with the knowledge that patients with the same baseline levels may have vastly different responses to drug, meaning that the LDL and HDL of a patient at baseline are not enough to predict the efficacy of treatment for this patient. The LIFE method enables us to advance mechanistic hypotheses on the factors driving this variable drug response. We can create populations with the same baseline values but different biology to analyze the effect of biological and PK variability on treatment outcome. Previous work by Hosseini and MacGabhann⁹ shows some analysis of VPs with different parameterizations but a similar time course of disease progression, which speaks to this idea. Our methodology gives the user an analytical representation of this set of patients and an understanding of how they relate so that we can efficiently generate a population of these VPs using the flux relationship structure rather than numerically determining individual patient profiles empirically. This is of key importance in identifying responder subpopulations so that we can better target trial populations to include patients who have a higher probability of being treated by drug because of their underlying biology. This approach can also be connected to a disease progression model, to help us predict how patients with the same clinical end point levels in the short term will have different long-term outcomes.

We have demonstrated here the ability of the LIFE method to create VP populations and the advantages that it has over existing virtual population development methods, including more restricted variability in key identified parameters, enhanced variability in other parameters in relevant pathways, and more applicable range of therapeutic outcomes when both PK and PD parameters are varied. Our ultimate goal is to use this method to match clinical data for different patient subgroups and to hypothesize mechanistic characteristics likely to lead a patient to best respond to therapy. Existing methods for VP generation have been used to this effect,^7,9,10 and we would like to see what additional information can come from our understanding of the model as a system of connected fluxes. Our method can give insight into key parameters to use in optimizing parameter values and in generating VPs. In the QSP model presented here, from an original set of 101 parameters, our method generates 49 core fluxes which are independently responsible for variability in the model and can be used for VP creation. We would like to further develop our method to determine from these 49 parameters, which are most important to vary, and how many parameters are necessary to encompass all variability seen in the clinical data. We believe that the LIFE method can make a significant contribution toward improving the efficiency and robustness of existing VP methods and ultimately allowing for more comprehensive QSP simulators that advance mechanistic hypotheses ascertaining a drug’s mechanism of action, and disease mechanisms commensurate with drug mechanism of action, linking the right drug to the right patient.