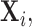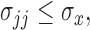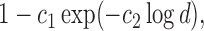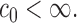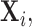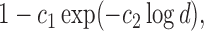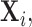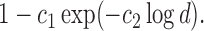Summary
This paper is motivated by the recent interest in the analysis of high-dimensional microbiome data. A key feature of these data is the presence of “structural zeros” which are microbes missing from an observation vector due to an underlying biological process and not due to error in measurement. Typical notions of missingness are unable to model these structural zeros. We define a general framework which allows for structural zeros in the model and propose methods of estimating sparse high-dimensional covariance and precision matrices under this setup. We establish error bounds in the spectral and Frobenius norms for the proposed estimators and empirically verify them with a simulation study. The proposed methodology is illustrated by applying it to the global gut microbiome data of Yatsunenko and others (2012. Human gut microbiome viewed across age and geography. Nature 486, 222–227). Using our methodology we classify subjects according to the geographical location on the basis of their gut microbiome.
Keywords: Classification, High dimension, Microbiome data, Missing data, Sparsity
1. Introduction
With the advancement of high-throughput technologies it is now common to encounter high-dimensional data where the number of parameters  exceeds the sample size
exceeds the sample size  . One of many such examples is the human microbiome data obtained by the 16s rRNA sequencing technology. The resulting data, known as operational taxonomic units (OTUs), represent counts of thousands of microbial taxa (Mandal and others, 2015). In this setting it is often of interest to investigate relationships among the microbes to understand their effects on health outcomes. These relationships can in turn be used to predict the health status of an individual based on his/her microbial composition.
. One of many such examples is the human microbiome data obtained by the 16s rRNA sequencing technology. The resulting data, known as operational taxonomic units (OTUs), represent counts of thousands of microbial taxa (Mandal and others, 2015). In this setting it is often of interest to investigate relationships among the microbes to understand their effects on health outcomes. These relationships can in turn be used to predict the health status of an individual based on his/her microbial composition.
Many such objectives can be achieved via the estimation of the covariance matrix  or its inverse, the precision matrix
or its inverse, the precision matrix 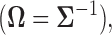 which characterize the dependence or the conditional dependence structure between variables, respectively. In the high-dimensional setting, estimation of
which characterize the dependence or the conditional dependence structure between variables, respectively. In the high-dimensional setting, estimation of 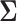 and
and 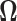 has been discussed extensively in the literature and the existing literature can be broadly classified into two categories, the first approach involves estimation of the precision matrix by exploiting its natural sparsity in comparison to the covariance matrix (Friedman and others, 2008; Rothman, Bickel and others, 2009; Cai and others, 2011). A limitation of this approach is that it does not apply to low-rank matrices
has been discussed extensively in the literature and the existing literature can be broadly classified into two categories, the first approach involves estimation of the precision matrix by exploiting its natural sparsity in comparison to the covariance matrix (Friedman and others, 2008; Rothman, Bickel and others, 2009; Cai and others, 2011). A limitation of this approach is that it does not apply to low-rank matrices 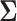 since the precision matrix does not exist in this case. The second popular approach is to estimate
since the precision matrix does not exist in this case. The second popular approach is to estimate 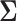 by assuming that
by assuming that 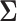 is itself sparse. One of several methods for this purpose is to threshold each element of the sample covariance matrix (Bickel and Levina, 2008; Rothman, Levina and others, 2009).
is itself sparse. One of several methods for this purpose is to threshold each element of the sample covariance matrix (Bickel and Levina, 2008; Rothman, Levina and others, 2009).
The current literature assumes the availability of independent and identically distributed (i.i.d.) copies of the vector 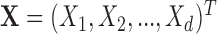 whose distribution is Gaussian or more generally sub-Gaussian with
whose distribution is Gaussian or more generally sub-Gaussian with 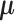 and
and 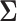 as the
as the 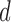 -dimensional mean vector and covariance matrix, respectively. Note that a real-valued random variable (r.v.)
-dimensional mean vector and covariance matrix, respectively. Note that a real-valued random variable (r.v.) 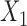 is said to be sub-Gaussian if there exists a
is said to be sub-Gaussian if there exists a 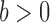 such that for every
such that for every 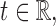 one has
one has 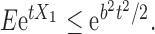
In contrast to typical high-dimensional data, not all variables (i.e. microbes) are observed in a sample of microbiome data. Thus if 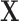 represents a vector of abundances of
represents a vector of abundances of 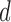 microbes in a specimen, then not all components of
microbes in a specimen, then not all components of 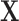 may be observed. We refer to this missingness as structural zeros, and it is due to the underlying biology and not due to error in measurement or values below the minimum detection level. For example, it is known that the bacterial genus Bacteroides is prevalent in the human gut when the associated diet is high protein/fat diet, whereas it may not be present otherwise, e.g. carbohydrate rich diet. The total abundance of such bacteria is coded as 0 counts in the observational vector
may be observed. We refer to this missingness as structural zeros, and it is due to the underlying biology and not due to error in measurement or values below the minimum detection level. For example, it is known that the bacterial genus Bacteroides is prevalent in the human gut when the associated diet is high protein/fat diet, whereas it may not be present otherwise, e.g. carbohydrate rich diet. The total abundance of such bacteria is coded as 0 counts in the observational vector 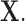
The missing structure required to model structural zeros is more general than typical notions of missingness in the literature. More precisely, in the classical notions of missingness, such as missing completely at random or missing at random (MAR), it is assumed that in place of 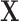 we observe a surrogate vector
we observe a surrogate vector 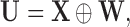 where
where  represents a component-wise product and
represents a component-wise product and 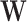 is a
is a 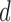 -dimensional vector of independent Bernoulli r.v.’s. In effect, not all components of
-dimensional vector of independent Bernoulli r.v.’s. In effect, not all components of 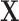 are observed in
are observed in 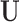 . For example,
. For example, 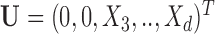 corresponds to the case where the first two components of
corresponds to the case where the first two components of 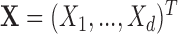 are not observed in
are not observed in 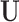 with
with 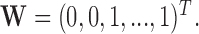 In this example, although
In this example, although 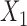 and
and 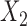 are absent in
are absent in 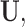 they still influence the distribution of the remaining components
they still influence the distribution of the remaining components 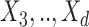 through the underlying dependence structure of
through the underlying dependence structure of 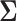 and are only hidden by the corresponding multiplicative Bernoulli noise vector
and are only hidden by the corresponding multiplicative Bernoulli noise vector 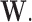 In contrast, for the case of structural zeros the observed vector itself is
In contrast, for the case of structural zeros the observed vector itself is 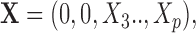 i.e. the first two components are truly absent from the observation and thus the missing components should not influence the distribution of the remaining components. It should also be noted from this example that in the latter case, implementing classical methods of imputation under such conditions would be a logical error due to the definition of a structural zero.
i.e. the first two components are truly absent from the observation and thus the missing components should not influence the distribution of the remaining components. It should also be noted from this example that in the latter case, implementing classical methods of imputation under such conditions would be a logical error due to the definition of a structural zero.
In this paper we introduce a framework which allows for structural zeros in the model and discuss consistent methods of estimating sparse high-dimensional covariance and precision matrices. We establish consistency in estimation of the proposed methodology and empirically support it with a simulation study. We also apply our methodology to classify observations to geographical locations based on the global human gut microbiome data of Yatsunenko and others (2012).
Some work related to ours in the literature is that of Kurkland and Heagerty (2005) who provide a regression setting for the analysis of longitudinal data truncated by deaths, here they make a similar distinction between zeros in response variable due to an individual dropping out of the study or due to death, in this context the zero due to death can be described as a structural zero in our definition. Estimation of covariance and precision matrices in the traditional missing values setting has also been discussed in the literature (Loh and Wainwright, 2012; Lounici, 2014; Kaul and others, 2016). As noted above and as shall become more apparent in the following sections, our model allows for a more general notion of missingness while assuming weaker conditions in comparison to typical notions of missingness.
2. Notations and framework
For any matrix 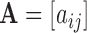 define the
define the 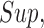
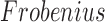 and
and 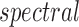 norms as
norms as 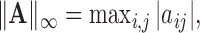
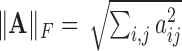 and
and 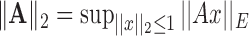 , respectively, where
, respectively, where 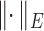 represents the usual Euclidean norm of a vector. We shall also require the matrix
represents the usual Euclidean norm of a vector. We shall also require the matrix 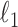 norm,
norm, 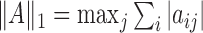 and the elementwise
and the elementwise 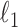 norm,
norm, 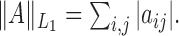 The notation
The notation 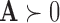 indicates the matrix
indicates the matrix 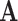 is positive definite and symbols
is positive definite and symbols 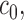
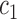 , and
, and 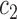 represent generic constants which may change according to the context but are independent of any model parameters. The notation
represent generic constants which may change according to the context but are independent of any model parameters. The notation 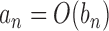 represents that
represents that 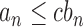 for some constant
for some constant 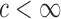 and
and 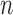 large enough. For any set of indices
large enough. For any set of indices 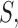 its cardinality is denoted by
its cardinality is denoted by 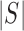 and for a subset
and for a subset 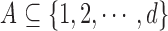 ,
, 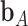 denotes the vector of components of
denotes the vector of components of 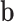 with indices in
with indices in 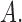 Finallyw we partition a
Finallyw we partition a 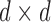 matrix
matrix 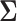 as follows:
as follows:
| (2.1) |
We begin by describing a framework that characterizes structural zeros. As stated in the previous section, these structural zeros represent components that are biologically absent in the specimen. Thus, the framework should allow for the distribution of the specimen to be determined by only the observed components. For this purpose, let 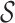 be the sample space of possible configurations of missing components be as follows.
be the sample space of possible configurations of missing components be as follows.
| (2.2) |
Here 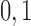 correspond to the cases where a component is unobserved or observed in the sample, respectively. We represent each of the above
correspond to the cases where a component is unobserved or observed in the sample, respectively. We represent each of the above 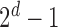 events of the sample space by Configuration (Config.)
events of the sample space by Configuration (Config.) 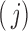 ,
, 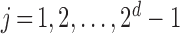 , in the order written in (2.2). For example, Config. (
, in the order written in (2.2). For example, Config. (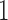 ) is the case where all components are observed and Config.
) is the case where all components are observed and Config. 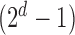 corresponds to the configuration where only the first component is observed. Assume for the
corresponds to the configuration where only the first component is observed. Assume for the 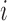 th sample, the missing structure is generated by independent r.v.’s
th sample, the missing structure is generated by independent r.v.’s 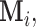
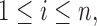 with sample space described in (2.2).
with sample space described in (2.2).
In many applications, including the analysis of microbiome data, it may be unreasonable to assume that the missingness is generated by identically distributed r.v.’s since this distribution function may be influenced by factors or covariates such as geographical location, age, race, and gender of the subject. We allow for this flexibility by defining the distribution of the r.v.’s 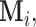
 as follows,
as follows,
| (2.3) |
Under this general definition each sample may have a different probability of each configuration. This feature of allowing the missingness to be acting independently but not identically is reminiscent of the MAR structure. We now proceed to define the conditional distribution of the observed components of a specimen.
Let 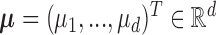 and
and 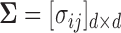 be a
be a 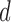 -dimensional vector and positive definite matrix, respectively. For the
-dimensional vector and positive definite matrix, respectively. For the 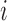 th subject, with missing configuration given by the r.v.
th subject, with missing configuration given by the r.v. 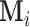 , we denote the observed components by the index set
, we denote the observed components by the index set
| (2.4) |
Note that the index set 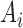 is a random set which is determined by the r.v.
is a random set which is determined by the r.v. 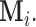 Now assume that conditioned on
Now assume that conditioned on 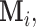 the components of
the components of 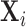 with indices in the index set
with indices in the index set 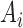 jointly follow a Gaussian distribution with mean and covariance being the corresponding sub-vector of
jointly follow a Gaussian distribution with mean and covariance being the corresponding sub-vector of 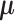 and sub-matrix of
and sub-matrix of 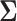 , respectively, i.e. for any
, respectively, i.e. for any 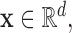
| (2.5) |
where 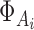 represents the Gaussian distribution function with mean
represents the Gaussian distribution function with mean 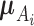 and covariance matrix
and covariance matrix 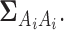 For example let
For example let 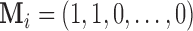 , then the observed vector is
, then the observed vector is 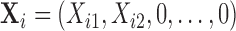 with the conditional distribution of the observed components as
with the conditional distribution of the observed components as 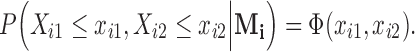 This completes the description of the distributional structure assumed in this paper. Under this definition, the zero components of an observation do not influence the distribution of the nonzero components, thus characterizing what we refer to as structural zeros.
This completes the description of the distributional structure assumed in this paper. Under this definition, the zero components of an observation do not influence the distribution of the nonzero components, thus characterizing what we refer to as structural zeros.
To proceed further we shall require the following definitions. For all 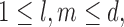 let
let 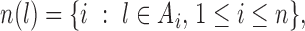 and
and 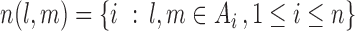 be the number of subjects where
be the number of subjects where 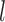 th component is observed and the number of subjects where both
th component is observed and the number of subjects where both 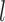 th and
th and 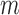 th components are observed, respectively. Note that these are random quantities determined by the random set
th components are observed, respectively. Note that these are random quantities determined by the random set 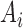 which in turn is determined by the r.v.’s
which in turn is determined by the r.v.’s 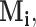
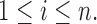 Also define for each observation
Also define for each observation 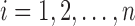 , and the indices
, and the indices 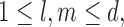 the collections,
the collections,
In the sequel we make the following additional assumption over the missing structure.
- (A1) There exists a constant
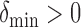 such that for any
such that for any 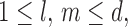
The condition (A1) is a mild assumption on the missing structure. If the r.v.’s 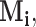
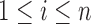 are assumed to be i.i.d., then (A1)(i) requires that each component is present in an observation with a nonzero probability, i.e.
are assumed to be i.i.d., then (A1)(i) requires that each component is present in an observation with a nonzero probability, i.e. 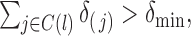 and (A1) (ii) requires that every pair of components are present in each observation vector with a nonzero probability, i.e.
and (A1) (ii) requires that every pair of components are present in each observation vector with a nonzero probability, i.e. 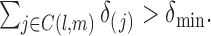
3. Methodology
In this section we discuss methodologies to estimate the covariance and precision matrices. First we provide a 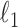 minimization approach to estimate the precision matrix
minimization approach to estimate the precision matrix 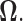 Then a generalized thresholding procedure to estimate the covariance matrix
Then a generalized thresholding procedure to estimate the covariance matrix 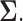 We shall provide error bounds for estimates obtained by these methods that hold with asymptotic probability
We shall provide error bounds for estimates obtained by these methods that hold with asymptotic probability 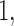 unconditional on the missing structure. These error bounds shall also allow for the dimension
unconditional on the missing structure. These error bounds shall also allow for the dimension 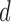 to increase exponentially with the sample size, thus allowing for high dimensions. To describe our methodology we require the following definitions. For each
to increase exponentially with the sample size, thus allowing for high dimensions. To describe our methodology we require the following definitions. For each 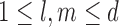 let
let
| (3.1) |
and define a “re-normalized sample covariance” matrix 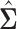 as follows,
as follows,
| (3.2) |
The matrix 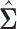 forms an initial estimator for obtaining consistent estimates of the covariance matrix and the precision matrices in the high-dimensional setting. The following lemma provides an approximation result between
forms an initial estimator for obtaining consistent estimates of the covariance matrix and the precision matrices in the high-dimensional setting. The following lemma provides an approximation result between 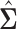 and
and 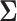 in the
in the 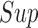 norm and shall be key to providing convergence rates of the estimators to follow later in this section.
norm and shall be key to providing convergence rates of the estimators to follow later in this section.
Lemma 3.1.
Suppose the observations
follow the distribution (2.5) and that the missing structure satisfies condition (A1). In addition assume that the variance components of the covariance matrix
are bounded above, i.e.
for a constant
Then with probability at least
(3.3) for some universal constant
To appreciate this result note that the re-normalized sample covariance matrix 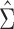 is defined through the r.v.’s
is defined through the r.v.’s 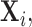
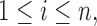 whose distribution is in turn defined conditionally of the missing structure
whose distribution is in turn defined conditionally of the missing structure 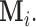 However, Lemma 3.1 provides an unconditional probability bound on the desired random quantity with only a mild assumption (A1) on the missing structure. The proof of this result relies on the observation that
However, Lemma 3.1 provides an unconditional probability bound on the desired random quantity with only a mild assumption (A1) on the missing structure. The proof of this result relies on the observation that 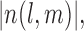
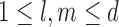 is a sum of independent r.v.’s, i.e.
is a sum of independent r.v.’s, i.e. 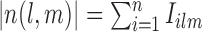 where
where 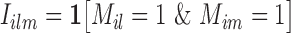 for every
for every 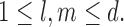 Here
Here 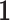 represents the indicator function. This observation allows the applicability of the Hoeffding’s inequality (Hoeffding, 1963) in combination with conditional expectation arguments. The details of the proof are provided in the supplementary material available at Biostatistics online. To proceed with the estimation of
represents the indicator function. This observation allows the applicability of the Hoeffding’s inequality (Hoeffding, 1963) in combination with conditional expectation arguments. The details of the proof are provided in the supplementary material available at Biostatistics online. To proceed with the estimation of 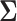 and
and 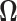 we require these matrices to belong to the following class of approximately sparse matrices.
we require these matrices to belong to the following class of approximately sparse matrices.
- (A2) Assume that the covariance and precision matrices belong to the following classes of matrices, respectively: define for
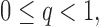
The quantity 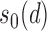 is allowed to depend on
is allowed to depend on 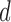 and thus is not and explicit restriction on sparsity. Two examples of matrices which satisfy this restrictions are, a p-diagonal matrix that satisfies this condition with any
and thus is not and explicit restriction on sparsity. Two examples of matrices which satisfy this restrictions are, a p-diagonal matrix that satisfies this condition with any 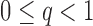 and
and  Second, an
Second, an 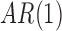 covariance matrix where
covariance matrix where 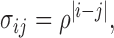 which satisfies the restriction with
which satisfies the restriction with 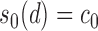 for some constant
for some constant 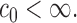
3.1 Estimation of the precision matrix 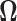
The problem of estimation of the precision matrix 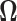 has received wide attention in the literature. Several solutions have been proposed in the context of i.i.d. sub-Gaussian observation and one such solution has been the penalized likelihood method for which exploits the i.i.d. Gaussian structure of observations (Friedman and others, 2008; Ravikumar and others, 2011). In our setup however, the observations
has received wide attention in the literature. Several solutions have been proposed in the context of i.i.d. sub-Gaussian observation and one such solution has been the penalized likelihood method for which exploits the i.i.d. Gaussian structure of observations (Friedman and others, 2008; Ravikumar and others, 2011). In our setup however, the observations 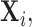
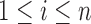 are no longer identically distributed, and hence such likelihood-based approaches are no longer feasible. However this problem can be overcome by adapting penalized moment-based approaches such as the method “Clime” of Cai and others (2011) under our setting. Such moment-based approaches to the estimation of high-dimensional precision matrices do not rely on an explicit likelihood functions, instead only require probabilistic bounds on the quantity
are no longer identically distributed, and hence such likelihood-based approaches are no longer feasible. However this problem can be overcome by adapting penalized moment-based approaches such as the method “Clime” of Cai and others (2011) under our setting. Such moment-based approaches to the estimation of high-dimensional precision matrices do not rely on an explicit likelihood functions, instead only require probabilistic bounds on the quantity 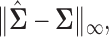 and thus Lemma 3.1 stated earlier forms the connecting link between such approaches and the distributional structure of Section 1 without requiring the observations
and thus Lemma 3.1 stated earlier forms the connecting link between such approaches and the distributional structure of Section 1 without requiring the observations 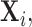
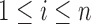 to be identically distributed.
to be identically distributed.
Let 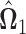 be the solution of the following convex program,
be the solution of the following convex program,
| (3.4) |
with a suitable choice of 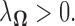 Here
Here 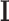 represents the identity matrix and
represents the identity matrix and 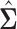 as defined in (3.2). Since the solution
as defined in (3.2). Since the solution 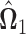 may not be symmetric in general, the final estimate
may not be symmetric in general, the final estimate 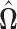 is obtained by symmetrizing
is obtained by symmetrizing 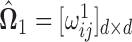 by choosing the smaller of
by choosing the smaller of 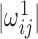 and
and 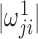 in the final estimate
in the final estimate 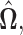 i.e.
i.e. 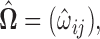 with
with 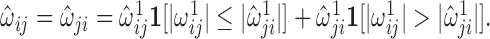
The estimator 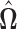 is not guaranteed to be positive definite; however, the following theorem shows that it converges to a positive definite limit with asymptotic probability 1. To ensure positive definiteness, in practice one may add a small constant to the diagonal elements of this matrix, or project the matrix onto the cone of positive definite matrices.
is not guaranteed to be positive definite; however, the following theorem shows that it converges to a positive definite limit with asymptotic probability 1. To ensure positive definiteness, in practice one may add a small constant to the diagonal elements of this matrix, or project the matrix onto the cone of positive definite matrices.
Theorem 3.1.
Suppose
follow the distribution (2.5) and that the missing structure satisfies condition (A1). Also assume that
and the regularizer is chosen
then the following bounds hold with probability at least
This methodology was introduced by Cai and others (2011) under the standard i.i.d. Gaussian setup, which is implemented using the sample covariance matrix 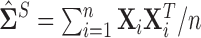 as the initial estimate. The proof for the error bounds of Theorem 3.1 follows by deterministic arguments on the event where the inequality (3.3) holds and follows from the arguments of Cai and others (2011), a sketch of this proof has been provided in the supplementary material available at Biostatistics online.
as the initial estimate. The proof for the error bounds of Theorem 3.1 follows by deterministic arguments on the event where the inequality (3.3) holds and follows from the arguments of Cai and others (2011), a sketch of this proof has been provided in the supplementary material available at Biostatistics online.
3.2 Estimation of the covariance matrix 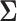
In this sub-section we discuss thresholding methods of estimating the covariance matrix 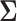 in our setting with structural zeros. These methods were first proposed in the standard i.i.d. setting by Wu and Pourahmadi (2003) and have also been studied by Bickel and Levina (2008) and Levina and others (2008) amongst several others. Although assuming sparsity on the covariance matrix is a stronger assumption than assuming the same on the precision matrix, however thresholding carries very little computational burden in comparison to the penalized methods such as the one described in the previous sub-section. Thus this procedure forms an attractive alternative to estimating the precision matrix, especially in very high-dimensional problems and real time applications. We adopt this methodology in our setup with structural zeros as follows.
in our setting with structural zeros. These methods were first proposed in the standard i.i.d. setting by Wu and Pourahmadi (2003) and have also been studied by Bickel and Levina (2008) and Levina and others (2008) amongst several others. Although assuming sparsity on the covariance matrix is a stronger assumption than assuming the same on the precision matrix, however thresholding carries very little computational burden in comparison to the penalized methods such as the one described in the previous sub-section. Thus this procedure forms an attractive alternative to estimating the precision matrix, especially in very high-dimensional problems and real time applications. We adopt this methodology in our setup with structural zeros as follows.
Let 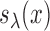 be a generalized thresholding operator as defined by Rothman, Levina and others (2009). We restate the definition for the convenience of readers. A function
be a generalized thresholding operator as defined by Rothman, Levina and others (2009). We restate the definition for the convenience of readers. A function 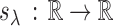 satisfying
satisfying
| (3.5) |
is said to be a generalized thresholding operator. In view of this definition, the covariance matrix 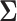 can be estimated by elementwise thresholding as,
can be estimated by elementwise thresholding as, 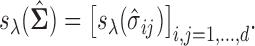 The two common examples of these operators are the hard- and soft-thresholding operators defined as,
The two common examples of these operators are the hard- and soft-thresholding operators defined as,
| (3.6) |
respectively. The soft-thresholding operator can also be defined as 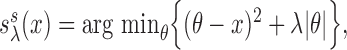 and has been studied by various authors, including Donoho and others (1995) and Tibshirani (1996). The hard-thresholding operator has been investigated by Bickel and Levina (2008) among others. Additional examples of thresholding operators include SCAD of Fan and Li (2001), adaptive Lasso of Zou (2006). The following result provides the consistency of this estimator.
and has been studied by various authors, including Donoho and others (1995) and Tibshirani (1996). The hard-thresholding operator has been investigated by Bickel and Levina (2008) among others. Additional examples of thresholding operators include SCAD of Fan and Li (2001), adaptive Lasso of Zou (2006). The following result provides the consistency of this estimator.
Theorem 3.2.
Suppose
follow the distribution (2.5) and that the missing structure satisfies condition (A1). Also assume that
satisfies condition (3.5). Then uniformly on
choosing the regularizer
we obtain
(3.7) with probability at least
In the standard i.i.d. setting, Rothman, Levina and others (2009) introduced this generalized thresholding methodology based on usual sample covariance matrix 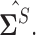 The proof of this theorem relies on deterministic arguments of Rothman, Levina and others (2009) on the set where the bound provided in Lemma 3.1 holds and a sketch is provided in the supplementary material available at Biostatistics online.
The proof of this theorem relies on deterministic arguments of Rothman, Levina and others (2009) on the set where the bound provided in Lemma 3.1 holds and a sketch is provided in the supplementary material available at Biostatistics online.
4. Simulation study
In this section we numerically illustrate that the methodology of Section 3 provides consistent estimates of 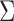 and
and 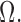 We confirm that our method provides a significant improvement over the typical method of using the sample covariance
We confirm that our method provides a significant improvement over the typical method of using the sample covariance 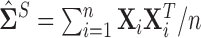 as the initial estimate in the methods of Sections 3.1 and 3.2, note that using the sample covariance matrix ignores the presence of these structural zeros.
as the initial estimate in the methods of Sections 3.1 and 3.2, note that using the sample covariance matrix ignores the presence of these structural zeros.
4.1 Simulation setup and results
The missingness is generated by r.v.’s 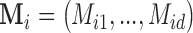 where each
where each 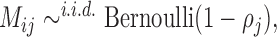
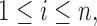
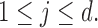 Here
Here 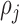 denotes the probability of
denotes the probability of 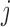 th component being a structural zero. These
th component being a structural zero. These 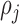 ’s
’s 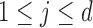 are chosen by uniformly between
are chosen by uniformly between  Finally, for each
Finally, for each 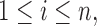 the components of
the components of 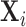 with indices in the set
with indices in the set 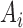 defined in (2.5) are assumed to be zero mean Gaussian r.v.’s with the covariance being the corresponding sub-block of the matrix
defined in (2.5) are assumed to be zero mean Gaussian r.v.’s with the covariance being the corresponding sub-block of the matrix 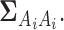
We set the covariance matrix as 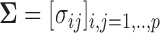 where
where 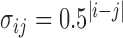 and all entries
and all entries 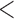 0.01 are set to zero. Under this setting we estimate
0.01 are set to zero. Under this setting we estimate 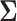 as described in Section 3.2 by the hard- and soft-thresholding operations of (3.6) on the initial re-normalized (RN) estimate (3.2), we shall refer to these estimates as “RN-hard” and “RN-soft,” respectively. Similarly we estimate
as described in Section 3.2 by the hard- and soft-thresholding operations of (3.6) on the initial re-normalized (RN) estimate (3.2), we shall refer to these estimates as “RN-hard” and “RN-soft,” respectively. Similarly we estimate 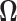 as described in Section 3.1 and refer to the estimates obtained as “RN-clime.” We also illustrate that our method provides a significant improvement over the standard method of using the sample covariance
as described in Section 3.1 and refer to the estimates obtained as “RN-clime.” We also illustrate that our method provides a significant improvement over the standard method of using the sample covariance 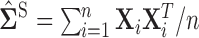 as the initial estimate for the hard/soft thresholding and clime procedures, we refer to these as “S-hard,” “S-soft,” and “S-clime,” respectively.
as the initial estimate for the hard/soft thresholding and clime procedures, we refer to these as “S-hard,” “S-soft,” and “S-clime,” respectively.
We repeat simulations on 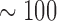 independent data sets that are generated under the following settings. (i)
independent data sets that are generated under the following settings. (i) 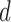 is fixed at
is fixed at 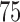 and
and 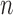 is allowed to vary from
is allowed to vary from 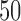 to
to 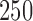 with increments of
with increments of 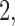 leading to 101 independent data sets; and (ii)
leading to 101 independent data sets; and (ii) 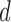 is allowed to vary from
is allowed to vary from 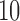 to
to 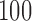 with increments of
with increments of 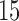 and
and 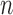 is allowed to vary from
is allowed to vary from 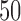 to
to 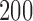 with increments of
with increments of 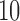 leading to 112 independent data sets.
leading to 112 independent data sets.
Figures 1 and 2 illustrate the results of our simulation. Here each dot (triangle) represents Frobenius norm of estimation error for each independent data set. To measure the average performance over the simulated models, nonparametric regression lines are fit via the Loess method with its smoothing parameter set at 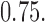 The solid line represents the average performance of our methods and the dotted line represents the average performance of the standard method which ignores the presence of structural zeros. For the soft-/hard-thresholding case, the tuning parameter
The solid line represents the average performance of our methods and the dotted line represents the average performance of the standard method which ignores the presence of structural zeros. For the soft-/hard-thresholding case, the tuning parameter 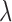 is chosen via cross-validation under the Frobenius loss, and for the “clime” method, the tuning parameter is chosen by cross-validating with the loss function
is chosen via cross-validation under the Frobenius loss, and for the “clime” method, the tuning parameter is chosen by cross-validating with the loss function 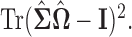
Fig. 1.
Comparisons of Frobenius norms of error in estimation due to soft (left) and hard (right) thresholding, x-axis: n, y-axis: 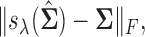 results at d=75.
results at d=75.
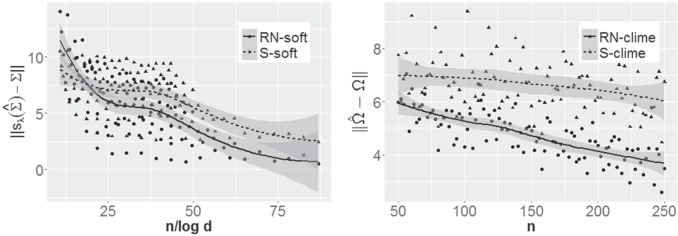
Fig. 2.
Left panel: Comparison of Frobenius norms of error in estimation due to soft thresholding the renormalized sample covariance at scaled sample size, x-axis: 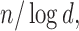
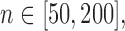
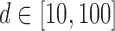 ; y-axis:
; y-axis: 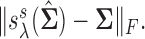 Right panel: Comparison of spectral norms of error in estimation due to Clime procedure on the renormalized sample covariance,
Right panel: Comparison of spectral norms of error in estimation due to Clime procedure on the renormalized sample covariance, 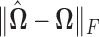 and Clime procedure on the standard sample covariance
and Clime procedure on the standard sample covariance 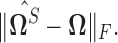 Results at
Results at 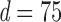 .
.
Results of thresholding procedures are provided in Figure 1. This figure plots 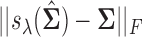 for different sample sizes
for different sample sizes 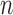 for the case
for the case 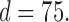 From this figure, it is clear that the error corresponding to the proposed estimator under both soft and hard thresholding tends to get smaller with sample size faster than the standard estimator that ignores the structural zeros. The left panel of Figure 2 plots of the errors for different values of scaled sample sizes
From this figure, it is clear that the error corresponding to the proposed estimator under both soft and hard thresholding tends to get smaller with sample size faster than the standard estimator that ignores the structural zeros. The left panel of Figure 2 plots of the errors for different values of scaled sample sizes 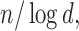 for the soft-thresholding operator. This figure seems to confirm the result of Theorem 3.2 regarding the rate of convergence of the estimator. Similarly, the right panel of Figure 2 describes the results of the simulation for the “clime” methodology described in Section 3.1.
for the soft-thresholding operator. This figure seems to confirm the result of Theorem 3.2 regarding the rate of convergence of the estimator. Similarly, the right panel of Figure 2 describes the results of the simulation for the “clime” methodology described in Section 3.1.
5. Analysis of global human gut microbiome data
In this section we analyze the global human gut microbiome data of Yatsunenko and others (2012) available at the repository MG-RAST (http://metagenomics.anl.gov/) under accession numbers qiime:621 for fecal microbiome shotgun sequencing data sets. Here we estimate the precision matrix 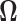 and use this estimate to classify observations according to geographical locations. Further details on the availability of data have been provided in the supplementary material available at Biostatistics online.
and use this estimate to classify observations according to geographical locations. Further details on the availability of data have been provided in the supplementary material available at Biostatistics online.
The data consist of microbial OTU counts obtained from individuals of United States (US), Venezuela (VE), and Malawi (MA). Our analysis is based on the “genus” level of bacterial taxonomy. We subdivide the data into two age categories “under 2 years” and “at least 2 years.” This stratification is done since it is known that microbial composition of infants changes drastically when they switch over from breast milk (or formula milk) to solid food (Lozupone and others, 2013). The sample sizes in the two strata (under 2 years, at least 2 years) for US, VE and MA samples are (70, 225), (15, 74) and (32, 72), respectively. After several pre-processing steps of the raw OTU data we obtain for each age group and each location, a matrix of observations with 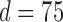 microbes and inherent structural zeros. Each row of these matrices is assumed to follow the conditional Gaussian distribution of (2.5). Note that for the “under 2 years” category for the pair VE–MA, the total number of observations is
microbes and inherent structural zeros. Each row of these matrices is assumed to follow the conditional Gaussian distribution of (2.5). Note that for the “under 2 years” category for the pair VE–MA, the total number of observations is 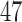 and thus we have a high-dimensional scenario. The pre-processing of data is described in detail in the supplementary material available at Biostatistics online. For each pair of locations, we randomly split
and thus we have a high-dimensional scenario. The pre-processing of data is described in detail in the supplementary material available at Biostatistics online. For each pair of locations, we randomly split 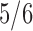 -th data into training set and the remaining one-sixth as the test set. The training set is used to estimate the common precision matrix using the procedure described in Section 3.
-th data into training set and the remaining one-sixth as the test set. The training set is used to estimate the common precision matrix using the procedure described in Section 3.
5.1 Tuning parameter
The regularizer 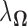 is chosen via 5-fold cross-validation within the combined training data for each pair of locations. The loss function used to evaluate cross-validation error is
is chosen via 5-fold cross-validation within the combined training data for each pair of locations. The loss function used to evaluate cross-validation error is 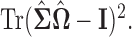 Also, in the construction of
Also, in the construction of 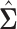 in (3.2) if a pair
in (3.2) if a pair 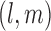 does not occur then we set the pairwise covariance to zero.
does not occur then we set the pairwise covariance to zero.
5.2 Classification of subjects to geographical locations
In this section we exploit the assumed conditional Gaussian structure of observations to classify subjects of the test set to one of two geographical locations by using estimates of the corresponding precision matrices.We perform pairwise classifications of samples into (i) US and MA, (ii) US and VE, and finally (iii) VE and MA. Let 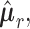
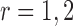 be the estimated
be the estimated 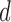 -dimensional mean vector obtained as in (3.1) for each of the two populations under consideration, and
-dimensional mean vector obtained as in (3.1) for each of the two populations under consideration, and 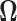 be the common precision matrix of the two locations.
be the common precision matrix of the two locations.
Let 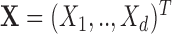 represent the observation to be classified and let
represent the observation to be classified and let 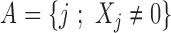 denote the collection of indices of the non-zero components of
denote the collection of indices of the non-zero components of 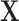 . For location
. For location 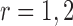 , We implement the following classification rule: let
, We implement the following classification rule: let
| (5.1) |
denote the linear discriminant function where an observation 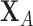 is classified into population 1 if
is classified into population 1 if 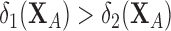 , otherwise classified into population 2. The percentage of correctly classified observations from the test set is computed and the above process is repeated 20 times to obtain average correct classification percentages. The results for the two age groups and for every pair of locations are summarized in Table 1.
, otherwise classified into population 2. The percentage of correctly classified observations from the test set is computed and the above process is repeated 20 times to obtain average correct classification percentages. The results for the two age groups and for every pair of locations are summarized in Table 1.
Table 1.
Percentages of correct classification between locations
| US–MA | US–VE | VE–MA | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Age/ %Correct | US | MA | Total | US | VE | Total | VE | MA | Total |
Age  2 years 2 years |
87.5 | 80.9 | 85.6 | 79.6 | 81.2 | 79.8 | 76.1 | 60.5 | 69.4 |
Age  2 years 2 years |
92.8 | 95.0 | 93.3 | 80.9 | 73.3 | 73.3 | 62.1 | 57.5 | 60.0 |
The classification results depend on the two populations under consideration. The trends in the correct classification rates (column “Total” in Table 1) are the same in both age categories, the best being US–MA and the worst VE–MA. A possible reason for this is that the microbial composition between US and MA is more different relative to the other two pairs. This is illustrated in Figure 3, which plots the largest 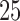 absolute differences in the signal-to-noise ratios (SNR) for each of the three pairs of location for the “at least 2 years” age group. More precisely, for each
absolute differences in the signal-to-noise ratios (SNR) for each of the three pairs of location for the “at least 2 years” age group. More precisely, for each 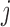 ,
, 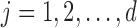 , we plot
, we plot 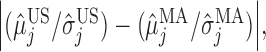
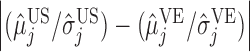 , and
, and 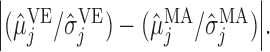 This decreasing trend in the absolute difference of SNRs is a possible reason for the lower correct classification rate between MA and VE than between US and MA.
This decreasing trend in the absolute difference of SNRs is a possible reason for the lower correct classification rate between MA and VE than between US and MA.
Fig. 3.

Comparison of absolute difference in SNR for each pair of locations in descending order for the top 25 microbes. Results for the “at least 2 years age” category.
6. Discussion
New technologies such as the 16s RNA sequencing have yielded high-dimensional data with characteristics that cannot be modeled by standard i.i.d. formulations of multivariate data. In this paper we describe one such characteristic, namely “structural zeros,” which are encountered in microbiome studies. We proposed a conditional Gaussian distributional structure that characterizes these zeros and provide methods to estimate covariance and precision matrices in this context. We show that in spite of the distribution being conditional, it is indeed possible to obtain results that are unconditional. As future work, we believe that the conditional Gaussian distributional structure proposed in this paper can be used to carry forward the work of Kurkland and Heagerty (2005) in the high-dimensional setting where the covariates are subjected to structural zeros.
Acknowledgement
We thank a reviewer and the associate editor for several useful suggestions that helped improve this manuscript. Conflict of Interest: None declared.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Funding
Intramural Research Program of the NIH, NIEHS (Z01 ES101744-04) to S.D.P. and A.K.; Israeli Science Foundation (1256/13) to O.D.
References
- Bickel, P. and Levina, E. (2008). Covariance regularization by thresholding. Annals of Statistics 36, 2577–2604. [Google Scholar]
-
Cai, T., Liu, W. and Luo, X. (2011). A constrained
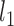 minimization approach to sparse precision matrix estimation. Journal of American Statistical Association, 106, 594–607. [Google Scholar]
minimization approach to sparse precision matrix estimation. Journal of American Statistical Association, 106, 594–607. [Google Scholar] - Donoho, D. L., Johnstone, I. M., Kerkyacharian, G. and Pickard, D. (1995). Wavelet shrinakge: asymptopia? Journal of the Royal Statistical Society, Series. B, 57, 301–369. [Google Scholar]
- Fan, J. and Li, R. (2001). Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American Statistical Association, 96,1348–1360. [Google Scholar]
- Friedman, J.,, Hastie, T.,, Tibshirani, R. (2008). Sparse inverse covariance estimation with the graphical lasso. Biostatistics, 9, 432–441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoeffding, W. (1963). Probability inequalities for sums of bounded variables. Journal of American Statistical Association, 58, 13–30. [Google Scholar]
- Kaul, A., Koul, H. L., Chawla, A. and Lahiri, S. N. (2016). Two stage non-penalized corrected least squares for high dimensional linear models with measurement error or missing covariates. arXiv preprint arXiv:1605.03154v1. [Google Scholar]
- Kurkland, B. F. and Heagerty, P. J. (2005). Directly parameterized regression conditioning on being alive: analysis of longitudinal data truncated by deaths. Biostatistics 6, 241–258. [DOI] [PubMed] [Google Scholar]
- Levina, E., Rothman, A., and Zhu, J. (2008). Sparse estimation of large covariance matrices via a nested Lasso penalty. Annals of Applied Statistics, 1,245–263. [Google Scholar]
- Loh, P., and Wainwright, M. J. (2012). High-dimensional regression with noisy and missing data: provable guarantees with non-convexity. Annals of Statistics 40, 1637–1664. [Google Scholar]
- Lounici, K. (2014). High dimensional covariance matrix estimation with missing observations. Bernoulli 20, 1029–1058. [Google Scholar]
- Lozupone, C. A.,, Stombaugh, J.,, Gonzalez, A.,, Ackerman, G.,, Wendel, D.,, Vazquez-Baeza, Y.,, Jansson, J. K.,, Gordon, J. I.,, Knight R. (2013). Meta-analyses of studies of the human microbiota. Genome Research 23(10), 1704–1714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandal, S., Teuren, W. V., White, R. A., Eggesbo, M., Knight, R. and Peddada, S. (2015) Analysis of composition of microbiomes: a novel method for studying microbial composition. Microbial Ecology in Health and Disease 261651–2235. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
Ravikumar, P., Wainwright, M., Raskutti, G., and Yu, B. (2011). High dimensional covariance estimation by minimizing
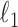 -penalized log-determinant divergence. Electronic Journal of Statistics 5, 935–980. [Google Scholar]
-penalized log-determinant divergence. Electronic Journal of Statistics 5, 935–980. [Google Scholar] - Rothman, A., Bickel, P., Levina, E., and Zhu, J. (2009). Sparse permutation invariant covariance estimation. Electronic Journal of Statistics 2, 494–515. [Google Scholar]
- Rothman, A., Levina, E., and Zhu, J. (2009). Generalized thresholding of large covariance matrices. Journal of American Statistical Association 104, 177–186. [Google Scholar]
- Tibshirani, R. (1996). Regression shrinkage and selection via the Lasso. Journal of the Royal Statistical Society Series B, 58,267–288. [Google Scholar]
- Wu, W. B. and Pourahmadi, M. (2003). Nonparametric estimation of large covariance matrices of longitudinal data. Biometrika 90, 831–844. [Google Scholar]
- Yatsunenko, T.,, Rey, F. E.,, Manary, M. J.,, Trehan, I.,, Dominguez-Bello, M. G.,, Contreras, M.,, Magris, M.,, Hidalgo, G.,, Baldassano, R. N.,, Anokhin, A. P., and others (2012). Human gut microbiome viewed across age and geography. Nature, 486, 222–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou, H. (2006). The adaptive Lasso and its oracle properties. Journal of the American Statistical Association, 101,1418–1429. [Google Scholar]