Analysis of accelerated failure time data with dependent censoring using auxiliary variables via nonparametric multiple imputation

Abstract

We consider the situation of estimating the marginal survival distribution from censored data subject to dependent censoring using auxiliary variables. We had previously developed a nonparametric multiple imputation approach. The method used two working proportional hazards (PH) models, one for the event times and the other for the censoring times, to define a nearest neighbor imputing risk set. This risk set was then used to impute failure times for censored observations. Here, we adapt the method to the situation where the event and censoring times follow accelerated failure time models and propose to use the Buckley–James estimator as the two working models. Besides studying the performances of the proposed method, we also compare the proposed method with two popular methods for handling dependent censoring through the use of auxiliary variables, inverse probability of censoring weighted and parametric multiple imputation methods, to shed light on the use of them. In a simulation study with time-independent auxiliary variables, we show that all approaches can reduce bias due to dependent censoring. The proposed method is robust to misspecification of either one of the two working models and their link function. This indicates that a working proportional hazards model is preferred because it is more cumbersome to fit an accelerated failure time model. In contrast, the inverse probability of censoring weighted method is not robust to misspecification of the link function of the censoring time model. The parametric imputation methods rely on the specification of the event time model. The approaches are applied to a prostate cancer dataset.

1. Introduction

The event times for censored observations can be regarded as missing data [1]. Missing data methods such as the data augmentation algorithm [2] and multiple imputation [3] have been proposed to handle censored observations to recover lost information due to censoring [4–6] or to simplify doubly censored data into right censored data [7]. Not only does censoring result in a loss of efficiency of estimators but also a potential for bias too if the censoring mechanism is not independent of the event time mechanism. In many studies, auxiliary variables predictive of the failure time often are also available, for example, Gleason score and prostate-specific antigen (PSA) level in studies of prostate cancer. In this paper, our interest is in estimating the marginal survival distribution when the data are subject to dependent censoring; thus, the auxiliary variables will only be used to provide some additional information on endpoint occurrence times for censored observations.

Incorporating auxiliary variables has the potential to reduce bias due to dependent censoring in estimating the marginal survival distribution. A few statistical approaches have been proposed to handle dependent censoring through the use of auxiliary variables. Of the existing approaches, the inverse probability of censoring weighted (IPCW) method [8], where the weight is derived from a model for the censoring times with auxiliary variables as the covariates, and parametric multiple imputation (PMI) method, where a specific parametric model is used to impute event times for censored observations, are two popular methods. Both approaches use a model to directly incorporate auxiliary variables into estimation of the marginal survival function. To weaken the reliance on the model, we previously developed a nonparametric multiple imputation approach using auxiliary variables to recover information for censored observations. The approach uses two working semiparametric models to indirectly incorporate auxiliary variables into estimation of the marginal survival function. Specifically, we use two working Cox proportional hazards (PH) models, one for the failure time and one for the censoring time. The parameter estimates from these models are then used to give two risk scores for each subject, defined as the linear combination of covariates. The method then selects an imputing risk set of observations for each censored observation [9], which consists of subjects who survive longer than the censored subject and have similar risk scores as the censored subject. Then the event time was drawn from a nonparametric distribution derived from this imputing risk set. The idea is similar to predictive mean matching [10] and propensity score matching [11] in the missing data literature. By incorporating predictive auxiliary variables into the multiple imputation method, one can both increase efficiency and reduce bias due to dependent censoring. We also showed that conditions under which the nonparametric imputation enhanced estimate is consistent and reproduces the weighted Kaplan–Meier estimator, a method for incorporating categorical auxiliary variables. This approach has nice properties; however, the two working models assume that the hazards are proportional.

When the PH assumption is questionable, the accelerated failure time (AFT) model is an alternative to the Cox PH model. It is often characterized by specifying that the logarithm of a failure time be linearly related with covariates. In that sense, the AFT model is more appealing and easier to interpret than the PH model because of its quite direct physical interpretation [12]. Based on how the AFT model is often characterized, one would use conventional linear regression methods to perform estimation. However, often, there are censored observations, which complicate the estimation. One popular approach to deal with censored observations in estimation of the AFT model is the Buckley–James method [13, 14], which is an iterative method based on the expectation-maximization (EM) algorithm. The estimation of the Buckley–James method can be highly unstable, especially in a situation with a small sample size. Also, the estimation of its variance involves the density and the derivative of the density of an unknown distribution [14].

In this paper, we adapt our nonparametric multiple imputation approach to handle the case of the data from an AFT model when the goal is estimating the marginal survival function. Specifically, we propose to use two Buckley–James estimators, one for the failure time and one for the censoring time, to derive two risk scores to select an imputing risk set for each censored observation. The two Buckley–James estimators are only used to derive two risk scores to select an imputing risk set. Hence, the approach is expected to be less affected by unstable estimation, and it is not required to estimate the variance of the Buckley–James estimator. In this paper, not only will we study the performances of the proposed multiple imputation approaches but also will compare their performances with these two existing popular approaches, IPCW and PMI, and, furthermore, shed light on the use of IPCW and PMI approaches when the true model for the event time is from an AFT model.

This paper is organized as follows. In Section 2, we review estimation for the AFT model and the relationship between PH and AFT models. In Section 3, we briefly describe the IPCW and the PMI methods. In Section 4, we describe multiple imputation procedures and discuss their properties. In Section 5, we apply the techniques to data from a prostate cancer study. In Section 6, we give results from a simulation study. A discussion follows in Section 7.

2. Estimation for the accelerated failure time model

Let T denote the failure time, C denote the censoring time, X = min(T, C), δ = I(T ≤ C), and Z^T = (Z₁, Z₂, …, Z_p) denote the time-independent auxiliary variables. Assume that there are n independent observations of X, δ, and Z.

2.1. Buckley–James estimator

Under the AFT model, one can specify log(T) = α₀+α^TZ+σW to study the relationship between T and Z, where α^T = (α₁, …, α_p), σ > 0 are unknown parameters and W has density f (w) and distribution function F(w). Without censoring, the ordinary least square (OLS) method can be performed on the logarithm of T to estimate α₀ and α by minimizing $n^{-1}{\displaystyle {\sum }_{i=1}^n{[\log (T_i)-({\alpha }_0+{\alpha }^{T}Z)]}^2}$ with respect to α₀ and α. With censoring, the OLS method cannot be performed directly because log(T) is unobserved for censored observations. The Buckley–James estimator [13,14] has been proposed to handle censored observations by adapting the OLS method. The method iterates between replacing each censored log(T) with the expected value of log(T) conditional on the current parameter estimate, censoring indicator, and Z (i.e., the E step) and then performing the OLS method on the ‘complete’ data (i.e., the M step). It has been shown that it is difficult to derive the variance of the Buckley–James estimator, and the estimation can be unstable. However, we only use the Buckley–James estimator to derive risk scores (defined as α^TZ) to select an imputing set for each censored observation, therefore, we do not need to derive the variance. Specifically, in this paper, we propose to use two Buckley–James estimators, one for the failure time and one for the censoring time, only to summarize the auxiliary variables into two risk scores.

2.2. Relationship between Cox proportional hazards and accelerated failure time models

In practice, often, people use a PH model to study the relationship between T and Z regardless of the underlying distribution of T. In other words, the hazard function given Z is specified as $\lambda (t;Z)={\lambda }_0(t)e^{{\beta }^{T}Z}$, where β^T = (β₁, …, β_p) is a vector of regression coefficients and λ₀(t) is the unspecified baseline hazard function. The regression coefficients β can be estimated based on the partial likelihood. There are some known relationships between the AFT and PH models. Specifically, when the AFT model has the extreme value distribution, the partial likelihood of the PH model estimates the parameter β = σ⁻¹α. In addition, based on first-order approximations, several studies [15–17] have shown that the relative importance of the covariates derived from the PH model remains unchanged approximately when the true model is an AFT model. The relative importance of the covariates is measured using the ratios of the estimated regression coefficients to the estimated regression coefficient of a reference covariate. This is equivalent to the coefficients from the two models being the same up to an unknown scale factor. In symbols, the property is that α_j∕‖α‖ ≈ β_j∕‖β‖, j = 1, …, p. A consequence of this property is that the rank order of the estimated regression coefficients from a PH model should be the same as the rank order of the estimated regression coefficients of the AFT model. In practice, with finite samples that introduce uncertainty in to the estimates, and because the result is based on an approximation, the relative importance from the two estimated models will not be exactly the same, but it can be expected to be similar. Because on this property of preserving the relative importance, PH models can be expected to produce good estimates of the risk scores even if the true models are AFT models. Thus, if two subjects have similar risk scores under one model, they will very likely have similar risk scores under the other model. Therefore, the nonparametric multiple imputation approach based on two working PH models is expected to produce similar survival estimates as the imputation method based on the two working Buckley–James estimators when the true models are the AFT models.

3. Alternative methods

3.1. Inverse probability of censoring weighted method

In survival analysis, the IPCW method [8] is a popular way to correct potential bias due to dependent censoring. Specifically, the IPCW method uses the auxiliary variables Z to derive censoring weights and then incorporates the weights into estimation. The weights are derived from a regression model for the censoring time. Once the weights are estimated, the expression of the point estimator for the marginal survival rate at time t [8, Equation 10] can be specified as follows: $\widehat{S}(t)={\displaystyle {\prod }_{\{i:X_i<t\}}\left(1-\frac{{\delta }_i{\widehat{W}}_i(X_i)}{{\displaystyle {\sum }_{j=1}^n{Y}_j(X_i){\widehat{W}}_j(X_i)}}\right)}$, where Y(u) = I(X ⩾ u) is the at-risk indicator and ${\widehat{W}}_i(X_i)={\widehat{K}}_i^0(X_i)/{\widehat{K}}_i^Z(X_i)$ is the subject-specific weight at time X_i for subject i. ${\widehat{K}}_i^0(X_i)$ is the usual Kaplan–Meier estimator of the probability being uncensored by time X_i, and ${\widehat{K}}_i^Z(X_i)$ is the conditional probability of being uncensored by time X_i given Z_i derived from a model for censoring time using the auxiliary variables Z as the covariates. When a Cox PH model is used for the censoring time, the expressions for the standard errors of the IPCW method involve complicated formulas and can be found in the appendix of [8]. Besides using a PH model to derive the censoring weights (denoted as IPCW_PH), we will also use a specific parametric AFT model (a lognormal (denoted as IPCW_Lognormal) or log-logistic (denoted as IPCW_Loglogistic) model) to derive the censoring weights. The standard error formulas in [8] are only for the censoring weights derived from a PH model. When the censoring weights are derived from an AFT model, the estimate of the standard error is derived from 500 bootstrap samples. When the censoring time model is indeed an AFT model, then IPCW using the AFT model to derive the weights is expected to perform well. In this paper, we will study their performances and compare them with the proposed imputation methods in simulation when the true censoring time model is from an AFT model.

3.2. Parametric multiple imputation

In this method, a parametric AFT model is fit to a bootstrap sample of the event time data, with the auxiliary variables as covariates. Based on the parameter estimates derived from the bootstrap sample, the residual time distribution is calculated for each censored observation in the original sample. An event time is then imputed for each censored case in the original sample by drawing from this residual time distribution [18]. The procedure is repeated M times. A Kaplan–Meier estimator is obtained from each completed dataset. The final estimates and standard errors are obtained from the results of the M analyses using the standard combining rules for multiple imputation.

4. Nonparametric multiple imputation

To conduct nonparametric multiple imputation, for each censored observation, we seek an imputing risk set consisting of subjects who survive longer than the censored subject and have similar risk scores as the censored subject. We describe the imputation procedures in the following four steps.

4.1. Imputation procedures

Step 1. Estimate the two risk scores on a bootstrap sample

To define each imputing risk set, we first reduce the auxiliary variables to two scalar indices (risk scores), which provide an indicator of an individual’s risk of failure and censoring. This strategy summarizes the multidimensional structure of the auxiliary variables into a two-dimensional summary. The hope is that this two-dimensional summary contains most, if not all, of the information about the future event and censoring times. Here, we assume that the data arise from an AFT model. Hence, we propose to use two Buckley–James estimators, one for the failure time and one for the censoring time, to derive two risk scores, summarizing the associations between the auxiliary variables and the failure and censoring times. Two Buckley–James estimators will be derived on a nonparametric bootstrap sample [19] of the original dataset to incorporate the uncertainty of parameter estimates from the working models. This step results in proper multiple imputation ([20] and references therein). More specifically, let (X^B, δ^B, Z^B) denote the bootstrap sample. Two Buckley–James estimators are conducted on the bootstrap sample to calculate two risk scores, $S_T^{(B)}=Z^B{\widehat{\alpha }}_T^B$ (failure) and $S_C^{(B)}=Z^B{\widehat{\alpha }}_C^B$ (censoring), for each individual in the bootstrap sample. We further standardize these scores by subtracting their sample mean and dividing by their standard deviation and denote the standardized scores by $S_T^{c(B)}$ and $S_C^{c(B)}$, respectively.

Combinations of these two risk scores will be studied to see to what extent a double robustness property for model misspecification can be established [21]. In addition, two working PH models will also be fit to the bootstrap sample to calculate the two risk scores to study whether a robustness property for link function misspecification can be established for the nonparametric multiple imputation method [15–17].

Step 2. Calculate the distance between subjects

For a censored subject j in the original dataset with covariate values Z_j, two risk scores are derived using the regression coefficient estimates obtained from the bootstrap sample (i.e., $S_T(j)=Z_j{\widehat{\alpha }}_T^B$ and $S_C(j)=Z_j{\alpha }_C^B$) and then standardized by subtracting the sample mean of the corresponding bootstrap sample risk scores and dividing by the standard deviation of the corresponding bootstrap sample risk scores, respectively (denoted as $S_T^c(j)$ and $S_C^c(j)$). The distance between subject j in the original dataset and subject k in the bootstrap sample is then defined as $d(j,k)=\sqrt{w_1{[S_T^c(j)-S_T^c(k)]}^2+w_2{[S_C^c(j)-S_C^c(k)]}^2}$, where w₁ and w₂ are non-negative weights that sum to 1. Non-zero weights for w₂ may be useful in reducing the bias resulting from model misspecification. Specifically, a small weight w₂ (e.g., 0.2) will result in incorporating the risk scores from the censoring time model into defining a set of nearest neighbors for censored subjects. Based on our previous study [9], we found that w₁ = 0.8 and w₂ = 0.2 gave reasonable results even when the working failure time model is misspecified. Hence, we set w₁ = 0.8 and w₂ = 0.2 in this paper.

Step 3. Define the imputing risk set

For each censored subject j, the distance derived in step 2 is then employed to define a set of nearest neighbors. This neighborhood, R(j⁺, NN), consists of NN subjects who have longer survival time than the censoring time of subject j and a small distance from the censored subject j. For example, R(j⁺, NN = 10) consists of 10 subjects, including both censored and uncensored subjects, with the 10 nearest distances from subject j among those who have longer survival time than the censoring time for subject j. When the number of individuals still at risk is less than NN, then they are all included in the imputing risk set. We previously studied NN in the range of 5 to 50 and found that NN = 10 gave the most reasonable results in terms of having the minimum mean square error [9]. Hence, in this paper, we set NN = 10.

Step 4. Impute a value from the imputing risk set

After the imputing risk set R(j⁺, NN) is defined, the Kaplan–Meier imputation (KMI) scheme developed in [6] and briefly described in the succeeding text can be easily used. The KMI method draws an event time from a KM estimator of the distribution of failure times based on the imputing risk set. Thus, the procedure imputes only observed failure times unless the longest time in the imputing risk set is censored, in which case, some imputed times may include this censored time. Specifically, for each censored time t_j, a survival curve, ${\widehat{S}}_{j^{+}}(t)$, is estimated from among those individuals in R(j⁺, NN). Then the KMI method imputes a value $t_j^{\ast }$ by drawing at random from the corresponding estimated distribution function $1-{\widehat{S}}_{j^{+}}(t)$. The KMI method using two Buckley–James estimators to derive the risk scores is denoted as KMI_BJ. The KMI method using two PH models to derive the risk scores is denoted as KMI_PH.

Step 5. Repeat steps 1 to 4 independently M times

Each of the M imputed datasets is based on a different bootstrap samples. Once the M multiply imputed datasets are obtained, we carry out the multiple imputation (MI) analysis procedure established in [3]. Specifically, for our purposes, Kaplan–Meier estimation of the marginal survival distribution is performed on the M imputed datasets. The final estimate of S(t) (denoted as Ŝ^M(t)) is the average of the M Kaplan–Meier estimates (i.e., Ŝ(t)), and the final variance (denoted as var[Ŝ^M(t)]) is the sum of the sample variance (denoted as B) of the M Kaplan–Meier estimates and the average (denoted as U) of the M variance estimates of the Kaplan–Meier estimator. The quantity $[{\widehat{S}}^M(t)-S(t)]/\sqrt{\mathit{var}[{\widehat{S}}^M(t)]}$ approximately follows a t distribution with a degree of freedom v = (M − 1) ∗ [1 + {U ∗ M∕(M + 1)}∕B]² [3]. We use a value of 10 or higher for M.

4.2. Properties of the proposed multiple imputation approach

We have previously shown in large samples that by conditioning on the two risk scores, a situation of independent censoring can be induced within each imputing risk set if one of the two working models is correctly specified [9]. Based on this property, we have further shown that the proposed KMI approach has a double robustness property: if one of the two working models is correctly specified, then the estimate derived from the multiple imputation method is consistent. In addition, based on the relationship between PH and AFT models, we expect that the KMI method has a second robustness property. Specifically, if one of the two true models is from the AFT model family, then fitting two PH models still gives good estimates of the regression coefficients [15–17]. Because it is only the regression coefficients, and not the link function that is used in defining the imputing risk set, the KMI method is robust to misspecification of the link function. The aforementioned properties of the KMI method apply in large sample conditions. In small sample size situations, this nearest-neighborhood approach could produce biased survival estimates due to the lack of availability of suitable donor observations even if one of the two working models is correctly specified, especially when the failure time model is misspecified.

5. Illustration of the method on a prostate cancer dataset

We demonstrate the nonparametric multiple imputation approach using auxiliary variables on a prostate cancer dataset, which consists of 503 patients with localized prostate cancer treated with external-beam radiation therapy at the University of Michigan and affiliated institutions between July 1987 and February 2000. This dataset has been previously used to develop individualized prediction models of disease progression using serial PSA [22–24] and to develop a weighted Kaplan–Meier approach to adjust for dependent censoring using linear combinations of prognostic variables where the linear combination is categorized to define risk groups, and the final Kaplan–Meier estimate is the weighted average of the Kaplan–Meier estimates from all of the risk groups [25].

There are several variables collected at baseline, including age, Gleason score, PSA, T stage, and total radiation dose. T stage, PSA, and Gleason score are well-known prognostic variables of prostate cancer. In addition, age and total radiation dose are expected to be predictive of the patient’s survival or censoring time. In this paper, we treat those five variables as the auxiliary variables for estimating the distribution of recurrence/prostate cancer-free survival. To assess the PH assumption, time-dependent variables consisting of an interaction between the auxiliary variables and log(time) are included. Non-PH are detected for age and Gleason score with a p-value of 0.04 and 0.02, respectively.

To demonstrate the MI approach when potential non-PH exist, baseline PSA value, age, Gleason score, total radiation dose, and T stage are treated as time-independent covariates in the two working Buckley–James estimators and two working PH models. The results for estimation of the two working Buckley–James estimators and PH models are provided in Table I. Based on the two working Buckley–James estimators, all of the five auxiliary variables are significantly associated with failure time. Age, Gleason score, T stage, and total radiation dose are significantly associated with censoring time. Based on the two working PH models, Gleason score, T stage, and total radiation dose are significantly associated with failure time. All of the five auxiliary variables are significantly associated with censoring time. Even though the Buckley–James estimators pick up the significant covariates slightly different from the PH models (this could be due to unstable estimates of the standard errors for Buckley–James estimators), they show similar relative importance of the covariates as the PH models, as shown in the relative importance columns in the table. Specifically, negative/positive estimates (shorter/longer survival time) of the regression coefficients for Buckley–James estimators always correspond to positive/negative estimates (higher/lower hazard) of the regression coefficients for the PH models, the rank order of the estimated regression coefficient remains unchanged, and the ratio of regression coefficients is quite similar.

Table I.

Data analysis: estimation of two working Cox PH models.

	Failure time model				Censoring time model
Covariates	Estimate	SE	p-value	Rel-Import	Estimate	SE	p-value	Rel-Import
Cox PH model
Age	−0.024	0.0170	0.15	−0.02	0.031	0.0078	<0.01	−0.05
Log(PSA)	0.173	0.1267	0.17	0.13	−0.115	0.0536	0.03	0.17
Gleason	0.405	0.1037	<0.001	0.30	0.092	0.0494	0.06	−0.14
T stage	1.355	0.2184	<0.001	1.00	−0.679	0.0849	<0.001	1.00
Total dose	−0.111	0.0300	<0.001	−0.08	0.176	0.0141	<0.001	−0.26
Buckley–James estimators
Age	0.024	0.012	0.05	−0.02	−0.011	0.004	<0.01	−0.03
Log(PSA)	−0.198	0.090	0.03	0.20	0.015	0.030	0.61	0.05
Gleason	−0.360	0.083	<0.001	0.34	−0.066	0.025	0.01	−0.23
T stage	−1.062	0.198	<0.001	1.00	0.286	0.047	<0.001	1.00
Total dose	0.050	0.022	0.02	−0.05	−0.073	0.006	<0.001	−0.26

Rel-Import denotes coefficient estimate relative to T stage coefficient.

PH, proportional hazards; PSA, prostate-specific antigen; SE, standard error.

The risk scores derived from the two working Buckley–James estimators and the two working PH models, respectively, are used to calculate the distance between subjects and then to select the imputing risk set for each censored observation. The two risk scores derived from the two Buckley–James estimators are highly correlated with a Spearman correlation coefficient of −0.59. The two risk scores derived from the two PH models are also highly correlated with a Spearman correlation coefficient of −0.77. Based on principal component analysis, about 90% of variation of the two risk scores derived from both the Buckley–James estimators and the PH models is explained by the first principal component.

The results for estimating the recurrence-free probability are provided in Table II and Figure 1. Table II displays selected estimates from the partially observed (PO) analysis, which is the Kaplan–Meier estimation based on the observed censored event time data, IPCW_PH, IPCW_Lognormal, KMI_BJ, and KMI_PH methods. In addition, two PMI methods (PMI_Lognormal and PMI_Weibull), where a parametric model (log-normal or Weibull model) is fitted to the observed data to impute residual life times for each censored observation, are also performed. KMI_BJ and KMI_PH methods, as well as both PMIs and both IPCW methods, produce slightly higher estimated survival at both 5 and 10 years and slightly lower associated estimated standard errors than the PO analysis at 5 years. Both IPCW methods produce slightly greater survival estimates than the two KMI methods especially at the tail. KMI_BJ and KMI_PH produce almost identical results for both survival and associated standard error estimates. Figure 1 displays the estimated survival curves for all of the aforementioned methods. The PMI_Lognormal, PMI_Weibull, IPCW, KMI_BJ, and KMI_PH methods consistently produce slightly higher estimated survival compared with the PO analysis, especially the IPCW methods. This indicates that the IPCW and KMI methods both have potential to reduce bias due to dependent censoring.

Table II.

Data analysis: estimation of recurrence-free probability at 5 and 10 years.

	t = 5 years		t = 10 years
Methodb	Ŝ(t)	SEa	Ŝ(t)	SEa
PO	0.852	0.018	0.742	0.029
KMIPH	0.863	0.017	0.766	0.030
KMIBJ	0.863	0.016	0.766	0.029
IPCWLognormal	0.869	0.013	0.763	0.023
IPCWPH	0.868	0.016	0.770	0.028
PMILognormal	0.866	0.016	0.748	0.027
PMIWeibull	0.864	0.016	0.769	0.024

IPCW (Lognormal): a lognormal model is fitted to derive the censoring weights.

IPCW(PH): a PH model is fitted to derive the censoring weights.

PMI(Lognormal): a lognormal model is fitted to impute residual lifetime.

PMI(Weibull): a Weibull model is fitted to impute residual lifetime.

KMI(BJ): two Buckley–James estimators are used to define imputing risk sets.

KMI(PH): two PH models are fitted to define imputing risk sets.

PO, partially observed; KMI, Kaplan–Meier imputation; IPCW, inverse probability of censoring weighted; PMI, parametric multiple imputation.

^aEstimated standard error.

^bPO: KM estimates derived from the observed censored data.

Figure 1.

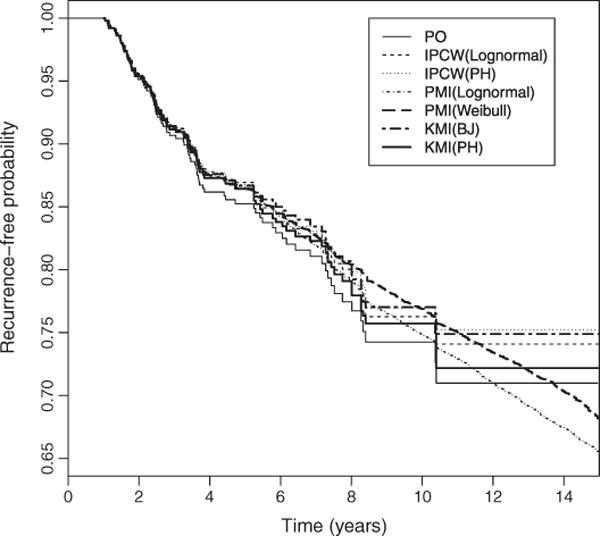
Prostate cancer study: recurrence-free curves derived from the methods considered in this paper. PO: KM estimates are derived from the observed censored data. IPCW (Lognormal): a lognormal model is fitted to derive the censoring weights. IPCW(PH): a PH model is fitted to derive the censoring weights. PMI(Lognormal): a lognormal model is fitted to impute residual lifetime. PMI(Weibull): a Weibull model is fitted to impute residual lifetime. KMI(BJ): two Buckley–James estimators are derived to define imputing risk sets. KMI(PH): two PH models are fitted to define imputing risk sets.

6. Simulation study

We perform several simulation studies to investigate the properties of the KMI, IPCW, and PMI methods when failure and censoring times are from AFT models, and the quantity of interest is the marginal survival distribution of the event time. We consider a situation with multiple time-independent prognostic covariates and dependent censoring. We investigate the effects of the magnitude of dependent censoring, which is measured by Spearman correlation coefficient (ρ) between failure and censoring times, sample size, misspecification of one of the two working models, and misspecification of the two link functions. The simulation program is written in R and is available upon request.

For each of the 500 independent simulated datasets, there are five hypothetical auxiliary variables (Z₁, …, Z₅) independently generated from a U(0, 1) distribution. The true failure and censoring time models are from an AFT family, the failure time T is generated from a hypothetical AFT model conditional on auxiliary variables, where log(T) = 0.10 − 2Z₁ + 0.5Z₂ − 2Z₃ + 2Z₄ + 2Z₅ + residual. The censoring time C is generated from a hypothetical AFT model, as well, where log(C) = 0.08 − 2.5Z₁ + 0.5Z₂ − 2Z₃ + 2Z₄ + 2Z₅ + residual. The regression coefficients and residual distributions are selected to give a censoring rate of approximately 50%. The residuals for log(T) and log(C) are generated either from a Normal(0, σ²), where σ is selected to control the correlation between failure and censoring times, or from a logistic(0, 1) distribution.

For the ‘fully observed’ (FO) analysis, treated as the gold standard, we derive KM estimates for each simulated dataset before any censoring is applied. For the ‘partially observed’ (PO) analysis, we derive KM estimates from the observed censored data. The estimate of the standard error for both FO and PO analyses is based on Greenwood’s formula. For the IPCW methods, all five auxiliary variables (Z₁, …, Z₅) are included in the PH and AFT models for the censoring time to derive the weights. For the PMI methods (i.e., PMI_Lognormal, PMI_Weibull and PMI_Loglogistic), an AFT model (lognormal/Weibull/log-logistic) with the five auxiliary variables as covariates is fitted to each of the M bootstrap samples and then used to impute residual times for each censored observation. For the KMI_BJ method, when both working Buckley–James estimators are correctly specified (i.e., including all five auxiliary variables in both estimators), it is denoted by KMI_BJ55. When the working Buckley–James estimator for failure time is correctly specified and the working Buckley–James estimator for censoring time is misspecified (i.e., by only including Z₁, Z₂ and Z₃ in the model), it is denoted by KMI_BJ53. When the working Buckley–James estimator for failure time is misspecified and the working Buckley–James estimator for censoring time is correctly specified, it is denoted by KMI_BJ35. For the KMI_PH method, the same inclusion of covariates as for KMI_BJ is considered, and is denoted by KMI_PH55, KMI_PH53, and KMI_PH35. All three KMI_PH estimators are considered as misspecified even if both working PH models include all five auxiliary variables in the models (i.e., KMI_PH55) because the true models are not PH models.

The results are provided in Tables III–V. The FO analysis, which is the gold standard method, targets the true values in all situations and produces coverage rates comparable with the nominal level, 95%. The PO analysis as expected produces biased survival estimates in all situations and has a lower coverage rate.

Table III.

Monte Carlo results for the marginal survival estimate at the median and 75th percentile survival times, where log(T) = 0.10 − 2Z₁ + 0.5Z₂ − 2Z₃ + 2Z₄ + 2Z₅ + Normal(0, 2²) and log(C) = 0.08 − 2.5Z₁ + 0.5Z₂ − 2Z₃ + 2Z₄ + 2Z₅ + Normal(0, 2²).

	S(t) = 0.50					S(t) = 0.25
Methode	Esta	Bias	SDb	SEc	CRd	Est	Bias	SD	SE	CR
N = 200
FO	0.5035	0.0035	0.0367	0.0353	92.6	0.2510	0.0010	0.0288	0.0306	94.4
PO	0.5482	0.0482	0.0432	0.0420	78.4	0.3049	0.0549	0.0480	0.0475	78.8
KMIBJ55	0.5078	0.0078	0.0460	0.0446	93.2	0.2606	0.0106	0.0472	0.0464	94.8
KMIPH55	0.5075	0.0075	0.0463	0.0446	94.4	0.2601	0.0101	0.0474	0.0461	93.4
KMIBJ53	0.5088	0.0088	0.0447	0.0438	93.4	0.2621	0.0121	0.0481	0.0459	94.2
KMIPH53	0.5076	0.0076	0.0452	0.0441	93.0	0.2600	0.0100	0.0481	0.0458	93.8
KMIBJ35	0.5149	0.0149	0.0450	0.0442	91.8	0.2681	0.0181	0.0487	0.0463	93.4
KMIPH35	0.5152	0.0152	0.0458	0.0440	91.8	0.2684	0.0184	0.0476	0.0465	92.6
IPCWLognormal	0.5029	0.0029	0.0479	0.0445	92.2	0.2505	0.0005	0.0522	0.0505	93.0
IPCWPH	0.5036	0.0036	0.0554	0.0440	89.4	0.2413	−0.0087	0.0663	0.0420	78.0
PMILognormal	0.5014	0.0014	0.0380	0.0418	97.4	0.2490	−0.0010	0.0345	0.0404	97.0
PMIWeibull	0.5028	0.0028	0.0395	0.0423	96.4	0.2308	−0.0192	0.0349	0.0395	92.2
N = 400
FO	0.5000	0.0000	0.0243	0.0250	96.2	0.2487	−0.0013	0.0218	0.0216	93.2
PO	0.5454	0.0454	0.0285	0.0298	68.0	0.3052	0.0552	0.0337	0.0337	62.6
KMIBJ55	0.5037	0.0037	0.0304	0.0315	96.8	0.2578	0.0078	0.0335	0.0329	94.4
KMIPH55	0.5035	0.0035	0.0309	0.0314	96.2	0.2574	0.0074	0.0333	0.0327	93.4
KMIBJ53	0.5050	0.0050	0.0307	0.0314	95.4	0.2587	0.0087	0.0338	0.0326	93.8
KMIPH53	0.5045	0.0045	0.0304	0.0314	95.8	0.2575	0.0075	0.0335	0.0325	94.0
KMIBJ35	0.5086	0.0086	0.0309	0.0312	95.8	0.2623	0.0123	0.0343	0.0328	93.6
KMIPH35	0.5088	0.0088	0.0305	0.0312	96.2	0.2623	0.0123	0.0338	0.0326	94.4
IPCWLognormal	0.5005	0.0005	0.0324	0.0321	95.8	0.2499	−0.0001	0.0365	0.0355	94.2
IPCWPH	0.5016	0.0016	0.0376	0.0324	92.6	0.2393	−0.0107	0.0528	0.0333	79.0
PMILognormal	0.4999	−0.0001	0.0256	0.0296	97.6	0.2492	−0.0008	0.0249	0.0282	96.6
PMIWeibull	0.5019	0.0019	0.027	0.0299	97.6	0.2311	−0.0189	0.0264	0.0276	89.0

Censoring rate = 50%, the Spearman correlation coefficient between T and C (i.e.,ρ) = 0.27.

FO, fully observed; PO, partially observed; KMI, Kaplan–Meier imputation; IPCW, inverse probability of censoring weighted; PMI, parametric multiple imputation.

^aAverage of 500 point estimates.

^bEmpirical standard deviation.

^cAverage estimated standard error.

^dCoverage rate of 500 95% confidence intervals.

^eSubscripts BJ(PH) that indicate Buckley–James (PH) are used for the two working models. Subscripts n, m indicate that n covariates are used in the working failure time model, and m covariates are used in the working censoring time model.

Table V.

Monte Carlo results for Monte Carlo results for the marginal survival estimate at the median and 75^th percentile survival times, where log(T) = 0.10 − 2Z₁ + 0.5Z₂ − 2Z₃ + 2Z₄ + 2Z₅ + logistic(0, 1) and log(C) = 0.08 − 2.5Z₁ + 0.5Z₂ − 2Z₃ + 2Z₄ + 2Z₅ + logistic(0, 1).

	S(t) = 0.50					S(t) = 0.25
Method	Esta	Bias	SDb	SEc	CRd	Est	Bias	SD	SE	CR
N = 200
FO	0.5011	0.0011	0.0360	0.0353	93.4	0.2529	0.0029	0.0314	0.0306	92.6
PO	0.5594	0.0594	0.0422	0.0416	70.6	0.3222	0.0722	0.0499	0.0472	68.6
KMIBJ55	0.5092	0.0092	0.0449	0.0443	92.4	0.2658	0.0158	0.0488	0.0460	91.8
KMIPH55	0.5085	0.0085	0.0445	0.0447	94.4	0.2642	0.0142	0.0479	0.0460	92.2
KMIBJ53	0.5113	0.0113	0.0443	0.0441	93.0	0.2676	0.0176	0.0487	0.0461	91.6
KMIPH53	0.5099	0.0099	0.0447	0.0442	92.8	0.2649	0.0149	0.0490	0.0455	91.8
KMIBJ35	0.5171	0.0171	0.0448	0.0440	89.8	0.2743	0.0243	0.0488	0.0458	90.6
KMIPH35	0.5173	0.0173	0.0445	0.0437	91.8	0.2742	0.0242	0.0489	0.0458	89.0
IPCWLoglogistic	0.5020	0.0020	0.0475	0.0452	92.4	0.2579	0.0079	0.0536	0.0498	92.8
IPCWPH	0.5030	0.0030	0.0532	0.0440	87.4	0.2508	0.0008	0.0695	0.0418	77.4
PMILoglogistic	0.5013	0.0013	0.0372	0.0417	96.6	0.2526	0.0026	0.0355	0.0396	96.6
PMIWeibull	0.5023	0.0023	0.0391	0.0418	95.8	0.2361	−0.0139	0.0372	0.0389	93.6
N = 400
FO	0.5003	0.0003	0.0244	0.0250	95.8	0.2505	0.0005	0.0208	0.0216	95.8
PO	0.5571	0.0571	0.0286	0.0295	51.2	0.3168	0.0668	0.0323	0.0334	48.0
KMIBJ55	0.5037	0.0037	0.0310	0.0317	94.6	0.2588	0.0088	0.0307	0.0323	95.4
KMIPH55	0.5029	0.0029	0.0310	0.0317	95.2	0.2578	0.0078	0.0309	0.0320	95.0
KMIBJ53	0.5048	0.0048	0.0310	0.0315	95.4	0.2595	0.0095	0.0308	0.0319	94.8
KMIPH53	0.5036	0.0036	0.0310	0.0314	94.4	0.2583	0.0083	0.0309	0.0316	95.8
KMIBJ35	0.5092	0.0092	0.0308	0.0312	93.6	0.2642	0.0142	0.0315	0.0317	94.2
KMIPH35	0.5096	0.0096	0.0304	0.0312	94.4	0.2643	0.0143	0.0314	0.0321	92.8
IPCWLoglogistic	0.4994	−0.0006	0.0328	0.0327	94.2	0.2501	0.0001	0.0339	0.0355	94.8
IPCWPH	0.5005	0.0005	0.0390	0.0328	90.4	0.2389	−0.0111	0.0557	0.0332	78.4
PMILoglogistic	0.4988	−0.0012	0.0249	0.0293	98.8	0.2486	−0.0014	0.0225	0.0278	97.6
PMIWeibull	0.5008	0.0008	0.0265	0.0297	97.4	0.2336	−0.0164	0.0246	0.0275	92.4

Censoring rate = 50%, the Spearman correlation coefficient between T and C (i.e.,ρ) = 0.32.

FO, fully observed; PO, partially observed; KMI, Kaplan–Meier imputation; IPCW, inverse probability of censoring weighted; PMI, parametric multiple imputation.

^aAverage of 500 point estimates.

^bEmpirical standard deviation.

^cAverage estimated standard error.

^dCoverage rate of 500 95% confidence intervals.

In all situations, both KMI_BJ and KMI_PH methods produce reasonable survival estimates and coverage rates, for KMI_BJ55 and KMI_PH55, that is, when both working models include all five auxiliary variables, and adequate performance if covariates are omitted. For both weak (Tables III and V) and strong (Table IV) dependent censoring, when the working Buckley–James estimator or PH model for the failure time only includes the first three auxiliary variables (i.e., KMI_BJ35 and KMI_PH35), the KMI methods have a larger bias. KMI_BJ and KMI_PH methods produce almost identical survival estimates and the associated standard error estimates. Their bias increases with the correlation between the failure and censoring times but decreases with sample size in all situations.

Table IV.

Monte Carlo results for the marginal survival estimate at the median and 75th percentile survival times, where log(T) = 0.10 − 2Z₁ + 0.5Z₂ − 2Z₃ + 2Z₄ + 2Z₅ + Normal(0, 0.8²) and log(C) = 0.08 − 2.5Z₁ + 0.5Z₂ − 2Z₃ + 2Z₄ + 2Z₅ + Normal(0, 0.8²).

	S(t) = 0.50					S(t) = 0.25
Method	Esta	Bias	SDb	SEc	CRd	Est	Bias	SD	SE	CR
N = 200
FO	0.5033	0.0033	0.0347	0.0353	94.8	0.2518	0.0018	0.0296	0.0306	94.2
PO	0.6291	0.1291	0.0408	0.0397	13.6	0.3984	0.1484	0.0463	0.0464	11.2
KMIBJ55	0.5256	0.0256	0.0461	0.0441	90.6	0.2823	0.0323	0.0426	0.0426	91.2
KMIPH55	0.5246	0.0246	0.0461	0.0442	90.8	0.2808	0.0308	0.0429	0.0424	91.0
KMIBJ53	0.5288	0.0288	0.0460	0.0436	89.4	0.2847	0.0347	0.0435	0.0425	88.4
KMIPH53	0.5279	0.0279	0.0462	0.0435	89.6	0.2830	0.0330	0.0429	0.0419	88.8
KMIBJ35	0.5441	0.0441	0.0445	0.0430	81.0	0.3014	0.0514	0.0443	0.0429	80.4
KMIPH35	0.5440	0.0440	0.0451	0.0433	81.4	0.3012	0.0512	0.0441	0.0432	80.6
IPCWLognormal	0.5060	0.0060	0.0587	0.0515	92.4	0.2599	0.0099	0.0516	0.0505	94.4
IPCWPH	0.4850	−0.0150	0.0979	0.0436	70.8	0.2311	−0.0189	0.0795	0.0371	62.8
PMILognormal	0.5023	0.0023	0.0355	0.0398	97.6	0.2519	0.0019	0.0302	0.0354	97.8
PMIWeibull	0.4958	−0.0042	0.0362	0.0394	96.8	0.2397	−0.0103	0.0297	0.0340	96.6
N = 400
FO	0.5003	0.0003	0.0255	0.0250	94.8	0.2490	−0.0010	0.0217	0.0216	93.8
PO	0.6275	0.1275	0.0284	0.0282	0.8	0.3958	0.1458	0.0321	0.0329	0.2
KMIBJ55	0.5202	0.0202	0.0315	0.0315	89.6	0.2767	0.0267	0.0287	0.0304	89.8
KMIPH55	0.5199	0.0199	0.0317	0.0317	90.2	0.2764	0.0264	0.0287	0.0305	89.8
KMIBJ53	0.5229	0.0229	0.0315	0.0313	88.2	0.2790	0.0290	0.0283	0.0302	88.2
KMIPH53	0.5226	0.0226	0.0318	0.0311	88.6	0.2779	0.0279	0.0284	0.0300	88.6
KMIBJ35	0.5324	0.0324	0.0315	0.0309	81.8	0.2895	0.0395	0.0294	0.0305	78.0
KMIPH35	0.5329	0.0329	0.0317	0.0309	81.6	0.2895	0.0395	0.0295	0.0303	76.6
IPCWLognormal	0.5029	0.0029	0.0409	0.0388	93.6	0.2529	0.0029	0.0384	0.0366	94.2
IPCWPH	0.4699	−0.0301	0.0953	0.0353	69.4	0.2071	−0.0429	0.0813	0.0283	55.8
PMILognormal	0.5005	0.0004	0.0250	0.0281	97.6	0.2498	−0.0002	0.0219	0.0250	98.0
PMIWeibull	0.4941	−0.0059	0.0261	0.0277	94.6	0.2381	−0.0119	0.0218	0.0241	94.2

Censoring rate = 51%, the Spearman correlation coefficient between T and C (i.e.,ρ) = 0.69.

FO, fully observed; PO, partially observed; KMI, Kaplan–Meier imputation; IPCW, inverse probability of censoring weighted; PMI, parametric multiple imputation.

^aAverage of 500 point estimates.

^bEmpirical standard deviation.

^cAverage estimated standard error.

^dCoverage rate of 500 95% confidence intervals.

The performance of the IPCW method depends on whether a correct model is used to derive the censoring weights and the correlation between the failure and censoring times (i.e., the magnitude of dependent censoring). In all situations, when a correct censoring time model is used to derive the weights (i.e., IPCW_Lognormal in Tables III and IV and IPCW_Loglogistic in Table V), IPCW produces survival estimates almost identical to the FO analysis and the coverage rates comparable with the nominal level. When a wrong censoring time model is used to derive the weights (i.e., IPCW_PH) and the correlation between failure and censoring times is weak (Tables III and V), IPCW produces survival estimates very close to the FO analysis, and the bias decreases with sample size. However, when the correlation is strong (Table IV), IPCW using a wrong censoring time model produces biased survival estimates, and the bias increases with sample size. In all situations, when a wrong censoring time model is used, IPCW’s standard errors tend to underestimate the variability of its survival estimates, and the underestimate is substantial when the correlation between the failure and censoring times is strong. As a result, IPCW’s coverage rates are lower than the nominal level even when the correlation between the failure and censoring times is weak. When the correlation between the failure and censoring times is weak (Tables III and V), IPCW methods have a bias slightly smaller than KMI methods. However, when the correlation between the failure and censoring times is strong (Table IV), KMI methods have a bias smaller than IPCW. The KMI methods are more efficient than the IPCW method as seen by the smaller SD and MSE values. In some scenarios, the difference superiority of KMI over IPCW in efficiency is substantial.

The performance of the PMI method depends on whether a correct model is used to impute residual times for each censored observation. In all situations, when a correct residual time model is used for imputation (i.e., PMI_Lognormal in Tables III and IV and PMI_Loglogistic in Table V), PMI produces survival estimates almost identical to the FO analysis. The coverage rates are slightly higher than the nominal level due to over-estimation of the variability of its survival estimates. In all situations, when a wrong residual time model is used for imputation (i.e., PMI_Weibull), PMI produces survival estimates very close to the FO analysis at the median survival time. However, PMI produces biased survival estimates at the 75th percentile survival time. When the correlation between the failure and censoring times is high (Table IV), PMI methods have a bias smaller than KMI methods at both median and 75th percentile survival times. When the correlation between the failure and censoring times is weak (Tables III and V), PMI methods using a wrong residual time model could produce a bias slightly larger but comparable with KMI methods at the 75th percentile survival time, especially when the sample size is equal to 400. In all situations, PMI methods have a smaller mean squared error estimate than KMI methods.

In simulation results not shown, we assessed the properties of the IPCW and PMI methods, which only used the first three auxiliary variables. We found that this substantially increased the bias, and that the standard error estimates were poor for the IPCW method.

In summary, all methods reduced the bias of the standard PO analysis, but the amount of the remaining bias, the efficiency, and the validity of the estimated standard errors varied between methods. The performance of the IPCW method depends on whether a correct censoring time model is used to derive the weights, especially when the dependent censoring is strong. In contrast, the KMI methods in which two risk scores are derived from either two working Buckley–James estimators or two working PH models can provide reasonable survival estimates for both weak and strong dependent censoring and is robust to misspecification of either one of the two working models and is robust to misspecification of the link functions in the failure time and censoring time models. The performance of the PMI approach depends on whether a correct residual time model is used for imputation, especially in the tail area of the survival curve.

7. Discussion

In this paper, we adapt the nonparametric multiple imputation approach we previously proposed to recover information for censored observations and compare it with the two existing popular approaches when the data are from AFT models. Based on the simulation results, the performance of the PMI method depends on whether the failure time model is correctly specified, especially in the tail area. The performance of the IPCW method depends on whether the censoring time model is correctly specified. This indicates that while performing the PMI and IPCW methods, one has to be sure that the corresponding model is correct, and specifically requires all aspects of the models including the link functions and choice of covariates to be correct. In contrast, for the nonparametric multiple imputation approach, the two working Buckley–James estimators or PH model estimators are only used to derive two risk scores to select imputing risk sets for censored observations. Once the imputing risk sets are selected, nonparametric multiple imputation procedures are conducted on the risk sets. Therefore, this approach is expected to have weak reliance on the two working models compared with the IPCW method. As expected, the simulation study shows that the multiple imputation approaches based on two working Buckley–James estimators and two working PH models produce similar results for both point survival estimates and the associated standard error estimates when the data are from AFT models. This is because the PH model preserves the relative importance of the covariates in the AFT model. This indicates that the multiple imputation approach [9] we previously proposed is robust to misspecification of the link functions of the two working PH models when the data are from AFT models. In other words, the multiple imputation approach in [9] has good properties even when the true model is from an AFT family. In addition, the multiple imputation approach based on the two working Buckley–James estimators is also robust to misspecification of either one of the two working estimators when the data are from AFT models. Even though both the nonparametric multiple imputation approaches are robust to misspecification of either one of the two working models and misspecification of the link functions, the nonparametric multiple imputation approach based on two working PH models is preferred because in general, the estimation of a PH model is easier and more stable.

Although the double robustness property of the KMI methods is attractive, simulation results do show that in a situation with a finite sample size when the working Buckley–James or PH model estimators for the failure time are misspecified, the bias is greater than when it is correctly specified. This suggests that it is more important to try to find a reasonable working model for the failure time than the censoring time because the main interest is in estimating the survival function for the failure time, not for the censoring time. Hence, it is important to identify all of the prognostic variables for the failure time and evaluate how prognostic they are.

The performances of the proposed nonparametric multiple imputation method will depend on the censoring rate. Specifically, the censoring rate will affect the number of available ‘donors’ for each censored observation, especially at the tail of the survival function. In a situation with a high censoring rate, say, 0.90, a much larger sample size is required for the proposed method to perform well, than a situation with a low censoring rate.

In this paper, we assume that censoring only depends on the observed auxiliary variables. This assumption is untestable. It is possible that censoring also depends on some unobserved auxiliary variables. This indicates that informative censoring may still remain even conditioning on all of the observed auxiliary variables. Sensitivity analysis [26, 27] would be a possible way to evaluate the impact of unobserved auxiliary variables on the proposed multiple imputation approaches.