Abstract
The mean amplitude of glycemic excursions (MAGE) is an essential index for glycemic variability assessment, which is treated as a key reference for blood glucose controlling at clinic. However, the traditional “ruler and pencil” manual method for the calculation of MAGE is time-consuming and prone to error due to the huge data size, making the development of robust computer-aided program an urgent requirement. Although several software products are available instead of manual calculation, poor agreement among them is reported. Therefore, more studies are required in this field. In this paper, we developed a mathematical algorithm based on integer nonlinear programming. Following the proposed mathematical method, an open-code computer program named MAGECAA v1.0 was developed and validated. The results of the statistical analysis indicated that the developed program was robust compared to the manual method. The agreement among the developed program and currently available popular software is satisfied, indicating that the worry about the disagreement among different software products is not necessary. The open-code programmable algorithm is an extra resource for those peers who are interested in the related study on methodology in the future.
1. Introduction
Clinical researches have suggested that high glycemic variability may cause more serious damage to the body than high level stable blood glucose [1], which relates to the development of diabetic complication [2–6] and the increase of mortality in critically serious patients without diabetes [7, 8]. In such circumstances, how to quantitatively evaluate the glycemic variability in diabetic blood glucose monitor is essential for the clinical diagnosis and treatment. Several indexes have been proposed for the quantitative evaluation of the glycemic variability, such as MBG, SDBG, IQR, LAGE, M-value, %CV, J-index, IGC, GRADE, MODD, LBGI, HBGI, ADRR, TI, LI, PGS, CONGA, and MAGE [9–16]. Presently, clinicians and researchers trend to choose MAGE as the preferred index [17, 18], making it a “popular standard” in the quantitative evaluation of the within-day glycemic variability.
MAGE is an arithmetic average of either the upward or downward of all glycemic excursions exceeding the threshold (standard deviation of blood glucose (SDBG) obtained from all blood glucose concentrations within 24-hour period); the direction of the calculation is determined by the first countable excursion [19–21]. Following the original definition by Service et al. [19], clinicians and researchers applied the “ruler and pencil” graphical approach to calculate MAGE. However, this kind of manual approach is time-consuming and error-prone, when dealing with huge amount of data typically characterized by 288 observations in 5 minutes apart over a 24-hour period, generated from continuous glucose monitoring (CGM). Thus, the development of computer-aided programs to calculate MAGE becomes an urgently needed task.
To address the urgent need above, several automatic programs have been developed [22–25], making great contribution to the automatic calculation of MAGE. However, it was pointed out that the agreement among them is poor [26]. Therefore, more studies are required to explore the automatic calculation of MAGE. Currently available programs can be roughly divided into two groups. One group has detailed descriptions about algorithm with graphical display, such as the automated algorithm described by Baghurst [22] and the computer software described by Fritzsche et al. (Fritzsche) [23]. The other group only provides executable software for automatic calculation, without detailed descriptions of the algorithms used in the software, such as the web-based application “GlyCulator” [24] and the Excel-based workbook “EasyGV” [25]. However, to the best of our knowledge, all of these methods did not provide programmable open codes, which are important resources required for peers to implement more studies on methodology in this field.
Therefore, in this report, we developed a mathematical algorithm based on integer nonlinear programming method. Following the proposed mathematical method, a computer-aided program named MAGECAA v1.0 was developed. The code of our program is open; if peers are interested in it, please contact xuefeiyu@smu.edu.cn for downloading. To validate the developed program, comparison study was implemented using blood glucose CGM datasets obtained from T1D, T2D, and gestational diabetes patients against the manual method (MAGEo) and other currently popular software products.
2. Materials and Methods
2.1. The Proposed Mathematical Algorithm
Let f(t) (t = t1, t2,…, tL) represent the discrete blood glucose values obtained in CGM; then f is a discrete function defined in time set {t1, t2,…, tL}. Let SDBG be the standard deviation of f(t) (t = t1, t2,…, tL). A graph depicting the glycemic variability can be formed by connecting all the discrete values of function f. When the difference of a peak and an adjacent nadir exceeds SDBG, the corresponding peak is labeled as a valid peak. The key point for the calculation of MAGE is to correctly count the valid peak or nadir.
Amplitude is the difference of functional values in a peak and a nadir of the function graph. A valid amplitude is labeled and counted when it is bigger than SDBG. To compute MAGE, these valid amplitudes of function f should be firstly searched. From the mathematical perspective, a peak or nadir should be an extreme point of the function. These extreme points related to valid amplitudes are called valid extreme points. The MAGE computation problem can be solved by calculating all valid extreme points.
Suppose that {tl1, tl2,…, tlN} is the sequence of all extreme points of function f. We know that the local maximum points and local minimum points of function f should be arranged as follows: interleaved between a maximum point and a minimum point. For simplicity, {tl1, tl2,…, tlN} is denoted as {1,2,…, N}, and {n1, n2,…, nK} is an arbitrary valid subsequence of sequence {1,2,…, N}. These local maximum points and local minimum points can be staggered in subsequence {n1, n2,…, nK}. Then
| (1) |
where 2 ≤ K ≤ N. This equation ensures that the selected extreme points are staggered.
Thus, the above MAGE computation problem can be transformed to an integer nonlinear programming (INLP) problem.
| (2) |
| (3) |
According to the principle of INLP problem, function (2) should have an optimum solution {n1∗, n2∗,…, nK∗} and an optimum value ZK∗ with respect to a constant K; it should also have an optimum value ZK−1∗ for constant K − 1, and
| (4) |
Suppose that K∗ is the maximal K with respect to the optimal solution of function (2), and then the optimal solution {n1∗, n2∗,…, nK∗∗} represents the valid extreme points to compute MAGE.
If the extreme point n1∗ is the local minimum point, then
| (5) |
If the extreme point n1∗ is the local maximum point, then
| (6) |
Now, our object is to get the optimal solution {n1∗, n2∗,…, nK∗∗} of function (2). If the INLP problem is solved by enumeration algorithm, the amounts of different subsequences {n1, n2,…, nK} should be . For 3 ≤ K ≤ N, the amounts of all subsequences are
| (7) |
It is difficult to directly solve function (2) when N is large. A faster optimization algorithm is usually used to solve the above INLP problem. For example, a penalty function algorithm [27, 28] was used here to transform the above INLP problem (2) to an unconstrained optimization problem as follows.
Set
| (8) |
The new unconstrained integer optimization problem becomes
| (9) |
where 3 ≤ K ≤ N and μk and λk (k = 1,…, K − 1) are penalty coefficients and tend to be +∞.
When the optimum value YK∗ > 0, problem (9) has no optimal solution.
Differential evolution (DE) algorithm, a faster optimization algorithm proposed by Storn and Price [29], is a simple but powerful population-based stochastic search technique to solve global optimization problems over continuous domains. Many researchers modified DE algorithm to improve its performance when it was applied to a specific problem [30–33]. The idea of a modified DE algorithm proposed by Lin [34] to solve mixed-integer nonlinear programming problem is used here.
DE searches for a global optimal point in an n-dimensional hyperspace. Let be the K-dimensional search space of the INLP problem under consideration. The DE evolves a population of NP n-dimensional individual vectors, that is, solution candidates, , i = 1, …, NP, from one generation to the next. The evolution begins with a randomly initialized population of n-dimensional integer parameter vectors in space {1,2,…, N}K. In each vector, integer parameters are sorted in an ascending order. Each vector forms a candidate solution to the unconstrained optimization problem. At each generation G, DE employs the mutation and crossover operations to produce a trial vector UiKG for each individual vector NiKG, also called target vector, in the current population.
The details of the employment of the DE algorithm to solve the above INLP problem are as follows from (a) to (d).
(a) Initialization. A randomly initialized population is created to cover the entire search space uniformly as in the following form:
| (10) |
where ρij is a random number in the range [0,1] and NINT[B] is expressed as the nearest integer vector to real vector B.
(b) Mutation Operation. For each target vector NiKG at generation G, randomly sample three other individuals Nr1KG, Nr2KG, and Nr3KG from the same generation, where r1, r2, and r3 are random and mutually different integers generated over the range [1, NP], which should be different from the current trial vector's index i. Then an associated mutant vector ViKG = (vi1G,…, viKG) can be generated by using strategy:
| (11) |
where F is a factor in [0,1] for scaling differential vectors.
(c) Crossover Operation. The crossover operation is applied to each pair of the generated mutant vector ViKG and its corresponding target vector NiKG to generate a trial vector UiKG = (ui1G, ui2G,…, uiKG).
| (12) |
where CR ∈ [0,1] is a crossover constant that is determined by users. jrand is a randomly chosen index in [1, K] which ensures that uijG gets at least one parameter from vijG. The integer parameters of target vector NiKG are also sorted from small to big.
(d) Selection Operation. The trial vector UiKG is compared to its corresponding target vector NiKG using the greedy criterion to decide whether a member of generation G + 1 existed or not. If vector UiKG yields a smaller cost function value Y(UiKG) than Y(NiKG), then NiKG+1 is set to UiKG; otherwise, the old vector is retained. The operation is expressed as follows:
| (13) |
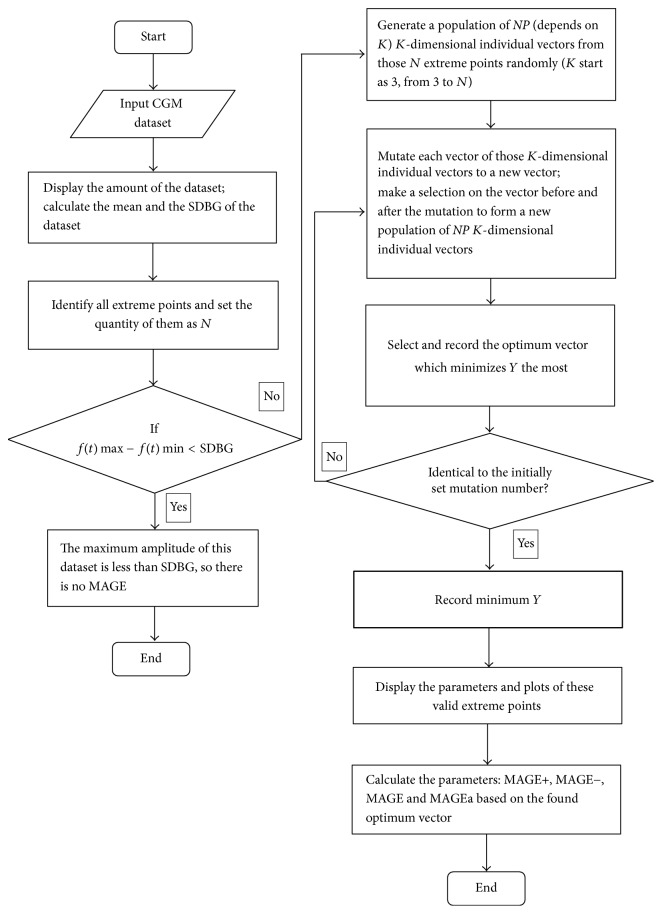
The above (b) to (d) steps are repeated till the evolution times arrived to certain number (general G = 200); from the last evolutionary generation, the individual vector NiKG with the smallest value of the objective function Y is the optimal solution of the problem of the current K-dimensional extreme point combination. The algorithm will search K from 3 to N till the objective function Y obtains the minimum value so as to obtain the optimal extreme point combination {n1∗, n2∗,…, nK∗∗} and then use formulas (5)~(6) to calculate the MAGE value. Figure 1 shows the entire algorithm.
Figure 1.
Flow of the algorithm of the program of MAGECAA v1.0.
2.2. The Developed Program Based on the Proposed Mathematical Method
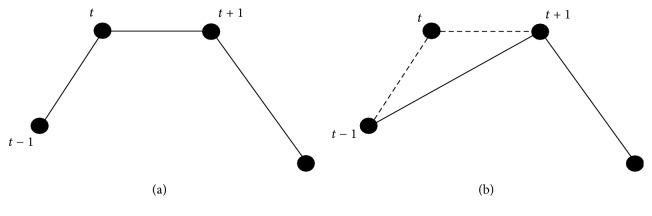
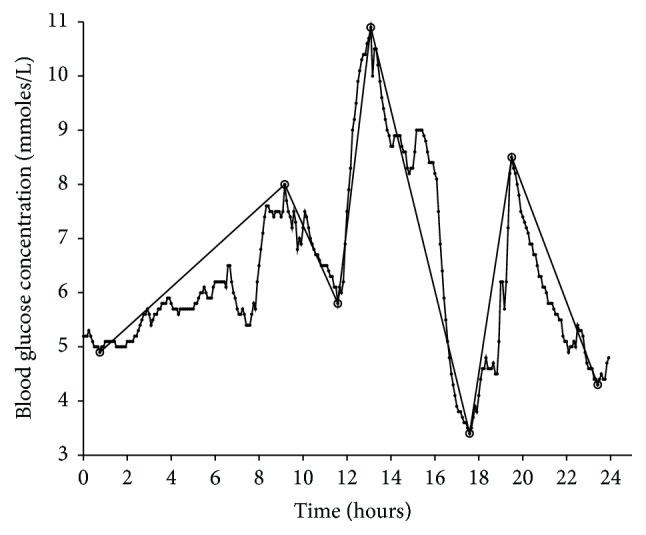
Based on the proposed mathematical method, a computer automated program named MAGECAA v1.0 was developed. The MAGE calculation program can be described as a process that selects valid extreme points from a time-ordered set of glucose concentrations whose adjacent differences are all greater than the threshold (typically 1 SDBG obtained from 24-hour period blood glucose concentrations). It can be summarized as finding the optimum vector combination solution of the valid extreme points and using INLP to establish the mathematic method, which can be solved by differential evolution (DE) algorithm. Once all valid extreme points of countable excursions have been identified, the MAGE is determined by MAGE+ or by MAGE−, depending on the direction of the first countable excursion. For more in-depth understanding, it depends on the first valid extreme point of the vector combination, because that point indicates the direction. In addition, the average of both MAGE+ and MAGE−, designated as MAGEa, is also calculated. MAGECAA v1.0 is based on INLP and has several different outputs: SDBG, MAGE+, MAGE−, MAGE, MAGEa, and so forth. Besides it also needs plot to show all valid extreme points joined by straight lines; MATLAB (MathWorks®, USA) is chosen as the programming environment accordingly. Generally, some data points could not be extreme point according to the mathematical definition, like points shown in Figure 2, which shows turning points t and t + 1 which are equal in values (not being extreme points) but there is an amplitude from peak point t − 1 to nadir point t, so we combine points t and t + 1 as one point t + 1 or remove point t and then let point t + 1 be a local maximum point. If the points appear to be opposite, then point t + 1 should be a local minimum point.
Figure 2.
(a) shows turning points t and t + 1 to be equal in values (not being extreme points) but there is an amplitude from peak point t − 1 to nadir point t. (b) shows the combination of points t and t + 1 as one point t + 1 or remove point t; then let point t + 1 be a local maximum point.
MAGECAA v1.0 consists of the following major modules: (1) import CGM data and calculate the SDBG as the threshold; (2) identify all extreme points; (3) find the optimum vector combination solution of valid extreme points; and (4) display the calculated parameters and plots.
2.3. Collection of CGM Data
The CGM datasets obtained by using CGMS® Gold™ (Medtronic®, USA), collected from clinical treatment, are used to evaluate the proposed program. All CGM datasets were provided by the Third Affiliated Hospital of Southern Medical University. Only complete 24-hour CGM data were selected for comparison study. All patients have provided their written informed consent. 5 CGM recordings from 3 T1D patients, 116 CGM measurements contributed by 58 T2D patients, and 127 CGM measurements based on gestational diabetes patients have been collected. Outpatients had been treated with either diet, oral hypoglycemic agents, oral hypoglycemic agents plus insulin, or insulin alone, depending on their glycemic control.
2.4. Data Analysis
The validation of MAGECAA v1.0 was implemented by comparison against MAGEo and MAGEc. A doctor who has been well trained in using the original manual method to analyze CGM data was invited from Department of Endocrinology of the Third Affiliated Hospital of Southern Medical University, and he did not know the effect of MAGECAA v1.0. Our research team analyzed the complete patient population (n = 248) CGM measurements using MAGECAA v1.0 and two other popular software products, EasyGV and Fritzsche, whereas the doctor performed a manual analysis on a randomly drawn sample (n = 60). As calculator, Fritzsche allows the analyzer to choose whether or not to consider the first and/or the final glucose value of the CGM trace as a start or end point of a glucose excursion; it will result in four different MAGE values per CGM trace. To keep following the original description of the calculation of MAGE and for the comparison of the different software products, the first and final glucose values were both taken into account.
2.5. Statistical Analyses
Spearman's correlation analysis was applied in evaluating the relationship between the MAGE values obtained by different methods with respect to the same patients. Bland-Altman plots were used to represent the agreement of the methods [35, 36]. P < 0.01 was considered significant.
3. Results
Figure 3 presents the screenshot of the graphical user interface of the developed software named MAGECAA v1.0.
Figure 3.
Screenshot of the graphical user interface of the MAGECAA v1.0 based on the MATLAB® programming environment for the mean amplitude of glycemic excursions (MAGE) calculation. After computation, 24-hour continuous glucose monitoring profiles are shown in the plots with all valid extreme points joined by straight lines. Besides the calculation of MAGE, it also calculates the standard deviation of blood glucose (SDBG), the average of all upward valid excursions (MAGE+), the average of all downward valid excursions (MAGE−), and the average of all valid excursions (MAGEa). The CGM data were collected from patients with type 1 diabetes. After calculation, the results are as follows: SDBG = 1.63 mmoles/L, MAGE+ = 4.43 mmoles/L, MAGE− = 4.63 mmoles/L, MAGEc = 4.43 mmoles/L (the first account excursion is from nadir to peak), and MAGEa = 4.53 mmoles/L.
3.1. Comparison of MAGECAA v1.0 with the Original Manual Method
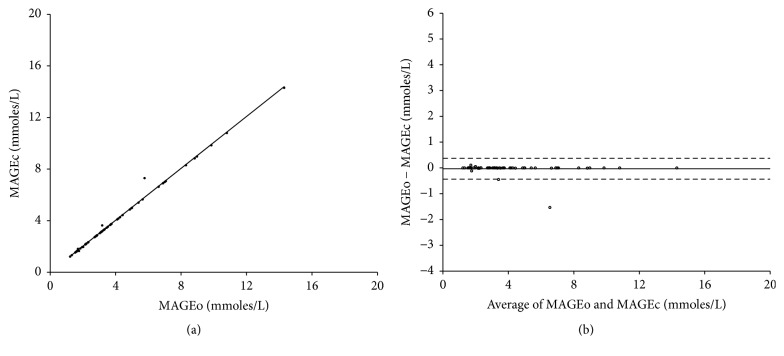
As shown in Figure 4, Spearman's correlation analysis identified that there is a highly significant linear correlation between MAGEc and MAGEo (r = 0.998, resp.; P < 0.01), and the mean difference found in Bland-Altman plot was −0.03 ± 0.21, which was statistically significantly small. This result indicated that the developed program was robust compared with the manual method.
Figure 4.
(a) Correlation of the mean amplitude of glycemic excursions values (MAGE) obtained from the proposed program (MAGEc) and the original manual methods (MAGEo). The data of 60 continuous glucose monitoring (CGM) measurements were randomly chosen from all collected CGM data. (b) Bland-Altman plot shows the difference between MAGEc and MAGEo on y-axis and the mean of the two computed indices on x-axis. The dashed lines represent the 95% confidence limit of the differences between the two methods, and the solid line indicates that the mean difference between the methods is close to 0.
3.2. Agreement of MAGECAA v1.0 with Fritzsche and EasyGV
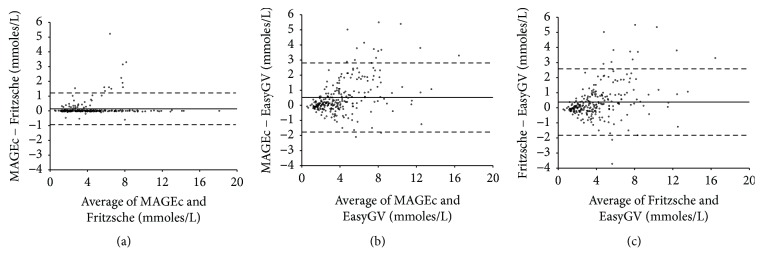
To evaluate the agreement of MAGECAA v1.0 with two currently available popular software products, that is, Fritzsche and EasyGV, we did pairwise comparison of MAGE among them. Table 1 shows the correlation coefficients for MAGE calculation between the calculators, which ranged from 0.926 to 0.987 (P < 0.01 for all). Figure 5 shows the Bland-Altman plot among the three software products; the dashed lines represent the 95% confidence limit of the differences between the two methods, and the solid line demonstrates that the mean difference between the methods is close to 0, indicating that little difference existed among them. The mean differences are 0.14 ± 0.55 (MAGEc versus Fritzsche), 0.52 ± 1.17 (MAGEc versus EasyGV), and 0.38 ± 1.12 (Fritzsche versus EasyGV), showing the good agreement between these three software products.
Table 1.
The correlation coefficient and difference of the results separately calculated using MAGEc, Fritzsche, and EasyGV software.
| MAGEc | Fritzsche | |||
|---|---|---|---|---|
| r | mean ± SD | r | mean ± SD | |
| (mmoles/L−1) | (mmoles/L−1) | |||
| MAGEc | — | — | — | — |
| Fritzsche | 0.987 | 0.14 ± 0.55 | — | — |
| EasyGV | 0.926 | 0.52 ± 1.17 | 0.926 | 0.38 ± 1.12 |
Note. P < 0.01.
Figure 5.
Bland-Altman plots showing the mean difference between MAGEc, EasyGV, and Fritzsche when applied to the same continuous glucose monitoring datasets.
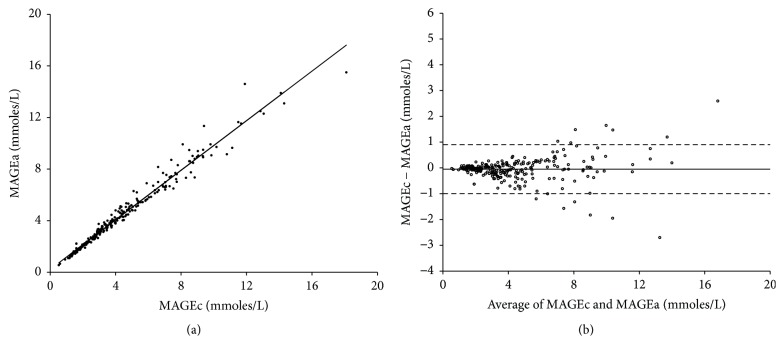
3.3. Comparison of MAGEc with MAGEa
In the original definition of MAGE, its direction of the calculation is determined by the first countable excursion. So MAGEc = MAGE+ or MAGEc = MAGE−; it is somewhat arbitrary and ignores half of the valid excursions. However, MAGEa represents the average of MAGE+ and MAGE−; it does not consider the direction, thus involving all the valid excursions.
To explore whether MAGEa may be a more useful index than MAGEc which depends on MAGE+ or MAGE−, the relationship between MAGEc and MAGEa was tested by using all the 248 CGM measurements via Spearman's correlation analysis and Bland-Altman analysis. As shown in Figure 6, the correlation coefficient was r = 0.993 (P < 0.01) and the mean difference was −0.05 ± 0.48. The results showed that little difference was observed between using MAGEa and MAGEc, indicating that MAGEa may be a useful index for evaluating glycemic variability.
Figure 6.
(a) Correlation between the mean amplitudes of glycemic excursions computerized (MAGEc) and the average of all valid glycemic excursions (MAGEa) for the total collected 248 continuous glucose monitoring measurements. (b) Bland-Altman plot shows the mean difference between MAGEc and MAGEa.
4. Discussions
We developed a computer-aided open-code program named MAGECAA v1.0 based on INLP algorithm for automatic calculation of MAGE. Compared with the existing methods, the proposed novel method turns to search the optimal solution of the combination of extreme points from overall CGM measurements instead of searching adjacent extreme points from the beginning to the end step by step. As for the computational time, if used for one person, the proposed method is comparable with currently available methods; if used for batch calculation, the proposed method is more powerful. The programmable open codes are useful for the study of methodology for automatic calculation of MAGE. The comparison study using MAGECAA v1.0 against manual method indicated that the agreement is satisfied. The pairwise comparison study between MAGECAA v1.0 and two other available software products, Fritzsche and EasyGV, based on Spearman's correlation analysis and Bland-Altman plots, demonstrated that the agreements between them met the requirement. Our study showed that the worry about the disagreement among the currently available popular software products is not necessary, which is different from the proposal by Sechterberger et al. [26]. The reason may be the increased amount of CGM data used in our research.
The MAGE value depends on MAGE+ or MAGE−, following the direction of the first accountable glucose excursion. Considering the fact that only one direction of glucose excursion is adopted in current popular software, unavoidably resulting in the omission of the other directions of valid excursions, we implemented an extra experiment in which data from both directions of the valid glycemic excursions are utilized. MAGEa was used to represent the mean of MAGE+ and MAGE− for the calculation of MAGE. As shown by our data, a close linear correlation between MAGEa and MAGEc was observed, indicating that the difference between MAGE+ and MAGE− is significantly small. Therefore, we proposed that MAGEa might be another suitable parameter to quantify glycemic variability.
To conclude, an open-code software program named MAGECAA v1.0 for automatic calculation of MAGE based on a mathematical algorithm has been proposed and evaluated. The programmable open codes are useful for further methodology study in the future. The comparison study indicated that the agreement among the proposed software and existing software is satisfied, and the worry about the disagreement among currently available different popular software products is not necessary.
Acknowledgments
This study was partially supported by the National Key Research and Development Program of China (nos. 2016YFC0100800 and 2016YFC0100801), the National Natural Science Foundation of China (Grants nos. 61671229 and 61528102), Science and Technology Program of Guangdong, China (nos. 2015B020214006 and 2016A050502026), Guangdong Natural Science Foundation (no. 2015A030313234), and Science and Technology Program of Guangzhou, China (no. 201704020091).
Abbreviations
- MAGE:
Mean amplitude of glycemic excursions
- SDBG:
Standard deviation of blood glucose
- CGM:
Continuous glucose monitoring
- Fritzsche:
Fritzsche et al.'s software
- INLP:
Integer nonlinear programming
- MAGEo:
Calculated values obtained from the original manual method
- MAGEc:
Calculated values obtained from MAGECAA v1.0
- MAGE+:
The average of all upward valid glycemic excursions
- MAGE−:
The average of all downward valid glycemic excursions
- MAGEa:
The average of all downward validated glycemic excursions
- DE:
Differential evolution.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
References
- 1.Monnier L., Mas E., Ginet C., et al. Activation of oxidative stress by acute glucose fluctuations compared with sustained chronic hyperglycemia in patients with type 2 diabetes. The Journal of the American Medical Association. 2006;295(14):1681–1687. doi: 10.1001/jama.295.14.1681. [DOI] [PubMed] [Google Scholar]
- 2.Hirsch I. B., Brownlee M. The effect of glucose variability on the risk of microvascular complications in type 1 diabetes: Response to Kilpatrick et al. and Bolli [9] Diabetes Care. 2007;30(1):186–187. doi: 10.2337/dc06-1610. [DOI] [PubMed] [Google Scholar]
- 3.Bragd J., et al. Can glycemic variability, as calculated form blood glucose self-monitoring, predict the development of complications in type 1 diabetes over a decade? Diabetes & Metabolism. 2008;34(6):612–616. doi: 10.1016/j.diabet.2008.04.005. [DOI] [PubMed] [Google Scholar]
- 4.Škrha J., et al. Glucose variability, HbA1c and microvascular complications. Reviews in Endocrine & Metabolic Disorders. 2016;17(1):1–8. doi: 10.1007/s11154-016-9356-1. [DOI] [PubMed] [Google Scholar]
- 5.Prázný M., et al. Short-term study and long-term glycemic variability and its relationship to microvascular complications of diabetes. Vnitrni Lekarstvi. 2016;62(Supply 4):85. [PubMed] [Google Scholar]
- 6.Caprnda M. Glycemic variability and Vascular Complication in Patients with Type 2 Diabetes Mellitus. Folia Med. 2017;59(3):270–278. doi: 10.1515/folmed-2017-0048. [DOI] [PubMed] [Google Scholar]
- 7.Eslami S., Taherzadeh Z., Schultz M. J., Abu-Hanna A. Glucose variability measures and their effect on mortality: a systematic review. Intensive Care Medicine. 2011;37(4):583–593. doi: 10.1007/s00134-010-2129-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hermanides J., Vriesendorp T. M., Bosman R. J., Zandstra D. F., Hoekstra J. B., Devries J. H. Glucose variability is associated with intensive care unit mortality. Critical Care Medicine. 2010;38(3):838–842. doi: 10.1097/CCM.0b013e3181cc4be9. [DOI] [PubMed] [Google Scholar]
- 9.Schlichtkrull J., Munck O., Jersild M. The M-Value, an Index of Blood-sugar Control in Diabetics. Journal of Internal Medicine. 1965;177(1):95–102. doi: 10.1111/j.0954-6820.1965.tb01810.x. [DOI] [PubMed] [Google Scholar]
- 10.Wojcicki J. M. Mathematical descriptions of the glucose control in diabetes therapy. Analysis of the Schlichtkrull 'M'-value. Hormone and Metabolic Research. 1995;27(1):1–5. doi: 10.1055/s-2007-979895. [DOI] [PubMed] [Google Scholar]
- 11.Wójcicki J. “J”-Index. A New Proposition of the Assessment of Current Glucose Control in Diabetic Patients. Hormone and Metabolic Research. 1995;27(01):41–42. doi: 10.1055/s-2007-979906. [DOI] [PubMed] [Google Scholar]
- 12.Kovatchev B. P., Cox D. J., Gonder-Frederick L. A., Clarke W. Symmetrization of the blood glucose measurement scale and its applications. Diabetes Care. 1997;20(11):1655–1658. doi: 10.2337/diacare.20.11.1655. [DOI] [PubMed] [Google Scholar]
- 13.Hill N. R., Hindmarsh P. C., Stevens R. J., Stratton I. M., Levy J. C., Matthews D. R. A method for assessing quality of control from glucose profiles. Diabetic Medicine. 2007;24(7):753–758. doi: 10.1111/j.1464-5491.2007.02119.x. [DOI] [PubMed] [Google Scholar]
- 14.Kovatchev B. P., Otto E., Cox D., Gonder-Frederick L., Clarke W. Evaluation of a new measure of blood glucose variability in diabetes. Diabetes Care. 2006;29(11):2433–2438. doi: 10.2337/dc06-1085. [DOI] [PubMed] [Google Scholar]
- 15.Rodbard D., Bailey T., Jovanovic L., Zisser H., Kaplan R., Garg S. K. Improved quality of glycemic control and reduced glycemic variability with use of continuous glucose monitoring. Diabetes Technology & Therapeutics. 2009;11(11):717–723. doi: 10.1089/dia.2009.0077. [DOI] [PubMed] [Google Scholar]
- 16.Hirsch I. B., Balo A. K., Sayer K., Garcia A., Buckingham B. A., Peyser T. A. A simple composite metric for the assessment of glycemic status from continuous glucose monitoring data: Implications for clinical practice and the artificial pancreas. Diabetes Technology & Therapeutics. 2017;19:S38–S48. doi: 10.1089/dia.2017.0080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Monnier L., Colette C., Owens D. R. Glycemic variability: The third component of the dysglycemia in diabetes. Is it important? how to measure it? Journal of Diabetes Science and Technology. 2008;2(6):1094–1100. doi: 10.1177/193229680800200618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rodbard D. New and improved methods to characterize glycemic variability using continuous glucose monitoring. Diabetes Technology & Therapeutics. 2009;11(9):551–565. doi: 10.1089/dia.2009.0015. [DOI] [PubMed] [Google Scholar]
- 19.Service F. J., Molnar G. D., Rosevear J. W., Ackerman E., Gatewood L. C., Taylor W. F. Mean amplitude of glycemic excursions, a measure of diabetic instability. Diabetes. 1970;19(9):644–655. doi: 10.2337/diab.19.9.644. [DOI] [PubMed] [Google Scholar]
- 20.Service F. J., Nelson R. L. Characteristics of glycemic stability. Diabetes Care. 1980;3(1):58–62. doi: 10.2337/diacare.3.1.58. [DOI] [PubMed] [Google Scholar]
- 21.Service F. J., O'Brien P. C., Rizza R. A. Measurements of glucose control. Diabetes Care. 1987;10(2):225–237. doi: 10.2337/diacare.10.2.225. [DOI] [PubMed] [Google Scholar]
- 22.Baghurst P. A. Calculating the mean amplitude of glycemic excursion from continuous glucose monitoring data: An automated algorithm. Diabetes Technology & Therapeutics. 2011;13(3):296–302. doi: 10.1089/dia.2010.0090. [DOI] [PubMed] [Google Scholar]
- 23.Fritzsche G., Kohnert K.-D., Heinke P., Vogt L., Salzsieder E. The use of a computer program to calculate the mean amplitude of glycemic excursions. Diabetes Technology & Therapeutics. 2011;13(3):319–325. doi: 10.1089/dia.2010.0108. [DOI] [PubMed] [Google Scholar]
- 24.Czerwoniuk D., Fendler W., Walenciak L., Mlynarski W. GlyCulator: A glycemic variability calculation tool for continuous glucose monitoring data. Journal of Diabetes Science and Technology. 2011;5(2):447–451. doi: 10.1177/193229681100500236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hill N. R., et al. Normal Reference Range for Mean Tissue Glucose and Glycemic Variability Derived from Continuous Glucose Monitoring for Subjects Without Diabetes in Different Ethnic Groups. Diabetes Technology & Therapeutics. 2011;13(9):921–928. doi: 10.1089/dia.2010.0247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sechterberger M. K., Luijf Y. M., Devries J. H. Poor agreement of computerized calculators for mean amplitude of glycemic excursions. Diabetes Technology & Therapeutics. 2014;16(2):72–75. doi: 10.1089/dia.2013.0138. [DOI] [PubMed] [Google Scholar]
- 27.Anjidani M., Effati S. Steepest descent method for solving zero-one nonlinear programming problems. Applied Mathematics and Computation. 2007;193(1):197–202. doi: 10.1016/j.amc.2007.03.088. [DOI] [Google Scholar]
- 28.M. Kılınç. Exploiting integrality in the global optimization of mixed-integer nonlinear programming problems with BARON. Optimization Methods & Software. 2017:1–23. [Google Scholar]
- 29.Storn R., Price K. Differential Evolution - A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. Journal of Global Optimization. 1997;11(4):341–359. doi: 10.1023/A:1008202821328. [DOI] [Google Scholar]
- 30.Kukkonen S., Coello Coello C. A. Generalized differential evolution for numerical and evolutionary optimization. Studies in Computational Intelligence. 2017;663:253–279. doi: 10.1007/978-3-319-44003-3_11. [DOI] [Google Scholar]
- 31.Rakshit P. Uncertainty Management in Differential Evolution Induced Multiobjective Optimization in Presence of Measurement Noise. IEEE Transactions on Systems Man Cybernetics Systems. 2017;44(7):922–937. [Google Scholar]
- 32.Das S., Konar A., Chakraborty U. K. Two improved differential evolution schemes for faster global search. Proceedings of the Genetic and Evolutionary Computation Conference (GECCO '05); June 2005; pp. 991–998. [DOI] [Google Scholar]
- 33.Qin A. K., Suganthan P. N. Self-adaptive differential evolution algorithm for numerical optimization. Proceedings of the IEEE Congress on Evolutionary Computation (CEC '05); September 2005; IEEE; pp. 1785–1791. [DOI] [Google Scholar]
- 34.Lin Y. C. A mixed-coding scheme of evolutionary algrithms to solve mixed-integer nonlinear programming problems. Computer Mathematics with Applications. 2004;47(8-9):1295–1307. doi: 10.1016/S0898-1221(04)90123-X. [DOI] [Google Scholar]
- 35.Bland J. M., Altman D. G. Measuring agreement in method comparison studies. Statistical Methods in Medical Research. 1999;8(2):135–160. doi: 10.1191/096228099673819272. [DOI] [PubMed] [Google Scholar]
- 36.Giavarina D. Understanding Bland Altman analysis. Biochemia Medica. 2015;25(2):141–151. doi: 10.11613/BM.2015.015. [DOI] [PMC free article] [PubMed] [Google Scholar]