Comparative study of joint analysis of microarray gene expression data in survival prediction and risk assessment of breast cancer patients

Abstract

Microarray gene expression data sets are jointly analyzed to increase statistical power. They could either be merged together or analyzed by meta-analysis. For a given ensemble of data sets, it cannot be foreseen which of these paradigms, merging or meta-analysis, works better. In this article, three joint analysis methods, Z -score normalization, ComBat and the inverse normal method (meta-analysis) were selected for survival prognosis and risk assessment of breast cancer patients. The methods were applied to eight microarray gene expression data sets, totaling 1324 patients with two clinical endpoints, overall survival and relapse-free survival. The performance derived from the joint analysis methods was evaluated using Cox regression for survival analysis and independent validation used as bias estimation. Overall, Z -score normalization had a better performance than ComBat and meta-analysis. Higher Area Under the Receiver Operating Characteristic curve and hazard ratio were also obtained when independent validation was used as bias estimation. With a lower time and memory complexity, Z -score normalization is a simple method for joint analysis of microarray gene expression data sets. The derived findings suggest further assessment of this method in future survival prediction and cancer classification applications.

Introduction

Microarray data are (i) noisy owing to missing or erroneous values; (ii) high dimensional owing to a large number of genes versus a low number of samples in which their expression levels are measured; (iii) costly owing to expensive microarray experiments. As the number of samples is few, specifically in cancer studies, the learning ability of machine learning methods depends on the sample size of the training set, and the robustness of their prognosis is based on the sample size of the testing set; microarray gene expression data must be jointly analyzed to increase prognosis performance.

Two types of methods have been used for this purpose: Meta-analysis and data integration or data merging. While the former increases sample size by combining the results of different studies [ 1–12 ], the latter pools the gene expression data into a single set [ 13–30 ]. As the results of studies are aggregated in meta-analysis, no data adjustment or transformation is required, and heterogeneity between studies is often taken into account by the assumption of random effect. In data integration, however, heterogeneity in the data source is a more complicated issue that needs to be addressed to avoid biases. To this end, data merging methods adjust data generated from different sources or batches before their combination into a single set.

Various data integration methods have been developed to remove batch effects. Singular Value Decomposition (SVD) [ 31 ]/Principal Component Analysis (PCA), Distance Weighted Discrimination (DWD) [ 32 ], ComBat [ 33 ] and Z -score normalization [ 34 ] can be recognized among these methods. SVD/PCA, DWD and ComBat are known to be complex, more so than Z -score normalization. DWD requires large batch sizes, whereas Z -score normalization and ComBat can be applied to the data ensembles containing few samples per batch. There may be two other disadvantages with DWD: This method is applied to two data sets at a time, and its application to many data sets can be time-consuming and tedious. Furthermore, DWD may not adjust data if the data population is strongly spread [ 32 ].

In previous studies, only one joint analysis method, either data merging or meta-analysis, was applied to ensemble of data sets generated from different sources or batches in subtype tumor classification or survival prediction [ 1–4 , 11 , 13–23 , 35–48 ]. Few of these studies applied a joint analysis method to predict survival as a quantitative outcome [ 2 , 4 , 12 , 29 , 30 , 35–37 , 46 ]. In this article, three joint analysis methods, namely, Z -score normalization, ComBat and meta-analysis, were applied to the simulated and breast cancer data sets for cross-comparison of joint analysis methods and to investigate their performance in identifying gene signatures in survival prediction and risk assessment. These approaches were evaluated by using identical feature selection and bias reduction methods so that the results would mainly reflect the differences of the joint analysis methods.

Results and Discussion

Simulation

To test and compare the different strategies, four survival data sets were simulated. Each combined a number of gene expressions together with a randomly generated survival time. The characteristics of the survival time were a function of a known linear combination, a gene signature. The best fitting gene signatures were selected from the single and merged data sets adjusted by ComBat and Z -score normalization. Their performance was evaluated in pair-wise manner and leave-one-data set-out (for more details, see ‘Methods' section).

In both the cases, whether the genes were highly correlated (correlation = 0.8) or whether the genes were (linearly) independent (correlation = 0), the performance generated from the merged data sets was significantly higher than the performance obtained from the single data sets ( Supplementary Table S1–S8 ). This outperformance was more pronounced when there was correlation among the genes compared with the case where the genes were not correlated. While the selection of predictive genes from the single data sets was often misled by the correlation among the genes, the increase of sample size achieved by merging helped to identify the true survival genes.

By increasing the size of the gene signatures being considered from 1000 to 5000, the performance slightly decreased for the merged data sets but considerably for the majority of single data sets, both for correlated and uncorrelated genes. In the case of single data sets, when the genes were correlated, the area under the receiver operating characteristic (ROC) curve (AUC) decreased by up to 28% and the Hazard Ratio (HR) decreased by up to 4.75 units. In the case of uncorrelated genes, the AUC decreased by up to 25% and the HR decreased by up to 2.52 units, respectively. While the AUC and HR derived from the single data sets adjusted by ComBat or Z -score normalization decreased as the number of genes increased from 1000 to 5000, the performance obtained from the merged data sets adjusted by the three methods remained similar in the case of correlated genes. This may be explained by the fact that the increase from 1000 to 5000 leads to increased correlations and thus to deterioration, whereas the sample size of the merged data sets is sufficient to resist such deteriorating effects.

Among the data merging methods, the two variants of Z -score normalization ( Z -score1 normalizations and Z -score2 normalization) systematically outperformed ComBat when the genes were strongly correlated (increase of the AUC: 20–30%, increase of the HR: 0.60–2.38, Supplementary Tables S1–S4 ). In the case of uncorrelated genes, however, the performance of the genes signatures derived from the three merged data sets remained comparable ( Supplementary Tables S5–S8 ).

Data integration

To evaluate the reproducibility of the performance obtained from the data sets generated from different microarray platforms, the breast cancer data sets were analyzed in a pair-wise manner and leave-one/two-data set(s)-out (see bias estimation section). The results generated from the single data sets and the merged data sets adjusted by ComBat and Z -score1 normalization were presented in Yasrebi et al. 2009 [ 49 ]. In this article, the results obtained from the merged data sets adjusted by Z -score2 normalization are presented.

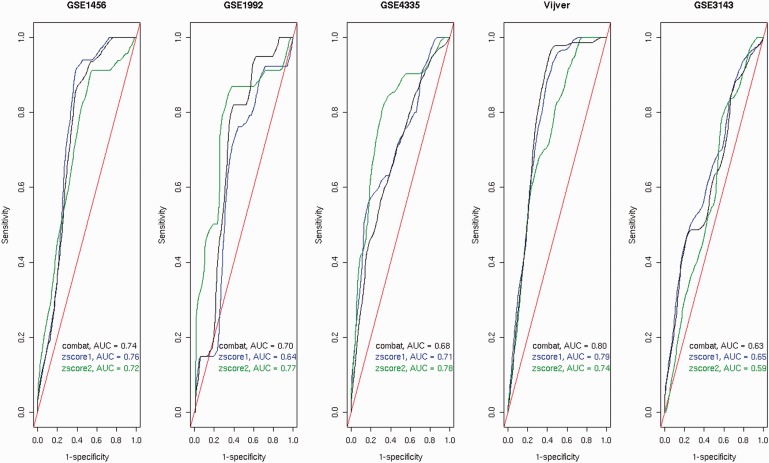
Survival prediction and risk association were partially improved when the results derived from the merged data set adjusted by Z -score2 normalization ( Table 1 ). While the performance obtained from the merged data sets was improved compared with the performance obtained from some individual data sets, it remained similar or decreased compared with the prognosis built from the other individual data sets. With respect to Overall Survival (OS), the survival prediction based on Z -score normalization (performed by Zscore1 normalization [ 49 ] or Zscore2 normalization) was higher than the prognosis accuracy achieved with ComBat [ 49 ] (difference of AUCs: 0.02–0.10 for four of five data sets and 0.05–0.10 for two of five data, Table 1 and Figure 1 ). The difference of AUCs is less significant than the difference of AUCs obtained from simulation. With respect to bias estimation, the performance based on independent validation ( Table 1 ) was higher than the performance derived from cross-validation [ 49 ] (difference of AUCs: 0.04–0.10 for four of five data sets).

Table 1.

Cross-data set performance of the breast cancer predictors (top 100 ranked) trained on the combined data sets with respect to OS

OS
	Z -score2		Meta-analysis
Testing set	AUC	HR	AUC	HR
GSE1456	0.72	3.17 (1.53–6.58) P  =  0.0019	0.74	10.23 (3.09–33.82) P  =  0.00014
GSE1992	0.77	4.19 (1.68–10.45) P  =  0.0021	0.71	3.49 (1.4–8.72) P  =  0.0073
GSE4335	0.78	6.48 (2.96–14.21) P  =  3e-06	0.72	2.78 (1.4–5.52) P  =  0.0034
Vijver	0.74	2.73 (1.66–4.46) P  =  6.4e-05	0.79	5.95 (3.27–10.85) P  =  5.5e-09
GSE3143	0.59	1.90 (1.02–3.53) P  =  0.042	0.64	P  > 0.05

Significant AUC ( $\ge$ 0.60) and HR ( P$\le$ 0.05) are shown in bold. Z -score2 normalization refers to the separate application of Z -score normalization to the training and the testing sets. The predictor was trained from all data sets (GSE1456, GSE1992, GSE4335, Vijver and GSE3143) except the testing set.

Figure 1.

ROC curves of the 100-gene signatures built from the merged data sets with respect to the OS endpoint assessed by independent validation.Four data sets (among GSE1456, GSE1992, GSE4335, Vijver and GSE3143) were used for the training set. The data sets composing the training set were adjusted by Z -score1 normalization (or Z -score1 for short), Z -score2 normalization (or Z -score2 for short) or ComBat and then validated on the testing set. The testing set is indicated at the top of each plot. Random prediction (AUC = 0.50) is illustrated by the diagonal red line.

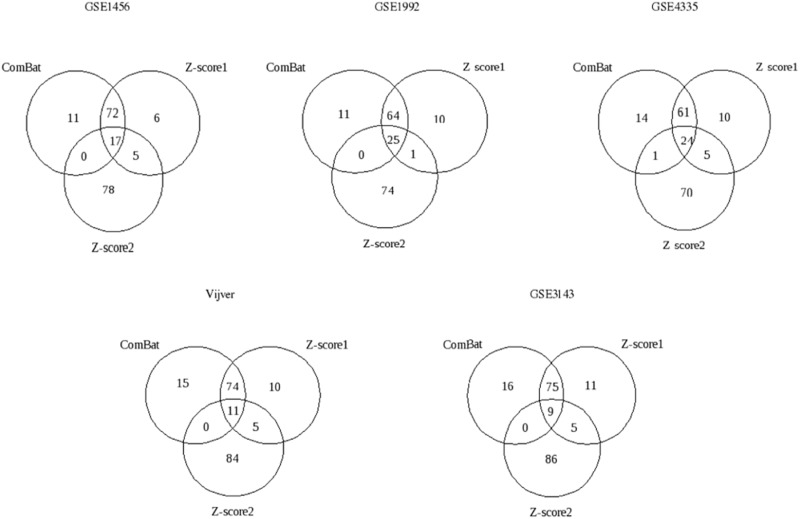
The overlap between the gene signatures derived from the three data integration methods can be compared in Figure 2 . Based on Figure 1 , it was interesting to know whether there would be a large overlap between the gene signatures built from the merged data sets adjusted by ComBat or Z -score1 normalization and a poor overlap between the gene signatures derived after the application of Z -score2 normalization and the two other methods. This expectation was based on the ROC curves and the AUC values obtained from the data sets adjusted by ComBat or normalized by Z -score1 normalization, which were similar but different from the results obtained from the merged data set normalized by Z -score2 normalization. As shown in Figure 2 , this is indeed the case.

Figure 2.

Venn diagrams of the 100-gene signatures derived from the merged data sets with respect to the OS endpoint assessed by independent validation.Four data sets (of five, GSE1456, GSE1992, GSE4335, Vijver and GSE3143) were merged by ComBat, Z -score1 normalization ( Z -score1 for short) or Z -score2 normalization ( Z -score2 for short) and validated on the remaining fifth data set, i.e. testing set. The testing set is indicated at the top of each diagram.

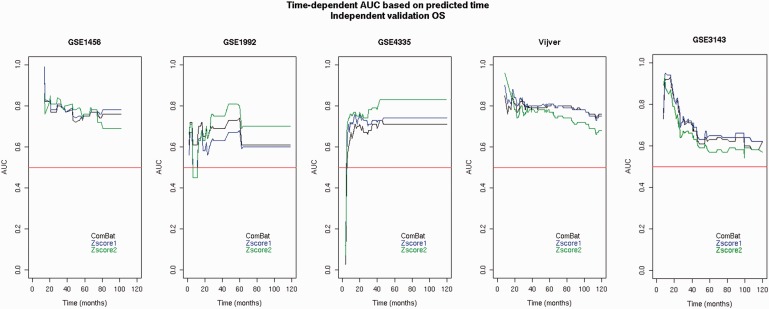
As the prediction accuracy can be different at different time points, the performance of the breast cancer gene signatures prognostic of OS was evaluated based on different time points ranging from 0 to 10 years [ 49 ] by independent validation ( Figure 3 ). The trends are consistent with the trends observed in Figure 1 . The performance accuracies obtained from the merged data sets adjusted by ComBat or normalized by Z -score1 normalization are similar to each other but different from Z -score2 normalization. As none of the methods provided the highest results for at least the majority of the data sets (three of five), none of them were preferred for survival prediction with respect to different time points.

Figure 3.

Time-dependent AUC based on different predicted time points generated from the merged data sets with respect to the OS endpoint assessed by independent validation.Four data sets (among GSE1456, GSE1992, GSE4335, Vijver and GSE3143) were used for the training set. The data sets composing the training set were merged and adjusted by Z -score1 normalization ( Z -score1 for short), Z -score2 normalization ( Z -score2 for short) or ComBat and then validated on the remaining set (testing set). The testing set is indicated at the top of each plot. Random prediction (AUC = 0.50) is illustrated by the diagonal red line.

The partial improvement of the survival prediction and risk assessment that was observed for the OS endpoint was also obtained with respect to Relapse Free Survival (RFS) ( Table 2 ). Between the merged data sets, Z -score2 normalization provided better results than ComBat [ 49 ] (difference of AUCs: 0.03–0.11 for four of seven data sets) even though the difference is not significant for the majority of data sets. The similarity between the results generated from Z -score1 normalization and ComBat was also observed with respect to RFS [ 49 ].

Table 2.

Cross-data set performance of the breast cancer predictors (top 100 ranked) trained on the combined data sets with respect to RFS

RFS
	Z -score2		Meta-analysis
Testing set	AUC	HR	AUC	HR
GSE1456	0.76	6.61 (2.77–15.77) P  =  2e-05	0.73	4.83 (2.22–10.49) P  =  7.06e-05
GSE1992	0.66	2.49 (1.22–5.10) P  =  0.012	0.69	3.39 (1.62–7.08) P  =  0.0012
GSE4335	0.60	2.83 (1.24–6.47) P  =  0.013	0.64	2.06 (1.04–4.06) P  =  0.038
Vijver	0.73	5.17 (2.84–9.41) P  =  7.6e-08	0.72	2.91 (1.96–4.33) P  =  1.22e-07
GSE2034	0.60	1.97 (1.3–2.99) P  =  0.001	0.60	1.75 (1.19–2.57) P  =  0.004
GSE2990	0.71	4.43 (2.43–8.07) P  =  1.2e-06	0.66	1.86 (1.08–3.19) P  =  0.02
GSE4922	0.63	2.34 (1.48–3.71) P  =  0.00028	0.64	2.38 (1.54–3.69) P  =  0.0001

Significant AUC ( $\ge$ 0.60) and HR ( P$\le$ 0.05) are shown in bold. Z -score2 normalization refers to the separate application of Z -score normalization to the training and the testing sets. The predictor was trained from all data sets (GSE1456, GSE1992, GSE4335, Vijver, GSE2034, GSE2990 and GSE4922) except the testing set.

It was intriguing to observe how the integration methods would perform if the testing set is pooled from the combination of different data sets. To this end, two data sets with the OS endpoint were pooled together to compose the testing set, and the remaining data sets with the same clinical endpoint were merged together to constitute the training set ( Table 3 ). Among the three methods, i.e. Z -score2 normalization, Z -score1 normalization and ComBat normalization, Z -score1 normalization provided better results (higher AUC and/or HR) for the majority of data sets (6 out of 10 combinations of testing sets) compared with Z -score2 normalization.

Table 3.

Cross-data set performance of the breast cancer predictors trained and tested on the combined data sets with respect to OS

	Z -score2		Z -score1		ComBat
Testing set	AUC	HR	AUC	HR	AUC	HR
GSE4335 GSE1992	0.64	2.32 (1.22–4.43) P  < 0.05	0.69	3.51 (2.03–6.05) P  < 0.05	0.70	3.42 (1.92–6.11) P  < 0.05
GSE4335 GSE3143	0.79	7.77 (2.39–25.29) P  < 0.05	0.65	2.25 (1.42–3.58) P  < 0.05	0.70	4.45 (2.82–7.02) P  < 0.05
GSE4335 GSE1456	0.82	5.01 (2.59–9.72) P  < 0.05	0.75	4.24 (2.45–7.36) P  < 0.05	0.68	2.72 (1.67–4.44) P  < 0.05
GSE4335 Vijver	0.70	2.62 (1.39–4.96) P  < 0.05	0.76	4.51 (2.83–7.20) P  < 0.05	0.75	4.07 (2.68–6.16) P  < 0.05
GSE1992 GSE3143	0.70	5.05 (1.74–14.69) P  < 0.05	0.66	2.51 (1.54–4.09) P  < 0.05	0.61	2.58 (1.67–3.99) P  < 0.05
GSE1992 GSE1456	0.78	3.17 (1.43–7.01) P  < 0.05	0.74	4.74 (2.55–8.84) P  < 0.05	0.72	3.39 (1.94–5.93) P  < 0.05
GSE1992 Vijver	0.71	3.40 (1.36–8.48) P  < 0.05	0.74	4.00 (2.51–6.38) P  < 0.05	0.75	6.49 (3.86–10.91) P  < 0.05
GSE3143 GSE1456	0.57	1.33 (0.76–2.33) P  > 0.05	0.69	2.97 (1.84–4.80) P  < 0.05	0.71	2.55 (1.52–4.29) P  < 0.05
GSE3143 Vijver	0.59	1.93 (1.07–3.51) P  < 0.05	0.72	3.30 (2.18–5.00) P  < 0.05	0.71	4.58 (2.85–7.35) P  < 0.05
GSE1456 Vijver	0.63	2.08 (0.95–4.58) P  > 0.05	0.76	4.71 (3.02–7.36) P  < 0.05	0.71	3.44 (2.34–5.05) P  < 0.05

AUC ( $\ge$ 0.60) and HR ( P$\le$ 0.05) are considered as significant. Z -score2 normalization refers to the separate application of Z -score normalization to the training and the testing sets. The predictor was trained from all data sets (GSE1456, GSE1992, GSE4335, Vijver and GSE3143) except the testing set, which was pooled from the two data sets indicated in the Testing set column.

Finally, it was interesting to assess the significance of the survival prediction derived from the merged data sets. This interest was motivated from the fact that there are so many genes whose expression levels are significantly associated with survival of breast cancer patients that most random gene sets can predict breast cancer outcome [ 50 ]. In effect, there are an enormous number of genes that are correlated with cell proliferation, and cell proliferation is strongly correlated with prognosis (estrogen receptor expression is strongly associated with outcome and prognosis and there are thousands of estrogen receptor target genes) ( http://www.ncbi.nlm.nih.gov/myncbi/richard.simon.1/comments/ ). Hence, random signatures were generated for testing the significance of the breast cancer gene signatures prediction generated from the merging data sets with respect to OS.

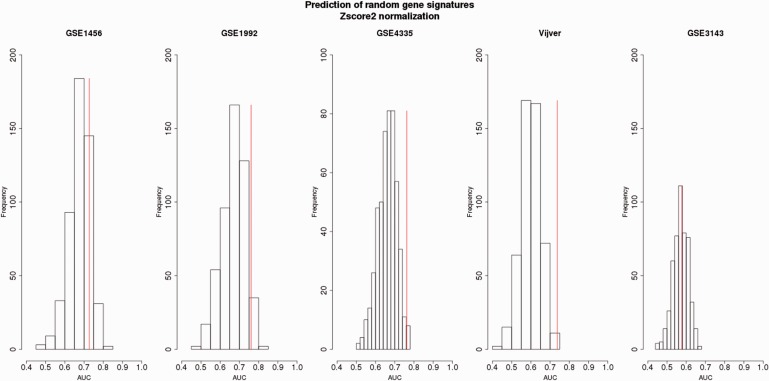
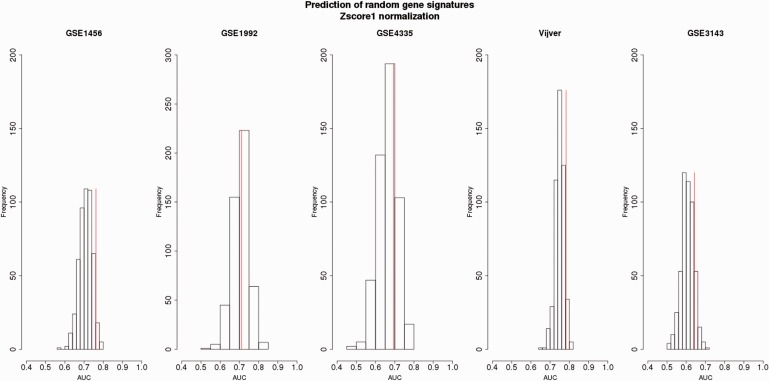
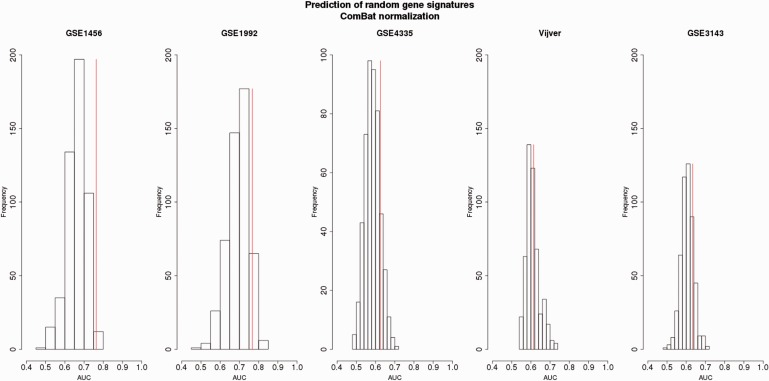
For the majority of data sets (four of five data sets), the non-random gene signatures fall in the third quartile of the random gene signatures distributions illustrating their outperformance compared with the performance of the random gene signatures ( Figures 4–6 ). The AUCs derived from the random gene signatures built from the data sets merged by Z -score2 and assessed by independent validation ranged on average from 0.57 to 0.67 (standard deviation, SD = [0.04,0.05]) ( Figure 4 ). Up to 45% AUCs generated from the random gene signatures was equal to or higher than the AUCs obtained by the non-random gene signatures. For the merged data set adjusted by Z -score1, the AUCs derived from the random gene signatures ranged from 0.60 to 0.71, on average (SD = [0.02,0.05]) ( Figure 5 ). Up to 46% of these AUCs was equal to or higher than AUCs obtained from the non-random gene signatures. As for ComBat, the AUCs derived from the random gene signatures ranged from 0.58 to 0.70, on average (SD = [0.03,0.05]) ( Figure 6 ). Up to 33% AUCs was equally well or higher than the AUCs obtained from the non-random gene signatures.

Figure 4.

Survival prediction of random gene signatures (top 100-ranked) generated from the Z -score2-normalized merged data sets with respect to the OS endpoint assessed by independent validation.Four data sets (among GSE1456, GSE1992, GSE4335, Vijver and GSE3143) were used for the training set. The data sets composing the training set were merged and adjusted by Z -score2 normalization. The top 100 random genes were derived from the training set and then validated on the remaining set (testing set). The testing set is indicated at the top of each plot. The prediction of non-random gene signature is illustrated by the vertical red line.For each testing data set, the average of AUCs, SD of AUCs and the percentage of AUCs higher than the AUC of the non-random gene signatures were obtained as follows:GSE1456: Mean (AUC): 0.67 ± 0.04, 15% AUCs;GSE1992: Mean (AUC): 0.67 ± 0.05, 4% AUCs;GSE4335: Mean (AUC): 0.65 ± 0.05, 2% AUCs;Vijver: Mean (AUC): 0.60 ± 0.04, 0% AUCs;GSE3143: Mean (AUC): 0.57 ± 0.04, 45% AUCs.

Figure 5.

Survival prediction of random gene signatures (top 100 ranked) generated from the Z -score1-normalized merged data sets with respect to the OS endpoint assessed by independent validation.Four data sets (among GSE1456, GSE1992, GSE4335, Vijver and GSE3143) were used for the training set. The data sets composing the training set were merged and adjusted by Z -score1 normalization. The top 100 random genes were derived from the training set and then validated on the remaining set (testing set) normalized by Z -score1 normalization. The testing set is indicated at the top of each plot. The prediction of non-random gene signature is illustrated by the vertical red line.For each testing data set, the average of AUCs, SD of AUCs and the percentage of AUCs higher than the AUC of the non-random gene signatures were obtained as follows:GSE1456: Mean (AUC): 0.71 ± 0.03, 6% AUCs;GSE1992: Mean (AUC): 0.70 ± 0.04, 46% AUCs;GSE4335: Mean (AUC): 0.66 ± 0.05, 25% AUCs;Vijver: Mean (AUC): 0.74 ± 0.02, 5% AUCs;GSE3143: Mean (AUC): 0.60 ± 0.03, 13% AUCs.

Figure 6.

Survival prediction of random gene signatures (top 100 ranked) generated from the ComBat-normalized merged data sets with respect to the OS endpoint assessed by independent validation.Four data sets (among GSE1456, GSE1992, GSE4335, Vijver and GSE3143) were used for the training set. The data sets composing the training set were merged and adjusted by ComBat normalization. The top 100 random genes were derived from the training set and then validated on the remaining set (testing set) adjusted by ComBat. The testing set is indicated at the top of each plot. The prediction from non-random gene signature is illustrated by the vertical red line.For each testing data set, the average of AUCs, SD of AUCs and the percentage of AUCs higher than the AUC of the non-random gene signatures were obtained as follows:GSE1456: Mean (AUC): 0.66 ± 0.04, 0.6% AUCs;GSE1992: Mean (AUC): 0.70 ± 0.05, 7% AUCs;GSE4335: Mean (AUC): 0.58 ± 0.03, 12% AUCs;Vijver: Mean (AUC): 0.61 ± 0.03, 33% AUCs;GSE3143: Mean (AUC): 0.60 ± 0.03, 17% AUCs.

It should be noted that for the majority of the testing sets (three or four of five data sets) and for all merging data sets normalized by different methods, the maximum of 15% AUCs predicted by the random gene signatures was equally well or higher than the AUCs provided by the non-random gene signatures. The prediction on only one data set of five adjusted by different normalization methods represented around 40% equally well or higher than the prediction obtained from the non-random gene signatures. These findings demonstrate the reliability of the survival prediction of the breast cancer gene signatures owing to the selection of the genes strongly associated with survival based on the lowest Cox P -value.

Meta-analysis

Meta-analysis was applied to the breast cancer data sets with respect to two clinical endpoints, OS and RFS, so that the performance generated from this joint analysis method can be compared with the performance obtained from the data integration methods. The aim was to find out which method (meta-analysis or merging) would outperform when applied to the breast cancer data sets.

Overall, the results are comparable with the results of the data integration methods ( Tables 1 and 2 ). For the breast cancer data sets, both data integration and meta-analysis achieve similar performance. Here, Z -score2 normalization provided higher HR than meta-analysis for the majority of data sets with respect to OS and RFS (three of five OS data sets and four of seven RFS data sets, respectively). The difference of AUC is not significant.

It is worth noting that the two types of joint analysis methods, data integration and meta-analysis, stratified the patients differently into high versus low risk: While the risk score threshold was based on the median score of the ‘training' samples for data merging [ 49 ], the risk score threshold was set based on the median score of the ‘testing' set in meta-analysis. The HR, which was calculated based on the risk score, might then not be comparable between data merging and meta-analysis. The AUC was, however, independent of this difference.

Conclusions

Joint analysis methods, namely, data merging and meta-analysis were evaluated on the simulated and breast cancer data sets. Because of data sets heterogeneity, it was expected that meta-analysis provide better results, as it combines the findings generated from different data sets and it does not require data adjustment or transformation. However, it was Z -score normalization that provided overall the higher AUC and HR despite (i) the heterogeneity of microarray technologies, (ii) the heterogeneity of patients cohorts, (iii) the heterogeneity of patients treatments and (iv) the heterogeneity of breast cancer disease. This might be owing to the fact that Z -score normalization homogenizes the data, and this homogenization may reduce the effect of bias introduced by the heterogeneity. On comparing the findings obtained from data merging methods, the survival prediction, risk assessment and the gene signatures generated from ComBat and Z -score1 normalization were found to be more similar than the performance and gene signatures obtained from Z -score2 normalization.

Random gene signatures were generated to assess the performance of the gene signatures derived from the breast cancer data sets. The survival prediction derived from the non-random gene signatures of the breast cancer data sets with respect to OS was overall reliable, as it was systematically>50% of the AUCs predicted by the random gene signatures. These findings are noteworthy, as the non-random gene signatures outperformed the random gene signatures despite (i) the heterogeneity of microarray technologies, (ii) the heterogeneity of patients cohorts, (iii) the heterogeneity of patients treatments and (iv) the heterogeneity of breast cancer disease.

It should be noted that the methods used in this study can be applied to one or more cohorts of patients but are not applicable for the prognosis of a new individual patient. This is owing to the facts that (i) the principle of these methods is based on the adjustment of the expression values of different samples and (ii) their performance evaluation relies on population averages.

To summarize and conclude, the Z -score normalization method is attractive, as (i) it is simple, (ii) it does not require any assumption on data distribution and (iii) its time and memory complexity is less than it is for ComBat. This method should be applied in survival prognosis of other cancer types as well as cancer classification to validate whether it could also provide high prognosis for other types of cancer and outcome. For bias estimation, independent validation outperformed cross-validation, as it generated better and more robust prediction.

Methods

Statistical analysis was performed using R [ 51 ], version 3.1.1 and BioConductor [ 52 ], release 3.1. All the methods applied in Yasrebi et al. 2009 [ 49 ] were used for the breast cancer data sets if not specified otherwise. These methods were implemented in the R survJamda package [ 53 ].

Data

Eight breast cancer data sets comprising 1324 samples with two clinical endpoints OS and RFS were used [ 49 ] ( Table 4 ). The data sets were selected based on the following criteria:

Table 4.

Survival breast cancer data sets with the OS and RFS endpoints

Data set	Platform	Pre-normalization	Gene nb	Sample size	Ref.	Treatment	Survival outcome
GSE3143	Affymetrix, HG-U95A	MAS5.0	8660	158	Bild 06 [ 56 ]	Unknown	OS
GSE1456A&B	Affymetrix, HG-U133A&B	MAS5.0, global mean	15848	159	Pawitan 05 [ 57 ]	Adj. Chemotherapy (incl. Tamoxifen)	OS, RFS
GSE4335	cDNA	Scaling	12793	122	Sorlie 03 [ 54 ]	Neoadj. Chemo/chemo (Tamoxifen)-82 patients	OS, RFS
GSE1992	Agilent	LOWESS	15528	170	Hu 06 [ 22 ]	Treated	OS, RFS
Vijver	Agilent	Scaling	13628	295	Van de Vijver 02 [ 55 ]	Chemo/hormonal therapy (90 patients)	OS, RFS
GSE2990	Affymetrix, HG-U133A	RMA	12010	189	Sotiriou 06 [ 58 ]	Tamoxifen (64 patients)	RFS
GSE2034	Affymetrix, HG-U133A	MAS5.0	12010	286	Wang 05 [ 59 ]	None	RFS
GSE4922A&B	Affymetrix, HG-U133A&B	MAS5.0, global mean	15848	289	Ivshina 06 [ 60 ]	Systemic/endocrine therapy (147 vs. 66 patients)	RFS
Merged OS	Affymetrix, Agilent, cDNA		7049	849			OS
Merged RFS	Affymetrix, Agilent, cDNA		9181	1324			RFS

Gene nb refers to the number of genes. MAS 5.0 refers to Affymetrix Microarray Suite version 5.0 and LOWESS stands for LOcally WEighted Scatterplot Smoothing and RMA for Robust Microarray Analysis, respectively. Adj. stands for adjuvant and chemo for chemotherapy. Merged OS refers to merged data sets with OS endpoint and Merged RFS refers to the merged data sets with RFS endpoint. The expression values of dual channel data were already ${\log }_2$ -transformed. Among the data sets generated by Affymetrix, the absolute intensity values of GSE3143, GSE2034 and GSE2990 were ${\log }_2$ -transformed for this study as the rest of Affymetrix data sets were already ${\log }_2$ -transformed by the authors.

1. Availability of the two clinical endpoints, namely OS and RFS.

2. Platform heterogeneity. The data from three different platforms, cDNA, Affymetrix and Agilent, were selected for this study.

3. Quality of the data sets, i.e. with the least amount of missing/incorrectly annotated values in both gene expression data and clinical outcomes.

4. Two most frequently used data sets in breast cancer studies, namely, GSE4335 [ 54 ] and Vijver [ 55 ].

5. Comparison of the results generated by Z -score2 normalization (presented in this study) with the results derived from ComBat and Z -score1 normalization presented in Yasrebi et al. 2009 [ 49 ].

Time to Overall Survival is defined as the time between surgery and death from breast cancer or the last date of follow-up. Time to Relapse-Free Survival is defined as the time between surgery and the first recurrence of local, regional or distant-metastatic breast tumor or the last date of follow-up. If OS or RFS time refers to death or recurrence of disease, the corresponding samples have a censoring status of 1 (event happened) or 0 otherwise. Note that throughout this document, clinical endpoints, clinical outcomes or prediction outcomes refer to OS and/or RFS.

Simulation

The aim of data simulation was 2-fold: (i) To compare the performance derived from the merged data sets adjusted by different merging methods and (ii) to determine if the benefits of data merging are countered by the correlation among genes. The latter expectation was inspired from real microarray gene expression data in which the genes are (highly) correlated. To these ends, gene signatures were built from artificial data to predict survival time and risk assessment using the Cox regression model. The derived gene signatures generated from the single and merged data sets were evaluated by independent validation, and their performance was measured by AUC and HR with the respective confidence interval and P -value.

The Weibull model was used to generate survival times, as it is a more general (parametric) survival model compared with the exponential model. The survivor and hazard functions of the Weibull model are defined as follows:

$$S(t)=\exp (-\lambda t^{\gamma })$$ (1)

$$h(t)=\lambda \gamma t^{\gamma -1}$$ (2)

where t denotes survival time, λ and γ (with $\lambda >0,\hspace{0.17em}\gamma >0$ ) are scale and shape parameters on which the mean and variance of the Weibull distribution depend. When we replace λ by $\lambda \exp (\beta .x)$ , where β and x are the vectors of Cox coefficients and gene expression values, respectively, we obtain a Cox model with baseline risk $\lambda \gamma t^{\gamma }-1$ [ 61 ].

Simulation of survival times can be started with the generation of random values following a uniform distribution in [0,1] (using the runif function in the R stats package). Then, having the source random variable U , the target random variable representing survival time, T can be obtained based on the following result:

Lemma: Let the random variable U be uniformly distributed between 0 and 1 and define

$$T={\left(\frac{-1}{\lambda }\log (U)\right)}^{\frac{1}{\gamma }}$$ (3)

It then follows that T has a Weibull distribution with parameters λ and γ .

To demonstrate the effect of the correlation between the genes on the performance derived from data merging, four artificial data sets containing different numbers of genes (1000 or 5000) with 100 samples were generated. In one analysis, the genes had a constant pairwise correlation of 0.8, and in another analysis, they had no correlation with each other (correlation = 0). The corgen function in the R ecodist package was used to generate the gene expression values with a correlation (0 or 0.8 in this study). This function generates random values based on the rnorm function.

Shape and scale ( γ and λ ) were set to different values like 1, 1.5 and 2. Survival time points were simulated as described above with components of β set as follows: all coefficients except six were set to zero. These six coefficients were considered as the coefficients of the true survival genes. Three of them were set to positive values (between 0.4 and 0.7), whereas the remaining three were set to negative values (between −0.7 and −0.4). The purpose of this analysis was to recover the true Cox coefficients through model fitting.

The censoring status denoted by c was initialized randomly between the minimum and 90 percentile of the maximum survival time. The choice of 90 percentile was determined experimentally so as not to generate more than 30 percent censoring. The censoring status was then set as follows:

$$T_i=\min (T_i,c_i)$$ (4)

$$censoring\hspace{0.17em}status=1\hspace{0.17em}\text{if}\hspace{0.17em}{T}_i\le c_i$$ (5)

$$censoring\hspace{0.17em}status=0\hspace{0.17em}\text{if}\hspace{0.17em}{T}_i\hspace{0.17em}>\hspace{0.17em}{c}_i$$ (6)

The gene expression values, the survival time points and the censoring status were then fitted in a Cox model (the coxph function in the R survival package). The genes were fitted in a univariate model, and the top-6 ranked were selected based on the smallest Cox P -value.

Preprocessing data

The data analysis was limited to 10 years of follow-up, as the majority of breast cancer patients had a follow-up of maximum 10 years. All patients having an OS or RFS >10 years were censored and their respective clinical endpoint was set to 10 years. All patients in GSE4335 deceased from any other cause than breast cancer were also censored. Fibroadenoma or normal breast samples were discarded from the study (GSE4335, GSE1992). Replicate samples in GSE1992 were eliminated from the study too. Note that throughout this document, GSE1456 refers to the merged data set of GSE1456A and GSE1456B, GSE4922 to the merged data set of GSE4922A and GSE4922B, respectively. GSE4335 and Vijver are data sets from clinical trials.

The data sets used in this study were pre-normalized in various ways by the authors of the original studies. The data sets were pre-normalized in the following ways: Global mean normalization was used for GSE1456A&B and GSE4922A&B. The probe set values were natural log-transformed followed by an adjustment of the mean intensity to a target signal value of log 500. The pre-normalization of Vijver data set was performed on an array-by-array basis. Raw intensities from each channel (red or green) were divided by the mean intensity (in linear scale) of the corresponding channel. The other data sets were pre-normalized as described in the legend to Table 4 .

K Nearest Neighbor (KNN) imputation [ 62 ] was used to impute missing expression values in the source data sets, using the impute.knn function of the R impute package with default parameters (including k = 10). When multiple probes/probe sets were mapped to the same gene, the expressions of multiple probes/probe sets were averaged (after KNN imputation).

Feature selection

Genes were selected based on univariate Cox P -value ranking using the coxph function in the R survival package. In this feature selection method, the genes were ranked based on their likelihood ratio P -value, and the 100 genes with the smallest P -values were retained as the gene signature for the breast cancer data, as it was experimentally found to be the best cutoff [ 49 ]. The random gene signatures were generated by first fitting the genes in a Cox model and then, selecting randomly 100 genes in 500 iterations. The top-6 ranked genes were used for the simulated data.

Prediction method

Patient risk score was calculated as the linear combination of the Cox coefficients estimated from the training set and the corresponding gene expression values ( Equation 7 ).

$$lp(x,\beta )={\displaystyle \sum _{i=1}^G{\beta }_i}{x}_i$$ (7)

where G is the total number of genes.

The advantage of linear prediction is 2-fold: (i) It is simple, and (ii) It can be easily interpreted by clinicians by dichotomizing the patients into two groups for example high- versus low-risk.

Performance measures

Survival prediction and risk assessment were expressed by time-dependent AUC [ 49 , 63 ] and HR, respectively [ 49 ].

Time-dependent ROC curves [ 63 ] were used to evaluate the prediction accuracy at the average of time points for the testing data set(s) using the nearest neighbor estimator (the R survivalROC package). The AUC $\ge$ 0.60 was considered as significant.

The association of the gene signatures to survival (OS or RFS) was measured by a HR. To this end, the patients of the testing set had to be stratified into predicted high- and low-risk groups based on the median score of the patients in the training set [ 49 ]. The HR with P -value $\le$ 0.05 was considered as significant.

Bias estimation

1. Pair-wise method: Two data sets are selected at a time. One data set was used as the training set and the other one as the testing set. This process was iterated until all data sets were used as the training set and the testing set [ 49 , 53 ].

2. Independent validation or leave-one/two-data set(s)-out: All data sets except one/two were merged together to constitute the training set, and the left-out set(s) constituted the testing set (see the ‘Joint analysis methods' section). This process was iterated until all data sets were used in the training and testing sets [ 49 , 53 ]. Leave-one-data set-out was used in the simulation study.

Joint analysis methods

1. Merging methods

   • 1.1. ComBat [ 33 , 53 ].
   • 1.2. Z -score normalization [ 34 ]. Z -score normalization was applied in two ways as described in [ 53 ]:

   • 1.2.1. In Z -score1 normalization, all data sets were Z -score normalized before their selection for the training and testing sets. Then, the data sets composing the training set were merged together, and the left-out set was used as the testing set. This method was applied in Yasrebi et al. 2009 [ 49 ]. When two data sets were used for the testing set, they were pooled together, and the combined set was subsequently used as the testing set.
   • 1.2.2. Z -score2 normalization. In Z -score2 normalization, the data sets were first selected for the training and testing sets. Then, the data sets composing the training set were merged together and Z -score normalized subsequently. The testing set composing of one or two data sets was also Z -score normalized but independently and separately from the training set. When the testing set was composed of two data sets, the two data sets were merged together and Z -score normalized subsequently, independently and separately from the training set.

Z -score normalization was first applied to the samples and then to the genes. Scale in the R stats package was used for Z -score normalization.

$$Z=\frac{{\displaystyle \sum _{s=1}^S{Z}_s}}{\sqrt{S}}$$ 08

where S is the number of studies.

1. Meta-analysis The inverse normal method [ 64 ] was used for meta-analysis. This approach integrates the Z -tests or Z -scores of different studies by averaging them. Different scales of data from different studies were adjusted by standardization (division of Z -scores by standard error). The aggregation of Z -scores is defined as the sum of the different Z -scores divided by the square root of the number of studies ( Equation 8 ).

This method transforms the combined Z -score to a P -value.

$$p={\Phi }^{-1}(|Z|)$$ (9)

A null hypothesis is rejected if the P -value is less than α , the level of significance.

In this study, the Z -tests or Z -scores represent the standardized univariate Cox coefficients. Standardization of Cox coefficients refers to the division of Cox coefficients by their standard error. The null hypothesis used for meta-analysis suggests that the Cox coefficient is zero and consequently, the associated covariate has no effect on OS or RFS. The alternative hypothesis suggests that the Cox coefficient is not null and therefore, the related covariate has an effect on OS or RFS.

For each gene, the Z -test was calculated. Then, the Z -tests from different studies were combined as described above. Note that this combined Z -test was used as a Cox coefficient in the calculation of the patient’s risk score. The patient’s risk score is the linear predictor described in linear predictor section. The combined Z -test of each gene was transformed to a P -value ( Equation 9 ), which was subsequently used for feature selection.

While in the data integration methods, the patients in the testing set were stratified into high- versus low-risk based on the median score of the patients in the training set [ 49 ] to be used for HR, in meta-analysis, the patients in the testing set were stratified into high- versus low-risk based on the median score of the patients in the testing set.

The coxph function in the R survival package was used to calculate the gene Z -scores.

Key Points

• Microarray gene expression data can be merged to increase statistical power.

• Among Z -score normalization, ComBat and the inverse normal method, Z -score in overall outperformed in the survival prediction of breast cancer data sets.

• With a lower time and memory complexity, Z -score normalization is a simple method that could be used for survival prediction and cancer classification applications.

Supplementary Data

Supplementary data are available online at http://bib.oxfordjournals.org/ .

Funding

This project was funded by Roche Research foundation in Basel, Switzerland for 2 years. The open access fee was supported by the grant from the Swiss federal government to SIB.