Improving protein identification from tandem mass spectrometry data by one-step methods and integrating data from other platforms

Abstract

Motivation: Many approaches have been proposed for the protein identification problem based on tandem mass spectrometry (MS/MS) data. In these experiments, proteins are digested into peptides and the resulting peptide mixture is subjected to mass spectrometry. Some interesting putative peptide features (peaks) are selected from the mass spectra. Following that, the precursor ions undergo fragmentation and are analyzed by MS/MS. The process of identification of peptides from the mass spectra and the constituent proteins in the sample is called protein identification from MS/MS data. There are many two-step protein identification procedures, reviewed in the literature, which first attempt to identify the peptides in a separate process and then use these results to infer the proteins. However, in recent years, there have been attempts to provide a one-step solution to protein identification, which simultaneously identifies the proteins and the peptides in the sample.

Results: In this review, we briefly introduce the most popular two-step protein identification procedure, PeptideProphet coupled with ProteinProphet. Following that, we describe the difficulties with two-step procedures and review some recently introduced one-step protein/peptide identification procedures that do not suffer from these issues. The focus of this review is on one-step procedures that are based on statistical likelihood-based models, but some discussion of other one-step procedures is also included. We report comparative performances of one-step and two-step methods, which support the overall superiorities of one-step procedures. We also cover some recent efforts to improve protein identification by incorporating other molecular data along with MS/MS data.

Introduction

Identification of sensitive biomarker proteins from solid tissues and complex biological fluids such as saliva, urine, blood or serum plays a significant role in early detection of complex diseases such as cancer. Though mass spectrometry (MS) is one of the most widely used platforms for the discovery of biomarker proteins, there are several issues associated with protein identification and inference through this technique. There has been a lack of sufficient attention to determining proper statistical methods used in analyzing the data obtained from an MS experiment [1].

In a typical tandem mass spectrometry (MS/MS) experiment, the first step is to digest the mixture of proteins into smaller peptides, often by the enzyme trypsin. Each of these proteins can be digested into more than one peptide. As a result, peptide mixtures are usually more complex than protein mixtures. The sample peptides are then ionized and subjected to MS. Following that, the precursor ions undergo fragmentation and are then analyzed by MS/MS. The mass-to-charge ratios (m/z) of these smaller fragmented ion pieces and their relative abundances (intensities) are recorded as MS/MS spectra. These observed MS/MS spectra are matched against theoretical spectra predicted from individual peptides from a protein database using algorithms such as the SEQUEST scoring scheme [2] to identify the associated peptides. This is called the database search method. The peptides with the highest scores are considered as proper peptide identifications, which are further used for protein identifications. Modifications to SEQUEST that improve the speed of the process have been proposed in [3] and [4]. Other popular database search programs include X!TANDEM [5], Mascot [6], MS-Tag [7] and MS-GF+ [8, 9] available through Percolator [10]. The overall steps of a typical MS/MS experiment are illustrated in Figure 1. There are other methods of peptide identifications such as de novo sequencing and hybrid approaches.

Figure 1.

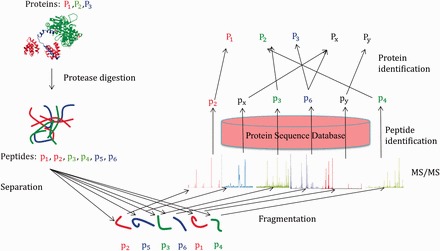
A cartoon explaining the protein identification process and the sources of errors from an MS/MS experiment (adapted from Shen et al. [11]). ${\text{P}}_1,\hspace{0.17em}{\text{P}}_2{\text{\hspace{0.17em}and\hspace{0.17em}P}}_3$ are parent proteins, which generates the peptides ${\text{p}}_1,{\text{p}}_2,{\text{p}}_3,{\text{p}}_4,{\text{p}}_5$ and${\text{p}}_6$. The MS/MS spectra of the two peptides ${\text{p}}_5$ and ${\text{p}}_1$incorrectly identify the peptides ${\text{p}}_{\text{x}}$ and${\text{\hspace{0.17em}p}}_{\text{y}}$, resulting in the incorrect identifications of the proteins ${\text{P}}_{\text{x}}$ and${\text{P}}_{\text{y}}$. A colour version of this figure is available at BIB online: http://bib.oxfordjournals.org.

Peptide and protein identifications from an MS/MS experiment are highly error-prone owing to experimental errors and lack of adequate search algorithms. In absence of proper filtering, even 80–90% of identified peptides may be incorrect [12, 13]. However, in recent years, there have been significant improvements in both of these areas. Several efforts have been made for developing powerful scoring mechanisms to identify the peptides accurately. These include scoring systems based on the number of shared peaks [2], incorporating stochastic modeling of the fragmentation process [14], the peak intensity [15], a Bayesian approach [16], Mowse scores [6], modeling the distribution of hits to the m/z values of a spectrum using the Hypergeometric distribution [17, 18], the Poisson distribution [17, 19] and regression models [20]. See Nesvizhskii et al. [21] for a detailed account of peptide identification processes. Also see [22] and [23] for other important reviews of two-step methods of protein identification following peptide scoring. Despite these diverse approaches, peptide and the subsequent protein identification is still not an easy task. This clearly indicates a need for statistical evaluation of the peptide and protein inferences.

In this review, we first describe two-step protein identification processes with a focus on the PeptideProphet and ProteinProphet combination. Following that, we explain the potential shortcomings of a two-step procedure. Next, we focus on more recently developed one-step procedures, which attempt to alleviate problems associated with two-step identification of peptides and proteins. We include summaries of results from analyses of various data sets in the literature, which compare one or more of the one-step procedures with the two-step procedure based on PeptideProphet and ProteinProphet combination and demonstrate that the one-step procedures that simultaneously identify the peptides and proteins generally perform better. Finally, we review recent methods of protein identification, which integrate data from other platforms outside the MS/MS experiment in an attempt to improve the performance of methods based only on the MS/MS experiment.

Methods for protein identifications

Two-step processes

Several statistical two-step procedures have been proposed, which first provide confidence to the peptide identifications followed by confidence measures for protein identifications. These measures include P-value or E-value [6, 17, 18, 24] or false discovery rate (FDR) [25–30]. Among these, the most popular method is PeptideProphet [28] coupled with ProteinProphet [29]. In the sequel, we will refer to this combined (two-step) procedure as ProteinProphet. To our knowledge, ProteinProphet is a highly regarded procedure in this field and the first protein identification method that is probabilistically motivated. Thus, ProteinProphet is a two-step process where peptides are identified first through PeptideProphet [28] and their corresponding confidences are estimated. The second step involves the estimation of probabilities for protein presence, assuming the assignments of the peptides to the observed spectra are correct. PeptideProphet is based on the expectation-maximization (EM) algorithm, which generates a probability-based mixture model of correct and incorrect peptide identifications from the data. The observed data, denoted by$D$, includes scores, number of tryptic termini, number of missed cleavages and the mass difference of the observed precursor ion mass and the weight of the theoretical peptide. This information, in the observed data$D$, is used to separate the correct (denoted by $\prime +\prime$) from the incorrect (denoted by $\prime -\prime$) peptide assignments. The probability of correct peptide assignment to a spectrum, given the data$D$, is estimated using Bayes’ theorem:

$$p\left(+|D\right)=\frac{p\left(D|+\right)p(+)}{p\left(D|+\right)p(+)+p\left(D|-\right)p(-)}$$

where $p(+)$ and $p(-)$ are the proportions of correct and incorrect peptide assignments to an observed spectra in the population, respectively. The probabilities that a peptide, assigned to a spectrum, have information $D$ among correctly and incorrectly assigned peptides are denoted by $p\left(D|+\right)$ and$p\left(D|-\right)$, respectively. It is to be noted that PeptideProphet assumes each peptide to spectrum matches (PSM) for MS/MS data in the context of the whole population of correct and incorrect PSMs. The other PSMs in the data set that identify the same peptide sequence are not taken into account. So, the statistical unit of posterior probability of PSM and the peptide sequence is the same in PeptideProphet. PeptideProphet calculates this posterior probability individually for each search engine output. Opposed to that, procedures such as iProphet [31] uses the evidence from multiple PSM database search engines and computes peptide-based probability by introducing grouping variables such as number of sibling searches, replicate spectra, sibling experiments, sibling ions and sibling modifications. For a detailed description of the iProphet procedure, please refer to Figure 1 of the above mentioned paper.

The identified peptides, along with their confidences from PeptideProphet, are then further used in ProteinProphet to estimate the protein confidences, assuming that the peptide assignments are correct. The probability that a protein is present in the sample is estimated by

$$P=1-{\displaystyle \prod }_i\left(1-ma{x}_{j}p\left(+|D_j^i\right)\right)$$

where $i$ is the index for the peptide corresponding to the protein of interest and $j$ is the index for the assignment of peptide $i$ to a spectrum. The probability that the $j^{th}$ assignment of the $i^{th}$ peptide to a spectrum is correct is denoted by$p\left(+|D_j^i\right)$ and the product in the expression for P is computed assuming the independence of the accuracy of the assignments for all peptides. Note that, while estimating the protein probabilities, this method considers only the maximum assignment score for each peptide instead of all assignment scores. ProteinProphet also incorporates grouping information of all assigned peptides according to their corresponding proteins in the database, under the assumption that correct peptide assignments are more likely to correspond to ‘multihit’ proteins than the incorrect peptide assignments. Applying iProphet along with the initial PeptideProphet results produces adjusted PSM probabilities at the unique peptide level, and applying ProteinProphet on this modified PSM probabilities with the additional adjustment of number of sibling peptides gives the final protein probabilities. It has been shown in [31] that the protein probabilities computed with the help of iProphet are more accurate than the standard PeptideProphet/ProteinProphet probabilities.

Although ProteinProphet is one of the most widely used methods for protein identifications, it has certain issues that need attention. Firstly, the fact that ProteinProphet considers the maximum assignment score for each peptide while estimating the protein probabilities may be overoptimistic as an incorrect peptide may, by chance, have a high score if it is assigned more than once. Also, in reality, the spectra are often subjected to noise, which may lead to incorrect peptide identifications and thus incorrect protein identifications. This problem with a two-step process is clear from Figure 1. Here, there are three parent proteins, namely, $P_1,P_2$ and $P_3$, which generate the peptides $p_1,p_2,p_3,p_4,p_5$ and$p_6$. The MS/MS spectra of the two peptides $p_5$ and $p_1$incorrectly identify the peptides $p_x$ and$p_y$, resulting in the incorrect identifications of the proteins $P_x$ and$P_y$. The situation is more complicated when there is a presence of degenerate peptides, that is, the peptides that are generated by more than one protein. Additionally, from Figure 1 it is clear that if we know that peptide $p_3$ is present, then we know that protein $P_2$ is present and it will increase the likelihood of the presence of peptide$p_4$. So, there is an indirect feedback from peptide $p_3$ to$p_4$. It is clear that knowing the presence/absence of a peptide/protein influences the likelihood of the presence/absence of other peptides/proteins. Thus, a two-step process is inefficient in protein identifications in these situations, and construction of joint likelihood of peptides/proteins and identifying the uncertainties in both peptides/proteins in one step seems to be a logical step.

One-step processes

One-step methods involve simultaneous identification of which proteins are present and which peptides are identified correctly in a single step as opposed to the two-step process in ProteinProphet. One-step models incorporate a feedback loop between the proteins and their constituent peptides. The difference between a one-step process and a two-step process is shown graphically in Figure 2. As evident from Figure 2, in a two-step process there is no way of going back to update the peptide list (probabilities) after obtaining the protein list (probabilities). But, in a one-step process the peptide and protein lists are updated simultaneously through the feedback loop. Hence, unlike a two-step process, a one-step process can take into account the fact that the presence/absence of a peptide/protein can influence the likelihood of the presence/absence of other peptides/proteins.

Figure 2.

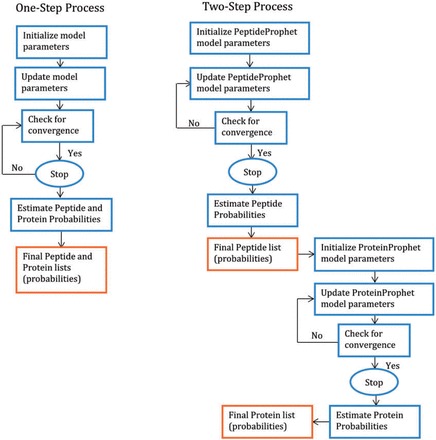
A cartoon showing the algorithms of a two-step process and a one-step process. In a two-step process, there is no way of going back to update the peptide list (probabilities) after obtaining the protein list (probabilities). But, in a one-step process the peptide and protein lists are updated simultaneously.

In the current literature, there are only two published papers on one-step methods incorporating rigorous statistical joint likelihood models for the presence of proteins and peptides, namely, the hierarchical statistical model (HSM) by Shen et al. [11] and the nested mixture model (NMM) by Li et al. [32]. Additionally, our group is currently working on a one-step protein identification process using a Bayesian hierarchical model (BHM) and we have received some encouraging initial results. We include some of the results here.

There are other important one-step protein identification procedures, which follow different methodologies. For example, [33] proposes a two-dimensional target decoy method called ProteinsFirst, which can control the FDR of protein and peptide-to-spectrum match (PSM) levels simultaneously. They modify the PSM score depending on the confidence of the protein identification score (feedback). This algorithm and other such algorithms mentioned in [33] fall into the category of ‘protein-centric’ approaches. ProteinsFirst [33] provides comparative performances of ProteinsFirst with similar ‘protein-centric’ methods. However, no comparison is provided with ProteinProphet. Another approach is proposed in [34] using a Barista model, which represents the protein identification problem as a single optimization procedure of a tripartite graph with three different layers corresponding to the spectrum, peptide and protein levels using machine learning techniques. This method is compared with ProteinProphet at a wide range of fixed FDR levels using six data sets; for each data set, it identifies more true proteins than ProteinProphet (Figure 2 of [34]). Like any supervised learning method, the Barista model requires discrimination of training and test data to avoid overfitting, so the choice of the training set for real data may be a problem if suitable reference data is unavailable. Furthermore, a couple of methods [35, 36] have been proposed, which consider feedback from high-confidence proteins to the selection of peptides. The method proposed in [35] considers an iterative process to compute peptide and protein probabilities simultaneously. Unlike the other one-step methods described herein, it uses peptide confidence results from PeptideProphet as input. The method outperforms ProteinProphet in experimental results presented in [35]. However, this method may need more computational time and cost compared with the other one-step methods, as the iteration stops only if the protein list converges. Also, the method in [35] has not been tested on any real complex data set, and the authors have advised against direct implementation of this method for practical purposes. The method in [36] uses a feedback loop in a different way; it starts with peptide identification results from database search mechanisms to get an initial list of proteins, which in turn is used to derive a peptide adjacency matrix. This adjacency matrix is used to compute regularized scores of peptides, which are further used to calculate peptide identification probabilities through a logistic regression model. These peptide probabilities are then used to update the protein list and consequently the adjacency matrix between the peptides. Although the authors claimed that the feedback loop converged to a stable list of proteins in a few number of steps for the data they analyzed, no justification has been given for the guarantee of convergence or estimate of convergence time in general. Experimental results are presented in [36] to compare their proposed method with ProteinProphet. Overall, the method from [36] has more coverage in protein identification and produces better results in terms of identifying the number of true and false peptides/proteins at a given level of false positive rate.

The joint likelihood-based models of one-step protein identification are the main focus of this manuscript. As indicated earlier, the above one-step methods [33–36] do not exactly fall into the category of the joint likelihood modeling of the peptides and proteins unlike [11] and [32]. The HSM by Shen et al. [11] assumes that a protein can generate multiple peptides and a peptide can be generated by multiple proteins. Using this interdependence, HSM fits a hierarchical statistical model that consists of four connected layers that models the uncertainty of the identified peptides and proteins, given the peptide matching scores for all the peptides from MS/MS data. The joint likelihood of the data is then used to estimate the parameters of the model and find the protein-identification probability through an Empirical-Bayes [37] framework. To briefly describe the four connected layers, the following notations are introduced: $Y_i$ is an indicator (binary) variable denoting the presence (given by$Y_i=1$) or absence (given by$Y_i=0$) status of the $i^{th}$ protein. $Z_j$ is an indicator variable denoting the presence (given by $Z_j=1$) or absence (given by $Z_j=0$) status of the peptide $j$in the sample. Next, $W_{jk}$ is another binary variable taking value 1 (if the $k^{th}$ assignment of peptide $j$ is correct) or 0 (otherwise), with $S_{jk}$ as the corresponding matching score. Also, $N$ is denoted as the number of proteins with at least one peptide hit and $M$ as the number of peptides assigned to at least one spectrum. These notations are used to define the following marginal/conditional models. In the first layer, the marginal distribution of $Y_i$ is assumed to be Bernoulli$\left(\rho \right)$, with $\rho$ being the proportion of truly identified proteins. The second layer consists of the conditional distribution of $Z_j$, given$Y=\left\{Y_i\right\}$, $$which is denoted as$\left[Z_j|Y\right]$. Given $Z, W$ and $Y$ are assumed to be independent. So, the conditional distribution of $W$, given $Z$ is considered in the third layer, denoted by$\left[W_{jk}|Z_j\right]$. The fourth layer consists of the conditional probability density of scores $S,$ given$W$, denoted as$\left[S_{jk}|W_{jk}\right]$. The likelihood of the presence of protein is also affected by the number of peptide hits involved. This fact leads to the modeling of the number of peptide hits through a binary random variable $V_i$ for protein$i$, indicating whether the number of peptide hits is beyond a threshold. The conditional distribution of $V_i$, given$Y_i$, is denoted by$\left[V_i|Y_i\right]$. Finally, the joint likelihood is obtained by integrating all the marginal and conditional models and is given by:

$$\left({\displaystyle \prod }_{i=1}^N\left[Y_i\right]\right)\left({\displaystyle \prod }_{i=1}^N\left[V_i|Y_i\right]\right)\left({\displaystyle \prod }_{j=1}^M\left[Z_j|Y\right]\right)\left({\displaystyle \prod }_{j=1}^M{\displaystyle \prod }_{k=1}^{T_j}\left[W_{jk}|Z_j\right]\left[S_{jk}|W_{jk}\right]\right)$$

Here, $[.]$ denotes the distribution (density/probability) of the variable involved. HSM uses the EM algorithm to estimate the parameters involved in the joint likelihood. So, if $\theta$denotes the vector containing all the model parameters, then the confidences of peptides and proteins are estimated by $Pr\left[Z_j=1|S,V;\widehat{\theta }\right]$ and$Pr\left[Y_i=1|S,V;\widehat{\theta }\right]$, respectively.

The NMM [32] considers the nested structure owing to the fact that there is a subsequence relationship between lower-level elements (peptides) and higher-level elements (proteins), whereas the lower-level elements (peptides) are the ones that are usually observed. NMM incorporates the evidence feedback from proteins to peptides, as in HSM. This feature helps in the distinction of correctly identified peptides with low scores from incorrectly identified peptides with high scores. To describe the model, the following notations are introduced: $T_k$ is an indicator variable taking value 1 (or 0) if the $k^{th}$protein is present (or absent) in the sample. $P_{k,i }^{\prime }s$are also indicator variables taking values 1 or 0 depending on whether the peptide $i$on protein $k$ is correctly assigned. Assuming that there are $N$protein identifications, ${\pi }_j^{*}$is defined as $Pr\left(T_k=j\right)$where $j$can be 0 or 1 and$k=1,\dots ,N$. Also, it is assumed that there are $n_k$peptide identifications corresponding to protein$k$, along with a score vector$x_k=\left(x_{k,1},\dots ,x_{k,n_k}\right)$. NMM assumes that given the protein indicators, the peptide indicators are independent and identically distributed. Also, it is assumed that if the protein is absent in the sample, all its constituent peptides are incorrectly identified, while, if a protein is present, some of its constituent peptides may be correctly identified. NMM also models the number of peptide hits to a protein and scores for identified peptides. Based on all the assumptions, the joint likelihood for the proposed NMM is given by

$${\displaystyle \prod }_{k=1}^N\left[P\left(T_k=0\right)\left[x_k|n_k,T_k=0\right]\left[n_k|T_k=0\right]+P\left(T_k=1\right)\left[x_k|n_k,T_k=1\right]\left[n_k|T_k=1\right]\right]$$

As before, $[.]$ denotes the distribution (density/probability) of the variable involved. Let $\psi$denote the vector containing all of the model parameters. Then $\psi$ is estimated by maximizing the likelihood using the EM algorithm, and the estimated parameters are used to obtain the confidences of peptide and protein identifications.

Although HSM and NMM both model the uncertainties of peptides and proteins simultaneously, these two methods differ in several aspects. HSM handles the issue of degeneracy (when a peptide is generated by multiple proteins or a protein generates multiple peptides) by assuming that a peptide will be present in the sample, provided at least one of the proteins containing that peptide generates it, and by assuming that the generation of the peptides are independent events. But the NMM admittedly did not account for degeneracy, which is an important consideration for estimating the protein confidences, especially, in high-level organisms. There are many other subtle differences in the assumptions of the two models, which we skip for the brevity of this review.

In our full Bayesian approach (BHM), we consider the fact that the proteins in the same biological pathway or in the same subcellular locations may not be independent. But both [11] and [32] assume independence of the proteins in the sample. In BHM, we incorporate the prior information by grouping functionally related proteins. Moreover, both [11] and [32] use the EM algorithm for the estimation of the peptide and protein confidences from the joint likelihood, which does not have any guarantee of convergence. In the BHM, the peptides and proteins are modeled simultaneously in the joint likelihood, and full posterior inference is carried out by applying a Gibbs sampling scheme.

Evaluations of HSM, NMM and BHM

These three models fall into the same category of statistical modeling and so they are collectively evaluated in this section. A comparison between the two-step process ProteinProphet and one-step processes (HSM and NMM) is given in [32], by applying all the methods on a standard protein mixture [38]. This data set consists of MS/MS spectra generated from a sample of stand-alone peptides and trypsin-digested proteins. SEQUEST is used to match the generated MS/MS spectra against a database containing both the sample peptides/proteins and proteins from Shewanella oneidensis as a decoy data set. A comparison between the empirical FDR and the estimated FDR at the peptide level, using all the methods, is shown in Figure 3. It should be noted that for PeptideProphet, FDR refers to the FDR of peptide identification, whereas for the rest it refers to the FDR of protein identification. As seen from this figure, PeptideProphet, ProteinProphet and HSM underestimate the FDR at lower values of the FDR, whereas NMM is conservative in estimating the FDR in the entire range.

Figure 3.

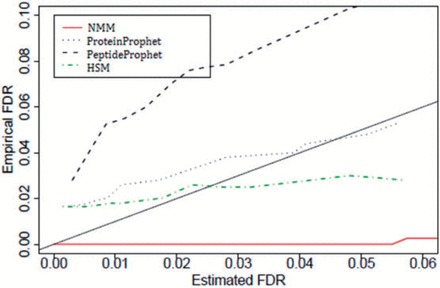
Comparative performances of ProteinProphet, PeptideProphet, HSM and NMM based on FDR estimates for peptide identifications using a standard protein mixture (adapted from Li et al. [32]). The solid diagonal line represents a perfect method. A colour version of this figure is available at BIB online: http://bib.oxfordjournals.org.

Figure 4 compares the discriminating powers of all the methods at the peptide level through the receiver operating characteristic (ROC) curves using the same data. It can be seen from Figure 4 that at a given level of specificity, the one-step processes (HSM and NMM) have higher sensitivity compared with that of the two-step process ProteinProphet, with NMM showing the maximum discriminating power. Thus, overall, these figures show that both the one-step processes are performing better than ProteinProphet in terms of peptide identifications for these data.

Figure 4.

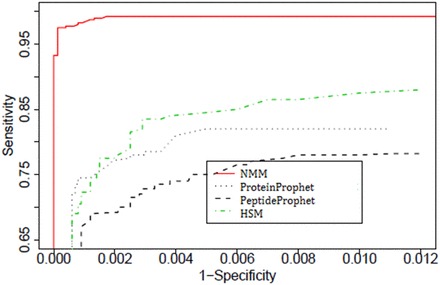
Comparisons among ProteinProphet, PeptideProphet, HSM and NMM using a standard protein mixture, based on ROC curves for peptide identifications (adapted from Li et al. [32]). A colour version of this figure is available at BIB online: http://bib.oxfordjournals.org.

As we are currently working on the full Bayesian model (BHM), we compared the performances of HSM and NMM with BHM using a yeast proteomics experiment where the true proteins are assumed to be known. The spectra scores of the yeast peptide fragments are obtained from a QSTAR mass spectrometer as done in [39]. The generated MS/MS spectra are matched, using SEQUEST, against a combined search database that contains both yeast proteins and proteins from Caenorhabditis elegans as a decoy data set. The number of true detected proteins against false positives is plotted at a fixed posterior threshold for the three one-step methods, which is shown in Figure 5. It is evident from Figure 5 that BHM picks up more true positives than HSM and NMM at each fixed number of false positives. Thus, a full Bayesian approach appears to perform better than the other two one-step processes in identifying the proteins from MS/MS data if we allow the number of false positives to go beyond eight.

Figure 5.

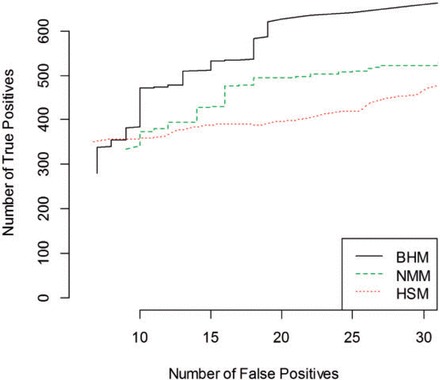
Comparisons among BHM, NMM and HSM using a ‘Yeast’ proteomics experiment. The number of true detected proteins against false positives is plotted at a fixed posterior threshold. A colour version of this figure is available at BIB online: http://bib.oxfordjournals.org.

We have also analyzed one more data set of Haemophilus influenzae (Hinf_Hum) data originally analyzed in [29] and compared the performances of NMM, BHM and ProteinProphet in Figure 6. Overall, BHM in this case performs better than ProteinProphet and NMM.

Figure 6.

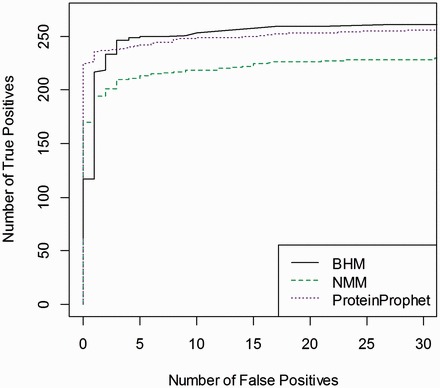
Comparisons among BHM, NMM and ProteinProphet using H. influenzae data. The number of true detected proteins against false positives is plotted at a given posterior threshold. A colour version of this figure is available at BIB online: http://bib.oxfordjournals.org.

Integration of other platforms

Protein identification methods described so far only use MS/MS data and database search. Recently, efforts have been made to improve protein identification using additional data outside the MS/MS experiment. The method proposed by Shanmugan et al. [40] uses external information [RNA-seq transcript abundances and/or Global Proteome Machine Database (GPMDB) [41] identification frequencies] to adjust the estimated protein identification probabilities via Bayes’ theorem. Specifically, positive protein identification is made when the corresponding probability exceeds a specified FDR threshold; the FDRs are estimated using a target-decoy approach [42] with reverse decoy sequences.

Some other information used for protein identification in addition to just MS/MS data are microarray data [43], protein–protein interaction network data [44], gene functional network data [45] and RNA-seq abundance information [46]. This additional information is especially useful for samples with low to moderate proteome coverage. The values of the external variables for the decoy proteins must be carefully simulated from the distribution of proteins with lengths similar to the decoy protein, and conditional probabilities of bins of possible values for the external variable are computed, given the type of protein (decoy or forward identification). This method was applied to real MS/MS data from a human prostate cancer cell line VCaP [47], which included RNA-seq data obtained from the same lab as well as from MS/MS data on a human embryonic kidney cell line HEK293 [48, 49], which included RNA-seq data from a different source [50]. When applied to each full data set, a large number of positive protein identifications were obtained at 1% FDR, so subsets were sampled to assess the performance of the method under various levels of proteome coverage. It was found that the method is most effective at improving the percentage of positive protein identifications when there is low to moderate proteomic coverage. Each MS/MS data set was also analyzed with GPMDB frequencies instead of with RNA-seq abundances, and similar results were obtained, demonstrating that the method can be applied in the absence of matching RNA-seq data. In summary, including additional information from external sources along with the traditional protein identification process using MS/MS data can improve the sensitivity of the process especially for the low to medium coverage proteins.

Conclusion

This review summarizes the recent improvements on protein identification from MS/MS data. In particular, we promote the idea of using one-step protein identification. We echo the same sentiment as [34] that peptide- and protein-level tasks are cooperative and the optimal identification solution has to be made using both peptide- and protein-level information simultaneously. We provide performance comparisons of one-step methods with the best two-step procedure, ProteinProphet, when available. The Barista model [34] clearly demonstrates superiority over ProteinProphet in all the six data sets that they had analyzed. The other three one-step procedures with joint likelihood modeling ([11, 32] and work in progress in BHM) vary in terms of model complexities such as incorporation of degeneracies and dependencies of proteins and peptides. This partly explains why the performance of any one of them is not always uniformly better than the other two. In many situations they perform better than ProteinProphet (Fig 3–6). However, it really depends on the tuning parameters of the models and the complexity of the data set. We anticipate that these one-step models can be improved further to make them uniformly better than the two-step procedures. Additionally, incorporation of data from other platforms also will improve the task of protein identification. Generally speaking, availability of more and more complex real and simulated protein-mixture data and transparent software will lead to progressively accurate protein identification procedures using MS/MS data. We hope that this review will inspire other researchers to delve into this area of proteomics research for better protein identification from complex mixtures of proteins using MS/MS experiments.

Key Points

• Protein identification from MS/MS data is still a fertile area of research.

• One-step protein-identification processes generally perform better than two-step processes.

• Incorporating additional molecular information along with the MS/MS data may provide better protein identification.

Funding

This study was supported by the research funding from NCI/NIH grant CA 170091−01A1 to Susmita Datta.