Cross-Talk between Ionic and Nanoribbon Current Signals in Graphene Nanoribbon-Nanopore Sensors for Single Molecule Detection

Abstract

Nanopores are now being used not only as an ionic current sensor but also as a means to localize molecules near alternative sensors with higher sensitivity and/or selectivity. One example is a solid-state nanopore embedded in a graphene nanoribbon (GNR) transistor. Such a device possesses the high conductivity needed for higher bandwidth measurements and, because of its single-atomic-layer thickness, could improve the spatial resolution of the measurement. Here we show two-channel measurements of ionic current through the nanopore during double-stranded DNA (dsDNA) translocation, along with the simultaneous response of the neighboring GNR due to changes in the surrounding electric potential. We observe cross-talk originating from capacitive coupling between the two measurement channels, resulting in a transient response in the GNR during DNA translocation; however, we do not observe a modulation in device conductivity via an electric field effect response, due to changes in local solution potential during DNA translocation. A field effect response would scale with GNR source-drain voltage (V_ds), whereas the capacitive coupling does not scale with V_ds. In order to take advantage of the high bandwidth potential of such sensors, the field effect response must be enhanced. We present potential field calculations to outline a phase diagram for detection within the device parameter space, charting a roadmap for future optimization of such devices.

1. Introduction

There has been encouraging progress toward high-spatial-resolution molecular sensing using both biological and solid-state nanopores.^[1–3] There are two main approaches toward improving the signal-to-noise of nanopore measurements: 1) slowing down the speed of DNA translocation so that the ionic current measurement can be made using commercial amplifiers at lower bandwidths with less high frequency noise^[4–6] (the high capacitance of the lipid bilayer necessitates this approach for biological nanopores) and/or 2) reducing the noise stemming from the amplifier and nanopore chip in order to measure at high bandwidths and preserve the intrinsic speed of the molecule translocation.^[7,8]

Electronic detection using a single-layer graphene nanoribbon at the nanopore may be an alternative, advantageous technique for molecular detection at even higher bandwidths (>10 MHz) than ionic current measurements and a spatial resolution that in principle could be as fine as the graphene thickness (~ 0.3 nm, approximately the same as the separation between nucleotides along the DNA backbone). For the example of DNA sequencing, the nanopore localizes the DNA molecule near the sensor, ensuring that the bases flow past the sensor linearly while both the ionic current signal and the current through the graphene device are measured simultaneously (Figure 1a). As nucleotides pass one-by-one through the nanopore and past the sensor, only one base abuts the GNR at a time, offering the potential for base-by-base read-out. Graphene nanoribbon-nanopore devices have been explored theoretically and experimentally^[9–14]; however, the scarcity of experimental data calls for clarification of the graphene device response and measured signals.

Figure 1. GNR-nanopore device fabrication and characterization.

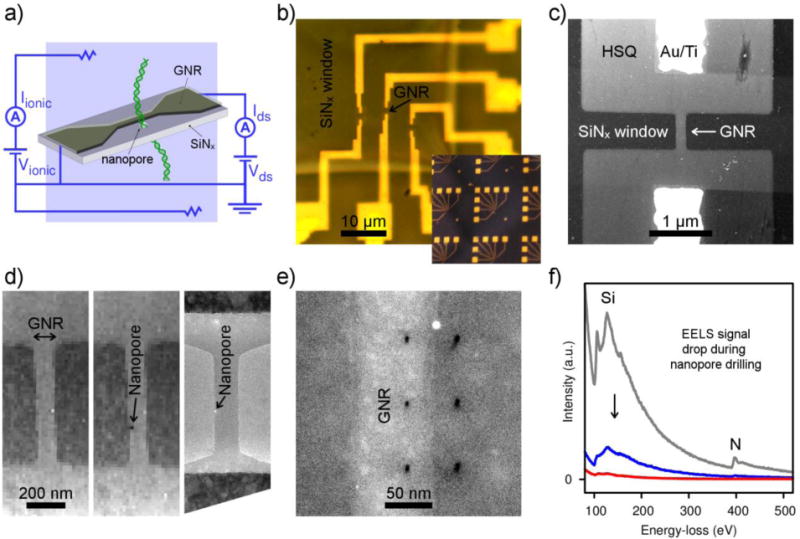
a) Diagram of GNR-nanopore device during DNA translocation. b) Optical microscope image of a 50 nm thick Si₃N₄ window containing three GNR devices. The inset shows an array of GNR chips (5 mm × 5 mm each). c) HAADF STEM image of GNR. The contrast is given by the HSQ layer. d) HAADF STEM images before (left) and after (center) nanopore formation with the electron probe, and TEM image of GNR with nanopore (right). All images have the same magnification. e) HAADF STEM image showing the precision in placement along the GNR of nanopores formed in STEM. f) EELS signal before (gray), during (blue) and after (red) a nanopore has been formed with the electron probe. Si and N peaks are indicated at 100 and 400 eV, respectively.

In this letter we describe the robust design and measurement procedure of a nanopore with embedded GNR (GNR widths down to 50 nm and lengths of 600 nm, on Si₃N₄ membranes), such that the nanopore provides stable open-pore ionic current with linear dependence on ionic voltage. We report dsDNA translocations through these nanopores while running currents of several hundred nAs up to 2 μA through the GNR at low V_ds (< 100 mV). During DNA translocation, there is cross-talk between the two channels, which appears in the ionic channel as the familiar ionic current blockade and in the nanoribbon channel as the time derivative of the ionic signal. Because the ionic signal during DNA translocation typically appears as a rectangular pulse, the graphene nanoribbon signal can be pictured as up and down current spikes that occur in time at the beginning and end of the ionic signal, respectively. This time derivative signal is a result of a capacitive coupling between the measurement channels. The cross-talk does not scale with V_ds on the device and is present for measurements at both high salt (1 M KCl) and low salt concentrations (10 mM KCl). This experimental data contributes clarity and controls to pre-existing reports in the literature.

We also perform circuit simulations confirming that cross-talk should be observed given the high capacitance between the gold electrodes and ionic solution. A reduction of that capacitance (e.g., with the use of an insulation layer) diminishes the cross-talk. Importantly, the circuit simulation also predicts that for an increase in device leakage current (i.e., a decrease in resistance to electrochemistry between the GNR and ionic solution) it is possible to obtain rectangular pulses in the GNR channel that mirror signals in the ionic channel.

By calculating the electric potential in the vicinity of the device, we quantify the potential change (ΔV) due to DNA translocation as a function of position across the GNR. Considering the GNR sensitivity to changes in local potential (i.e. the GNR gating curve), Si₃N₄ membrane thickness, nanopore size, salt concentration, insulation thickness, and ionic voltage (V_ionic), we use the potential field calculations to generate a phase diagram for molecule detection within the device parameter space. According to these calculations, given the magnitude of ΔV for the range of device parameters measured here, it would be unlikely to observe a GNR response based on a field effect mechanism. However, the calculations suggest future device modifications that can amplify that response. While the capacitive coupling reported here provides a means for counting molecules, it does not provide the high magnitude signals and scaling that could eventually be obtained from a field effect mechanism.

2. Results and Discussion

2.1. Graphene Nanoribbon-Nanopore Sensor Fabrication and Characterization

In designing the graphene nanoribbon sensors for detection of DNA translocation through a nanopore, we considered the following criteria: visibility of the device in the transmission electron microscope (TEM) during nanopore drilling, wetting of the nanopore, and leakage currents between device and solution.

Graphene nanoribbons are made from chemical vapor deposition (CVD) grown, continuous-sheet graphene using a commonly employed electron-beam lithography technique involving the negative HSQ resist. During development,^[15] the exposed sections of the HSQ resist harden into a ~ 15 nm thick SiO₂ layer, serving as an etch mask to define the nanoribbon pattern in the graphene sheet. Typical dimensions for the nanoribbons were 600 nm long and 50–200 nm wide, with resistances in the range of 10–80 kΩ. GNR widths as thin as ~ 20 nm were achieved in HSQ dose tests, but they were not employed because the yield of working devices at that width is low. Example devices are shown in Figure 1b–d. Some devices were also made from CVD grown, single-crystal graphene hexagons (Figure S1), making it possible to optically determine the crystal orientation (Figure S2).

The HSQ layer serves not only as an etch mask to define the nanoribbon but also makes the graphene visible in the TEM (necessary for nanopore positioning)^[16] and masks the graphene after the nanopore is formed so that H₂/O₂ plasma cleaning can be used to generate a clean, hydrophilic nanopore. However, there are also a few disadvantages that should be noted: if the nanopore is in the center of the nanoribbon, the HSQ layer increases the total thickness of the nanopore, reducing the ionic current; the resist displays different nanopore formation dynamics than Si₃N₄ and can take longer to drill through with the TEM; as spun for this concentration, it is ~ 15 nm thick and has a low dielectric constant, reducing the potential change in solution seen by the GNR.

The STEM-based procedure that we routinely use to form nanopores for nanoribbon-nanopore experiments is described in a previous publication^[16] (although some of the data shown in this paper was collected from nanopores drilled in standard TEM mode as well). With this procedure we have precise control over nanopore placement (Figure 1d–f) while generating little to no damage in the GNR itself, as demonstrated by the almost unchanged device resistance and transconductance after nanopore drilling.^[16] For a given Si₃N₄ membrane thickness, by adjusting the electron probe dwell time and monitoring the electron energy-loss spectroscopy (EELS) signal, we are able to calibrate and control the size of the nanopore that we create in scanning transmission electron microscopy (STEM) mode (Figure S3).

The EELS signal provides a precise indication of material composition (including, most importantly, the Si content) in the area of the electron probe^[17] and allows us to monitor in real-time the sputtering of atoms in the membrane while the nanopore is being formed (Figure 1f). All devices measured here consisted of nanopores formed on the side of nanoribbons and therefore through pure Si₃N₄. We observe other elements in the EELS spectra when atomic layer deposition (ALD) insulation is added, when the nanopore is formed through the HSQ, or when the device is not sufficiently clean (Figure S4) (e.g., oxygen for HSQ, titanium for a TiO₂ ALD layer, an increasing carbon peak for dirty devices, etc.). When a nanopore is fully formed and opened, the intensity of the EELS Si peak drops to zero. Longer dwell times, past the initial point of nanopore formation, generate larger nanopore sizes.

Once the nanopore is formed, the device is cleaned again with H₂/O₂ plasma and mounted on a home-built PDMS microfluidic channel, which feeds KCl solution to the bottom side of the membrane. A silicone well is placed on the opposite side (top side) of the device and filled with KCl solution. Ag/AgCl electrodes are inserted into solution on both sides of the membrane and connected to a HEKA patch-clamp amplifier operated in voltage-clamp mode in order to measure ionic current flow through the nanopore (typical V_ionic = ± 500 mV). Micro-manipulators connected to a second HEKA patch-clamp amplifier (also operated in voltage-clamp mode) are used to interface with the gold contact pads connecting with the GNR in order to measure the GNR current during DNA translocation (typical V_ds < 100 mV). A home-built acquisition software simultaneously monitors the currents through both patch-clamp channels.

In these experiments, the grounded Ag/AgCl electrode was always placed on the GNR side of the Si₃N₄ membrane. This results in lower noise and also limits electrochemistry at the GNR surface because the difference in potential between the GNR and the grounded ionic electrode is small (usually < 100 mV).

The GNR sensitivity is characterized by measuring the response of the graphene nanoribbon to a gate voltage applied to the ionic solution on the nanoribbon side of the Si₃N₄ membrane (Figure 2a). We see the characteristic ambipolar gate response of graphene devices.^[18] As the ionic concentration is reduced, there is a shift in the charge neutrality point toward higher gate voltages,^[19] and the transconductance of the device is reduced (Figure 2b).

Figure 2.

GNR gating and sensitivity. a) Schematic showing GNR gating measurement in ionic solution. b) Response of GNR resistance (R_ds) to a gate voltage (V_g) applied to an Ag/AgCl electrode in KCl solution for different ionic solution concentrations.

For a typical STEM drilled GNR with resistance < 100 kΩ, a perturbation of the potential uniformly across the nanoribbon of ~ 10 mV at the most sensitive region of the gating curve should generate > 50 nA change in GNR current from a baseline current of > 1 μA, a variation significantly higher than the GNR noise level of I_rms ~ 12 nA at 1 MHz bandwidth in solution.

2.2. DNA Translocation through Graphene Nanoribbon-Nanopore Sensors

Measurements consisting of hundreds of individual DNA translocations were observed in the ionic current in nanopores next to graphene nanoribbons for ionic concentrations from a) 1 M KCl on both sides of the membrane down to b) 1 mM (GNR side)/1M (bottom side) and down to c) 10 mM KCl on both sides of the membrane. At 1 M KCl a cross-talk between the GNR and ionic current translocation measurement is visible in the GNR current trace (Figure 3a). As V_ds increases (for both positive and negative polarity), the magnitudes of the nanoribbon current and noise increase, but the magnitude of the cross-talk remains the same. Therefore, the cross-talk becomes gradually less visible as V_ds increases (Figure 3b).

Figure 3.

Measurement of ionic current and GNR current during 15,000 base-pair long dsDNA translocations. a-c) Each ionic current time trace is in black, with representative single translocation events shown on the right. Corresponding GNR current time trace are in red, below the ionic data. a) High salt concentration on both sides of the membrane (1 M KCl, screening length ~ 0.3 nm) with the GNR at ground (V_ds = 0). Nanopore diameter (d) = 4.7 nm, membrane thickness (t) = 50 nm, GNR width (w) = 130 nm, GNR length (l) = 680 nm. b) High salt concentration on both sides of the membrane (1 M KCl, screening length ~ 0.3 nm) with high current through the GNR (~ 229 nA). Same GNR as in (a). c) Low salt concentration on the GNR side of the membrane (10 mM KCl, screening length ~ 3 nm) with high current through the GNR (~ −472 nA). d = 8.5 nm, t = 50 nm, w = 230 nm, l = 600 nm. The concentration on bottom side of the membrane is 1 M KCl.

A lower salt concentration (e.g., 10 mM KCl) would be amenable for sensing in two ways: it provides a longer screening length (~ 3 nm for 10 mM KCl vs. ~ 0.3 nm for 1 M KCl) over which the charge of the molecule can be detected, and it results in a smaller electric potential gradient outside of the nanopore, which falls off over a larger distance than it would at higher salt concentrations. The practical consequence of the later is that the physical act of blocking ion flow through the nanopore during DNA translocation generates changes in electric potential even as far as tens of nanometers away from the pore.^[20]

In essence this mechanism is, as pointed out by Xie et al.,^[20] an amplification of the ionic signal via the transconductance of the sensor. A molecule translocating through the nanopore increases the nanopore resistance (measured in the ionic current as ΔI_nanopore), resulting in a change in the potential in solution. That ΔV is amplified by the GNR and observed in the GNR current as ΔI_GNR. We expect that at high salt concentrations only a small area of the device is affected, resulting in no detection of DNA. At lower salt concentrations, however, a larger area of the device sees the change in potential.

Upon transitioning to lower salt concentration on the GNR side of the membrane, however, there is no increase in signal-to-noise of the cross-talk, and at high nanoribbon currents the cross-talk is convoluted with the noise (Figure 3c). This behavior was true for both damaged (after TEM drilling) and undamaged GNR devices (after STEM drilling), even though the sensitivity of the STEM drilled devices is much higher.^[16]

The magnitude of the cross-talk observed at 1 M KCl does not scale with V_ds, indicating that this signal is not a field effect response of the GNR to a change in surrounding potential. As a control, the same measurement was made with the GNR replaced by a single gold contact held at ground near the nanopore (Figure S5). In this instance, any measured current flows directly in to/out of the gold contact. The same cross-talk was observed, indicating that it is induced by the presence of a conductor in solution near the pore (the signal was not present when the probe was not attached. i.e. the device must be connected, and the cross-talk is not induced in the electronics alone).

2.3. Discussion of Circuit Simulation

The cross-talk in the nanoribbon appears as the time derivative of the ionic current (Figure 3a,b and Figure 4). The fact that we observe the same correlation in a grounded electrode near the nanopore (Figure S5) suggests a capacitive source. An effective circuit diagram for the single gold electrode is shown in Figure 4d, where R_soln is the solution resistance, R_{electrode-soln} is the resistance to current leakage from the electrode to solution, and C_{electrode-soln} is the capacitance between solution and the gold electrode (or GNR). Circuit simulations of this effective circuit reveal, in response to translocation-like pulses on the ionic channel (Figure 4e), a similar time derivative signal on I_electrode (Figure 4f) when both of the following are true:

1. R_soln << R_{electrode-soln}. i.e. the electrochemical resistance for current flow from solution into the device (or vice versa) is much greater than resistance of the solution (R_soln) — this is certainly the case in our devices,

2. the capacitance between the source/drain electrodes and solution is C_{electrode-soln} ~ 1 nF. The magnitude of C_{electrode-soln} determines how quickly the correlated spikes in I_electrode decay (smaller C_{electrode-soln} means faster decay).

Figure 4.

GNR-nanopore circuit simulations. A single DNA translocation as measured experimentally in a) the ionic current and c) the GNR current. b) The calculated negative time derivative of the measured ionic current signal shown in (a). Graphs a–c share the same horizontal axis. d) Effective circuit used to model the GNR response to changes in R_pore. The following simulation parameters were used: R_soln = 1 kΩ, R_pore = 50 MΩ before DNA translocation, R_pore = 100 MΩ during DNA translocation, C_membrane = 40 pF, R_{electrode-soln} = 100 Ω (green trace), 1 kΩ (orange trace), and 10 MΩ (black trace), C_{electrode-soln} = 1 nF, V_electrode = 0 V, and V_ionic = 500 mV. e) The simulated ionic current signal due to a change in R_pore for the three different values of R_{electrode-soln}. f) The simulated GNR current signal due to the same change in R_pore for the three different values of R_{electrrode-soln}. The C_{electrode-soln} value determines the decay rate for the derivative spikes shown in the black and orange traces, which resemble the experimental data in (c). Graphs (e) and (f) share the same horizontal axis.

In short, the capacitive coupling between the ionic electrode and the GNR (or even simply a lone gold electrode) in solution is high enough that any change in potential (a result of DNA translocation through the nanopore) produces a transient current in the device (I_electrode = dq/dt = C × dV/dt), observed as the time derivative of the ionic translocation event. For C_{electrode-soln} several orders of magnitude smaller (which could be achieved with thick ALD insulation), the derivative signal should be negligible. However, thick device insulation additionally buffers the sensitivity of the device.

If the GNR leakage current into solution becomes high enough such that R_{electrode-soln} is comparable to R_soln (modeled here as 1 kΩ) then the GNR events mirror the shape of the ionic translocations (orange and green traces, Figure 4f). This describes a leakage current flowing directly to/from the GNR, and both channels would show rectangular pulses that are fully correlated.

The capacitive coupling shown in Figures 3 and 4 does provide an alternative means for DNA detection, but the signal does not contain any unique information that cannot be generated directly from the ionic current. At 10 mM KCl, where changes in the electric potential could cause conductance modulations in the GNR via a field effect mechanism, we do not see any positive correlation.

2.4. Discussion of Electric Potential Calculations

The length-scale and magnitude of the change in potential caused by DNA translocation through the nanopore is depicted in Figures 5a–b, based on the analytic expressions derived by Xie et al.^[20] (a comparison with COMSOL simulations is shown in Figure S6). From this picture it is clear that the largest ΔV occur within a few nanometers of the nanopore. To amplify detection of DNA translocation based on a field effect response from the GNR, the entire width of the nanoribbon must be subject to a perturbation in potential, and the absolute value of the electric potential should match with the gate values in the sensitive region of the GNR gating curve (Figure 2). The absolute potential around the GNR can be shifted by choosing the ionic voltage such that the resulting electric potential lies in the nanoribbon’s sensitive region. Figure 5f gives an example of how the absolute potential falls off as a function of distance from the nanopore, with and without a DNA molecule blocking some of the ion flow. The nanopore size (Figure 5c), Si₃N₄ membrane thickness (Figure 5d), and salt concentration ratio (C_cis/C_trans) (Figure 5e) can all be tuned to maximize ΔV around the nanoribbon during translocation. In general, small nanopore size, reduced membrane thickness, and a high salt concentration ratio generate conditions most amenable to DNA detection with the GNR. Given the experimental conditions for the data shown in Figure 3 we can see that while the portion of the nanoribbon near the nanopore is subjected to ΔV that could in principle produce a measurable change in nanoribbon current, the majority of the nanoribbon does not see a significant ΔV.

Figure 5. Calculation of electric potential near the nanopore.

a) Cross-sectional schematic of a GNR-nanopore device before and during DNA translocation. The DNA is treated as a hard cylinder. The ionic voltage (V) is applied across two reservoirs (trans and cis chambers) separated by an insulating membrane containing a nanopore. The change in potential is calculated upon DNA entry into the nanopore. b) Two-dimensional distribution of potential change in the trans chamber. c) Potential change distribution as a function of nanopore size (D). d) Potential change distribution as a function of membrane thickness (L). e) Potential change distribution as a function of salt concentration ratio (C_cis/C_trans). f) Absolute potential distribution with various salt concentration ratios with and without a DNA molecule in the nanopore.

3. Conclusions

In conclusion, we show DNA translocation results from a solid-state nanopore embedded in a single-layer graphene sensor. The device shows a distinct cross-talk between ionic and nanoribbon currents during DNA translocation. This cross-talk does not scale with V_ds or ionic concentration, and we show with a circuit simulation that this signal is generated by a capacitive coupling between the GNR and the ionic measurement channels. By considering the absolute electric potential around the graphene nanoribbon sensor and the change in potential during DNA translocation, it will be possible to further tune the device and measurement parameters to optimize detection based on a field effect mechanism.

4. Experimental Section

GNR devices were fabricated on top of Si₃N₄ membranes (suspended area ~ 50 μm × 50 μm) fabricated on 5 mm × 5 mm, 500 μm thick Si chips coated with an inner layer of 5 μm SiO₂ and an outer layer of 50 nm Si₃N₄ on each side. Large gold contact pads (titanium adhesion layer) were placed near the window using photolithography and thermal evaporation. Continuous, mostly monolayer graphene was grown on a copper substrate via CVD and transferred onto the Si₃N₄ windows via a wet-transfer procedure with FeCl₃. A second set of gold contacts were defined onto the suspended window via electron-beam lithography (EBL) and thermal evaporation.

HSQ resist (Dow Corning, XR1541, 2% solution in MIBK) was patterned into ribbons via EBL. Large HSQ pads were defined around the gold contacts leading to the ribbon, and these large HSQ pads were crucial for device yield. GNRs were defined by using the HSQ as an etch mask during a 10-20 s, 50 W O₂ plasma etch.

Transmission-electron beam nanopore drilling was carried out in a JEOL 2010F TEM/STEM at 200 kV, using a procedure^[16] to limit damage to the GNRs caused by the electron beam.

Currents through the nanopore and through the GNR were recorded in voltage-clamp mode using HEKA patch-clamp amplifiers at 10 kHz bandwidth (50 kHz sampling) using a custom LabVIEW acquisition software. 15,000 base-pair double-stranded DNA molecules (Fermentas Life Sciences) were used for all DNA translocation experiments.

Circuit simulations were performed using LTspice. Each head-stage of the Heka patch-clamp amplifiers was modeled as an ideal ammeter in series with a ideal voltage source, with an added white-noise voltage noise of 1 μV RMS. The nanopore was modeled as a resistor with a capacitor in parallel, and the DNA translocation events were represented by a change in the nanopore resistance. The simulation was run for 300 μs with a 10 ns step size.

The values for the circuit simulation were chosen based on the following: The estimate for R_soln was obtained by measuring the resistance between two Ag/AgCl electrodes in solution for different electrode spacings. C_{electrode-soln} is strongly dependent on geometry of the device. We directly measured C_{electrode-soln} using a triangle wave technique outlined in the supplement of reference 21.^[21] The simulation yields visible cross-talk for C_{electrode-soln} > 0.1 nF. The higher the C_{electrode-soln} value, the more slowly the cross-talk decays. R_{electrode-soln} depends on electrode material, area, and insulation. We estimated this value to be ~ 10 MΩ by measuring the resistance between the gold electrode and the ionic electrode in solution above it. In instances when further insulation is added, R_{electrode-soln} increases even more. If a non-inert metal were used for the electrode or corrosion caused R_{electrode-soln} to decrease, one could obtain the alternative signals for lower R_{electrode-soln} values shown in Figure 4f.