Abstract
The precision of estimates in many statistical models can be expressed by a confidence interval (CI). CIs based on standard errors (SE) are common in practice, but likelihood-based CIs are worth consideration. In comparison to SEs, likelihood-based CIs are typically more difficult to estimate, but are more robust to model (re)parameterization. In latent variable models, some parameters may take on values outside of their interpretable range. Therefore, it is desirable to place a bound to keep the parameter interpretable. For likelihood-based CI, a correction is needed when a parameter is bounded. The correction is known (Wu & Neale, 2012), but is difficult to implement in practice. A novel automatic implementation that is simple for an applied researcher to use is introduced. A simulation study demonstrates the accuracy of the correction using a latent growth curve model and the method is illustrated with a multilevel confirmatory factor analysis.
Keywords: Wald test, Wilks test, confidence intervals, likelihood ratio test
Introduction
Once a model is fit to data, it is routine practice to examine the precision of the parameter estimates. An approximation of this information is found in the parameter covariance matrix V, and in summary form, as standard errors, (Wald, 1943). Standard errors (SE) can be used for null hypothesis significance testing, but the information is better communicated by confidence intervals (CIs; Wilkinson, 1999), which may not be symmetric. A CI is constructed by finding the set of values that cannot be rejected by the test; the exact method depends on the particular significance test.
SE-based CIs are widely used and easy to compute, often simply the parameter estimate ±1.96 times the SE. However, SE-based CIs are not parameterization-invariant. For example, the upper and lower limits of a CI constructed for a variance are usually not the squares of those of a CI for the corresponding standard deviation (Neale, Heath, Hewitt, Eaves, & Fulker, 1989). The accuracy of SE-based CIs depends on whether the Wald statistic is close to normally distributed. For example, Fisher’s z transformation of a correlation usually requires a smaller sample size to achieve asymptotic normality than does the original correlation parameter. Hence, the CI coverage of the z transformed value is usually closer to the nominal level than the CI coverage of the original value.
To avoid the problem of parameterization sensitivity, Neale and Miller (1997) implemented a likelihood-based CI constructed by inverting the likelihood ratio test (LRT; Wilks, 1938). Since the LRT is parametrization-invariant, the resultant CIs are as well. Likelihood-based CIs are accurate in many cases, but do not always perform well near certain parameter space boundaries.
Natural and attainable boundaries can be distinguished. A natural boundary is a boundary of the model distribution beyond which the distribution is invalid or degenerate. For example, a binomial parameter p outside the interval (0, 1) does not define a valid binomial distribution, and similarly, a population correlation between observed variables cannot be outside of the interval (−1, 1). In contrast, an attainable boundary separates the interpretable part of a distribution from the uninterpretable part. For example, in factor analysis, an uninterpretable correlation (e.g., |r| > 1) between latent variables may still generate a valid positive-definite expected multivariate normal distribution given sufficiently large variable-specific residual variances. The values ±1 are attainable boundaries of such a latent correlation parameter.
Figure 1 exhibits a latent growth curve model. In this model, the variance of the slope has a natural boundary near −0.1 instead of 0. Since negative variances are not interpretable in this context, it is desirable to place an attainable lower bound at 0. An adjustment has been developed to produce likelihood-based CIs for this situation (Wu & Neale, 2012). The adjusted CIs are exhibited in Figure 2. Formerly, bound-adjusted CIs were not trivial to compute. A decision tree is involved and, in some cases, the original model needs to be augmented with 3 non-linear constraints and carefully optimized to obtain the adjusted limits. Here we report that OpenMx v2.7 and later versions automatically compute bound-adjusted CIs of parameters when either an upper or lower bound is set. OpenMx (Neale et al., 2016) is a free and open-source software originally designed for structural equation modeling (SEM). OpenMx runs inside the R statistical programming environment (R Core Team, 2014) in most popular computer operating systems.
Figure 1.
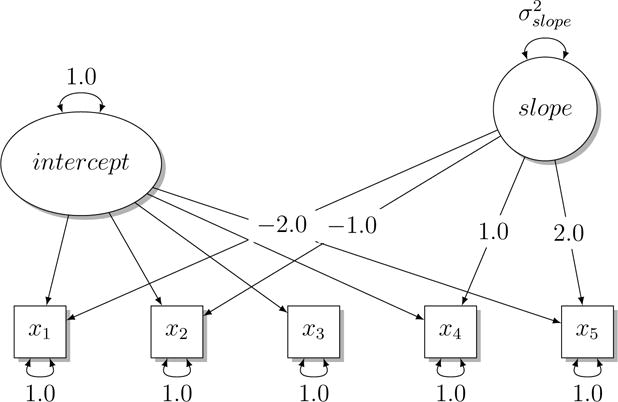
Latent growth curve model used to illustrate the confidence interval adjustment when a lower bound of 0 is placed on . The natural lower bound of is near −0.1. Simulated values are shown. Indicator residual and latent variances were freely estimated. The intercept-slope covariance was fixed at zero and not estimated.
Figure 2.
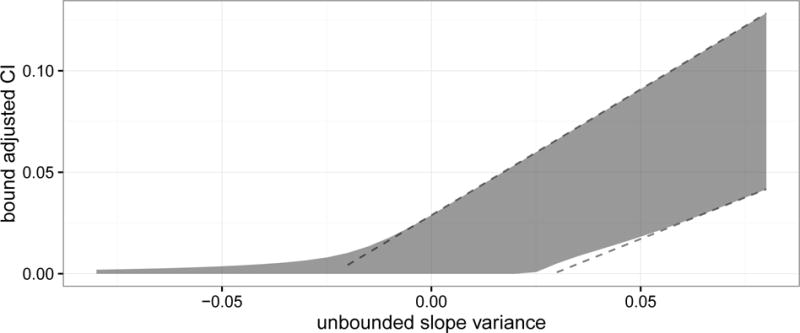
Adjusted CI of (shaded) with unadjusted CI indicated by dashed lines. The model used is shown in Figure 1 with a sample size of 150. Only is manipulated. The unadjusted CIs do not use a lower bound and extend below the figure. The adjusted CIs narrow from 0.025 to 0.05, and smoothly transition from a two-sided to one-sided interval from 0 to −0.05.
Likelihood-based CIs
We describe issues common to likelihood-based CIs and then describe the implementation of bound adjusted CIs. Let ξ = (θ, ζ)′ be the parameter vector in a model where θ is the single parameter of interest and ζ is the set of other parameters. Let f(ξ) be the −2 log likelihood (deviance) function of our model and the maximum likelihood estimates (MLE). For a single parameter, under certain regularity conditions (Steiger, Shapiro, & Browne, 1985), the difference between model deviance is χ2 distributed with a single degree of freedom. Let za be the 1 − a quantile of the standard normal distribution such that . Given false positive rate α, a 100(1 − α)% CI of θ is the set of all test values such that the statistical test does not reject the null hypothesis at level α.
Profile likelihood confidence intervals have only one theoretical definition, but there are at least four distinct ways to communicate how to locate these limits to an optimization algorithm. Throughout, we will take the point of view of deviance minimization even though the MLE is customarily regarded as the likelihood maximum. Two equivalent formulations to find the lower limit of θ are:
| (1) |
| (2) |
These two search regions are described geometrically in Figure 3. In addition to a choice of geometry, there is a choice in how to communicate the constraints to an optimizer. Some optimization algorithms are specially tailored to handle non-linear constraints (e.g., Birgin & Martínez, 2008; Luenberger & Ye, 2008). However, constraints can also be expressed as the sum of a fit function and penalty term. The unconstrained functions are typically of the form,
| (3) |
| (4) |
These composite functions are minimized as a whole. Equations 3 and 4 correspond to Equations 1 and 2, respectively.
Figure 3.
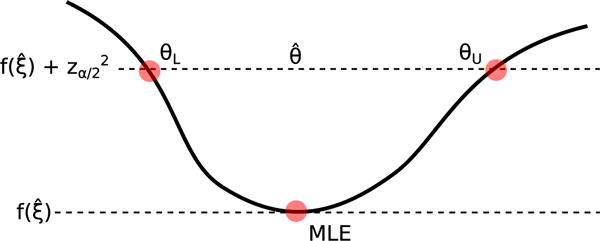
Search region for upper θU and lower θL limits of . An equality constraint (Equation 1) guides the optimizer to search on the θL↔θU line segment. An inequality constraint (Equation 2) guides the optimizer to search in the region bounded below by f and above by the θL ↔ θU line segment. Both formulations of the problem are equivalent, but may obtain somewhat different results depending on the optimization algorithm.
The concern with the unconstrained formulations is that units of θ are equated with the deviance units of the penalty function. Due to this fungibility, the optimizer will accept some constraint violation if the change in θ is large relative to the change in the penalty function. The constrained version of the problem provides to the optimizer more information so it can potentially do a better job. In addition, the constrained version often has no performance disadvantage. When searching for limits of a parameter, evaluation of the two versions of the problem take the same amount of time because the gradient of the fit function is known in the constrained version of the problem.
The MLE is identified as long as there is a global minimum deviance. Likelihood-based confidence intervals require a much stronger condition for identification: that deviance values within units of the MLE are close to the MLE. Figure 4 exhibits the problem geometrically. The analyst ought to examine the parameter vector at the lower bound ξL and decide whether it looks reasonable. One way to check the CI is to compare it to the Wald SE. If a CI interval is much wider or narrower than the Wald SE then additional scrutiny is warranted. An important CI diagnostic is to examine the value of the other parameters ζ at the limits of the parameter of interest θ. This information is readily available from OpenMx using the “verbose=TRUE” option to the summary function.
Figure 4.
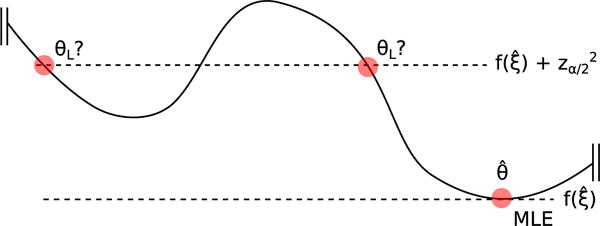
More than one point can satisfy the lower bound θL in a sufficiently flat deviance space. The lowest lower bound can be much further away from than might be expected from its Wald standard error.
For example, consider the model in Figure 1 and with set to 0.03 and sample size 150. Assume there is no sampling error; we set the covariance data equal to the model implied distribution. If we find CIs for then output from the summary function includes:
## parameter value side fit residual vari vars method ## 1 vars 0.066 upper 1057 0.96 1.00 0.066 neale-miller-1997 ## 2 vars 0.005 lower 1056 1.05 0.98 0.005 wu-neale-2012 ## diagnostic statusCode ## 1 success OK ## 2 success OK
The first column parameter gives the parameter name vars. This corresponds to . The second column value gives the limits. The column side indicates whether it is an upper or lower limit of the CI. The column fit is the deviance value at the CI. For unbounded parameters, the fit should be the MLE plus . The next three columns (residual, vari, and vars) give the parameter values at the CI limit. The method column describes which algorithm was used. If the algorithm fails, the diagnostic and statusCode columns give some idea of why.
If CIs seem suspicious then it is important to check whether the model is locally identified and search for a better deviance minima. To address these needs, OpenMx offers mxCheckIdentification (in part based on Bollen & Bauldry, 2010) and mxTryHard, respectively. The mxTryHard algorithm repeatedly perturbs starting values and optimizes the model in an effort to find the best minimum. For models that include ordinal data, a variation, mxTryHardOrdinal, is available.
Implementation
OpenMx implements likelihood-based confidence intervals for a parameter with an attainable upper or lower bound (i.e., Wu & Neale, 2012, Section 3.3). For the purpose of exposition, instead of regarding the confidence limits as upper and lower, the limits will be identified by their relative closeness to the attainable parameter bound θb. The algorithm for the far limit θF then the near limit θN will be described. Whether θ or −θ is minimized depends on whether the far or near limit corresponds to the upper or lower limit. This algorithm can commence after model optimization has completed. Let be the MLE obtained during model optimization. Be aware that determination of the CIs may require additional optimizations. The MLE of these optimizations will be notated with a hat and suitable subscript to distinguish them from . Let ε > 0 be some small threshold that will be used to compare whether values are close enough to be considered equal.
For the far limit θF, if then the parameter bound is irrelevant and the standard Neale and Miller (1997) algorithm is used. Otherwise, the MLE with the attainable bound on the parameter removed is found, . Recall that the bound θb is attainable, and likely, values somewhat beyond the bound define a valid model distribution. For example, if θ is a latent variance with an attainable bound at zero (θb = 0) then may obtain some small negative value. Once is found, the following optimization is performed,
| (5) |
| (6) |
| (7) |
| (8) |
where
| (9) |
| (10) |
and Φ is the standard normal cumulative distribution function.
If then the near limit θN is immediately set at the parameter bound θb. Otherwise, the MLE with the parameter fixed to its bound is found, . For example, if the parameter is a latent variance with a lower bound θb at 0 then an optimization is performed to obtain the MLE with θ fixed at 0 and ζ free. Let d0 be the square root of the distance between the MLE at the parameter bound and the original MLE, . If d0 < zα then θN is set to the parameter bound and we are done. If then the parameter bound is irrelevant and the standard Neale and Miller (1997) algorithm is used. Otherwise, with and dU ≡ min(d0, z0.5α) the following optimization is performed,
| (11) |
| (12) |
| (13) |
where
| (14) |
and Φ is the standard normal cumulative distribution function.
Establishing both the near and far limit can involve one or more optimizations. If an optimization terminates with violated constraints then optimization is re-attempted with perturbed starting values. Optimization failure is not uncommon, but is often resolved by slightly different starting values (e.g., Shanno, 1985).
Estimation of bound-adjusted far and near limits involve three non-linear constraints. While it is possible to formulate these searches as unconstrained problems, penalty fungibility seems to result in frequent failures to satisfy constraints. Constrained optimization seems to perform better. At the time of writing, OpenMx offers three different optimizers: NPSOL (Gill, Murray, Saunders, & Wright, 1986), SLSQP (Johnson, n.d.; Kraft, 1994), and CSOLNP (Zahery, Gillespie, & Neale, 2014). Both NPSOL and CSOLNP have difficulty with constrained optimization. NPSOL is proprietary and is unlikely to be fixed. CSOLNP is in development. In contrast, SLSQP performs well on constrained problems and was used exclusively throughout this report. SLSQP uses a Broyden family algorithm with a gradient approximated by finite differences (Gilbert & Varadhan, 2012; Richardson, 1911).
Simulation study
In spite of the possible peril of treacherously flat deviance functions (e.g., Figure 4) and constrained optimization difficulties, adjusted CIs often work well. A simulation study was conducted using a latent growth model (Figure 1) with and without the attainable lower bound at zero and data generated with . For each condition, 25 thousand replications were completed. For each replication, data were generated, the model fit to the data, and 95% CIs found (false positive rate α = .05). All optimizations converged. The percentages of CIs that did not cover the true are exhibited in Table 1.
Table 1.
Percentage chance that the true is outside the confidence limits with false positive rate α set to 5%. These results represent 25 thousand Monte Carlo replications.
|
|
lower | upper | total | ||
|---|---|---|---|---|---|
| 0.0 | 2.364 | 2.840 | 5.204 | ||
| unadjusted | 0.3 | 2.248 | 2.672 | 4.920 | |
| 0.6 | 2.244 | 2.696 | 4.940 | ||
|
| |||||
| 0.0 | 4.780 | 0.000 | 4.780 | ||
| adjusted | 0.3 | 2.248 | 2.672 | 4.920 | |
| 0.6 | 2.244 | 2.696 | 4.940 | ||
Example
CIs were estimated for a multilevel confirmatory factor analysis (CFA) of affect. Sixty two undergraduate students reported on current affect three times per day for seven days using a smartphone-based app. Affect was assessed using the nine item scale developed by Diener and Emmons (1984). Participants completed the study for course credit; the study was approved by the institutional review board of St. Joseph’s University, where the data were collected. Separate latent factors were assigned to positive (e.g., “pleased”) and negative affect items (e.g., “frustrated”). Additionally, a variance was included to account for common measurement error or the variance with respect to time (Maydeu-Olivares & Coffman, 2006). CFA models may use a multilevel structure to account for nesting of observations within person. The present analysis focused on the intraindividual affect. For this reason, interindividual (i.e. level 2) variance in affect was fit with a saturated model and was not interpreted. Model fit for intraindividual variation in affect (i.e. level 1) was estimated using partially saturated model fit indices (Ryu & West, 2009).
Participants showed high compliance with the method; 59 participants (95.16%) completed at least 80% of the measurement occasions. The 2-factor model with a random intercept showed reasonable fit, χ2(25) = 137.68, p < 0.0001, RMSEAlevel1 = 0.06. Path estimates indicated the appropriateness of a two factor solution for intraindividual variation in affect (see Figure 5). Likelihood-based CIs were computed for the variance with respect to time and intraindividual correlation between negative and positive affect both with and without bounds. For interpretability, a variance needs an attainable lower bound at 0 and a correlation needs attainable bounds at ±1. However, OpenMx needs to know whether to adjust the CI with respect to the upper or lower bound. Since the estimate of the correlation was negative, the attainable lower bound at −1 was retained and the attainable upper bound at 1 was omitted. CIs with and without bounds are presented in Table 2. With the adjustment for attainable bounds, the lower CI of the variance with respect to time was very close to but statistically different from 0.
Figure 5.
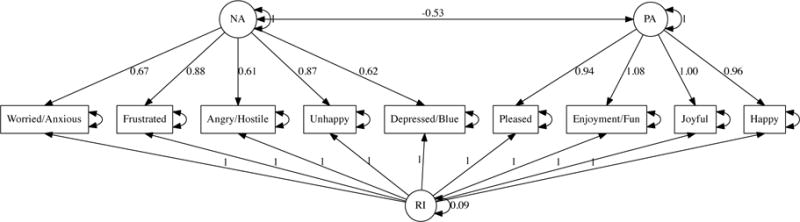
Lower level of a 2-level confirmatory factor analysis. RI accounts for common measurement error or the variance with respect to time. Variances NA and PA are fixed to 1. Upper level (not shown) is a fully saturated covariance matrix of the manifest variables.
Table 2.
CIs with and without parameter bounds. Deviance at the MLE was 32468.74 and the false positive rate α was set to 0.05. Wu and Neale (2012) was automatically selected for the lower (i.e. near) bound of . Parameter corPA−NA was automatically determined to be far enough away from its bound at −1 that no adjustment was needed.
| Model | Variable | Lower
|
Estimate | Upper
|
|||
|---|---|---|---|---|---|---|---|
| Estimate | Fit | Estimate | Fit | ||||
| Unbounded |
|
0.07† | 32470.3 | 0.09 | 0.17 | 32472.59 | |
| corPA−NA | −17.23† | 32550.71 | −0.53 | −0.34 | 32472.59 | ||
| Bounded |
|
0.01 | 32471.45 | 0.09 | 0.17 | 32472.59 | |
| corPA−NA | −0.73 | 32472.59 | −0.53 | −0.34†† | 32472.59 | ||
Note.
non-linear constraints were not satisfied during optimization. The optimizer might have converged to a satisfactory solution if given more time.
At the upper bound of corPA−NA, was at its attainable lower bound of 0.
Discussion
The pros and cons of likelihood-based CIs in comparison to Wald-based CIs are reviewed with a particular emphasis on a recent refinement to likelihood-based CIs that make an adjustment for the presence of an upper or lower bound. Two kinds of parameter bounds can be distinguished: natural and attainable. A natural boundary is a boundary of the model distribution beyond which the distribution is invalid or degenerate. For example, a correlation between manifest variables has natural boundaries (−1, 1). In contrast, attainable boundaries separate the interpretable part of a distribution from the uninterpretable part. For example, a latent correlation may have natural boundaries at absolute values greater than 1. However, attainable boundaries of (−1, 1) are desirable for interpretability. It must be stressed that the attainable bound adjustment for likelihood-based CIs (Wu & Neale, 2012) is only applicable when the boundary of concern is actually attainable and not a natural boundary.
OpenMx, a free and open-source software originally designed for structural equation modeling, has implemented likelihood-based CIs since version 1.0 and recently added automatic support for the attainable boundary adjustment. While the theoretical definition of CIs is neat and tidy, a number of implementation decisions influence performance. The applied analyst is relieved from the need to attend to these details by our novel, fully automatic implementation. Given current tools, the CI problem seems best formulated with constrained optimization using OpenMx’s SLSQP optimizer. Once CIs are estimated, a number of diagnostic should be taken into account. Likelihood-based CI widths should be compared to Wald-based CI widths. When CIs are suspect, the model can be checked for local identification, the likelihood space searched for better minima, and the other parameters at the CI limits inspected.
At the time of writing, OpenMx uses finite differences to approximate the gradient of the deviance function during optimization. The finite differences algorithm is easy to implement, but is not as accurate as analytic derivatives or automatic differentiation (e.g. Griewank, 1989). It seems likely that optimization could be performed more quickly and with greater accuracy if higher accuracy gradients were available.
The boundary adjusted CI procedure is only valid when the parameter of interest is the only one close to a boundary. Since the sampling distributions of the LRT statistics are affected by boundary conditions of all parameters, the proposed CIs may not produce desired coverage if a parameter not being considered is close to its boundary or the parameter of interest is subject to additional boundary conditions. However, in such cases, it is still advisable to use the proposed adjustments instead of a CI that neglects all boundary conditions. This is because the current approach still includes partial boundary information of the parameter space in such cases and is expected to produce CIs whose coverage probabilities are closer to the nominal ones (Wu & Neale, 2012). Unfortunately, it appears difficult to generalize the boundary adjustment to more complex cases. For example, similar adjustments for a bivariate ACE model are drastically more complex (Wu & Neale, 2013).
To conduct inference, likelihood-based CIs are an important tool. Applied researchers often do not have time to carefully program an intricate adjustment for parameters with bounds. Our novel, fully automatic implementation makes more precise inference available to applied researchers in a manner that is easy for them to enjoy.
Acknowledgments
This research was supported in part by National Institute of Health grants R01-DA018673 and R25-DA026119. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Institutes of Health. L. R. contributed the example. We thank Hao Wu for technical advice and Josephine Shih for assistance in data collection.
Contributor Information
Joshua N. Pritikin, Department of Psychiatry and Virginia Institute for Psychiatric and Behavior Genetics, Virginia Commonwealth University
Lance M. Rappaport, Department of Psychiatry and Virginia Institute for Psychiatric and Behavior Genetics, Virginia Commonwealth University
Michael C. Neale, Department of Psychiatry and Virginia Institute for Psychiatric and Behavior Genetics, Virginia Commonwealth University
References
- Birgin EG, Martínez JM. Improving ultimate convergence of an augmented lagrangian method. Optimization Methods and Software. 2008;23(2):177–195. [Google Scholar]
- Bollen KA, Bauldry S. Model identification and computer algebra. Sociological Methods & Research. 2010;39(2):127–156. doi: 10.1177/0049124110366238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diener E, Emmons RA. The independence of positive and negative affect. Journal of Personality and Social Psychology. 1984;47(5):1105–1117. doi: 10.1037//0022-3514.47.5.1105. [DOI] [PubMed] [Google Scholar]
- Gilbert P, Varadhan R. numDeriv : Accurate numerical derivatives. R package version 2012.9-1. 2012 Retrieved from http://CRAN.R-project.org/package=numDeriv.
- Gill PE, Murray W, Saunders MA, Wright MH. User’s guide for NPSOL (version 4.0): A Fortran package for nonlinear programming. DTIC Document 1986 [Google Scholar]
- Griewank A. On automatic differentiation. Mathematical Programming: Recent Developments and Applications. 1989;6(6):83–107. [Google Scholar]
- Johnson SG. The NLopt nonlinear-optimization package. n.d. Retrieved Aug 2016 from http://ab-initio.mit.edu/nlopt.
- Kraft D. Algorithm 733: TOMP–Fortran modules for optimal control calculations. ACM Trans Math Softw. 1994 Sep;20(3):262–281. doi: 10.1145/192115.192124. [DOI] [Google Scholar]
- Luenberger DG, Ye Y. Linear and nonlinear programming. Springer-Verlag; 2008. [Google Scholar]
- Maydeu-Olivares A, Coffman DL. Random intercept item factor analysis. Psychological Methods. 2006;11(4):344–362. doi: 10.1037/1082-989X.11.4.344. [DOI] [PubMed] [Google Scholar]
- Neale MC, Heath AC, Hewitt JK, Eaves LJ, Fulker DW. Fitting genetic models with LISREL: Hypothesis testing. Behavior genetics. 1989;19(1):37–49. doi: 10.1007/BF01065882. [DOI] [PubMed] [Google Scholar]
- Neale MC, Hunter MD, Pritikin JN, Zahery M, Brick TR, Kirkpatrick R, Boker SM. OpenMx 2.0: Extended structural equation and statistical modeling. Psychometrika. 2016;81(2):535–549. doi: 10.1007/s11336-014-9435-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neale MC, Miller MB. The use of likelihood-based confidence intervals in genetic models. Behavior genetics. 1997;27(2):113–120. doi: 10.1023/a:1025681223921. [DOI] [PubMed] [Google Scholar]
- R Core Team. R Foundation for Statistical Computing. Vienna, Austria: 2014. R: A language and environment for statistical computing. Retrieved from http://www.R-project.org. [Google Scholar]
- Richardson LF. The approximate arithmetical solution by finite differences of physical problems involving differential equations, with an application to the stresses in a masonry dam. (Series A, Containing Papers of a Mathematical or Physical Character).Philosophical Transactions of the Royal Society of London. 1911;210:307–357. [Google Scholar]
- Ryu E, West SG. Level-specific evaluation of model fit in multilevel structural equation modeling. Structural Equation Modeling. 2009;16(4):583–601. [Google Scholar]
- Shanno DF. On Broyden-Fletcher-Goldfarb-Shanno method. Journal of Optimization Theory and Applications. 1985;46(1):87–94. [Google Scholar]
- Steiger JH, Shapiro A, Browne MW. On the multivariate asymptotic distribution of sequential chi-square statistics. Psychometrika. 1985;50(3):253–263. [Google Scholar]
- Wald A. Tests of statistical hypotheses concerning several parameters when the number of observations is large. Transactions of the American Mathematical society. 1943;54(3):426–482. [Google Scholar]
- Wilkinson L. Statistical methods in psychology journals: Guidelines and explanations. American Psychologist. 1999;54(8):594. [Google Scholar]
- Wilks SS. The large-sample distribution of the likelihood ratio for testing composite hypotheses. The Annals of Mathematical Statistics. 1938;9(1):60–62. [Google Scholar]
- Wu H, Neale MC. Adjusted confidence intervals for a bounded parameter. Behavior genetics. 2012;42(6):886–898. doi: 10.1007/s10519-012-9560-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu H, Neale MC. On the likelihood ratio tests in bivariate ACDE models. Psychometrika. 2013;78(3):441–463. doi: 10.1007/s11336-012-9304-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zahery M, Gillespie N, Neale MC. High-performance constrained optimization in R: Applications to substance use. Presented at the poster session of the 26th Annual Convention of Association for Psychological Science; San Francisco, CA.. 2014. May, [Google Scholar]


