An advection-deposition-survival model to assess the risk of introduction of vector-borne diseases through the wind: Application to bluetongue outbreaks in Spain

Abstract

This work develops a methodology for estimating risk of wind-borne introduction of flying insects into a country, identifying areas and periods of high risk of vector-borne diseases incursion. This risk can be characterized by the role of suitable temperatures and wind currents in small insects’ survival and movements, respectively. The model predicts the number density of introduced insects over space and time based on three processes: the advection due to wind currents, the deposition on the ground and the survival due to climatic conditions. Spanish livestock has suffered many bluetongue outbreaks since 2004 and numerous experts point to Culicoides transported by wind from affected areas in North Africa as a possible cause. This work implements numerical experiments simulating the introduction of Culicoides in 2004. The model identified southern and eastern Spain, particularly between June and November, as being at greatest risk of wind-borne Culicoides introduction, which matches field data on bluetongue outbreaks in Spain this year. This validation suggests that this model may be useful for predicting introduction of airborne pathogens of significance to animal productivity.

Introduction

Introduction of vector-borne diseases can substantially harm public and animal health, causing significant sanitary and financial loss. Long-range wind-borne transportation of infected flying insects has previously been linked to the introduction of viruses affecting humans and/or animals such as West Nile virus, dengue or Rift Valley fever. Therefore, modeling the movement of wind-borne midges or mosquitoes may help identify geographic regions and seasons at higher risk of incursion of several arboviral diseases, improving surveillance efforts.

Bluetongue is a viral disease of ruminants transmitted by biting midges of the genus Culicoides. Culicoides imicola is considered the main vector of Bluetongue in South Europe and Africa [1]. This virus has traditionally been considered endemic to tropical and subtropical regions, between parallels 35°S and 40°N; however, recently several outbreaks have occurred further North and it is considered to be a re-emerging disease in new latitudes [2]. So far, the disease has been reported in Australia, USA, Africa, Middle East, Asia and Europe, although the geographic distribution of the 27 virus serotypes differs by region [3].

Previous studies suggest that Culicoides could be transported by the wind to distances of up to 170 km from their original location [4]. Wind-borne movement of bluetongue virus-infected Culicoides is thought to explain the northward spread of bluetongue in Europe, primarily through routes from Turkey to Greece-Bulgaria, from Algeria-Tunisia to Italy and from Morocco-Algeria to Spain [5]. Specifically, wind-borne introduction of these insects to Spain from North Africa has been suggested as the cause of the numerous bluetongue outbreaks in Spain in 2004–05 [6–8] and in other countries and periods [9, 10]. In October 2004, 121 bluetongue outbreaks were reported in Spain; this number increased to 322 in December 2004 and to 328 at the start of 2005 [11–13].

The goal of the present work was to develop a model that could identify geographic areas and time periods at highest risk of introduction of small insects potentially infected with human and/or animal pathogens. The model takes into account three processes: (1) advection, in which insects are considered as particles in the air, and move according to wind currents; (2) deposition, in which wind-borne insects are deposited on the ground; and (3) survival, reflecting insects’ survival or mortality as a function of climatic factors. This model was numerically implemented to simulate wind-borne Culicoides introduction from North Africa into Spain and was validated using field data on bluetongue outbreaks reported in Spain in 2004.

Materials and methods

Model’s scheme

Culicoides are 1–3 mm in size, they weigh less than 1 mg and, under favorable conditions, they can be found as high as 200 m above the ground [14]. Previous studies consider that the long-range transportation of Culicoides is likely caused by wind currents at high altitudes [1, 5, 15]. Therefore the model assumes that the movement of small insects in the air shows a similar behaviour to wind-borne small particles [16]. Then, the model takes into consideration the following processes:

• (1)Wind advection. Particle movement in the air due to wind currents is computed using an advection partial differential equation (PDE). The same kind of PDE has been used to predict the movements of dust [17, 18], sediments [19, 20], oil [21, 22] or gaseous substances [23, 24].
• (2)Vertical deposition. The model assumes that Culicoides deposited onto the ground from the air in a manner similar to other airborne particles. Thus, deposition is computed using particles’ sedimentation and flotation theory based on settling principles through the air, adapted here to the specific characteristics of Culicoides.
• (3)Survival. Dead insects do not pose an introduction risk. Consequently, the model estimates a mortality rate during wind-borne transport on the basis of climatic variables.

Mathematical model

We consider the spatial domain $\mathrm{\Omega }\subset {\mathbb{R}}^3$ and time interval [0, T]. We denote by Γ_g and Γ_s(t) the subsets of the boundary of Ω corresponding, respectively, to the ground and to the source of Culicoides entering into Ω at time t ∈ [0, T]. C(x, y, z, t) is the spatial and temporal distribution of the number density of insects (i.e. the number of insects per unit volume) at point (x, y, z) ∈ Ω at time t ∈ [0, T]. Since the number density of insects varies according to wind advection, vertical deposition and survival, the evolution of C is governed by the following equations

$$\{\begin{array}{ll}\frac{\partial C}{\partial t}+\text{div}\left(Cw\right)=-\sigma \left(f,C\right)\hfill & \text{in}\mathrm{\Omega }\times \left(0,T\right],\hfill \\ C=C_0\hfill & \text{in}\mathrm{\Omega }\times \left\{0\right\},\hfill \\ C=C_s\hfill & \text{on}\left\{\left(x,y,z,t\right):\left(x,y,z\right)\in {\mathrm{\Gamma }}_{\text{s}}\left(t\right)\right\},\hfill \end{array}$$ (1)

where C₀ is the initial distribution of the number density of Culicoides in Ω, C_s(x, y, z, t) is the number density of insects at point (x, y, z) ∈ Γ_s(t) at time t ∈ [0, T], w = (w_x, w_y, w_z) is the velocity field related to the wind and deposition effects, which satisfies w_z = 0 on Γ_g × (0, T], and σ(f, C) is the mortality function (i.e. the number of Culicoides that die per unit volume and unit time), which depends on C and the spatio-temporal distribution of climatic factors f associated with survival.

Model implementation for the case of Culicoides

Here, the model formulated above is tailored for studying the case of the introduction of Culicoides from North Africa to Iberian Peninsula and Balearic Islands. The model has been fully developed in Matlab.

Domain’s discretization

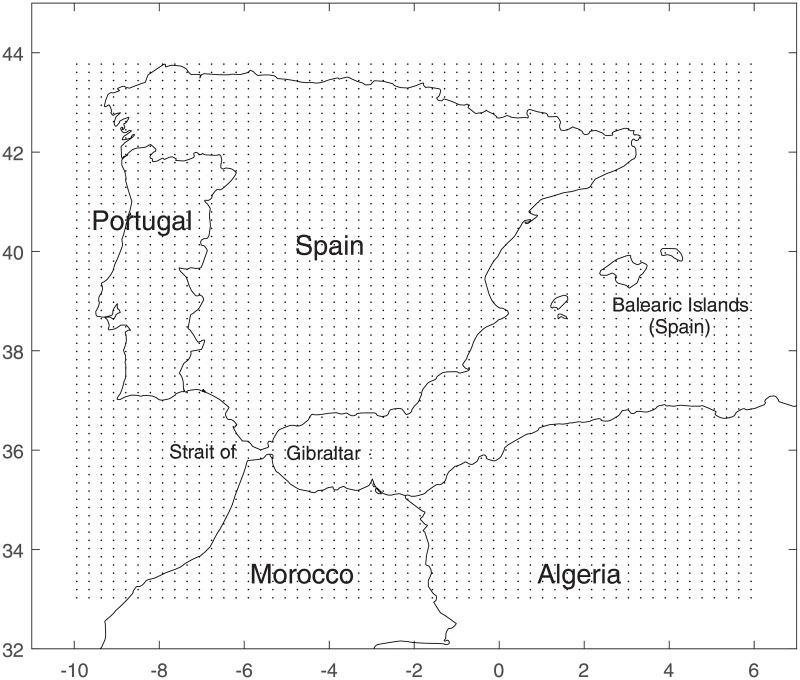
We discretized Γ_g into a two-dimensional regular meshgrid of n_x × n_y grid points, where $n_x,n_y\in \mathbb{N}$. Here we considered n_x = n_y = 50, covering the area extending from latitude 34°N to 44°N and from longitude 10°W to 4.25°E (around 22 and 26 km between vertical and horizontal grid points, respectively), comprising parts of Spain, Portugal, northern Morocco and northern Algeria (Fig 1).

Fig 1. Domain Γ_g in numerical experiments, extending from latitude 34°N to 44°N and from longitude 10°W to 4.25°E.

Black lines demarcate country boundaries and black dots locate the fixed 2,500 grid points.

We also discretized the temporal domain [0, T] into $N\in \mathbb{N}$ steps, using a fixed time step Δt > 0, given by Δt = T/N. Here, we considered Δt = 1/24 days (1 hour).

Climatic data source and interpolation

Wind and temperature data on Γ_g were sourced from Forecast.io website (www.forecast.io). This data consisted of hourly measurements of mean temperature (θ, in Celsius degrees °C), mean horizontal wind direction (from 0° to 359°) and mean horizontal wind speed (in m/s) taken along 2004 at each grid point on the surface (2,500 source points). Climatic data at intermediate points on the ground within the domain, Γ_g, were estimated through linear interpolation at every time step.

At high altitudes, z > 10 m, temperature values were estimated through the standard free atmospheric lapse rate of 6.5°C decrease per kilometer of increasing elevation estimated for Mediterranean atmosphere [25]:

$$\begin{array}{c}\hfill \theta \left(z\right)=\theta \left(z_0\right)-\gamma z,\end{array}$$ (2)

where θ(z₀) is the temperature on the ground z₀, and γ = 0.0065 °C/m.

Horizontal wind speed values at high altitudes, z > 10 m, were estimated using the following polynomial variation [26]:

$$\begin{array}{c}w\left(z\right)=w\left(z_0\right){\left(\frac{z}{10}\right)}^{\alpha },\end{array}$$ (3)

where w(z₀) is the wind speed on the ground z₀, and α is the Hellman exponent for particles above sea and land surfaces (in this work, α = 0.10 and α = 0.16, respectively).

Deposition

Vertical deposition of Culicoides from high altitudes was assumed to be governed by processes similar to those affecting the deposition velocity of dust particles. This deposition is due to the combined action of gravitational settling, wind drag capacity and the aerodynamic properties of the particles (here, the Culicoides).

In general, flying insects use integrated systems consisting of wings to generate aerodynamic forces, muscles to move the wings, and sensing and control systems to guide and manoeuvre [27]. The Reynolds number, Re, and the drag coefficient, C_d, are two dimensionless quantities used in fluid mechanics to predict the relative internal movement and drag of particles in different fluid velocities [28]. In particular, as the size of a flier is reduced, the wing-to-body mass ratio tends to decrease paired with the Reynolds number as well [27] (in this work, Re = 100, assumed for small flying insects with slow flights [27, 29]). Following Haider et. al. [30], the drag coefficient was computed as a function of the Reynolds number adjusted for small spherical particles:

$$\begin{array}{c}\hfill C_d=\frac{24}{Re}(1+0.173R{e}^{0.657})+\left(\frac{0.413}{1+16,300R{e}^{-1.09}}\right).\end{array}$$ (4)

The settling velocity for Culicoides was assumed to be governed by the same processes affecting the settling velocity of spherical particles, V_g(z) [31]:

$$\begin{array}{c}\hfill V_g{\left(z\right)}^2={\displaystyle \frac{8gR}{3C_d}}({\displaystyle \frac{\rho }{{\rho }_{\text{air}}\left(\theta \left(z\right)\right)}}-1),\end{array}$$ (5)

where R is the radius of the Culicoides, here assumed to be R = 2 ⋅ 10⁻³ m [32]; M is the weight of the Culicoides, here assumed to be M = 0.5 ⋅ 10⁻³ kg [33]; ρ is the density of the Culicoides, here approximated to an spherical particle ρ = M/(4/3πR³); g is the gravity acceleration, assumed constant, g = 9.81 m/s²; and ρ_air(θ) is the mass air density at temperature θ, see Table 1 [34].

Table 1. Effect of temperature on air density.

θ (°C)	35	30	25	20	15	10	5	0	-5	-10	-15	-20	-25
ρair (kg/m3)	1.15	1.16	1.18	1.20	1.22	1.25	1.27	1.29	1.32	1.34	1.37	1.39	1.42

However, when wind becomes sufficiently strong, particles in the air are susceptible to enter into long-term suspension and are therefore transported long-range [35]. Since one of the main variables for modeling sediment transport is the force exerted on the soil by the wind, a fundamental variable used to predict aeolian particle transport is the shear velocity, ${\overrightarrow{u}}_{*}$, whose module is calculated as $u_{*}=\left|{\overrightarrow{u}}_{*}\right|=\sqrt{|\overrightarrow{\tau }|/{\rho }_{\text{air}}}$ [36, 37]; where $\overrightarrow{\tau }$ is the surface shear stress, i.e. the vertical flux of horizontal momentum measured near the surface; which can be computed as $\overrightarrow{\tau }={\rho }_{\text{air}}{C}_{d}w{\left(z_0\right)}^2$ [38, 39]. Thus,

$$\begin{array}{c}\hfill u_{*}^2=C_{d}w{\left(z_0\right)}^2.\end{array}$$ (6)

We may now use the dimensionless parameter $\mathrm{\lambda }\left(z\right)=\frac{V_g\left(z\right)}{u_{*}}$ to distinguish three types of flight for Culicoides [36, 37]: i) a long term suspension, when λ < 0.1; ii) a short term suspension, when 0.1 < λ < 0.7; iii) and vertical settling, when λ > 0.7. Concretely, the settling velocity of Culicoides, w_z, was computed in terms of V_g (see Eq 5) through the following continuous function:

$$\begin{array}{c}\hfill w_z\left(z\right)=\{\begin{array}{cc}0\hfill & \text{if}\mathrm{\lambda }\left(z\right)\le 0.1,\hfill \\ \frac{\mathrm{\lambda }\left(z\right)-0.1}{0.6}{V}_g\left(z\right)\hfill & \text{if}0.1<\mathrm{\lambda }\left(z\right)<0.7,\hfill \\ V_g\left(z\right)\hfill & \text{if}\mathrm{\lambda }\left(z\right)\ge 0.7.\hfill \end{array}\end{array}$$ (7)

Since the number density of wind-borne particles is generally greater at lower altitudes than at higher ones [40, 41], we assumed the center of mass of wind-borne living midges to lie at an altitude of 1 km. On the other hand, according to the literature, while long-range transportation of Culicoides is caused by wind currents at high altitudes, favorable temperatures and wind speeds for natural Culicoides outdoor mobility are often located less than 200 m above the ground [1, 5, 14, 15]. Thus, the model assumes that below this altitude, the Culicoides do not move through wind currents (i.e. w = (0, 0, 0) if z < 200 m).

Mortality function

The mortality function predicts the number density of insects based on temperature, since this is one of the most important determinants of Culicoides life cycle and lifespan [42, 43]. Although other climatic parameters, such as relative humidity and precipitation, can also affect insect survival, neglecting these factors only moderately affects the accuracy of model predictions [44]. In order to simplify the model, we only considered the impact of temperature in the Culicoides mortality function σ; i.e. f = θ, with θ(x, y, z, t) being the temperature value (here in °C) at point (x, y, z) ∈ Ω and at time t ∈ [0, T]. Therefore the mortality function is defined by

$$\begin{array}{c}\hfill \sigma (\theta ,C)=\{\begin{array}{cc}\mu (-6)C\hfill & \text{if}\theta <-6,\hfill \\ \mu \left(\theta \right)C\hfill & \text{if}-6\le \theta \le 42,\hfill \\ \mu \left(42\right)C\hfill & \text{if}\theta >42,\hfill \end{array}\end{array}$$ (8)

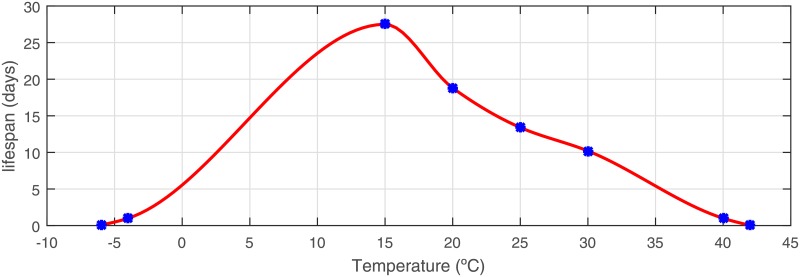
where μ is the Culicoides mortality rate (i.e. the inverse of lifespan) as a function of temperature. This function was derived based on studies reporting total Culicoides mortality after 2 h at 42°C or −6°C [45] and Culicoides lifespan was assumed to be shorter than 24 h after exposure to 40.5°C or −4°C [45]. Culicoides lifespan of 27.5, 18.8, 13.4 and 10.2 days were observed at temperature of 10°C, 15°C, 20°C and 30°C, respectively [46]. These values were used to estimate intermediate values for arbitrary temperatures through the Hermite cubic interpolation computed with the Matlab function pchip and denoted by 1/μ(.). Thus the inverse function μ(.) returns the estimated mortality rate of the Culicoides depending on the value of the temperature (Table 2).

Table 2. Estimated mean lifespan of Culicoides imicola at different temperatures, based on field data [45, 46].

Temperature (°C)	-6	-4	15	20	25	30	40.5	42
Lifespan (days)	1/12	1	27.5	18.8	13.4	10.2	1	1/12

Culicoides sampling data and activity function

Data on the number of Culicoides imicola trapped per day along the Spanish territory between 2004 and 2013 and average temperatures associated with each capture were collected from the Ministry of Agriculture, Fisheries, Food and Environment (www.mapama.gob.es) within the Spanish national surveillance programme.

Field data on the mean number of Culicoides trapped in Spain at temperatures between 0°C and 35°C were fitted to a polynomial function computed with the polyfit command in Matlab, which was defined as the activity function and denoted by δ(.). We used this function to estimate the outdoor number density of Culicoides in source locations, Γ_s(t).

Numerical implementation

The system of Eq (1) was solved numerically using a Lagrangian particle approach. The source of the Lagrangian particles remained constant (i.e. Γ_s(t) = Γ_s, ∀t ∈ [0, T]) and was defined as lying in $M\in \mathbb{N}$ fixed cells at an altitude of 1 km over northern Morocco and/or northern Algeria. At each time step, M new particles started from Γ_s, such that the model included (k + 1) × M particles at time step k ∈ {0, …, N − 1}, and the total amount of particles per simulation was N × M. All particles were assigned with an index i ∈ {1, …, N × M}. Therefore, at time step k, M particles with indexes {k × M + 1, ⋯, (k + 1) × M} started from Γ_s.

Particle trajectories were estimated by considering the velocity field w through the explicit scheme:

$$\begin{array}{c}\hfill X_{n+1}^i=X_n^i+\mathrm{\Delta }t{\mathbf{w}}_n^i,\end{array}$$ (9)

where $X_n^i$ is the position of the Lagrangian particle with index i = {1, …, (n + 1) × M} at time step n = n(i), ‥, N, ${\mathbf{w}}_n^i$ is the wind velocity vector at position $X_n^i$ at time step n and $n\left(i\right)=\lfloor \frac{i-1}{M}\rfloor$ (i.e. n(i) is the greatest integer less than or equal to $\frac{i-1}{M}$). Then, the number density of Culicoides transported at step n by particle i (which was located at $X_n^i$) was denoted as $C_n^i$.

Given the difficulty of estimating the number of Culicoides placed in a specific location, several epidemiological works assume an initial ratio of mosquitoes or midges instead [47, 48]. In our case, the number density of Culicoides transported by particle i situated in Γ_s at step n was assumed to be proportional to the Culicoides activity function, δ(.), as follows

$$\begin{array}{c}\hfill C_n^i=\delta \left(\theta \left(X_n^i\right)\right)\text{,}\text{if}{X}_n^i\in {\mathrm{\Gamma }}_{\mathrm{s}}.\end{array}$$ (10)

Next, the evolution of this particle number density function was governed by the following scheme:

$$\begin{array}{c}\hfill C_{n+1}^i=C_n^i-\frac{\mathrm{\Delta }t}{2}(\mu \left(\theta \left(X_n^i\right)\right)C_n^i+\mu \left(\theta \left(X_{n+1}^i\right)C_{n+1}^i\right)),\end{array}$$ (11)

where i = {1, …, (n + 1) × M} and n ∈ {n(i), ‥, N − 1}.

According to the features of the Culicoides, the number density of Culicoides deposited on Γ_g was calculated at each time step n as the sum of all particles below 200 m altitude; consequently, Eq (11) was not applied to such particles.

Simulations

Three numerical experiments were performed to evaluate the risk of Culicoides introduction in Spain from North Africa and thereby allow validation of our model against field data of bluetongue outbreaks reported in 2004. The first experiment compared the introduction of Culicoides along an entire year from the cells located at 1 km above the ground of Morocco alone, Algeria alone, and both countries (i.e. the choice of three different sources Γ_s). Each simulation started on the first day of 2004 and finished after T = 365 days. The goal of this experiment was to identify areas at high risk of midge introduction during one year from different African countries.

The second experiment examined the risk of wind-borne Culicoides introduction from both Morocco and Algeria for each month of a year; thus, 12 simulations were performed, each starting on the first day of every month. The goal of this experiment was to identify months associated with higher risk of Culicoides introduction.

A third experiment aimed to study the influence that variation in the values of input parameters affect in the model outcomes, especially the climatic factors and the physical features of the Culicoides on the final depositions in the target territory. Thus, a sensitivity analysis was carried out by increasing ±1 to ±5% and ±5 to ±25% the value of the following climatic and physical variables, respectively, in an entire year of simulation from initial Culicoides positions located at 1 km above the ground of Morocco and Algeria: temperature, θ, wind speed, w, Hellman exponent, α, temperature lapse rate, γ, and insect’s weight, M, radius, R, Reynolds number, Re. The results of the model is also associated to the initial altitude at source locations, Γ_s, here located at 1 km high. Thus, a sensitivity analysis was carried out by increasing ±5 to ±25% the initial altitude.

The results of the numerical experiments were compared with field data from the bluetongue outbreaks in Spain in 2004. This allowed us to validate the model.

Results

Mortality and activity functions

Fig 2 shows the lifespan associated to different values of temperature (blue dots) displayed in Table 2 and the cubic Hermite interpolation computed for intermediate values (red line). Thus, the mean lifespan of Culicoides is

$$\begin{array}{c}\hfill \frac{1}{\mu \left(\theta \right)}=\sum _{i=0}^3{a}_k\left(\theta \right){(\theta -b\left(\theta \right))}^k,\end{array}$$ (12)

where the value of a_k(θ), for each k ∈ {0, …, 4}, and b(θ) are given in Table 3, depending on the value of θ.

Fig 2. Culicoides lifespan used in the present model according to temperature variations based on field data (blue dots) and cubic Hermite approximation (red line), 1/μ(.).

Table 3. Piecewise cubic Hermite interpolating polynomial parameters for the mean lifespan of Culicoides according to temperature values from −6°C to 42°C, see Eq (12).

θ range (°C)	a0 (days)	a1 (days/°C)	a2 (days/°C2)	a3 (days/°C3)	b (°C)
-6 ≤ θ ≤ -4	1/12	3.69⋅10−1	1.48⋅10−2	1.49⋅10−2	-6
-4 ≤ θ ≤ 15	1	6.07⋅10−1	1.56⋅10−1	-6.04⋅10−3	-4
15 ≤ θ ≤ 20	27.5	0	-7.77⋅10−1	8.59⋅10−2	15
20 ≤ θ ≤ 25	18.8	-1.33	4.58⋅10−2	9.40⋅10−4	20
25 ≤ θ ≤ 30	13.4	-8.04⋅10−1	8.55⋅10−2	-1.05⋅10−2	25
30 ≤ θ ≤ 40.5	10.2	-7.40⋅10−1	-6.91⋅10−2	5.11⋅10−3	30
40.5 ≤ θ ≤ 42	1	-5.89⋅10−1	7.30⋅10−2	-9.06⋅10−3	40.5

Fig 3 shows the mean number of Culicoides captured (blue dots) and the approximation polynomial fitting (red line). Thus, considering a midges abundance higher or equal to zero, the Culicoides activity function is defined as

$$\begin{array}{c}\hfill \delta \left(\theta \right)=\sum _{i=0}^8{c}_k{\theta }^k,\end{array}$$ (13)

where c₀ = −0.226, c₁ = 0.344 °C⁻¹, c₂ = −0.178 °C⁻², c₃ = 4.24 ⋅ 10⁻² °C⁻³, c₄ = −4.85 ⋅ 10⁻³ °C⁻⁴, c₅ = 2.89 ⋅ 10⁻⁴ °C⁻⁵, c₆ = −9.04 ⋅ 10⁻⁶ °C⁻⁶, c₇ = 1.38 ⋅ 10⁻⁷ °C⁻⁷ and c₈ = −7.90 ⋅ 10⁻¹⁰ °C⁻⁸, if θ ∈ [1.25, 33.45] °C; and c_k = 0 °C^−k, for each k ∈ {1, …, 8}, otherwise.

Fig 3. Averaged Culicoides trapped per capture (blue dots) and polynomial approximation curve (red line), δ(.).

Annual risk of introduction

Fig 4 shows the number density of Culicoides deposited (in logarithmic scale) across the entire year on target territory via wind-borne transport from the skies over Morocco, Algeria or both. The most exposed areas were the south and east of the Iberian Peninsula and Balearic Islands. Midge deposition patterns varied considerably depending on whether the source was Morocco or Algeria.

Fig 4. Simulated spatial distribution of the number density of Culicoides deposited on the target territory throughout 2004, when the midge source was both Morocco and Algeria (left), Morocco alone (center) or Algeria alone (right).

Number densities were plotted in logarithmic scale, log(C + 1) (log1). Blue dots represent the source of Culicoides, Γ_s.

When Morocco was the source, midge depositions constituted the 50.99% of the total depositions, and they occurred mainly in the south cost of the Iberian Peninsula, and especially close to the Strait of Gibraltar. However, the Culicoides spread might reach the inland west areas of the Iberian Peninsula, reaching even the north of Portugal. On the other hand, a low number density of Culicoides reached the Balearic Islands, discarding the introduction of Culicoides in the center of the Iberian Peninsula.

When Algeria was the source, midge depositions constituted the 49.01% of the total depositions, and they occurred mainly in the region from southeastern Spain to the eastern coast and Balearic Islands. In some cases, the Culicoides spread may reach the center and the northeast of the Iberian Peninsula, but in very low quantity.

Monthly risk of introduction

Since changes in wind currents and temperature during the year can affect the dynamics of midge transport from North Africa, we simulated the spatial density of deposited Culicoides over all 12 months of the year. Table 4 shows the percentage of the number densities of Culicoides deposited on the target territory during each month of 2004. Despite having strong wind currents between December and February, the low temperatures do not favor the Culicoides activity and it represented a low risk for introduction, reaching 12.65% of the total depositions in a year. Despite favorable temperatures between March to May, the wind currents were not sufficiently strong to transport high amount of Culicoides, only reaching 19.40%. The period of high risk of introduction is concentrated in the remaining half of the year, reaching 29.43% between June and August; and 38.52% between September and November, when strong wind streams and suitable temperatures for Culicoides activity in African territories are optimal.

Table 4. Simulated percentage of number density of Culicoides deposited on the ground during each month of 2004.

Jan	Feb	Mar	Apr	May	Jun	Jul	Aug	Sep	Oct	Nov	Dec
5.21	1.44	5.43	9.70	4.27	7.50	15.11	6.81	9.33	15.33	13.85	6.00

Next we examined the spatial distribution of depositions over the 12 months of the year. Fig 5 shows the monthly distribution of Culicoides number density deposited on target territory from the source in both Morocco and Algeria. The largest densities of deposition occurred in the southern and eastern parts of the Iberian Peninsula and Balearic Islands, consistent with the annual-level simulation. Risk of wind-borne incursions were high throughout the year in the southern part of the Iberian Peninsula, specifically close to the Strait of Gibraltar. Central areas of the Iberian Peninsula and the north of Portugal were scarcely reached in specific periods with strong wind streams. However, the Balearic Islands were reached frequently with a high amount of depositions, as mentioned above, mainly from Algeria but also could be reached from Morocco.

Fig 5. Simulated spatial distribution of the number density of Culicoides deposited on Spanish territory for each month of 2004, when the midge source was both Morocco and Algeria.

Number densities were plotted in logarithmic scale, log(C + 1) (log1). Blue dots represent the source of Culicoides, Γ_s.

Sensitivity analysis

Table 5 shows the changes in the output number density deposited over target territory, under the assumption of slight variations in climatic variables and in physical features of the Culicoides. Among all climatic variables computed, the wind speed and the Hellmann exponent, both associated directly with wind speed at higher altitudes, represented the most relevant variables in terms of particle transportation. Indeed, an increase/decrease of 5% in the wind speed (e.g. from 20 m/s to 21 m/s) may increase/decrease the final number density around ±10%. In contrast, variables affecting temperature slightly varied the final number density. Indeed, a temperature increase/decrease of 5% (e.g. from 20°C to 21°C) may increase/decrease the final number density around ±3%.

Table 5. Percentage of output variation of final number density of Culicoides deposited over target territory, C, after a whole year simulation for input variation of {±5%, ±4%, ±3%, ±2%, ±1%} for climatic variables and {±25%, ±20%, ±15%, ±10%, ±5%} for insect’s variables.

Percentage of variation	-5%	-4%	-3%	-2%	-1%	+1%	+2%	+3%	+4%	+5%
Temperature, θ	-3.65	-2.86	-1.89	-1.14	-0.35	0.98	1.52	2.01	2.40	2.84
Wind speed w	-9.07	-7.18	-5.23	-3.43	-1.60	2.14	4.12	6.04	8.01	9.98
Hellman exponent, α	-5.89	-4.75	-3.65	-2.40	-0.84	1.76	3.16	4.48	5.95	7.36
Temperature lapse rate, γ	2.15	1.69	1.25	0.75	0.28	-0.22	-0.85	-1.38	-1.63	-2.02
Percentage of variation	-25%	-20%	-15%	-10%	-5%	+5%	+10%	+15%	+20%	+25%
Insect’s weight, M	10.09	7.99	5.88	4.02	2.13	-1.11	-2.64	-4.22	-5.73	-7.27
Insect’s radius, R	-18.90	-14.84	-10.77	-6.80	-2.82	3.65	6.82	10.01	12.69	15.49
Reynolds number, Re	8.54	6.87	5.17	3.50	1.80	-3.27	-4.55	-5.80	-7.27	-8.79
Percentage of variation	-25%	-20%	-15%	-10%	-5%	+5%	+10%	+15%	+20%	+25%
Initial source altitude, 1000 m	-16.22	-11.68	-8.74	-5.75	-2.43	2.74	4.93	7.15	9.06	11.01

A reduction in the weight of the Culicoides, or an increment in the radius decreases the density of the wind-borne particle, ρ, which reduces the settling velocity accordingly to Eq 5. On the contrary, a reduction in Reynolds number increases the drag coefficient, C_d, which decreases the settling velocity, see Eqs 4 and 5. These cases implied a reduction in settling velocity, which extends long-suspension in the air reaching longer distances.

Model validation

Since October 2004 to January 2005, a total of 328 bluetongue outbreaks were reported in the Iberian Peninsula, with no previous outbreaks reported since 1960 [6, 11–13]. Among them, 82% were located in the south of Spain, and only 18% were located in the south-west. Since September 2004 to December 2004, a total of 230 outbreaks were reported in Morocco, with no previous outbreaks reported it that year. Concretely, 28 new outbreaks were reported in September in north-northeastern Morocco. Other works consider that a period of 4 weeks is the time necessary to detect an infected animal once the infected vector lands in the surroundings [15, 49]. According to this, the virus could have been introduced in September from infected areas of Morocco, to the Spanish territory, concretely to areas close to the Strait of Gibraltar (see Fig 6).

Fig 6. Bluetongue outbreaks reported in Spain in between October 2004 and January 2005 (green dots).

First outbreaks reported between October 12th and 19th (white diamonds). Simulated spatial distribution of the number density of Culicoides deposited on the Iberian Peninsula throughout 2004 when the midge source was the sky over Morocco (see Fig 5), plotted in logarithmic scale, log(C + 1) (log1).

Discussion

In this work, we developed a methodology for estimating risk of long-range wind-borne transport and deposition of small insects, while taking into account the likelihood of insect survival given certain climatic conditions. The methodology relies on a mathematical advection model that is solved numerically using Lagrangian particle tracking, based on the wind velocity field, and particles’ sedimentation and flotation theory for deposition, that takes into account temperature-based insect lifespan and activity. In particular, we focused on assessing the risk of introduction of Culicoides from North Africa to Spain, in order to explain the bluetongue outbreaks that occurred in this territory during 2004.

Two numerical experiments were carried out to simulate the incursion of Culicoides through wind currents in 2004 in Spain, one yearly and one monthly. The results showed that the highest number density of Culicoides deposited on regions agreed with the real primary bluetongue reported outbreaks in the period of study. Concretely, since September 2004, several bluetongue outbreaks were reported in Morocco. In this period, the model showed that main incursions of Culicoides from Moroccan territory were deposited close to the Strait of Gibraltar, showing a high rate of matching between model results and bluetongue notifications.

For the remaining reported outbreaks and for future reported ones in 2005 [13], Calvete et al. [50] identified suitable areas for Culicoides based on climatic factors and livestock distribution in Spain. Those regions were distributed mainly in the south and south-west of Spain. The model developed in this work aimed to assess midges’ incursions from North Africa due to wind currents, not the spread within the Iberian Peninsula. In future works, this model should link continuous updated bluetongue status in North African areas, with the host population distribution and with spatio-temporal suitable conditions for vector survival in target, as proposed by Calvete et al. [50], in order to estimate not only the risk of introduction, but also the risk of spread.

Our results suggest that the Culicoides source can substantially affect midge deposition in Spain: when midges came from over northern Morocco, they usually deposited close to the Strait of Gibraltar; when they came from over northern Algeria, they usually deposited along southeastern Spain and the Balearic Islands. Our results further showed risk variation during the year: risk of introduction was relatively high between June and November, and moderate during other months. These findings illustrate the power of our approach for helping to focus surveillance efforts in space and time.

This work was motivated because, first, different authors foretold the Strait of Gibraltar as one of the main bluetongue introduction pathways in Europe [2, 5] and, second, the presence of Culicoides and bluetongue outbreaks were reported along the region and period of study, which allowed the validation of our predictions [11, 12]. The use of the methodology presented here may serve to assess regions and periods at high risk of incursion of several vectors such as midges or mosquitoes. Indeed, Culicoides may also be a vector for African horse sickness, and many species of mosquitoes are vectors for diseases such as West Nile virus, dengue, Rift Valley fever, Zika, etc. Currently, the system developed in this work embeds a wind and climatic databases automatically, which allows surveillance of real-time (hourly) wind patterns and Culicoides deposition under friendly configurable features, which are easily adaptable to other insects. However, an important quantitative validation of this model should be carried out with more bluetongue outbreaks in territories with no previous disease notifications in a long period; e.g. the bluetongue outbreaks in other European territories or possible infections of African territories from Spanish source locations. The application of this system is to launch risk alerts when suspicious initial infected areas that may spread the vector to long-range distances, especially where livestock population may be exposed. This development could contribute to an effective early warning system for preventing and controlling vector-borne disease incursions.

Supporting information

S1 File. Video simulation.

Video file of particle movement in the air and ground concentration on Spanish territory during September 2004.

(MP4)

Data Availability

Climatic data can be downloaded from www.forecast.io. Further source data are displayed within this manuscript.

Funding Statement

This work has been funded by the EU project “Understanding pathogen, livestock, environment interactions involving bluetongue” (PALE-BLU, H2020-SFS-2016-2); the Spanish Ministry of Economy and Competitiveness (project MTM2015-64865-P); the Junta de Andalucía and European Regional Development Fund (project P12-TIC301); and the MOMAT research group (Ref. 910480), supported by the Universidad Complutense de Madrid. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.